An Optimized Fuzzy Based Control Solution for Frequency Oscillation Reduction in Electric Grids
Abstract
:1. Introduction
- Modelling different HPS like PV, FC, and ESS.
- Verifying the transient behaviors for system performances.
- Investigate the robust performance of the suggested fuzzy PD-PI controller over conventional and proportional, integral, derivative (PID) controllers tuned with the GOA.
- Improved frequency deviation in the HPS.
Research Problem
- The main challenge in these hybrid power systems (HPS) is the variation in the frequency from its nominal or rated value, which causes failure in the system. This frequency deviation results from a networked structure’s demand and supply. As a result, it is highly efficient at returning the frequency back to its prescribed range in no time. Practically, the LFC strategy is used to recover the frequency disturbances by utilizing an appropriate secondary controller (SC).
- Choosing appropriate controller parameters is one of the challenges in improving the system’s performance.
- After selecting a suitable controller, the manual tuning of its parameters has difficulties.
2. Related Work
2.1. Control Algorithms for Frequency Regulation
2.2. Load Frequency Control (LFC)
2.3. Mechanism of Frequency Control in Traditional Grid
- Primary control;
- Secondary control; and
- Tertiary control
2.4. Frequency Control in Hybrid Power Systems
- Rate of change of frequency (ROCOF): a metric used to calculate the frequency decline/incline rate.
- Frequency nadir: the maximum frequency excursion point.
- Primary settling frequency: the stabilized frequency resulting from governor response.
| Reference Number | Proposed Technique | Predicted Results | Limitations |
|---|---|---|---|
| [18] | Direct Load Control Algorithm | 1000 HVAC provided 24 h regulation services | They cannot provide long term services. |
| [19] | Hierarchical Control Algorithm | Full responsive Load Control | Their practical implementation is difficult. |
| [20] | Power Control Algorithm | Balanced supply and demand | It has a poor response if any sudden fault occurs in the system. |
| [21] | Internal Model Control Scheme | Stabilized Frequency | Faces limitations in case of the uncertain atmosphere. |
| [22,23] | Conventional Controllers | Smooth Frequency | Capital install cost |
| [24] | Neuro-Fuzzy hybrid controller | Improved dynamic response | Deteriorated performance for complex dynamical system. |
| [25] | BAT Algorithm | Stabilized frequency | Complex calculations |
| [26] | Modified Harmony Optimization Algorithm | Stabilized Frequency for MG | A limited selection of M.F. |
| [27] | Sliding-Mode Technique | Feasible results under load disturbances | The high switching frequency can damage the controller. |
| [28] | PID controller for LFC | Mitigated frequency oscillations | Slow Time Response. |
| [29,30] | Fractional-Order Controller | Reduced Frequency Deviation | Sensitive to system’s variations. |
| [31,32] | Optimal Fractional-order Fuzzy PD + I controller | Controlled Frequency Oscillations | LFC heavily reliant on controller parameters. |
| [33,34,35,36,37,38,39] | Meta-Heuristic Algorithms | Improved System Stability | Highly dependent upon controller parameters. |
| Proposed Work | GOA based FPD-PI Controller | Stabilized Frequency | Computational time is a little bit complex. |
3. Proposed Framework
- To propose a GOA and validate its utility.
- To propose a robust fuzzy PD-PI controller as a load frequency controller for the HPS under consideration.
- To compare the effectiveness and robustness of a GOA-based fuzzy PD-PI controller with that of a traditional PID controller and conventional controllers.
- To evaluate the GOA tuned FPD-PI controller in a widely used and projected frequency control approach by recommending tuning parameters.
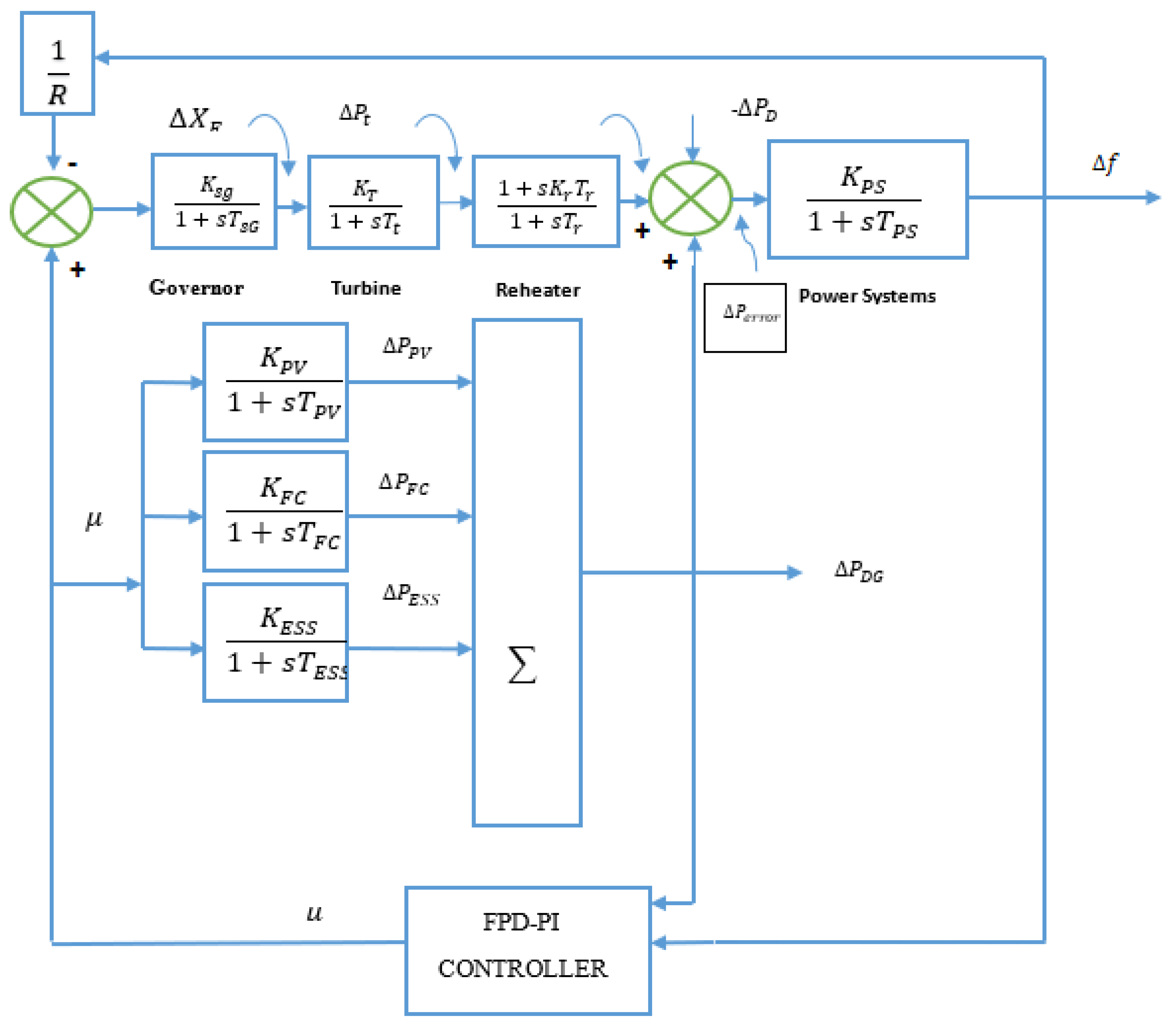
3.1. Hybrid Power System under Study
3.2. Mathematical Modelling of the Components:
3.3. System Modelling
3.4. Proposed Controller
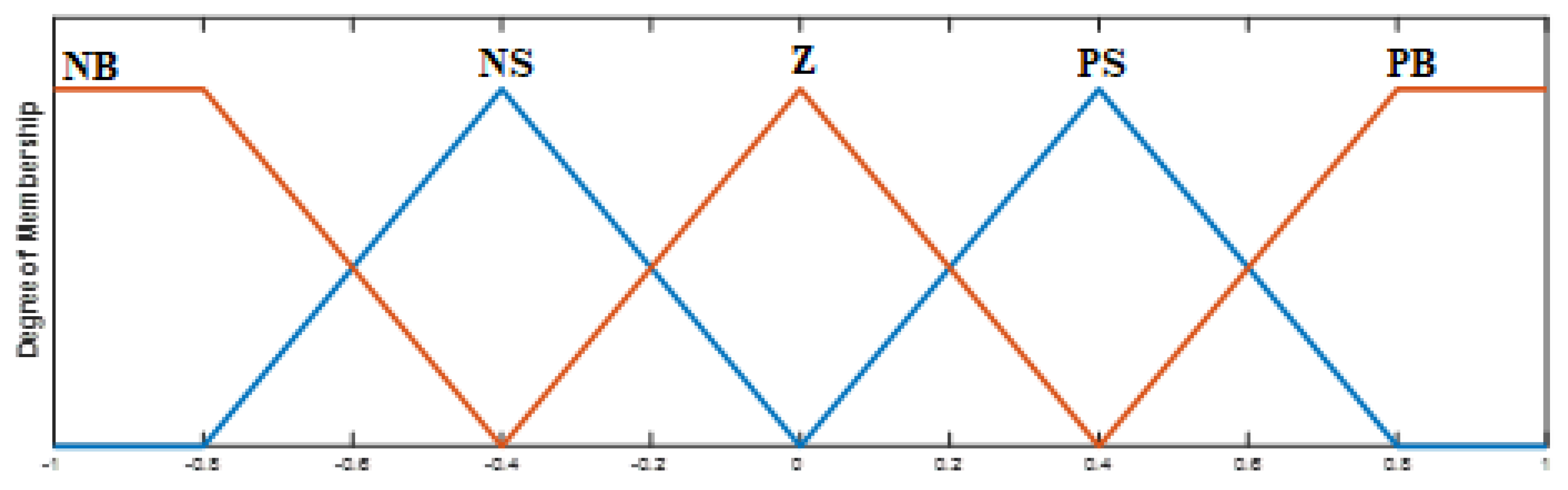
3.4.1. Fuzzy Logic Controller
3.4.2. Structure of the Fuzzy Logic PD-PI Controller
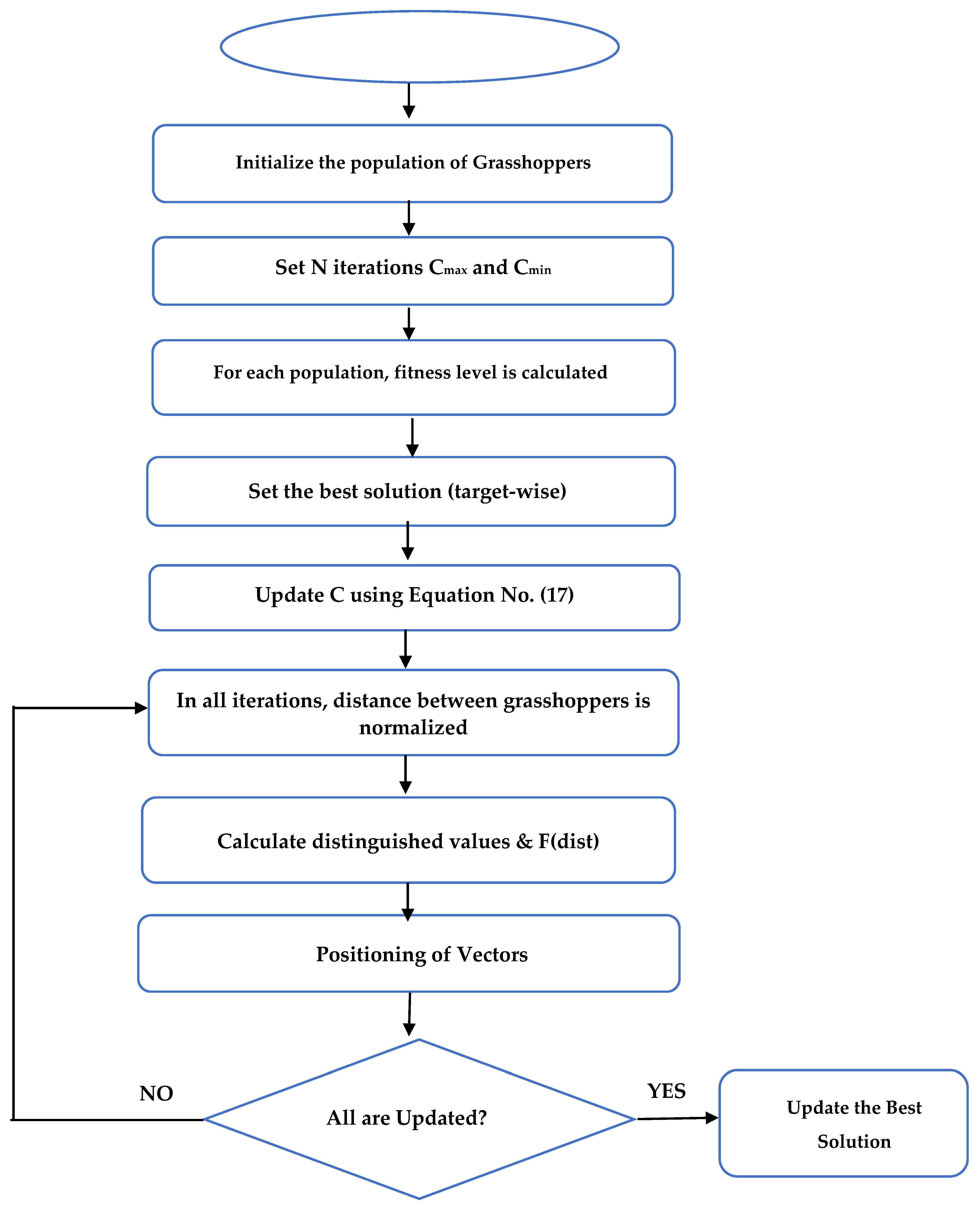
3.5. Optimization Algorithm
Grasshopper Optimization Algorithm
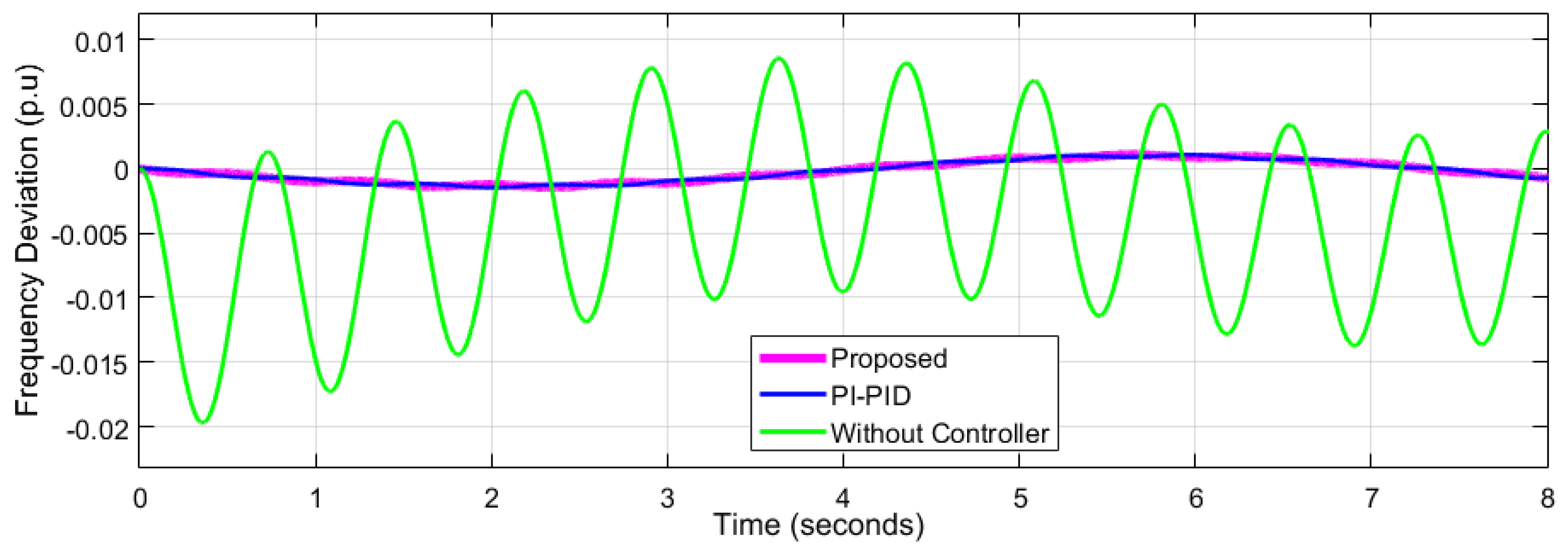
4. Results and Discussion
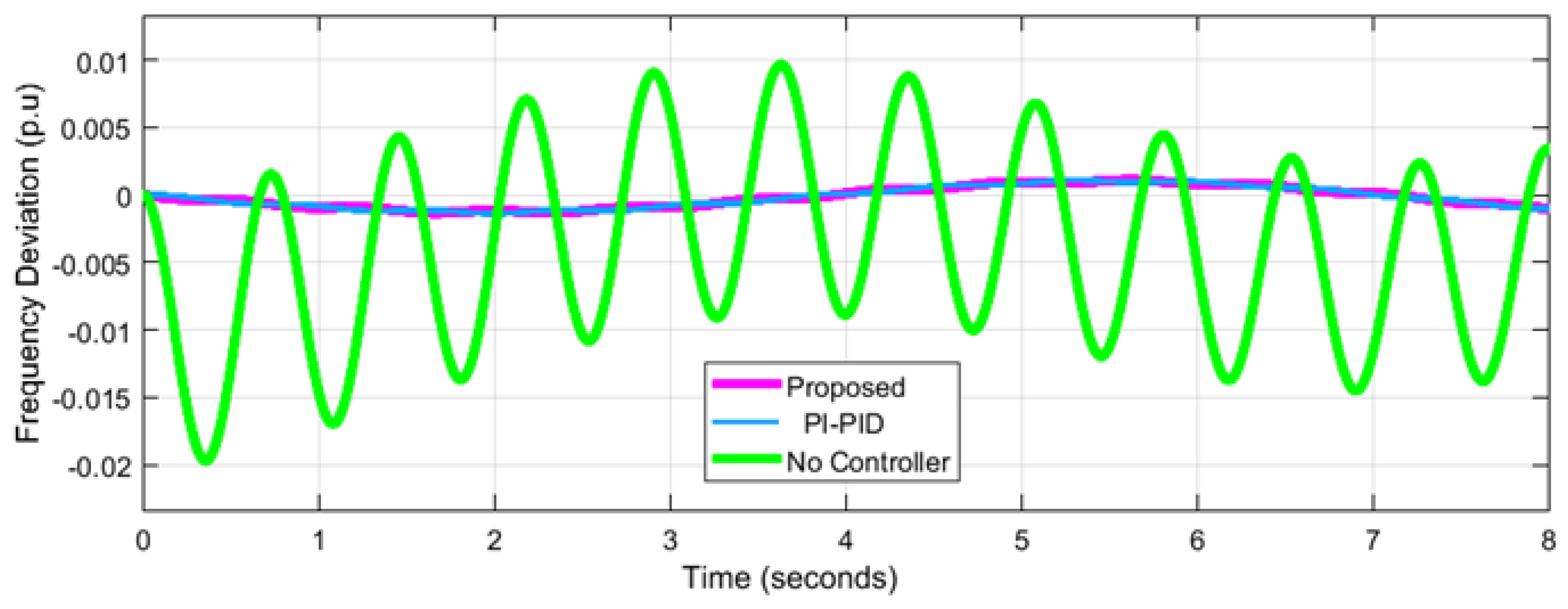
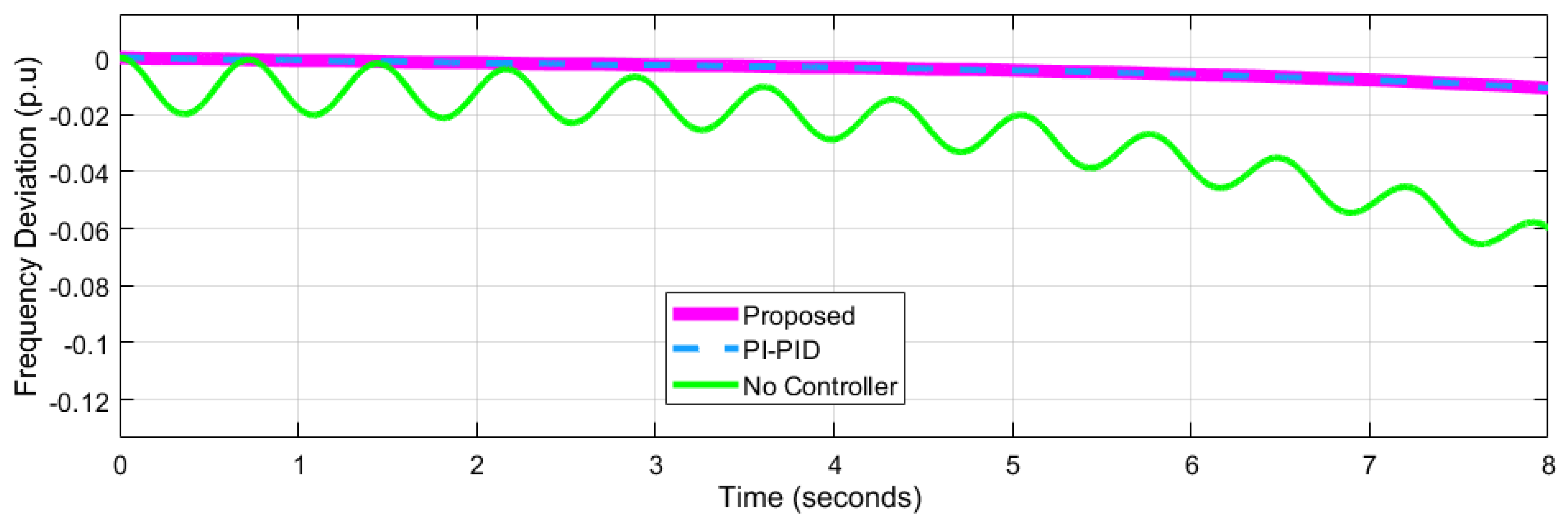
4.1. Performance Analysis for Network 1
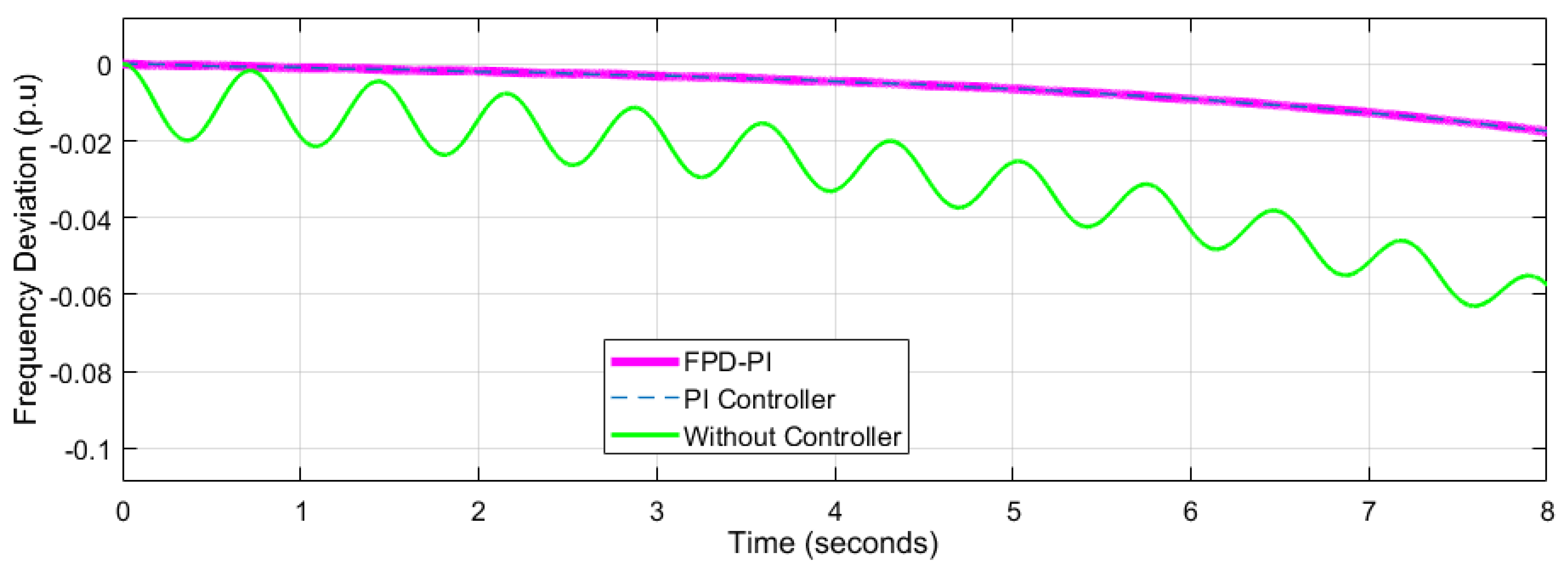
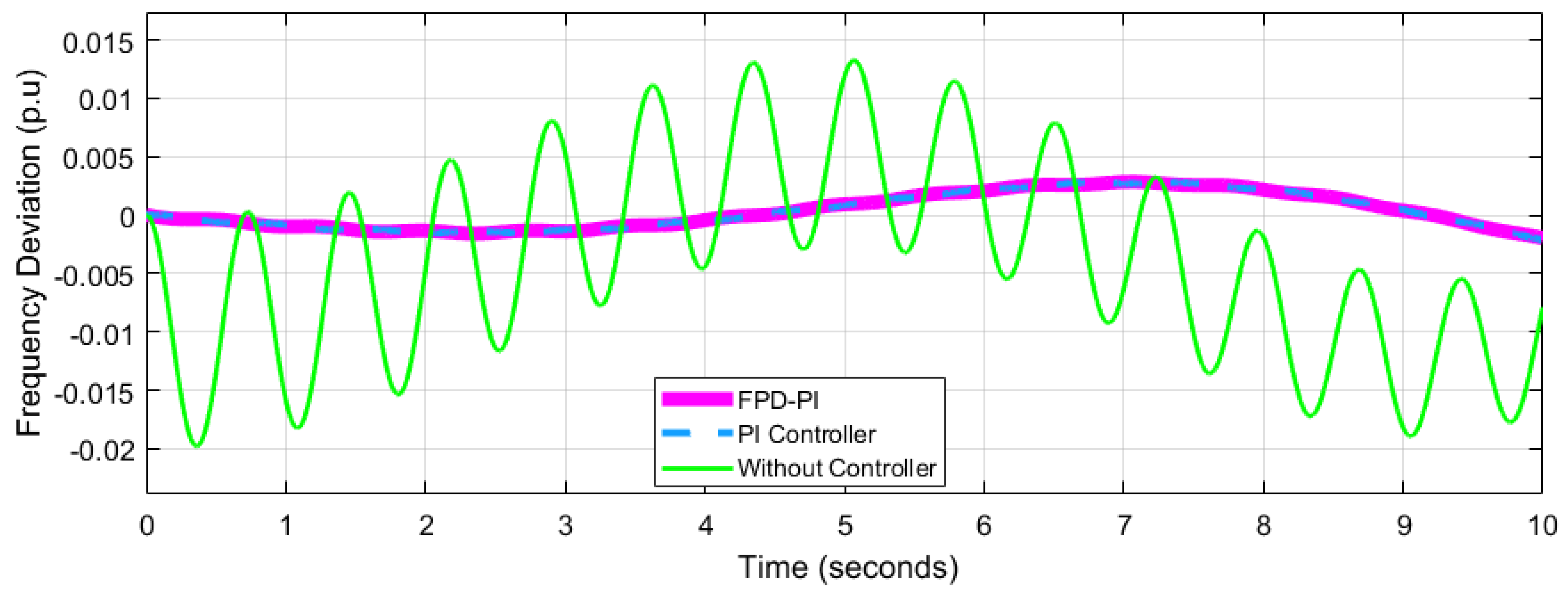
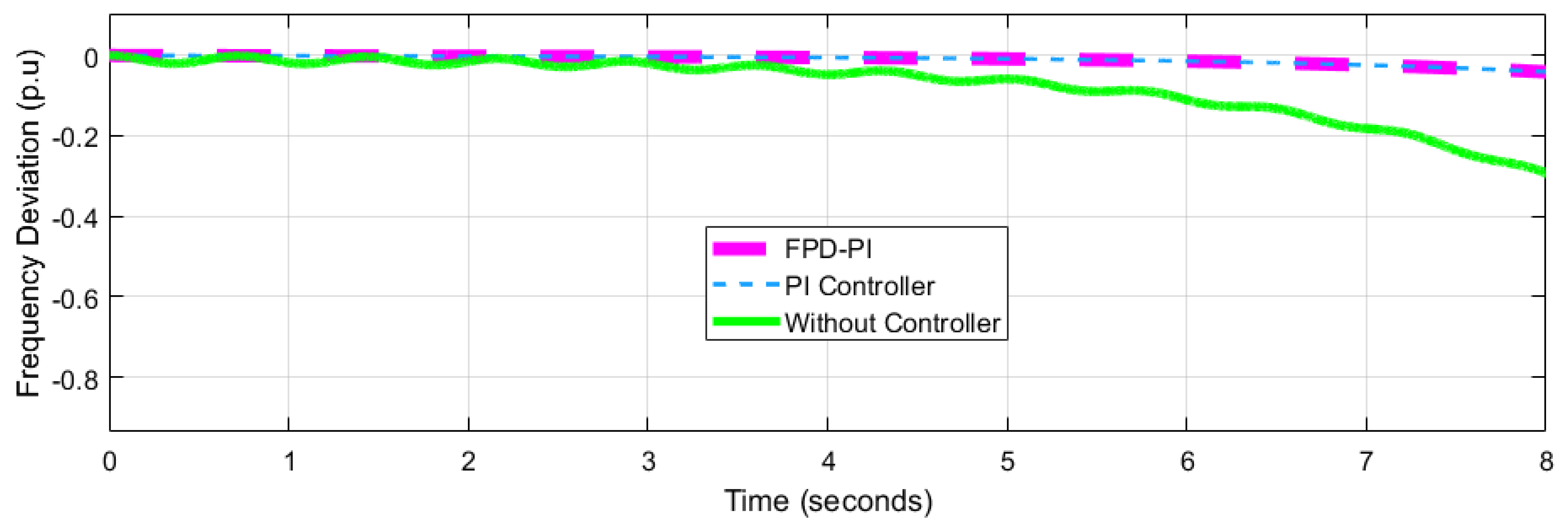
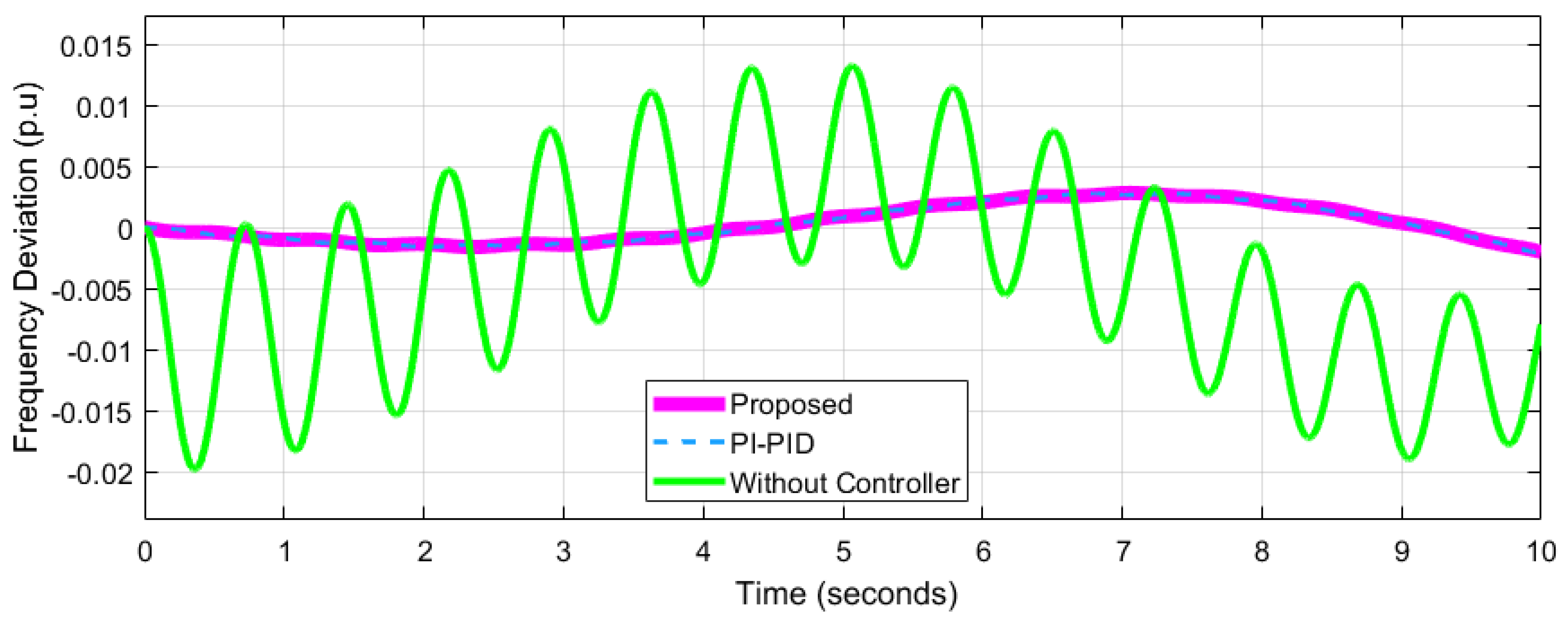
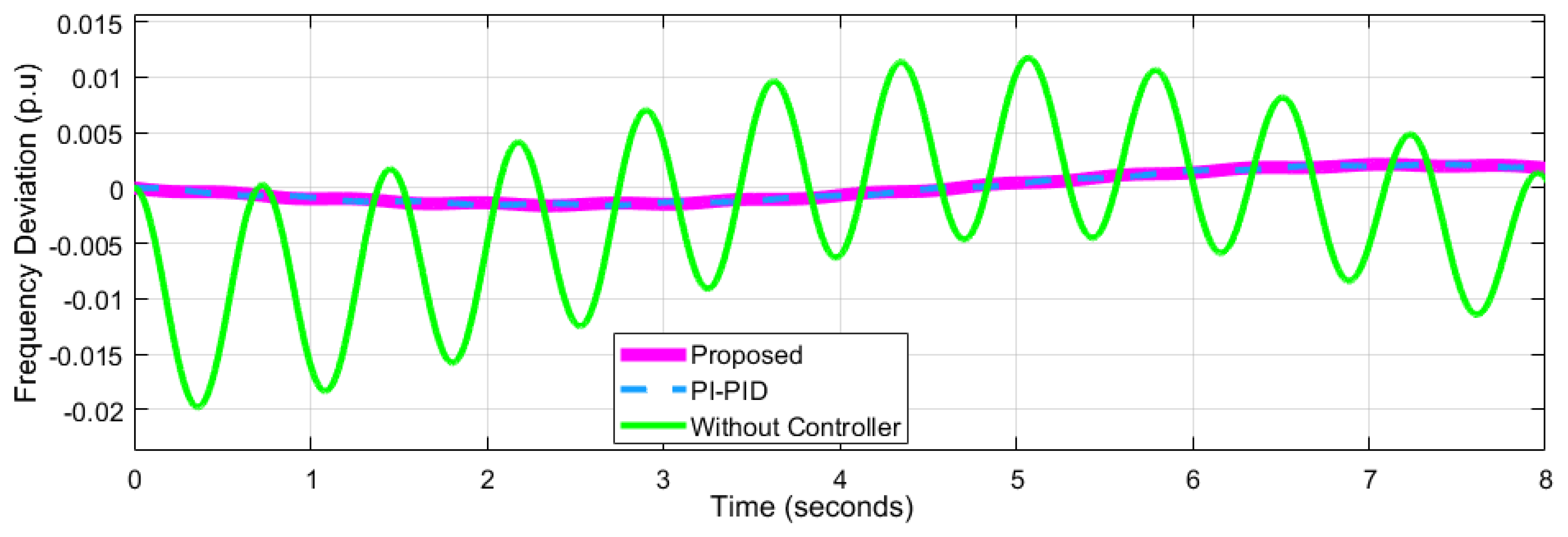
4.2. Performance Analysis of Network 2
5. Conclusions and Future Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barik, A.K.; Das, D.C. Expeditious frequency control of solar photovoltaic/biogas/biodiesel generator based isolated renewable microgrid using grasshopper optimisation algorithm. IET Renew. Power Gener. 2018, 12, 1659–1667. [Google Scholar] [CrossRef]
- Barisal, A.K.; Mishra, S. Improved PSO based automatic generation control of multi-source nonlinear power systems interconnected by AC/DC links. Cogent Eng. 2018, 5, 1422228. [Google Scholar] [CrossRef]
- Padhan, S.; Sahu, R.K.; Panda, S. Application of firefly algorithm for load frequency control of multi-area interconnected power system. Electr. Power Compon. Syst. 2014, 42, 1419–1430. [Google Scholar] [CrossRef]
- Mostafa Elsaied, M.; Abdallah Attia, M.; Abdelhamed Mostafa, M.; Fouad Mekhamer, S. Application of different optimization techniques to load frequency control with WECS in a multi-area system. Electr. Power Compon. Syst. 2018, 46, 739–756. [Google Scholar] [CrossRef]
- Yang, J.; Zeng, Z.; Tang, Y.; Yan, J.; He, H.; Wu, Y. Load frequency control in isolated micro-grids with electrical vehicles based on multivariable generalized predictive theory. Energies 2015, 8, 2145–2164. [Google Scholar] [CrossRef]
- Khan, M.I.; Khan, I.A.; Chang, Y.C. An overview of global renewable energy trends and current practices in Pakistan—A perspective of policy implications. J. Renew. Sustain. Energy 2020, 12, 056301. [Google Scholar] [CrossRef]
- Goyal, H.; Handmandlu, M.; Kothari, D.P. A novel modelling technique for automatic load frequency control of small hydro power plants. Int. J. Model. Simul. 2007, 27, 186–192. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Fractional-order load-frequency control of interconnected power systems using chaotic multi-objective optimization. Appl. Soft Comput. 2015, 29, 328–344. [Google Scholar] [CrossRef]
- Debbarma, S.; Saikia, L.C.; Sinha, N. Automatic generation control using two degree of freedom fractional order PID controller. Int. J. Electr. Power Energy Syst. 2014, 58, 120–129. [Google Scholar] [CrossRef]
- Khooban, M.H.; ShaSadeghi, M.; Niknam, T.; Blaabjerg, F. Analysis, control and design of speed control of electric vehicles delayed model: Multi-objective fuzzy fractional-order PIλDμ controller. IET Sci. Meas. Technol. 2017, 11, 249–261. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. Design an optimal fuzzy fractional proportional integral derivative controller with derivative filter for load frequency control in power systems. Trans. Inst. Meas. Control 2019, 41, 2563–2581. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Hamedani-Golshan, M.E.; Heydarian-Forushani, E.; Al-Sumaiti, A.S.; Siano, P. Decentralized fractional order control scheme for LFC of deregulated nonlinear power systems in presence of EVs and RER. In Proceedings of the IEEE 2018 International Conference on Smart Energy Systems and Technologies (SEST), Seville, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar]
- Arya, Y.; Kumar, N. BFOA-scaled fractional order fuzzy PID controller applied to AGC of multi-area multi-source electric power generating systems. Swarm Evol. Comput. 2017, 32, 202–218. [Google Scholar] [CrossRef]
- Peddakapu, K.; Mohamed, M.R.; Srinivasarao, P.; Leung, P.K. Frequency stabilization in interconnected power system using bat and harmony search algorithm with coordinated controllers. Appl. Soft Comput. 2021, 113, 107986. [Google Scholar] [CrossRef]
- Paliwal, N.; Srivastava, L.; Pandit, M. Application of grey wolf optimization algorithm for load frequency control in multi-source single area power system. Evol. Intell. 2022, 15, 563–584. [Google Scholar] [CrossRef]
- Guchhait, P.K.; Banerjee, A. Stability enhancement of wind energy integrated hybrid system with the help of static synchronous compensator and symbiosis organisms search algorithm. Prot. Control. Mod. Power Syst. 2020, 5, 11. [Google Scholar] [CrossRef]
- Khamari, D.; Kumbhakar, B.; Patra, S.; Laxmi, D.A.; Panigrahi, S. Load Frequency Control of a Single Area Power System using Firefly Algorithm. Int. J. Eng. Res. 2020, 9, 1318–1320. [Google Scholar]
- Amini, M.; Almassalkhi, M. Investigating delays in frequency-dependent load control. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 448–453. [Google Scholar]
- Bakar Siddique, M.A.; Asad, A.; Asif, R.M.; Rehman, A.U.; Sadiq, M.T.; Ullah, I. Implementation of Incremental Conductance MPPT Algorithm with Integral Regulator by using Boost Converter in Grid Connected PV Array. IETE J. Res. 2021, 67. [Google Scholar] [CrossRef]
- Habib, A.; Sou, C.; Hafeez, H.M.; Arshad, A. Evaluation of the effect of high penetration of renewable energy sources (RES) on system frequency regulation using stochastic risk assessment technique (an approach based on improved cumulant). Renew. Energy 2018, 127, 204–212. [Google Scholar] [CrossRef]
- Hernández, J.C.; Sanchez-Sutil, F.; Vidal, P.G.; Rus-Casas, C. Primary frequency control and dynamic grid support for vehicle-to-grid in transmission systems. Int. J. Electr. Power Energy Syst. 2018, 100, 152–166. [Google Scholar] [CrossRef]
- Panwar, A.; Sharma, G.; Bansal, R.C. Optimal AGC design for a hybrid power system using hybrid bacteria foraging optimization algorithm. Electr. Power Compon. Syst. 2019, 47, 955–965. [Google Scholar] [CrossRef]
- Yousaf, A.; Asif, R.M.; Shakir, M.; Rehman, A.U.; S. Adrees, M. An Improved Residential Electricity Load Forecasting Using a Machine-Learning-Based Feature Selection Approach and a Proposed Integration Strategy. Sustainability 2021, 13, 6199. [Google Scholar] [CrossRef]
- Tielens, P.; Van Hertem, D. Grid inertia and frequency control in power systems with high penetration of renewables. In Proceedings of the Young Researchers Symposium in Electrical Power Engineering, Delft, The Netherlands, 16–17 April 2012. [Google Scholar]
- Mosca, C.; Bompard, E.; Aluisio, B.; Migliori, M.; Vergine, C.; Cuccia, P. HVDC for frequency stability under RES penetration: The Sardinia island case. In Proceedings of the 2019 AEIT HVDC International Conference (AEIT HVDC), Florence, Italy, 9–10 May 2019; pp. 1–6. [Google Scholar]
- Shams, N.; Wall, P.; Terzija, V. Active power imbalance detection, size and location estimation using limited PMU measurements. IEEE Trans. Power Syst. 2018, 34, 1362–1372. [Google Scholar] [CrossRef]
- Siddique, M.A.B.; Khan, M.A.; Asad, A.; Rehman, A.U.; Asif, R.M.; Rehman, S.U. Maximum Power Point Tracking with Modified Incremental Conductance Technique in Grid-Connected PV Array. In Proceedings of the 2020 5th International Conference on Innovative Technologies in Intelligent Systems and Industrial Applications (CITISIA), Sydney, Australia, 25–27 November 2020; pp. 1–6. [Google Scholar]
- Lu, N. An evaluation of the HVAC load potential for providing load balancing service. IEEE Trans. Smart Grid 2012, 3, 1263–1270. [Google Scholar] [CrossRef]
- Dechanupaprittha, S.; Jamroen, C. Self-learning PSO based optimal EVs charging power control strategy for frequency stabilization considering frequency deviation and impact on EV owner. Sustain. Energy Grids Netw. 2021, 26, 100463. [Google Scholar] [CrossRef]
- Rebours, Y.G.; Kirschen, D.S.; Trotignon, M.; Rossignol, S. A survey of frequency and voltage control ancillary services—Part I: Technical features. IEEE Trans. Power Syst. 2007, 22, 350–357. [Google Scholar] [CrossRef]
- Yousaf, A.; Asif, R.M.; Shakir, M.; Rehman, A.U.; Alassery, F.; Hamam, H.; Cheikhrouhou, O. A Novel Machine Learning-Based Price Forecasting for Energy Management Systems. Sustainability 2021, 13, 12693. [Google Scholar] [CrossRef]
- Saxena, S.; Hote, Y.V. Load frequency control in power systems via internal model control scheme and model-order reduction. IEEE Trans. Power Syst. 2013, 28, 2749–2757. [Google Scholar] [CrossRef]
- Shiva, C.K.; Mukherjee, V. A novel quasi-oppositional harmony search algorithm for AGC optimization of three-area multi-unit power system after deregulation. Eng. Sci. Technol. Int. J. 2016, 19, 395–420. [Google Scholar] [CrossRef]
- Masood, B.; Khan, M.A.; Baig, S.; Song, G.; Rehman, A.U.; Rehman, S.U.; Rasheed, M.B. Investigation of deterministic, statistical and parametric NB-PLC channel modeling techniques for advanced metering infrastructure. Energies 2020, 13, 3098. [Google Scholar] [CrossRef]
- Rahman, A.; Saikia, L.C.; Sinha, N. Automatic generation control of an interconnected two-area hybrid thermal system considering dish-stirling solar thermal and wind turbine system. Renew. Energy 2017, 105, 41–54. [Google Scholar] [CrossRef]
- Asif, R.M.; Ur Rehman, A.; Ur Rehman, S.; Arshad, J.; Hamid, J.; Tariq Sadiq, M.; Tahir, S. Design and analysis of robust fuzzy logic maximum power point tracking based isolated photovoltaic energy system. Eng. Rep. 2020, 2, e12234. [Google Scholar] [CrossRef]
- Prakash, S.; Sinha, S.K. Simulation based neuro-fuzzy hybrid intelligent PI control approach in four-area load frequency control of interconnected power system. Appl. Soft Comput. 2014, 23, 152–164. [Google Scholar] [CrossRef]
- Satapathy, P.; Dhar, S.; Dash, P.K. Stability improvement of PV-BESS diesel generator-based microgrid with a new modified harmony search-based hybrid firefly algorithm. IET Renew. Power Gener. 2017, 11, 566–577. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T.; Blaabjerg, F.; Dragičević, T. A new load frequency control strategy for micro-grids with considering electrical vehicles. Electr. Power Syst. Res. 2017, 143, 585–598. [Google Scholar] [CrossRef]
- Ullah, A.; Nawi, N.M.; Khan, M.H. BAT algorithm used for load balancing purpose in cloud computing: An overview. Int. J. High Perform. Comput. Netw. 2020, 16, 43–54. [Google Scholar] [CrossRef]
- Meinhardt, M.; Cramer, G. Past, present and future of grid connected photovoltaic-and hybrid-power-systems. In Proceedings of the IEEE 2000 Power Engineering Society Summer Meeting (Cat. No. 00CH37134), Seattle, WA, USA, 16–20 July 2000; Volume 2, pp. 1283–1288. [Google Scholar]
- Khamari, D.; Sahu, R.K.; Panda, S. Adaptive differential evolution based PDF plus (1+ PI) controller for frequency regulation of the distributed power generation system with electric vehicle. Int. J. Ambient Energy 2022, 43, 3040–3054. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Grasshopper optimization algorithm scaled fractional order PI-D controller applied to reduced order model of load frequency control system. Int. J. Model. Simul. 2020, 40, 217–242. [Google Scholar] [CrossRef]
- Tripathy, D.; Behera, S.; Dev Choudhury, N.B. Implementation of Grasshopper optimization algorithm based cascaded fuzzy PD-PI controller for frequency stability in a multi-area power system. J. Interdiscip. Math. 2020, 23, 335–345. [Google Scholar] [CrossRef]
- Antoniou, A.; Lu, W.S. Practical Optimization: Algorithms and Engineering Applications; Springer: New York, NY, USA, 2007; Volume 19, p. 669. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Omar, M.; Soliman, M.; Ghany, A.M.A.; Bendary, F. Optimal tuning of PID controllers for hydrothermal load frequency control using ant colony optimization. Int. J. Electr. Eng. Inform. 2013, 5, 348. [Google Scholar] [CrossRef]
- Abd-Elazim, S.M.; Ali, E.S. Load frequency controller design via BAT algorithm for nonlinear interconnected power system. Int. J. Electr. Power Energy Syst. 2016, 77, 166–177. [Google Scholar] [CrossRef]
- Kouba, N.E.L.Y.; Menaa, M.; Hasni, M.; Boudour, M. Optimal control of frequency and voltage variations using PID controller based on particle swarm optimization. In Proceedings of the 2015 4th International Conference on Systems and Control (ICSC), Sousse, Tunisia, 28–30 April 2015; pp. 424–429. [Google Scholar]


| Control Mechanism | Time Slots | Auxiliary Services |
|---|---|---|
| Primary Control | 10–60 s | Frequency Response |
| Secondary Control | 1–10 min | Regulation |
| Tertiary Control | 10 min–few hours | Imbalance/Reserve |
| Symbols | Description |
|---|---|
| The output power of PV cell | |
| The efficiency of PV cells, i.e., 8% | |
| Area of PV array | |
| Change in solar irradiation | |
| Temperature | |
| Transfer function (T.F) of PV cell in s-domain | |
| The T.F of fuel cell in s-domain | |
| Gain of fuel cell | |
| A constant of time for fuel cell | |
| l | Number of units |
| The T.F of ESS | |
| Gain of energy storage system | |
| A constant of time for ESS | |
| U | Incremental action of the proposed controller |
| R(s) | Transfer function of power system |
| Frequency deviation | |
| Power dynamics in response to oscillations | |
| Damping constant | |
| Ps | Inertia constant |
| D(s) | Load disturbance |
| F(s) | s-domain area frequency |
| Transfer function of fuzzy logic (PD-PI) controller | |
| Proportional, integral & derivative gain of the proposed controller |
| Components | Formulations | Description of Variable |
|---|---|---|
| Grasshopper swarming Behaviour | Random swarming behaviour of grasshoppers: where shows the i-th grasshopper location, the social interaction of grasshoppers is denoted by Si, the gravity force on i-th grasshopper is depicted by Gi, and the wind advection is denoted by Ai. | |
| Social interaction of grasshoppers | Number of grasshoppers is shown by N, and the displacement between i-th and j-th grasshopper is denoted by | |
| Social forces of grasshopper | The force of attraction is taken as: [2.079,4], while repulsion is taken as. [0,2.079]. Note that no force should be precisely at 2.079. This is referred a ’comfort zone.’ | |
| The component of gravity | The . is a gravitational constant referring to the centre of earth, i.e., | |
| The advection of wind | is the ‘drift constant’ and is a unity vector following the direction of the wind. A baby grasshopper has no wings, so its movements are highly dependent upon the wind. | |
| The substituted equation for swarming behaviour of grasshoppers | In the next step, S, G, and A are all replaced by the defined equations. | |
| Improved calculation of Equation (15) | The issues like reaching of grasshoppers to comfort zone quickly and the non-convergent behaviour of swarm system to the target location does not permit to directly solve the problem of optimization. This is why is transformed into | |
| The decreasing coefficients | The comfort zone is reduced by the coefficient c, which is proportional to the number of iterations |
| No. of Trials | Proportional Gain Kp | Derivative Gain KD | Integral Gain Ki |
|---|---|---|---|
| 1. | −1.6066 | −1.0150 | −0.0024 |
| 2. | −1.9600 | −1.7808 | −0.0011 |
| 3. | −1.7251 | −0.4057 | −0.0012 |
| 4. | −1.8811 | −1.9678 | −0.0014 |
| No. of Trials | Proportional Gain Kp | Derivative Gain KD | Integral Gain Ki |
|---|---|---|---|
| 1. | −1.9185 | −1.7166 | −0.0030 |
| 2 | −1.8703 | −1.7753 | −0.0051 |
| 3 | −1.8196 | −0.6802 | −0.0009 |
| No. of Trials | Proportional Gain Kp | Derivative Gain KD | Integral Gain Ki |
|---|---|---|---|
| 1 | −1.9111 | −1.6176 | −0.0080 |
| 2 | −1.8700 | −1.8783 | −0.0040 |
| 3 | −1.8914 | −0.5002 | −0.0007 |
| No. of Iteration | Particle Swam Optimization On Wind Power Based Power System [49] | Ant Colony Algorithms On Hydrothermal Power Plant [47] | Bat Algorithms For Nonlinear Interconnected Power Systems [48] | Proposed | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kp | KD | Ki | Kp | KD | Ki | Kp | KD | Ki | Kp | KD | Ki | |
| Network- | 3.1205 | 2.4641 | 2.7821 | 0.9 | 0.98 | 0.98 | 0.152 | 0.164 | 0.124 | 1.8811 | 1.9678 | 0.0014 |
| Network-2 | 3.1205 | 2.4641 | 2.7821 | 0.4 | 0.88 | 0.15 | 0.152 | 0.164 | 0.124 | −1.8196 | −0.6802 | −0.0009 |
| Network-3 | ------ | ------ | ------ | 0.56 | 0.27 | 0.21 | 0.152 | 0.164 | 0.124 | −1.8914 | −0.5002 | −0.0007 |
| Frequency Deviation p.u | Network-1 = 0.04547 Network-2= 0.007218 ---------------------- | Network-1 = 0.06 Network-2 = 0.03 Network-3 = 0.02 | Network-1 = 0.05 Network-2 = 0.025 Network-3 = 0.20 | Network-1= 0.08 Network-2= 0.02 Network-3= 0.02 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maqbool, H.; Yousaf, A.; Asif, R.M.; Rehman, A.U.; Eldin, E.T.; Shafiq, M.; Hamam, H. An Optimized Fuzzy Based Control Solution for Frequency Oscillation Reduction in Electric Grids. Energies 2022, 15, 6981. https://doi.org/10.3390/en15196981
Maqbool H, Yousaf A, Asif RM, Rehman AU, Eldin ET, Shafiq M, Hamam H. An Optimized Fuzzy Based Control Solution for Frequency Oscillation Reduction in Electric Grids. Energies. 2022; 15(19):6981. https://doi.org/10.3390/en15196981
Chicago/Turabian StyleMaqbool, Hina, Adnan Yousaf, Rao Muhammad Asif, Ateeq Ur Rehman, Elsayed Tag Eldin, Muhammad Shafiq, and Habib Hamam. 2022. "An Optimized Fuzzy Based Control Solution for Frequency Oscillation Reduction in Electric Grids" Energies 15, no. 19: 6981. https://doi.org/10.3390/en15196981
APA StyleMaqbool, H., Yousaf, A., Asif, R. M., Rehman, A. U., Eldin, E. T., Shafiq, M., & Hamam, H. (2022). An Optimized Fuzzy Based Control Solution for Frequency Oscillation Reduction in Electric Grids. Energies, 15(19), 6981. https://doi.org/10.3390/en15196981









