Numerical Investigation of the Effect of Hub Gaps on the 3D Flows Inside the Stator of a Highly Loaded Axial Compressor Stage
Abstract
:1. Introduction
2. Investigated Compressor
3. Numerical Setup
3.1. CFD Solver
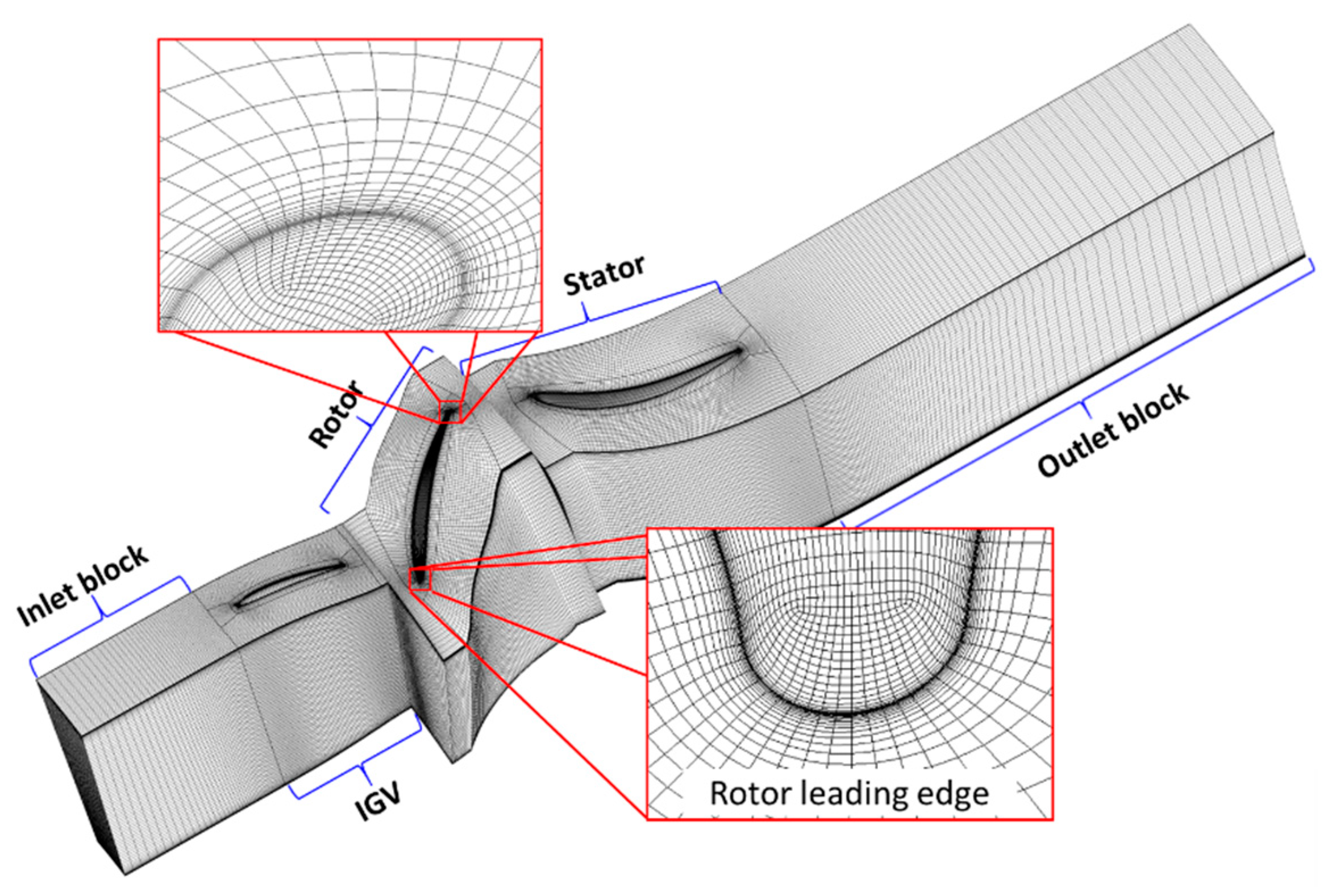
3.2. Grid Generation
3.3. Boundary Conditions
3.4. Turbulence Model
3.5. Numerical Schemes and Convergence Criteria
4. Numerical Results
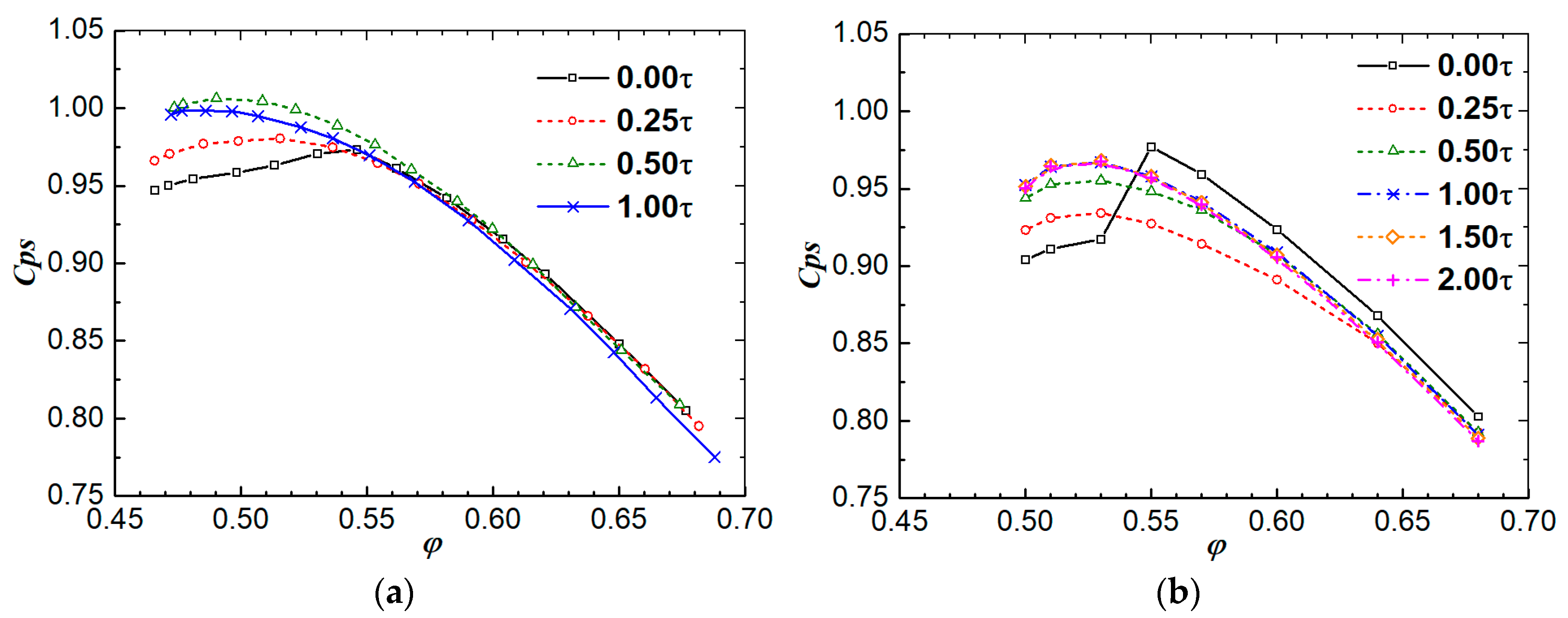
4.1. The Compressor Characteristics
4.2. 3D Flow Structures inside the Stator Passage
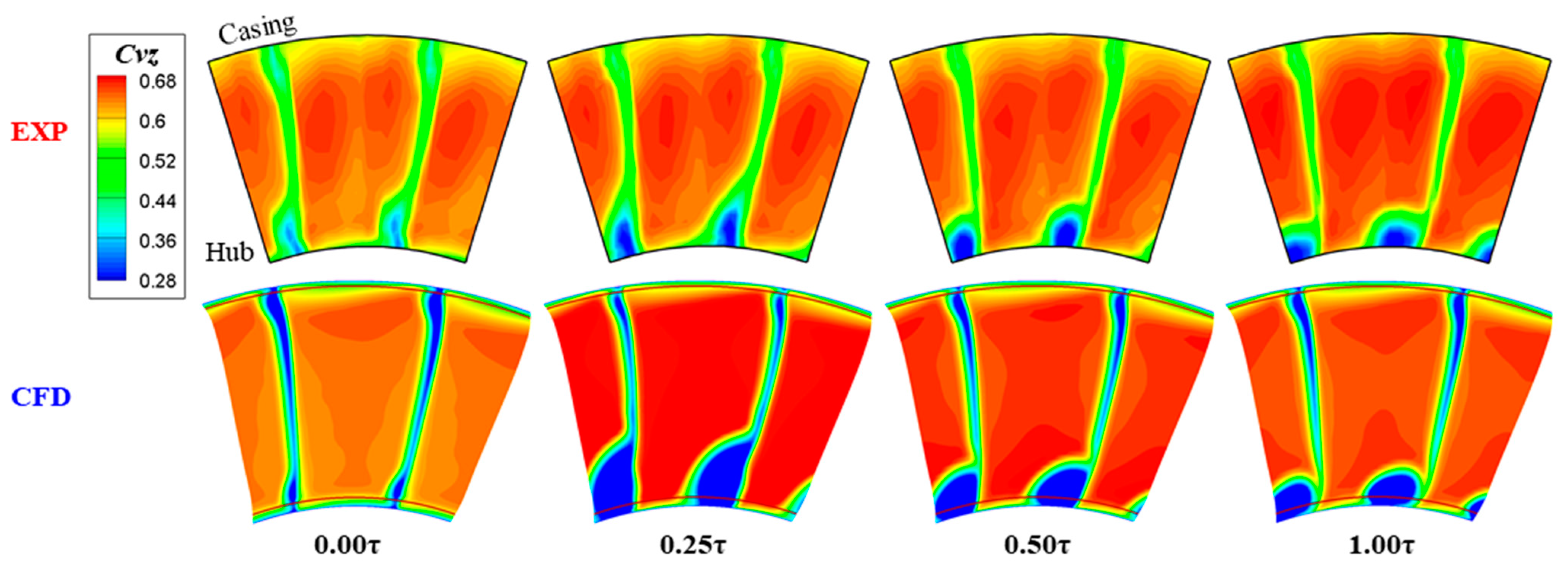
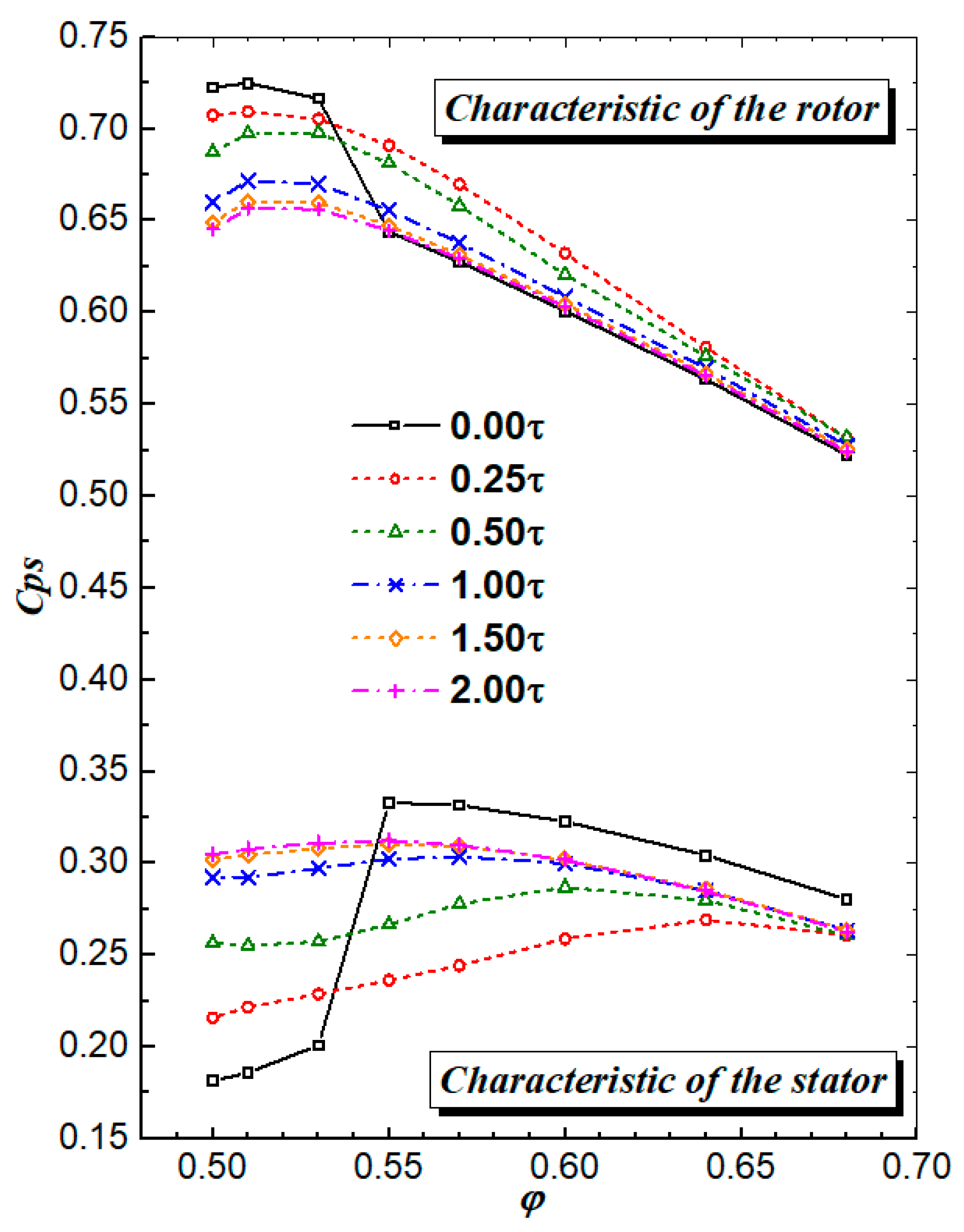
4.3. Flow Fields at the Stator Outlet
5. Flow Mechanisms of the Effect of the Hub Clearance on the 3D Flows of the Stator
5.1. Interaction between the Hub Corner Separation and the Leakage Flow
5.2. Effect of the Hub Clearance on the Leakage Flow
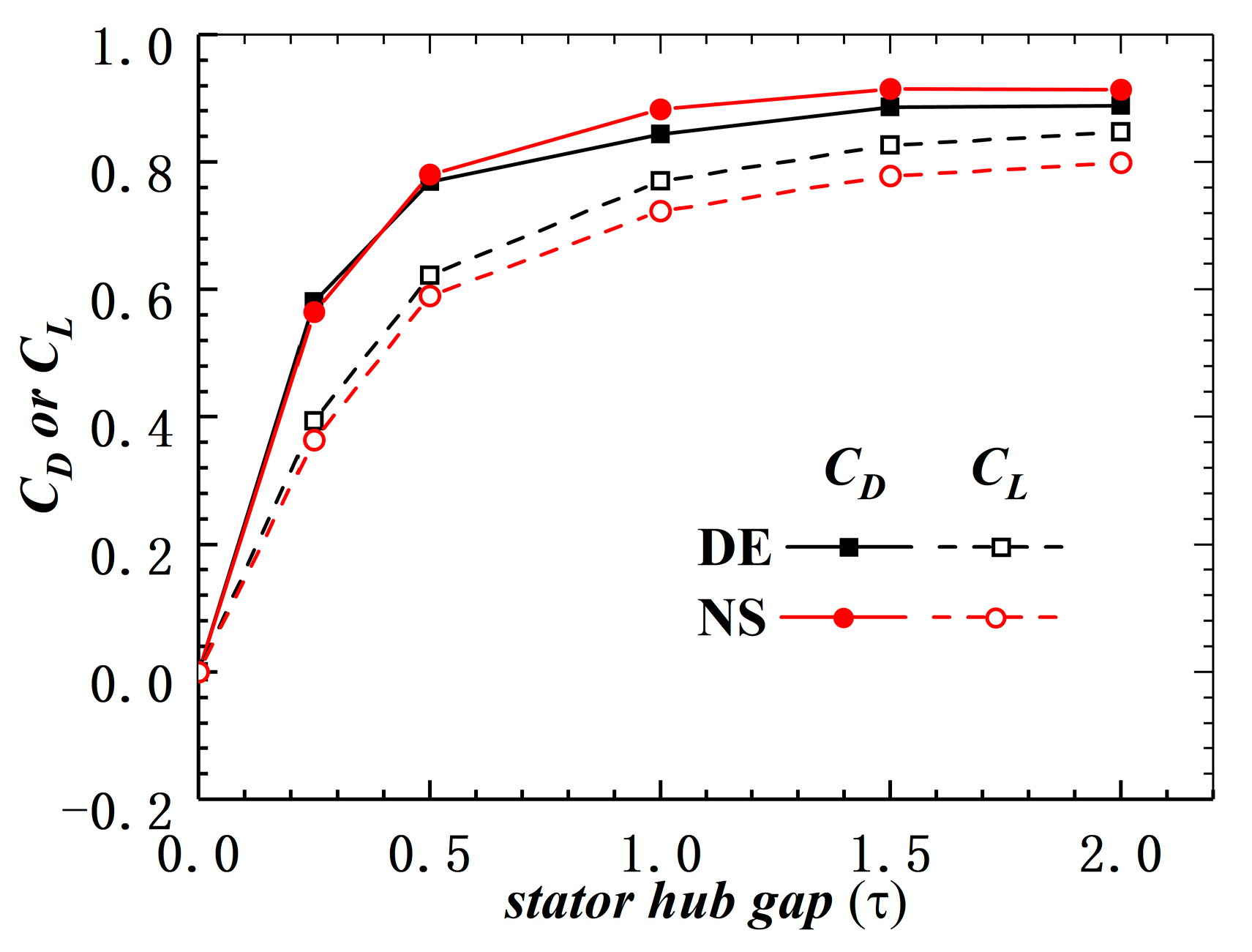
5.3. Discussion of the Optimum Hub Clearance
6. Effect of the Stator Hub Gap on the Stator Inlet Flow Fields and the Rotor Performance
6.1. Variation of the Rotor Performance
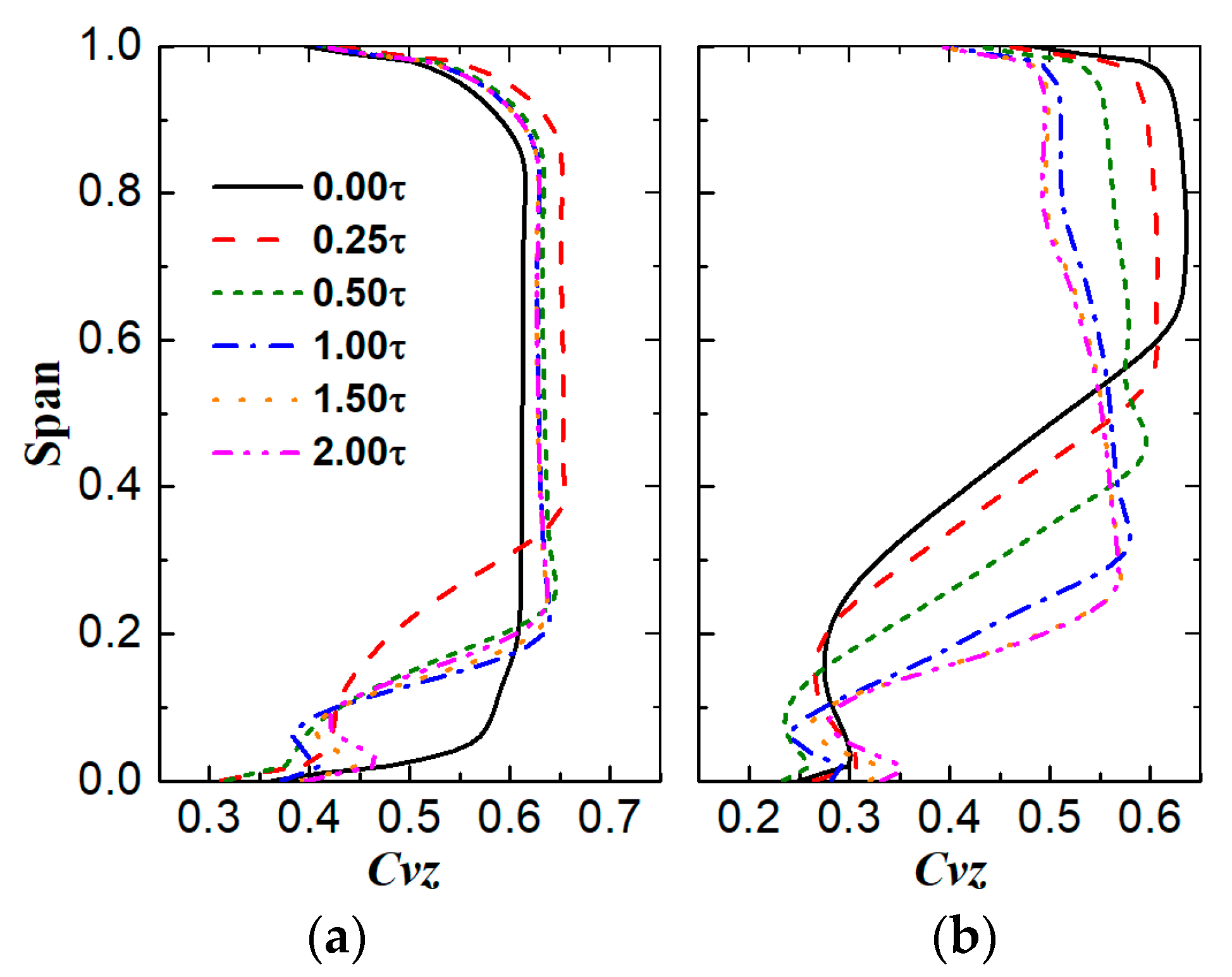
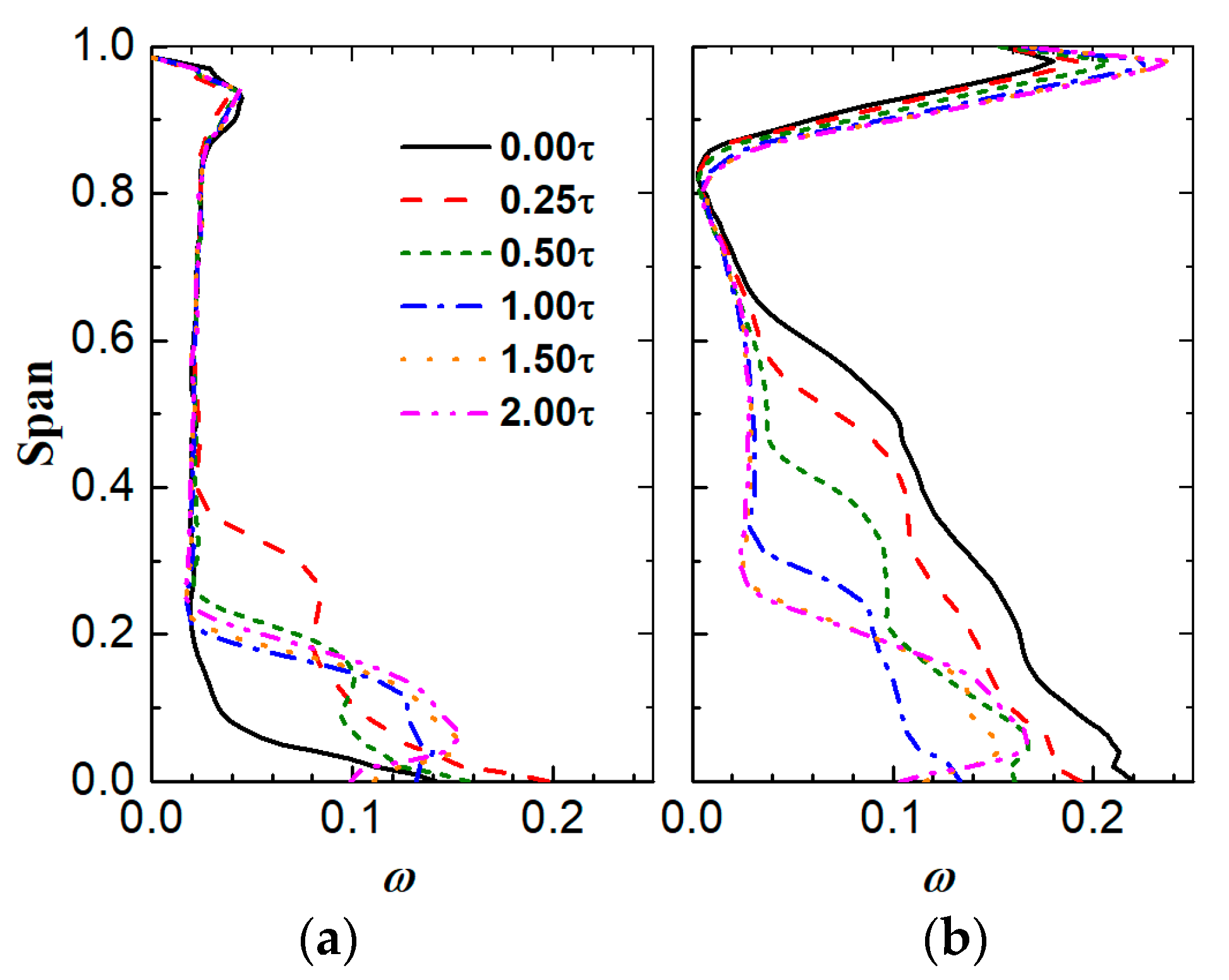
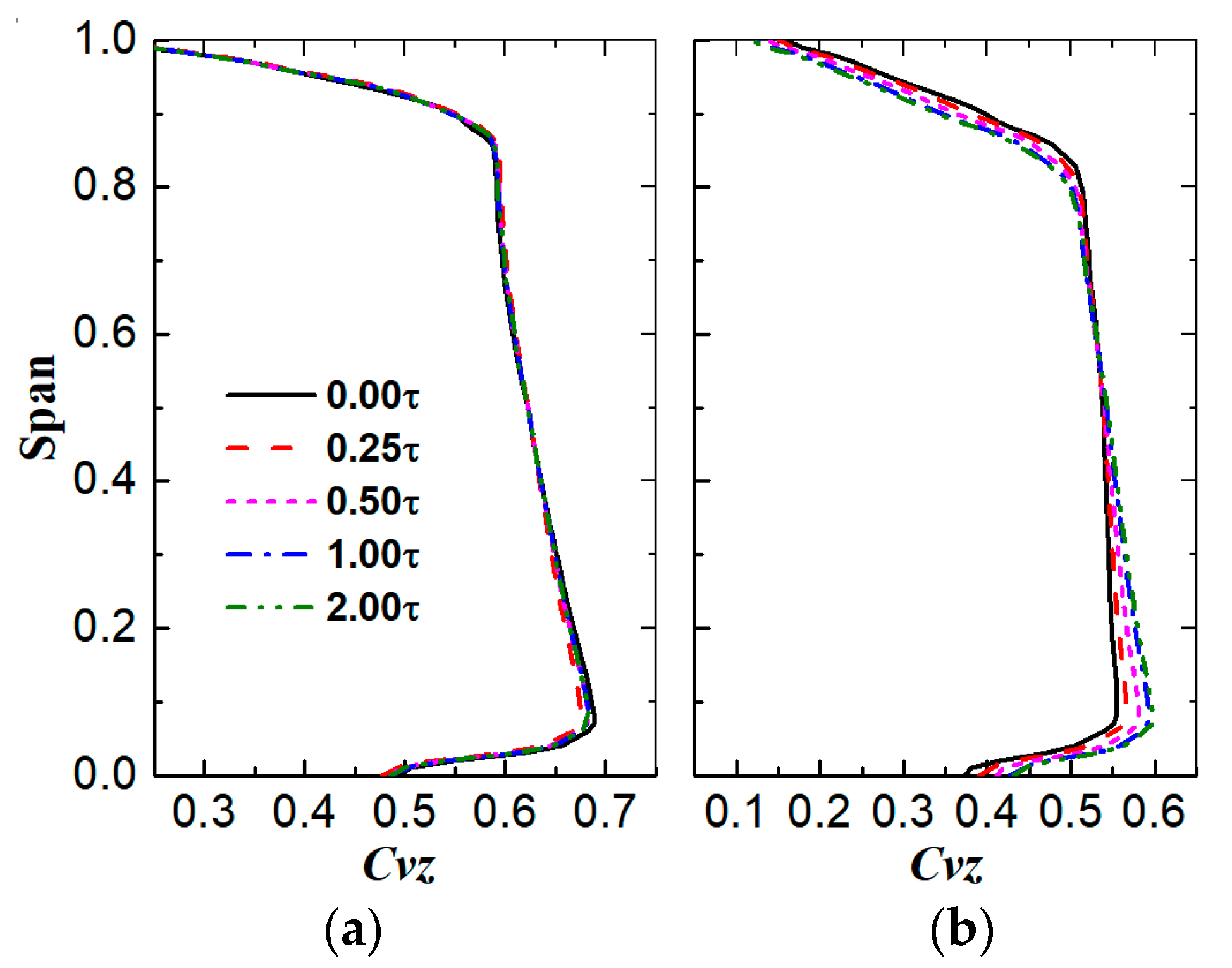
6.2. Variation in the Stator Inlet Flow Fields
7. Conclusions and Prospects
- The CFD solver and the corresponding setup used in this paper can almost reproduce the 3D separating flows inside the stator passage as the stator hub gap changes, not only in tendency but also in scale. Hence, it is feasible enough to be used to analyse the detailed flow mechanisms when the stator hub gap is induced.
- The 3D flow structure inside the stator passage depends on the interaction between the leakage flow and the corner separation. Furthermore, it mainly depends on the velocity of the leakage flow. When the hub gap is too small, the velocity of the leakage flow is very low; in the DE condition, this becomes a low-energy flow, which will make the hub corner flow worse. However, in the NS condition, when a shrouded stator has a corner stall, this low-velocity leakage flow helps to improve the flow. The hub corner stall, or corner separation, gradually disappears as the stator hub gap widens, which increases the velocity of the leakage flow and, in turn, reduces flow loss and blockage. This trend continues until the stator hub gap increases to where the viscosity in the gap can be ignored. From then on, the velocity of the leakage flow will no longer increase apparently. Instead, as the gap increases, the leakage flow will increase, and the mixing between the leakage flow and the mainflow can also induce extra flow loss, and hence the compressor performance declines again.
- There exists an optimum stator hub gap where the leakage flow is comparable to the corner separation and the compressor performance is the best. This optimum gap, however, is equal to the gap where the viscosity in the gap can be ignored. Hence, using the method proposed by Rain, a simple metric was proposed to choose the optimum stator hub gap. By comparing our results with the results from published studies, this metric was proven to be feasible.
- Finally, it was also explained how the stator hub gap affected the stator inlet flow and rotor performance. It was demonstrated that the stator passage flow blockage can affect the upstream flow field. As a result, the performance of the rotor tends to vary in the opposite direction to that of the stator.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | three-dimensional |
| DE | compressor design condition |
| LE | blade leading edge |
| NS | compressor near-stall condition |
| PS | blade pressure side |
| SS | blade suction side |
| SL | separating line |
| Span | normalized blade height |
| TE | blade trailing edge |
| Cvz | normalized axial velocity, Vaxial/Umid |
| Cps | static pressure-rise coefficient, (p2-p1)/(1/2ρU2mid) |
| CD | discharge coefficient, Vn/Vnideal |
| Vaxial | axial flow velocity (m/s) |
| Vstr | normalized streamwise velocity of the leakage flow |
| Vnideal | ideal normalized normal velocity of the leakage flow (viscosity ignored) |
| Vn | normalized normal velocity of the leakage flow |
| Umid | rotor speed at the middle span (m/s) |
| A | flow yaw angle (°) |
| φ | mass flow coefficient, Vaxial/Umid |
| ρ | air density (kg/m3) |
| ω | the total pressure loss coefficient, (P1-P2)/(1/2ρU2mid) |
| η | compressor efficiency |
References
- Dean, R.C. Secondary Flow in Axial Compressors; Massachusetts Institute of Technology: Cambridge, MA, USA, 1954. [Google Scholar]
- Lakshminarayana, B.; Horlock, J.H. Tip-Clearance Flow and Losses for an Isolated Compressor Blade; Aeronautical Research Council London: London, UK, 1962. [Google Scholar]
- Lakshminarayana, B.; Horlock, J.H. Leakage and Secondary Flows in Compressor Cascades; HM Stationery Office: Richmond, UK, 1965. [Google Scholar]
- Lakshminarayana, B. Methods of Predicting the Tip Clearance Effects in Axial Flow Turbomachinery. J. Fluids Eng. 1970, 92, 467–480. [Google Scholar] [CrossRef]
- Singh, U.K.; Ginder, R.B. The Effect of Hub Leakage Flow in a Transonic Compressor Stator. In Proceedings of the ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition, Stockholm, Sweden, 2–5 June 1998. [Google Scholar] [CrossRef]
- Lee, C.; Song, J.; Lee, S.; Hong, D. Effect of a Gap Between Inner Casing and Stator Blade on Axial Compressor Performance. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar] [CrossRef]
- George, K.K.; Agnimitra Sunkara, S.N.; George, J.T.; Joseph, M.; Pradeep, A.M.; Roy, B. Investigations on Stator Hub End Losses and its Control in an Axial Flow Compressor. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Dong, Y.; Gallimore, S.J.; Hodson, H.P. Three-Dimensional Flows and Loss Reduction in Axial Compressors. J. Turbomach. 1987, 109, 354–361. [Google Scholar] [CrossRef]
- Gbadebo, S.A.; Cumpsty, N.A.; Hynes, T.P. Interaction of Tip Clearance Flow and Three-Dimensional Separations in Axial Compressors. J. Turbomach. 2007, 129, 679–685. [Google Scholar] [CrossRef]
- Peacock, R.E. A review of turbomachinery tip gap effects: Part 1: Cascades. Int. J. Heat Fluid Flow 1982, 3, 185–193. [Google Scholar] [CrossRef]
- Sakulkaew, S.; Tan, C.S.; Donahoo, E.; Cornelius, C.; Montgomery, M. Compressor Efficiency Variation with Rotor Tip Gap from Vanishing to Large Clearance. J. Turbomach. 2013, 135, 031030. [Google Scholar] [CrossRef]
- Wennerstrom, A.J. Experimental Study of a High-Throughflow Transonic Axial Compressor Stage. J. Eng. Gas Turbines Power 1984, 106, 552–560. [Google Scholar] [CrossRef]
- McDougall, N.M. A Comparison Between the Design Point and Near-Stall Performance of an Axial Compressor. J. Turbomach. 1990, 112, 109–115. [Google Scholar] [CrossRef]
- Liu, B.; Qiu, Y.; An, G.; Yu, X. Experimental Investigation of the Flow Mechanisms and the Performance Change of a Highly Loaded Axial Compressor Stage with/without Stator Hub Clearance. Appl. Sci. 2019, 9, 5134. [Google Scholar] [CrossRef]
- Yu, X.J.; Liu, B.J. Research on three-dimensional blade designs in an ultra-highly loaded low-speed axial compressor stage: Design and numerical investigations. Adv. Mech. Eng. 2016, 8, 1–16. [Google Scholar] [CrossRef]
- Liu, B.J.; An, G.F.; Yu, X.J. Assessment of Curvature Correction and Reattachment Modification into the Shear Stress Transport Model within the Subsonic Axial Compressor Simulations. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 910–927. [Google Scholar] [CrossRef]
- Dener, C.; Hirsch, C. IGG—An Interactive 3D Surface Modelling and Grid Generation System. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Storer, J.A.; Cumpsty, N.A. Tip Leakage Flow in Axial Compressors. J. Turbomach. 1991, 113, 252–259. [Google Scholar] [CrossRef]
- Rains, D.A. Tip Clearance Flows in Axial Compressors and Pumps. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1954. [Google Scholar]
- Wang, Z.; Geng, S.; Zhang, H. Influence of clearance variation on aerodynamic performance of a compressor stator cascade. Acta Aeronaut. Astronaut. Sin. 2016, 37, 3304–3316. [Google Scholar]
- Chen, S.; Tsai, C.-R. The effect of tip clearance flow on compressor performance. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998. [Google Scholar] [CrossRef]
- Yang, C.; Lu, X.; Zhang, Y.; Zhao, S.; Zhu, J. Numerical Investigation of a Cantilevered Compressor Stator at Varying Clearance Sizes. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar] [CrossRef]







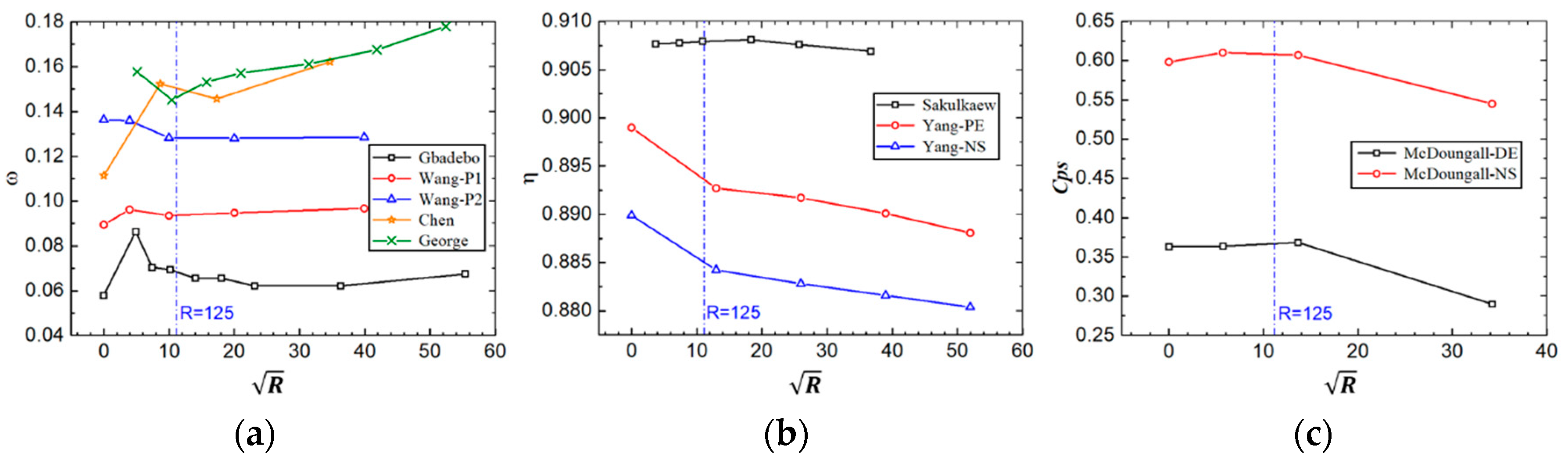

| Researcher | Research Object | Methodology | Re | Blade Thickness/Chord |
|---|---|---|---|---|
| Gbadebo [9] | Cascade | CFD | 4.8 × 105 | 5% |
| Wang [22] | Cascade | Experiment | 3.2 × 105 | 8% |
| Chen [23] | Cascade | CFD | 3 × 105 | 10% |
| George [7] | Low-speed compressor stator | CFD | 1.1 × 105 | 10% |
| Sakulkaew [11] | High-speed compressor rotor | CFD | 2 × 106 | 5% |
| Yang [24] | High-speed compressor stator | CFD | 3 × 105 | 10% |
| McDougall [13] | Low-speed compressor rotor | Experiment | 1.3 × 105 | 10% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, G.; Fan, Z.; Qiu, Y.; Wang, R.; Yu, X.; Liu, B. Numerical Investigation of the Effect of Hub Gaps on the 3D Flows Inside the Stator of a Highly Loaded Axial Compressor Stage. Energies 2022, 15, 6993. https://doi.org/10.3390/en15196993
An G, Fan Z, Qiu Y, Wang R, Yu X, Liu B. Numerical Investigation of the Effect of Hub Gaps on the 3D Flows Inside the Stator of a Highly Loaded Axial Compressor Stage. Energies. 2022; 15(19):6993. https://doi.org/10.3390/en15196993
Chicago/Turabian StyleAn, Guangfeng, Zhu Fan, Ying Qiu, Ruoyu Wang, Xianjun Yu, and Baojie Liu. 2022. "Numerical Investigation of the Effect of Hub Gaps on the 3D Flows Inside the Stator of a Highly Loaded Axial Compressor Stage" Energies 15, no. 19: 6993. https://doi.org/10.3390/en15196993
APA StyleAn, G., Fan, Z., Qiu, Y., Wang, R., Yu, X., & Liu, B. (2022). Numerical Investigation of the Effect of Hub Gaps on the 3D Flows Inside the Stator of a Highly Loaded Axial Compressor Stage. Energies, 15(19), 6993. https://doi.org/10.3390/en15196993






