An Approach for Determining Voltage Imbalance Contributions Based on Complex Independent Component Analysis
Abstract
:1. Introduction
2. The Proposed Method for Determining Voltage Imbalances Contributions
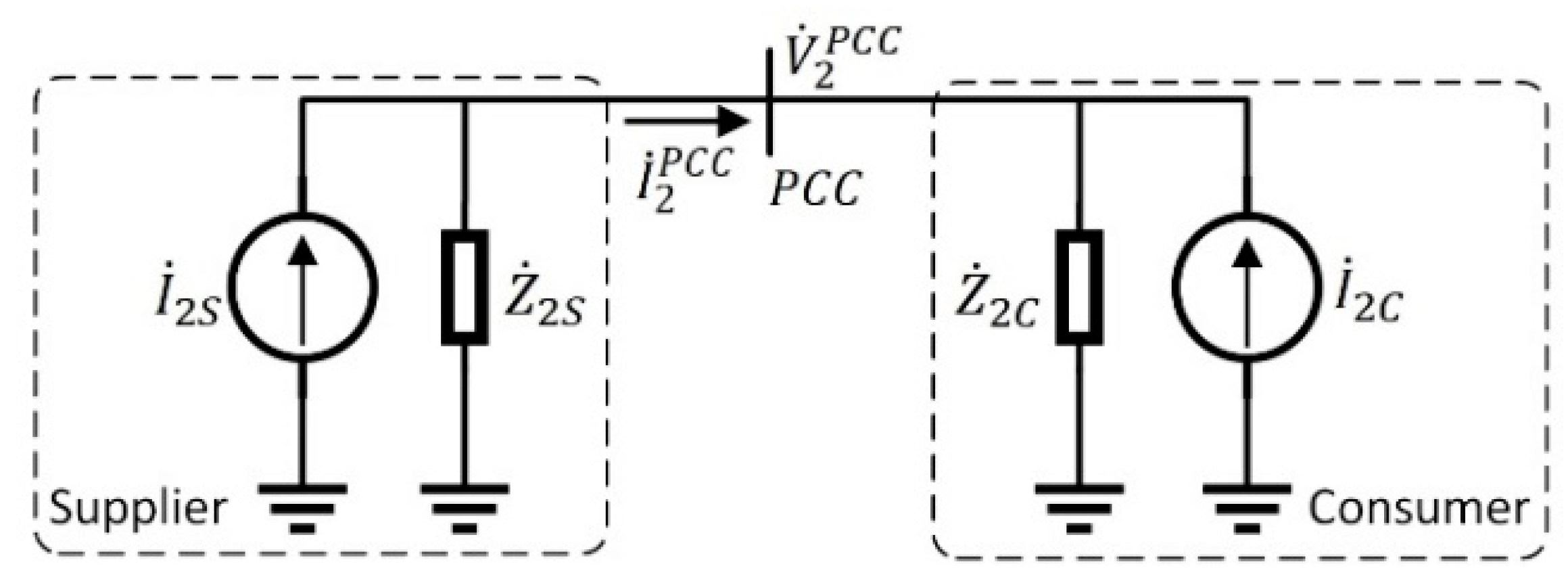
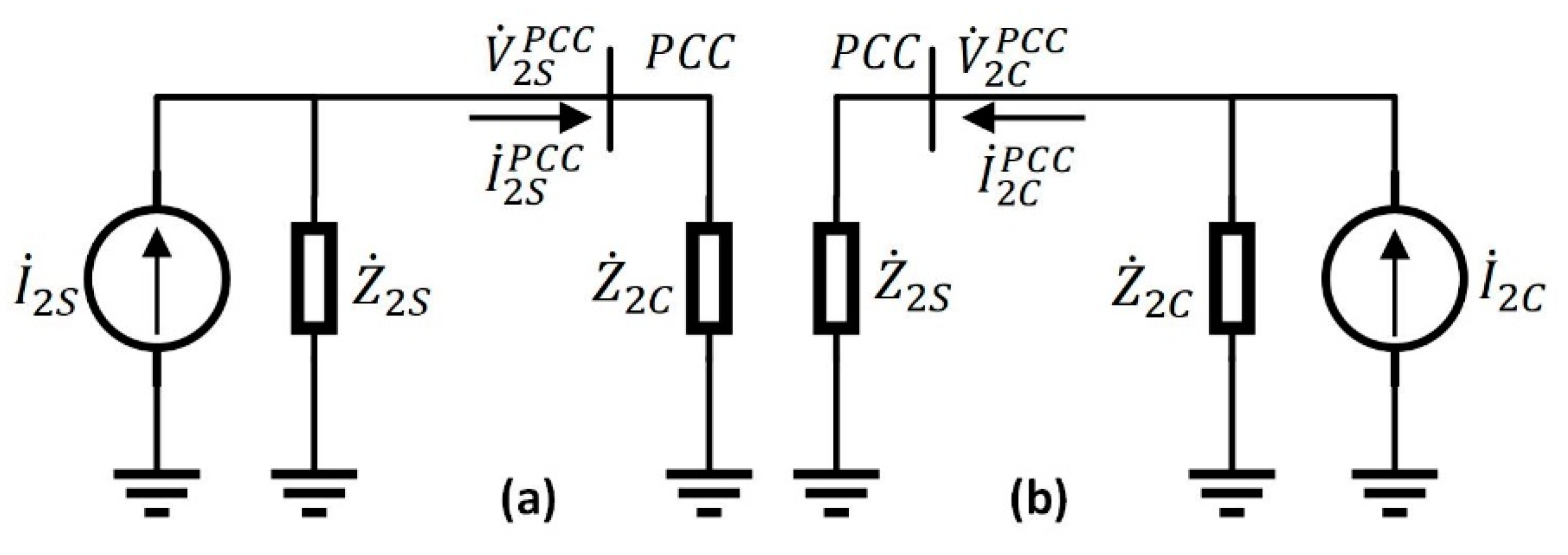
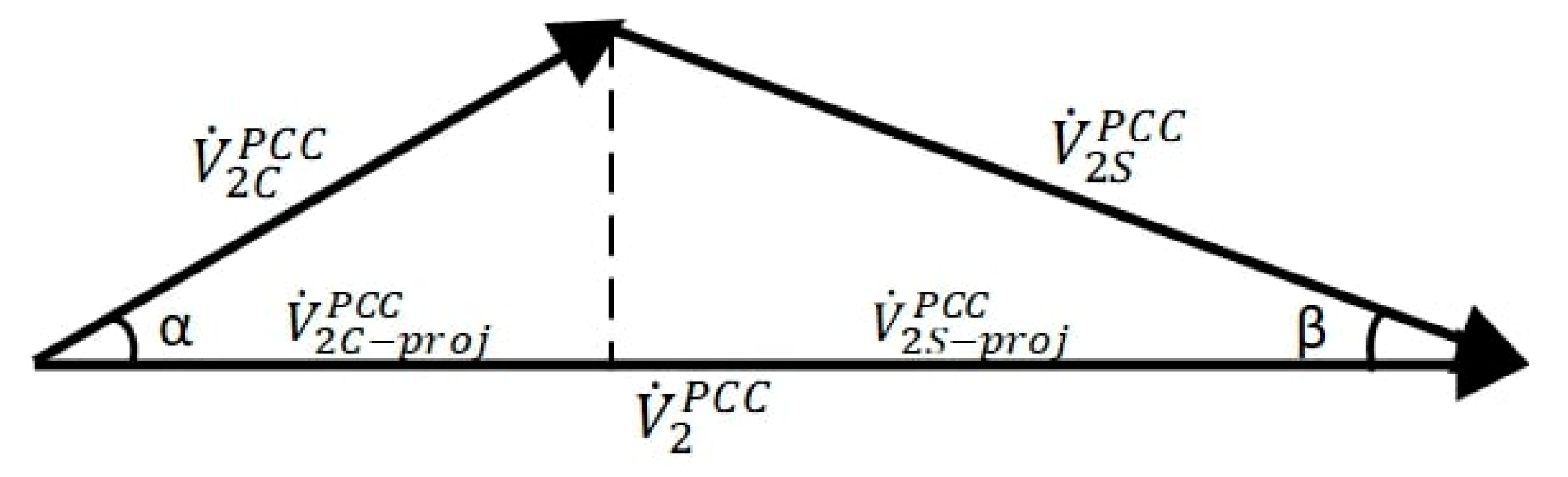
2.1. Superposition Method
2.2. Complex Independent Component Analysis Technique
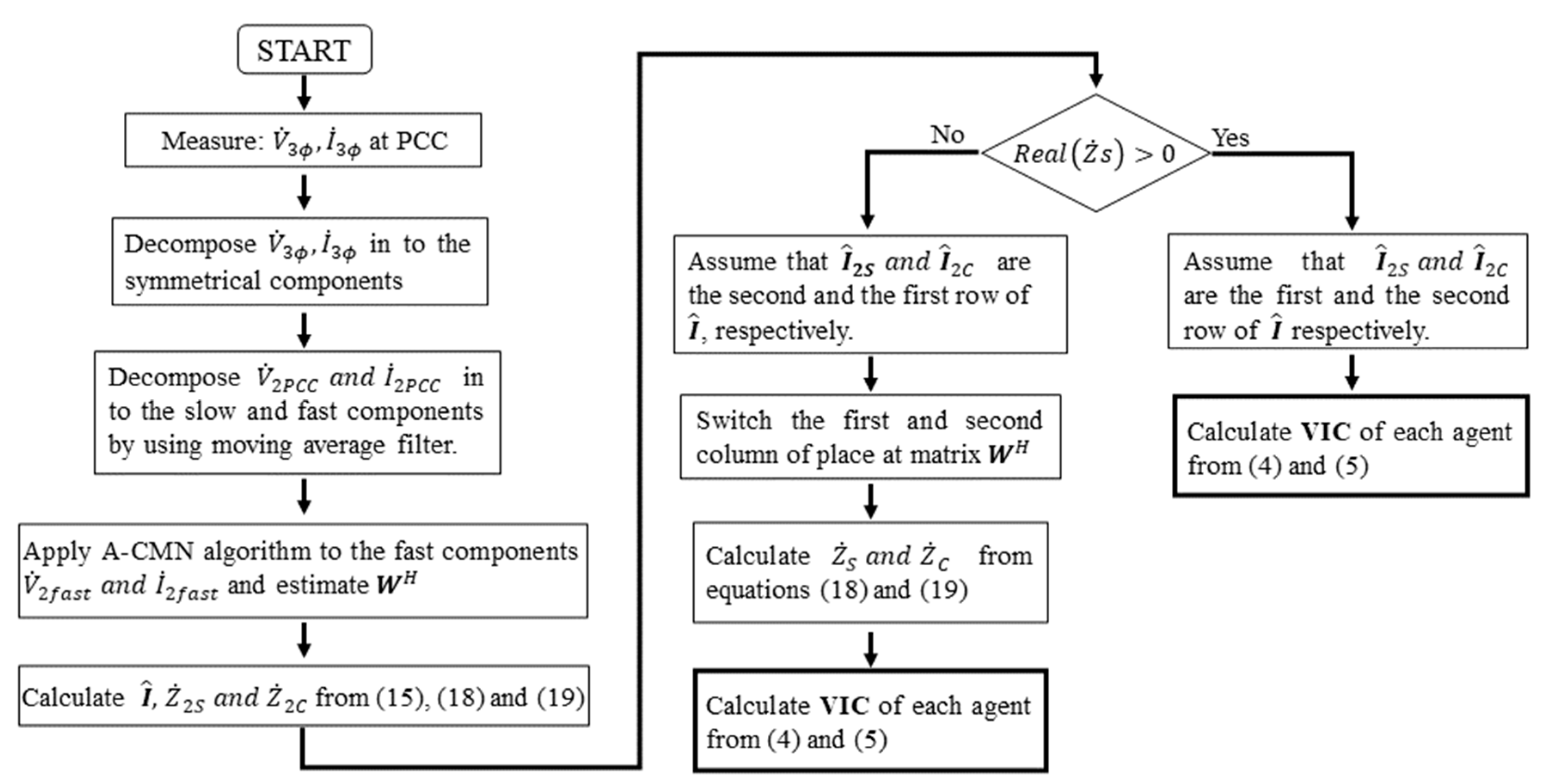
3. The CICA Technique for Determining Voltage Imbalance Contributions
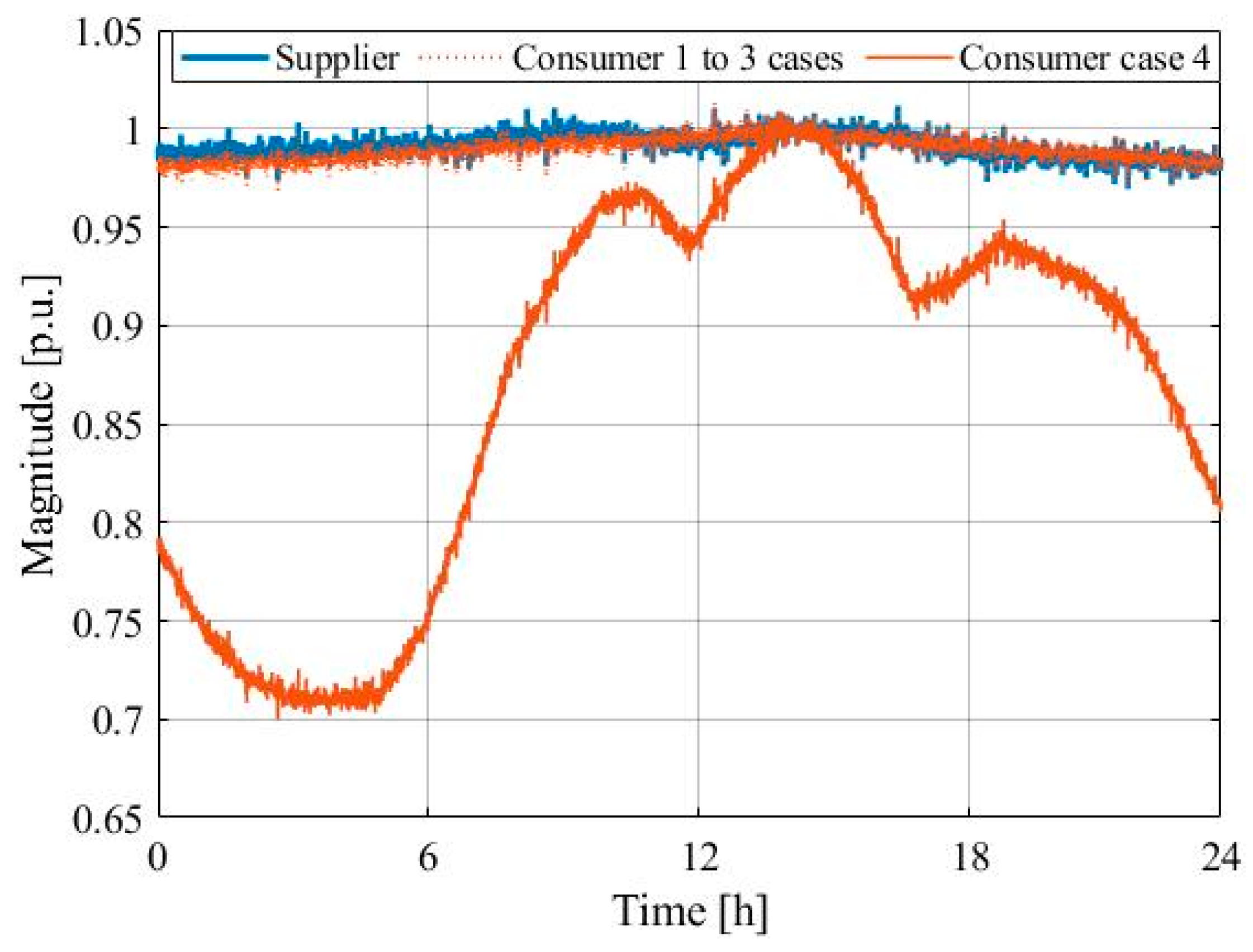
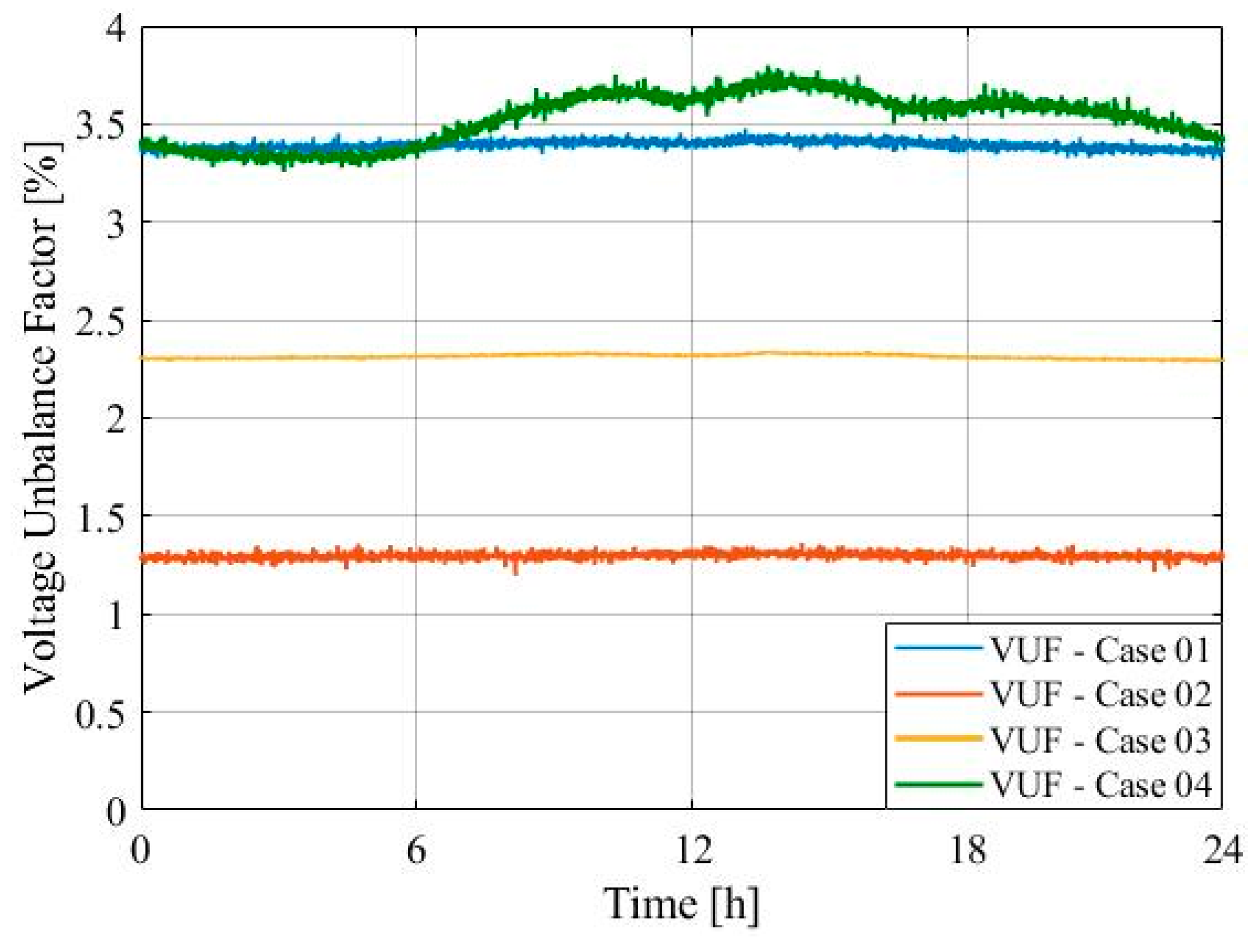
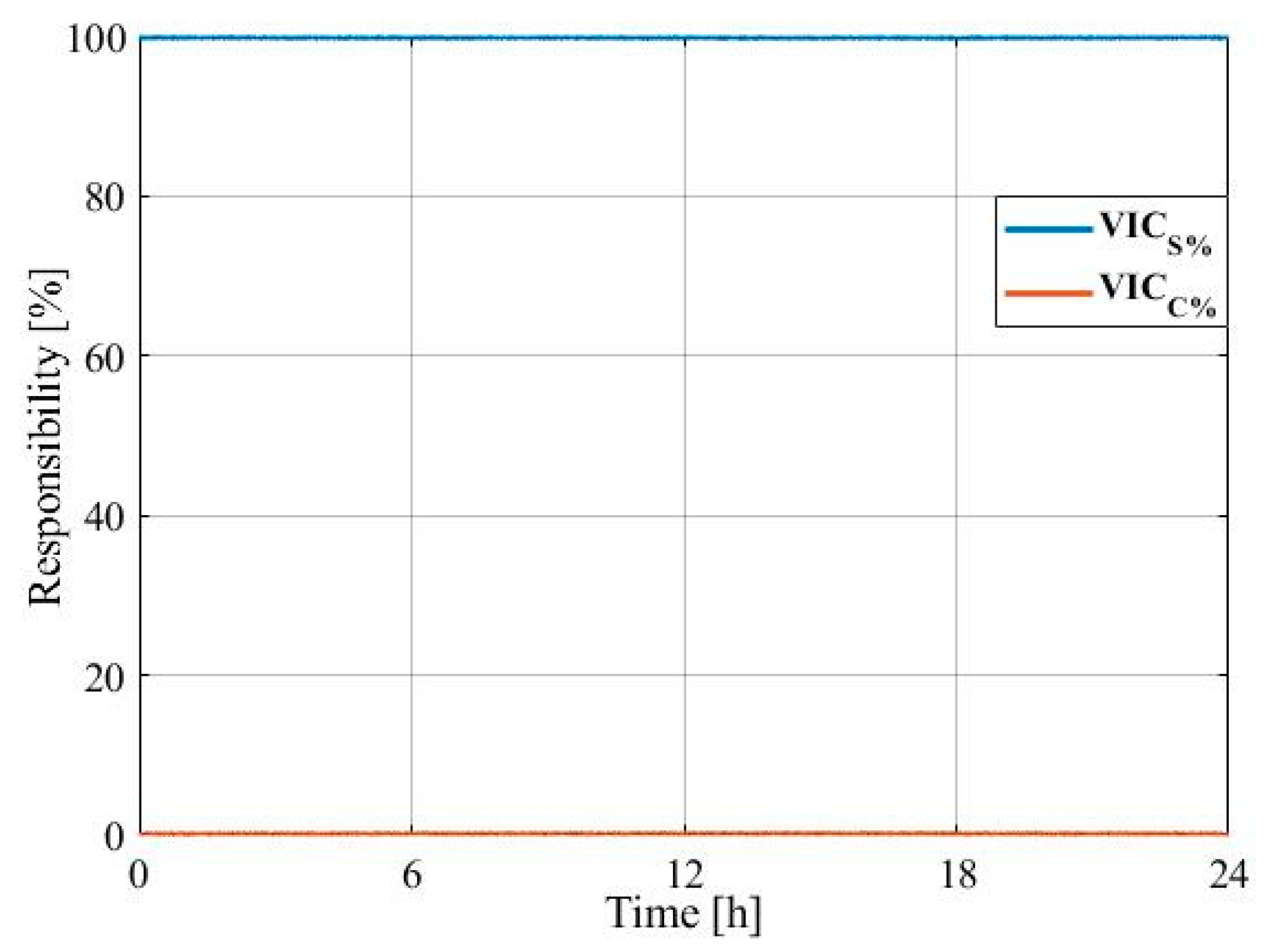
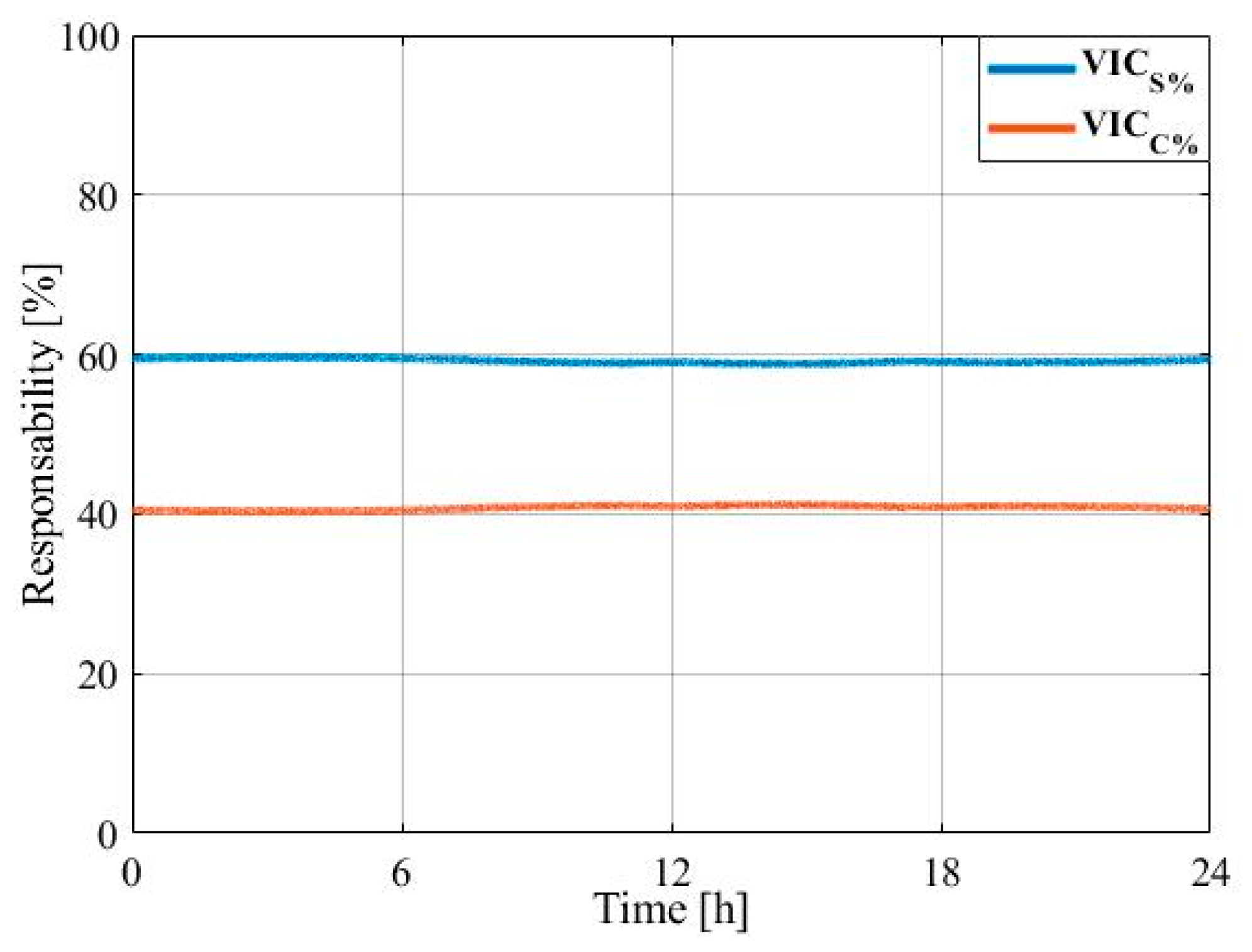
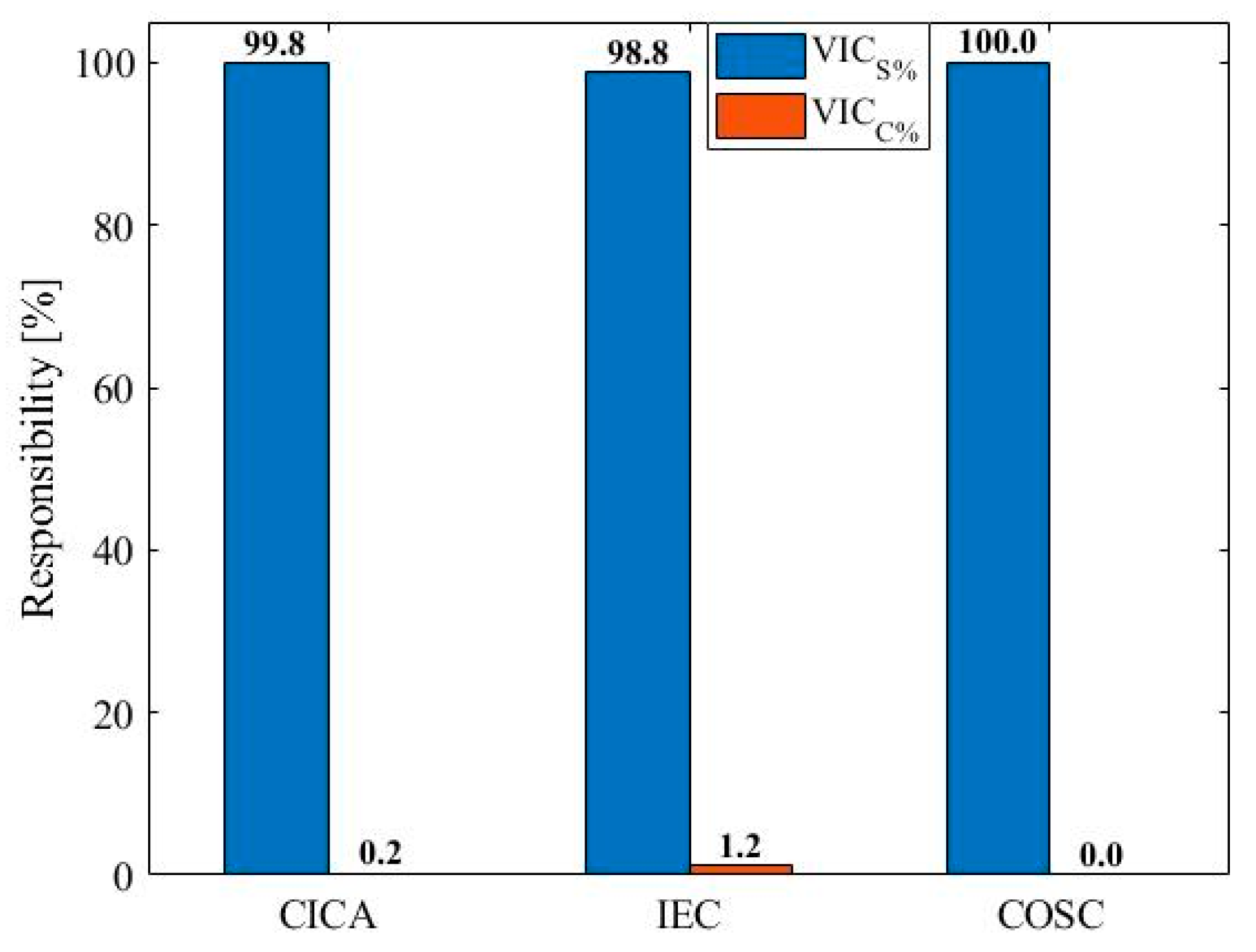
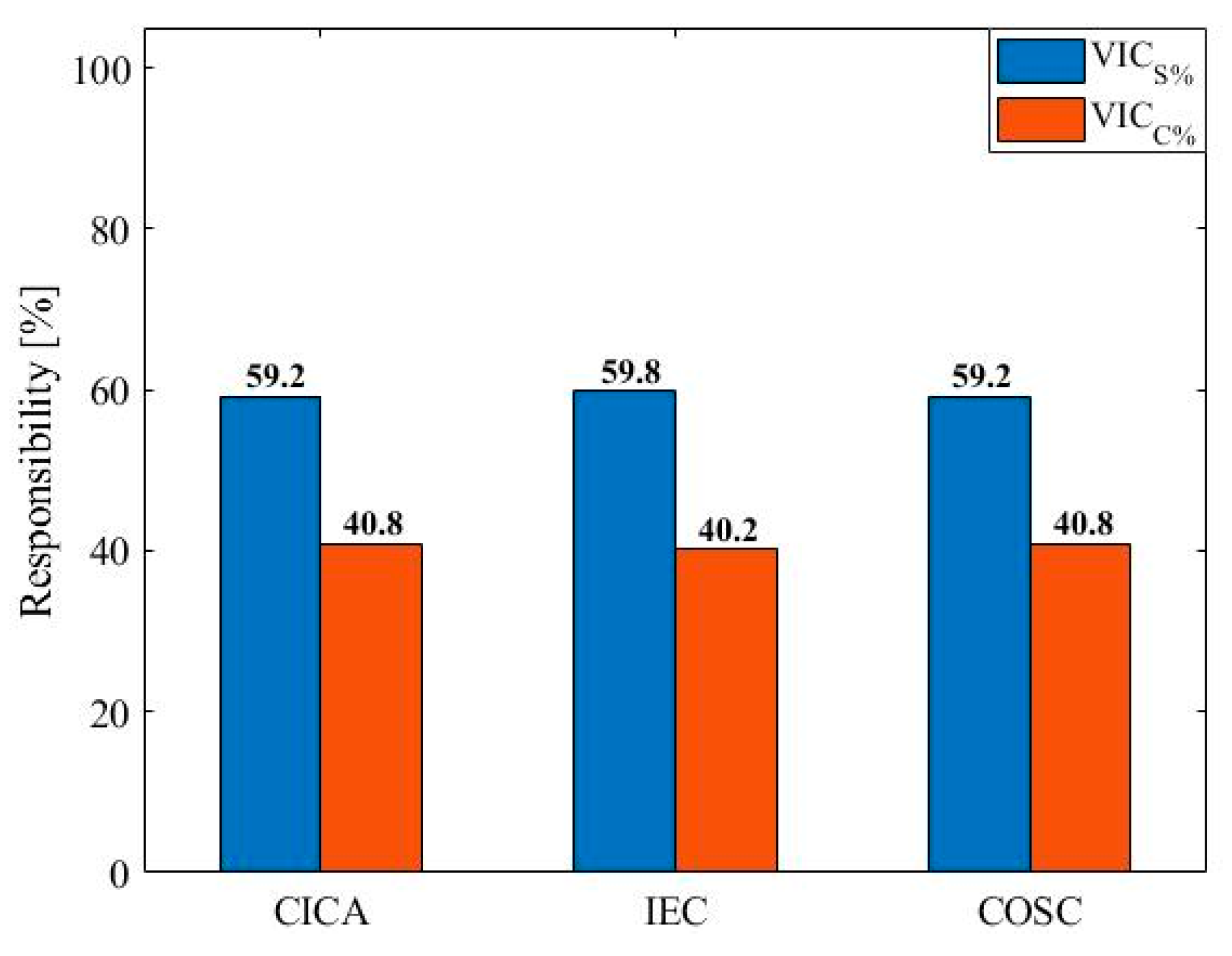
4. Case Studies
- Case 1: Both supplier and consumer with smoothly unbalanced voltage profiles;
- Case 2: Balanced voltage supply condition and consumer with smoothly unbalanced voltage profile;
- Case 3: Smoothly unbalanced voltage supply profile with balanced consumer loads;
- Case 4: Smoothly unbalanced voltage supply condition with significant consumer unbalanced load profile changes.
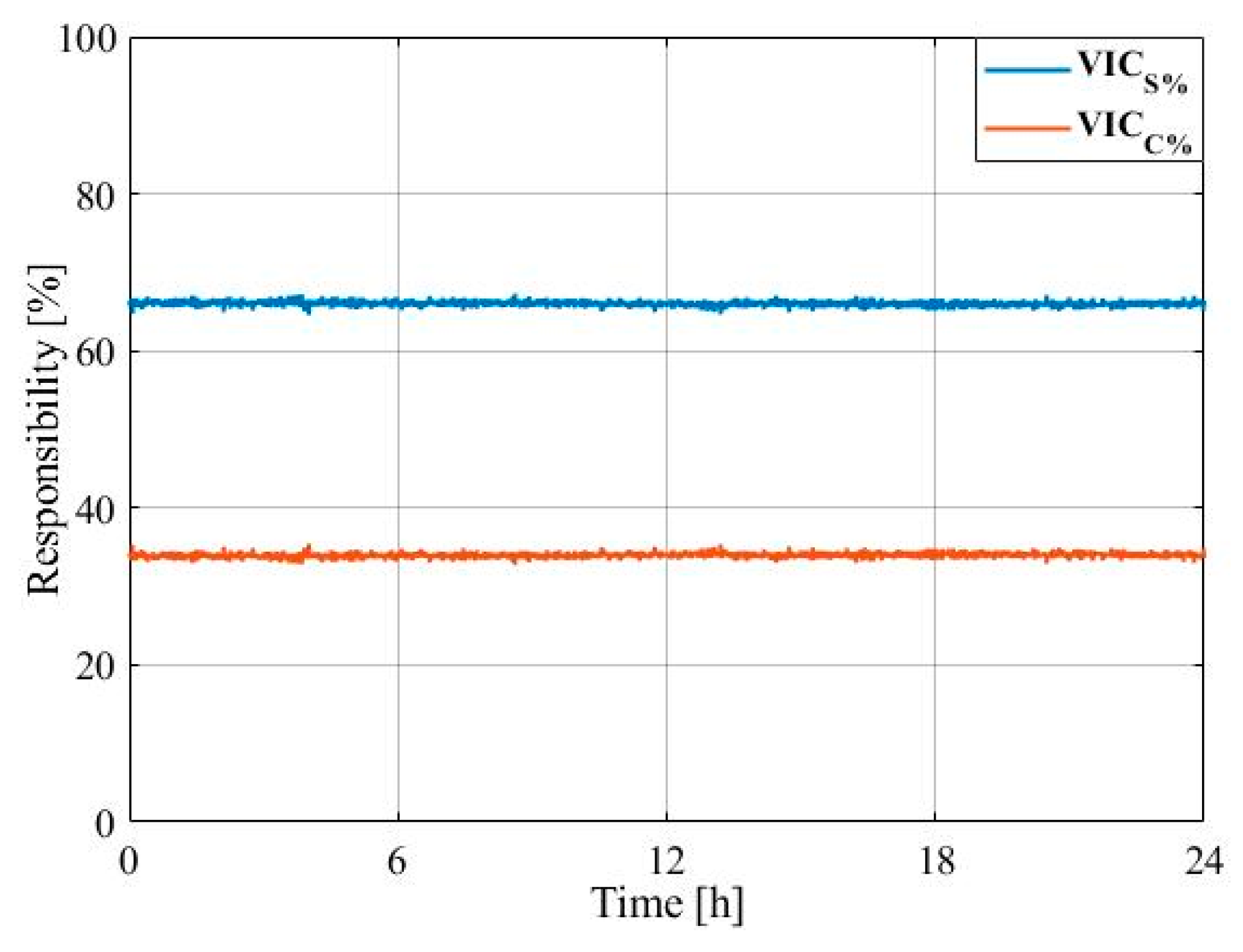
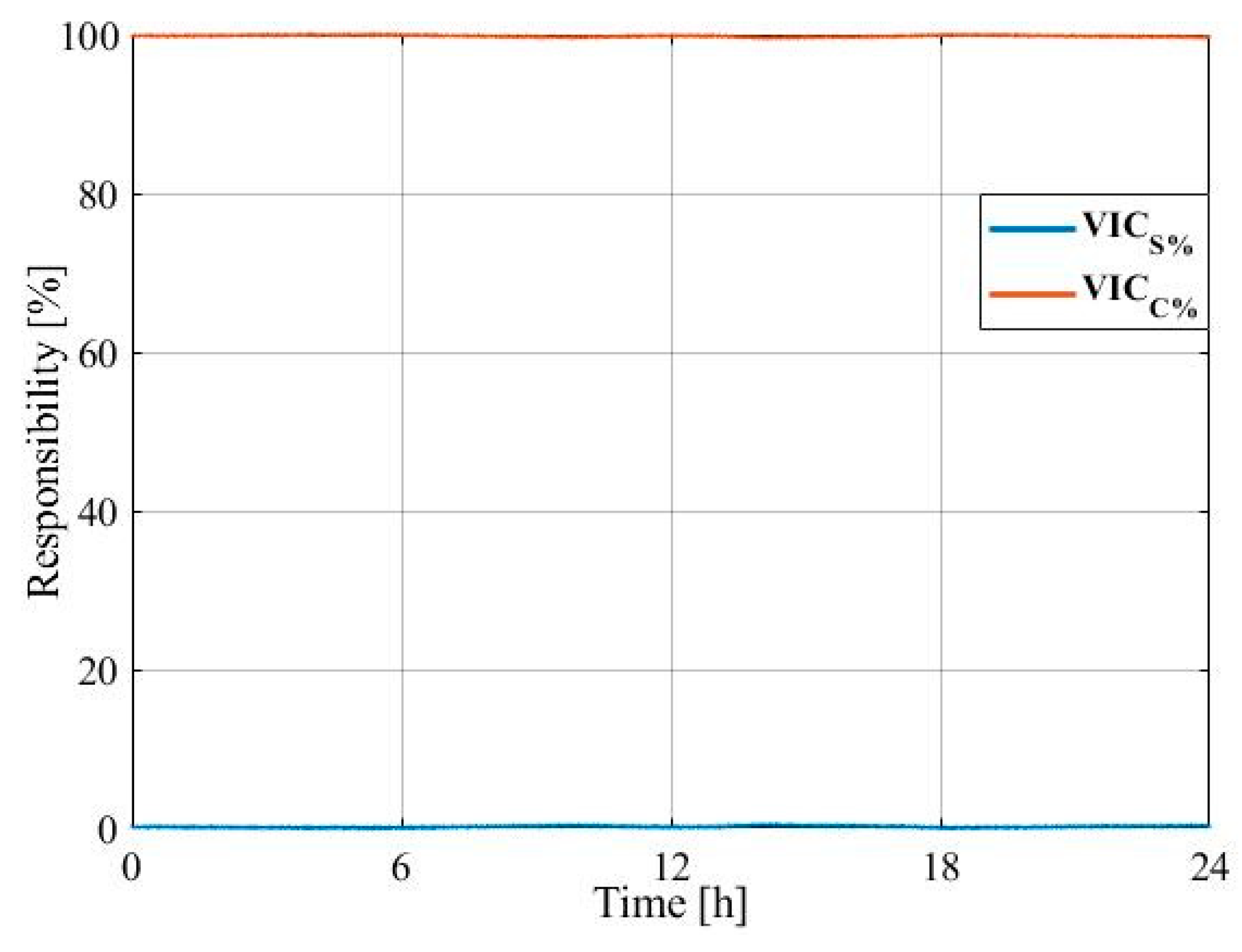
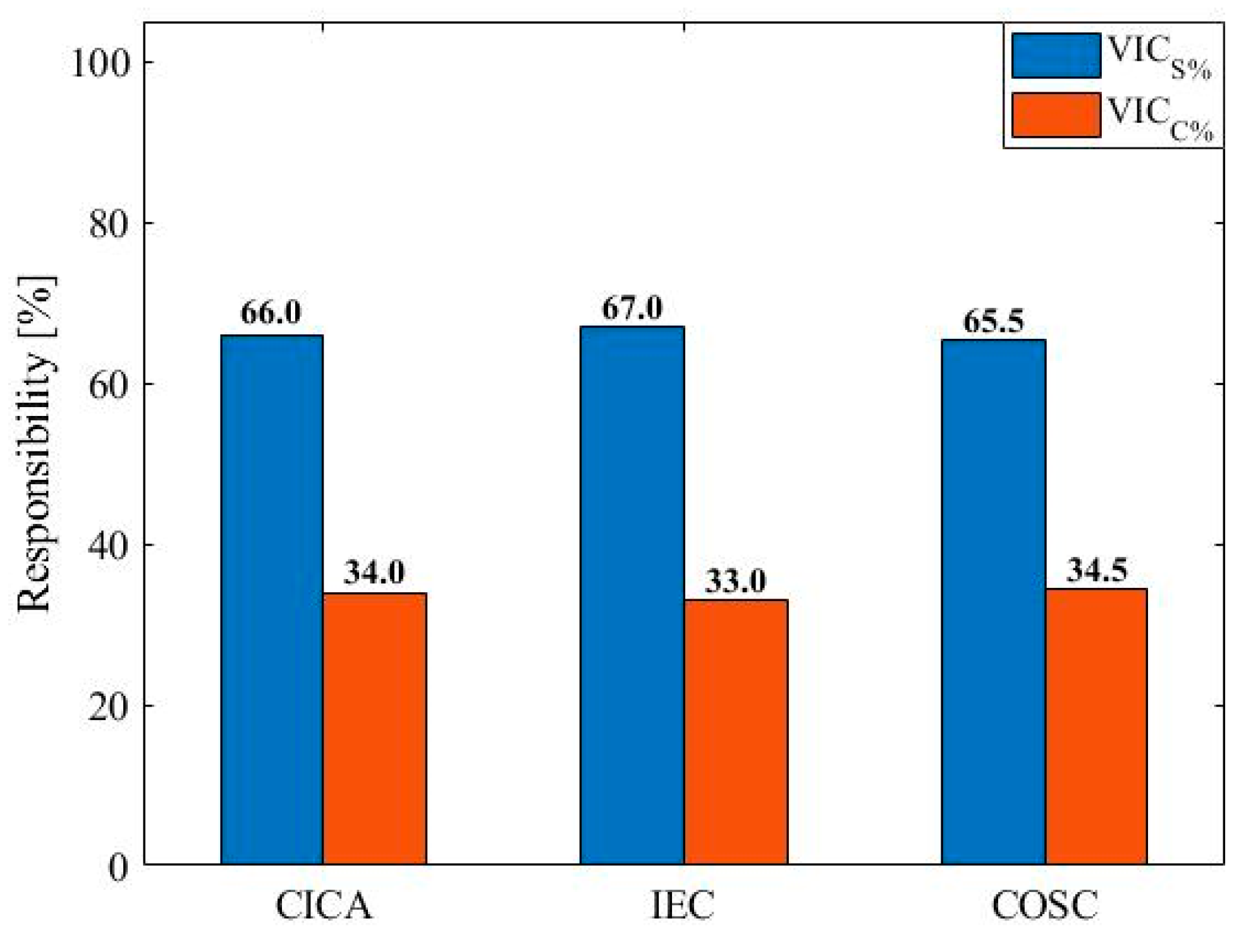
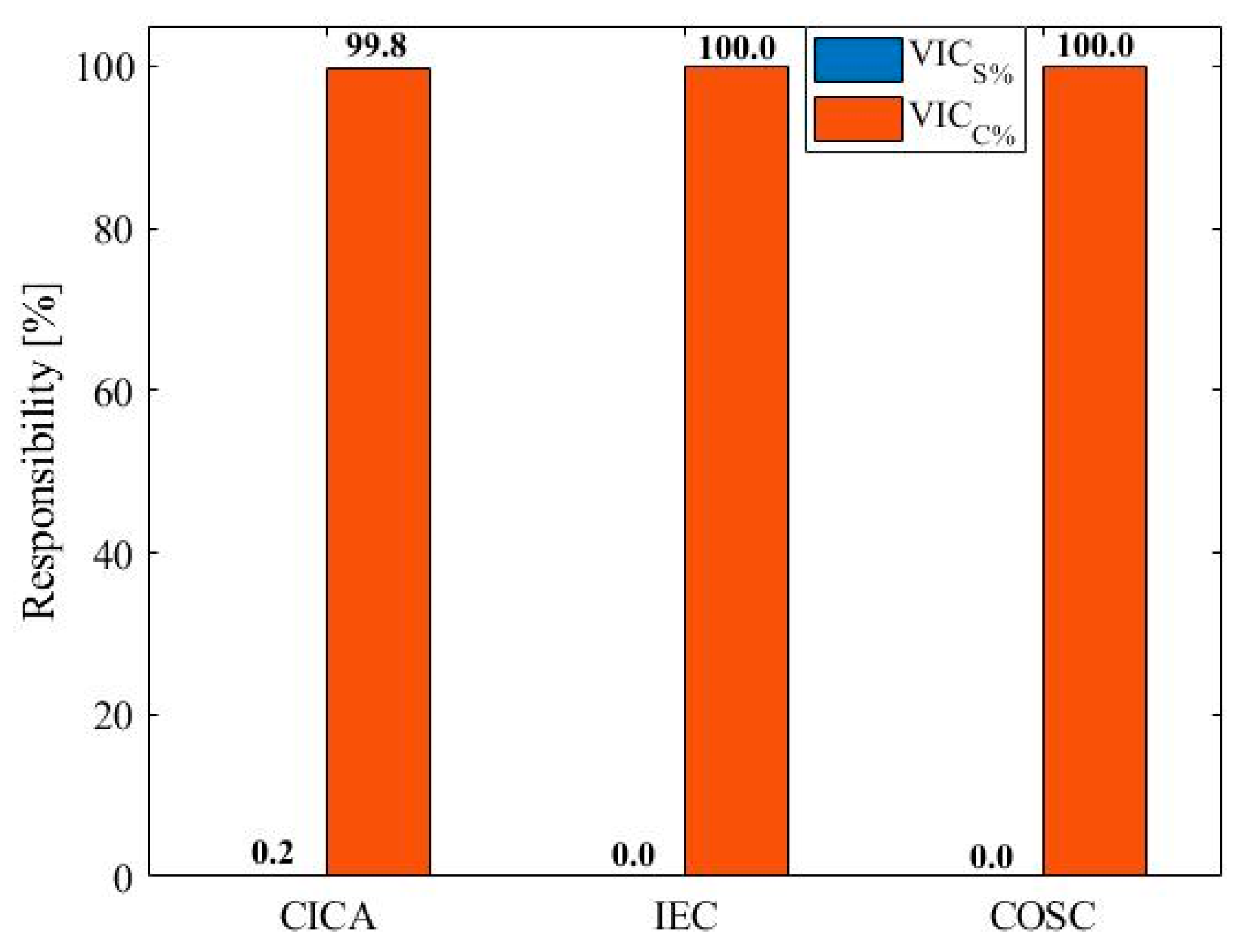
5. Comparative Evaluation of the CICA, IEC, and COSC Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Li, P.; Li, S.; Zhang, L. Contribution Determination for Multiple Unbalanced Sources at the Point of Common Coupling. Energies 2017, 10, 171. [Google Scholar] [CrossRef]
- Li, Y.; Crossley, P.A. Voltage Balancing in Low-Voltage Radial Feeders Using Scott Transformers. IET Gener. Transm. Distrib. 2014, 8, 1489–1498. [Google Scholar] [CrossRef]
- Ciontea, C.I.; Iov, F. A Study of Load Imbalance Influence on Power Quality Assessment for Distribution Networks. Electricity 2021, 2, 5. [Google Scholar] [CrossRef]
- Sayenko, Y.; Kalyuzhniy, D.; Bolgov, V.; Baranenko, T. Evaluating Responsibility for Voltage Unbalance Emission in Three-Phase Three-Wire Networks. In Proceedings of the International Conference on Electrical Power Quality and Utilisation (EPQU), Krakow, Poland, 14–15 September 2020. [Google Scholar] [CrossRef]
- Dadashzade, A.; Aminifar, F.; Davarpanah, M. Unbalanced Source Detection in Power Distribution Networks by Negative Sequence Apparent Powers. IEEE Trans. Power Deliv. 2021, 36, 481–483. [Google Scholar] [CrossRef]
- El-Kharashi, E.; Massoud, J.G.; Al-Ahmar, M.A. The Impact of the Unbalance in Both the Voltage and the Frequency on the Performance of Single and Cascaded Induction Motors. Energy 2019, 181, 561–575. [Google Scholar] [CrossRef]
- Liao, R.-N.; Yang, N.-C. Evaluation of Voltage Imbalance on Low-Voltage Distribution Networks Considering Delta-Connected Distribution Transformers with a Symmetrical NGS. IET Gener. Transm. Distrib. 2018, 12, 1644–1654. [Google Scholar] [CrossRef]
- Nascimento, C.F.; Watanabe, E.H.; Diene, O.; Dietrich, A.B.; Goedtel, A.; Gyselinck, J.J.C.; Dias, R.F.S. Analysis of Noncharacteristic Harmonics Generated by Voltage-Source Converters Operating under Unbalanced Voltage. IEEE Trans. Power Deliv. 2017, 32, 951–961. [Google Scholar] [CrossRef]
- de Paula Silva, S.F.; de Oliveira, J.C. The Sharing of Responsibility between the Supplier and the Consumer for Harmonic Voltage Distortion: A Case Study. Electr. Power Syst. Res. 2008, 78, 1959–1964. [Google Scholar] [CrossRef]
- Jia, Y.; Liu, Y.; Wang, B.; Lu, D.; Lin, Y. Power Network Fault Location with Exact Distributed Parameter Line Model and Sparse Estimation. Electr. Power Syst. Res. 2022, 108137. [Google Scholar] [CrossRef]
- Nagata, E.A.; Ferreira, D.D.; Duque, C.A.; Cequeira, A.S. Voltage Sag and Swell Detection and Segmentation Based on Independent Component Analysis. Electr. Power Syst. Res. 2018, 155, 274–280. [Google Scholar] [CrossRef]
- Stefanidou-Voziki, P.; Sapountzoglou, N.; Raison, B.; Dominguez-Garcia, J.L. A Review of Fault Location and Classification Methods in Distribution Grids. Electr. Power Syst. Res. 2022, 209, 108031. [Google Scholar] [CrossRef]
- Sun, Y.; Li, P.; Wang, Y.; Yin, Z. Determination of the Main Unbalance Sources on PCC in the Distribution System. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 5 October 2015; pp. 1–4. [Google Scholar]
- Arão, L.F.L.; Filho, A.L.F.; Mendonça, M.V.B.; Ferreira Filho, A.L.; Mendonça, M.V.B. Comparative Evaluation of Methods for Attributing Responsibilities Due to Voltage Unbalance. IEEE Trans. Power Deliv. 2016, 31, 743–752. [Google Scholar] [CrossRef]
- Srinivasan, K.; Jutras, R. Conforming and Non-Conforming Current for Attributing Steady State Power Quality Problems. IEEE Trans. Power Deliv. 1998, 13, 212–217. [Google Scholar] [CrossRef]
- Seiphetlho, T.E.; Rens, A.P.J. On the Assessment of Voltage Unbalance. In Proceedings of the ICHQP 14th International Conference on Harmonics and Quality of Power, Bergamo, Italy, 26–29 September 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Neto, A.F.T.; Cunha, G.P.L.; Mendonça, M.V.B.; Filho, A.L.F. A Comparative Evaluation of Methods for Analysis of Propagation of Unbalance in Electric Systems. In Proceedings of the 2012 6th IEEE/PES Transmission and Distribution: Latin America Conference and Exposition, T and D-LA 2012, Montevideo, Uruguay, 3–5 September 2012; pp. 1–8. [Google Scholar] [CrossRef]
- IEC TR 61000-3-13; Electromagnetic Compatibility (EMC)—Part 3.13: Limits—Assessment of Emission Limits for the Connection of Unbalanced Installations to MV, HV and EHV Power Systems. International Electrotechnical Commission: Geneva, Switzerland, 2008.
- Abasi, M.; Ghodratollah Seifossadat, S.; Razaz, M.; Sajad Moosapour, S. Determining the Contribution of Different Effective Factors to Individual Voltage Unbalance Emission in N-Bus Radial Power Systems. Int. J. Electr. Power Energy Syst. 2018, 94, 393–404. [Google Scholar] [CrossRef]
- Jayatunga, U.; Perera, S.; Ciufo, P. Voltage Unbalance Emission Assessment in Radial Power Systems. IEEE Trans. Power Deliv. 2012, 27, 1653–1661. [Google Scholar] [CrossRef]
- Jayatunga, U.; Perera, S.; Ciufo, P.; Agalgaonkar, A.P. Voltage Unbalance Emission Assessment in Interconnected Power Systems. IEEE Trans. Power Deliv. 2013, 28, 2383–2393. [Google Scholar] [CrossRef]
- Sun, Y.; Xie, X.; Li, P. Unbalanced Source Identification at the Point of Evaluation in the Distribution Power Systems. Int. Trans. Electr. Energy Syst. 2018, 28, e2460. [Google Scholar] [CrossRef]
- Jayatunga, U.; Perera, S.; Ciufo, P.; Agalgaonkar, A.P. Deterministic Methodologies for the Quantification of Voltage Unbalance Propagation in Radial and Interconnected Networks. IET Gener. Transm. Distrib. 2015, 9, 1069–1076. [Google Scholar] [CrossRef]
- Gregory, R.C.F. Proposals for Methodologies for Determining Voltage Imbalance Contributions in Three-Phase Electric Systems. Ph.D. Thesis, Federal University of Uberlandia UFU, Uberlândia, Brazil, 2020. [Google Scholar]
- Xu, W.; Liu, Y. A Method for Determining Customer and Utility Harmonic Contributions at the Point of Common Coupling. IEEE Trans. Power Deliv. 2000, 15, 804–811. [Google Scholar] [CrossRef]
- Pereira, F.A.; Silva, S.F.d.P.; Santos, I.N. Blind Source Separation Methods Applied to Evaluate Harmonic Contribution. Int. Trans. Electr. Energy Syst. 2021, 31, e13149. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, H.; Pan, A.; Xu, F. An Improved Complex ICA Based Method for Wind Farm Harmonic Emission Levels Evaluation. Electr. Power Syst. Res. 2020, 179, 106105. [Google Scholar] [CrossRef]
- Xiao, X.; Zheng, X.; Wang, Y.; Xu, S.; Zheng, Z. A Method for Utility Harmonic Impedance Estimation Based on Constrained Complex Independent Component Analysis. Energies 2018, 11, 2247. [Google Scholar] [CrossRef]
- Karimzadeh, F.; Esmaeili, S.; Hosseinian, S.H. Method for Determining Utility and Consumer Harmonic Contributions Based on Complex Independent Component Analysis. IET Gener. Transm. Distrib. 2016, 10, 526–534. [Google Scholar] [CrossRef]
- Karimzadeh, F.; Esmaeili, S.; Hosseinian, S.H. A Novel Method for Noninvasive Estimation of Utility Harmonic Impedance Based on Complex Independent Component Analysis. IEEE Trans. Power Deliv. 2015, 30, 1843–1852. [Google Scholar] [CrossRef]
- Chen, F.; Mao, N.; Wang, Y.; Wang, Y.; Xiao, X. Improved Utility Harmonic Impedance Measurement Based on Robust Independent Component Analysis and Bootstrap Check. IET Gener. Transm. Distrib. 2019, 14, 910–919. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Ma, X. Determining the Responsibility of Three-Phase Unbalanced Sources Based on RICA. Energies 2019, 12, 2849. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Ma, X.; Yao, W.; Wang, H.; Tang, Z. Unbalanced Responsibility Division Considering Renewable Energy Integration. IET Gener. Transm. Distrib. 2020, 14, 5816–5822. [Google Scholar] [CrossRef]
- Novey, M.; Adali, T. Adaptable Nonlinearity for Complex Maximization of Nongaussianity and a Fixed-Point Algorithm. In Proceedings of the 2006 16th IEEE Signal Processing Society Workshop on Machine Learning for Signal Processing IEEE, Maynooth, Ireland, 6–8 September 2006; pp. 79–84. [Google Scholar]
- Gregory, R.C.F.; Scotti, T.M.; Oliveira, J.C. Performance Evaluation of Unbalance Sharing Responsibility Procedures. In Proceedings of the 7th Brazilian Electrical Systems Symposium (SBSE 2018), Rio de Janeiro, Brazil, 12–18 May 2018. [Google Scholar] [CrossRef]
- Gregory, R.C.F.; dos Santos, A.C.; Santos, I.N.; Ran, L.; de Oliveira, J.C. A Practical Approach for Determining Voltage Imbalance Contributions from Suppliers and Consumers. Int. Trans. Electr. Energy Syst. 2020, 30, e12627. [Google Scholar] [CrossRef]
- Kutz, J.N. Data-Driven Modeling and Scientific Computation, 1st ed.; Oxford University Press: New York, NY, USA, 2013. [Google Scholar]
- Niebur, D.; Gursoy, E.; Liao, H. Independent Component Analysis Techniques for Power System Load Estimation. In Applied Mathematics for Restructured Electric Power Systems; Chow, J.H., Wu, F.F., Momoh, J.A., Eds.; Springer: Boston, MA, USA, 2005; pp. 287–317. [Google Scholar]
- Hyvärinen, A.; Karhune, J.; Oja, E. Independent Component Analysis, 1st ed.; John Wiley and Sons Ltd.: New York, NY, USA, 2001. [Google Scholar]
- Hyvärinen, A.; Oja, E. A Fast Fixed-Point Algorithm for Independent Component Analysis. Neural Comput. 1997, 9, 1483–1492. [Google Scholar] [CrossRef]
- Hirst, E.; Kirby, B. Defining Intra and Interhour Load Swings. IEEE Trans. Power Syst. 1998, 13, 1379–1385. [Google Scholar] [CrossRef] [Green Version]
- ONS Hourly Consumption Profile. Available online: http://www.ons.org.br/paginas/resultados-da-operacao/historico-da-operacao/curva_carga_horaria.aspx (accessed on 21 November 2021).
- IEEE Std 1159TM; Recommended Practice for Monitoring Electric Power Quality. Institute of Electrical and Electronics Engineers: New York, NY, USA, 2009.
- Moraes, M.A.; Gregory, R.C.F.; Gianesini, B.M.; Santos, I.N.; de Oliveira, J.C. Comparative Analysis of Methods for Sharing the Responsibility of Voltage Imbalances in Electrical Systems. In Proceedings of the XIV Brazilian Conference on Power Quality, Foz do Iguaçu, Brazil, 29 August–1 September 2021. [Google Scholar]

| Method | Physical Fundaments | Analysis |
|---|---|---|
| Conforming and Non-Conforming Current | The approach shares the negative sequence currents measured in the PCC in components assigned to agents using impedances estimated by the positive sequence. | Since the method considers that the positive and negative sequence impedances are equal, this yields significant inconsistencies. |
| Three-Phase Power Flow | The procedure is based on positive and negative sequence three-phase power measurements. | The method does not allow sharing responsibility for imbalances but only identifies the predominant source. |
| IEC (IEC/TR 61000-3-13) | The proposal includes two measurement steps. A first one with the consumer agent disconnected and a second one with its insertion. | In its physical essence, the method is consistent; however, its practical implementation is unfeasible for most installations in operation. |
| Controlled Operational State Change | The proposition is based on equations of electrical quantities under different and controlled conditions of operation of the electrical network by the successive connection and disconnection of an electrical component with pre-known unbalanced characteristics. | Despite recognizing the satisfactory performance of the method, its application presents as invasive to the operational conditions of the electrical network. This factor presents itself as a restrictive possibility for many installations. |
| Component | Parameters |
|---|---|
| Supply system | |
| Distribution lines L01 and L02 | ; distance L01 = 0.3 km; distance L01 = 0.2 km |
| Transformer TR01 | S = 50 MVA; Vpri. = 138 kV/s = 13.8 kV; Z% = 6% |
| Transformer TR02 | S = 10 MVA; Vpri. = 13.8 kV/s = 4.16 kV; Z% = 7% |
| Transformer TR03 | S = 500 kVA; Vpri. = 13.8 kV/s = 0.38 kV; Z% = 6% |
| Load 01 | |
| If unbalanced: SA = k(7.7 + j1.9)MVA; SB = k(6.8 + j3.0)MVA; | |
| Load 02 | |
| Load 03 | |
| If unbalanced: SA = k(3.3 + j0.8)MVA; SB = k(3.7 + j0.6)MVA; | |
| Load 04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moraes, M.A.; Brito, V.H.F.; de Oliveira, J.C. An Approach for Determining Voltage Imbalance Contributions Based on Complex Independent Component Analysis. Energies 2022, 15, 7014. https://doi.org/10.3390/en15197014
Moraes MA, Brito VHF, de Oliveira JC. An Approach for Determining Voltage Imbalance Contributions Based on Complex Independent Component Analysis. Energies. 2022; 15(19):7014. https://doi.org/10.3390/en15197014
Chicago/Turabian StyleMoraes, Márcio Arvelos, Vinícius Henrique Farias Brito, and José Carlos de Oliveira. 2022. "An Approach for Determining Voltage Imbalance Contributions Based on Complex Independent Component Analysis" Energies 15, no. 19: 7014. https://doi.org/10.3390/en15197014
APA StyleMoraes, M. A., Brito, V. H. F., & de Oliveira, J. C. (2022). An Approach for Determining Voltage Imbalance Contributions Based on Complex Independent Component Analysis. Energies, 15(19), 7014. https://doi.org/10.3390/en15197014







