Type-B Energy Process: Asymmetric Function-Gated Isothermal Electricity Production

Abstract

Recently, we identified two types (A and B) of energy processes that naturally occur on Earth. Type-A energetic process such as the classical heat engines follows well the thermodynamic second law; Type-B energy process follows the first law of thermodynamics, but does not have to be constrained by the second law, owning to its special asymmetric function. The identification of type-B process inspired a novel invention on isothermal electricity production through an asymmetric function-gated power generation system. This article highlights the fundamental embodiments, scientific principles, and physics equations for the asymmetric function-gated isothermal electricity generator that comprises an exceptionally low electron-work-function surface as an isothermal electron emitter and a space gap that permits the isothermally emitted electrons to travel ballistically to a collector. The physics equations for the density of isothermal electricity current, voltage and power all clearly show that the type-B energy technology can isothermally utilize the limitless environmental heat energy to generate electricity power as long as the electron-work function of the emitter $\left[WF\left(e\right)\right]$ is substantially lower than that of the collector $\left[WF\left(c\right)\right]$. It has the potential capability to forever energize many electronic devices such as mobile phones and laptops, which is of great scientific and practical importance.

1. Introduction

The ambient-temperature-associated thermal (heat) energy widely existing in our natural environments is known as the “environmental heat energy” that is the dissipated form of thermal (heat) energy. It is also known as the environmental temperature-dependent molecular thermal motion kinetic energy or latent heat. If the limitless environmental heat energy could be utilized isothermally to do useful work, that would be a giant breakthrough step in helping solve the world’s energy problem of today. In the past for centuries, probably due to some monolithic thinking with the thermodynamic second law, many people believed that one could not utilize the environmental heat energy to do useful work unless there is a temperature gradient. That classic belief is also known as one of the rules for the thermodynamic second law [1,2,3,4]. Recently, our studies with the transmembrane-electrostatically localized protons (TELP) theory [5,6,7,8,9,10,11] surprisingly revealed a “thermotrophic function” that can “isothermally utilize environmental heat energy through TELP at a liquid-membrane interface to help drive ATP synthesis in many biological systems” [12,13,14,15,16,17] including human mitochondria [18]. This has led to an important discovery for the two thermodynamically distinct types (A and B) of energetic processes that are now identified to naturally exist on Earth [19].

Type-A energy processes such as classical heat engines, and many of the known chemical, electrical, and mechanical processes apparently well follow the second law; Type-B energy process as exemplified by the thermotrophic function that does not have to be constrained by the second law, owning to its special asymmetric function [18,19,20]. The discovery of Type-B energy process indicates that there is an entirely new world of physics, chemistry, and biochemistry yet to be fully explored [4].

We all understand that the second law remains still as an incredibly good law. However, it does not necessarily have to be always absolute or universal as implicated also by a number of well-documented independent studies [3,12,21,22,23,24,25,26,27,28,29,30,31,32]. The special type-B process perfectly follows the first law (conservation of mass and energy) of thermodynamics but does not have to obey the thermodynamic second law. In other words, the TELP-associated thermotrophic function as a type-B process clearly represents an example of a natural “second law violation”, since type-B process by its definition is not constrained by the second law, owing to its special asymmetric function [4].

There are many formulations and discussions about the second law of thermodynamics including its challenges and debates that can be found in the literatures [1,33]. Its violability and/or applicability issues are now increasingly recognized by some researchers across the world [27,32,34,35,36,37]. Anyhow, the thermodynamic second law was developed primarily from the Sadi Carnot cycle [38] that “was based on the ideal gas law (nRT = PV; here P is pressure, V is volume and n is the number of moles) where the ideal molecular particles were assumed to have freedoms in a 3-dimensional space (volume) without the consideration of any asymmetric structures”. Furthermore, the TELP [5,6,8,9,10,11,13,17,39] “are on a 2-dimensional membrane surface with asymmetric properties, which is quite different from the assumed 3-dimensional space (volume) system that the second law was based on”. Consequently, as recently pointed out [4], “one must be careful not to mindlessly apply something like the second law derived from a 3-dimensional space (volume) system to a two-dimensional and/or one-dimensional system without looking into the specific facts”.

Furthermore, the thermodynamic-spatial asymmetric features that may be human-made [19,24,40] and/or resulted from the billion years of natural evolution were not considered by the formulation of the second law per se. As recently pointed out [4], “this is another reason that one shall be careful not to apply the second law with monolithic thinking mindlessly or blindly to certain special cases involving asymmetric systems without looking into the specifics”.

That is, the second law can be well applied to the type-A processes such as the classical heat engines, and many of the known chemical, electrical, and mechanical processes where the second law belongs to; The second law should not be blindly applied to type B energy processes owning to their special asymmetric functions [4]. It is important now for our scientific communities to avoid monolithic thinking and keep an open minder to consider the type-B processes and their related phenomena in certain physical, chemical, and/or biological processes especially where asymmetric mechanisms are involved. The scientific communities may well benefit from the new fundamental understanding of type-B processes uncovered in the natural Earth environment. To avoid the blind faith in the second law, the scientific community must pay attention to what this law was really based on and to better understand its limitations that are of great scientific and practical importance.

For a world in which the second law is now known to be not absolute, type-B processes may be created to utilize the limitless environmental thermal energy to do useful work such as generating isothermal electricity to power the modern electricity-based world economy. For example, a novel invention on isothermal electricity for energy renewal (WO 2019/136037 A1) has now been made to generate isothermal electricity by innovatively translating the concept of the asymmetric protonic membrane capacitor-enabled Type-B process into an isothermal electrons-based power generation system, which is now referred as “an asymmetric function-gated isothermal electricity generator system” that could be made into a chip device [29]. Its proof-of-principle experimental data that demonstrated the production of isothermal electricity through a prototype asymmetric function-gated isothermal electricity production system have recently been disclosed with details in the Lee 2019 PCT international patent application publication number WO 2019/136037 A1 [29].

In scientific principles, the asymmetric function-gated isothermal electricity power density could be so surprisingly good that its chip with a size of about 40 cm² “may be sufficient to continuously power a smart mobile phone device forever” [19]. Therefore, the novel type-B energy technologies such as the asymmetric function-gated isothermal electricity production technology [29] may have the potential capabilities for use to permanently power many electric devices, electric motors, machines and vehicles including (but not limited to) mobile phones, laptops, cars, buses, trains, ships, and airplanes utilizing the limitless environmental heat energy alone without requiring any fossil fuel energy [4,19]. Therefore, innovative scientific research and development efforts in mimicking and/or creating of type-B processes [19] to isothermally utilize the endless environmental heat energy [19,24,29,40,41] should be highly encouraged to help “ultimately liberate all peoples from their dependence of fossil fuel energy, thus helping to reduce greenhouse gas CO₂ emissions and control climate change” towards a common shared sustainable future for the humanity on Earth [4].

This article highlights the fundamental embodiments including the scientific principles, physics equations and special features of the novel type-B process invention on isothermal electricity generation for energy renewal (WO 2019/136037 A1) with an isothermal electrons-based power generation system which is now referred as “an asymmetric function-gated isothermal electricity generator system” that could be made into a chip device [29].

2. Results and Discussions on Novel Type-B Energy Invention for Isothermal Electricity Production

As inspired by the type-B energy process identified first as the thermotrophic function mentioned above, a novel invention (Lee 2019 PCT International Patent Application Publication Number WO 2019/136037 A1) was made on the methods for the creation and use of asymmetric function-gated isothermal electricity production systems to achieve energy renewal with “electrons isothermally utilizing environmental heat energy” [29].

2.1. Fundamental Embodiments of a Type-B Energy Process—Asymmetric Function-Gated Isothermal Electricity Generation

This invention (WO 2019/136037 A1) teaches how to make and use an asymmetric electron-function-gated isothermal electricity power generator system. One of its various examples is the asymmetric electron-function-gated isothermal electricity production system 1000 illustrated in Figure 1, which “comprises an asymmetric electron-gating function 1003 across a membrane-like barrier space (gap) 1004 that separates two electric conductors 1001 and 1002 acting as a pair of a thermal electron emitter and an electron collector, two electrically conducting leads 1006 and 1007 connected with each of these electrodes 1001 and 1002 as the two power outlet terminals that may be connected with an electrical load 1008. The barrier space 1004 is preferably a special electric insulator which contains no electric conduction materials (does not conduct electrons through any molecular orbital-associated conduction bands) but allows the thermally emitted electrons to fly through ballistically from the emitter to the collector” [29].

Accordingly, “the barrier space 1004 comprises a vacuum space (gap) that has no electric conductive materials with molecular orbital-associated electric conduction bands but allows the thermally emitted electrons to fly through ballistically. The asymmetric electron-gating function 1003 effectively allows freely emitted thermal electrons 1005 to ballistically fly predominantly from the electric conductor (emitter) 1001 through the barrier space 1004 to the electric conductor (collector) 1002 although the two electric conductors 1001 and 1002 are under the same temperature and pressure conditions. Since the barrier space 1004 is an electrical insulating space without the conventional conductor-based electrical conduction but has a unique property that allows thermal electrons to fly through ballistically, it prevents the excess thermal electrons captured by the collector 1002 from conducting back to the emitter except the minimal back emission from the collector that may be controlled by the asymmetric electron-gating function 1003. As a result, the excess thermal electrons captured by the collector 1002 may accumulate and electrostatically distribute themselves mostly to the collector 1002 electrode surface. Similarly, the excess positive charges (“holes”) left in the emitter may also accumulate and electrostatically distribute themselves mostly to the emitter 1001 electrode surface. This results in the creation of an electric voltage potential difference across the barrier space 1004 between the emitter electrode 1001 and the collector electrode 1102, in a manner that is analogous to the creation of a transmembrane potential (voltage difference, $\Delta \psi$) in the protonic bioenergetics systems” [9,11,18,19,20,29].

Note, in the cases of TELP [9,11,18,19,20], when a protonic load circuit with an F₀F₁-ATP synthase protonic channel as a load is given, “the excess protons typically flow through the ATP synthase protonic channel across the membrane to perform useful work in driving ATP synthesis”. Analogously, “when an external electric load circuit is connected between the emitter and the collector, the excess electrons in the collector will flow through the external load circuit back to the emitter. Consequently, the excess electrons in the collector electrode here will pass through an external circuit comprising an electrically conducting lead as an electric outlet 1007 (−) and an electrical load 1008 connected with another wire as electric outlet 1007 (+) back to the emitter 1001 (Figure 1). By doing so, a portion of the environmental heat energy associated with the ambient-temperature thermal electrons is utilized to perform work through use of the electrical load 1008” [29].

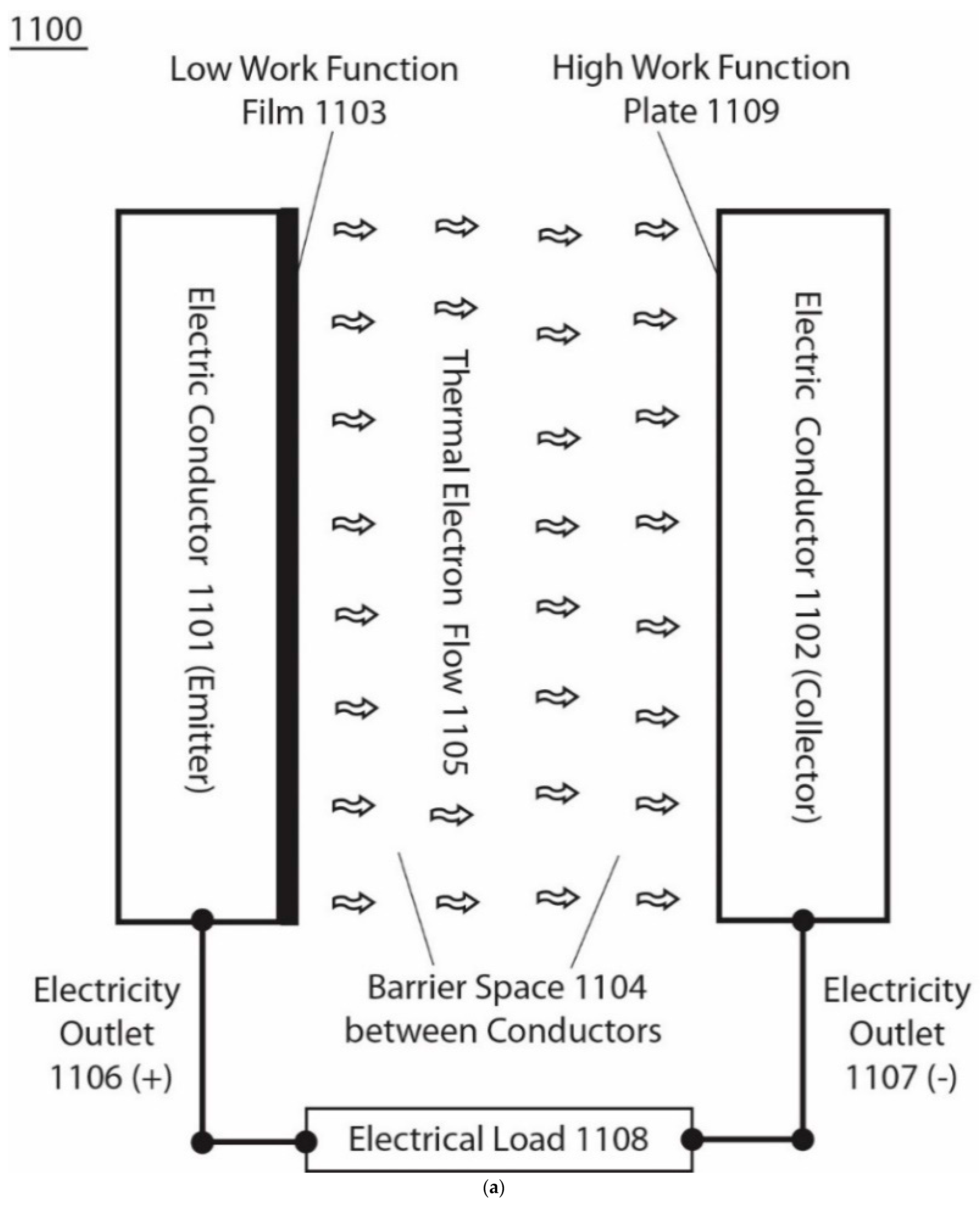
Figure 2a illustrates “a basic unit of an asymmetric function-gated isothermal electron power generator system 1100 comprising a barrier space 1104 such as a vacuum space gap that separates a pair of electric conductors 1101 and 1102: one of them has a low work function film 1103 surface and the other has a high work function plate 1109 surface. The surface film 1103 is made of a low work function material such as an Ag-O-Cs film surface that has an electron work function as low as about 0.7 eV to serve as the emitter. The barrier space 1104 is a special electric insulator space such as a space gap that does not conduct electricity by the conventional electric conduction but allow free thermal electrons 1105 to fly through ballistically. Use of such barrier space 1104 and low work function surface film 1103 enables significant amounts of the ambient temperature thermal electrons to emit from the film surface into the barrier space 1104 and fly ballistically towards the collector that is a high work function plate 1109 such as a copper plate which has an electron work function as high as about 4.6 eV. At ambient environmental temperature around 298 K, such a high work function plate 1109 practically has nearly zero emission of thermal electrons from its surface whereas it can accept the thermal electrons flying through the barrier space from the emitter 1101” [29].

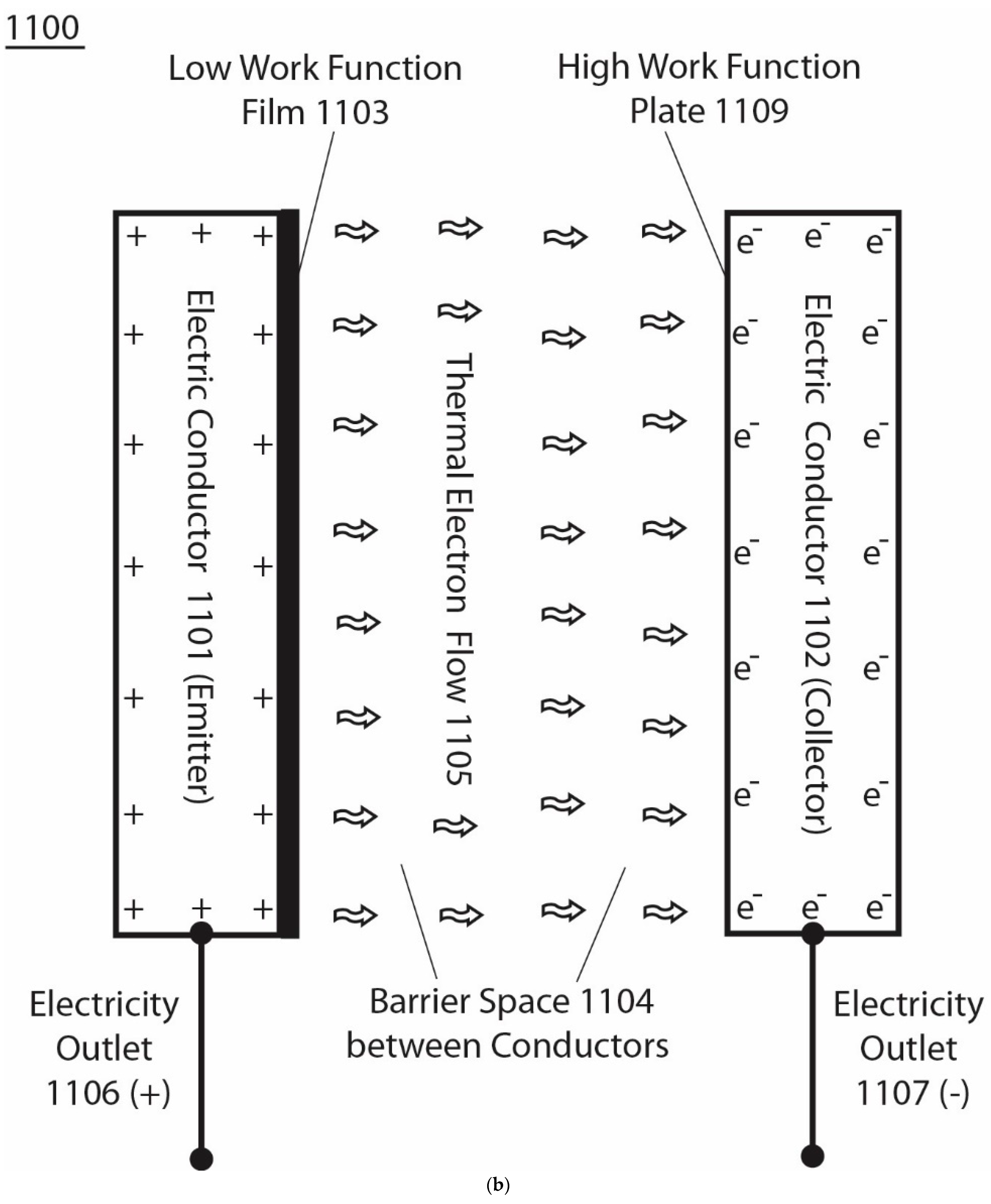
After the thermal electrons 1105 from the emitter 1101 flowing ballistically across the barrier space arrive at the collector 1102, they as “excess electrons will electrostatically repel each other and spread around the electric conductor 1102 (collector) surface” as shown in Figure 2b, which is “quite similar to the behavior of the excess protons in a proton-conductive water body” (WO2017/007762 A1 and US 2017/0009357 A1). Meanwhile, “the excess holes (positive charges) left at the emitter will also electrostatically spread around the electrode 1101 (emitter) surface (Figure 2b). As a result, this creates a voltage difference between the emitter 1101 and the collector 1102. Use of this voltage difference through the terminals of electricity outlets 1107 (−) and 1106 (+) can drive an electric current through the load resistance (such as an electric resistor) 1108 to do electric work as shown in Figure 2a. This conductive flow of electrons through the external load wire, better known as electricity, can continue as the excess electrons flow conductively through the external circuit back to the emitter where they will get re-emitted again for the next cycle etc. after gaining thermal motion kinetic energy from the environmental heat of the surrounding environment. This explains how the asymmetric function-gated system 1100 can isothermally generate electricity by isothermally utilizing heat energy from the environment” [29].

As mentioned above, this phenomenon (Figure 2b) is fundamentally “analogous to that of the excess protons in a water body separated by a membrane barrier with excess hydroxyl anions at the other side of the membrane” (WO2017/007762 A1 and US 2017/0009357 A1). Analogously, it is the excess electron population density ${\left[e_L^{-}\right]}^0$ accumulation at the collector electrode surface resulted from the activity of the asymmetric function-gated isothermal electricity generation system across the emitter and the collector that builds the output voltage $V_{output}$ which is defined as the electrical voltage potential difference between the emitter electrode and the collector electrode in isothermal electricity production. Consequently, the isothermal electricity output voltage $V_{output}$ under the “open circuit” conditions can be expressed as a function of the ideal effective concentration of the electrostatically localized excess electrons ${\left[e_L^{-}\right]}^0$ at the collector electrode surface using the following equation:

$$V_{output}=\frac{\mathrm{F}\cdot d\cdot l\cdot {\left[e_L^{-}\right]}^0}{\mathsf{\kappa }\cdot {\mathsf{\epsilon }}_{\mathrm{o}}}$$

(1)

where F is the Faraday constant; d is the barrier space thickness that is the distance between the emitter and the collector; κ is the barrier space dielectric constant; ε_o is the vacuum permittivity; and l is the localized excess electron layer thickness.

This equation (Equation (1)) mathematically explains how the accumulation of excess electron population density ${\left[e_L^{-}\right]}^0$ as a result from the capturing of thermally emitted electrons from the emitter by the collector can build the isothermal electricity output voltage $V_{output}$. Consequently, the excess electrons in the collector with such an output voltage $V_{output}$ can drive an electric current through an external circuit, which comprises an electric outlet 1107 (−) wire connected with an electrical load 1108 that is connected with another electric wire as electric outlet 1106 (+) back to the emitter 1101 as shown in Figure 2a. By doing so, a portion of the environmental heat energy (thermal motion energy) associated with the thermal electrons is utilized to perform useful work through the use of an electrical load 1108.

2.2. Energy Diagrams of Asymmetric Electron-Work-Function-Gated Isothermal Electricity Production Systems

According to one of the various embodiments, it is “a preferred practice” to ground the emitter with an Earth ground 1110 at the electricity outlet 1106 (+) terminal as shown in Figure 2c to prevent the accumulation of positive charges there. This is exaplained below through Figure 3 with the energy diagrams of the asymmetric electron-work-function-gated isothermal electricity production system.

Figure 3 presents the energy diagrams of the asymmetric electron-work-function-gated isothermal electricity production system 1100 (Figure 2). As shown in Figure 3a (left), the electron work function (WF(e)) of the emitter 1101 (Figure 2a) is the energy level difference between the Fermi energy level (E(F, e)) of the emitter and the vacuum energy level (E(vacuum, ∞) of a free electron that is considered “infinitely” (∞) far away from the emitter and collector surfaces; while the electron work function (WF(c)) of the collector 1102 is the difference between the collector’s Fermi energy level (E(F, c)) and the vacuum energy level (E(vacuum, ∞). As mentioned before, it is a preferred practice to employ an emitter with an electron work function as low as possible such as about 0.7 eV so that substantial amounts of the “ambient temperature thermal electrons” can self-emit from the emitter surface into the vacuum barrier space 1104 and fly ballistically with kinetic energy (E(k)) towards the collector 1109 that has an electron work function (WF(c)) much larger than that of the emitter (WF(e)). On the other hand, essentially no “ambient-temperature thermal electrons” can emit from the high work function collector surface into the vacuum barrier space 1104 since the electron work function of the collector (WF(c)) is so big (for example, above 3.0 eV) that the ambient-temperature thermal electrons are practically not able to escape from the collector surface. Consequently, there are statistically many more thermal electrons 1105 flying from the emitter 1101 into the collector 1102 than that in the opposite direction. After the emitted electrons arriving at the collector 1102, they will thermally equilibrate with the environment and electrostatically result in the creation of a voltage at the collector (V(c)) as expressed in Equation (1) that can drive an electric current through an external electric load 1108 back to the emitter 1101. This completes a cycle of the asymmetric electron-work-function-gated thermal electricity generation process and gets ready for the next cycles of thermal electron emission and collection as shown in Figure 2a.

When the asymmetric electron-work-function-gated isothermal electricity production system 1100 is under its “open circuit” condition (such as when the electric load 1108 is removed) as shown in Figure 2b, the activity of the asymmetric electron-work-function-gated thermal electron power generation process will result in the accumulation of excess electrons in the collector thus generating a negative voltage V(c) there; Meanwhile, this may also result in the accumulation of excess positive charges at the emitter thus generating a positive voltage V(e) there. The negative voltage V(c) at the collector will push up its effective Fermi level by the absolute value of V(c) to that of E(F, c) minus the negative voltage V(c) (labeled as “E(F, c) − V(c)” in the 1100 (b) of Figure 3); whereas the positive voltage V(e) at the emitter will push down its effective Fermi level to a lower level of (E(F, e) − V(e)) as shown in the 1100 (b) of Figure 3 (middle). Consequently, under the “open circuit” condition, the effective electron-work function of the emitter at the equilibrated state (WF(e)eq) is increased by the product e·V(e) of the electron charge e and the emitter voltage V(e) to a higher value (WF(e) + e·V(e)) while the effective work function of the collector (WF(c)eq) is decreased by the absolute value of e·V(c) to a lower (smaller) value (WF(c) + e·V(c)). The larger (higher) effective electron-work function of the emitter (WF(e) + e·V(e)) will reduce and eventually pretty much cut off the ambient-temperature electron emission at the emitter 1101 and consequently the accumulation of positive charges at the emitter will then stop, resulting in an equilibrated value of V(e) as shown in Figure 3b (middle, 1100(b)).

This explains why it is “a preferred practice” to ground the emitter with an Earth ground 1110 at the electricity outlet 1106 (+) terminal as shown in Figure 2c to prevent the accumulation of positive charges there. When the emitter is “Earth grounded” (V(e) = 0), the effective electron-work function of the emitter will be retained at the initial value of WF(e) even when the 1100 system is under the “open circuit” condition. In this way, the ambient-temperature electron emission at the emitter 1101 will continue until the effective Fermi level of the collector (E(F, c) − V(c)) will rise so much by the absolute value of V(c) that will match at the same level of the emitter E(F, e) with WF(e) as shown in the 1100(c) of Figure 3 (right). At this point, the back emission flow of the ambient-temperature electrons from the collector 1102 to the emitter 1101 will cancel the flow of the ambient-temperature electrons from the emitter 1101 to the collector 1102 at an equal rate. In this case, at its equilibrium state, V(c) will equal to the difference between the collector electron-work function WF(c) and emitter electron-work function WF(e) over the electronic unit charge (e for an electron e⁻).

2.3. Physical Equations for Isothermal Electricity Current, Voltage and Power Density

The asymmetric electron-work-function-gated thermal electricity power production system 1100 as illustrated in Figure 2 and Figure 3 “operates isothermally where the temperature at the emitter ($T_e$) equals to that of the collector ($T_c$). Under the isothermal operating conditions ($T=T_e=T_c)$, the ideal net flow density (flux) of the emitted electrons 1105 from the emitter 1101 to the collector 1102, which is defined also as the ideal isothermal electron flux ($J_{isoT}$) normal to the surfaces of the emitter and collector (also named as the ideal isothermal electricity current density defined as amps (A) per square centimeters of the cross-section area of the emitter-collector interelectrode space), can be calculated based on the Richardson-Dushman formulation using the following ideal isothermal current density ($J_{isoT}$) equation”:

$$J_{isoT}=A{T}^2(e^{-\left[WF\left(e\right)+e · V\left(e\right)\right]/kT} - e^{-\left[WF\left(c\right)+e · V\left(c\right)\right]/kT})$$

(2)

where “$A$ is the universal factor (as known as the Richardson-Dushman constant) can be expressed as $\frac{4\pi me{k}^2}{h^3}\approx 120 \mathrm{Amp}/\left({\mathrm{K}}^2·{\mathrm{cm}}^2\right)$ [where $m$ is the electron mass, $e$ is the electron unit charge,$k$ is the Boltzmann constant and $h$ is Planck constant]. $T$ is the absolute temperature in Kelvin (K) for both the emitter and the collector; $WF\left(e\right)$ is the electron-work function of the emitter surface; the term of $e·V\left(e\right)$ is the product of the electron unit charge $e$ and the voltage $V\left(e\right)$ at the emitter; $k$ is the Boltzmann constant in eV/K unit; $WF\left(c\right)$ is the electron-work function of the collector surface; and $e·V\left(c\right)$ is the product of the electron unit charge $e$ and the voltage $V\left(c\right)$ at the collector” [29].

Its key feature is the conversion of environmental heat energy isothermally (at the same temperature T as shown in Equation (2) to electrical power without the need for an external energy-consuming heater or an exhaust, heat sink or the like. Consequently, its energy efficiency as a type-B energetic process is essentially 100% without being constrained by the thermodynamic second law [29].

According to the invention (WO 2019/136037 A1), “when the voltage at the emitter (V(e)) is zero such as when the emitter is grounded, the ideal net isothermal electrons flow density across the vacuum space from the emitter 1101 to the collector 1102 can be calculated using the following modified ideal isothermal electricity current density ($J_{isoT\left(gnd\right)}$) equation”:

$$J_{isoT\left(gnd\right)}=A{T}^2(e^{-\left[WF\left(e\right)\right]/kT} - e^{-\left[WF\left(c\right)+e · V\left(c\right)\right]/kT})$$

(3)

When the voltage at both the emitter (V(e)) and the collector (V(c)) are zero such as at the initial state of an isothermal electricity generation system 1100 as illustrated in Figure 2a (or if/when the resistance of the circuit including the load 1108 and associated wire, electrodes and connection terminals 1106 and 1107, is zero), the maximum net isothermal electron flow density “across the vacuum space from the emitter 1101 to the collector 1102” reaches the highest attainable, which is regarded as the “saturation” (upper limit) flux after the effects of any negative space charge and other limiting factors are all eliminated. This ideal saturation electron flux can be calculated using the following ideal saturation isothermal electricity current density ($J_{isoT\left(sat\right)}$) equation:

$$J_{isoT\left(sat\right)}=A{T}^2(e^{-\left[WF\left(e\right)\right]/kT} - e^{-\left[WF\left(c\right)\right]/kT})$$

(4)

This isothermal current density ($J_{isoT\left(sat\right)}$) equation (Equation (4)) clearly shows that it can physically generate isothermal electricity as long as the electron work function $\left[WF\left(e\right)\right]$ of the emitter is substantially lower than that of the collector$\left[WF\left(c\right)\right]$.

Accordingly, the “open circuit” ideal saturation output voltage ($V_{sat}$) at the equilibrium between the emitter and collector terminals (1106 and 1107) as shown in Figure 2c can be expressed as the difference in the electron work functions:

$$V_{sat}=\frac{W{F}_{\left(c\right)}-W{F}_{\left(e\right)}}{e}$$

(5)

where $e$ is the electron charge which is 1 (an electron charge unit); and $W{F}_{\left(c\right)}$ and $W{F}_{\left(e\right)}$ are the collector work function and the emitter work function, respectively, as illustrated in the 1100 (c) of Figure 3 (right).

The steady-state operating output voltage ($V_{st}$) between the emitter and collector terminals (1106 and 1107) can be expressed as:

$$V_{st}=V_{\left(c\right)}-V_{\left(e\right)}$$

(6)

where $V_{\left(c\right)}$ and $V_{\left(e\right)}$ are the steady-state operating voltages at the collector and emitter, respectively, as illustrated in the 1100 (b) of Figure 3 (middle).

The ideal saturation electrical current ($I_{sat}$) across the inter electrode space between the emitter and collector as shown in Figure 2a can be expressed as the product of the inter electrode space cross section (emitter surface) area ($S$) and the ideal saturation isothermal electron flux as known as the saturation current density ($J_{isoT\left(sat\right)}$) with the following equation:

$$I_{sat}=S.J_{isoT\left(sat\right)}=S.A{T}^2(e^{-\left[WF\left(e\right)\right]/kT} - e^{-\left[WF\left(c\right)\right]/kT})$$

(7)

This isothermal current ($I_{sat}$) equation (Equation (7)) clearly shows that there can be isothermal electricity current as long as the electron-work function $\left[WF\left(e\right)\right]$ of the emitter is substantially lower than that $\left[WF\left(c\right)\right]$ of the collector.

Accordingly, the ideal steady-state operating electrical current ($I_{st}$) through the electrical load 1108 as shown in Figure 2a can be expressed as:

$$I_{st}= \frac{R_l+R_m}{V_{st}}$$

(8)

where $R_l$ is the resistance of the electrical load and $R_m$ is any possible miscellaneous resistance from the circuit including the electrodes and wire materials; $V_{st}$ is the steady-state operating output voltage as of Equation (6).

The effect of the asymmetric function-gated isothermal electricity generating activity is additive. That is, the asymmetric electron-work-function-gated isothermal electricity production systems like the one shown in Figure 2 can be used in series and/or in parallel. When a plurality (n) of the asymmetric electron-work-function-gated isothermal electricity production systems like the one shown in Figure 2 are used in the series, the total steady-state output voltage ($V_{\mathrm{st}\left(total\right)}$) is the summation of the steady-state output voltages ($V_{st \left(i\right)}$ as of Equation (6) from each of the asymmetric electron-work-function-gated isothermal electricity production systems:

$$V_{\mathrm{st}\left(total\right)}={\displaystyle \sum }_{i=1}^n{V}_{st \left(i\right)}={\displaystyle \sum }_{i=1}^n\left(V_{\left(c\right)i}-V_{\left(e\right)i}\right)$$

(9)

Similarly, the total saturation output voltage ($V_{\mathrm{sat}\left(total\right)}$) is the summation of the saturation output voltages ($V_{sat \left(i\right)}$ as of Equation (5)) from each of the asymmetric electron-work-function-gated isothermal electricity production systems operating in series:

$$V_{\mathrm{sat}\left(total\right)}={\displaystyle \sum }_{i=1}^n{V}_{sat \left(i\right)}={\displaystyle \sum }_{i=1}^n\left(\frac{ W{F}_{\left(c\right)i}-W{F}_{\left(e\right)i}}{e}\right)$$

(10)

When pluralities (n) of the asymmetric electron-work-function-gated isothermal electricity production systems are used in the parallel, the total ideal electrical current ($I_{\mathrm{sat}\left(total\right)}$) is the summation of the ideal electrical current ($I_{\mathrm{sat}\left(i\right)}$ as of Equation (7)) from each of the asymmetric electron-work-function-gated isothermal electricity production systems:

$$I_{\mathrm{sat}\left(total\right)}={\displaystyle \sum }_{i=1}^n{I}_{\mathrm{sat}\left(i\right)}$$

(11)

Therefore, the asymmetric electron-work-function-gated isothermal electricity production is additive. Pluralities (n) of the asymmetric electron-work-function-gated isothermal electricity production systems may be used in parallel and/or in series, depending on a given specific application and its associated operating conditions such as temperature conditions, and the properties of the barrier spaces such as their thickness and compositions, the properties of the emitter and collector electrodes and other physical chemistry properties.

When a plurality (n) of the asymmetric electron-work-function-gated isothermal electricity production systems operate in parallel, the total steady-state electrical current ($I_{\mathrm{st}\left(total\right)}$) is the summation of the steady-state electrical current ($I_{\mathrm{st}\left(i\right)}$) from each of the asymmetric electron-work-function-gated isothermal electricity production systems while the total steady-state output voltage ($V_{\mathrm{st}\left(total\right)}$) remains the same.

When a plurality (n) of the asymmetric electron-work-function-gated isothermal electricity production systems operate in series, the total steady-state output voltage ($V_{\mathrm{st}\left(total\right)}$) is the summation of the steady-state output voltages ($V_{st \left(i\right)}$) from each of the asymmetric electron-work-function-gated isothermal electricity generation systems while the total steady-state electrical current ($I_{\mathrm{st}\left(total\right)}$) remains the same.

2.4. Examples of Isothermal Electricity Production Systems

Figure 4 presents an example of a prototype for an isothermal electricity production system 1400A that has a pair of an emitter (electron-work function 0.7 eV) and a collector (electron-work function 4.36 eV) installed in a vacuum tube chamber. As illustrated in Figure 4, the system 1400A comprises a thin layer of low electron-work function Ag-O-Cs film 1403 coated on the right side surface of electric conductor plate 1401 to serve as the emitter, a vacuum space gap 1404 allowing the thermal electron flow 1405 to pass through ballistically between the emitter and collector, a high electron-work function Mo film/plate 1439 coated on the left side surface of the second electric conductor plate 1432 facing the emitter 1403 to serve as the collector, a vacuum tube wall 1450 that is in contact with the edges of the electric conductor plates 1401 and 1432 to allow environmental heat to transfer between the tube wall and the electric conductor plates 1401 (emitter) and 1432 (collector), a first electricity outlet 1406 connected with the first electric conductor plate 1401, an second electricity outlet 1477 connected with the second electric conductor plate 1432, a capacitor 1461 that is connected in between the two electricity outlets 1406 and 1477, and an Earth ground 1410 that is connected with the first electricity outlet 1406.

As illustrated in Figure 4, the effective heat-conduction contact of vacuum tube wall 1450 with the edges of the two electric conductor plates 1401 and 1432 in the system 1400A allow efficient transfer of environmental heat from the tube wall to both the emitter and collector system. Furthermore, the use of Earth ground 1410 and capacitor 1461 with the electricity outlets 1406 and 1477 provides more stable system performance for isothermal electricity generation and output delivery.

The electron work function of Mo film is about 4.36 eV and the electron work function of Ag-O-Cs film can be made to be anywhere between 0.5 and 1.2 eV. In the example with the isothermal electricity generator system 1400A, the electron work function of Ag-O-Cs film was selected to be 0.7 eV for use as the emitter while the work function of Mo film was 4.36 eV for use as the collector as illustrated in Figure 4. Accordingly, when the isothermal electricity is outputted through the outlet terminals 1406 and 1477, the steady-state operating output voltage can typically be about 3.5 V in this case. Its saturation isothermal electricity current density (at output voltage of 3.5 V) is 1.55 × 10⁻⁵ (A/cm²) at the standard ambient temperature of 298 K (25 °C). The characteristic pattern of the ideal isothermal electricity current density (A/cm²) as a function of operating temperature T at various output voltage V(c) for this system is also similar to that of the system with a pair of emitter electron-work function (0.70 eV) and collector electron-work function (4.56 eV, copper Cu(110)).

Figure 5 presents an example of a prototype for an integrated isothermal electricity production system 1400C that has three pairs of emitters (electron-work function 0.7 eV) and collectors (electron-work function 4.36 eV) installed in a vacuum tube. As illustrated in Figure 5, the system 1400 comprises: a thin layer of low electron-work function (0.7 eV) Ag-O-Cs film 1403 coated on the first electric conductor plate 1401 right side surface to serve as the first emitter; a first vacuum space gap 1404 allowing the thermal electron flow 1405 to pass through ballistically between the first pair of emitter and collector; a (high electron-work function of 4.36 eV) Mo film/plate 1409 coated on the second electric conductor plate 1402 left side surface facing the first emitter to serve as the first collector; a thin layer of low electron-work function (0.7 eV) Ag-O-Cs film 1423 coated on a second electric conductor plate 1402 right side surface to serve as the second emitter; a second vacuum space gap 1424 allowing the thermal electron flow 1425 to pass through ballistically between the second pair of emitter and collector; a (high electron-work function 4.36 eV) Mo film/plate 1429 coated on a third electric conductor plate 1421 left side surface facing the second emitter to serve as the second collector; a thin layer of low electron-work function (0.7 eV) Ag-O-Cs film 1433 coated on a third electric conductor plate 1421 right side surface to serve as the third emitter; a third vacuum space gap 1434 allowing the thermal electron flow 1435 to pass through ballistically between the third pair of emitter and collector; a (work function 4.36 eV) Mo film/plate 1439 coated on a fourth electric conductor plate 1432 left side surface facing the third emitter to serve as the terminal collector; a vacuum tube wall 1450 that is in contact with the edges of the electric conductor plates 1401, 1402, 1421 and 1432 to allow environmental heat to transfer from the tube wall to the electric conductor plates 1401 (emitter), 1402 (collector/emitter), 1421 (collector/emitter) and 1432 (collector); a first electricity outlet 1406 connected with the first electric conductor plate 1401; a second electricity outlet 1476 connected with the second electric conductor plate 1402; a third electricity outlet 1477 connected with the fourth electric conductor plate 1432; a first capacitor 1461 that is connected in between the first and second electric conductor plates 1401 and 1402; a second capacitor 1462 that is connected in between the second and third electric conductor plates 1402 and 1421; a third capacitor 1463 that is connected in between the third electric conductor plate 1421 and the fourth electric conductor plate 1432; and an Earth ground 1410 that is connected with the first electric conductor plates 1401.

As illustrated in Figure 5, the isothermal electricity in this example can be outputted for delivery through outlet terminals 1406 and 1476 or 1477 depending on the specific output power needs. When the isothermal electricity is outputted through outlet terminals 1406 and 1476 across a pair of emitter and collector, the steady-state operating output voltage equals to V(c), which typically can be around 3.5 V depending on the system operating conditions including the load impedance and the difference in electron-work function between the emitter and the collector. The saturation isothermal electricity current density (at output voltage of 7 V) is about 1.55 × 10⁻⁵ (A/cm²) at the standard ambient temperature of 298 K (25 °C).

When the isothermal electricity is outputted through outlet terminals 1406 and 1477 across three pairs of emitters and collectors, according to Equation (9), the steady-state operating output voltage typically can be as high as about 10.5 V. However, the total saturation isothermal electricity current density (at output voltage of 10.5 V) remains to be about 1.55 × 10⁻⁵ (A/cm²) at the standard ambient temperature of 298 K (25 °C).

More importantly, when the isothermal electricity is outputted through the outlet terminals1476 and 1477, the activity of the first emitter (1401 with Ag-O-Cs film 1403) and the first collector (Mo film/plate 1409) can be used to generate a V(c) of about 3.5 V to serve as a bias voltage for the second emitter (Ag-O-Cs film 1423) on the surface of the second conductor plate 1402. In this way, the second emitter (Ag-O-Cs film 1423) will more readily emit thermal electrons towards the second collector (Mo film/plate 1429) of the third conductor plate 1421. Subsequently, the enhanced generation of V(c) at the third collector 1429 of the third conductor plate 1421 can serve as a bias voltage for the third emitter to more readily emit thermal electrons towards the terminal collector 1439 at the fourth conductor plate 1432. Therefore, use of this customized feature can help better extract environmental heat energy especially when the operating environmental temperature is relatively low or when the electron-work function of certain emitters alone may not be entirely low enough to function effectively. When the isothermal electricity is outputted through the outlet terminals 1476 and 1477, the steady-state operating output voltage can typically be about 7 V according to Equation (9). The total saturation isothermal electricity current density (at output voltage of 7 V) remains to be about 1.55 × 10⁻⁵ (A/cm²) at the standard ambient temperature of 298 K (25 °C).

According to the invention (WO 2019/136037 A1), the system capacitance for a pair of parallel emitter and collector plates is inversely dependent on their separation distance (d). It is a preferred practice to increase the capacitance across each pair of emitter and collector by properly narrowing the space separation distance (d) between the emitter surface and the collector surface to a selected space gap size in a range from as big as 100 mm to as small as in a micrometer and/or sub-micrometer scale based on specific application and operation conditions. In this way, the need of using external capacitors may be eliminated. Furthermore, use of a narrow (micrometer and/or sub-micrometer) space gap between the emitter and the collector may also help to limit the formation of the static electron space-charge clouds in the inter electrode space for better system performance.

Figure 6 presents an integrated isothermal electricity production system 1500 that comprises a narrow inter electrode space gap size (separation distance d) for each of the three pairs of emitters and collectors installed in a vacuum tube chamber set up vertically. The system 1500 (Figure 6) has the following components installed in a vacuum tube chamber from its top to bottom: a LWF (low work function) film 1503 coated on the first electric conductor plate 1501 bottom surface to serve as the first emitter, a first narrow space gap 1504 allowing thermally emitted electrons 1505 to flow through ballistically between the first pair of emitter and collector, a HWF (high work function) film 1509 coated on the second electric conductor 1502 top surface to serve as the first collector, a LWF film 1523 coated on the second electric conductor 1502 bottom surface to serve as the second emitter, a second narrow space gap 1524 allowing thermally emitted electrons 1525 to flow through ballistically between the second pair of emitter and collector, a HWF film 1529 coated on the third electric conductor 1521 top surface to sever as the second collector, a LWF film 1533 coated on the third electric conductor 1521 bottom surface to serve as the third emitter, a third narrow space gap 1534 allowing thermally emitted electrons 1535 to flow through ballistically between the third pair of emitter and collector, a HWF film 1539 coated on the fourth electric conductor 1532 top surface to serve as the terminal (third) collector, a first electricity outlet 1506 (+) and a Earth ground 1510 that are connected with the first electric conductor plate 1501, and the second electric outlet 1537 (−) that is connected with the fourth electric conductor 1532.

The integrated isothermal electricity generator system 1500 (Figure 6) is similar to the system 1400C (Figure 5) except that only the first electric conductor plate 1501 and the terminal conductor plate 1532 are wired to provide electricity outlets 1506 and 1507. Therefore, in this example, each of the second and third electric conductor plates in between the first electric conductor plate 1501 and the terminal (fourth) conductor plate 1532 is designed to simultaneously serve as a collector on its top surface and an emitter at its bottom surface. For example, the conductor plate 1502 has a collector (HWF film 1509) on the top surface facing up to receive thermally emitted electrons 1505 from the first emitter (LWF film 1503) located above the narrow space gap 1504 and an emitter (LWF film 1523) on the bottom side to emit thermal electrons 1525 downwards. Meanwhile, the conductor plate 1521 has a HWF film 1529 on its top surface facing up to receive thermally emitted electrons 1525 from the second emitter (LWF film 1523) located above the narrow space gap 1524 and a LWF film 1533 on its bottom to emit thermal electrons 1535 downwards to the terminal collector (HWF 1539) on the terminal conductor 1532. When the isothermal electricity is outputted through outlet terminals 1506 and 1537 across three pairs of emitters and collectors, the maximum total steady-state operating output voltage typically can be about 9~12 V in this example.

Since the effect of the isothermal electricity production is additive, a number of emitter-collector pairs that may be used per integrated system as shown in Figure 6. Depending on a given specific application and its associated operating conditions such as temperature conditions, and the properties of the barrier space such as its thickness and composition, the emitter and collector electrodes and other physical chemistry properties, the number of emitter-collector pairs that may be used per integrated system as shown in Figure 6 for the purpose of isothermally extracting environmental heat energy to produce electricity may be selected from the group consisting of 1, 2, 3, 4, 5, 6, 7, 8, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 1000, 2000, 5000, 10,000, 100,000, 1,000,000, more and/or within a range bounded by any two of these values.

Figure 7 presents an integrated isothermal electricity production system 1600 in a compact device form that comprises three pairs of emitters and collectors installed in a vacuum tube chamber set up vertically to utilize the gravity to help pull the emitted electrons from an emitter down to a collector. The system 1600 (Figure 7) has the following components installed in a vacuum tube container from its top to bottom: a LWF (low work function) film 1603 coated onto the vacuum tube wall 1650 inner surface at the dome-shaped top end to serve as a first emitter that has an electricity outlet 1606 (+) wired with a capacitor 1611 that is connected with an Earth ground 1610, a first vacuum space gap 1604 allowing thermally emitted electrons 1605 to flow through ballistically, a HWF (high work function) film 1609 to serve as a first collector on the top surface of electric conductor 1602, a LWF film 1623 as the second emitter at the bottom surface of electric conductor 1602, a second vacuum space gap 1624 allowing thermally emitted electrons 1625 to flow through ballistically, a HWF film 1629 as the second collector on electric conductor 1621 top surface, a LWF film 1633 as the third emitter at electric conductor 1621 bottom surface, a third vacuum space gap 1634 allowing thermally emitted electrons 1635 to flow through ballistically, and a HWF film 1639 “coated on the inner surface of the inversed-dome-shaped bottom end of the vacuum tube to serve as the terminal collector” connected with an electricity outlet 1637 (−). When the isothermal electricity is outputted through outlet terminals 1606 and 1637 across three pairs of emitters and collectors, the maximum total steady-state operating output voltage typically can be about 9~12 V in this example.

The integrated isothermal electricity generator system 1600 (Figure 7) is similar to the system 1500 (Figure 6) except the following special features: (1) The system 1600 employs “the inner surface of dome-shaped top end of the vacuum tube chamber as a physical support to construct the first emitter” by coating an LWF (low work function) film 1603; (2) It utilizes “the inner surface of the inversed-dome-shaped bottom end of the vacuum tube chamber to construct the terminal collector” by coating a HWF (high work function) film 1639; and (3) the first emitter has an electricity outlet 1606 (+) wired with a capacitor 1611 that is connected with an Earth ground 1610 while the terminal collector connected with an electricity outlet 1637 (−). These features make the integrated isothermal electricity generator system 1600 much more compact than the system 1500. The optional use of capacitor 1611 between the electricity outlet 1606 (+) and the Earth ground 1610 also provides an additional way to reduce and/or modulate the possible voltage at the emitter for better system performance.

Accordingly, during the isothermal electricity generation, an effective emitter absorbs environmental heat from the outside environment and utilizes the environmental heat energy to emit electrons as shown in Figure 2, Figure 4, Figure 5, Figure 6 and Figure 7 It is important to provide effective heat conduction from the environment to the emitters. The system 1500 (Figure 6) provide an example where the environmental heat energy primarily flows through the tube wall-electric conductor plate joints to the emitters on the electric conductor plate surfaces. Therefore, it is “a preferred practice” to employ heat-conductive materials in making the tube wall and more importantly the tube wall-electric conductor plate joints to ensure effective conduction of latent heat from the environment to the emitters.

The integrated isothermal electricity generator system 1600 (Figure 7) provide an example of “an emitter constructed on the inner surface of dome-shaped top end of the vacuum tube chamber” by coating an LWF (low work function) film 1603. Such a close physical contact between the vacuum tube dome-shaped top wall inner surface and the emitter can favorably facilitate the heat transfer from the tube environment to the emitter.

2.5. Examples of Computed Isothermal Electricity Current and Power Density

The ideal isothermal electricity current density (A/cm²) “defined as amps (A) per square centimeters of the cross-section area of the emitter-collector interelectrode space” can be computed using Equation (3) as a function of operating temperature T at various output voltage V(c).

Figure 8 presents the computed isothermal electricity current density (A/cm²) as a function of operating temperature T at various output voltage V(c) from 0.00 to 3.86 V, as calculated using Equation (3) for a pair of emitter work function (WF(e) = 0.70 eV) and collector work function (WF(c) = 4.56 eV, copper Cu(110)), in which the emitter was grounded. Since the emitter was grounded, the output voltage equals to V(c), which is the difference between the collector voltage V(c) and the grounded emitter voltage (V(e) = 0). Consequently, the isothermal electricity current density (A/cm²) with the output voltage V(c) of 0.00 V in the initial state as illustrated with energy diagram in the 1110 (a) of Figure 3 represents the saturation isothermal current density as expressed in Equation (7).

As shown in Figure 8, the computed ideal isothermal electricity current density curve with an output voltage V(c) of 3.00 V pretty much overlaps with that of the saturation isothermal current density (with V(c) = 0.00 V) in a temperature (T) range from 225 K to 325 K. When the output voltage V(c) is raised to 3.80 V, the isothermal electricity current density curve lay only slightly below the maximum saturation isothermal current density curve. In these cases, the isothermal electricity current density increases dramatically as function of temperature T. However, when the output voltage V(c) is further raised to 3.86 V, the isothermal electricity current density is dramatically reduced to zero (a flat line), which represents the equilibrium state as shown in the 1110(c) of Figure 3 (right) where the thermal electron flow from the emitter to the collector equals to that from the collector to the emitter, resulting in a net isothermal electricity current density of zero.

Figure 9 presents the computed isothermal electricity current density (A/cm²) curves as a function of output voltage V(c) from 0.00 to 3.86 V at an operating environmental temperature of 273, 293, 298, and 303 K for a pair of emitter work function (WF(e) = 0.70 eV) and collector work function (WF(c) = 4.56 eV, copper Cu(110)) with the emitter grounded. These curves showed that the saturation isothermal electricity current density is pretty much constant (steady) in an output voltage V(c) range from 0.00 to 3.75 V at each of the operating environmental temperature of 273, 293, 298, and 303 K. Only when the output voltage V(c) is raised from 3.75 V to 3.86 V, the isothermal electricity current density is dramatically reduced to zero. At an output voltage in a range from 0 to 3.50 V, the level of the steady-state isothermal electricity current density increases with temperature dramatically from the level of 1.07 μA/cm² at 273 K (0 °C) to the levels of 9.39, 15.5, and 25.1 μA/cm² at 293 K (20 °C), 298 K (25 °C), and 303 K (30 °C), respectfully.

Figure 10 presents “the computed isothermal electricity current density Amps (A) per cm² (A/cm²) at an output voltage V(c) of 3.00 V as a function of operating environmental temperature T with a series of emitter work function (WF(e)) values including 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1 or 1.2 eV in pairing with the collector work function (WF(c) = 4.56 eV, copper Cu(110)) with the emitter grounded. The data showed that the use of an emitter with a lower work function is highly imperative to isothermally utilize environmental heat to generate electricity. Therefore, it is a preferred practice to employ an emitter with a low work function that is selected from the group consisting of 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1 and 1.2 eV and/or within a range bounded by any two of these values for isothermal electricity generation in a temperature range from 250 K to 673 K” [29].

Figure 11 presents “the computed isothermal electricity current density (A/cm²) curves as a function of output voltage V(c) from 0.00 to 4.10 V at operating environmental temperature of 273, 293, 298, and 303 K for a pair of emitter work function (WF(e) = 0.50 eV) and collector work function (WF(c) = 4.60 eV, graphene and/or graphite) with the emitter grounded”. These curves showed that the isothermal electricity current density is pretty much constant (steady) in a range of output voltage V(c) from 0.00 to 4.00 V at each of the operating environmental temperature of 273, 293, 298, and 303 K. Only when the output voltage V(c) is raised beyond 4.00 V up to the limit of 4.10 V, the isothermal electricity current density is dramatically reduced to zero. The level of the steady-state isothermal electricity current density at an output voltage of 3.50 V increases dramatically with temperature from 5.26 × 10⁻³ A/cm² at 273 K (0 °C) to 2.59 × 10⁻² A/cm² at 293 K (20 °C), 3.73 × 10⁻² A/cm² at 298 K (25 °C), and to 5.32 × 10⁻² A/cm² at 303 K (30 °C).

These data (Figure 8, Figure 9, Figure 10 and Figure 11) show that “significant amounts of isothermal electricity can be generated through the asymmetric function comprising a low work function (e.g., 0.7 eV, more preferably 0.5 eV) electron emitter and a high work function (about 5 eV) electric collector across a barrier space such as a vacuum space that allows the thermally emitted electrons to fly through ballistically”. The use of the asymmetric electron-work-function gate and the vacuum space (as a barrier space) “enables freely emitted thermal electrons to ballistically fly predominantly from the emitter through the barrier space to the electric collector although the emitter and collector are at the same environmental temperature. Since the barrier space is an electrical insulating space without the conventional conductor-based electrical conduction but has a unique property that allows thermal electrons to fly through ballistically, it prevents the excess thermal electrons captured by the collector from conducting back to the emitter. As a result, this creates a voltage difference between the emitter and the collector. This voltage difference can drive an electric current through a load resistance to do useful electric work. This electric current can continue as the excess electrons conduct through the external circuit back to the emitter where they will get re-emitted again for the next cycle, etc., after gaining thermal motion kinetic energy from environmental heat energy. Therefore, it has the potential to forever power electronic devices including mobile phones and laptops, likely transformative in energy science and technologies for sustainability” [29].

Table 1. Presents the computed ideal isothermal electricity current density (A/cm²) as a function of operating temperature T at various output voltage V(c) from 0.00 to 3.86 V, calculated using Equation (3) for a pair of emitter electron-work function (WF(e) = 0.70 eV) and collector electron-work function (WF(c) = 4.56 eV, copper Cu(110)). The emitter was grounded, and the output voltage V(c) is the voltage difference between the collector and the grounded emitter.

T (K)	V(c) 0.00	V(c) 1.50	V(c) 3.00	V(c) 3.50	V(c) 3.80	V(c) 3.86
203	2.07 × 10−11	2.07 × 10−11	2.07 × 10−11	2.07 × 10−11	2.00 × 10−11	0
213	1.49 × 10−10	1.49 × 10−10	1.49 × 10−10	1.49 × 10−10	1.43 × 10−10	0
223	9.04 × 10−10	9.04 × 10−10	9.04 × 10−10	9.04 × 10−10	8.64 × 10−10	0
233	4.71 × 10−9	4.71 × 10−9	4.71 × 10−9	4.71 × 10−9	4.47 × 10−9	0
243	2.15 × 10−8	2.15 × 10−8	2.15 × 10−8	2.15 × 10−8	2.03 × 10−8	0
253	8.74 × 10−8	8.74 × 10−8	8.74 × 10−8	8.74 × 10−8	8.18 × 10−8	0
263	3.20 × 10−7	3.20 × 10−7	3.20 × 10−7	3.20 × 10−7	2.97 × 10−7	0
273	1.07 × 10−6	1.07 × 10−6	1.07 × 10−6	1.07 × 10−6	9.86 × 10−7	0
283	3.29 × 10−6	3.29 × 10−6	3.29 × 10−6	3.29 × 10−6	3.01 × 10−6	0
293	9.39 × 10−6	9.39 × 10−6	9.39 × 10−6	9.39 × 10−6	8.52 × 10−6	0
298	1.55 × 10−5	1.55 × 10−5	1.55 × 10−5	1.55 × 10−5	1.40 × 10−5	0
310	4.81 × 10−5	4.81 × 10−5	4.81 × 10−5	4.81 × 10−5	4.30 × 10−5	0
313	6.30 × 10−5	6.30 × 10−5	6.30 × 10−5	6.30 × 10−5	5.62 × 10−5	0
323	1.50 × 10−4	1.50 × 10−4	1.50 × 10−4	1.50 × 10−4	1.32 × 10−4	0
333	3.39 × 10−4	3.39 × 10−4	3.39 × 10−4	3.39 × 10−4	2.97 × 10−4	0
343	7.32 × 10−4	7.32 × 10−4	7.32 × 10−4	7.32 × 10−4	6.36 × 10−4	0
353	0.00152	0.00152	0.00152	0.00152	0.00131	0
363	0.00302	0.00302	0.00302	0.00302	0.00258	0
373	0.00582	0.00582	0.00582	0.00582	0.00492	0
383	0.01083	0.01083	0.01083	0.01083	0.00907	0
393	0.01956	0.01956	0.01956	0.01956	0.01623	0
403	0.03435	0.03435	0.03435	0.03435	0.02824	0
413	0.05877	0.05877	0.05877	0.05877	0.04788	0
423	0.09814	0.09814	0.09814	0.09814	0.07922	0
433	0.16024	0.16024	0.16024	0.16023	0.12815	0
443	0.25616	0.25616	0.25616	0.25614	0.20296	0
453	0.40151	0.40151	0.40151	0.40147	0.31518	0
463	0.61782	0.61782	0.61782	0.61775	0.48049	0
473	0.93436	0.93436	0.93436	0.93422	0.71996	0
483	1.39028	1.39028	1.39028	1.39004	1.0614	0
493	2.03731	2.03731	2.03731	2.03688	1.54106	0
503	2.94281	2.94281	2.94281	2.94208	2.20558	0
513	4.1935	4.1935	4.1935	4.19229	3.11423	0
523	5.89976	5.89976	5.89976	5.89775	4.34142	0
533	8.20048	8.20048	8.20048	8.19725	5.97966	0
543	11.2688	11.2688	11.2688	11.26367	8.14272	0
553	15.31839	15.31839	15.31839	15.31037	10.96923	0
563	20.61061	20.61061	20.61061	20.59826	14.62655	0
573	27.46246	27.46246	27.46246	27.44373	19.31508	0
583	36.25534	36.25534	36.25534	36.22732	25.27281	0
593	47.44464	47.44464	47.44464	47.40327	32.78025	0
603	61.57024	61.57024	61.57023	61.5099	42.16566	0
613	79.26778	79.26778	79.26778	79.18081	53.81059	0
623	101.2809	101.2809	101.28089	101.15693	68.15564	0
633	128.47419	128.47419	128.47418	128.29937	85.70654	0
643	161.84712	161.84712	161.84709	161.60307	107.04041	0
653	202.54861	202.54861	202.54856	202.21123	132.81218	0
663	251.89254	251.89254	251.89246	251.43047	163.76124	0
673	311.37387	311.37387	311.37375	310.74663	200.71813	0

lists the ideal isothermal electricity current density (A/cm²) values as a function of operating temperature T in a range from 203 K (−70 °C) to 673 K (400 °C) at a number of output voltage V(c) values including 0.00, 1.50, 3.00, 3.50, 3,80 and 3.86 V, as calculated using Equation (3) for a pair of emitter electron-work function (WF(e) = 0.70 eV) and collector electron-work function (WF(c) = 4.56 eV, copper Cu(110)) where the emitter was grounded. The data showed that, with a reasonable output voltage V(c) of about 3 V, the isothermal electricity current density is strongly dependent on temperature T in a range from 2.07 × 10⁻¹¹(A/cm²) at 203 K (−70 °C) to 1.55 × 10⁻⁵ (A/cm²) at 298K (25 °C), and to as much as 311 (A/cm²) at 673 K (400 °C).

According to the invention (WO 2019/136037 A1), when the emitter is grounded, the ideal isothermal electricity power production density $P_{isoT\left(gnd\right)}$ (W/cm²) at various output voltage V(c) volts can be expressed as:

$$P_{isoT\left(gnd\right)}=A{T}^2(e^{-\left[WF\left(e\right)\right]/kT} · e^{-\left[WF\left(c\right)+e · V\left(c\right)\right]/kT}) V\left(c\right)$$

(12)

Table 2. Presents the computed isothermal electricity power production density defined as Watt (W) per square centimeters (W/cm²) as a function of operating temperature T at various output voltage V(c) from 0.00 to 3.86 V, calculated using Equation (12) for a pair of emitter electron-work function (WF(e) = 0.70 eV) and collector electron-work function (WF(c) = 4.56 eV, copper Cu(110)) where the emitter is grounded.

T (K)	V(c) 0.00	V(c) 1.50	V(c) 3.00	V(c) 3.50	V(c) 3.80	V(c) 3.86
203	0	3.10 × 10−11	6.21 × 10−11	7.24 × 10−11	7.61 × 10−11	0
213	0	2.24 × 10−10	4.47 × 10−10	5.22 × 10−10	5.45 × 10−10	0
223	0	1.36 × 10−9	2.71 × 10−9	3.16 × 10−9	3.28 × 10−9	0
233	0	7.07 × 10−9	1.41 × 10−8	1.65 × 10−8	1.70 × 10−8	0
243	0	3.23 × 10−8	6.45 × 10−8	7.53 × 10−8	7.71 × 10−8	0
253	0	1.31 × 10−7	2.62 × 10−7	3.06 × 10−7	3.11 × 10−7	0
263	0	4.80 × 10−7	9.60 × 10−7	1.12 × 10−6	1.13 × 10−6	0
273	0	1.60 × 10−6	3.21 × 10−6	3.74 × 10−6	3.75 × 10−6	0
283	0	4.93 × 10−6	9.86 × 10−6	1.15 × 10−5	1.14 × 10−5	0
293	0	1.41 × 10−5	2.82 × 10−5	3.29 × 10−5	3.24 × 10−5	0
298	0	2.32 × 10−5	4.64 × 10−5	5.41 × 10−5	5.31 × 10−5	0
310	0	7.21 × 10−5	1.44 × 10−4	1.68 × 10−4	1.63 × 10−4	0
313	0	9.45 × 10−5	1.89 × 10−4	2.20 × 10−4	2.13 × 10−4	0
323	0	2.25 × 10−4	4.49 × 10−4	5.24 × 10−4	5.03 × 10−4	0
333	0	5.08 × 10−4	1.02 × 10−3	1.19 × 10−3	1.13 × 10−3	0
343	0	1.10 × 10−3	2.20 × 10−3	2.56 × 10−3	2.42 × 10−3	0
353	0	2.28 × 10−3	4.56 × 10−3	5.32 × 10−3	4.98 × 10−3	0
363	0	4.53 × 10−3	9.06 × 10−3	1.06 × 10−2	9.80 × 10−3	0
373	0	8.73 × 10−3	1.75 × 10−2	2.04 × 10−2	1.87 × 10−2	0
383	0	1.62 × 10−2	3.25 × 10−2	3.79 × 10−2	3.45 × 10−2	0
393	0	2.93 × 10−2	5.87 × 10−2	6.85 × 10−2	6.17 × 10−2	0
403	0	5.15 × 10−2	1.03 × 10−1	1.20 × 10−1	1.07 × 10−1	0
413	0	8.82 × 10−2	1.76 × 10−1	2.06 × 10−1	1.82 × 10−1	0
423	0	1.47 × 10−1	2.94 × 10−1	3.43 × 10−1	3.01 × 10−1	0
433	0	2.40 × 10−1	4.81 × 10−1	5.61 × 10−1	4.87 × 10−1	0
443	0	3.84 × 10−1	7.68 × 10−1	8.96 × 10−1	7.71 × 10−1	0
453	0	6.02 × 10−1	1.20	1.41	1.20	0
463	0	9.27 × 10−1	1.85	2.16	1.83	0
473	0	1.40	2.80	3.27	2.74	0
483	0	2.09	4.17	4.87	4.03	0
493	0	3.06	6.11	7.13	5.86	0
503	0	4.41	8.83	1.03 × 10	8.38	0
513	0	6.29	1.26 × 10	1.47 × 10	1.18 × 10	0
523	0	8.85	1.77 × 10	2.06 × 10	1.65 × 10	0
533	0	1.23 × 10	2.46 × 10	2.87 × 10	2.27 × 10	0
543	0	1.69 × 10	3.38 × 10	3.94 × 10	3.09 × 10	0
553	0	2.30 × 10	4.60 × 10	5.36 × 10	4.17 × 10	0
563	0	3.09 × 10	6.18 × 10	7.21 × 10	5.56 × 10	0
573	0	4.12 × 10	8.24 × 10	9.61 × 10	7.34 × 10	0
583	0	5.44 × 10	1.09 × 102	1.27 × 102	9.60 × 10	0
593	0	7.12 × 10	1.42 × 102	1.66 × 102	1.25 × 102	0
603	0	9.24 × 10	1.85 × 102	2.15 × 102	1.60 × 102	0
613	0	1.19 × 102	2.38 × 102	2.77 × 102	2.04 × 102	0
623	0	1.52 × 102	3.04 × 102	3.54 × 102	2.59 × 102	0
633	0	1.93 × 102	3.85 × 102	4.49 × 102	3.26 × 102	0
643	0	2.43 × 102	4.86 × 102	5.66 × 102	4.07 × 102	0
653	0	3.04 × 102	6.08 × 102	7.08 × 102	5.05 × 102	0
663	0	3.78 × 102	7.56 × 102	8.80 × 102	6.22 × 102	0
673	0	4.67 × 102	9.34 × 102	1.09 × 103	7.63 × 102	0

list the computed isothermal electricity power production density defined as Watt (W) per square centimeters (W/cm²) as a function of operating temperature T in a range from 203 K (−70 °C) to 673 K (400 °C) at a number of output voltage V(c) values including 0.00, 1.50, 3.00, 3.50, 3,80 and 3.86 V, as calculated using Equation (12) for a pair of emitter electron-work function (WF(e) = 0.70 eV) and collector electron-work function (WF(c) = 4.56 eV, copper Cu(110)) where the emitter was grounded. The data showed that the output voltage V(c) that gave the best isothermal electricity power production density (W/cm²) was about 3.50 V in this example. The isothermal power production density (W/cm²) at output voltage V(c) of 3.50 V is strongly dependent on temperature T, which is in a range from 7.24 × 10⁻¹¹(W/cm²) at 203 K (−70 °C) to 5.41 × 10⁻⁵ (W/cm²) at 298 K (25 °C), and to as much as 1090 (W/cm²) at 673 K (400 °C).

2.6. Asymmetric Function-Gated Isothermal Electricity Generators Distinct in Comparing with Type-A Energy Processes

This asymmetric electron-work-function-gated isothermal electricity power production system 1100 (Figure 1, Figure 2 and Figure 3) is fundamentally different from the conventional temperature gradient-driven thermionic converter reported previously by Hatsopoulos and Gyftopoulos 1973 (Thermionic Energy Conversion, Volume I: Processes and Devices, The MIT Press, Cambridge, Massachusetts, and London, England). The conventional thermionic converter converts heat to electricity by boiling electrons from an extremely hot emitter surface (~2000 K) across a small inter electrode gap (<0.5 mm) to a cooler collector surface (~1000 K), which requires a large temperature gradient and clearly is not an isothermal operation in contrast to the isothermal electricity generation of the present invention (WO 2019/136037 A1). Since the thermionic converter is a form of heat engine which runs by the use of a temperature gradient, it is believed to be limited by the Carnot efficiency, at best. In the conventional temperature gradient-driven thermionic converter reported by King et al. 2004 (Sandia Report, SAND2004-0555, Unlimited Release, Sandia National Laboratory, Albuquerque, New Mexico) and by Chou 2014 (Discovering Low Work Function Materials For Thermionic Energy Conversion, PhD Dissertation, Stanford University, California), a high electron-work function electrode is typically used as the emitter that is heated up by a high temperature heat source while a low electron-work function electrode is used as the collector that is cooled by a cold heat sink so that the conventional thermionic electricity generation is believed to be driven by the temperature gradient from the heated emitter to the cooled collector in “following the second law of thermodynamics”, which is typical of the known type-A energy process.

The present invention of isothermal electricity (WO 2019/136037 A1) as shown through the examples of the asymmetric electron-work-function-gated isothermal electricity production system 1100 (Figure 1, Figure 2 and Figure 3) differs from the conventional thermoelectric approach including the “thermal diode for energy conversion” (WO 01/69657 A2) where “a highly doped n region can serve as an emitter region, from which carriers can be injected into a gap region”. The conventional thermoelectric approach represents a Type-A energy process since it requires the use of a temperature gradient from the heated emitter relative to the collector to generate an electron motive force which drives the electric current through a series load.

In contrast to the conventional thermoelectric approach (WO 01/69657 A2), the innovative asymmetric function-gated isothermal electricity production system (WO 2019/136037 A1) such as the one illustrated in Figure 2c, comprises a special low electron-work function conductor as the emitter electrode 1101 while the collector electrode 1102 is selected to have a higher electron-work function predominately from the nuclear (positive) charge force. More importantly, both the emitter 1101 and the collector 1102 can be used at the same ambient temperature (isothermal conditions) without requiring any temperature gradient between the emitter and the collector. The isothermal electricity power production system which isothermally extracts latent heat energy from the environment for generating useful electricity perfectly follows the first law of thermodynamics but without being constrained by the second law of thermodynamics owning to the utilization of the special asymmetric function-gated mechanisms.

In the conventional temperature gradient-driven thermionic converter, a conducting electrode (emitter) is heated to hot temperatures so that it emits electrons (Wanke et al. 2017 MRS Bulletin 42: 518-524). These thermionic electrons overcome the electrode’s work function and generate a thermionic emission current. It typically requires the emitter being heated by using an external energy/heat source such as focused solar irradiation, intensified chemical combustion, or nuclear decay reaction heat to a temperature as high as 2000K while the collector is cooled to below about 600K using a heat sink (Sandia Report, SAND2004-0555). Air-breathing chemical heat sources, such as common hydrocarbon burners, cannot achieve the desired thermionic temperatures (~2000K) unless substantial air-preheat is used. That is, the thermionic converter operation is based on an exceptionally elevated temperature at the emitter with a large temperature difference between the two electrodes (thermionic emitter and collector). The elevated hot temperatures required by the thermionic converter impose formidable technical problems concerning the structure of the fuel elements and the means of transferring heat to the converters. As a type-A energetic process, the Carnot efficiency here is believed to represent the ultimate efficiency limit (Khalid et al. 2016 IEEE Transactions on Electron Devices 63: 2231-2241).

In contrast, the asymmetric function-gated isothermal electron production generator system (WO 2019/136037 A1), as a type-B energetic process, does not require such an elevated hot temperature and is not constrained by the Carnot efficiency; since it can generate electricity by isothermally utilizing the ambient temperature latent heat energy from the surrounding environment without requiring any energy-intensive heating and/or cooling energy resources.

According to the present invention (WO 2019/136037 A1), the asymmetric electron-gating function 1003 (Figure 1) that comprises the utilization of low electron-work function emitter 1103 (Figure 2a) typically coated on the surface of an electric conductor 1101, which is able to emit thermal electrons even at the ambient temperature (such as 293 K (20 °C)) and the utilization of higher electron-work function collector 1109 on an electric conductor plate 1102 surface under the ambient temperature conditions that essentially will not emit electrons but be able to collect the thermal electrons from the emitter 1103. It is this asymmetric electron-gating function that enables the flow of thermal electrons 1105 through the vacuum barrier space 1104 from the emitter 1103 to the collector 1109 under the isothermal conditions, generating an electricity output with a voltage difference across the two outlets 1106 (+) and 1007(−) without being constrained by the thermodynamic second law. Therefore, this asymmetric electron-work-function-gated isothermal electricity power production system 1100 (Figure 1 and Figure 2) represents a special non-Second-Law energy technology that is capable of energy renewal by extracting the latent (existing hidden) heat energy from the ambient environment through the use of thermal electrons associated with the emitter and the collector and converting it to useful energy in the form of electricity under the isothermal conditions. Fundamentally, this type-B process-based isothermal electricity technology is somewhat similar to the non-Second-Law energy renewal function disclosed previously with the TELP systems (WO2017/007762 A1, US 2017/0009357 A1).

Previous study (by Hishinuma et al. 2001 Applied Physics Letters 78: 2572-2574) suggested that the conventional thermionic generators could be effective, but only at temperatures above 1000K. In contrast, the asymmetric electron-work-function-gated isothermal electricity power production system can operate isothermally at any temperatures from a freezing temperature such as 253 K (−20 °C), to ambient temperatures around 293 K (20 °C), to an elevated temperature as high as both above and/or below 1000 K where the conventional thermionic generators still cannot effectively operate. More importantly, the asymmetric function-gated isothermal electricity power production systems (Figure 1, Figure 2 and Figure 3) can isothermally generate electricity without requiring any temperature gradient between its emitter and collector.

According to the isothermal electricity invention (WO 2019/136037 A1), it is critically important to select a special low electron-work function conductor to serve as the emitter with consideration of its operating environmental temperature conditions. For example, for an asymmetric function-gated isothermal electricity power production system that is designed to operate at a room temperature (around 25 °C), the electron work function of the emitter is preferably selected to be less than 1.0 eV, more preferably less than 0.8 eV, even more preferably less than 0.7 eV or 0.6 eV, and most preferably less than 0.5 eV. For an asymmetric function-gated isothermal electricity power production system designed to isothermally operate at a higher environmental temperature such as 35 °C, 40 °C, 50 °C, 60 °C, 80 °C, 100 °C, 120 °C, 150 °C, and 200 °C, somewhat higher electron-work function materials may also be selected for use as the emitters. On the other hand, when the intended isothermally operating temperature is significantly lower, such as, at 15 °C, 10 °C, 5 °C, 0 °C, −5 °C, −10 °C, −15 °C, −20 °C, −30 °C, and −50 °C, exceptionally low electron-work function materials should be selected for use as the emitters.

2.7. Isothermal Electricity Generation as a Type-B Energy Process for a Shared Sustainable Future on Earth

For a world with isothermal electricity generation as a type-B energy process, the modern electricity-based world economy may be powered by isothermally utilizing the limitless environmental thermal energy to do useful work. For examples, the asymmetric electron-work-function-gated isothermal electricity production system could be made into a chip device [19,29]. As illustrated in Figure 7, a number of emitter-space-collector layers may be seamlessly built into a compact chip device. Consequently, its isothermal electricity power density could be so surprisingly good that its chip with a size of about 4 cm × 10 cm (40 cm²) may be sufficient to continuously power a smart mobile phone device forever [4,19]. A typical smart mobile phone device such as iPhone 12 consumes about 10.5 Watt-hours per day (24 h). The use of an asymmetric function-gated isothermal electricity production system disclosed here with a chip size of about 40 cm² that has a 3 V isothermal electricity output of 200 mA may be sufficient to permanently power a smart mobile phone device.

That is, based on the invention [29], the novel type-B energy technologies such as the asymmetric function-gated isothermal electricity production systems have the potential capabilities for use to permanently power many electric devices, electric motors, machines and vehicles including (but not limited to) mobile phones, laptops, cars, buses, trains, ships, and airplanes utilizing the limitless environmental heat energy alone without requiring any fossil fuel energy [4,19]. Therefore, innovative scientific research and development efforts in mimicking and/or creating of type-B processes [4,19] to isothermally utilize the endless environmental heat energy [19,24,29,40,41] should be highly encouraged to help ultimately liberate all peoples from their dependence of fossil fuel energy, thus helping to reduce greenhouse gas CO₂ emissions and control climate change towards a common shared sustainable future for the humanity on Earth.

3. Conclusions

As highlighted above with the type-B energetic equations and physical principles including the fundamental embodiments, it explains how an asymmetric electron-work-function-gated system can isothermally utilize environmental heat energy to generate electricity (WO 2019/136037 A1) [29]. Briefly, a basic asymmetric function-gated isothermal electricity power production system (Figure 1, Figure 2 and Figure 3) comprises a space gap that separates a pair of electric conductors: one of them has a low electron-work function film surface to serve as the emitter and the other is a high electron-work function plate to serve as the collector. The emitter surface film is made of an exceptionally low electron-work function material such as Ag-O-Cs that has an electron work function as low as 0.5−0.7 eV. The space gap does not conduct electricity by the regular electric conduction but allow free thermal electrons to fly through ballistically. Use of the space gap and low electron-work function surface film enables substantial amounts of the ambient temperature thermal electrons to emit from the film surface into the space gap and fly ballistically towards the collector that is a high electron-work function plate such as a copper plate which has an electron-work function as high as about 5 eV. At ambient temperature around 298 K, such a high electron-work function plate has nearly zero emission of thermal electrons from its surface whereas it can accept the thermal electrons flying through the space gap from the emitter. This enables freely emitted thermal electrons to ballistically fly predominantly from the emitter through the space gap to the electric collector although the emitter and collector are at the same environmental temperature. After the thermal electrons from the emitter flowing ballistically across the space gap arrive at the collector, they as excess electrons will electrostatically repel each other and spread around the electric conductor (collector) surface; Similarly, the excess positive charges left at the emitter will electrostatically spread around the electrode (emitter) surface. As a result, it creates a voltage difference between the emitter and the collector.

Use of this voltage difference through the terminals of electricity outlets can drive an electric current through a load resistance to do electric work as shown in Figure 2. This conductive flow of electrons through the external load wire, better known as electricity, can continue as the excess electrons flow conductively through the external circuit back to the emitter where they will get re-emitted again for the next cycle etc. after gaining thermal motion kinetic energy from the environmental heat of the surrounding environment. This explains how the asymmetric function-gated isothermal electricity production system can generate electricity by isothermally utilizing heat energy from the environment.

The physics equations (Equations (1)–(12)) of isothermal electricity current, voltage and power density mathematically show a number of the key properties and principles associated with the asymmetric function-gated isothermal electricity production systems as a type-B energetic process isothermally utilizing environmental heat energy. The ideal isothermal current density ($J_{isoT}$) equation (Equation (2)) for a basic asymmetric function-gated isothermal electricity generator (Figure 1 and Figure 2) with an emitter and a collector indicates that there will be isothermal current density and/or voltage as long as the electron work function of the emitter ($WF\left(e\right))$ is substantially lower than that of the collector ($WF\left(c\right))$.

When the emitter is grounded, the ideal isothermal current density ($J_{isoT\left(gnd\right)}$) can then be calculated through Equation (3) which clearly shows an isothermal electricity current density as long as the electron work function of the emitter (WF(e)) is substantially smaller than the collector’s electron work function plus the electric voltage at the collector [$WF\left(c\right)+e · V\left(c\right)].$

When the voltage at both the emitter (V(e)) and the collector (V(c)) are zero, the ideal saturation isothermal electricity current density ($J_{isoT\left(sat\right)}$ can be calculated through Equation (4), which also shows a non-zero isothermal electricity current density as long as the electron work function of the emitter (WF(e)) is substantially lower that of the collector (WF(c)). The “open circuit” ideal saturation output voltage ($V_{sat}$) at the equilibrium between the emitter and collector can be expressed as the difference in their electron work functions as shown in Equation (5). The isothermal saturation current ($J_{isoT\left(sat\right)}$) equation (Equation (7)) clearly shows that it can generate isothermal electricity current as long as the electron work function of the emitter $\left[WF\left(e\right)\right]$ is substantially lower than that of the collector $\left[WF\left(c\right)\right]$.

The ideal isothermal electricity power production density $P_{isoT\left(gnd\right)}$ (W/cm²) at various output voltage V(c) volts can be expressed by Equation (12). The asymmetric function-gated isothermal electricity generator systems have the potential capacity to generate substantial amounts of electricity (see the examples of isothermal electricity current and power density data in Table 1 and Table 2) to permanently power many electronic devices such as mobile phones, laptops, electric motors, machines and vehicles including (but not limited to) cars, buses, trains, ships, and airplanes utilizing the limitless environmental heat energy alone without requiring any fossil fuel energy [4,19]. Its forever clean energy renewal function may be made into a compact chip/device (Figure 4, Figure 5, Figure 6 and Figure 7) to isothermally utilize the end-less environmental heat energy to power the modern electricity-based economy, which thus could help to liberate all peoples from their dependence of fossil fuels energy, thus helping to reduce greenhouse-gas CO₂ emissions and control climate changes.

Therefore, the author hereby encourages both public and private supports to accelerate the R&D efforts [19,24,29,40,41] on type-B energy processes at national and/or international scales, to provide the envisioned forever clean energy for all peoples towards a shared common future for the humanity on the planet. That is, innovative scientific research and development efforts [19,24,29,40,41] in mimicking and/or creating of type-B processes [4,19] to isothermally utilize the endless environmental heat energy should be highly encouraged to help ultimately liberate all peoples from their dependence of fossil fuel energy, thus helping to reduce greenhouse gas CO₂ emissions and control climate change towards a common shared sustainable future for the humanity on Earth.

4. Materials and Methods

The computation of isothermal electricity current density (A/cm²) as a function of operating temperature T at various output voltage V(c) was performed using the modified ideal isothermal electricity current density ($J_{isoT\left(gnd\right)}$) equation (Equation (3)) for each pair of low electron-work-function (e.g., 0.7 eV) emitter and high electron-work-function (e.g., 4.56 eV) collector. The computed isothermal electricity current density (A/cm²) data are presented in Figure 8, Figure 9, Figure 10 and Figure 11 and Table 1.

The computation of isothermal electricity power production density defined as Watt (W) per square centimeters (W/cm²) as a function of operating temperature T at various output voltage V(c) from 0.00 to 3.86 V was performed using the ideal isothermal electricity power production density $P_{isoT\left(gnd\right)}$ equation (Equation (12)) for a pair of emitter electron-work function (WF(e) = 0.70 eV) and collector electron-work function (WF(c) = 4.56 eV, copper Cu(110)) where the emitter is grounded. The computed isothermal electricity power production density data are presented in Table 2.

The proof-of-principle experimental demonstration of sustainable isothermal electricity production was accomplished through the use of a prototype asymmetric election-work-function-gated isothermal electricity generator under isothermal experimental conditions using ambient environmental temperatures as disclosed with great details in [29]: the paragraphs 0097–0103 with the experimental data listed in the “Table 7” of the PCT international patent application publication (WO 2019/136037 A1); and in paragraphs 0172–0190 with the experimental data presented in the “Table 10” and “Table 11” of the patent application publication (WO 2019/136037 A1).