Performance Prediction for a Marine Diesel Engine Waste Heat Absorption Refrigeration System
Abstract
:1. Introduction
2. Description of the Ammonia–Water-Based Absorption Refrigeration System
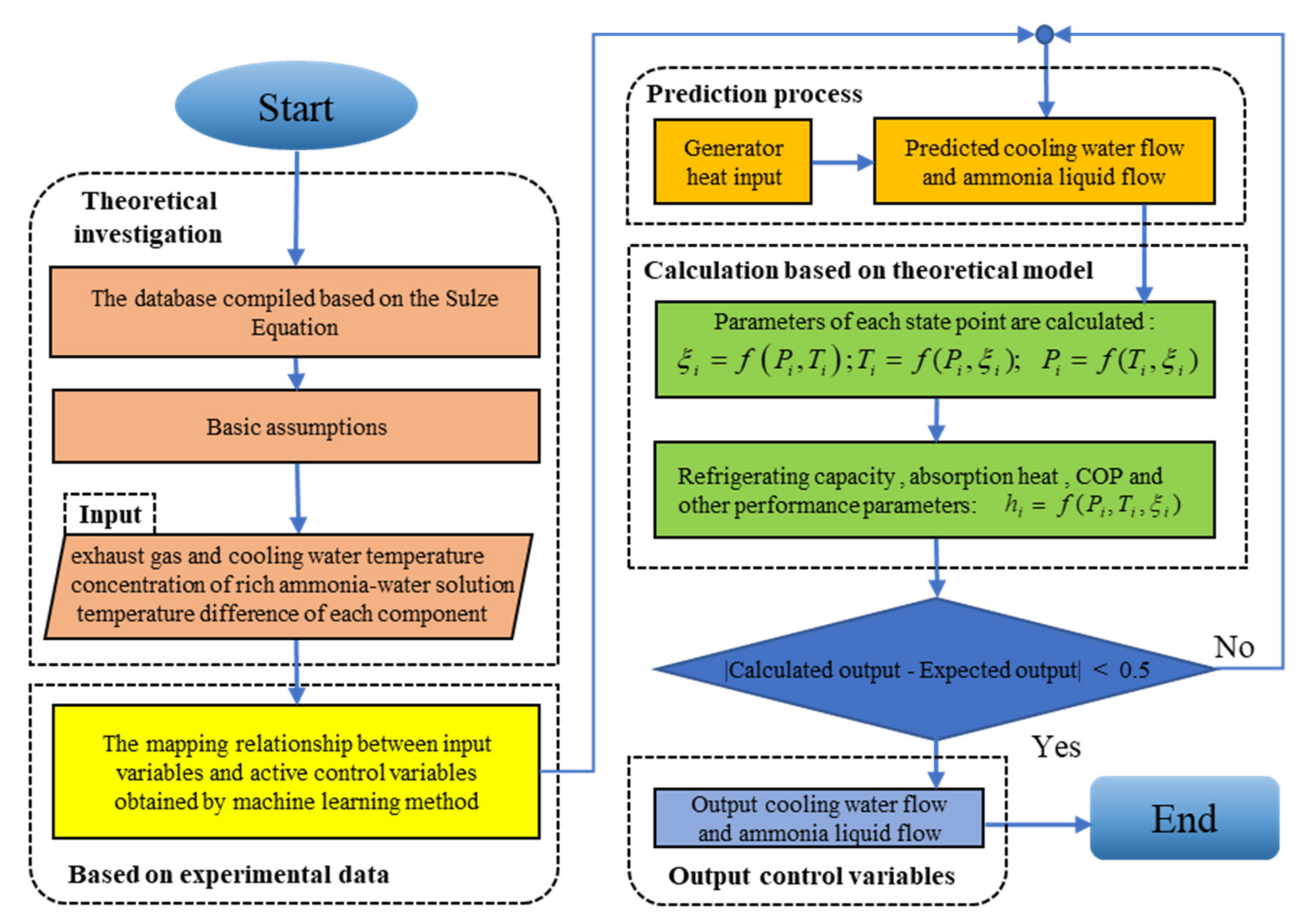
3. Basic Procedure of the Control Parameter Prediction
3.1. Prediction Principle and Solution Strategy
3.2. Experimental Setup
3.3. Experimental Plan
3.4. Experimental Results and Analyses
4. Combined Prediction Model Based on Machine-Learning Algorithms and Thermodynamics
4.1. BPNN Algorithm
4.2. ELM Algorithm
4.3. Elman Algorithm
4.4. Thermodynamic Model
- (1)
- The initial concentration of rich ammonia–water solution is available.
- (2)
- The inlet temperature of cooling water is available.
- (3)
- The NH3-H2O solution and vapor reaches saturation at the output end of the absorber and reflux condenser.
- (4)
- The components of the refrigeration system are in a steady state.
- (5)
- All heat exchangers can meet the minimum heat-transfer requirements.
4.5. Mathematical Model for Absorption Refrigeration Cycle
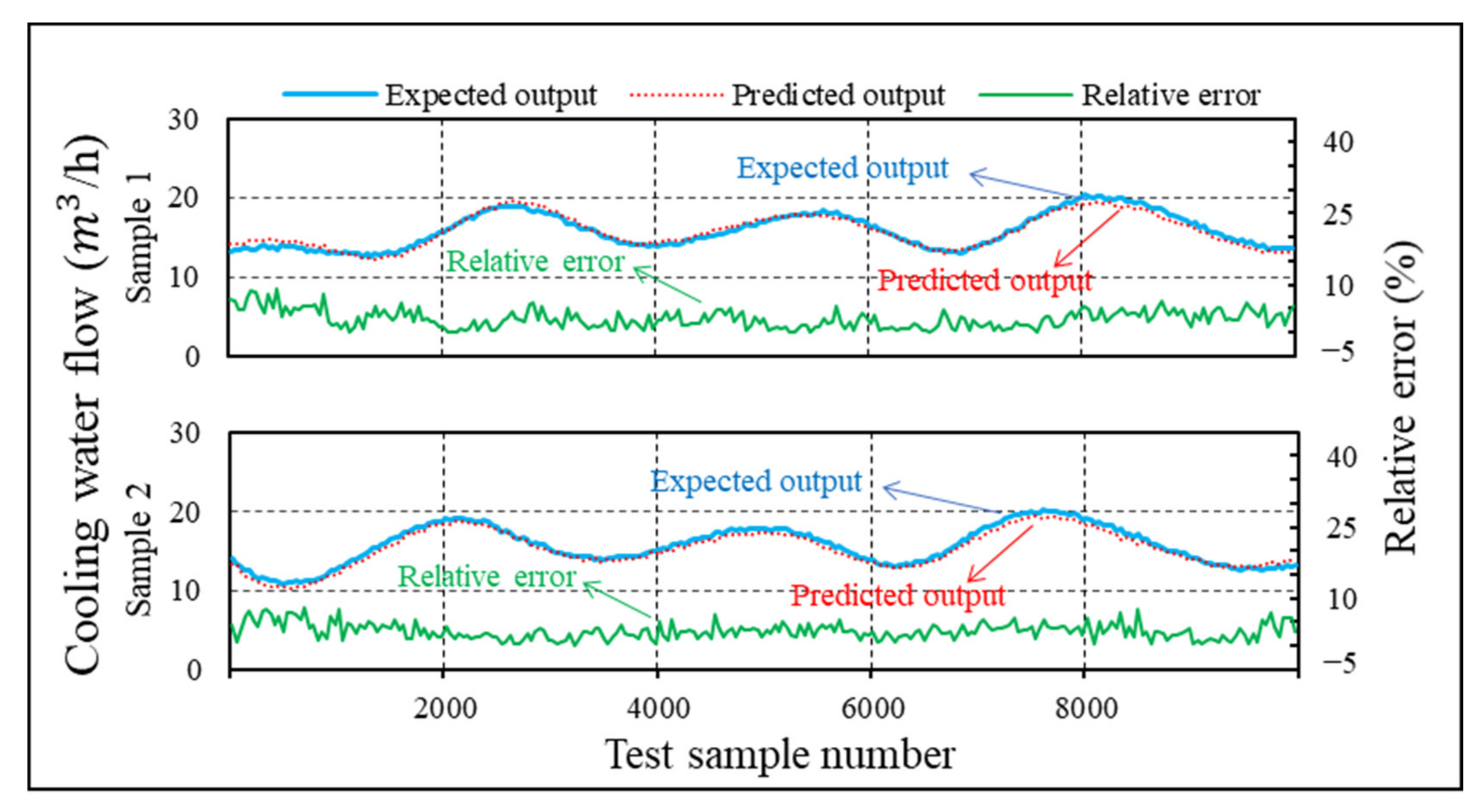
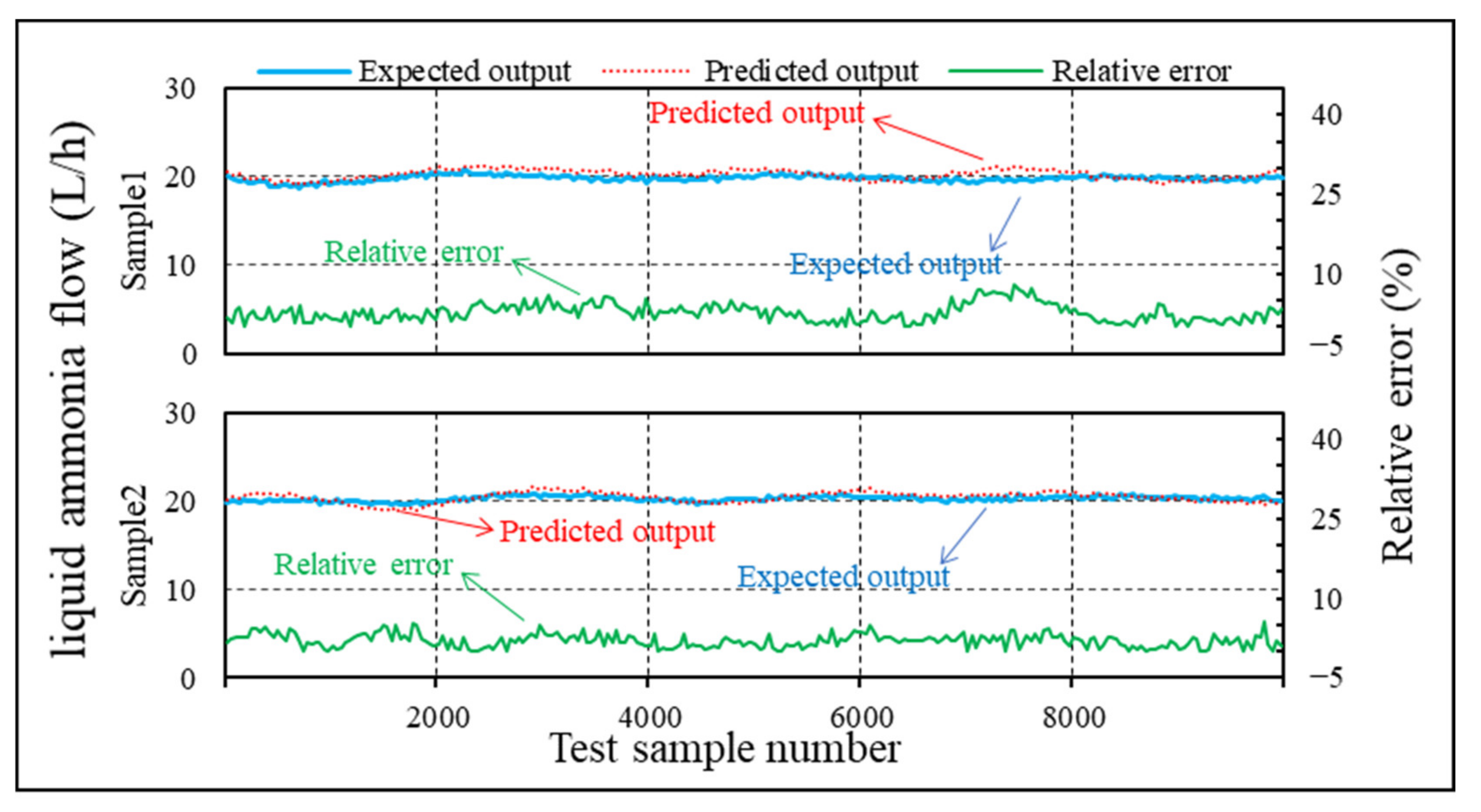
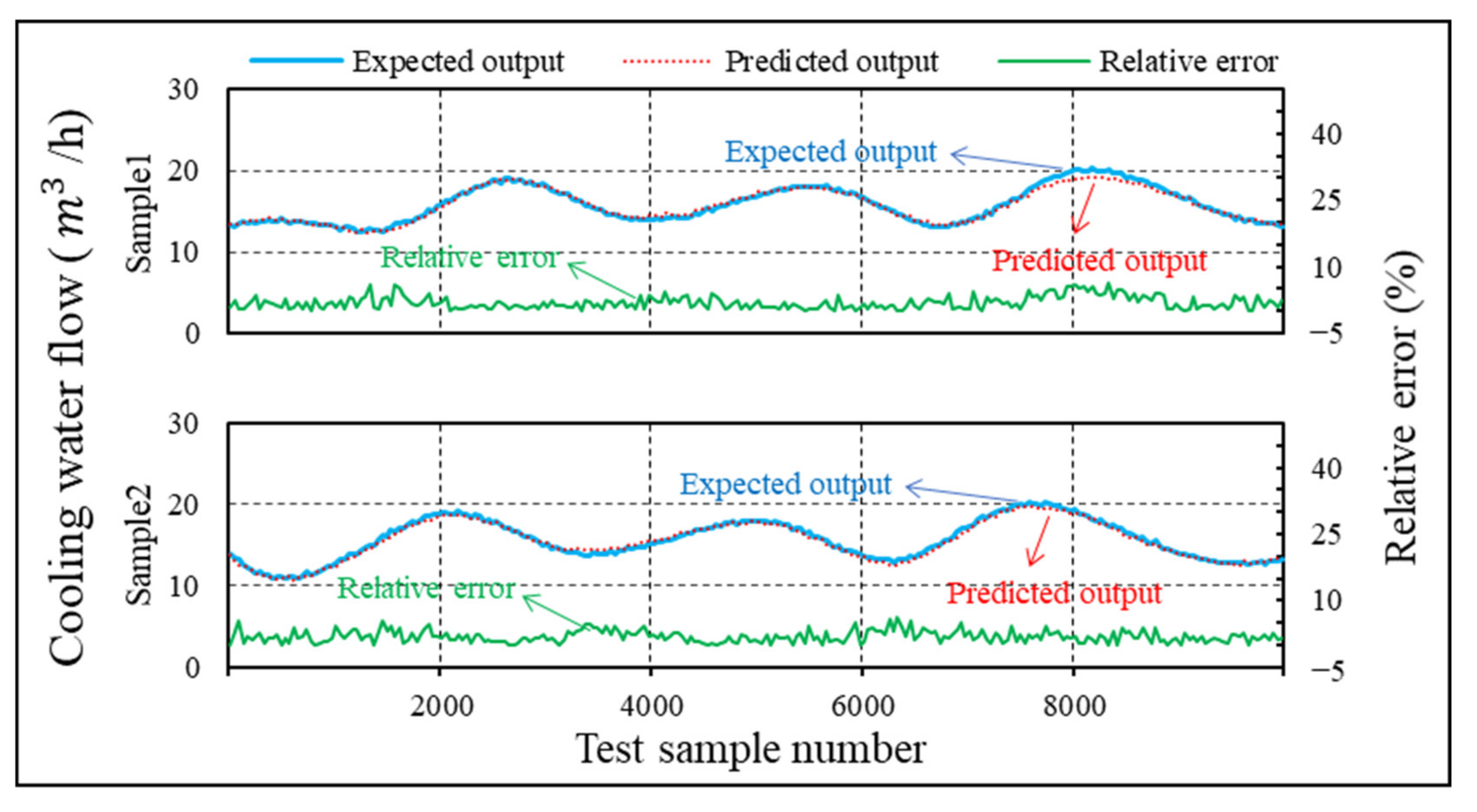
4.6. Comparison and Optimization of Prediction Algorithms
4.7. System Performance Based on the Predicted Value of the Optimization Algorithm
5. Conclusions
- The two most critical parameters affecting the system refrigeration performance, i.e., the cooling water flow into the absorber and liquid ammonia flow into the evaporator, were determined based on the experimental process and experimental data and were selected as the two manipulated variables.
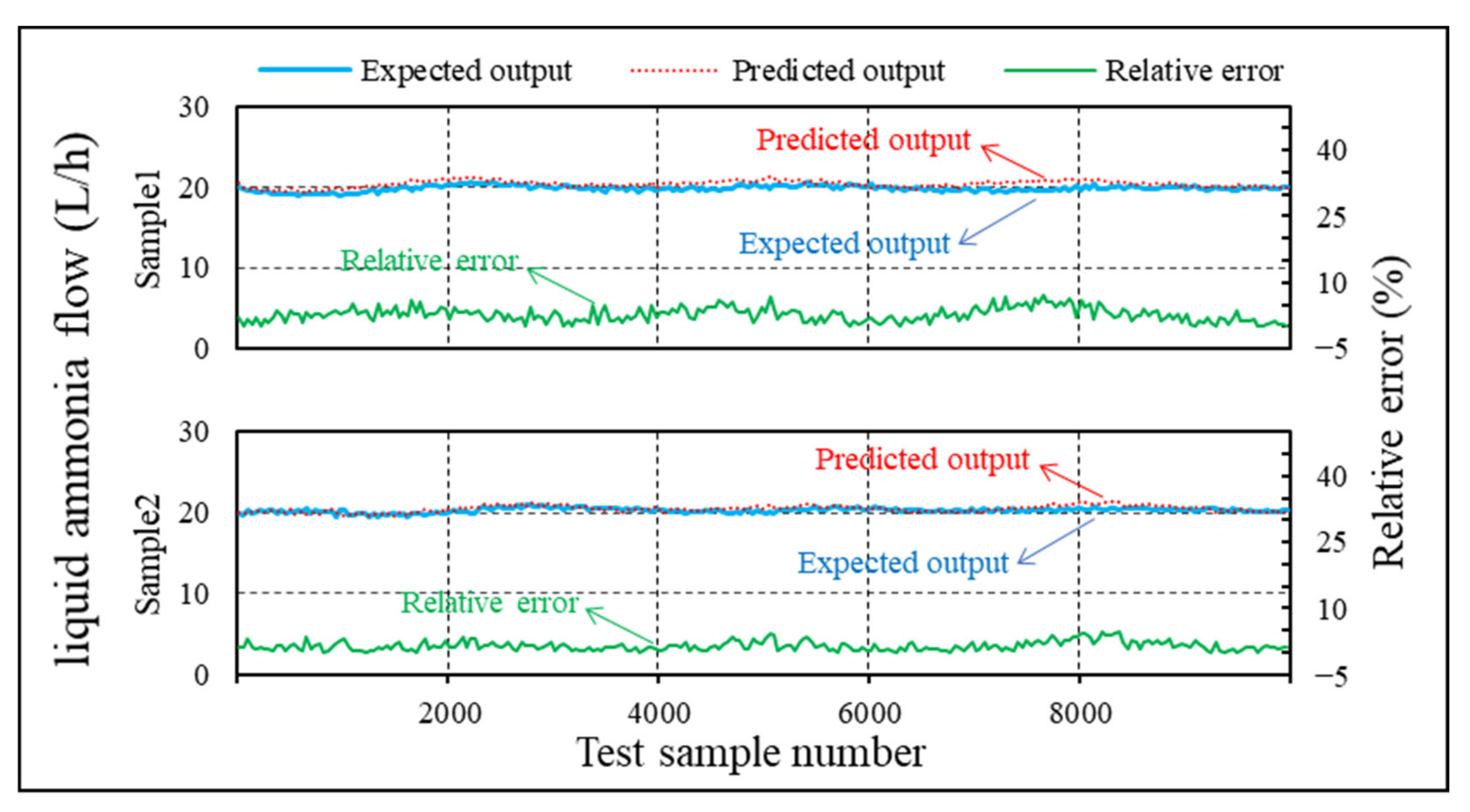
- The BPNN algorithm results show that the maximum relative error between the predicted cooling water flow and expected value is approximately 5.8%. The maximum relative error between the predicted liquid ammonia flow and expected value is approximately 7.2%. The ELM algorithm results show that the maximum relative error between the predicted cooling water flow and expected value is approximately 2.5%. The maximum relative error between the predicted liquid ammonia flow and expected value is approximately 5.1%. The Elman algorithm results show that the maximum relative error between the predicted cooling water flow and expected value is approximately 4.1%. The maximum relative error between the predicted liquid ammonia flow and the expected value is approximately 5.6%.
- The ELM algorithm was selected as the final optimal prediction algorithm owing to its relatively fast learning speed, good generalization performance, and small error sum of the test set.
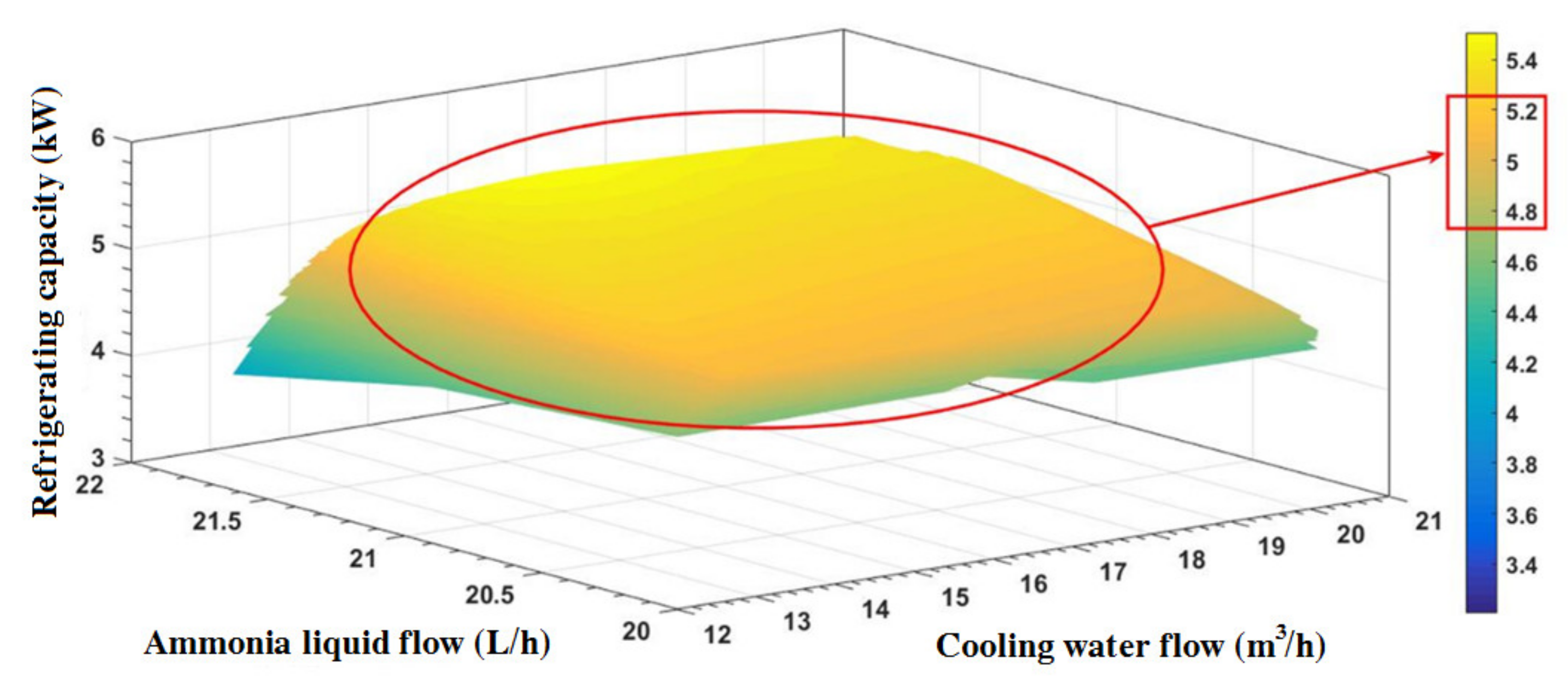
- The calculated refrigerating capacity output based on the ELM algorithm prediction ranged from 4.8 to 5.2 kW. The maximum relative error with the expected refrigerating capacity output of 4.85 kW was 7.2%.
- There is a certain coupling relationship between the exhaust heat of a marine diesel engine and the absorption refrigeration system. Application scenarios of absorption refrigeration systems, such as indoor refrigeration and cold-storage refrigeration, will also affect the performance of the refrigeration system. In addition, the aging of mechanical systems and sensors can affect the prediction accuracy, so online learning can be used to enhance the performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Greek symbols | ||
| A | Cross-sectional area, m2 | η | Learn rate, % |
| X | Sets of input values for the network | θ | Weight between hidden layer neurons |
| Y | Sets of output values for the network | ξ | Ammonia concentration |
| M, N | Dimension number | δ | Fouling factor of the heat exchange surface |
| a, b | Node thresholds | Subscript | |
| O | Predictive output | 1, 2, 3 … | State points |
| e | Prediction error | a, b, c | Cross section |
| d | Number of input layer neurons | uc | Feedback state vector |
| l | Number of hidden layer neurons | w3 | Connection weight between the middle layer and output layer |
| f | Activation function between the input layer and hidden layer | w2 | Connection weight between the input layer and middle layer |
| n | Total number of samples | w1 | Connection weight between the receiving layer and middle layer |
| w | Weight values | mi | Mass flow rate of the working fluid, L/min |
| H | Hidden layer | QG | Generation heat input, Kj |
| y | Output node vector | QE | Refrigerating capacity output |
| u | Unit vector of middle layer node | QC/A | Condensation/absorption heat output |
| x | Input vector | QD | Heat exchange of the components |
| g | Transfer function of the output layer neuron | UD | The overall heat transfer coefficient of the components |
| h | Enthalpy of the working fluid | AD | Heat exchange area of the components |
| Acronyms | ∆TD | Log mean temperature difference of the components | |
| ORC | Organic Rankine Cycle | Ao | External heat exchange areas, m3 |
| ELM | Extreme learning machine | Ain | Internal heat exchange areas, m3 |
| BPNN | Back propagation neural network | ho | Heat transfer coefficients of the outer side (heating/cooling side) |
| COP | Coefficient of performance | hin | The heat transfer coefficients of the inner side (working medium side) |
| MED | Multi-effect distillation | hw | The conductivity of the heat transfer wall |
| MLA | Machine-learning algorithms | ||
References
- Hossain, F.M.; Nabi, N.; Brown, R.J. Investigation of diesel engine performance and exhaust emissions of microalgae fuel components in a turbocharged diesel engine. Energy Convers. Manag. 2019, 186, 220–228. [Google Scholar] [CrossRef]
- Nour, M.; Attia, A.M.; Nada, S.A. Combustion, performance and emission analysis of diesel engine fuelled by higher alcohols (butanol, octanol and heptanol)/diesel blends. Energy Convers. Manag. 2019, 185, 313–329. [Google Scholar] [CrossRef]
- Petranović, Z.; Sjerić, M.; Taritaš, I.; Vujanović, M.; Kozarac, D. Study of advanced engine operating strategies on a turbocharged diesel engine by using coupled numerical approaches. Energy Convers. Manag. 2018, 171, 1–11. [Google Scholar] [CrossRef]
- Leng, L.; Shi, L.; Gui, Y.; Liu, B.; Deng, K. Research Progress on Intelligent Control Technology of Marine Diesel Engine. J. Propuls. Technol. 2021, 42, 1186–1194. [Google Scholar]
- Fu, J.; Liu, J.; Feng, R.; Yang, Y.; Wang, L.; Wang, Y. Energy and exergy analysis on gasoline engine based on mapping characteristics experiment. Appl. Energy 2013, 102, 622–630. [Google Scholar] [CrossRef]
- Wang, X.; Sun, B.-G.; Luo, Q.-H. Energy and exergy analysis of a turbocharged hydrogen internal combustion engine. Int. J. Hydrog. Energy 2018, 44, 5551–5563. [Google Scholar] [CrossRef]
- Kiani, M.K.D.; Rostami, S.; Eslami, M.; Yusaf, T.; Sendilvelan, S. The effect of inlet temperature and spark timing on thermo-mechanical, chemical and the total exergy of an SI engine using bioethanol-gasoline blends. Energy Convers. Manag. 2018, 165, 344–353. [Google Scholar] [CrossRef]
- Patel, K.R.; Dhiman, V.D. A review on emission and performance of water diesel micro-emulsified mixture-diesel engine. Int. J. Environ. Sci. Technol. 2021, 19, 8027–8042. [Google Scholar] [CrossRef]
- Di Blasio, G.; Belgiorno, G.; Beatrice, C. Effects on performances, emissions and particle size distributions of a dual fuel (methane-diesel) light-duty engine varying the compression ratio. Appl. Energy 2017, 204, 726–740. [Google Scholar] [CrossRef]
- Verhelst, S.; Turner, J.W.; Sileghem, L.; Vancoillie, J. Methanol as a fuel for internal combustion engines. Prog. Energy Combust. Sci. 2018, 70, 43–88. [Google Scholar] [CrossRef]
- Fontana, G.; Galloni, E.; Ianniello, R.; Lanni, D.; Beatrice, C.; Di Biasio, G. Numerical analyses of spray development and combustion process with diesel-gasoline-ethanol mixtures in compression-ignition engines. In Proceedings of the Second International Conference on Material Science, Smart Structures and Applications: ICMSS-2019, Erode, India, 21–22 November 2019. [Google Scholar] [CrossRef]
- Kyriakidis, F.; Sørensen, K.; Singh, S.; Condra, T. Modeling and optimization of integrated exhaust gas recirculation and multi-stage waste heat recovery in marine engines. Energy Convers. Manag. 2017, 151, 286–295. [Google Scholar] [CrossRef]
- Kim, S.; Choi, K.; Lee, K.; Kim, K. Evaluation of automotive waste heat recovery for various driving modes. Energy 2016, 106, 579–589. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Wang, Y.; Deng, B.; Yang, Y.; Feng, R.; Yang, J. A comparative study on various turbocharging approaches based on IC engine exhaust gas energy recovery. Appl. Energy 2014, 113, 248–257. [Google Scholar] [CrossRef]
- Vale, S.; Heber, L.; Coelho, P.; Silva, C. Parametric study of a thermoelectric generator system for exhaust gas energy recovery in diesel road freight transportation. Energy Convers. Manag. 2016, 133, 167–177. [Google Scholar] [CrossRef]
- Hoang, A.T. Waste heat recovery from diesel engines based on Organic Rankine Cycle. Appl. Energy 2018, 231, 138–166. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Li, D.; Xia, Y.; Zhang, J. A review on adsorption refrigeration technology and adsorption deterioration in physical adsorption systems. Renew. Sustain. Energy Rev. 2010, 14, 344–353. [Google Scholar] [CrossRef]
- Salek, F.; Moghaddam, A.N.; Naserian, M.M. Thermodynamic analysis of diesel engine coupled with ORC and absorption refrigeration cycle. Energy Convers. Manag. 2017, 140, 240–246. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Deng, B.; Feng, R.; Yang, J.; Zhou, F.; Zhao, X. An approach for exhaust gas energy recovery of internal combustion engine: Steam-assisted turbocharging. Energy Convers. Manag. 2014, 85, 234–244. [Google Scholar] [CrossRef]
- Mostafavi, S.A.; Mahmoudi, M. Modeling and fabricating a prototype of a thermoelectric generator system of heat energy recovery from hot exhaust gases and evaluating the effects of important system parameters. Appl. Therm. Eng. 2018, 132, 624–636. [Google Scholar] [CrossRef]
- Mohamed, E.S. Development and performance analysis of a TEG system using exhaust recovery for a light diesel vehicle with assessment of fuel economy and emissions. Appl. Therm. Eng. 2018, 147, 661–674. [Google Scholar] [CrossRef]
- Jiménez-Arreola, M.; Wieland, C.; Romagnoli, A. Direct vs indirect evaporation in Organic Rankine Cycle (ORC) systems: A comparison of the dynamic behavior for waste heat recovery of engine exhaust. Appl. Energy 2019, 242, 439–452. [Google Scholar] [CrossRef]
- Mohammadkhani, F.; Yari, M. A 0D model for diesel engine simulation and employing a transcritical dual loop Organic Rankine Cycle (ORC) for waste heat recovery from its exhaust and coolant: Thermodynamic and economic analysis. Appl. Therm. Eng. 2019, 150, 329–347. [Google Scholar] [CrossRef]
- Goyal, P.; Baredar, P.; Mittal, A.; Siddiqui, A.R. Adsorption refrigeration technology—An overview of theory and its solar energy applications. Renew. Sustain. Energy Rev. 2016, 53, 1389–1410. [Google Scholar] [CrossRef]
- Wang, R.; Xia, Z.; Wang, L.; Lu, Z.; Li, S.; Li, T.; Wu, J.; He, S. Heat transfer design in adsorption refrigeration systems for efficient use of low-grade thermal energy. Energy 2011, 36, 5425–5439. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Yuan, Z.; Chen, Q. Enhancement of heat transfer in adsorption bed of vacuum-tube with fins. Appl. Therm. Eng. 2019, 153, 291–298. [Google Scholar] [CrossRef]
- Cui, P.; Yu, M.; Liu, Z.; Zhu, Z.; Yang, S. Energy, exergy, and economic (3E) analyses and multi-objective optimization of a cascade absorption refrigeration system for low-grade waste heat recovery. Energy Convers. Manag. 2019, 184, 249–261. [Google Scholar] [CrossRef]
- Salmi, W.; Vanttola, J.; Elg, M.; Kuosa, M.; Lahdelma, R. Using waste heat of ship as energy source for an absorption refrigeration system. Appl. Therm. Eng. 2017, 115, 501–516. [Google Scholar] [CrossRef]
- She, X.; Yin, Y.; Xu, M.; Zhang, X. A novel low-grade heat-driven absorption refrigeration system with LiCl–H2O and LiBr–H2O working pairs. Int. J. Refrig. 2015, 58, 219–234. [Google Scholar] [CrossRef]
- Maryami, R.; Dehghan, A. An exergy based comparative study between LiBr/water absorption refrigeration systems from half effect to triple effect. Appl. Therm. Eng. 2017, 124, 103–123. [Google Scholar] [CrossRef]
- Cerezo, J.; Bourouis, M.; Vallès, M.; Coronas, A.; Best, R. Experimental study of an ammonia–water bubble absorber using a plate heat exchanger for absorption refrigeration machines. Appl. Therm. Eng. 2009, 29, 1005–1011. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, N.I.; Al-Sulaiman, F.A.; Ani, F.N. Performance characteristics of a solar driven lithium bromide-water absorption chiller integrated with absorption energy storage. Energy Convers. Manag. 2017, 150, 188–200. [Google Scholar] [CrossRef]
- Alelyani, S.M.; Fette, N.W.; Stechel, E.B.; Doron, P.; Phelan, P.E. Techno-economic analysis of combined ammonia-water absorption refrigeration and desalination. Energy Convers. Manag. 2017, 143, 493–504. [Google Scholar] [CrossRef]
- Srikhirin, P.; Aphornratana, S.; Chungpaibulpatana, S. A review of absorption refrigeration technologies. Renew. Sustain. Energy Rev. 2001, 5, 343–372. [Google Scholar] [CrossRef]
- Li, Y.; Hu, R. Exergy-analysis based comparative study of absorption refrigeration and electric compression refrigeration in CCHP systems. Appl. Therm. Eng. 2016, 93, 1228–1237. [Google Scholar] [CrossRef]
- Xinxing, Z.; Guozhen, X.; Fanying, K. Study on the Relationship between the Frequency Conversion Control and Stability of Lithium Bromide Absorption Chiller System. J. Beijing Univ. Civ. Eng. Archit. 2009, 8, 37–40. [Google Scholar]
- Yuan, H.; Sun, P.; Zhang, J.; Sun, K.; Mei, N.; Zhou, P. Theoretical and experimental investigation of an absorption refrigeration and pre-desalination system for marine engine exhaust gas heat recovery. Appl. Therm. Eng. 2019, 150, 224–236. [Google Scholar] [CrossRef]
- Machado, D.O.; Sánchez, A.J.; Gallego, A.J.; de Andrade, G.A.; Normey-Rico, J.E.; Bordons, C.; Camacho, E.F. Split-range control for improved operation of solar absorption cooling plants. Renew. Energy 2022, 192, 361–372. [Google Scholar] [CrossRef]
- Kim, B.; Park, J. Dynamic simulation of a single-effect ammonia–water absorption chiller. Int. J. Refrig. 2007, 30, 535–545. [Google Scholar] [CrossRef]
- Xu, Y.-J.; Zhang, S.-J.; Xiao, Y.-H. Modeling the dynamic simulation and control of a single effect LiBr–H2O absorption chiller. Appl. Therm. Eng. 2016, 107, 1183–1191. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Cornejo-Bueno, L.; Prieto, L.; Paredes, D.; García-Herrera, R. Feature selection in machine learning prediction systems for renewable energy applications. Renew. Sustain. Energy Rev. 2018, 90, 728–741. [Google Scholar] [CrossRef]
- Palagi, L.; Pesyridis, A.; Sciubba, E.; Tocci, L. Machine Learning for the prediction of the dynamic behavior of a small scale ORC system. Energy 2018, 166, 72–82. [Google Scholar] [CrossRef]
- Wang, S.X.; Wang, Y.M.; Liu, Y.; Zhang, N. Hourly solar radiation forecasting based on EMD and ELM neural network. Electr. Power Autom. Equip. 2014, 34, 7–12. [Google Scholar]
- Khosla, M.; Jamison, K.; Ngo, G.H.; Kuceyeski, A.; Sabuncu, M.R. Machine learning in resting-state fMRI analysis. Magn. Reson. Imaging 2019, 64, 101–121. [Google Scholar] [CrossRef]
- Castresana, J.; Gabiña, G.; Martin, L.; Uriondo, Z. Comparative performance and emissions assessments of a single-cylinder diesel engine using artificial neural network and thermodynamic simulation. Appl. Therm. Eng. 2020, 185, 116343. [Google Scholar] [CrossRef]
- Tan, Q.; Han, X.; Zheng, M.; Tjong, J. Neural Network Soft Sensors for Gasoline Engine Exhaust Emission Estimation. J. Energy Resour. Technol. Trans. ASME 2021, 144, 0821038. [Google Scholar] [CrossRef]
- Goyal, A.; Staedter, M.A.; Garimella, S. A review of control methodologies for vapor compression and absorption heat pumps. Int. J. Refrig. 2018, 97, 1–20. [Google Scholar] [CrossRef]
- Goyal, A.; Garimella, S. Computing thermodynamic properties of ammonia–water mixtures using artificial neural networks. Int. J. Refrig. 2019, 100, 315–325. [Google Scholar] [CrossRef]









| Working Fluid | Parameter | Value |
|---|---|---|
| Exhaust gas | Inlet temperature, °C | 253 |
| Outlet temperature, °C | 155 | |
| Flow, m3/h | 856 | |
| Ammonia | Before condenser, °C | 42.6 |
| After condenser, °C | 24.7 | |
| Generation pressure, MPa | 0.99 | |
| Absorption pressure, MPa | 0.03 | |
| Flow, m3/h | 18.6 | |
| Evaporation temperature, °C | −22.8 | |
| Return gas temperature, °C | −17.7 | |
| Rich solution | After absorber, °C | 27.8 |
| After heat exchanger, °C | 116.7 | |
| Weak solution | After generator, °C | 127.9 |
| After heat exchanger, °C | 43.1 | |
| Cooling water | Before absorber, °C | 25 |
| After absorber, °C | 26.9 | |
| Flow of absorber, m3/h | 12 | |
| After reflux condenser, °C | 42.6 | |
| Flow of reflux condenser, m3/h | 0.24 | |
| After condenser, °C | 27.2 |
| Input Exhaust Gas Temperature °C | Exhaust Gas Flow m3/h | Cooling Water Flow into the Absorber m3/h | Liquid Ammonia Flow into the Evaporator L/h | Refrigerating Capacity kW |
|---|---|---|---|---|
| 253 | 856 | 12.0 | 18.6 | 4.75 |
| 265 | 856 | 12.4 | 19.1 | 4.85 |
| 276 | 888 | 13.1 | 19.2 | 4.86 |
| 289 | 902 | 13.8 | 19.3 | 4.87 |
| 298 | 879 | 14.5 | 19.1 | 4.80 |
| 311 | 856 | 15.1 | 19.0 | 4.79 |
| 323 | 881 | 15.9 | 19.3 | 4.87 |
| 335 | 917 | 16.7 | 19.5 | 4.90 |
| 356 | 870 | 18.1 | 19.7 | 4.93 |
| 361 | 881 | 18.5 | 19.4 | 4.88 |
| Algorithm | The Maximum Relative Error (%) | |
|---|---|---|
| Cooling Water Flow | Liquid Ammonia Flow | |
| BPNN | 5.8 | 7.2 |
| ELM | 2.5 | 5.1 |
| Elman | 4.1 | 5.6 |
| Generation Temperature (°C) | Predicted Refrigeration Output (kW) | Experimental Refrigeration Output (kW) | The Relative Error (%) |
|---|---|---|---|
| 125 | 6.2 | 6.0 | 3.2 |
| 135 | 9.0 | 8.9 | 1.1 |
| 145 | 11.3 | 10.9 | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Sun, P.; Zhang, Z.; Zhang, S.; Zhao, J.; Mei, N. Performance Prediction for a Marine Diesel Engine Waste Heat Absorption Refrigeration System. Energies 2022, 15, 7070. https://doi.org/10.3390/en15197070
Sun Y, Sun P, Zhang Z, Zhang S, Zhao J, Mei N. Performance Prediction for a Marine Diesel Engine Waste Heat Absorption Refrigeration System. Energies. 2022; 15(19):7070. https://doi.org/10.3390/en15197070
Chicago/Turabian StyleSun, Yongchao, Pengyuan Sun, Zhixiang Zhang, Shuchao Zhang, Jian Zhao, and Ning Mei. 2022. "Performance Prediction for a Marine Diesel Engine Waste Heat Absorption Refrigeration System" Energies 15, no. 19: 7070. https://doi.org/10.3390/en15197070
APA StyleSun, Y., Sun, P., Zhang, Z., Zhang, S., Zhao, J., & Mei, N. (2022). Performance Prediction for a Marine Diesel Engine Waste Heat Absorption Refrigeration System. Energies, 15(19), 7070. https://doi.org/10.3390/en15197070





