Predictive Controller for Refrigeration Systems Aimed to Electrical Load Shifting and Energy Storage
Abstract
:1. Introduction
2. Literature Review
- A novel predictive controller based on a Dynamic Programming algorithm, which decides the best control action at every time-step, in order to minimize the implemented cost function.
- The development of an optimization strategy with the goal to investigate the possibility to save energy by varying the level of refrigerant in the separators of a vapor compression refrigeration system.
- The analysis of the possibility to store surplus renewable energy in the frozen product in the form of thermal energy and make the refrigeration systems a way of adding flexibility to the power grid.
3. Digital Twin
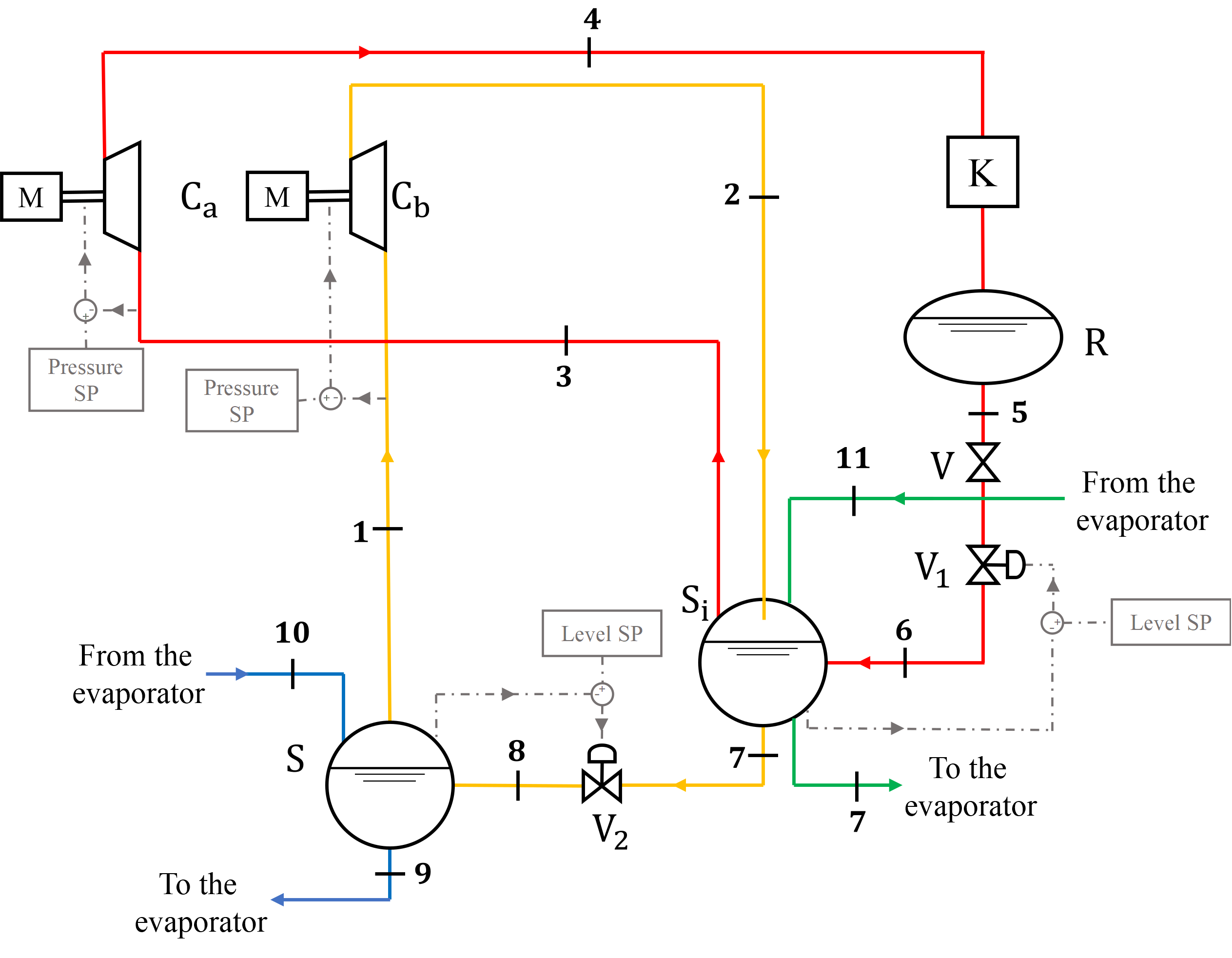
3.1. System Description
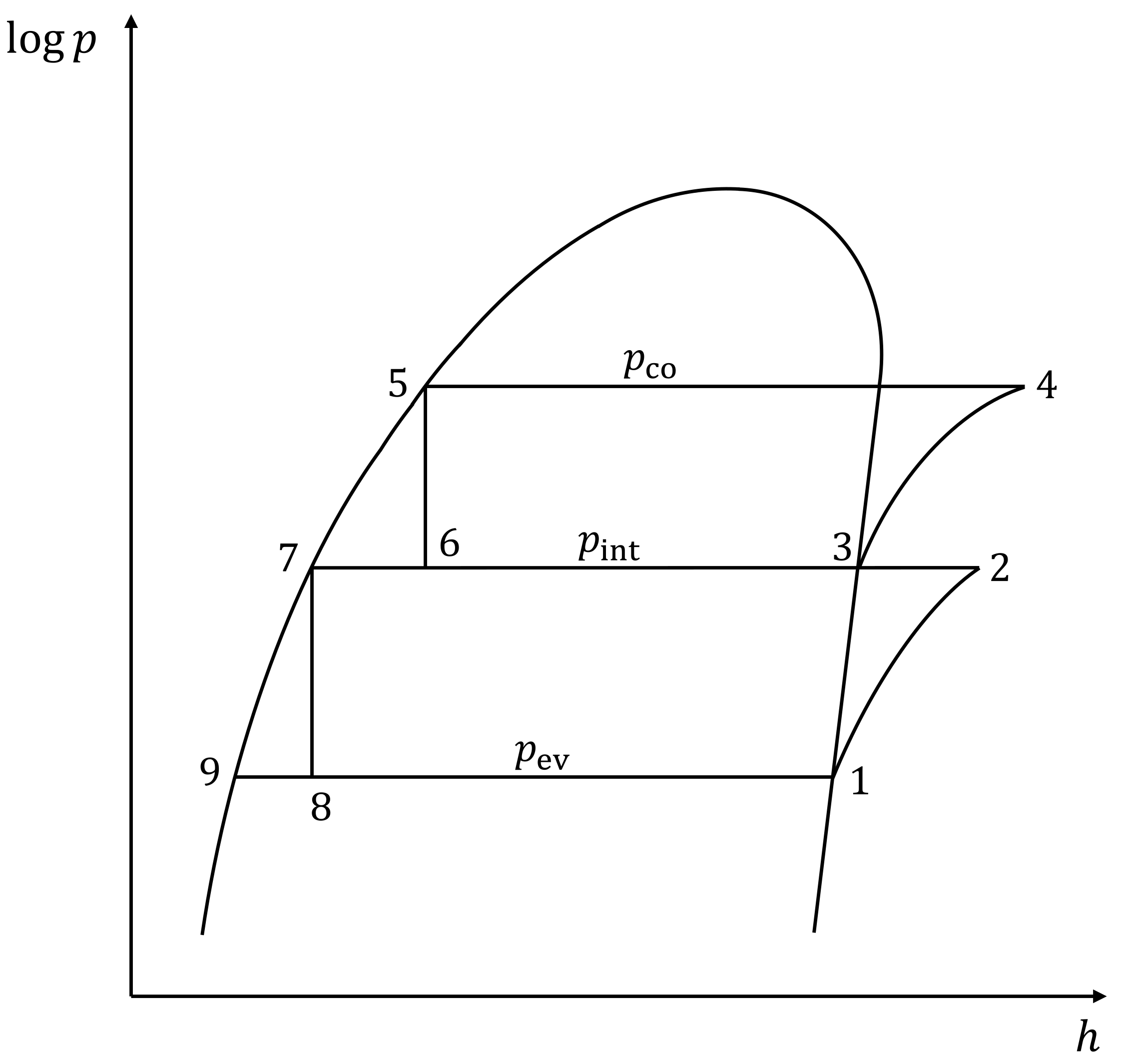
3.2. Twin-Screw Compressor Model
3.3. Separator and Receiver Models
3.4. Expansion Valve Model
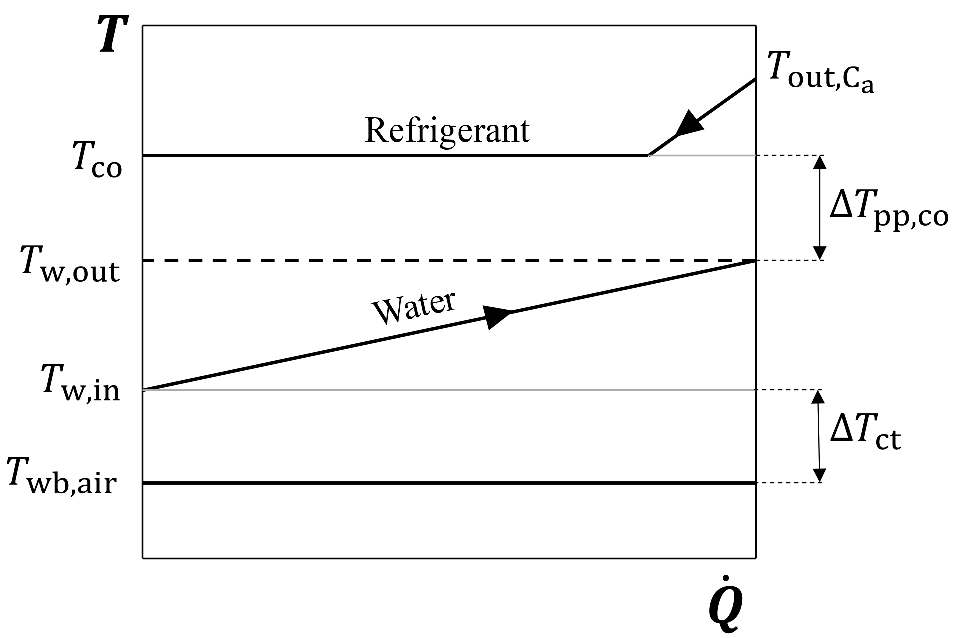
3.5. Condenser Model
4. Control Strategy
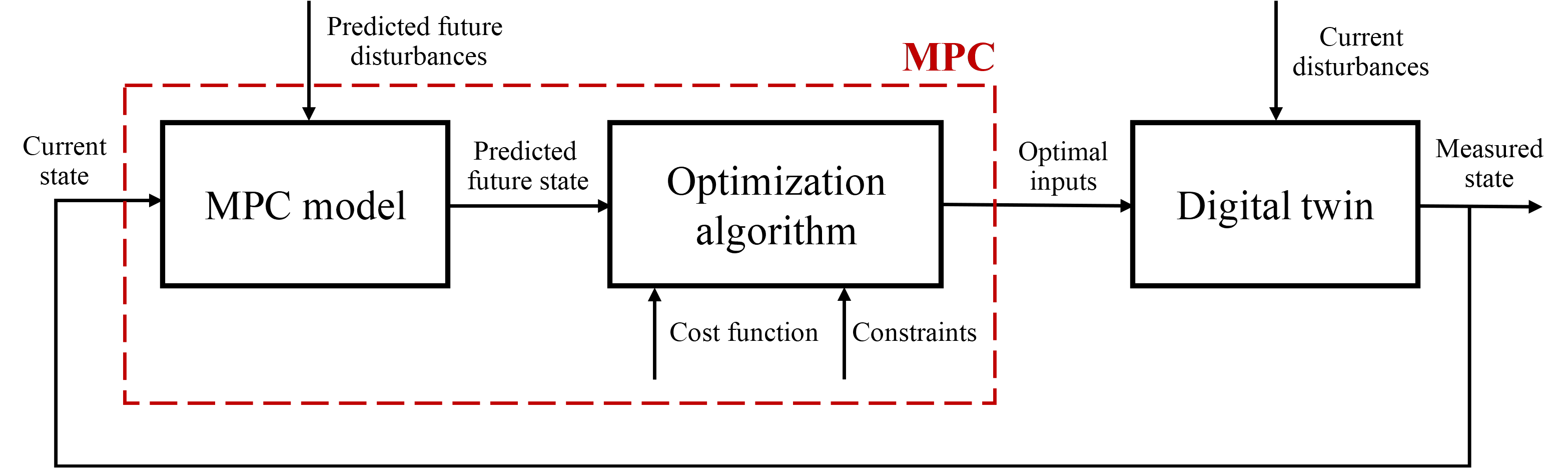
4.1. The Optimization Algorithm
4.2. MPC Model
- The optimization of level L of the low-pressure separator, which is given as a setpoint to the PI controller that regulates the opening ratio of valve V2.
- The optimization of the heat exchanged in the evaporator with the frozen product, which is given directly as an input to the evaporator.
5. Application
5.1. System Digital Twin
5.2. Description of the Case Studies
5.2.1. Single-Objective Case Study: Minimization of Total Energy Consumption
5.2.2. Multi-Objective Case Study: Minimization of Total Energy Consumption and Exploitation of Renewable Energy Production
- TC360, TC400, and TC440: in these three scenarios, a traditional control action is applied. In all scenarios, the low-pressure separator level setpoint is fixed at L = 1 m and they only differ in the value of the evaporation heat setpoint applied. These control strategies are useful to evaluate the results of the scenarios in which the MPC is implemented.
- MPC400: in this scenario, the MPC is applied; nevertheless, the evaporation heat is considered constant and equal to 400 kW, while the controller can only optimize low-pressure separator level L. The weights of the cost function are adequate to meet both objectives and they have been set after sensitivity analysis.
- MPC-ES: in this scenario, the MPC is applied, but only the first part of the cost function is considered, as and . Therefore, only the minimization of the total energy consumption is performed, and both level L and evaporation heat are optimized.
- MPC-ESRE: this scenario is the most complete. It considers both terms of the cost function, as in MPC400, with adequate weights, and both the evaporation heat and the low-pressure separator level are optimized, as in MPC-ES. Nevertheless, to estimate the benefits of this optimization, a comparison with the other considered scenarios is useful.
5.3. Key Performance Indicators
- Total energy consumption (kWh): this is the amount of energy utilized by the system, which consists of the electrical energy used by the compressors.
- CO2 emissions (kg): this is the amount of carbon dioxide emitted, which is entirely related to electrical energy consumption. Indeed, the emissions associated with renewable energy generation are considered nil, while for electricity purchased from the grid, an emission factor equal to 0.4455 kgCO2/kWh is assumed [47].
- Renewable energy utilization (%): this is the percentage of renewable energy utilized by the compressors on the total energy produced by the photovoltaic system, only applicable to the multi-objective case study.
6. Results and Discussion
6.1. Results of the Single-Objective Case Study
6.2. Results of the Multi-Objective Case Study
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A0 | orifice expansion valve area (m2) |
| am | average vapor-liquid volume ratio (-) |
| AR | receiver area (m2) |
| AS | separator area (m2) |
| c | specific heat capacity (kJ kg−1 °C−1) |
| Ca | high pressure compressor |
| Cb | low pressure compressor |
| ci | empirical valve coefficients (-) |
| Ct | heat capacity of the tubes (kJ °C−1) |
| Cv | valve flow coefficient (-) |
| eii | separator coefficients (different units) |
| FL | pressure recovery factor (-) |
| Fy | specific heat ratio (-) |
| h | specific enthalpy (kJ kg−1) |
| J | cost function (Wh) |
| K | condenser |
| L | separator level (m) |
| M | electrical motor |
| ṁ | mass flow rate (kg s−1) |
| compressor rotational speed (rad s−1) | |
| p | pressure (bar) |
| P | electrical power (W) |
| thermal power (W) | |
| R | receiver |
| S | low pressure separator |
| Si | intermediate pressure separator |
| t | time (s) |
| T | temperature (K) |
| v | specific volume (m3/kg) |
| V | volume (m3) |
| V1, V2 | expansion valves |
| x | vapor quality (-) |
| X | pressure ratio (-) |
| Xt | critical pressure ratio (-) |
| Y | expansion factor (-) |
| ρ | density (kg m−3) |
| πi | valve coefficients (-) |
| Δt | time step (s) |
| ω | weight (-) |
| Subscripts | |
| air | air |
| C,i | i-th compressor |
| co | condensation |
| ct | cooling tower |
| db | dry bulb |
| dc | downcomer |
| ES | Energy Saving |
| ev | evaporator |
| il | internal load |
| in | input |
| int | intermediate |
| l | liquid |
| out | output |
| pp | pinch-point |
| PV | photovoltaic |
| r | riser |
| RE | Renewable Energy |
| sat | saturation |
| sw | swept |
| v | vapor |
| vf | viscous friction |
| w | water |
| wb | wet bulb |
| Acronyms | |
| GHG | Greenhouse gas |
| IIAS | Istituto Italiano Alimenti Surgelati (Italian Institute for Frozen Food) |
| KPI | Key Performance Indicator |
| MiL | Model-in-the-Loop |
| MPC | Model Predictive Control |
| PI | Proportional-Integral |
| PID | Proportional-Integral-Derivative |
| SP | Setpoint |
| VCC | Vapor Compression Refrigeration Cycle |
Appendix A
References
- Dupont, J.; Domaski, P.; Lebrun, P.; Ziegler, F. The Role of Refrigeration in the Global Economy—38th Informatory Note of Refrigeration Technologies. 2019. Available online: https://iifiir.org/en/fridoc/the-role-of-refrigeration-in-the-global-economy-2019-142028 (accessed on 25 September 2022).
- Istituto Italiano Alimenti Surgelati (IIAS). I Consumi Dei Prodotti Surgelati, Rapporto 2020. Available in Italian. Available online: https://www.istitutosurgelati.it/wp-content/uploads/2021/07/IIAS_REPORTCONSUMI2020_low.pdf (accessed on 25 September 2022).
- Tassou, S.A.; Lewis, J.S.; Ge, Y.T.; Hadawey, A.; Chaer, I. A Review of Emerging Technologies for Food Refrigeration Applications. Appl. Therm. Eng. 2010, 30, 263–276. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The Role of Renewable Energy in the Global Energy Transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Richard, H.; Evangelos, G.; Jacqueline, E.; Aidan, R.; Rob, G. Unlocking the Potential of Energy Systems Integration; Imperial College London: London, UK, 2018. [Google Scholar]
- Xu, Y.C.; Chen, Q. A Theoretical Global Optimization Method for Vapor-Compression Refrigeration Systems Based on Entransy Theory. Energy 2013, 60, 464–473. [Google Scholar] [CrossRef]
- Ahmed, R.; Mahadzir, S.; Erniza B Rozali, N.; Biswas, K.; Matovu, F.; Ahmed, K. Artificial Intelligence Techniques in Refrigeration System Modelling and Optimization: A Multi-Disciplinary Review. Sustain. Energy Technol. Assess. 2021, 47, 101488. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A Survey of Industrial Model Predictive Control Technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Bejarano, G.; Alfaya, J.A.; Ortega, M.G.; Vargas, M. On the Difficulty of Globally Optimally Controlling Refrigeration Systems. Appl. Therm. Eng. 2017, 111, 1143–1157. [Google Scholar] [CrossRef]
- Lei, Z.; Zhou, Y. A Kind of Nonlinear PID Controller for Refrigeration Systems Based on Vapour Compression. In IFAC-PapersOnLine; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 51, pp. 716–721. [Google Scholar]
- Bejarano, G.; Alfaya, J.A.; Rodríguez, D.; Morilla, F.; Ortega, M.G. Benchmark for PID Control of Refrigeration Systems Based on Vapour Compression. In IFAC-PapersOnLine; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 51, pp. 497–502. [Google Scholar]
- Reynoso-Meza, G.; Sánchez, H.S.; Alves Ribeiro, V.H. Control of Refrigeration Systems Based on Vapour Compression Using Multi-Objective Optimization Techniques. In IFAC-PapersOnLine; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 51, pp. 722–727. [Google Scholar]
- Cajo, R.; Zhao, S.; Ionescu, C.M.; de Keyser, R.; Plaza, D.; Liu, S. IMC Based PID Control Applied to the Benchmark PID18. In IFAC-PapersOnLine; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 51, pp. 728–732. [Google Scholar]
- Carreño-Zagarra, J.J.; Villamizar, R.; Moreno, J.C.; Guzmán, J.L. Active Disturbance Rejection and PID Control of a One-Stage Refrigeration Cycle. In IFAC-PapersOnLine; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 51, pp. 444–449. [Google Scholar]
- Rodríguez, D.; Bejarano, G.; Alfaya, J.A.; Ortega, M.G. Robust and Decoupling Approach to PID Control of Vapour-Compression Refrigeration Systems. In IFAC-PapersOnLine; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 51, pp. 698–703. [Google Scholar]
- Salazar, M.; Méndez, F. PID Control for a Single-Stage Transcritical CO2 Refrigeration Cycle. Appl. Therm. Eng. 2014, 67, 429–438. [Google Scholar] [CrossRef]
- Zhao, B.Y.; Zhao, Z.G.; Li, Y.; Wang, R.Z.; Taylor, R.A. An Adaptive PID Control Method to Improve the Power Tracking Performance of Solar Photovoltaic Air-Conditioning Systems. Renew. Sustain. Energy Rev. 2019, 113, 109250. [Google Scholar] [CrossRef]
- Li, Y.; Ang, K.H.; Chong, G.C.Y. PID Control System Analysis and Design: Problems, Remedies, and Future Directions. IEEE Control Syst. 2006, 26, 32–41. [Google Scholar] [CrossRef]
- Yin, X.H.; Li, S.Y. Model Predictive Control for Vapor Compression Cycle of Refrigeration Process. Int. J. Autom. Comput. 2018, 15, 707–715. [Google Scholar] [CrossRef]
- Richardson, D.H.; Jiang, H.; Lindsay, D.; Radermacher, R. Optimization of Vapor Compression Systems via Simulation. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 16–19 July 2002. [Google Scholar]
- Zhao, L.; Cai, W.; Ding, X.; Chang, W. Model-Based Optimization for Vapor Compression Refrigeration Cycle. Energy 2013, 55, 392–402. [Google Scholar] [CrossRef]
- Zendehboudi, A.; Mota-Babiloni, A.; Makhnatch, P.; Saidur, R.; Sait, S.M. Modeling and Multi-Objective Optimization of an R450A Vapor Compression Refrigeration System. Int. J. Refrig. 2019, 100, 141–155. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Nejatolahi, M. Multi-Objective Optimization of a Cooling Tower Assisted Vapor Compression Refrigeration System. Int. J. Refrig. 2011, 34, 243–256. [Google Scholar] [CrossRef]
- Roy, R.; Mandal, B.K. Thermo-Economic Assessment and Multi-Objective Optimization of Vapour Compression Refrigeration System Using Low GWP Refrigerants. In Proceedings of the 2019 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Manama, Bahrain, 15–17 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Wang, H.; Cai, W.; Wang, Y. Optimization of a Hybrid Ejector Air Conditioning System with PSOGA. Appl. Therm. Eng. 2017, 112, 1474–1486. [Google Scholar] [CrossRef]
- Tian, J.; Feng, Q.; Zhu, R. Analysis and Experimental Study of MIMO Control in Refrigeration System. Energy Convers. Manag. 2008, 49, 933–939. [Google Scholar] [CrossRef]
- Kumlutaş, D.; Karadeniz, Z.H.; Avc, H.; Özşen, M. Investigation of Design Parameters of a Domestic Refrigerator by Artificial Neural Networks and Numerical Simulations. Int. J. Refrig. 2012, 35, 1678–1689. [Google Scholar] [CrossRef]
- Belman-Flores, J.M.; Mota-Babiloni, A.; Ledesma, S.; Makhnatch, P. Using ANNs to Approach to the Energy Performance for a Small Refrigeration System Working with R134a and Two Alternative Lower GWP Mixtures. Appl. Therm. Eng. 2017, 127, 996–1004. [Google Scholar] [CrossRef]
- Dangui, H.A.S.; Flesch, R.C.C.; Schwedersky, B.B.; Antonio, H.; Dangui, S.; César, R.; Flesch, C.; Schwedersky, B.B. Practical Guidelines for Tuning Model-Based Predictive Controllers for Refrigerant Compressor Test Rigs; Purdue University: West Lafayette, IN, USA, 2018. [Google Scholar]
- Yin, X.; Wang, X.; Liu, X.; Lin, M. Temperature Controller Design for Vapor Compression Refrigeration Cycle Systems. In Proceedings of the Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; IEEE: Piscataway, NJ, USA, 2017; pp. 7395–7400. [Google Scholar]
- Luchini, E.; Schirrer, A.; Kozek, M. A Hierarchical MPC for Multi-Objective Mixed-Integer Optimisation Applied to Redundant Refrigeration Circuits. In IFAC-PapersOnLine; Elsevier B.V.: Amsterdam, The Netherlands, 2017; Volume 50, pp. 9058–9064. [Google Scholar]
- Yin, X.; Li, S.; Cai, W. Enhanced-Efficiency Operating Variables Selection for Vapor Compression Refrigeration Cycle System. Comput. Chem. Eng. 2015, 80, 1–14. [Google Scholar] [CrossRef]
- Hovgaard, T.G.; Larsen, L.F.S.; Edlund, K.; Jørgensen, J.B. Model Predictive Control Technologies for Efficient and Flexible Power Consumption in Refrigeration Systems. Energy 2012, 44, 105–116. [Google Scholar] [CrossRef]
- Leducq, D.; Guilpart, J.; Trystram, G. Non-Linear Predictive Control of a Vapour Compression Cycle. Int. J. Refrig. 2006, 29, 761–772. [Google Scholar] [CrossRef]
- Gräber, M.; Kirches, C.; Schlöder, J.P.; Tegethoff, W. Nonlinear Model Predictive Control of a Vapor Compression Cycle Based on First Principle Models. IFAC Proc. Vol. 2012, 45, 258–263. [Google Scholar] [CrossRef]
- Yin, X.; Wang, X.; Li, S.; Cai, W. Energy-Efficiency-Oriented Cascade Control for Vapor Compression Refrigeration Cycle Systems. Energy 2016, 116, 1006–1019. [Google Scholar] [CrossRef]
- Yang, Z.; Pollock, D.T.; Wen, J.T. Optimisation et Commande Prédictive d’un Cycle à Compression de Vapeur Sous Charge Thermique d’impulsion Transitoire. Int. J. Refrig. 2017, 75, 14–25. [Google Scholar] [CrossRef]
- Arora, C.P. Refrigeration and Air Conditioning; Tata McGraw-Hill Education: New York, NY, USA, 2000. [Google Scholar]
- Di Mattia, E.; Gambarotta, A.; Morini, M.; Saletti, C. Application of Modelling Approaches of Twin-Screw Compressors: Thermodynamic Investigation and Reduced-Order Model Identification. E3S Web Conf. 2021, 312, 05001. [Google Scholar]
- Astrom, K.J.; Bell, R.D. Simple Drum-Boiler Models. IFAC Proc. Vol. 1988, 21, 123–127. [Google Scholar] [CrossRef]
- American National Standards Institute. Flow Equations for Sizing Control Valves: Standard; American National Standards Institute: New York, NY, USA, 1995; ISBN 0876648995. [Google Scholar]
- Knabben, F.T.; Melo, C.; Hermes, C.J.L. A Study of Flow Characteristics of Electronic Expansion Valves for Household Refrigeration Applications. Int. J. Refrig. 2020, 113, 1–9. [Google Scholar] [CrossRef]
- Parcol. Handbook for Control Valve Sizing; Parcol: Canegrate, Italy, 2016. [Google Scholar]
- Saletti, C.; Gambarotta, A.; Morini, M. Development, Analysis and Application of a Predictive Controller to a Small-Scale District Heating System. Appl. Therm. Eng. 2020, 165, 114558. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library coolprop. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [Green Version]
- Istituto Superiore per La Protezione e La Ricerca Ambientale (ISPRA). Fattori Di Emissione Atmosferica Di Gas a Effetto Serra Nel Settore Elettrico Nazionale e Nei Principali Paesi Europei. 303/2019. Available in Italian. Available online: https://tinyurl.com/ReportISPRA (accessed on 21 February 2022).





| Parameter | Symbol | Value |
|---|---|---|
| Area of the separator | 4 m2 | |
| Area of the receiver | 5 m2 | |
| Compressor swept volume | 2.33 × 10−4 m3 | |
| Compressor nominal mass flow rate | 0.4956 kg/s | |
| Condenser pinch-point temperature difference | 8 °C | |
| Cooling tower temperature difference | 10 °C |
| Parameter | Value |
|---|---|
| Evaporation pressure setpoint | 0.6 bar |
| Intermediate pressure setpoint | 2.7 bar |
| Level Si setpoint | 1.5 m |
| Level S setpoint (without MPC) | 1 m |
| Type of Control Action | Name | |||
|---|---|---|---|---|
| Traditional control | TC360 | 360 | n/a | n/a |
| Traditional control | TC400 | 400 | n/a | n/a |
| Traditional control | TC440 | 440 | n/a | n/a |
| MPC | MPC400 | 400 | 0.4 | 0.6 |
| MPC | MPC-ES | 360–440 | 1 | 0 |
| MPC | MPC-ESRE | 360–440 | 0.4 | 0.6 |
| Control Strategy (Three Central Days) | Total Energy Consumption (kWh) | CO2 Emissions (kg) | Renewable Energy Utilization (%) |
|---|---|---|---|
| Traditional control | 22,719 | 10,121 | n/a |
| MPC | 22,563 | 10,052 | n/a |
| Control Strategy (Three Central Days) | Total Energy Consumption (kWh) | CO2 Emissions (kg) | Renewable Energy Utilization (%) |
|---|---|---|---|
| TC400 | 22,734 | 4566 | 74.4% |
| MPC400 | 22,754 | 4514 | 75.2% |
| MPC-ES | 20,970 | 4143 | 69.5% |
| MPC-ESRE | 22,838 | 4275 | 78.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Mattia, E.; Gambarotta, A.; Marzi, E.; Morini, M.; Saletti, C. Predictive Controller for Refrigeration Systems Aimed to Electrical Load Shifting and Energy Storage. Energies 2022, 15, 7125. https://doi.org/10.3390/en15197125
Di Mattia E, Gambarotta A, Marzi E, Morini M, Saletti C. Predictive Controller for Refrigeration Systems Aimed to Electrical Load Shifting and Energy Storage. Energies. 2022; 15(19):7125. https://doi.org/10.3390/en15197125
Chicago/Turabian StyleDi Mattia, Edoardo, Agostino Gambarotta, Emanuela Marzi, Mirko Morini, and Costanza Saletti. 2022. "Predictive Controller for Refrigeration Systems Aimed to Electrical Load Shifting and Energy Storage" Energies 15, no. 19: 7125. https://doi.org/10.3390/en15197125
APA StyleDi Mattia, E., Gambarotta, A., Marzi, E., Morini, M., & Saletti, C. (2022). Predictive Controller for Refrigeration Systems Aimed to Electrical Load Shifting and Energy Storage. Energies, 15(19), 7125. https://doi.org/10.3390/en15197125








