Efficiency Improvement of an Electric-Grid Transformer Using the Diamagnetism Characteristics of a Bulk Superconductor
Abstract
:1. Introduction
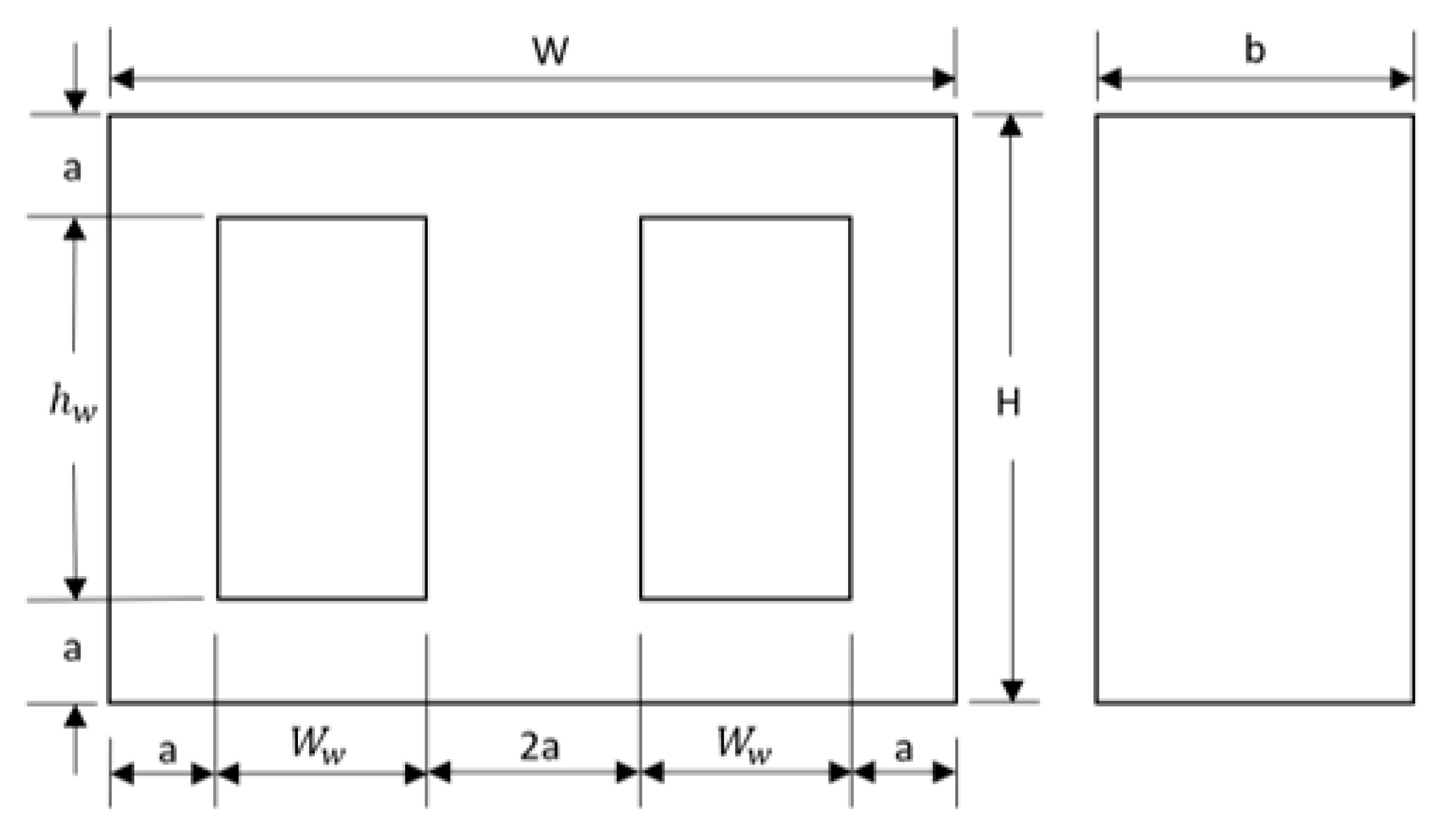
2. Transformers Design
2.1. The Conventional Transformer Model Design
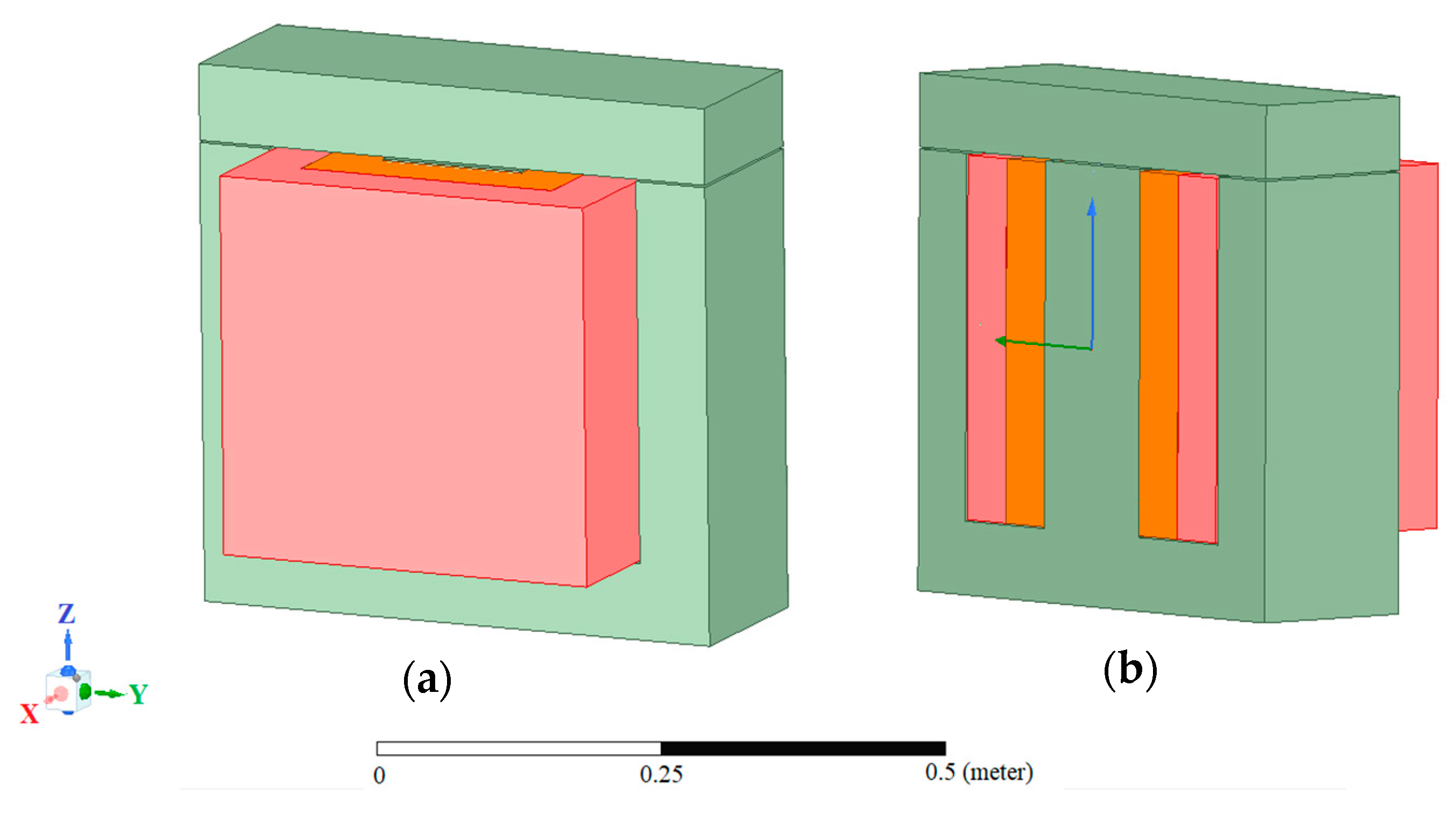
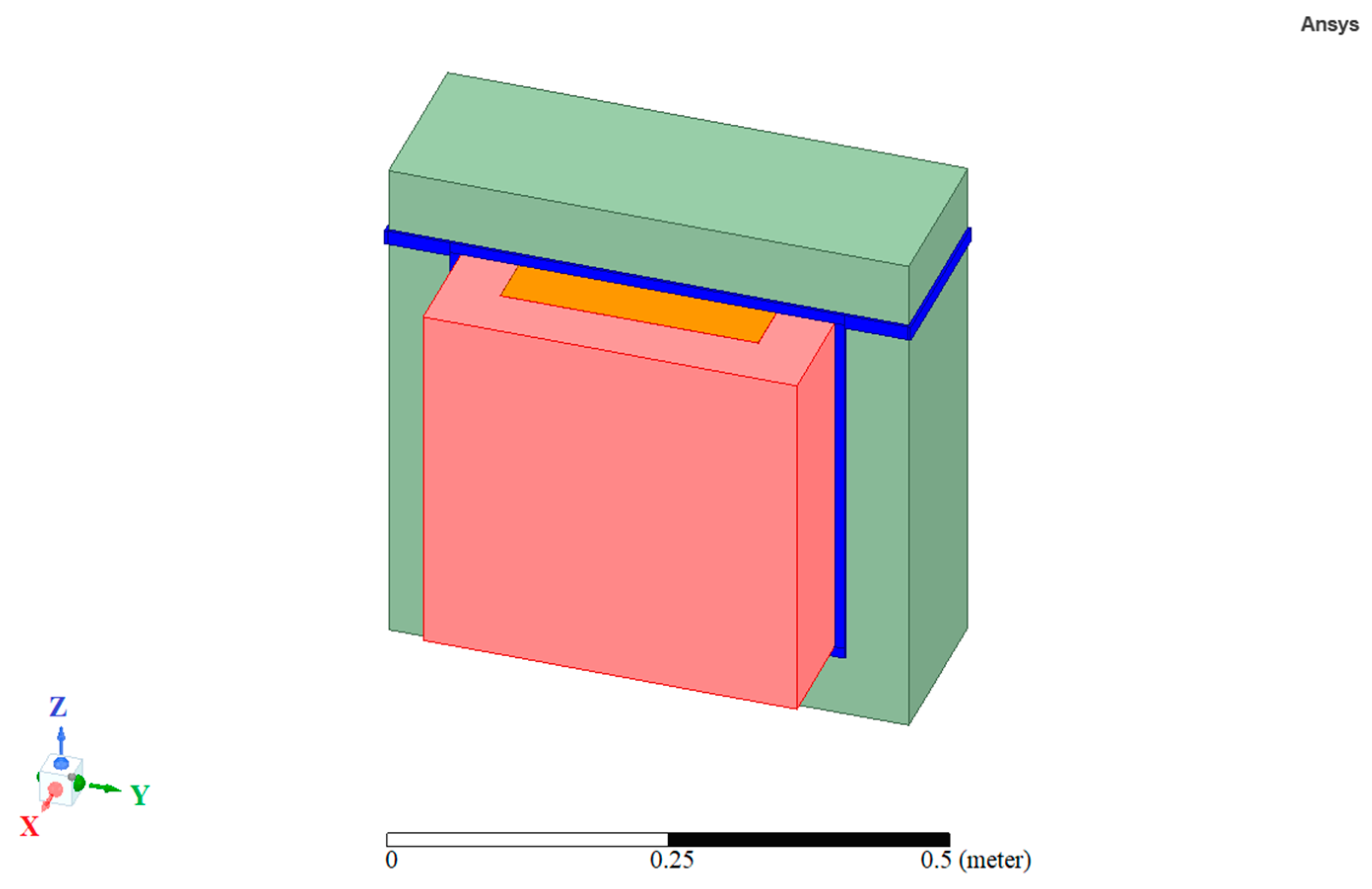
2.2. The HTS Bulk Transformer Model Design
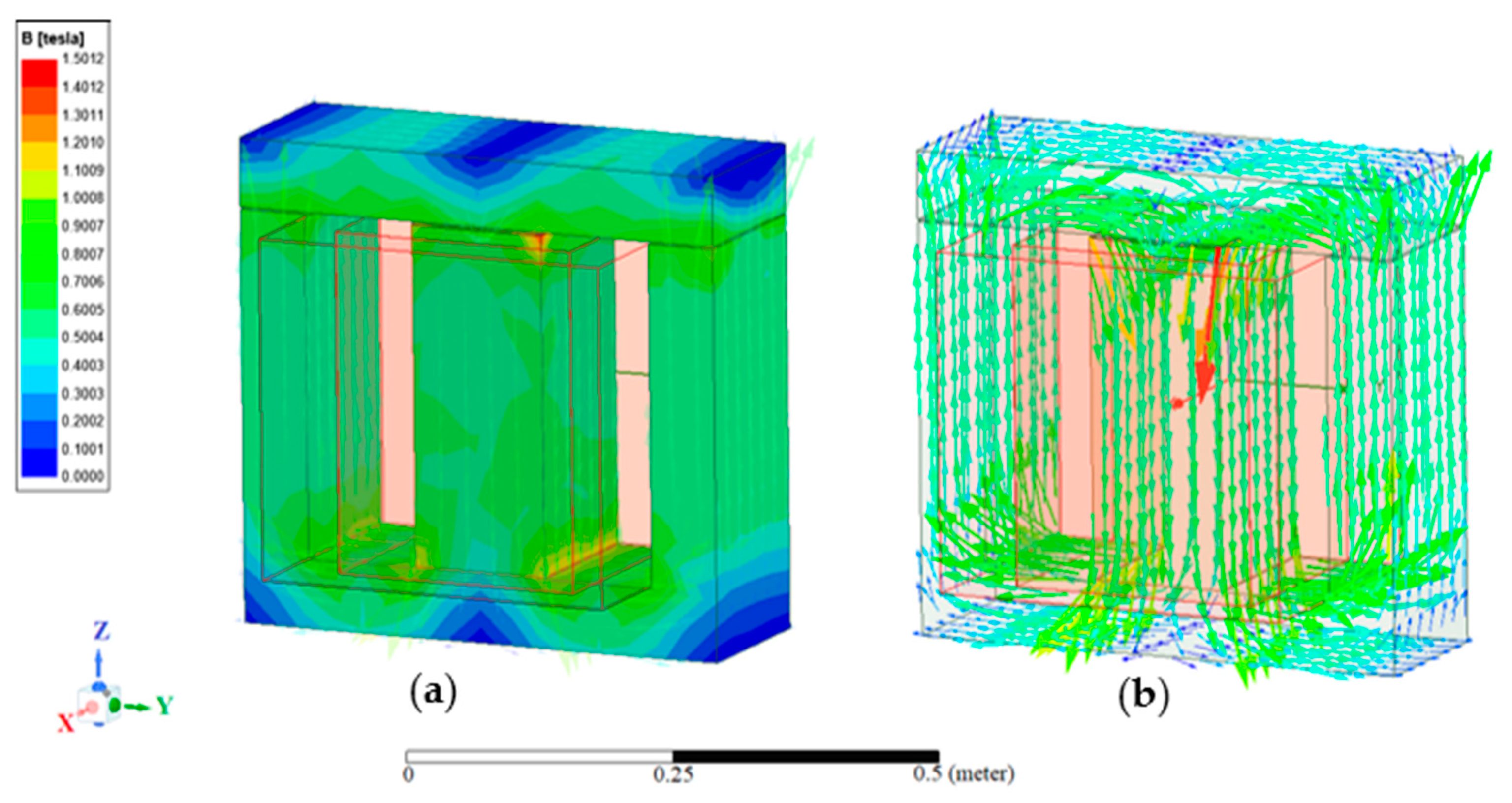
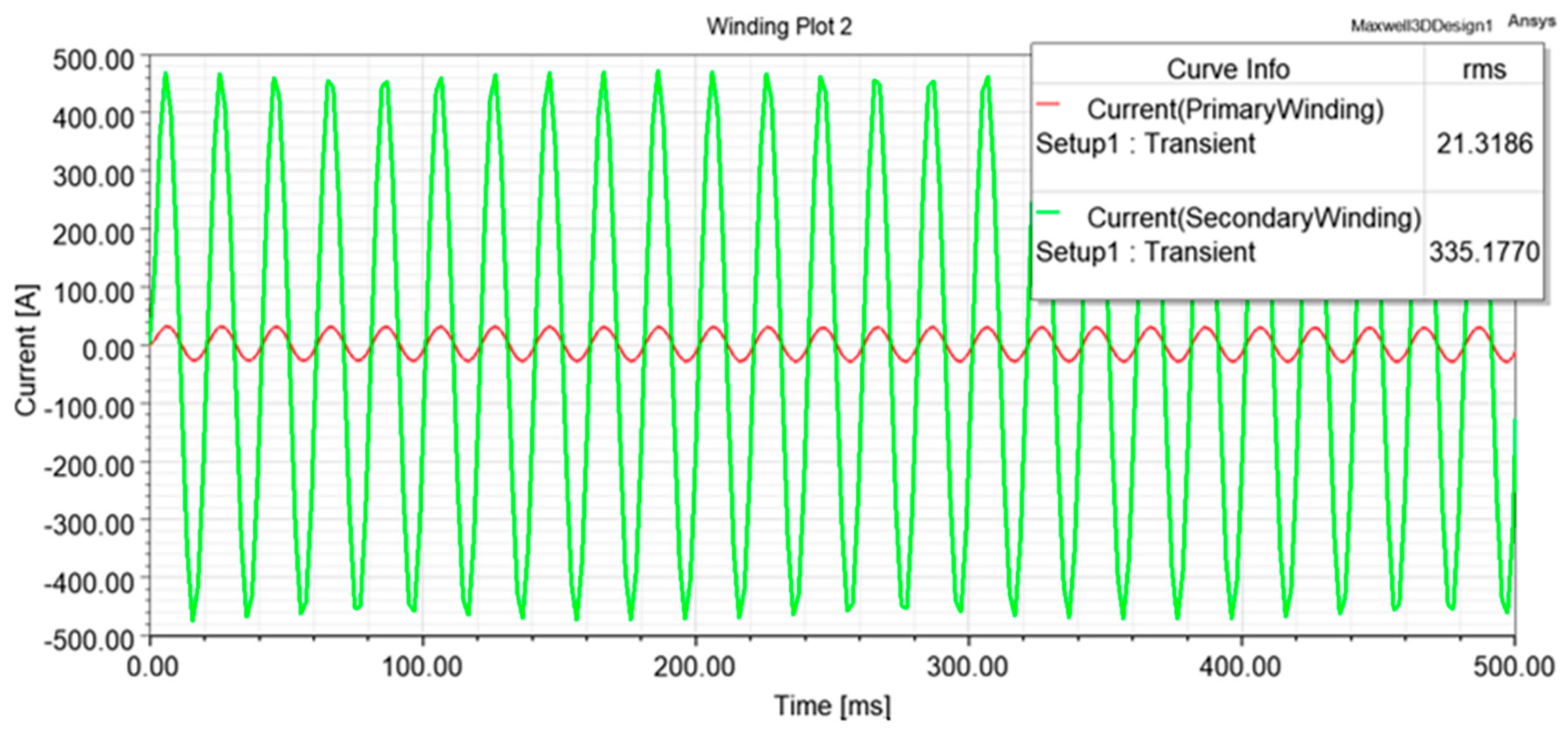
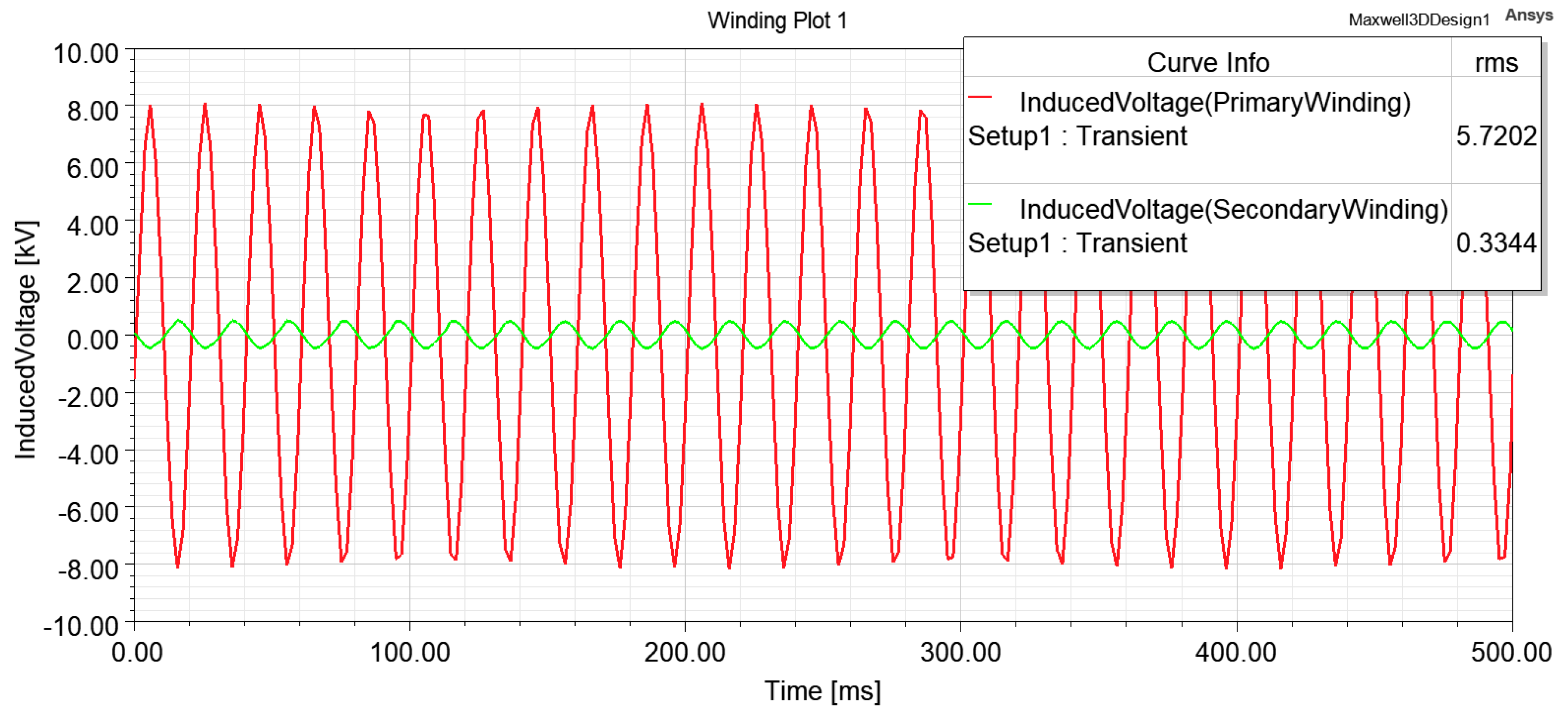
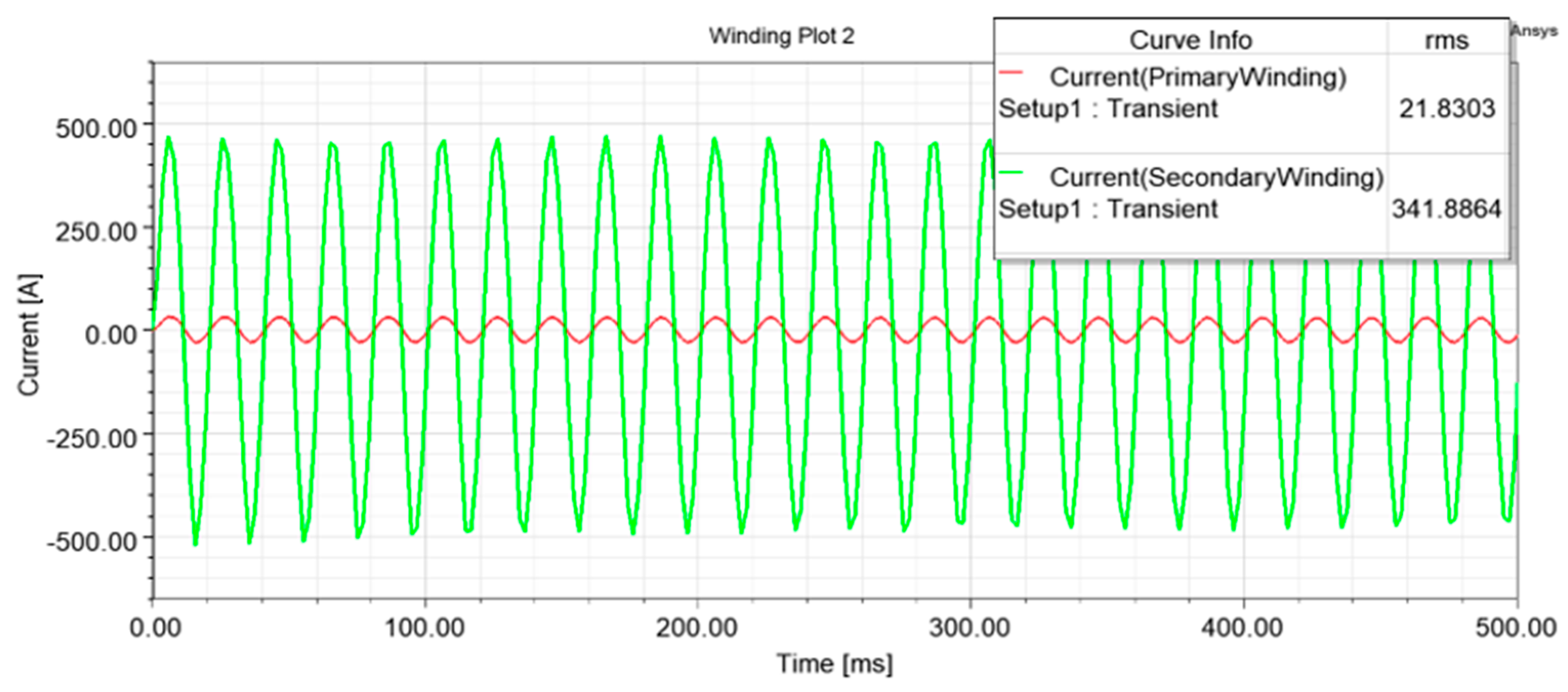
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karsai, K.; Kerenyi, D.; Kiss, L. Alternative Approaches for Distinguishing between Faults and Inrush Current in Power Transformers. Energy Power Eng. 2014, 6, 47620. [Google Scholar]
- Ashkezari, A.D.; Ma, H.; Saha, T.K.; Cui, Y. Investigation of feature selection techniques for improving efficiency of power transformer condition assessment. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 836–844. [Google Scholar] [CrossRef]
- Winders, J.J., Jr. Power Transformer Principles and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2002; Chapter 3; pp. 69–70. [Google Scholar]
- Karsai, K.; Kerenyi, D.; Kiss, L. Large Power Transformers; United States Department of Energy: Washington, DC, USA, 1987.
- Kulkarni, S.V.; Khaparde, S.A. Transformer Engineering, Design Technology and Diagnostics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012; Chapter 5; pp. 179–181. [Google Scholar]
- Baker, A.; Stefan, M.; Bertillon, H.; Bertillon, K. Contribution of Leakage Flux to the total Losses. Transformers with Magnetic Shunt. Int. J. Electr. 2020, 108, 558–573. [Google Scholar] [CrossRef]
- Al-Abadi, A.; Gamil, A.; Schatzl, F. Optimum Shielding Design for Losses and Noise Reduction in Power Transformers. In Proceedings of the 2019 6th International Advanced Research Workshop on Transformers (ARWtr), Cordoba, Spain, 7–9 October 2019; pp. 25–30. [Google Scholar]
- Li, F.M.; Jin, J.X.; Sun, R.M.; Zhu, Y.P.; Tang, C.L.; Chen, X.Y. Effects of inner air gaps on the leakage field optimization of HTS transformer windings. In Proceedings of the 2015 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Shanghai, China, 20–23 November 2015; pp. 19–20. [Google Scholar]
- Kladas, A.G.; Papadopoulos, M.P.; Tegopoulos, J.A. Leakage flux and force calculation on power transformer windings under short-circuit: 2D and 3D models based on the theory of images and the finite element method compared to measurements. IEEE Trans. Magn. 1994, 30, 3487–3490. [Google Scholar] [CrossRef]
- Moghaddami, M.; Sarwat, A.I.; De Leon, F. Reduction of stray loss in power transformers using horizontal magnetic wall shunts. IEEE Trans. Magn. 2016, 53, 8100607. [Google Scholar] [CrossRef]
- Chen, X.; Jin, J. Development and technology of HTS transformers. Res. Commun. 2007, 1, 2.1–2.7. [Google Scholar]
- Holdengreber, E.; Moshe, A.G.; Mizrahi, M.; Khavkin, V.; Schacham, S.E.; Farber, E. High Sensitivity High Tc Superconducting Josephson Junction Antenna for 200GHz Detection. J. Electromagn. Waves Appl. 2019, 33, 193–203. [Google Scholar] [CrossRef]
- Holdengreber, E.; Gao, X.; Mizrahi, M.; Schacham, S.E.; Farber, E. Superior Impedance Matching of THz Antennas with HTSC Josephson Junctions. Supercond. Sci. Technol. 2019, 32, 074006. [Google Scholar] [CrossRef]
- Holdengreber, E.; Moshe, A.G.; Schacham, S.E.; Mizrahi, M.; Dhasarathan, V.; Farber, E. THz Radiation Measurement with HTSC Josephson Junction Detector Matched to Planar Antenna. Appl. Sci. 2020, 10, 6482. [Google Scholar] [CrossRef]
- Dahan, Y.; Holdengreber, E.; Mizrahi, M.; Schacham, S.E.; Farber, E. Multi-Channel Transmitting System Based on High Temperature Superconducting Phase Shifter. IEEE Trans. Appl. Supercond. 2020, 30, 3500506. [Google Scholar] [CrossRef]
- Holdengreber, E.; Mizrahi, M.; Glassner, E.; Dahan, Y.; Castro, H.; Farber, E. Design and implementation of an RF coupler based on YBCO superconducting films. IEEE Trans. Appl. Supercond. 2015, 25, 1500905. [Google Scholar] [CrossRef]
- Fukuoka, K.; Hashimoto, M. Proposal of transformer using magnetic shielding with bulk high T/sub c/superconductors. IEEE Trans. Appl. Supercond. 2004, 14, 1126–1129. [Google Scholar] [CrossRef]
- Denis, S.; Dusoulier, L.; Dirickx, M.; Vanderbemden, P.H.; Cloots, R.; Ausloos, M.; Vanderheyden, B. Magnetic shielding properties of high-temperature superconducting tubes subjected to axial fields. Supercond. Sci. Technol. 2007, 20, 192–201. [Google Scholar] [CrossRef]
- Harlow, J.H. Electric Power Transformer Engineering, 2nd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2007; Chapter 3. [Google Scholar]
- Chapman, S.J. Electric Machinery Fundamentals, 5th ed.; BAE Systems Australia: Adelaide, Australia, 2012; Chapter 2; p. 25. [Google Scholar]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; Harvard University: Cambridge, MA, USA, 1996. [Google Scholar]
- Tomita, M.; Murakami, M. High Temperature Superconductor Bulk Magnet that can trap magnetic fields of over 17 T at 29 K. Nature 2003, 421, 517–520. [Google Scholar] [CrossRef] [PubMed]
- Douine, B.; Berger, K.; Ivanov, N. Characterization of high-temperature superconductor bulks for electrical machine application. Materials 2021, 14, 1636. [Google Scholar] [CrossRef] [PubMed]
- Holdengreber, E.; Mizrahi, M.; Farber, E. Quasi-dynamical multi-channel coupler based on high temperature superconducting films. In Proceedings of the 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Israel, Eliat, Israel, 14–17 October 2012; pp. 1–4. [Google Scholar]
- Holdengreber, E.; Moshe, A.G.; Dhasarathan, V.; Schacham, S.E.; Farber, E. Temperature Effect on Selectivity of HTSC Josephson Junction Detector. IEEE Trans. Appl. Supercond. 2021, 31, 1102004. [Google Scholar] [CrossRef]
- Holdengreber, E.; Schacham, S.E.; Farber, E. Impedance mismatch elimination for improved THz detection by superconducting Josephson junctions. In Proceedings of the Antennas and Propagation Conference 2019 (APC-2019), Birmingham, UK, 11–12 November 2019; pp. 1–3. [Google Scholar]
- Holdengreber, E.; Mizrahi, M.; Citron, N.; Schacham, S.E.; Farber, E. Very Low-Noise Figure HTSC RF Front-End. Electronics 2022, 11, 1270. [Google Scholar] [CrossRef]
- Holdengreber, E. A Serial Josephson Junction Antenna Array. In Proceedings of the 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 16–18 October 2020; pp. 1–2. [Google Scholar]
- Holdengreber, E.; Mizrahi, M.; Schacham, S.E.; Farber, E. Remote location of superconducting Josephson junction in planar antennas for improved THz detection. In Proceedings of the 2019 IEEE International Superconductive Electronics Conference (ISEC), Riverside, CA, USA, 28 July–1 August 2019; pp. 1–5. [Google Scholar]
- Dahan, Y.; Holdengreber, E.; Glassner, E.; Sorkin, O.; Schacham, S.E.; Farber, E. Measurement of Electrical Properties of Superconducting YBCO Thin Films in the VHF Range. Materials 2021, 14, 3360. [Google Scholar] [CrossRef] [PubMed]
- Citron, N.; Holdengreber, E.; Sorkin, O.; Schacham, S.E.; Farber, E. High-Performance RF Balanced Microstrip Mixer Configuration for Cryogenic and Room Temperatures. Electronics 2022, 11, 102. [Google Scholar] [CrossRef]

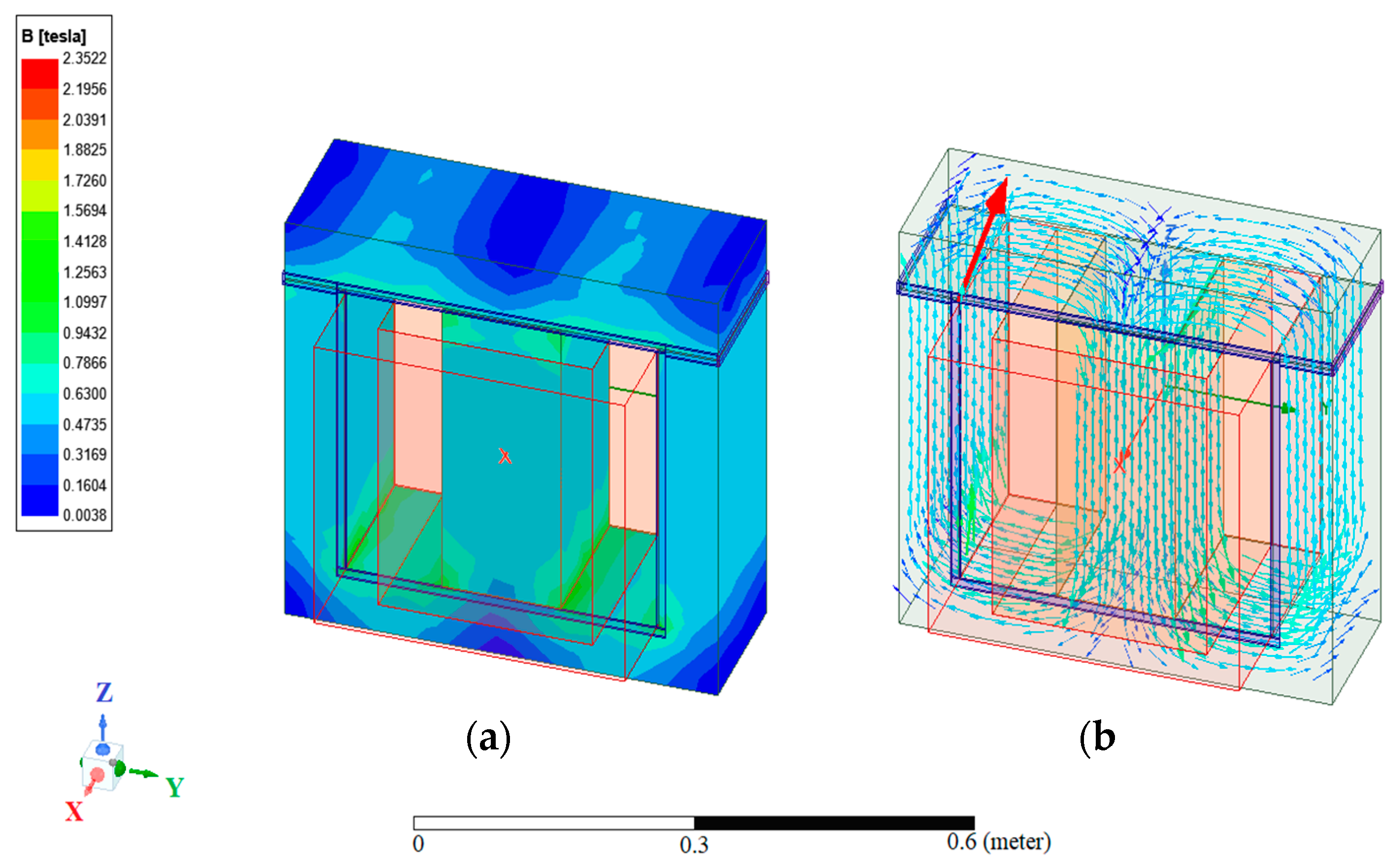

| Parameter | Value |
|---|---|
| Type | 1 phase Shell |
| kVA | 125 |
| Frequency | 50 Hz |
| HV Volts | 6600 |
| LV Volts | 400 |
| Parameter | Value |
|---|---|
| variable | |
| 28.91 | |
| 0.599 | |
| 2.887 | |
| 7872 kg/m3 | |
| variable |
| Model Type | PEC Thickness [mm] | PEC Width [mm] | Primary Induced Voltage [V] | Primary Induced Current [A] | Secondary Induced Voltage [V] | Secondary Induced Current [A] | Primary Induced Power [VA] | Secondary Induced Power [VA] |
|---|---|---|---|---|---|---|---|---|
| Conventional | - | - | 5687 | 21.3186 | 333.1 | 335.177 | 122,781 | 111,647 |
| BSST | 1 | 13.2 | 5637.9 | 21.3517 | 331.5 | 335.3547 | 120,379 | 111,170 |
| BSST | 2 | 13.2 | 5723.3 | 21.4258 | 335.5 | 336.6238 | 122,626 | 112,937 |
| BSST | 2.2 | 13.2 | 5731.3 | 21.8002 | 334.7 | 341.0928 | 124,943 | 114,164 |
| BSST | 2.4 | 13.2 | 5643.1 | 21.3379 | 332 | 335.2483 | 120,412 | 111,302 |
| BSST | 2.6 | 13.2 | 5720.2 | 21.8303 | 334.4 | 341.8864 | 124,874 | 114,327 |
| BSST | 2.8 | 13.2 | 5561.5 | 21.1708 | 326 | 329.9949 | 117,741 | 107,578 |
| BSST | 3 | 13.2 | 5591.4 | 21.0236 | 327.6 | 329.1144 | 117,551 | 107,818 |
| Transformer Type | Transformer Configuration/Dimensions | f (Hz) | Cooling | Primary Induced Voltage [V] | Secondary Induced Voltage [V] | No Load Loss (W) |
|---|---|---|---|---|---|---|
| CSP Auto protegido | Pole mounted Oil-immersed 1020 × 660 × 900 cm3 | 50 | Air/Dry | 13,200 | 200 | 210 |
| MT-DOE16-1P Isolation Transformer | Dry type 122 × 122 × 109 cm3 | 60 | Air/Dry | 480 | 240 | 350 |
| MT-ISX-3P Isolation Transformer | Dry type 76 × 83.5 × 105.5 cm3 | 60 | Air/Dry | 480 | 400 | 240 |
| Conventional | Shell type 46 × 34 × 7 cm3 | 50 | Air/Dry | 5687 | 333 | 129 |
| BSST | Shell type 46 × 34 × 7 cm3 | 50 | Cryogenic temperature | 5720 | 334 | 132 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaked, D.; Holdengreber, E. Efficiency Improvement of an Electric-Grid Transformer Using the Diamagnetism Characteristics of a Bulk Superconductor. Energies 2022, 15, 7146. https://doi.org/10.3390/en15197146
Shaked D, Holdengreber E. Efficiency Improvement of an Electric-Grid Transformer Using the Diamagnetism Characteristics of a Bulk Superconductor. Energies. 2022; 15(19):7146. https://doi.org/10.3390/en15197146
Chicago/Turabian StyleShaked, Daniel, and Eldad Holdengreber. 2022. "Efficiency Improvement of an Electric-Grid Transformer Using the Diamagnetism Characteristics of a Bulk Superconductor" Energies 15, no. 19: 7146. https://doi.org/10.3390/en15197146
APA StyleShaked, D., & Holdengreber, E. (2022). Efficiency Improvement of an Electric-Grid Transformer Using the Diamagnetism Characteristics of a Bulk Superconductor. Energies, 15(19), 7146. https://doi.org/10.3390/en15197146









