A Numerical Study on Heat Transfer Characteristics of a Novel Rectangular Grooved Microchannel with Al2O3/Water Nanofluids
Abstract
:1. Introduction
2. Numerical Method
2.1. Geometric Model
2.2. Mathematical Model
- The heat transfer and flow are in a steady state and are fully developed;
- The nanofluid is incompressible;
- The thermophysical properties are constant;
- The radiative and natural convection heat transfer between the external surfaces of the microchannel and the ambient are neglected;
- The viscous heating of nanofluid is considered.
2.3. Thermophysical Properties of Nanofluids
2.4. Boundary Conditions
- Inlet: Tin = 303.16 K; u = uin, v = 0, w = 0.
- Outlet: p = 1 atm.
- Interface between fluid and solid: Ts = Tf, ; u = 0, v = 0, w = 0.
- The bottom surface: (for model reliability verification), (for this study);
- At other wall surfaces: ;
2.5. Numerical Method
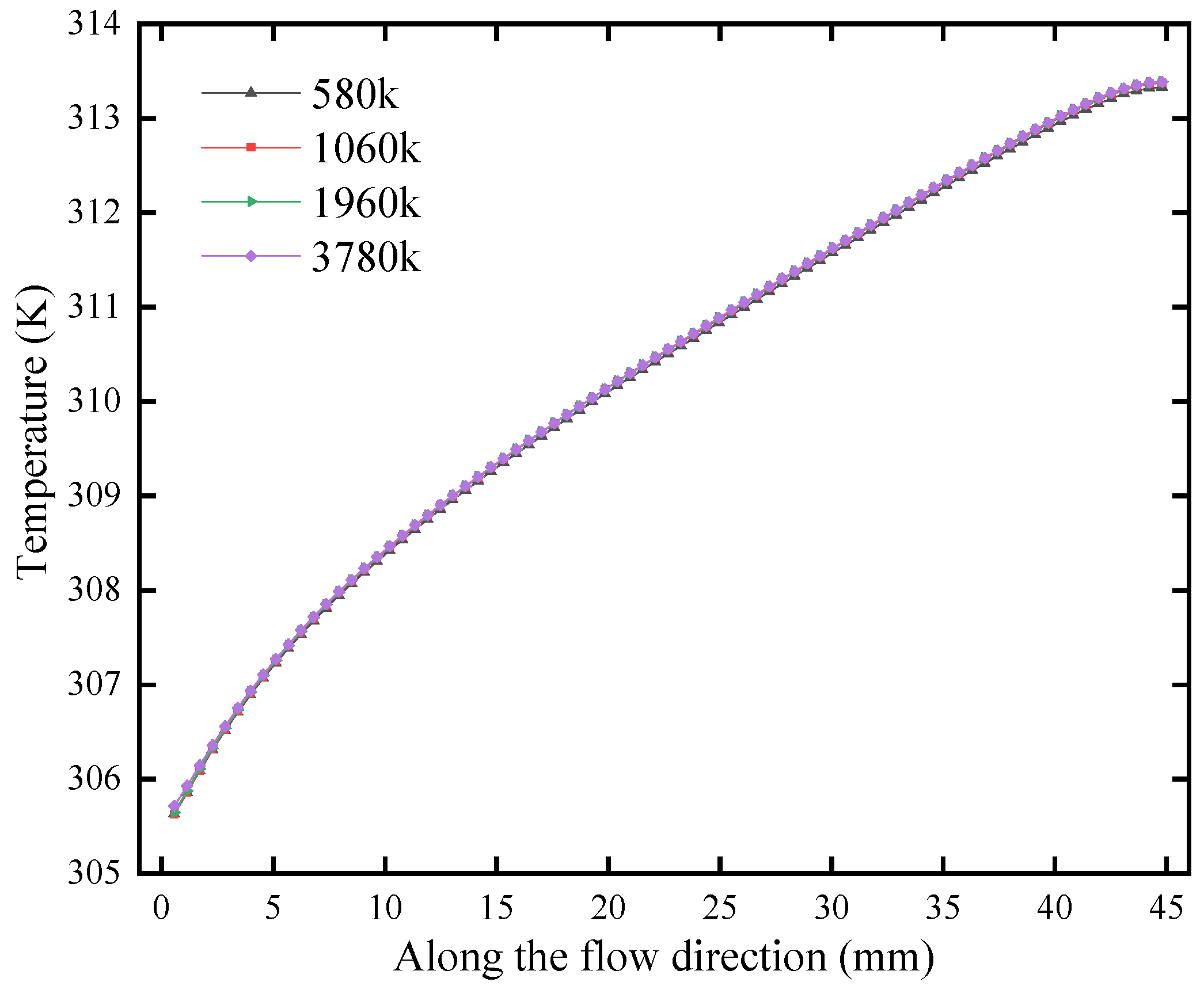
2.5.1. Mesh Sensitivity
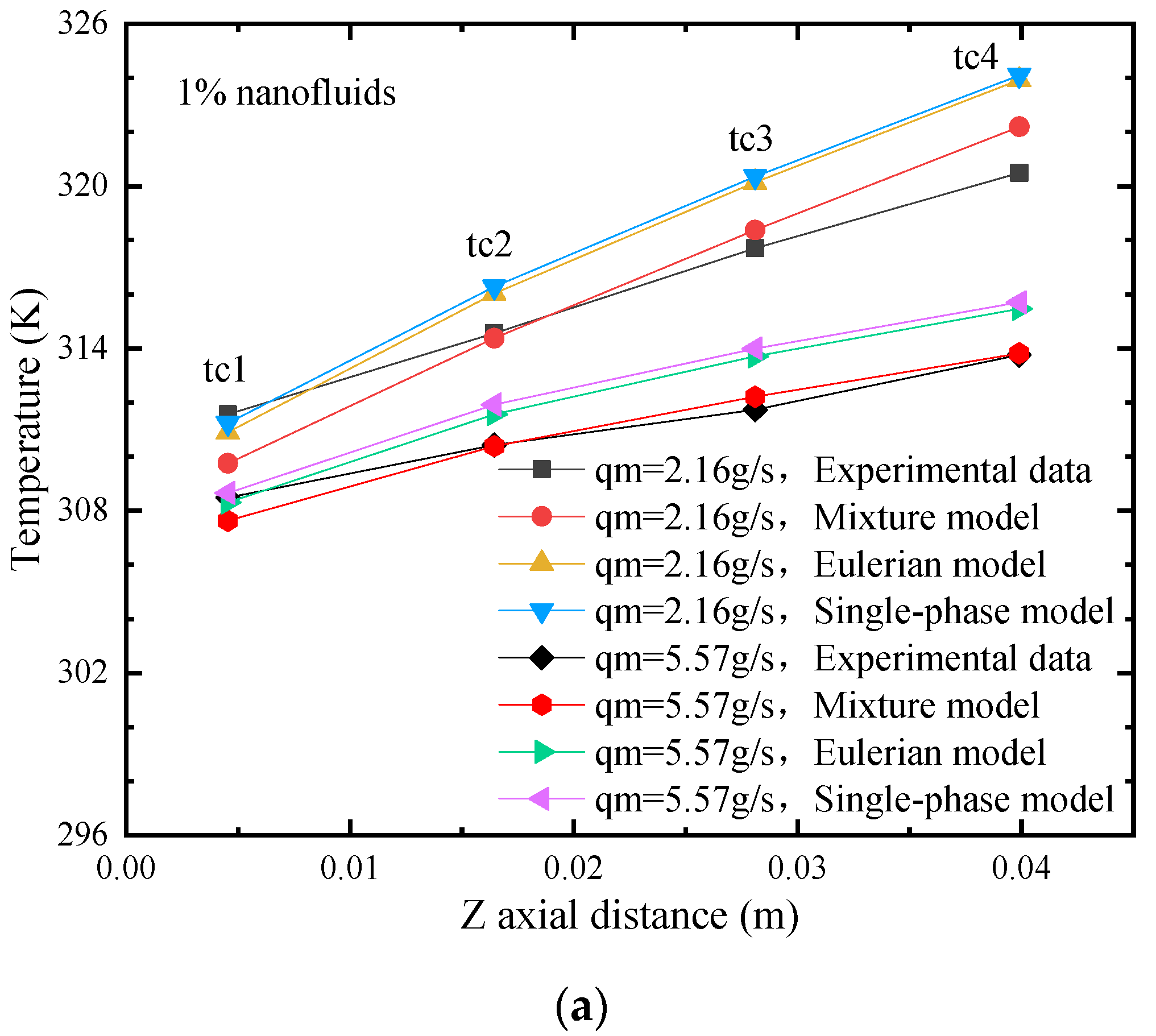
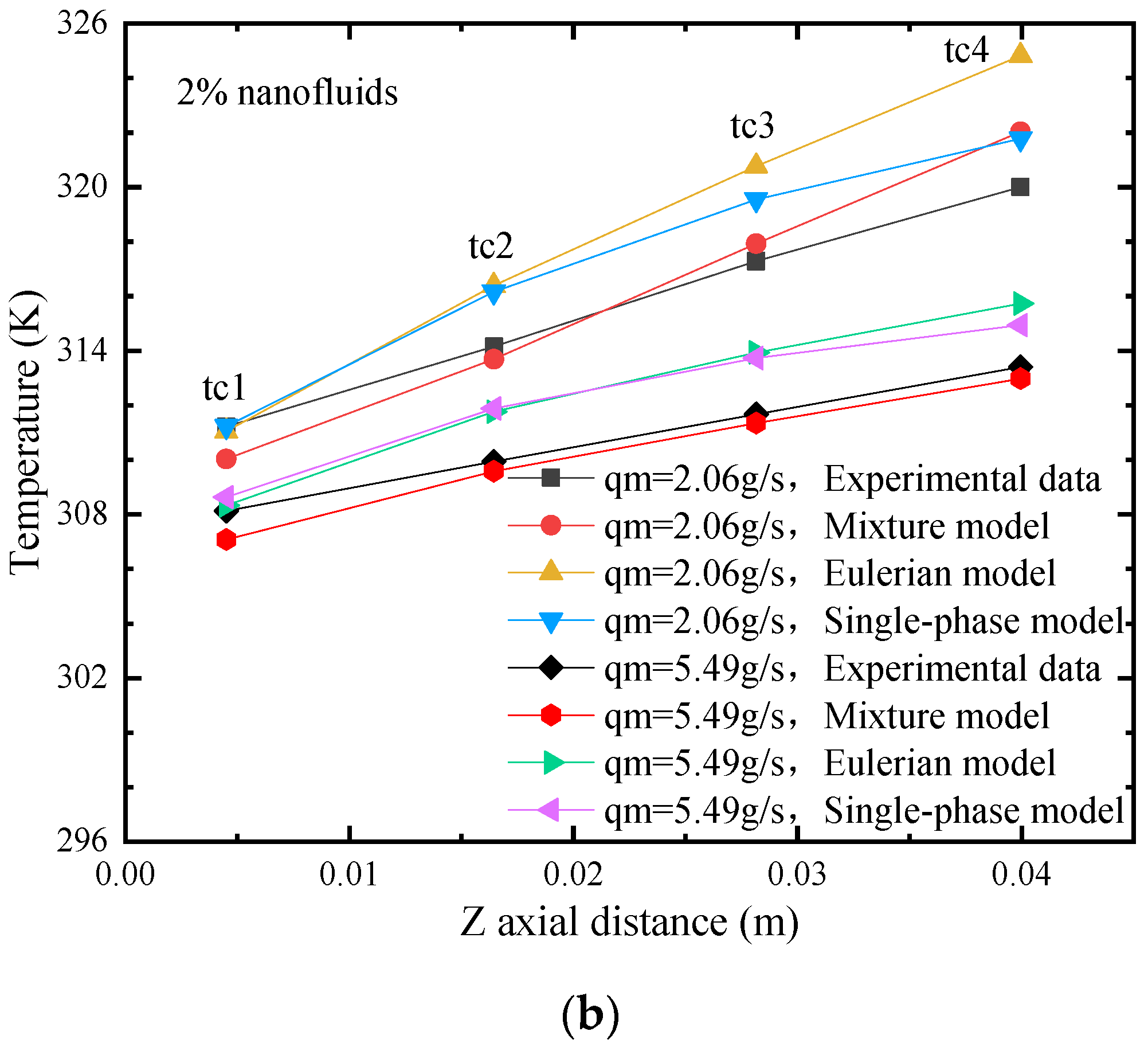
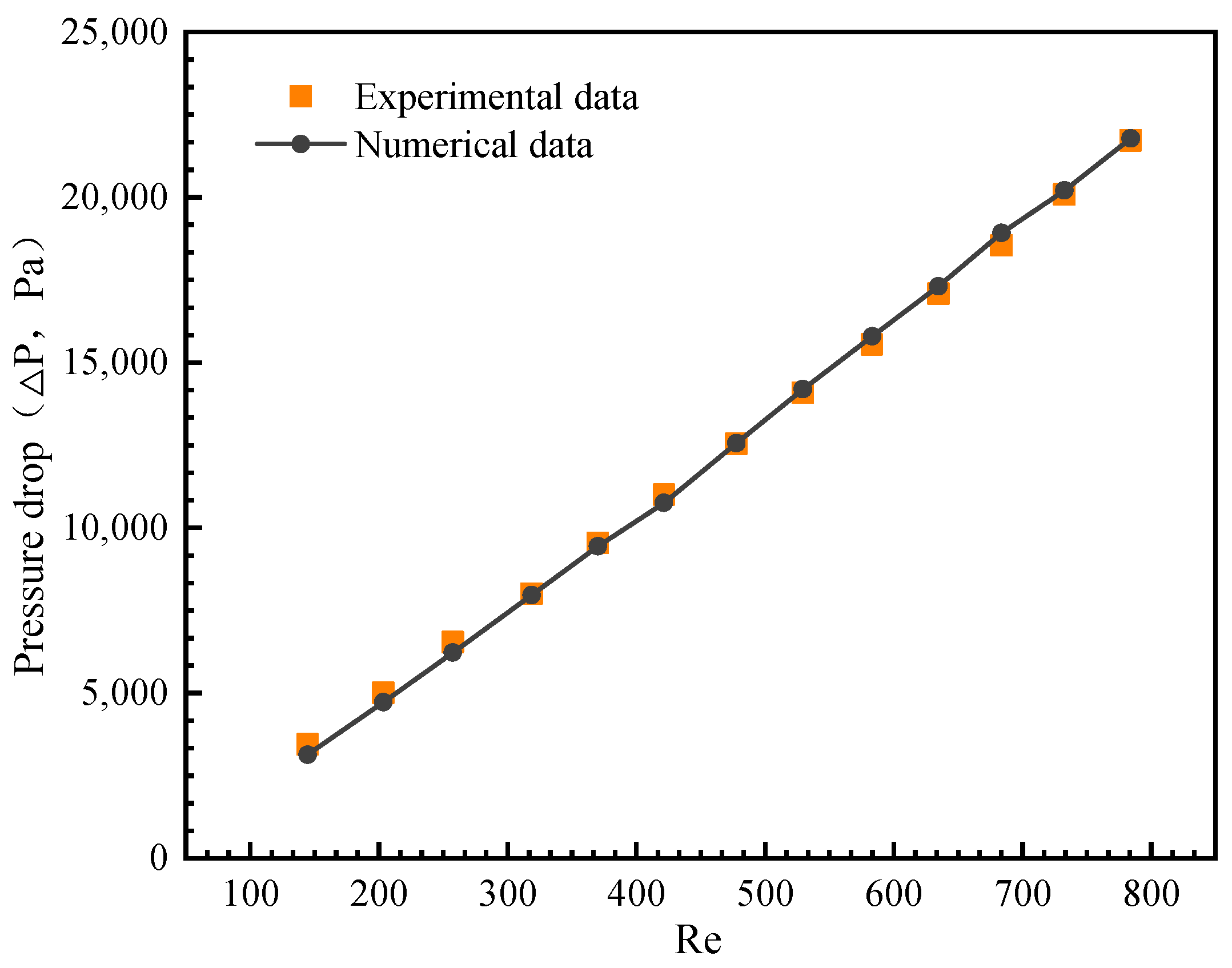
2.5.2. Model Validation
2.5.3. Study Cases
3. Results and Analysis
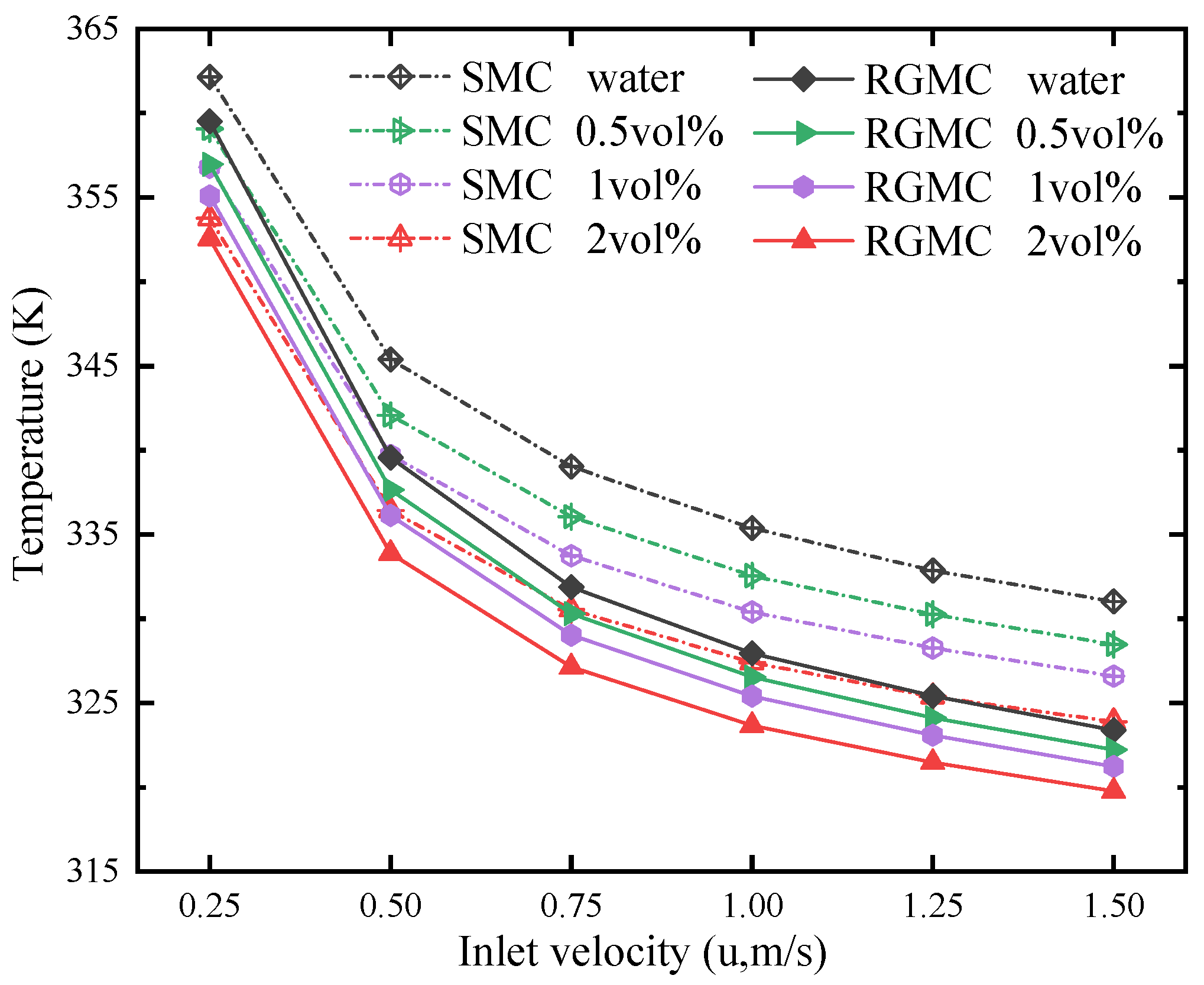
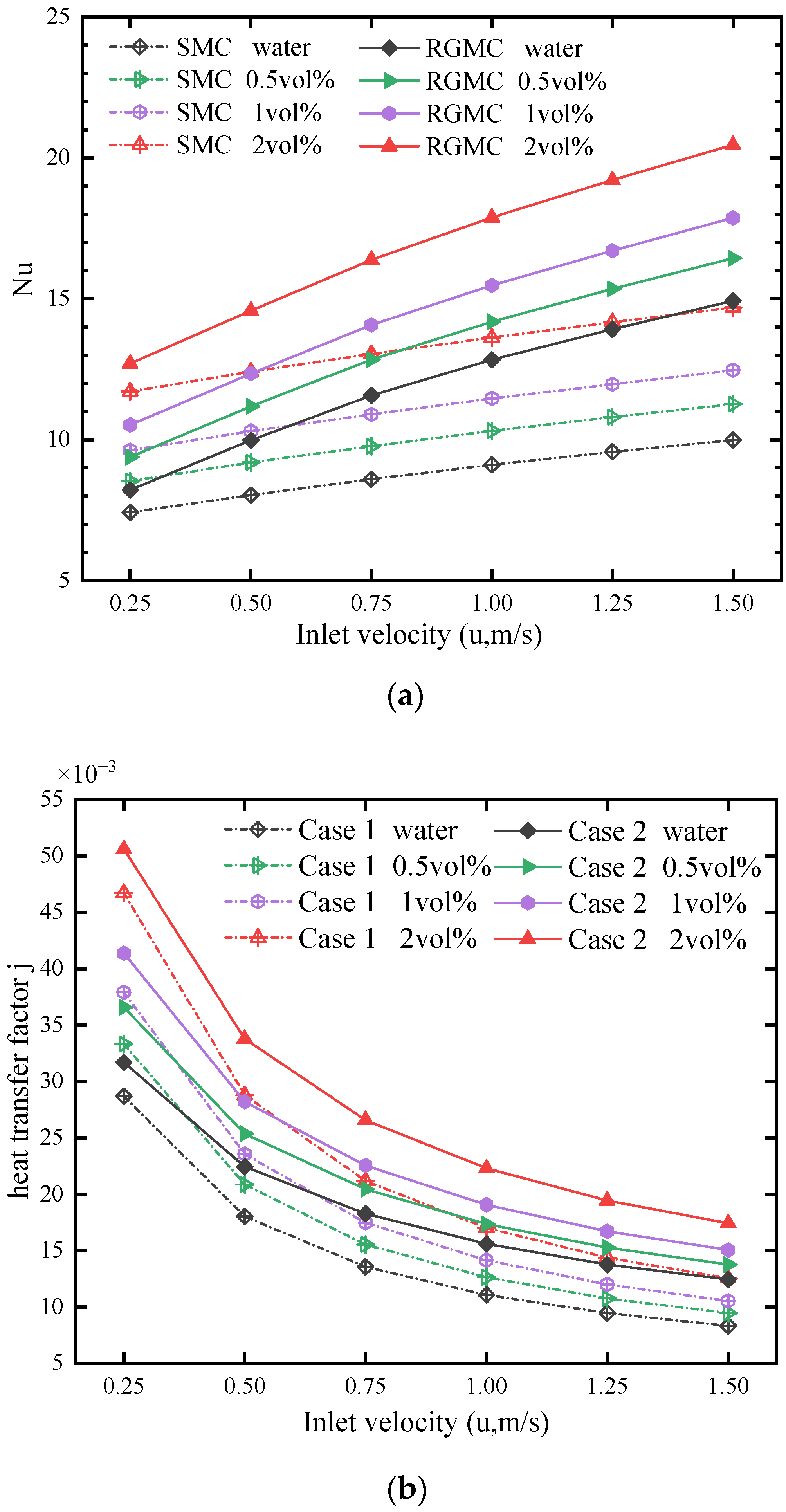
3.1. Heat Transfer Characteristics Analysis
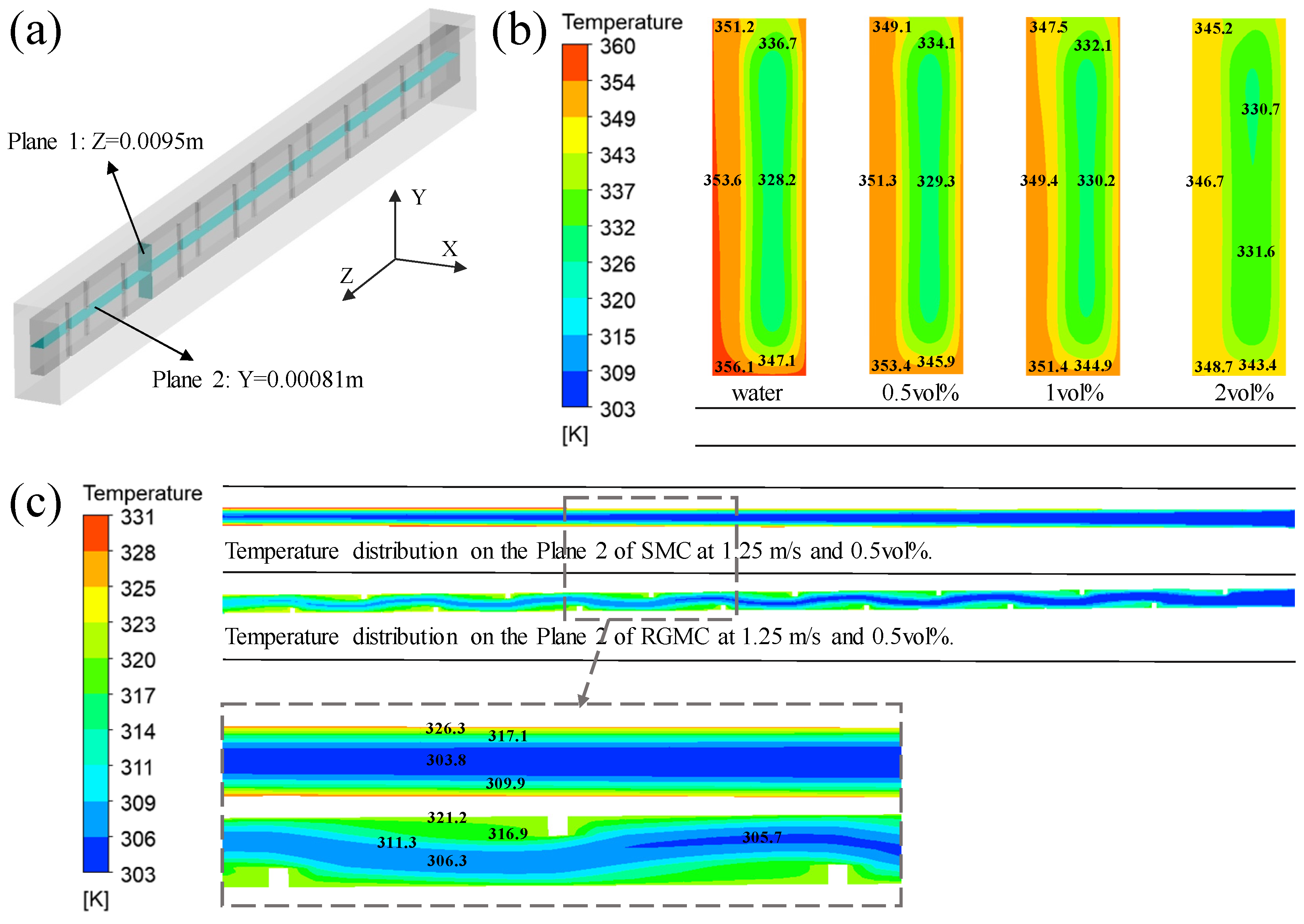
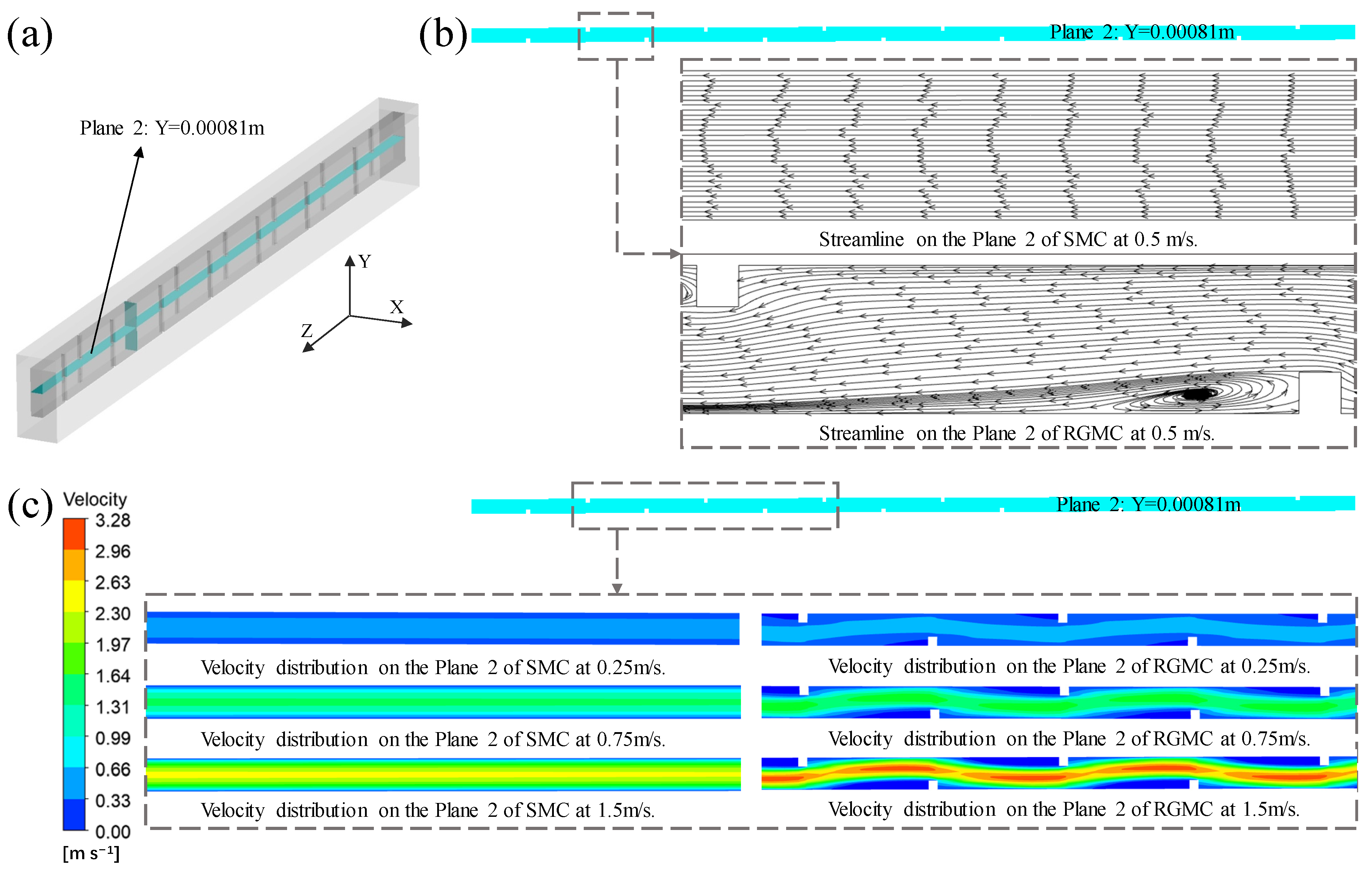
3.2. Effect of Grooves on Flow Disturbance
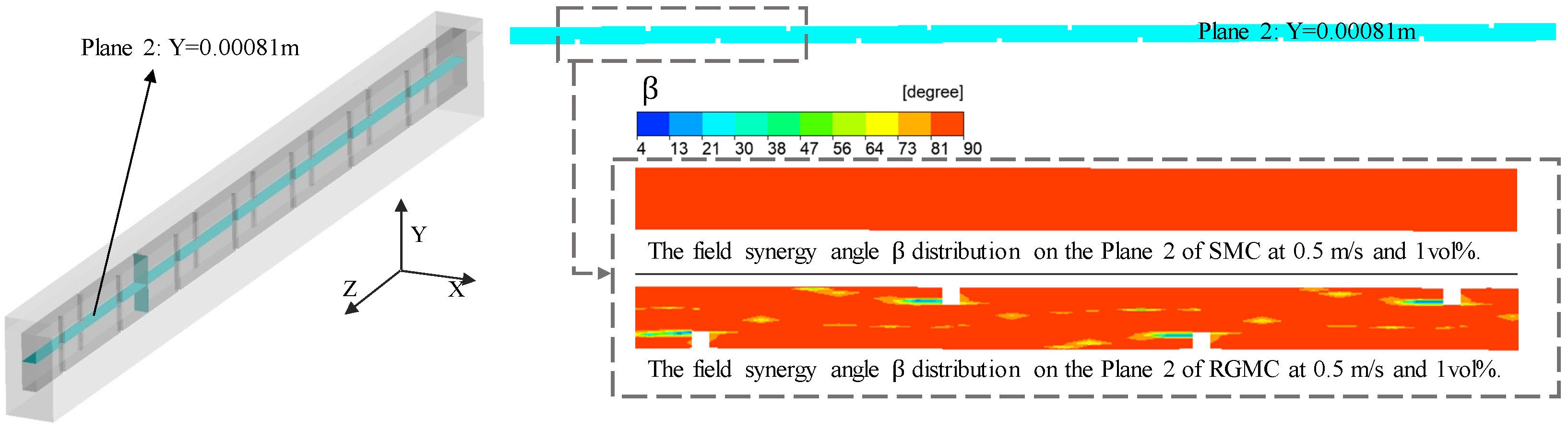
3.3. Integrated Effect of Rectangular Groove on Temperature and Flow Fields
3.4. Flow Characteristics Analysis
4. Conclusions
- The thermal performance is significantly improved by combining nanofluid and grooves rather than using only one of them. At 1.5 m/s, Nu of RGMC with 2 vol% nanofluid is 20.5, which 38.5% larger than that of SMC with the same nanofluid, and 36.7% larger than that of RGMC with pure water. Analyzing the heat transfer factor further shows that nanofluid enhances heat transfer more significantly at lower inlet velocity, while grooves enhance heat transfer more significantly at higher inlet velocity.
- Compared to SMC, the enhanced disturbance in RGMC can thin the thermal boundary layer and enhance the radial convection. The disturbance leads to more obvious flow irregularity. At 1.5 m/s, the maximum velocity difference of SMC is 2.1 m/s, while that of RGMC is 3.1 m/s, which is about 47.6% larger than the former.
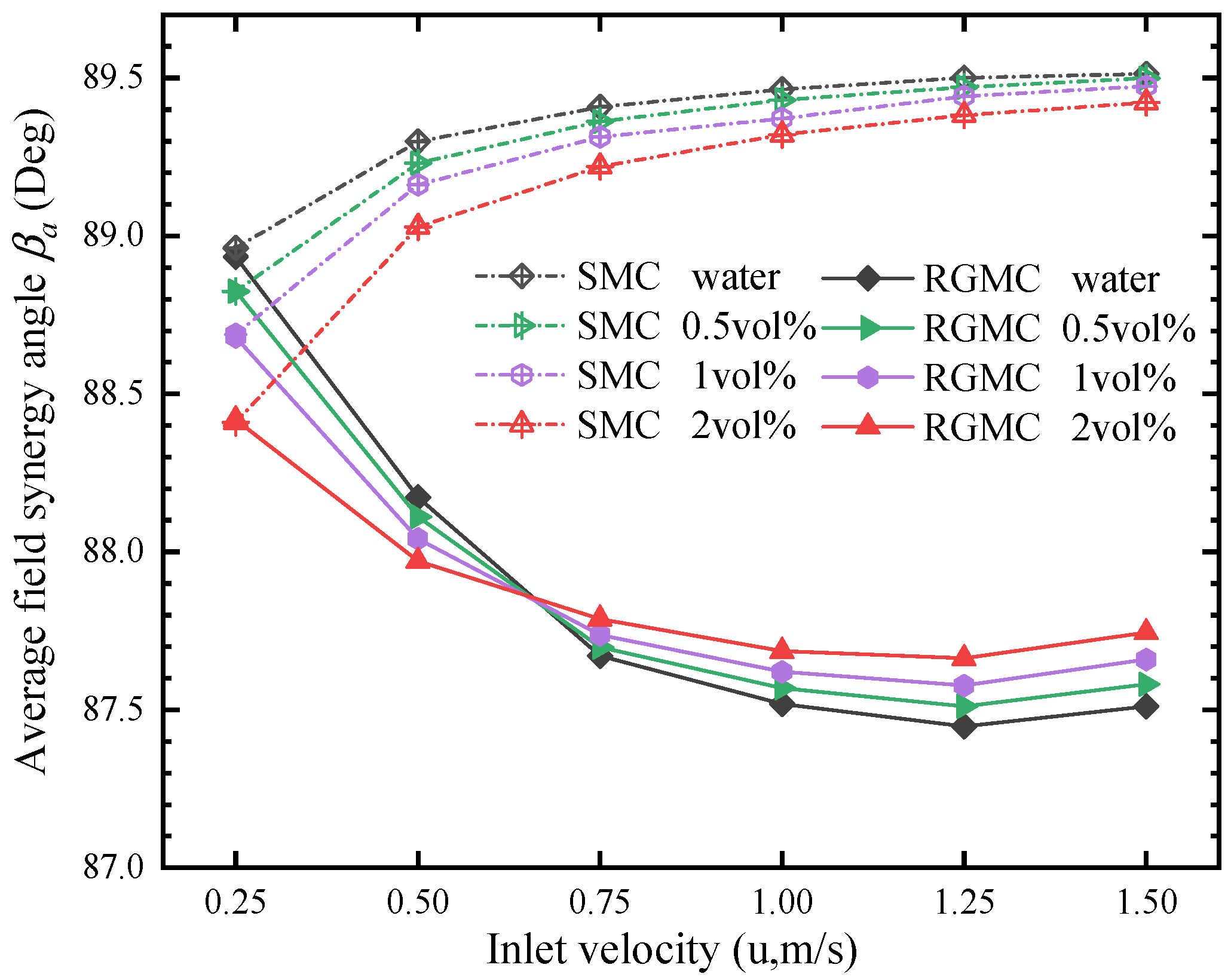
- The synergy angle β near the center line of RGMC is much lower than that of SMC, which represents better thermal performance. At 1.5 m/s, the average field synergy angle βα of RGMC with pure water is 2.1 Deg lower than that of SMC. At 0.25 m/s, βα of SMC with 2 vol% nanofluid is 0.55 Deg lower than that using pure water. Increasing volume fraction of nanofluid improves the synergic effect mainly at lower inlet velocity, while at higher inlet velocity, using grooves to make fluid disturbance improves the synergic effect more significantly.
- The flow resistance can be increased by using the rectangular grooves. It is found that friction factor f of RGMC is always about 0.3 larger than that of SMC.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Acceleration, m/s2 |
| Cp | Specific heat capacity, J/(kg·K) |
| d | Diameter, μm |
| D | Hydraulic diameter, μm |
| E | Depth of rectangular groove, μm |
| Fc | Field synergy number |
| g | Gravitational acceleration, m/s2 |
| H | Height of microchannel, μm |
| j | Heat transfer factor |
| Knf | Knudsen number |
| L | Length of microchannel heat sink, mm |
| Nu | Nusselt number |
| p | Pressure, Pa |
| Pr | Prandtl number |
| q | Heat flux, W/cm2 |
| Re | Reynolds number |
| T | Temperature, K |
| u | Inlet velocity, m/s |
| V | Velocity, m/s; Control volume, m3, used in FEM |
| W | Width of microchannel, μm |
| α | Field synergy angle between velocity vector and velocity gradient |
| β | Field synergy angle between velocity vector and temperature gradient |
| δ | Thermal boundary layer thickness, μm |
| φ | Nano particle concentration |
| ρ | Mass density of fluid, kg/m3 |
| µ | Kinematic viscosity, Pa·s |
| Subscripts | |
| Bf | Base fluid |
| Dr | Drift |
| F | Fluid domain |
| In | Inlet |
| K | Summation index |
| M | Mass-averaged |
| Max | Maximal value |
| Nf | Nanofluid |
| Out | Outlet |
| P | Particle |
| Pf | Nanoparticle relative to base fluid |
| S | Solid domain |
| T | Thermal |
| x, y, z | Cartesian coordinates |
| 0, 1, 2 | Case number |
References
- Kandlikar, S.G. High Flux Heat Removal with Microchannels—A Roadmap of Challenges and Opportunities. Heat Transf. Eng. 2005, 26, 5–14. [Google Scholar] [CrossRef]
- Tuckerman, D.B.; Pease, R.F.W. High-Performance Heat Sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Li, Z.X. Size Effect on Single-Phase Channel Flow and Heat Transfer at Microscale. Int. J. Heat Fluid Flow 2003, 24, 284–298. [Google Scholar] [CrossRef]
- Gad-el-Hak, M. Comments on “Critical View on New Results in Micro-Fluid Mechanics”. Int. J. Heat Mass Transf. 2003, 46, 3941–3945. [Google Scholar] [CrossRef]
- Kim, D.K.; Kim, S.J. Averaging Approach for Microchannel Heat Sinks Subject to the Uniform Wall Temperature Condition. Int. J. Heat Mass Transf. 2006, 49, 695–706. [Google Scholar] [CrossRef]
- Lee, P.S.; Garimella, S.V.; Liu, D. Investigation of Heat Transfer in Rectangular Microchannels. Int. J. Heat Mass Transf. 2005, 48, 1688–1704. [Google Scholar] [CrossRef]
- Adams, T.M.; Dowling, M.F.; Abdel-Khalik, S.I.; Jeter, S.M. Applicability of Traditional Turbulent Single-Phase Forced Convection Correlations to Non-Circular Microchannels. Int. J. Heat Mass Transf. 1999, 42, 4411–4415. [Google Scholar] [CrossRef]
- Shang, X.; Li, Q.; Cao, Q.; Li, Z.; Shao, W.; Cui, Z. Mathematical Modeling and Multi-Objective Optimization on the Rectangular Micro-Channel Heat Sink. SSRN Electron. J. 2022, 184, 107926. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles. Am. Soc. Mech. Eng. Fluids Eng. Div. FED 1995, 231, 99–105. [Google Scholar]
- Alawi, O.A.; Sidik, N.A.C.; Xian, H.W.; Kean, T.H.; Kazi, S.N. Thermal Conductivity and Viscosity Models of Metallic Oxides Nanofluids. Int. J. Heat Mass Transf. 2018, 116, 1314–1325. [Google Scholar] [CrossRef]
- Thansekhar, M.R.; Anbumeenakshi, C. Experimental Investigation of Thermal Performance of Microchannel Heat Sink with Nanofluids Al2O3/Water and SiO2/Water. Exp. Tech. 2017, 41, 399–406. [Google Scholar] [CrossRef]
- Li, C.; Huang, J.; Shang, Y.; Huang, H. Study on the Flow and Heat Dissipation of Water-Based Alumina Nanofluids in Microchannels. Case Stud. Therm. Eng. 2020, 22, 100746. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Roy, G.; Gauthier, C.; Galanis, N. Heat Transfer Enhancement Using Al2O3-Water Nanofluid for an Electronic Liquid Cooling System. Appl. Therm. Eng. 2007, 27, 1501–1506. [Google Scholar] [CrossRef]
- Varun Kumar, R.S.; Alhadhrami, A.; Punith Gowda, R.J.; Naveen Kumar, R.; Prasannakumara, B.C. Exploration of Arrhenius Activation Energy on Hybrid Nanofluid Flow over a Curved Stretchable Surface. ZAMM Z. Angew. Math. Mech. 2021, 101, 1–14. [Google Scholar] [CrossRef]
- Punith Gowda, R.J.; Naveen Kumar, R.; Jyothi, A.M.; Prasannakumara, B.C.; Sarris, I.E. Impact of Binary Chemical Reaction and Activation Energy on Heat and Mass Transfer of Marangoni Driven Boundary Layer Flow of a Non-Newtonian Nanofluid. Processes 2021, 9, 702. [Google Scholar] [CrossRef]
- Gowda, R.J.P.; Kumar, R.N.; Rauf, A.; Prasannakumara, B.C.; Shehzad, S.A. Magnetized Flow of Sutterby Nanofluid through Cattaneo-Christov Theory of Heat Diffusion and Stefan Blowing Condition. Appl. Nanosci. 2021. [Google Scholar] [CrossRef]
- Kumar, R.S.V.; Gowda, R.J.P.; Kumar, R.N.; Radhika, M.; Prasannakumara, B.C. Two-phase flow of dusty fluid with suspended hybrid nanoparticles over a stretching cylinder with modified Fourier heat flux. SN Appl. Sci. 2021, 3, 384. [Google Scholar]
- Punith Gowda, R.J.; Naveen Kumar, R.; Prasannakumara, B.C. Two-Phase Darcy-Forchheimer Flow of Dusty Hybrid Nanofluid with Viscous Dissipation Over a Cylinder. Int. J. Appl. Comput. Math. 2021, 7, 1–18. [Google Scholar] [CrossRef]
- Heris, S.Z.; Esfahany, M.N.; Etemad, G. Numerical Investigation of Nanofluid Laminar Convective Heat Transfer through a Circular Tube. Numer. Heat Transf. Part A Appl. 2007, 52, 1043–1058. [Google Scholar] [CrossRef]
- Akbari, M.; Galanis, N.; Behzadmehr, A. Comparative Analysis of Single and Two-Phase Models for CFD Studies of Nanofluid Heat Transfer. Int. J. Therm. Sci. 2011, 50, 1343–1354. [Google Scholar] [CrossRef]
- Haghshenas Fard, M.; Esfahany, M.N.; Talaie, M.R. Numerical Study of Convective Heat Transfer of Nanofluids in a Circular Tube Two-Phase Model versus Single-Phase Model. Int. Commun. Heat Mass Transf. 2010, 37, 91–97. [Google Scholar] [CrossRef]
- Moraveji, M.K.; Ardehali, R.M. CFD Modeling (Comparing Single and Two-Phase Approaches) on Thermal Performance of Al2o3/Water Nanofluid in Mini-Channel Heat Sink. Int. Commun. Heat Mass Transf. 2013, 44, 157–164. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gowda, R.J.P.; Alam, M.M.; Ahmad, I.; Mahrous, Y.M.; Gorji, M.R.; Prasannakumara, B.C. Inspection of Convective Heat Transfer and KKL Correlation for Simulation of Nanofluid Flow over a Curved Stretching Sheet. Int. Commun. Heat Mass Transf. 2021, 126, 105445. [Google Scholar] [CrossRef]
- Naveen Kumar, R.; Suresha, S.; Gowda, R.J.P.; Megalamani, S.B.; Prasannakumara, B.C. Exploring the Impact of Magnetic Dipole on the Radiative Nanofluid Flow over a Stretching Sheet by Means of KKL Model. Pramana-J. Phys. 2021, 95. [Google Scholar] [CrossRef]
- Xia, G.D.; Jiang, J.; Wang, J.; Zhai, Y.L.; Ma, D.D. Effects of Different Geometric Structures on Fluid Flow and Heat Transfer Performance in Microchannel Heat Sinks. Int. J. Heat Mass Transf. 2015, 80, 439–447. [Google Scholar] [CrossRef]
- Li, F.; Zhu, W.; He, H. Field Synergy Analysis on Flow and Heat Transfer Characteristics of Nanofluid in Microchannel with Non-Uniform Cavities Configuration. Int. J. Heat Mass Transf. 2019, 144, 118617. [Google Scholar] [CrossRef]
- Chen, Z.; Feng, Z.; Zhang, Q.; Zhang, J.; Guo, F. Effects of Regular Triangular Prisms on Thermal and Hydraulic Characteristics in a Minichannel Heat Sink. Int. J. Heat Mass Transf. 2022, 188, 122583. [Google Scholar] [CrossRef]
- Naqiuddin, N.H.; Saw, L.H.; Yew, M.C.; Yusof, F.; Poon, H.M.; Cai, Z.; Thiam, H.S. Numerical Investigation for Optimizing Segmented Micro-Channel Heat Sink by Taguchi-Grey Method. Appl. Energy 2018, 222, 437–450. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.D.; Wang, H.S. Numerical Study of Laminar Flow and Heat Transfer in Microchannel Heat Sink with Offset Ribs on Sidewalls. Appl. Therm. Eng. 2016, 92, 32–41. [Google Scholar] [CrossRef]
- Hong, F.; Cheng, P. Three Dimensional Numerical Analyses and Optimization of Offset Strip-Fin Microchannel Heat Sinks. Int. Commun. Heat Mass Transf. 2009, 36, 651–656. [Google Scholar] [CrossRef]
- Promvonge, P.; Sripattanapipat, S.; Kwankaomeng, S. Laminar Periodic Flow and Heat Transfer in Square Channel with 45° Inline Baffles on Two Opposite Walls. Int. J. Therm. Sci. 2010, 49, 963–975. [Google Scholar] [CrossRef]
- Xie, X.L.; Tao, W.Q.; He, Y.L. Numerical Study of Turbulent Heat Transfer and Pressure Drop Characteristics in a Water-Cooled Minichannel Heat Sink. J. Electron. Packag. Trans. ASME 2007, 129, 247–255. [Google Scholar] [CrossRef]
- Lee, J.; Mudawar, I. Assessment of the Effectiveness of Nanofluids for Single-Phase and Two-Phase Heat Transfer in Micro-Channels. Int. J. Heat Mass Transf. 2007, 50, 452–463. [Google Scholar] [CrossRef]
- Mokhtari Moghari, R.; Akbarinia, A.; Shariat, M.; Talebi, F.; Laur, R. Two Phase Mixed Convection Al2O3-Water Nanofluid Flow in an Annulus. Int. J. Multiph. Flow 2011, 37, 585–595. [Google Scholar] [CrossRef]
- Shi, X.; Li, S.; Wei, Y.; Gao, J. Numerical Investigation of Laminar Convective Heat Transfer and Pressure Drop of Water-Based Al2O3 Nanofluids in a Microchannel. Int. Commun. Heat Mass Transf. 2018, 90, 111–120. [Google Scholar] [CrossRef]
- Zhao, J.J.; Duan, Y.Y.; Wang, X.D.; Wang, B.X. Effect of Nanofluids on Thin Film Evaporation in Microchannels. J. Nanoparticle Res. 2011, 13, 5033–5047. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. A New Thermal Conductivity Model for Nanofluids. J. Nanoparticle Res. 2004, 6, 577–588. [Google Scholar] [CrossRef]
- Chon, C.H.; Kihm, K.D.; Lee, S.P.; Choi, S.U.S. Empirical Correlation Finding the Role of Temperature and Particle Size for Nanofluid (Al2O3) Thermal Conductivity Enhancement. Appl. Phys. Lett. 2005, 87, 1–3. [Google Scholar] [CrossRef]
- Jiang, F.; Sousa, A.C.M. Effective Thermal Conductivity of Heterogeneous Multi-Component Materials: An SPH Implementation. Heat Mass Transf. Stoffuebertragung 2007, 43, 479–491. [Google Scholar] [CrossRef]
- Lisy, V.; Tothova, J. On the (Hydrodynamic) Memory in the Theory of Brownian Motion. arXiv 2004, arXiv:cond-mat/0410222. [Google Scholar]
- Yu, H.; Zhuang, J.; Li, T.; Li, W.; He, T.; Mao, N. Influence of Transient Heat Flux on Boiling Flow Pattern in a Straight Microchannel Applied in Concentrator Photovoltaic Systems. Int. J. Heat Mass Transf. 2022, 190, 122792. [Google Scholar] [CrossRef]
- Sekulic, D.P. Compact Heat Exchangers. In Handbook of Thermal Science and Engineering; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
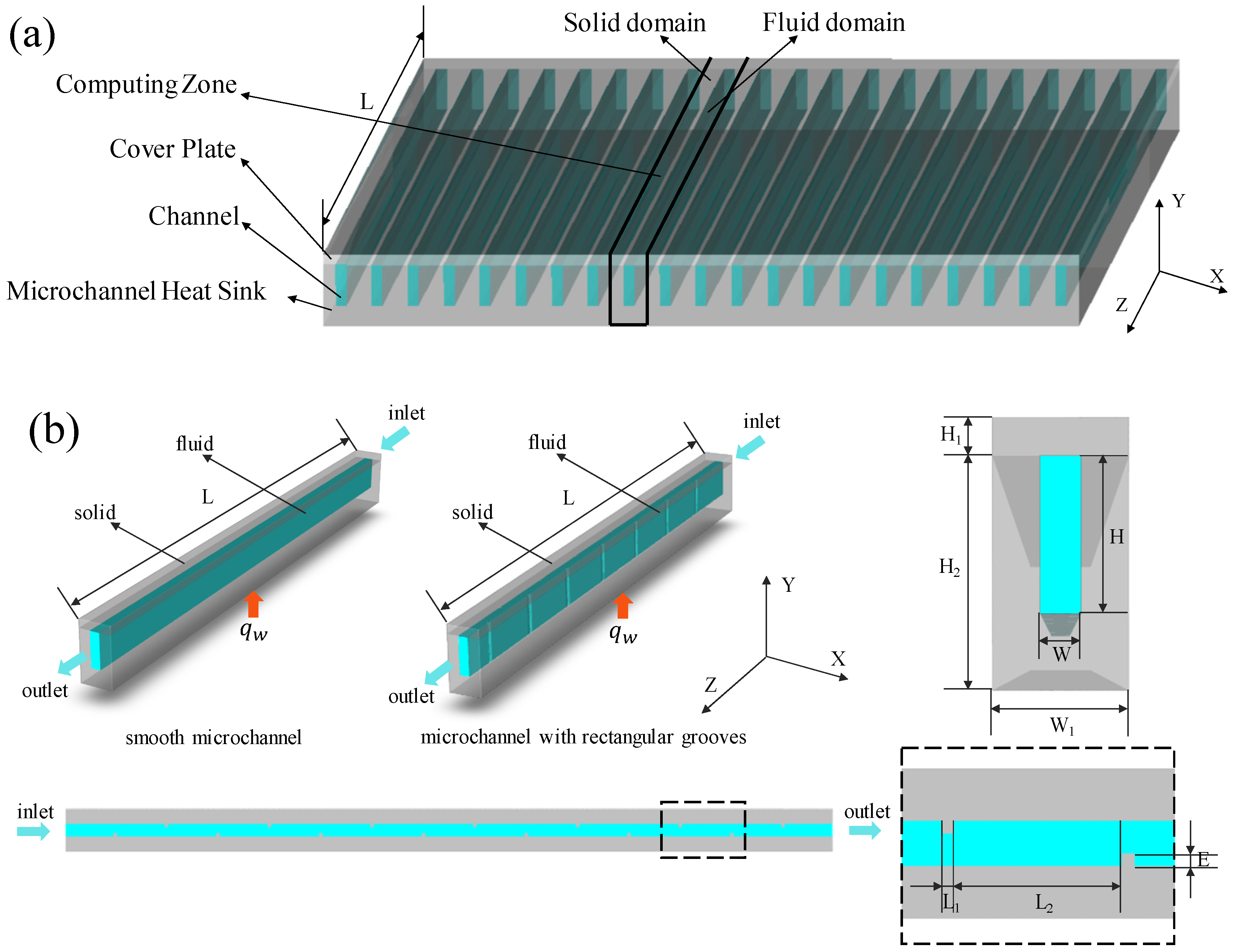

| L | L1 | L2 | E | H | H1 | H2 | W | W1 | |
|---|---|---|---|---|---|---|---|---|---|
| (mm) | (μm) | (μm) | (μm) | (μm) | (μm) | (μm) | (μm) | (μm) | |
| SMC0 | 44.8 | \ | \ | \ | 821 | 200 | 1221 | 215 | 715 |
| SMC | 12.84 | \ | \ | \ | 821 | 200 | 1221 | 215 | 715 |
| RGMC | 12.84 | 60 | 800 | 60 | 821 | 200 | 1221 | 215 | 715 |
| Property | Water | Al2O3 |
|---|---|---|
| Specific heat (J/kg·K) | 4182 | 765 |
| Density (kg/m3) | 998.2 | 3970 |
| Thermal conductivity (W/m·K) | −0.93314 + 0.00853·T − 0.000011259·T2 | 25 |
| Viscosity (kg/m·s) | 0.01723 − 9.25951 × 10−5·T + 1.2681 × 10−7·T2 | \ |
| Volume Fraction | Inlet Velocity | |
|---|---|---|
| SMC | Water, 0.5%, 1%, 2% | 0.25–1.5 m/s |
| RGMC | Water, 0.5%, 1%, 2% | 0.25–1.5 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Yu, H.; He, T.; Mao, N. A Numerical Study on Heat Transfer Characteristics of a Novel Rectangular Grooved Microchannel with Al2O3/Water Nanofluids. Energies 2022, 15, 7187. https://doi.org/10.3390/en15197187
Zeng X, Yu H, He T, Mao N. A Numerical Study on Heat Transfer Characteristics of a Novel Rectangular Grooved Microchannel with Al2O3/Water Nanofluids. Energies. 2022; 15(19):7187. https://doi.org/10.3390/en15197187
Chicago/Turabian StyleZeng, Xiaoxin, Hao Yu, Tianbiao He, and Ning Mao. 2022. "A Numerical Study on Heat Transfer Characteristics of a Novel Rectangular Grooved Microchannel with Al2O3/Water Nanofluids" Energies 15, no. 19: 7187. https://doi.org/10.3390/en15197187
APA StyleZeng, X., Yu, H., He, T., & Mao, N. (2022). A Numerical Study on Heat Transfer Characteristics of a Novel Rectangular Grooved Microchannel with Al2O3/Water Nanofluids. Energies, 15(19), 7187. https://doi.org/10.3390/en15197187








