Optimization of the Aircraft Air/Oil Separator by the Response Surface Determined from Modeling of Three-Dimensional Two-Phase Flow
Abstract
:1. Introduction
2. Numerical Model
2.1. Mathematical Model
2.2. Geometry of the Separator Domain and Boundary Conditions
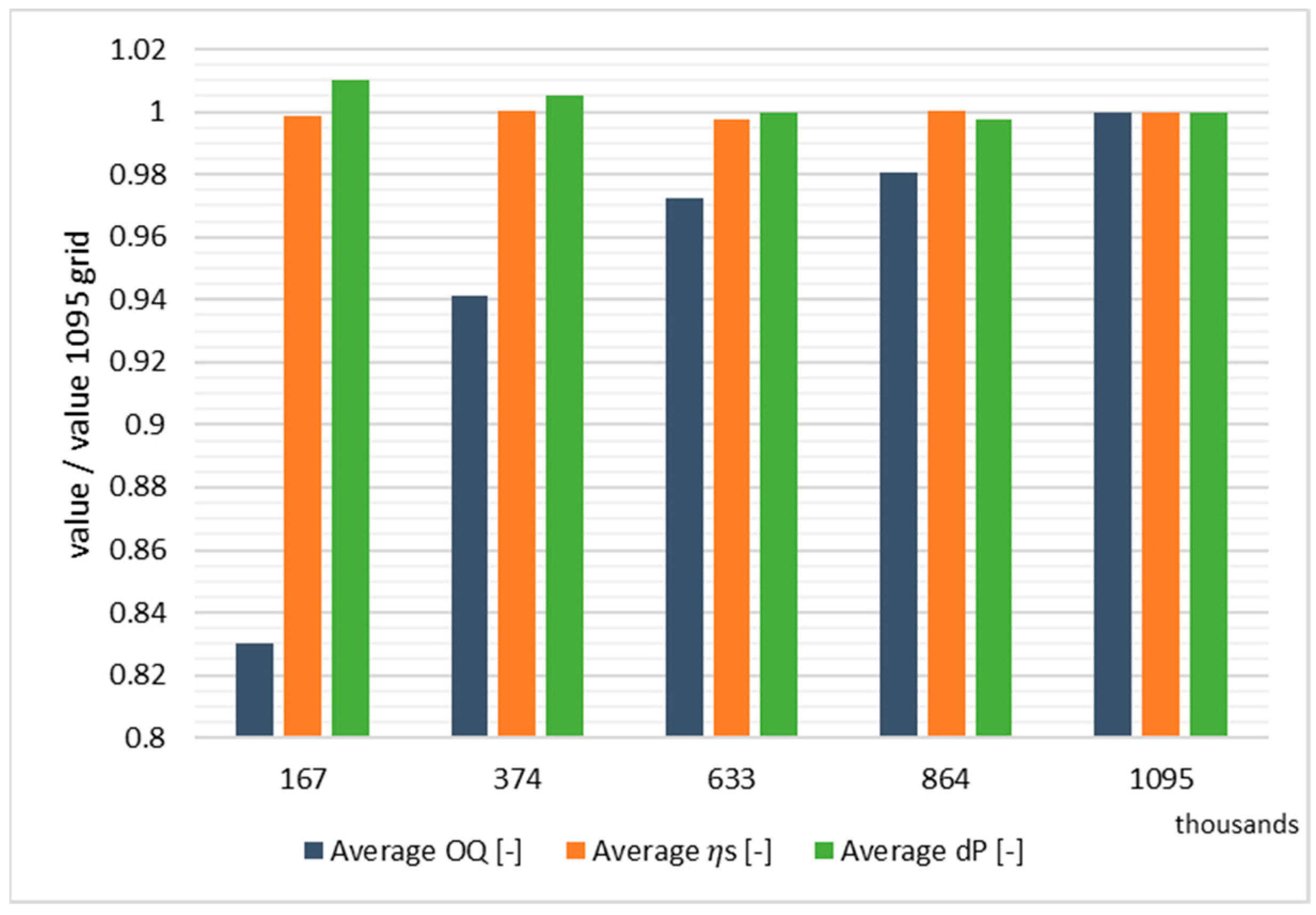
2.3. Selection of the Numerical Mesh
3. Design of the Experiment Selection and the Optimisation Algorithm
4. Separator Optimisation
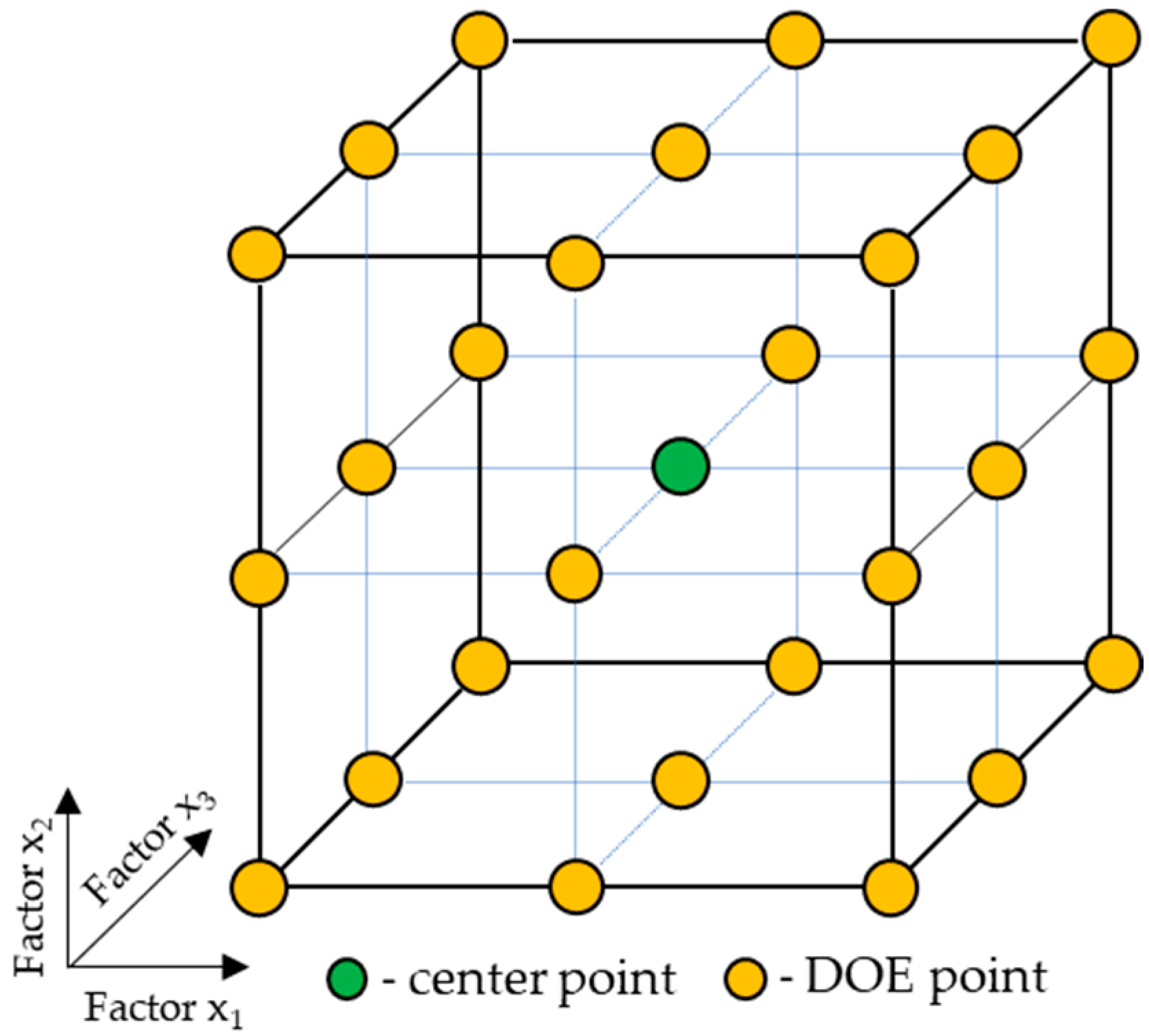
4.1. Design of Experiment
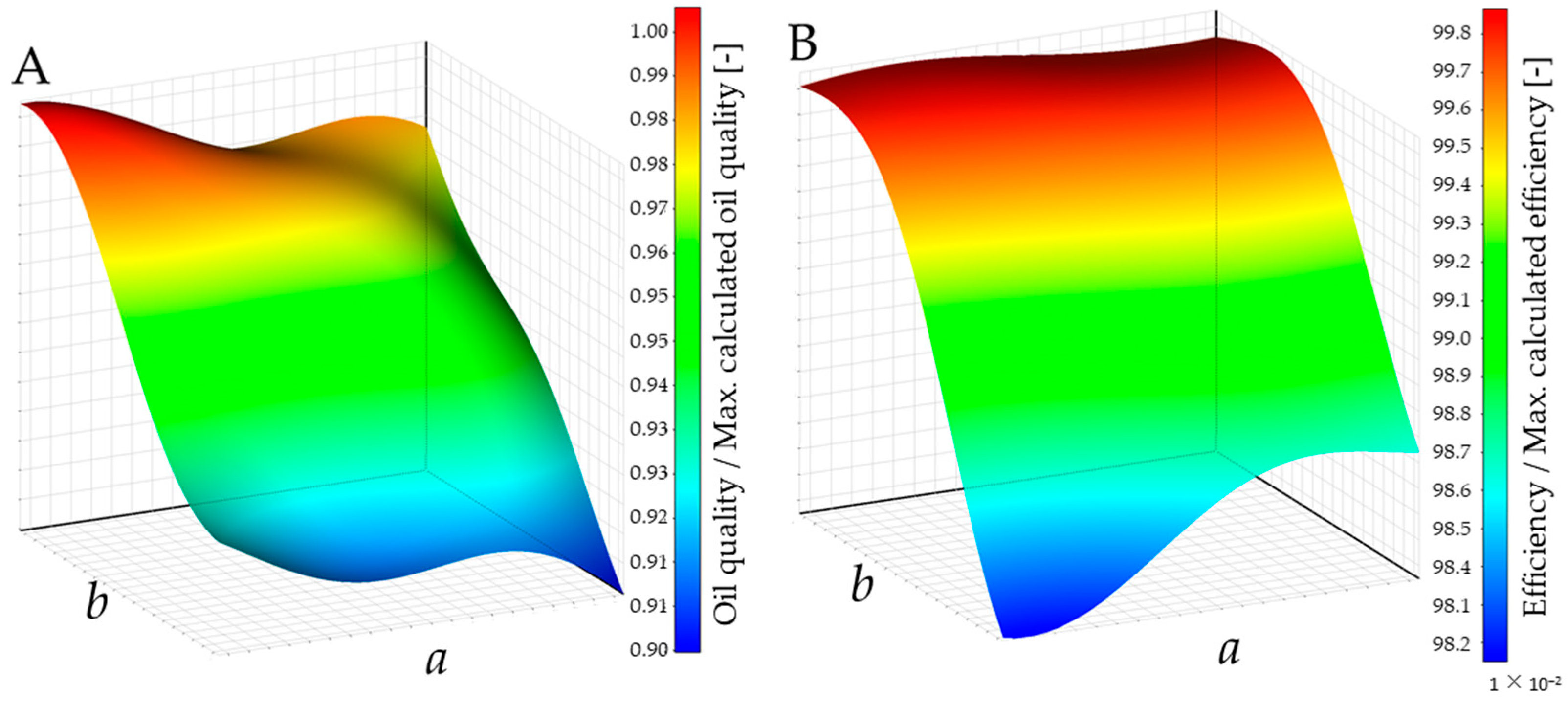
4.2. Response Surface
4.3. Optimization Task
5. Analysis of Results
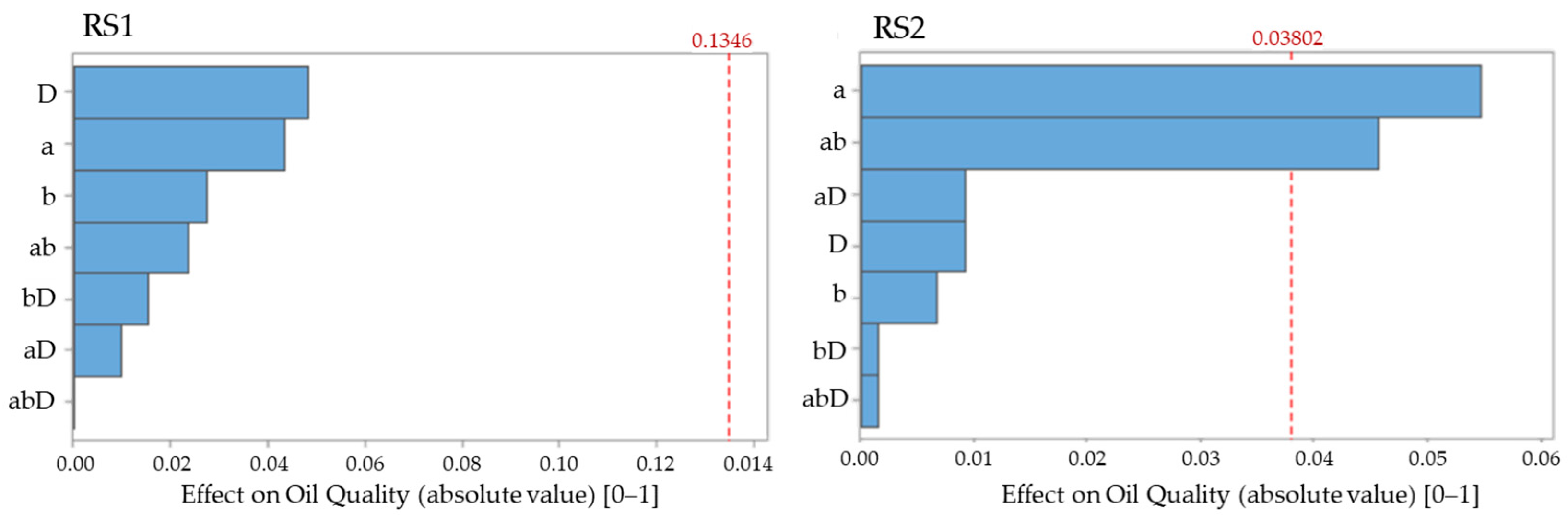
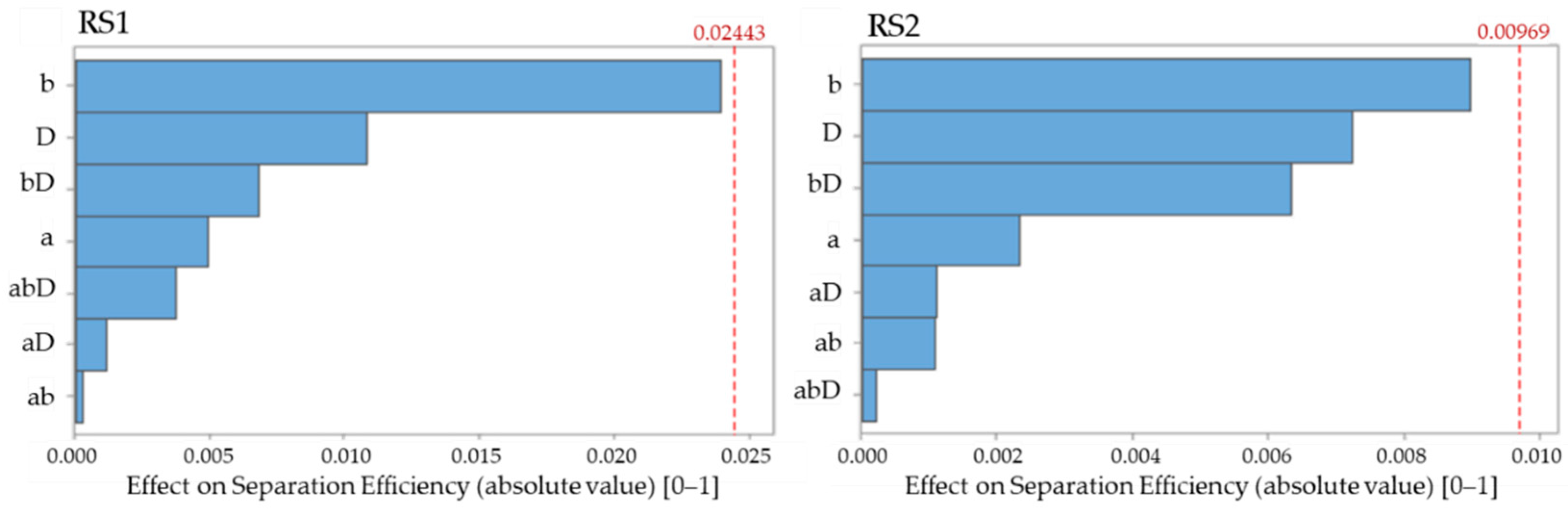
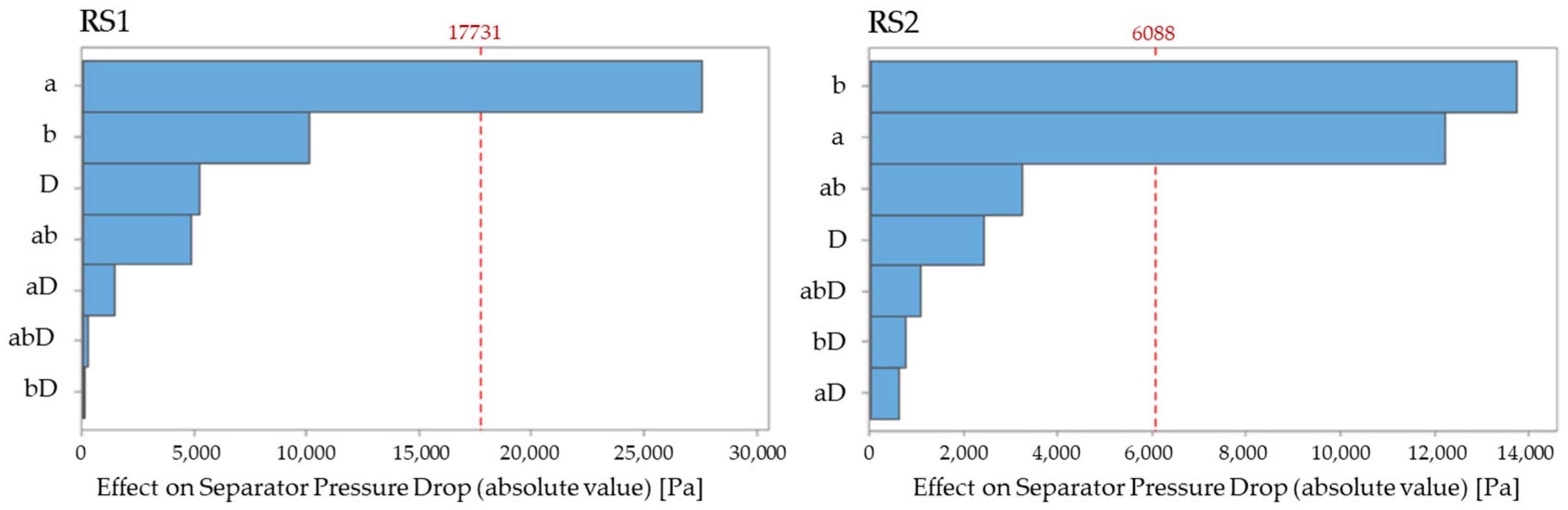
5.1. Pareto Analysis
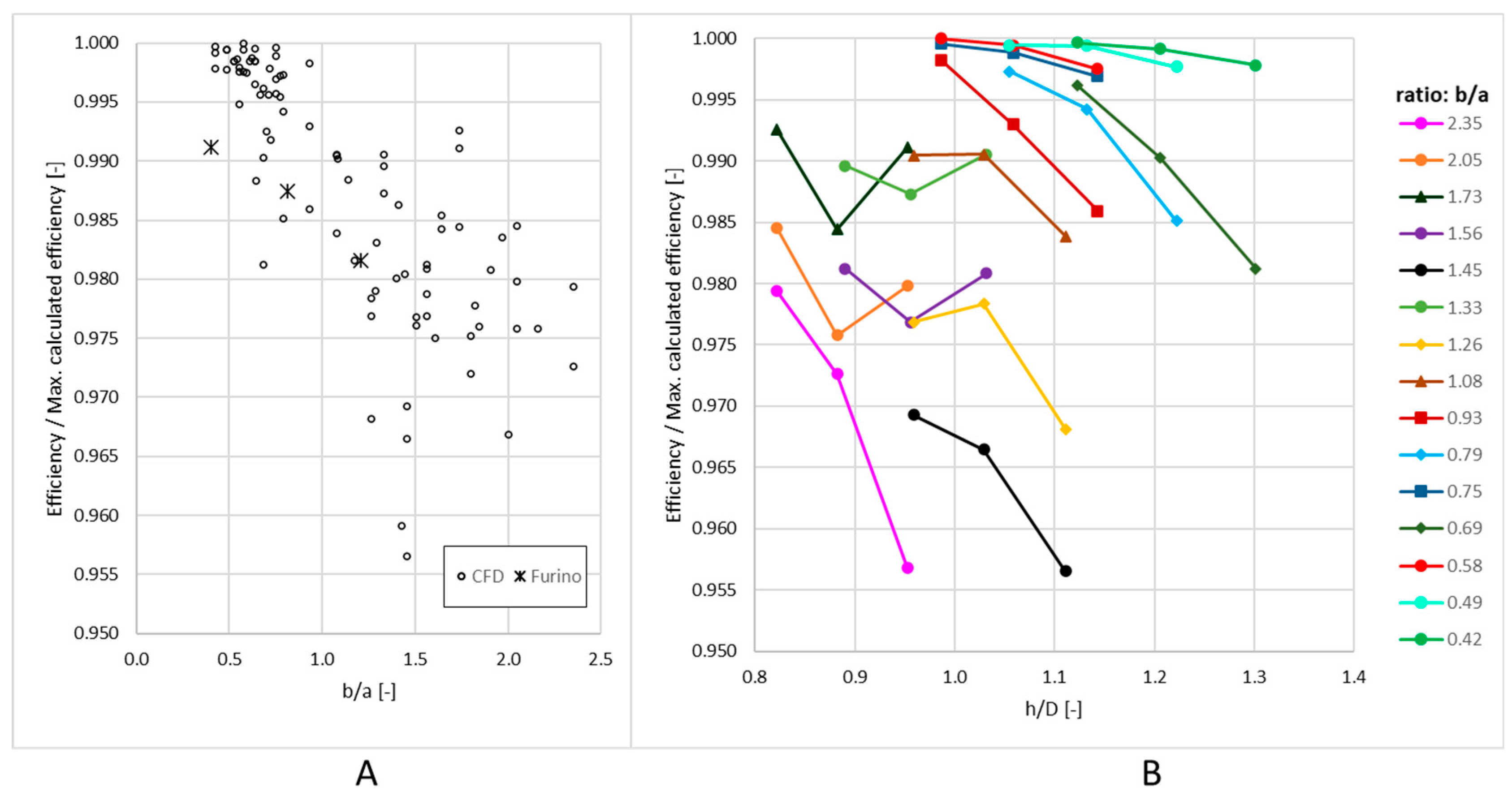
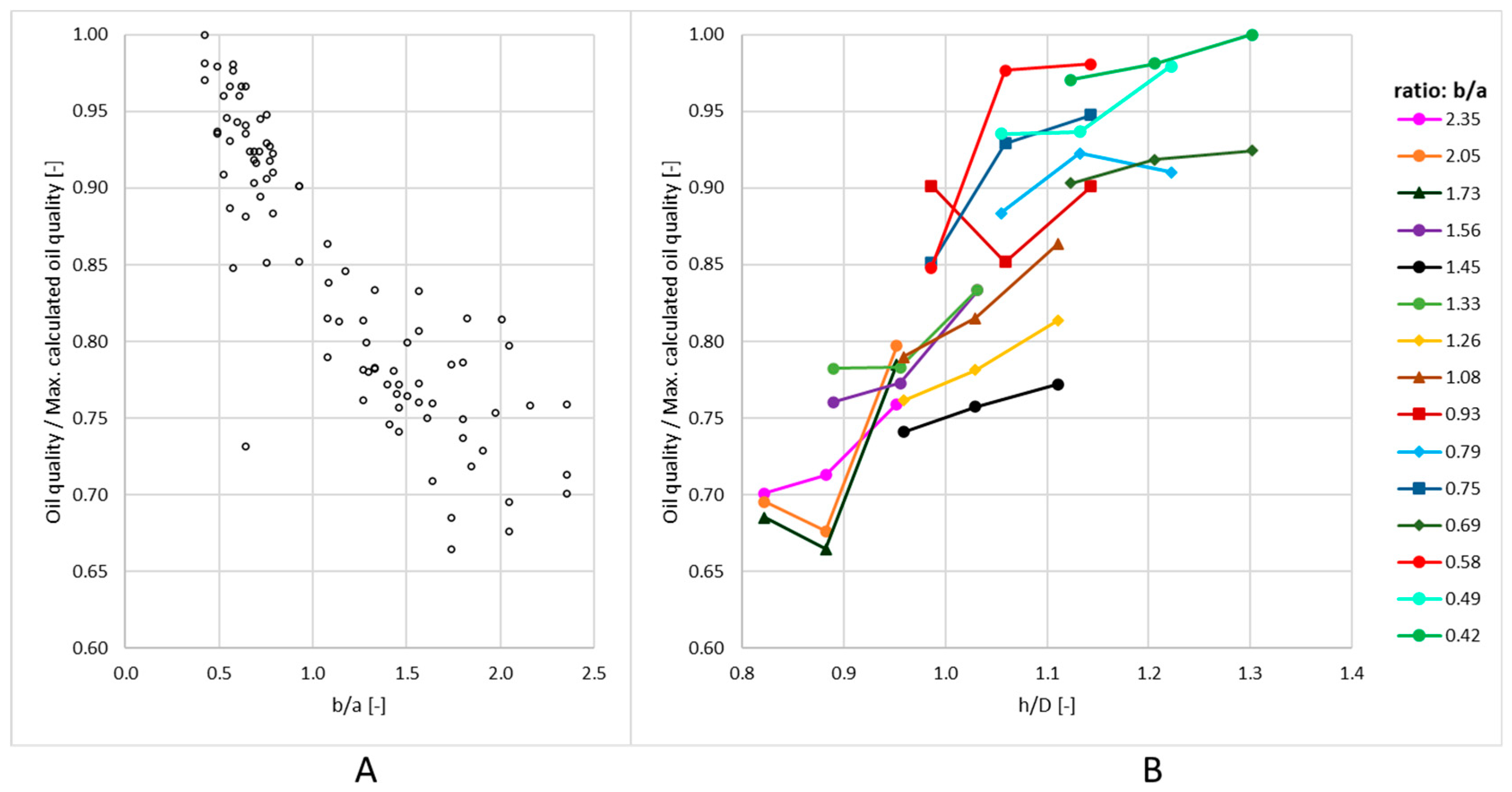
5.2. The Effect of Geometric Parameters on the Separator Operation
- -
- The highest efficiencies are obtained for and
- -
- The highest oil quality values are obtained for geometry with and
- -
- An increase of and decrease of ratios involves a higher pressure drop.
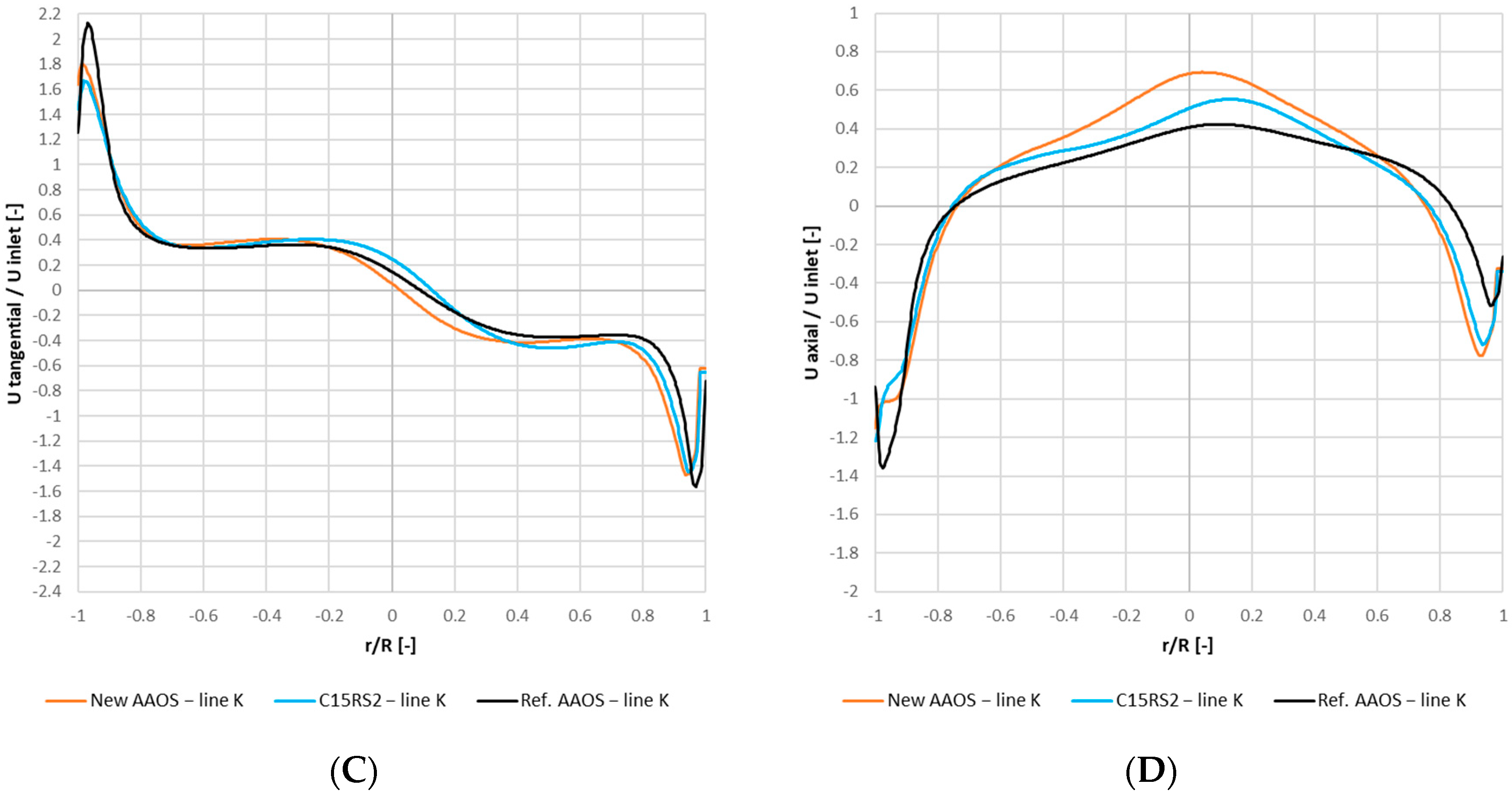
5.3. Comparison of Flow Field Structures for Different Configurations of the Separator
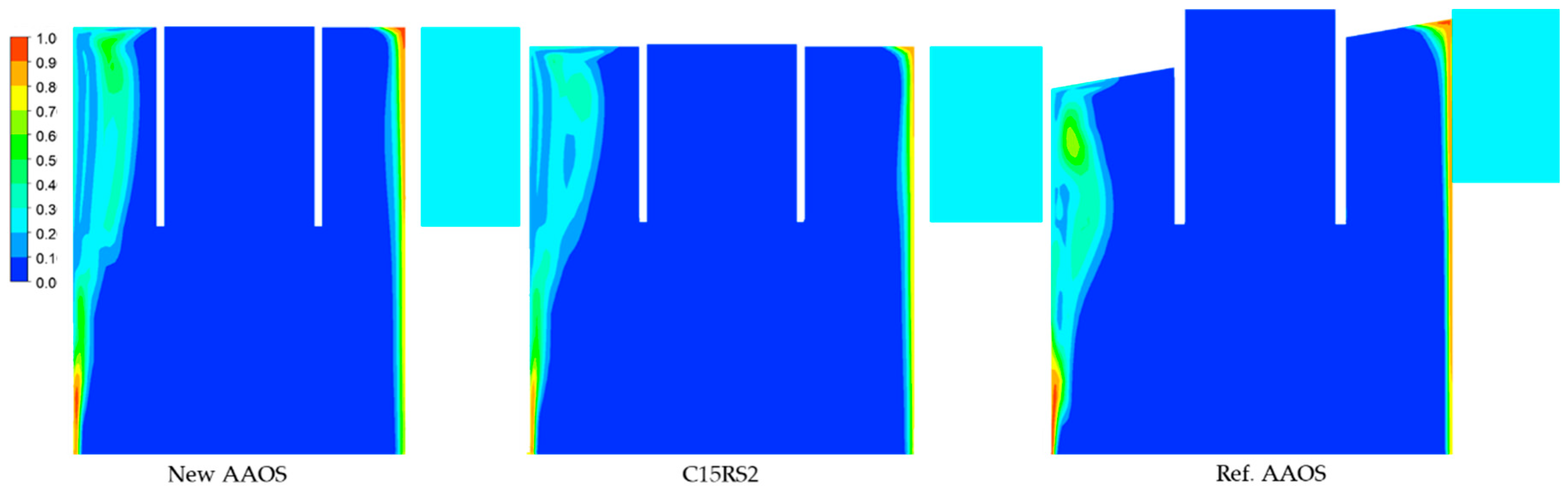
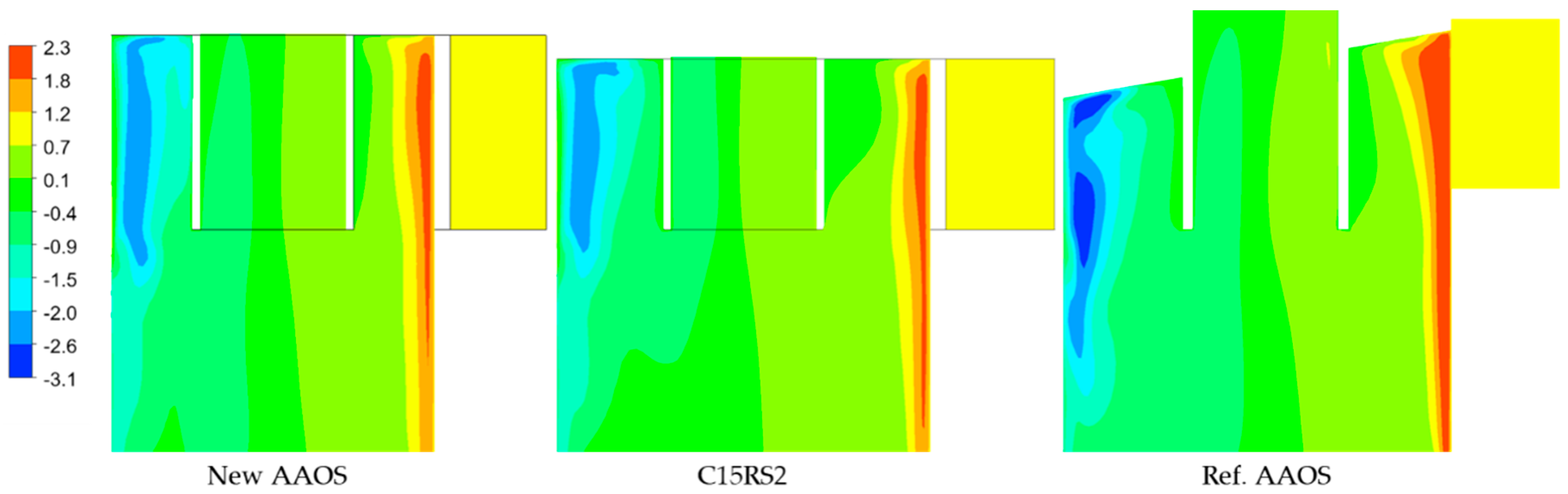
5.3.1. Oil Fraction Contours
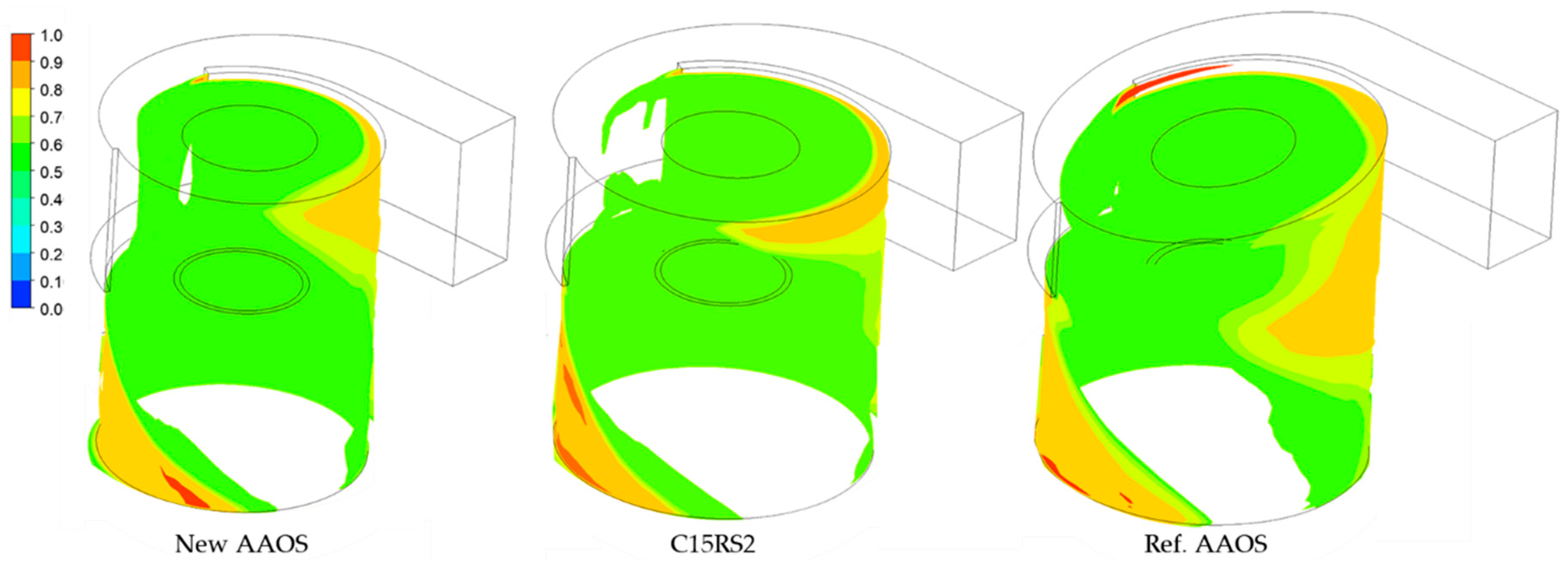
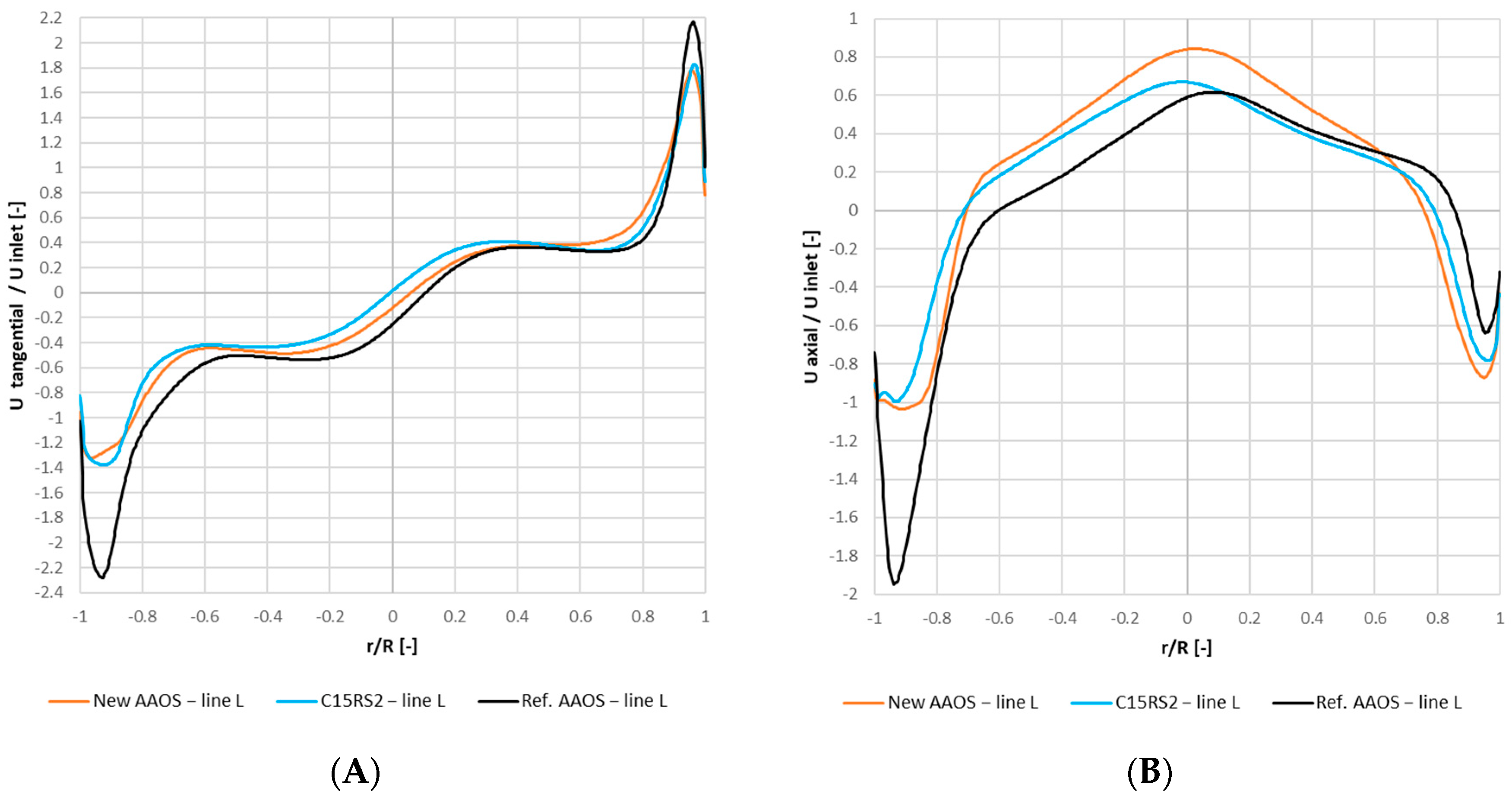
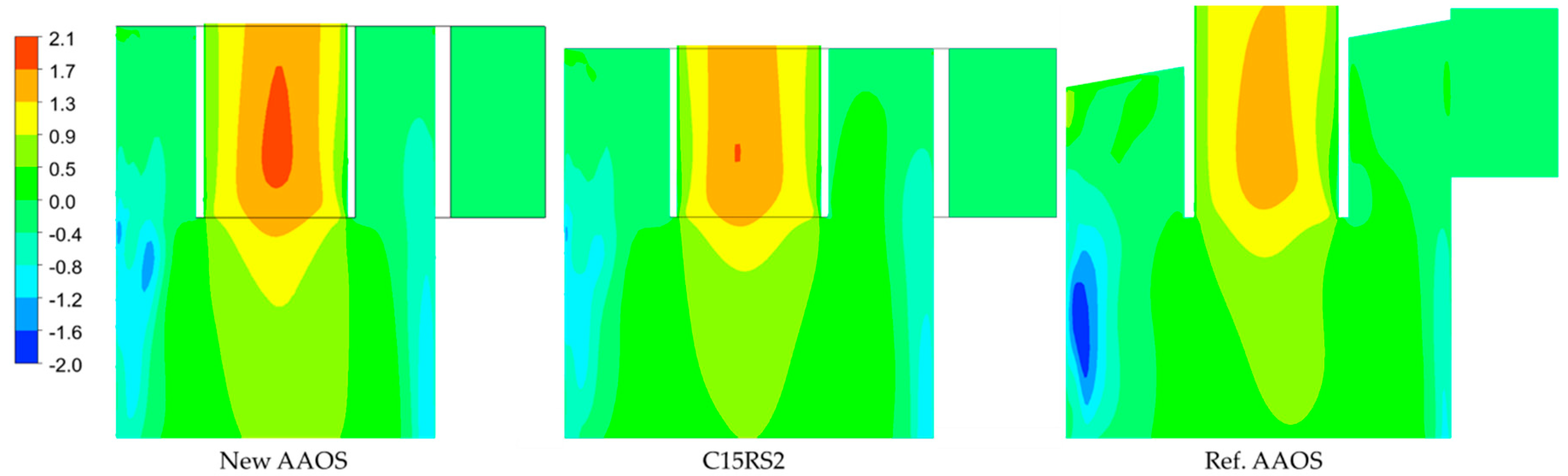
5.3.2. Velocity Contours
6. Summary and Conclusions
- -
- the applied CFD model enables simulations of the flow in the aircraft cyclone separator to analyse the impact of geometric parameters on the device performance,
- -
- the Pareto analysis results indicate that in the ranges under consideration geometric parameters and unlike diameter D, have a significant effect on the separator performance,
- -
- the RSM indicated the and the ratios for which the AAOS operating parameters are the best,
- -
- the comparison of the results of the CFD simulations for the New AAOS and the Ref. AAOS points to a difference in the formation of the oil film and a reduction in the velocity components at the separator wall, which translates into a higher value and a lower pressure drop for the New AAOS variant,
- -
- the obtained ratios of the separator dimensions differ from the Stairmand ratios; the separator inlet is higher and narrower,
- -
- the Ref. AAOS reached a 26% lower relative value of and a 50% higher pressure drop compared to the New AAOS,
- -
- it is important to direct the mixture stream properly so that it should perform as many full turns in the cylindrical part as possible.
- -
- investigations of the impact of the vortex finder geometry () and of the height of the separator cylindrical part below the inlet ; the studies should also concern the effect of the separator inlet inclination,
- -
- investigations of the impact of additional geometric features to avoid the mixing of separated oil with the stream of the inlet mixture,
- -
- numerical analysis of the oil level in the separator,
- -
- experimental testing of the new separator geometry.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barth, W. Design and layout of the cyclone separator on the basis of new investigations. Brennstow-Wäerme-Kraft 1956, 8, 1–9. [Google Scholar]
- Hoffmann, A.C.; Stein, L.E. Gas Cyclones and Swirl Tubeso; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Stairmand, C.J. Pressure drops in cyclone separators. Ind. Eng. Chem. 1949, 16, 409–411. [Google Scholar]
- Iozia, D.L.; Leith, D. The Logistic Function and Cyclone Fractional Efficiency. Aerosol Sci. Technol. 1990, 12, 598–606. [Google Scholar] [CrossRef] [Green Version]
- Ramachandran, G.; Leith, D.; Dirgo, J.; Feldman, H. Cyclone Optimization Based on a New Empirical Model for Pressure Drop. Aerosol Sci. Technol. 1991, 15, 135–148. [Google Scholar] [CrossRef]
- Casal, J.; Martinez-Benet, J.M. A better way to calculate cyclone pressure drop. Chem. Eng. 1983, 90, 99–100. [Google Scholar]
- Shepherd, C.B.; Lapple, C.E. Flow Pattern and Pressure Drop in Cyclone Dust Collectors Cyclone without Intel Vane. Ind. Eng. Chem. 1940, 32, 1246–1248. [Google Scholar] [CrossRef]
- Tauber, T.; D’Ambrosia, S.; Rudbarg, F. A lube system diagnostic monitor with deaeration capability. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME 1982 International Gas Turbine Conference and Exhibit, London, UK, 18–22 April 1982; American Society of Mechanical Engineers: New York, NY, USA, 1982; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Szwarc, T.; Wróblewski, W.; Borzęcki, T. Analysis of a cylindrical cyclone separator used in aircraft turbine engine. Tech. Sci. 2020, 23, 131–142. [Google Scholar] [CrossRef]
- Furino, S. Parametric Analysis of the Deaerator Flow Field Using CFD; Politecnico di Torino: Torino, Italy, 2020. [Google Scholar]
- Szwarc, T.; Wróblewski, W.; Borzęcki, T. Experimental and numerical study of the impact of the oil tank filling level on the aircraft separator. In Facta Universitatis, Series: Mechanical Engineering; University of Niš: Niš, Serbia, 2022. [Google Scholar] [CrossRef]
- Stairmand, C.J. The design and performance of cyclone separators. Ind. Eng. Chem. 1951, 29, 356–383. [Google Scholar]
- Zhu, Y.; Lee, K.W. Experimental study on small cyclones operating at high flowrates. J. Aerosol Sci. 1999, 30, 1303–1315. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. The effect of cyclone inlet dimensions on the flow pattern and performance. Appl. Math. Model. 2011, 35, 1952–1968. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Wang, J.; Liu, Z.; Wei, Y.; Wang, J.; Mao, Y. Effects of different inlet structures on the fl ow field of cyclone separators. Powder Technol. 2020, 372, 519–531. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. Numerical modeling of the flow field and performance in cyclones of different cone-tip diameters. Comput. Fluids 2011, 51, 48–59. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. Modeling and Pareto optimization of gas cyclone separator performance using RBF type arti fi cial neural networks and genetic algorithms. Powder Technol. 2012, 217, 84–99. [Google Scholar] [CrossRef]
- Kha, H.M.; Phuong, N.N.; Nam, N.T. The Effect of Different Geometrical Configurations of the Performances of Gas-Liquid Cylindrical Cyclone Separators (GLCC). In Proceedings of the 2017 International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 21–23 July 2017; pp. 646–651. [Google Scholar]
- Erdal, F.M.; Shirazi, S.A.; Shoham, O.; Kouba, G.E. CFD simulation of single-phase and two-phase flow in Gas-Liquid Cylindrical Cyclone separators. SPE J. 1997, 2, 436–445. [Google Scholar] [CrossRef] [Green Version]
- Erdal, F.M.; Shirazi, S.A.; Mantilla, I.; Shoham, O. CFD study of bubble carry-under in gas-liquid Cylindrical Cyclone separators. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LO, USA, 27–30 September 1998; Volume 1999, pp. 781–791. [Google Scholar] [CrossRef]
- Brar, L.S.; Sharma, R.P. Effect of varying diameter on the performance ofindustrial scale gas cyclone dust separators. Mater. Today Proc. 2015, 2, 3230–3237. [Google Scholar] [CrossRef]
- Elsayed, K. Analysis and Optimization of Cyclone Separators Geometry Using RANS and LES Methodologies Khairy Elsayed. In Turbulence and Interactions; Springer: Berlin/Heidelberg, Germany, 2011; pp. 65–74. [Google Scholar]
- Elsayed, K.; Lacor, C. Optimization of the cyclone separator geometry for minimum pressure drop using mathematical models and CFD simulations. Chem. Eng. Sci 2010, 65, 6048–6058. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. CFD modeling and multi-objective optimization of cyclone geometry using desirability function, Artificial neural networks and genetic algorithms. Appl. Math. Model. 2013, 37, 5680–5704. [Google Scholar] [CrossRef]
- Singh, P.; Couckuyt, I.; Elsayed, K.; Deschrijver, D.; Dhaene, T. Shape optimization of a cyclone separator using multi-objective surrogate-based optimization. Appl. Math. Model. 2016, 40, 4248–4259. [Google Scholar] [CrossRef]
- Sun, X. Multi-objective optimization of a Stairmand cyclone separator using response surface methodology and computational fluid dynamics. Powder Technol. 2017, 320, 51–65. [Google Scholar] [CrossRef]
- Sun, X.; Yoon, J.Y. Multi-objective optimization of a gas cyclone separator using genetic algorithm and computational fluid dynamics. Powder Technol. 2018, 325, 347–360. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Box, G.E.P.; Draper, N.R. Empirical Model Building and Response Surfaces; John Wiley and Sons: New York, NY, USA, 1987. [Google Scholar]
- Ravi, G.; Gupta, S.K.; Ray, M.B. Multiobjective optimization of cyclone separators using genetic algorithm. Ind. Eng. Chem. Res. 2000, 39, 4272–4286. [Google Scholar] [CrossRef]
- Sgrott, O.L.; Noriler, D.; Wiggers, V.R.; Meier, H.F. Cyclone optimization by COMPLEX method and CFD simulation. Powder Technol. 2015, 277, 11–21. [Google Scholar] [CrossRef]
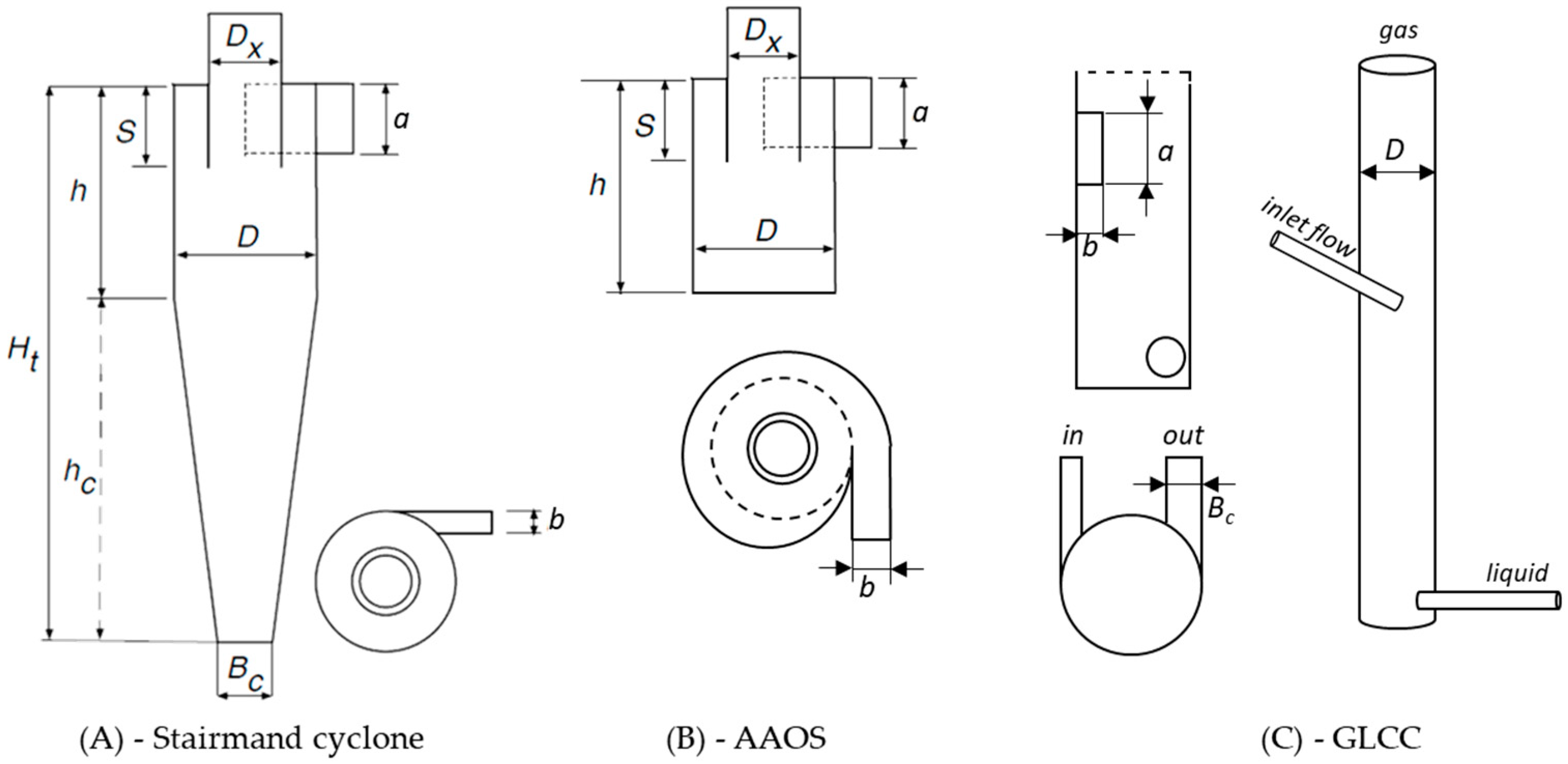



| a/D | b/D | Dx/D | Ht/D | h/D | S/D | Bc/D | |
|---|---|---|---|---|---|---|---|
| Stairmand [17] | 0.5 | 0.2 | 0.5 | 4 | 1.5 | 0.5 | 0.38 |
| AAOS [11] | 0.46 | 0.28 | 0.39 | 1.05 | 0.52 | 1.0 | |
| GLCC Minh [18] | 0.5 | 0.5 | 0.5 | 18.1 | 1 | 0.9 | |
| GLCC Farchi [19] | 0.5 | 0.1 | 1.0 | 2.5 | 1 | 0.2 | |
| GLCC Erdal [20] | 0.4 | 0.4 | 1.0 | 16.5 | 1 | 0.6 | |
| Case | RS1 | RS2 | ||||
|---|---|---|---|---|---|---|
| a/D | b/D | h/D | a/D | b/D | h/D | |
| 1 | 0.45 | 0.26 | 1.0 | 0.26 | 0.45 | 1.0 |
| 2 | 0.42 | 0.24 | 0.9 | 0.24 | 0.42 | 0.9 |
| 3 | 0.39 | 0.22 | 0.8 | 0.22 | 0.39 | 0.8 |
| 4 | 0.45 | 0.34 | 1.0 | 0.34 | 0.45 | 1.0 |
| 5 | 0.42 | 0.31 | 1.0 | 0.31 | 0.42 | 1.0 |
| 6 | 0.39 | 0.29 | 0.9 | 0.29 | 0.39 | 0.9 |
| 7 | 0.45 | 0.42 | 1.1 | 0.42 | 0.45 | 1.1 |
| 8 | 0.42 | 0.39 | 1.0 | 0.39 | 0.42 | 1.0 |
| 9 | 0.39 | 0.36 | 1.0 | 0.36 | 0.39 | 1.0 |
| 10 | 0.53 | 0.26 | 1.0 | 0.26 | 0.53 | 1.0 |
| 11 | 0.49 | 0.24 | 0.9 | 0.24 | 0.49 | 0.9 |
| 12 | 0.46 | 0.22 | 0.8 | 0.22 | 0.46 | 0.8 |
| 13 | 0.53 | 0.34 | 1.0 | 0.34 | 0.53 | 1.0 |
| 14 | 0.49 | 0.31 | 1.0 | 0.31 | 0.49 | 1.0 |
| 15 | 0.46 | 0.29 | 0.9 | 0.29 | 0.46 | 0.9 |
| 16 | 0.53 | 0.42 | 1.1 | 0.42 | 0.53 | 1.1 |
| 17 | 0.49 | 0.39 | 1.0 | 0.39 | 0.49 | 1.0 |
| 18 | 0.46 | 0.36 | 1.0 | 0.36 | 0.46 | 1.0 |
| 19 | 0.61 | 0.26 | 1.0 | 0.26 | 0.61 | 1.0 |
| 20 | 0.56 | 0.24 | 0.9 | 0.24 | 0.56 | 0.9 |
| 21 | 0.52 | 0.22 | 0.8 | 0.22 | 0.52 | 0.8 |
| 22 | 0.61 | 0.34 | 1.0 | 0.34 | 0.61 | 1.0 |
| 23 | 0.56 | 0.31 | 1.0 | 0.31 | 0.56 | 1.0 |
| 24 | 0.52 | 0.29 | 0.9 | 0.29 | 0.52 | 0.9 |
| 25 | 0.61 | 0.42 | 1.1 | 0.42 | 0.61 | 1.1 |
| 26 | 0.56 | 0.39 | 1.0 | 0.39 | 0.56 | 1.0 |
| 27 | 0.52 | 0.36 | 1.0 | 0.36 | 0.52 | 1.0 |
| Non-Parametric Regression | Genetic Aggregation | |||||
|---|---|---|---|---|---|---|
| Quality [%] | Eta [%] | dP [%] | Quality [%] | Eta [%] | dP [%] | |
| RS1 | ||||||
| DOE Points | 4.2 | 5.1 | 4.1 | 33.9 | 0.0 | 25.3 |
| Verification points | 4.8 | 5.4 | 5.2 | 36.6 | 0.0 | 27.2 |
| RS2 | ||||||
| DOE Points | 4.05 | 5.5 | 4.6 | 11.2 | 0.0 | 2.9 |
| Verification points | 4.3 | 9.2 | 6.4 | 13.5 | 0.0 | 5.4 |
| New AAOS | Ref. AAOS | Stairmand [12] | Sun [27] | Ravi [31] | Elsayed [23] | Elsayed [17] | Elsayed [24] | Elsayed [24] | Sgrott Jr. [32] | |
|---|---|---|---|---|---|---|---|---|---|---|
| a/D | 0.60 | 0.46 | 0.50 | 0.6 | 0.40 | 0.62 | 0.60 | 0.26 | 0.49 | 0.41 |
| b/D | 0.29 | 0.28 | 0.20 | 0.2 | 0.15 | 0.24 | 0.20 | 0.15 | 0.16 | 0.50 |
| Dx/D | 0.45 | 0.39 | 0.50 | 0.5 | 0.40 | 0.62 | 0.55 | 0.42 | 0.62 | 0.50 |
| h/D | 1.29 | 1.01 | 1.50 | 1.0 | 1.10 | 1.62 | 1.41 | 1.50 | 1.50 | 1.53 |
| S/D | 0.60 | 0.52 | 0.50 | 0.2 | 0.40 | 0.62 | 0.60 | 0.50 | 0.50 | 0.72 |
| Oil Quality/Max. Calculated Oil Quality [-] | Efficiency/Max. Calculated Efficiency [-] | Pressure Drop/Max. Calculated Pressure Drop [-] | |
|---|---|---|---|
| New AAOS | 0.99 | 0.997 | 0.38 |
| C15RS2 | 0.88 | 0.998 | 0.34 |
| Ref. AAOS | 0.73 | 0.999 | 0.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szwarc, T.; Wróblewski, W.; Borzęcki, T. Optimization of the Aircraft Air/Oil Separator by the Response Surface Determined from Modeling of Three-Dimensional Two-Phase Flow. Energies 2022, 15, 7273. https://doi.org/10.3390/en15197273
Szwarc T, Wróblewski W, Borzęcki T. Optimization of the Aircraft Air/Oil Separator by the Response Surface Determined from Modeling of Three-Dimensional Two-Phase Flow. Energies. 2022; 15(19):7273. https://doi.org/10.3390/en15197273
Chicago/Turabian StyleSzwarc, Tomasz, Włodzimierz Wróblewski, and Tomasz Borzęcki. 2022. "Optimization of the Aircraft Air/Oil Separator by the Response Surface Determined from Modeling of Three-Dimensional Two-Phase Flow" Energies 15, no. 19: 7273. https://doi.org/10.3390/en15197273
APA StyleSzwarc, T., Wróblewski, W., & Borzęcki, T. (2022). Optimization of the Aircraft Air/Oil Separator by the Response Surface Determined from Modeling of Three-Dimensional Two-Phase Flow. Energies, 15(19), 7273. https://doi.org/10.3390/en15197273






