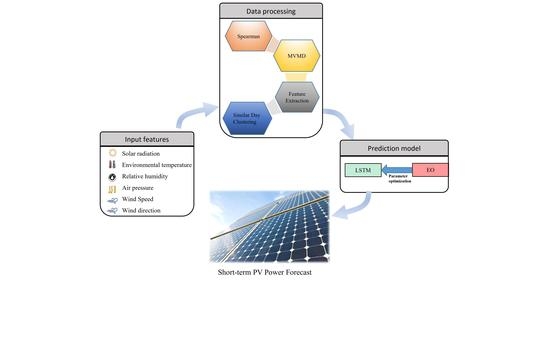
Development of MVMD-EO-LSTM Model for a Short-Term Photovoltaic Power Prediction
Abstract
1. Introduction
2. Data Preprocessing Based on MVMD for Feature Extraction
2.1. Spearman Correlation Analysis Method
2.2. Fundamentals of MVMD Algorithm
3. LSTM Power Prediction Model Based on EO Algorithm
3.1. EO Algorithm
- (1)
- Population particle initialization
- (2)
- Construct the equilibrium pool and select the candidate solution
- (3)
- Exponential term (F)
- (4)
- Generation rate (G)
3.2. The Procedure of EO Optimizing LSTM Parameter
- (1)
- Divide the dataset into a training set and a test set;
- (2)
- The number of iterations and learning rate of hidden layer neurons in LSTM are used as the object of EO optimization, i.e., the information of each particle concentration is a three-dimensional vector representing the number of hidden layer neurons, the number of iterations and the learning rate;
- (3)
- To guarantee global optimization results, the generation rate of EO algorithm GP is set as 0.5, and constant a1 = 2 and a2 = 1 [16]. Considering the convergence speed and time cost of the algorithm, the number of iterations T is set as 100 and the number of particles K is set as 30. and are the upper and lower limits of the particle search space, and the fitness function F(x) is the mean absolute error (MAE) of predicted value and output value in the photovoltaic power;
- (4)
- Random initialization is carried out in the search space through Equation (5);
- (5)
- The concentration information of each particle was imported into LSTM network, and the corresponding fitness value was calculated by training and prediction through the training set;
- (6)
- Compare the fitness values of each particle, filter out the four particles with the smallest fitness values as . At the same time, calculate the mean concentration of these four particles to construct the equilibrium pool ;
- (7)
- Update the coefficient of exponential term by Equation (7);
- (8)
- Randomly select guide particles from the equilibrium pool, and update the generation rate according to Equation (8);
- (9)
- Combine the guiding particle , the updated pointing coefficient and the generation rate . The concentration of each particle is updated one by one through Equation (11);
- (10)
- Judge whether the maximum number of iterations is reached. If the maximum number of iterations is reached, T, output the particle with the lowest fitness in the balance pool, and assign its corresponding parameters to LSTM for model training and prediction in combination with training set and test set; otherwise, return to Step (5).
4. The MVMD-EO-LSTM Model
- (1)
- Spearman is used to screen the correlation of input features of historical photovoltaic power station data to eliminate the low-correlation features;
- (2)
- MVMD is used to decompose the solar radiation sequence;
- (3)
- Spearman is used to calculate the correlation coefficient between each decomposition component and the output power, screening out the strong correlation component;
- (4)
- The strong correlation components are analyzed by cross-correlation number, grouped and screened as feature extraction results;
- (5)
- The feature extraction results are combined with the original feature screening results as the input feature of the prediction model, and the photovoltaic power is used as the output feature. The dataset is selected based on the K-means similar day clustering result, and the EO-LSTM is used for training and parameter optimization to achieve the photovoltaic power prediction under different weather conditions.
5. Performance Analysis
5.1. Results of Spearman Analysis
5.2. Feature Extraction Results
5.3. Verification of MVMD Feature Extraction
- (1)
- Compared with only original features input, all feature extraction methods (VMD, WPD and MVMD) can improve the prediction accuracy. Among them, the MVMD model presents the best performance, where the mean RMSE decreases by 0.64 and the mean MAE decreases by 0.35;
- (2)
- Compared with VMD and WPD models, the mean RMSE and mean MAE for the three weather conditions of the MVMD model were reduced by at least 18%. It exhibited that MVMD can better refine and decompose the input characteristics of photovoltaic power data, indicating that it is more conducive to mining the fluctuation characteristics of the data in the PV power prediction.
5.4. Comparison of Optimization Algorithms
6. Conclusions
- (1)
- For non-stationary photovoltaic historical data, the MVMD feature extraction method based on the fusion of VMD and WPD decomposition can effectively build up the relationship between input features and photovoltaic output power. This realizes the fine division of features so that the accuracy and stability in the short-term photovoltaic power prediction can be promised;
- (2)
- By way of EO algorithm with a strong global search ability and high process convergence, LSTM parameters can be determined to optimize the MVMD model. Compared with existing algorithms, the proposed method has better optimization performance, stronger stability and robustness under different weather conditions.
Author Contributions
Funding
Conflicts of Interest
References
- Colak, M.; Yesilbudak, M.; Bayindir, R. Daily Photovoltaic Power Prediction Enhanced by Hybrid GWO-MLP, ALO-MLP and WOA-MLP Models Using Meteorological Information. Energies 2020, 13, 901. [Google Scholar] [CrossRef]
- Serrano Ardila, V.M.; Maciel, J.N.; Ledesma, J.J.; Ando Junior, O.H. Fuzzy Time Series Methods Applied to (In)Direct Short-Term Photovoltaic Power Forecasting. Energies 2022, 15, 845. [Google Scholar] [CrossRef]
- Scolari, E.; Reyes-chamorro, L.; Sossan, F.; Paolone, M. A comprehensive assessment of the short-term uncertainty of grid-connected PV systems. IEEE Trans. Sustain. Energy 2018, 9, 1458–1467. [Google Scholar] [CrossRef]
- Liu, H.K.; Feng, J.X.; Yang, S.Q.; Jia, T. Wind power prediction model based on ARMA and improved BP-ANN. Adv. Mater. Res. 2014, 1008–1009, 183–187. [Google Scholar] [CrossRef]
- Biswas, A.K.; Ahmed, S.I.; Bankefa, T.; Prakash, R.; Salehfar, H. Performance Analysis of Short and Mid-Term Wind Power Prediction using ARIMA and Hybrid Models. In Proceedings of the 2021 IEEE Power and Energy Conference at Illinois (PECI), Urbana, IL, USA, 1–2 April 2021. [Google Scholar]
- Nguyen, R.; Yang, Y.; Tohmeh, A.; Yeh, H.-G. Predicting PV Power Generation using SVM Regression. In Proceedings of the IEEE Green Energy and Smart Systems Conference, Long Beach, CA, USA, 1–2 November 2021; pp. 1–5. [Google Scholar]
- Kim, G.G.; Choi, J.H.; Park, S.Y.; Bhang, B.G.; Nam, W.J.; Cha, H.L.; Park, N.S.; Ahn, H.K. Prediction Model for PV Performance With Correlation Analysis of Environmental Variables. IEEE J. Photovolt. 2019, 9, 832–841. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Wang, Z.; Cui, F.; Wang, S. A Power Prediction Method for PV system Based on Wavelet Decomposition and Neural Networks. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–16 July 2020. [Google Scholar]
- Zhao, Y.; Li, C.; Fu, W.; Liu, J.; Chen, H. A modified variational mode decomposition method based on envelope nesting and multi-criteria evaluation. J. Sound Vib. 2020, 468, 115099. [Google Scholar] [CrossRef]
- Sun, W.; Wang, A.; Zhang, T. Short-Term Photovoltaic Power Interval Prediction Based on VMD and GOA-KELM Algorithms. In Proceedings of the 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 7–10 May 2021. [Google Scholar]
- Ye, R.; Guo, Z.; Liu, R.; Liu, J. Short-term wind speed forecasting method based on wavelet packet decomposition and improved Elman neural network. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016. [Google Scholar]
- Yin, J.; Perakis, A.N.; Wang, N. An Ensemble Real-Time Tidal Level Prediction Mechanism Using Multiresolution Wavelet Decomposition Method. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4856–4865. [Google Scholar] [CrossRef]
- Li, Y.; Ye, F.; Liu, Z.; Wang, Z.; Mao, Y. A Short-Term Photovoltaic Power Generation Forecast Method Based on LSTM. Math. Probl. Eng. 2021, 2021, 6613123. [Google Scholar] [CrossRef]
- Ren, X.Q.; Liu, S.L.; Yu, X.D.; Dong, X. A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 2021, 234, 121236. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, Z.; Wang, H.; Yue, Y. Short-term Photovoltaic Power Prediction based on DE-GWO-LSTM. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Dalia, T.A.; Abdullah, M.S.; Waleed, A.S.; Walaa, I.G.; Ragab, A.E. Equilibrium optimizer based multi dimensions operation of hybrid AC/DC grids. Alex. Eng. J. 2020, 59, 4787–4803. [Google Scholar]
- Hossain, M.S.; Mahmood, H. Short-Term Photovoltaic Power Forecasting Using an LSTM Neural Network and Synthetic Weather Forecast. IEEE Access 2020, 8, 172524–172533. [Google Scholar] [CrossRef]
- Shi, M.; Xu, K.; Wang, J.; Yin, R.; Wang, T.; Yong, T. Short-Term Photovoltaic Power Forecast Based on Long Short-Term Memory Network. In Proceedings of the 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 7–9 September 2019. [Google Scholar]
- Bates, J.M.; Granger, C.W. The Combination of Forecasts. Oper. Res. Soc. 1969, 20, 451–468. [Google Scholar] [CrossRef]
- Eseye, A.T.; Zhang, J.; Zheng, D. Short-term Photovoltaic Solar Power Forecasting Using a Hybrid Wavelet-PSO-SVM Model Based on SCADA and Meteorological Information. Renew. Energy 2018, 18, 357–367. [Google Scholar] [CrossRef]
- Myers, J.I.; Well, A.D. Research Design and Statistical Analysis; Routledge: London, UK, 2003; pp. 305–309. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) Over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Krishna, V.B.; Wadman, W.S.; Kim, Y. Now Casting: Accurate and Precise Short-Term Wind Power Prediction Using Hyperlocal Wind Forecasts. In Proceedings of the Ninth International Conference on Future Energy Systems, Karlsruhe, Germany, 12–15 June 2018. [Google Scholar]
- Lorenz, E.; Hurka, J.; Heiemann, D. Irradiance Forecasting for the Power Prediction of Grid-connected Photovoltaic Systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 2–10. [Google Scholar] [CrossRef]







| Input Features | Solar Radiation | Environmental Temperature | Relative Humidity | Air Pressure | Wind Speed | Wind Direction |
|---|---|---|---|---|---|---|
| Spearman | 0.765 | 0.410 | −0.339 | 0.086 | −0.068 | −0.007 |
| Decomposition Method | Characteristic Components | Cross-Correlation |
|---|---|---|
| WPD | L1–LH1 | 0.994 |
| L1–IF1 | 0.988 | |
| LH1–IF1 | 0.992 | |
| VMD | IF1–IF4 | 0.582 |
| IF1–IF8 | 0.558 | |
| IF4–IF8 | 0.979 |
| Weather Types | Sunny | Cloudy | Rainy |
|---|---|---|---|
| Number of days | 51 | 31 | 10 |
| Models | Input Features |
|---|---|
| MVMD | MVMD decomposition feature extraction results (LH1 and IF2), solar irradiation intensity, ambient temperature, relative humidity |
| VMD | VMD decomposition feature extraction results (IF1 and IF4), solar irradiation intensity, ambient temperature, relative humidity |
| WPD | WPD feature extraction results (L1), solar irradiation intensity, ambient temperature, relative humidity |
| Original | Solar irradiation intensity, ambient temperature, relative humidity |
| Models | RMSE | ||
|---|---|---|---|
| Sunny | Cloudy | Rainy | |
| MVMD | 0.82709 | 0.93497 | 0.74021 |
| VMD | 0.95949 | 1.1857 | 0.93611 |
| WPD | 0.99308 | 1.5635 | 1.0313 |
| Original | 1.3219 | 1.7705 | 1.3491 |
| Models | MAE | ||
|---|---|---|---|
| Sunny | Cloudy | Rainy | |
| MVMD | 0.69789 | 0.69694 | 0.56436 |
| VMD | 0.75892 | 0.99214 | 0.723 |
| WPD | 0.80592 | 1.2282 | 0.88054 |
| Original | 0.83864 | 1.2836 | 0.91566 |
| Input | RMSE | ||
|---|---|---|---|
| Sunny | Cloudy | Rainy | |
| EO-LSTM | 0.82709 | 0.93497 | 0.74021 |
| PSO-LSTM | 0.88802 | 1.0711 | 0.82262 |
| GWO-LSTM | 0.90334 | 1.0947 | 0.8284 |
| Models | MAE | ||
|---|---|---|---|
| Sunny | Cloudy | Rainy | |
| EO-LSTM | 0.65789 | 0.69694 | 0.56436 |
| PSO-LSTM | 0.66806 | 0.89498 | 0.65755 |
| GWO-LSTM | 0.7632 | 0.83247 | 0.55425 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Gao, L.; Lin, H.-C.; Huo, Y.; Ren, Y.; Guo, W. Development of MVMD-EO-LSTM Model for a Short-Term Photovoltaic Power Prediction. Energies 2022, 15, 7332. https://doi.org/10.3390/en15197332
Gao X, Gao L, Lin H-C, Huo Y, Ren Y, Guo W. Development of MVMD-EO-LSTM Model for a Short-Term Photovoltaic Power Prediction. Energies. 2022; 15(19):7332. https://doi.org/10.3390/en15197332
Chicago/Turabian StyleGao, Xiaozhi, Lichi Gao, Hsiung-Cheng Lin, Yanming Huo, Yaheng Ren, and Wang Guo. 2022. "Development of MVMD-EO-LSTM Model for a Short-Term Photovoltaic Power Prediction" Energies 15, no. 19: 7332. https://doi.org/10.3390/en15197332
APA StyleGao, X., Gao, L., Lin, H.-C., Huo, Y., Ren, Y., & Guo, W. (2022). Development of MVMD-EO-LSTM Model for a Short-Term Photovoltaic Power Prediction. Energies, 15(19), 7332. https://doi.org/10.3390/en15197332