Unified Power Control of Permanent Magnet Synchronous Generator Based Wind Power System with Ancillary Support during Grid Faults
Abstract
:1. Introduction
2. Problem Formulation
2.1. Symmetrical Voltage Sag
2.2. Grid Imperfections with Both PSC and NSC
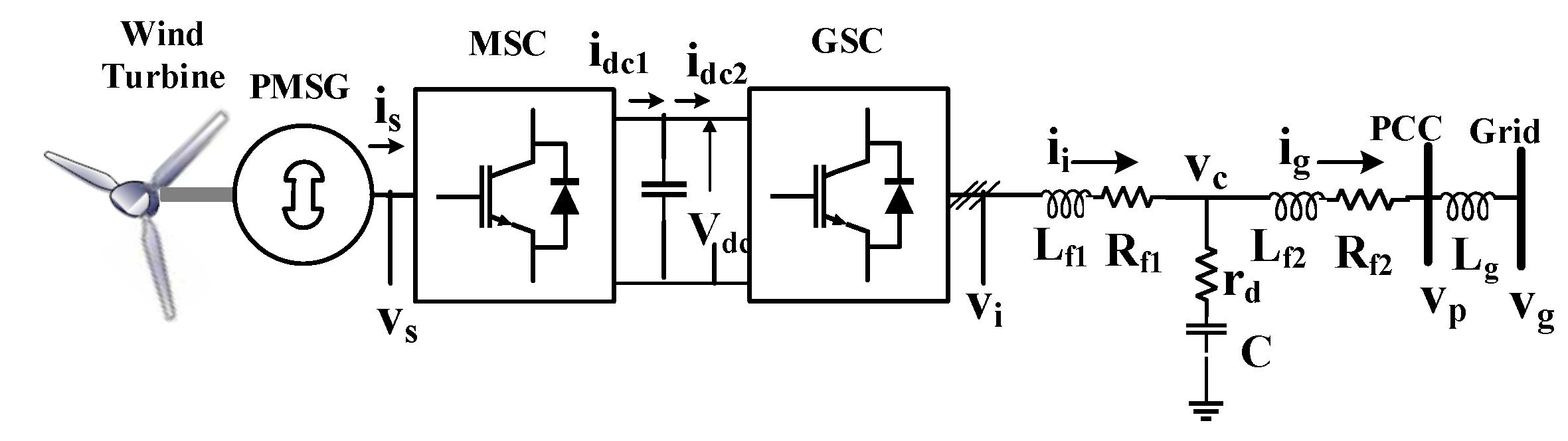
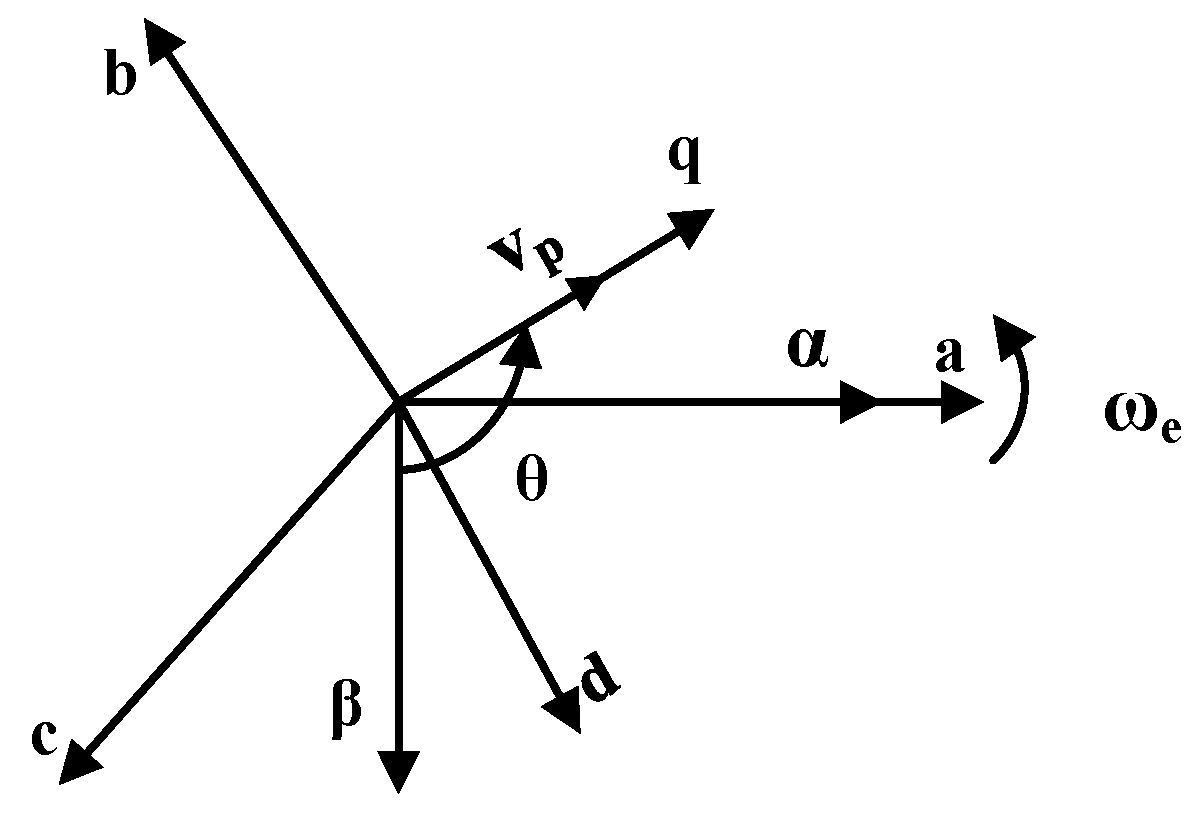
3. System Modelling and Proposed Controller Design
3.1. Modified MSC Controller
3.2. GSC Modelling
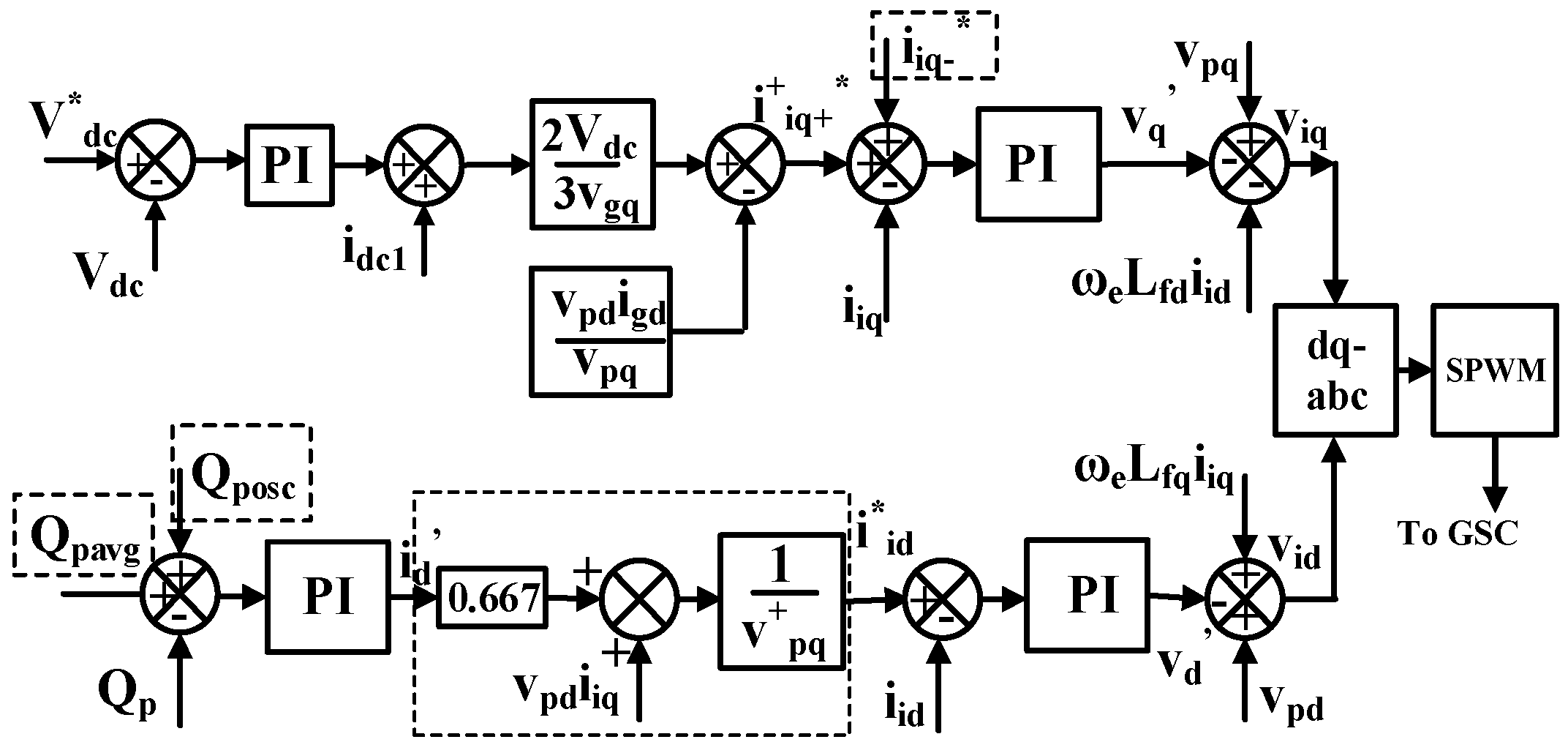
3.3. GSC Controller Design
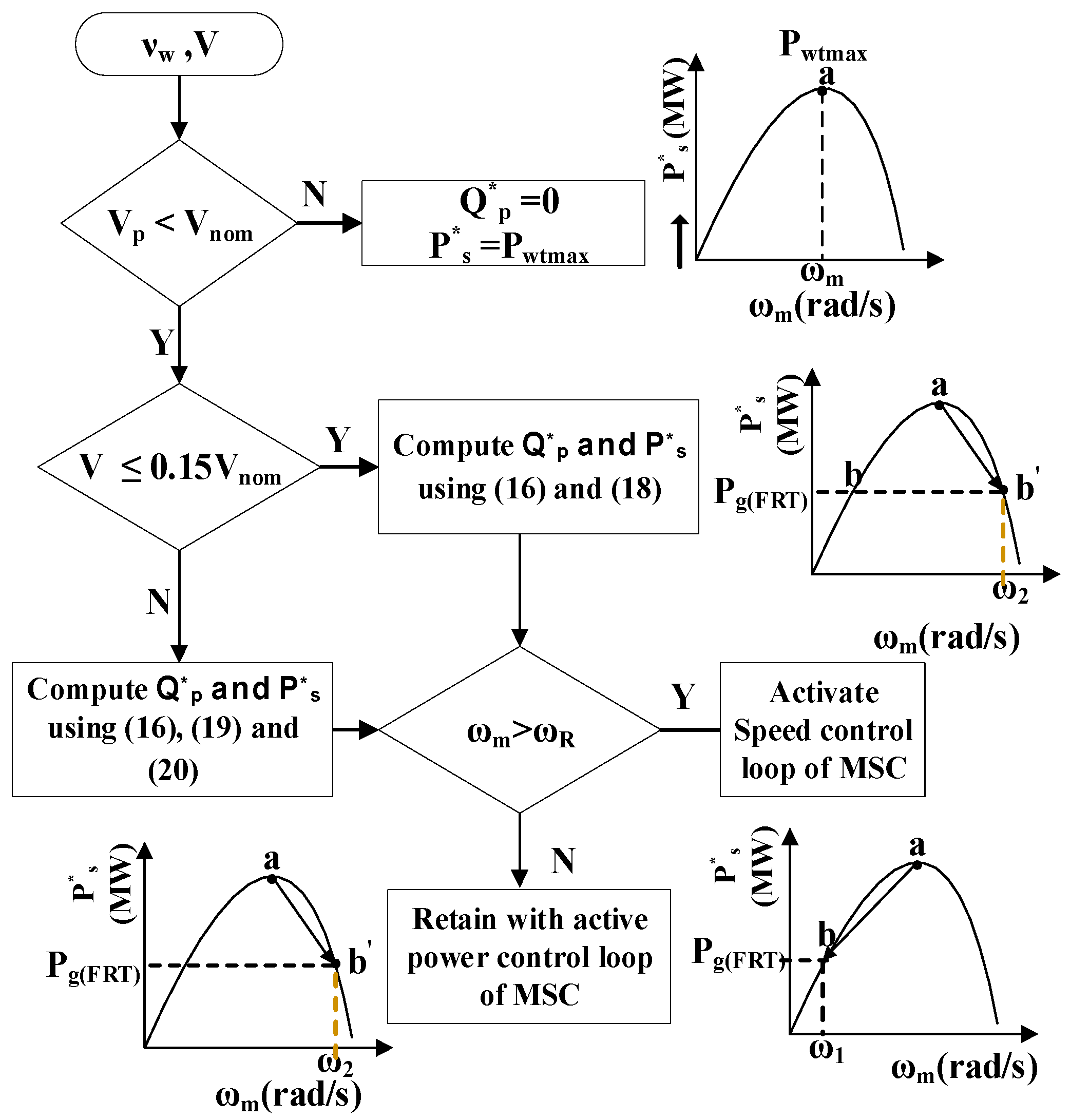
4. Proposed Reference Power Generation Scheme
4.1. Symmetrical Voltage Sag
4.1.1. Maximum Power Limits
4.1.2. Constant Current Control
4.1.3. Rotor Speed Regulation
4.2. Grid Imperfections with Both PSC and NSC
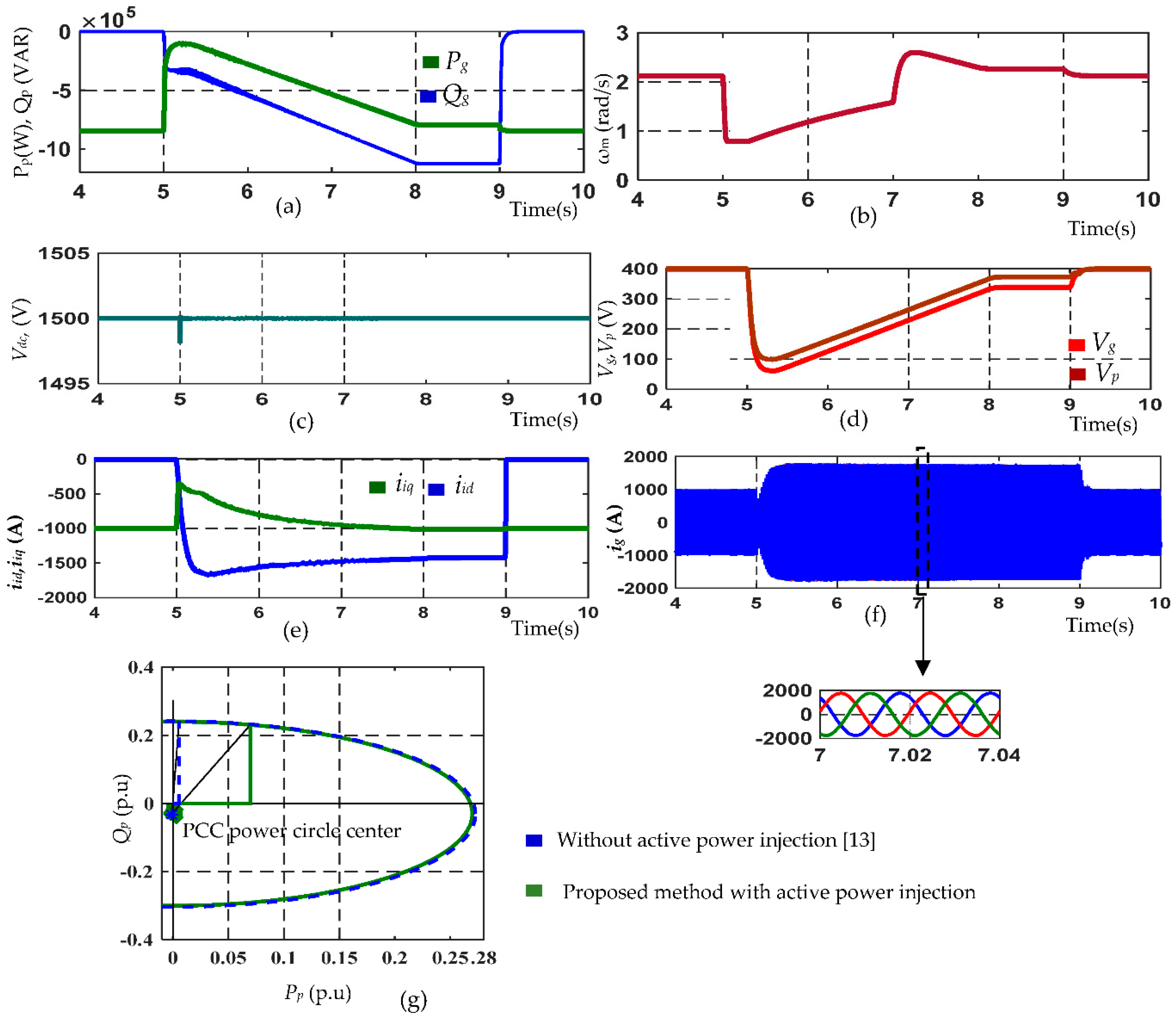
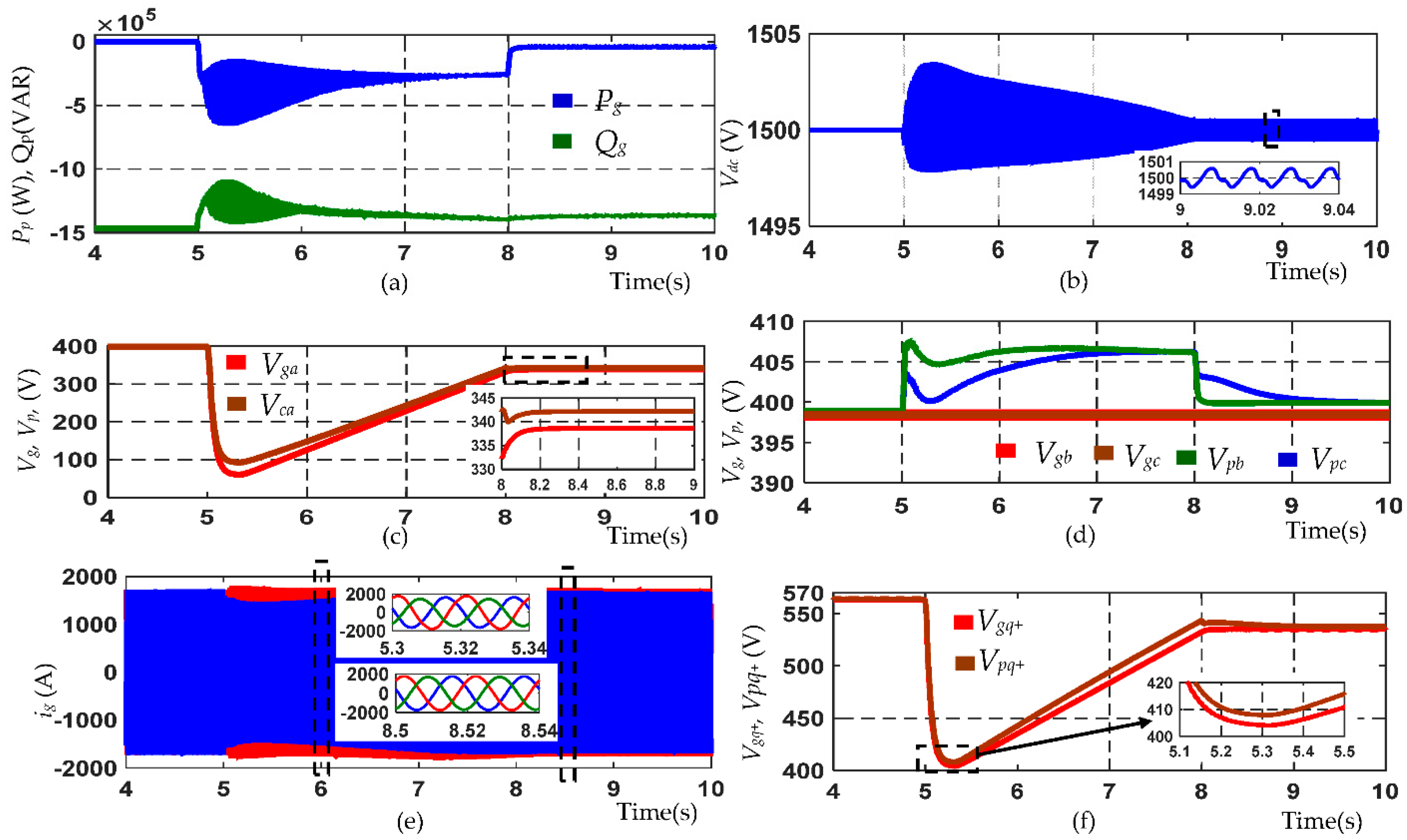
5. Simulation Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Central Electricity Regulatory Commission. Indian Electricity Grid Code Regulations (Fourth Amendment); Ministry of Power Government of India: New Delhi, India, 2016. [Google Scholar]
- Central Electricity Authority (Grid Standards). Indian Electricity Grid Code Regulations 2010. The Gazette of India, 26 June 2010. [Google Scholar]
- Adriana, M.; Pedro, P.; João, F.M. A Survey on Power Grid Faults and Their Origins: A Contribution to Improving Power Grid Resilience. Energies 2019, 12, 4667. [Google Scholar]
- Bollen, M.H.J.; Olguin, G.; Martins, M. Voltage dips at the terminals of wind power installations. Wind. Energy 2005, 8, 307–318. [Google Scholar] [CrossRef]
- Kanasottu, A.N.; Chandra, P.G.; Eugene, F. Complying the LVRT grid code requirement of a fixed speed wind energy system using unified voltage and pitch angle control strategy. Wind. Eng. 2022. [Google Scholar] [CrossRef]
- Kishor, V.B.; Dipak, P.P.; Sunildatta, S.K. Grid Integration of Wind Energy Generation System and Grid Code Requirements. In Deregulated Electricity Market: The Smart Grid Perspectives, 1st ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Amir, A.; Lorenzo, Z.; Nicolaos, A. Cutululis. Fault ride through capability of grid forming wind turbines: A comparison of three control schemes. IET Renew. Power Gener. 2022, 16, 1866–1881. [Google Scholar]
- Meng, Y.; Wu, K.; Jia, F.; Yan, S.; Yang, Y.; Wang, X. Grid integration and fault ride-through of fractional frequency offshore wind power system based on Y-connected modular multilevel converter. IET Gener. Transm. Distrib. 2022, 16, 2977–2988. [Google Scholar] [CrossRef]
- Wang, X.; Wu, H.; Wang, X.; Dall, L.; Kwon, J.B. Transient Stability Analysis of Grid-Following VSCs Considering Voltage-Dependent Current Injection during Fault Ride-Through. IEEE Trans. Energy Convers. (Early Access) 2022, 1–13. [Google Scholar] [CrossRef]
- Jlassi, I.; Cardoso, A.J.M. Fault-Tolerant Back-to-Back Converter for Direct-Drive PMSG Wind Turbines Using Direct Torque and Power Control Techniques. IEEE Trans. Power Elect. 2019, 34, 11215–11227. [Google Scholar]
- Ahmed, H.; Bhattacharya, A. PMSG-based VS-WECS for constant active power delivery to standalone load using direct matrix converter-based SST with BESS. IET Gener. Transm. Distrib. 2019, 13, 1757–1767. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Murata, R.T.T.; Tamura, J. A Variable Speed Wind Turbine Control Strategy to Meet Wind Farm Grid Code Requirements. IEEE Trans. Power Syst. 2010, 25, 331–340. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Wu, L.; Shen, C.; Ju, Y. LVRT Test data analysis of converter interfaced wind turbines. IET J. Eng. 2019, 16, 1550–1553. [Google Scholar] [CrossRef]
- Li, P.; Song, Y.-D.; Li, D.-Y.; Cai, W.-C.; Zhang, K. Control and Monitoring for Grid-Friendly Wind Turbines: Research Overview and Suggested Approach. IEEE Trans. Power Electron. 2015, 30, 1979–1986. [Google Scholar] [CrossRef]
- Valenciaga, F.; Fernandez, R.D. Multiple-input–multiple-output High-order Sliding Mode Control for a Permanent Magnet Synchronous Generator Wind-Based System with Grid Support Capabilities. IET Renew. Power Gener. 2015, 9, 925–934. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Swatloski, R.P.; Gathings, W. Optimal and Direct-Current Vector Control of Direct-Driven PMSG Wind Turbines. IEEE Trans. Power Electron. 2012, 27, 2325–2336. [Google Scholar] [CrossRef]
- Vijayapriya, R.; Raja, P.; Selvan, M.P. A Modified Active Power Control Scheme for Enhanced Operation of PMSG Based WGs. IEEE Trans. Sust. Energy 2018, 9, 630–638. [Google Scholar]
- Jahanpour-Dehkordi, M.; Vaez-Zadeh, S.; Mohammadi, J. Development of a Combined Control System to Improve the Performance of a PMSG-Based Wind Energy Conversion System Under Normal and Grid Fault Conditions. IEEE Trans. Energy Conver. 2019, 34, 1287–1295. [Google Scholar] [CrossRef]
- Alepuz, S.; Calle, A.; Busquets-Monge, S.; Kouro, S.; Wu, B. Use of Stored Energy in PMSG Rotor Inertia for Low Voltage Ride-Through in Back-to-Back NPC Converter Based Wind Power Systems. IEEE Trans. Ind. Electron. 2013, 60, 1787–1796. [Google Scholar] [CrossRef]
- Yassin, H.M.; Hanafy, H.H.; Hallouda, M.M. Enhancement Low-Voltage Ride Through Capability of Permanent Magnet Synchronous Generator-Based Wind Turbines using Interval Type-2 Fuzzy Control. IET Renew. Power Gener. 2016, 10, 339–348. [Google Scholar] [CrossRef]
- Geng, H.; Yang, G.; Xu, D.; Wu, B. Unified Power Control for PMSG based WECS Operating under different Grid Conditions. IEEE Trans. Energy Convers. 2011, 26, 822–830. [Google Scholar] [CrossRef]
- Nasiri, M.; Mohammadi, R. Peak Current Limitation for Grid Side Inverter by Limited Active Power in PMSG-Based Wind Turbines During Different Grid Faults. IEEE Trans. Sust. Energy 2014, 5, 1010–1017. [Google Scholar] [CrossRef]
- Kim, K.H.; Jeung, Y.C.; Lee, D.C. LVRT Scheme of PMSG Wind Power Systems Based on Feedback Linearization. IEEE Trans. Power Electron. 2012, 27, 2376–2384. [Google Scholar] [CrossRef]
- Kim, C.; Kim, W. Enhanced Low-Voltage Ride-Through Coordinated Control for PMSG Wind Turbines and Energy Storage Systems Considering Pitch and Inertia Response. IEEE Access 2020, 8, 212558–212567. [Google Scholar] [CrossRef]
- Hossain, M.I.; Abido, M.A. Positive-Negative Sequence Current Controller for LVRT Improvement of Wind Farms Integrated MMC-HVDC Network. IEEE Access 2020, 8, 93314–193339. [Google Scholar] [CrossRef]
- Thapa, K.B.; Jayasawal, K. Pitch Control Scheme for Rapid Active Power Control of a PMSG-Based Wind Power Plant. IEEE Tran. Indus. App. 2020, 56, 6756–6766. [Google Scholar] [CrossRef]
- Koiwa, K.; Li, Y.; Liu, K.Z.; Zanma, T.; Tamura, J. Full Converter Control for Variable-Speed Wind Turbines Without Integral Controller or PLL. IEEE Trans. Indus. Elect. 2020, 67, 9418–9428. [Google Scholar] [CrossRef]
- Boldea, I. The Electric Generators Handbook: Variable Speed Generators, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Vijayapriya, R.; Raja, P.; Selvan, M.P. Systematized Active Power Control of PMSG-based Wind-driven Generators. IEEE Syst. J. 2020, 14, 708–717. [Google Scholar]
- Vijayapriya, R.; Raja, P.; Selvan, M.P. A direct analytical predetermination of PMSG based WPS steady-state values under different operating conditions. Wind. Eng. 2022, 46. [Google Scholar] [CrossRef]
- Robles, E.; Ceballos, S.; Pou, J.; Martın, J.L.; Zaragoza, J.; Ibanez, P. Variable-Frequency Grid-Sequence Detector Based on a Quasi-Ideal Low-Pass Filter Stage and a Phase-Locked Loop. IEEE Trans. Power Electron. 2010, 25, 2552–2563. [Google Scholar] [CrossRef] [Green Version]
- Camacho, A.; Castilla, M.; Miret, J.; Vasquez, J.C.; Alarcón-Gallo, E. Flexible Voltage Support Control for Three-Phase Distributed Generation Inverters Under Grid Fault. IEEE Trans. Indus. Electron. 2013, 60, 1429–1441. [Google Scholar] [CrossRef]
- Liu, G.; Hu, J.; Tian, G.; Xu, L. Shengtie Wang, Study on high voltage ride through control strategy of PMSG-based wind turbine generation system with SCESU. J. Eng. 2019, 17, 4257–4260. [Google Scholar] [CrossRef]
- Miret, J.; Camacho, A.; Castilla, M.; de Vicuña, L.G.; Matas, J. Control Scheme with Voltage Support Capability for Distributed Generation Inverters Under Voltage Sags. IEEE Trans. Power Electron. 2013, 28, 5252–5262. [Google Scholar] [CrossRef]


| Variables | Phase/ Components | Before Fault | during Fault | ||
|---|---|---|---|---|---|
| without Reactive Power Support | with Reactive Power Support | ||||
| as per Section 4.1 | as per Section 4.2 | ||||
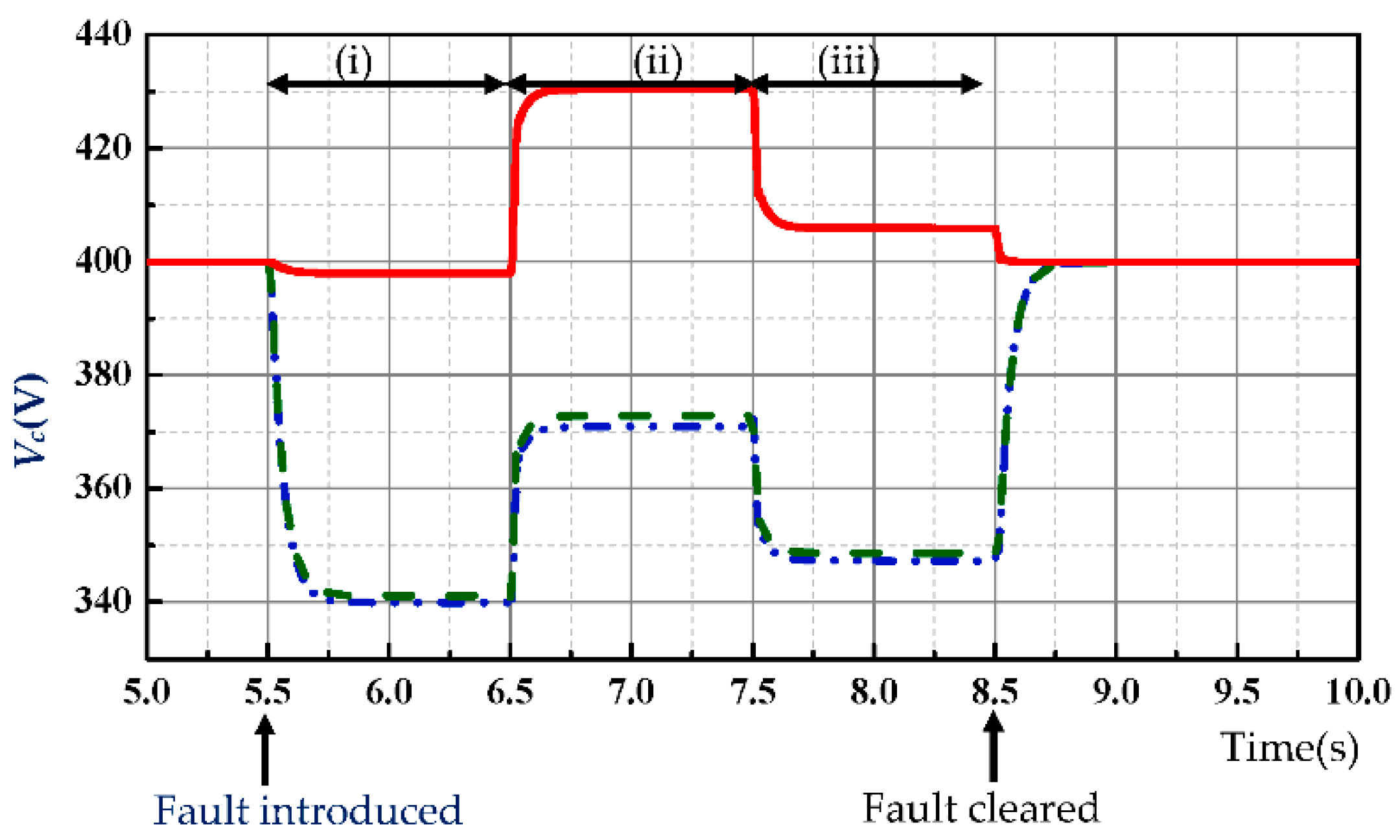
| Vc (V) | a-phase | 399.88 | 339.92 | 370.93 | 347.29 |
| b-phase | 399.88 | 341.08 | 372.86 | 348.63 | |
| c-phase | 399.88 | 397.9 | 430.38 | 405.8 | |
| PSC | 399.88 | 359.6 | 391.3 | 367.2 | |
| Ii (A) | a-phase | 706.2 | 782.31 | 1155 | 745.4 |
| b-phase | 706.2 | 806.5 | 1235.09 | 772.89 | |
| c-phase | 706.2 | 770.03 | 1134 | 723.38 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramachandran, V.; Perumal, A.S.; Lakshmaiya, N.; Paramasivam, P.; Dhanasekaran, S. Unified Power Control of Permanent Magnet Synchronous Generator Based Wind Power System with Ancillary Support during Grid Faults. Energies 2022, 15, 7385. https://doi.org/10.3390/en15197385
Ramachandran V, Perumal AS, Lakshmaiya N, Paramasivam P, Dhanasekaran S. Unified Power Control of Permanent Magnet Synchronous Generator Based Wind Power System with Ancillary Support during Grid Faults. Energies. 2022; 15(19):7385. https://doi.org/10.3390/en15197385
Chicago/Turabian StyleRamachandran, Vijayapriya, Angalaeswari Sendraya Perumal, Natrayan Lakshmaiya, Prabhu Paramasivam, and Seshathiri Dhanasekaran. 2022. "Unified Power Control of Permanent Magnet Synchronous Generator Based Wind Power System with Ancillary Support during Grid Faults" Energies 15, no. 19: 7385. https://doi.org/10.3390/en15197385








