Complex Heat Exchange in Friction Steam of Brakes

Abstract

In this article the structural features of friction pairs of brakes are analyzed. Heat transfer processes with new boundary conditions are described analytically with the addition of flow conditions and the appearance of a boundary thermal layer to convective heat transfer. The joint action of heat conduction and convection fields is presented. The release of heat during friction is due to the destruction of adhesive bonds in the actual contact zones, and the stress–strain state of micro-roughnesses. It should be said that due to the presence of accompanying transfer processes, complex heat transfer is much more complex compared to purely conductive, convective, and radiative heat transfer, which significantly complicates its analytical and experimental study. In this regard, the processes of complex heat transfer are currently studied little. From the point of view of non-equilibrium thermodynamics, the main task of describing the transfer process is to establish a relationship between the magnitude of the specific flux and the surface-volume temperatures that it causes in the metallic friction elements of the brakes. Additionally, as a result, an assessment of conductive and convective heat transfer in friction pairs of brake devices was made.

1. Introduction

From the standpoint of thermophysics, the friction assembly of various types of brakes is a system of many bodies with sources and absorbers of energy, distributed in a complex manner in space and time. It should be noted that complex systems of bodies occur not only in brake engineering but also in other areas of mechanics. Therefore, researchers are increasingly interested in the heat transfer theory, especially the interaction of heat conduction fields separately with convection and radiation [1,2].

The processes of heat exchange are essential and often critical in the intense thermal regimes of friction pairs of brakes, on which their effectiveness depends. They significantly influence brake operation and the intensity of wear of friction elements and can also cause failures of these elements. Temperature has a fundamental effect on the course of tribological phenomena on friction surfaces. As the temperature increases, the coefficient of friction changes, generally decreasing, which results in a decrease in braking efficiency [1,3]. In extreme cases, structural and chemical degradation of the friction material may occur [4,5]. An increase in temperature combined with the phenomenon of thermal expansion causes deformations and thermal stresses, which is the cause of ad hoc disorders of friction pair cooperation. A documented effect of cyclic stresses is the cracking of the drum or disc material, starting from the friction surface and progressing deep into the material [6,7]. For these reasons, thermal phenomena in brakes are subjects of numerous studies, both experimental and theoretical [6,8,9,10,11,12,13,14,15,16,17].

Thermal conductivity in solids, gases and liquids has been devoted to many books [18,19]. In a solid, the electronic phonon and photon thermal conductivity have been identified. In [20] attention was paid to the thermal radiation of a solid. The problems of heat transfer by radiation were of interest: for the case of given fields of surface-volume temperatures; when the transfer equation is “closed” by the heat conduction equation. The paper [21] highlighted the basics of radiation and complex heat transfer in technology. This complex heat transfer should include the following tasks:

(i)

radiation-conductive heat exchange in a flat layer of a selective and anisotropically scattering medium with a heat source;

(ii)

radiation-convective heat exchange of the medium flow with the channel walls.

In paper [22] on convective heat transfer in a homogeneous medium, attention was paid to thermal and dynamic boundary layers resulting from air-washing of metal brake friction.

Analysis of literature sources showed the following:

(i)

to take into account separately the peculiarities of each type of heat transfer, while highlighting the conductive type as a source of energy for certain types of heat transfer; therefore, it is necessary to consider in pairs conductive–convective, conductive–radiation and radiation–convection of heat exchanges;

(ii)

the relationship between the rough surface area forcedly cooled by air flows and polished heated surface and their emissivity has not been established;

(iii)

there is no method for assessing heat transfer from the surfaces of rims of pulleys and drums, as well as solid and self-ventilated discs [23].

In this paper attention will be focused on:

(i)

design and operation of frictional brake assemblies and their energy load;

(ii)

processes of heat exchange in friction pairs of brake devices;

(iii)

the combined action of convection fields from the washing air and thermal conductivity, and heat transfer from the metal friction elements of the brakes.

The paper aims to substantiate the features of complex heat transfer in friction pairs of brakes, and establish the reasons for its low efficiency in their open state.

2. Materials and Methods

The frictional units of the brakes have a different coefficient of mutual overlap of friction pairs, varying from 0.2 to 0.75, and therefore have unequal energy load. Figure 1a,b shows the friction pair of a disc-shoe brake. They consist of two friction linings which are located on the fixed brake pads. With the frictional interaction of the working surfaces of lining 2 with the rotating brake disc 1, under the action of the normal clamping force N, friction treadmill 3 is formed.

Figure 1c illustrates the friction assembly of a drawworks band brake. When tightening brake band 4 under the normal clamping force N, the working surface of friction lining 2 interacts with the friction track of the pulley rim 5. The latter is connected to the drum flange with the help of the fastening protrusion.

The frictional unit of the car drum-shoe brake is shown in Figure 1d. The unit contains brake drum rim 6 with flange 7, as well as friction lining 2 located on the brake pads. When expanding the latter in their toe and heel parts, the working surfaces of lining 2 frictionally interacts with the inner surface of the rim of brake drum 6.

The stress–strain state of microprotrusions of friction pairs with different types of contacts (ohmic, neutral, blocking) leads to volumetric heat release in the surface and subsurface layers of frictionally interacting materials. In this case, the friction power of the latter is a significant part of the total (taking into account the adhesive component) heat release power.

In braking devices of the tape– and drum–shoe type, the rim of the pulley and drum in cross-section can be represented as a horizontal plate (Figure 2a) and a solid disc—in the form of a vertical plate (Figure 2b). In this case, in a band-shoe brake, the upper surface of the pulley rim is polished, and the lower one is matte. In a drum–shoe brake, the opposite is true. In the considered brakes, a one-way supply of heat is carried out to the polished surfaces of the pulley rim. A solid-disc or a left half-disc of a self-ventilated brake disc with spikes is designed that a polished annular friction belt is surrounded by matt surfaces on the maximum and minimum radii sides of the friction belt. In addition, in a disc–shoe brake, a two-way supply of heat is carried out to the friction belts [23].

Heat transfer K through the rims, which are structural elements (thickness: lateral surfaces of the brake disc, pulley rim and drum) of metal friction element, is determined by the dependence of the type:

$$K=\frac{1}{\frac{1}{{\alpha }_1}+\frac{\delta }{\lambda }+\frac{1}{{\alpha }_2}},$$

(1)

where:

$\frac{1}{{\alpha }_1}$, $\frac{1}{{\alpha }_2}$—thermal resistance of heat transfer,

$\frac{\delta }{\lambda }$—thermal resistance of thermal conductivity,

$\lambda$—coefficient of thermal conductivity,

$\delta$—thickness of the metal friction elements.

3. Results and Discussions

3.1. Heat Transfer Processes in Friction Pairs of Brake Devices

Traditional sources of information about the temperature, convective, radiation and heat-conducting fields during frictional interaction of friction pairs of brakes are the theoretical and experimental studies that are carried out on full-scale samples and models.

From the point of view of non-equilibrium thermodynamics, the main task of describing the transfer process is to establish a relationship between the value of the specific flux q and the surface-volume temperatures that it causes in the metal friction elements of brakes. Concerning the heat transfer process, the main issue is to establish a relationship of the form [24]:

$$q=f\left(T\right).$$

(2)

The general nature of this relationship is determined by one of three possible forms of heat transfer—conductivity, convection and radiation.

There are two types of convection: free, when the elements of mass move in a gravitational field differ in volume due to the density of the system, and forced, in which the movement of the mass is carried out by external forces. Radiation is related to the ability of bodies to absorb, reflect, transmit and emit the energy of the electromagnetic field. Unlike the conduction and convection of heat, heat exchange by radiation between bodies is also possible in a vacuum. Upon encountering absorbing media, the energy of electromagnetic waves is converted into heat.

In

Table 1. Modified list of boundary conditions.

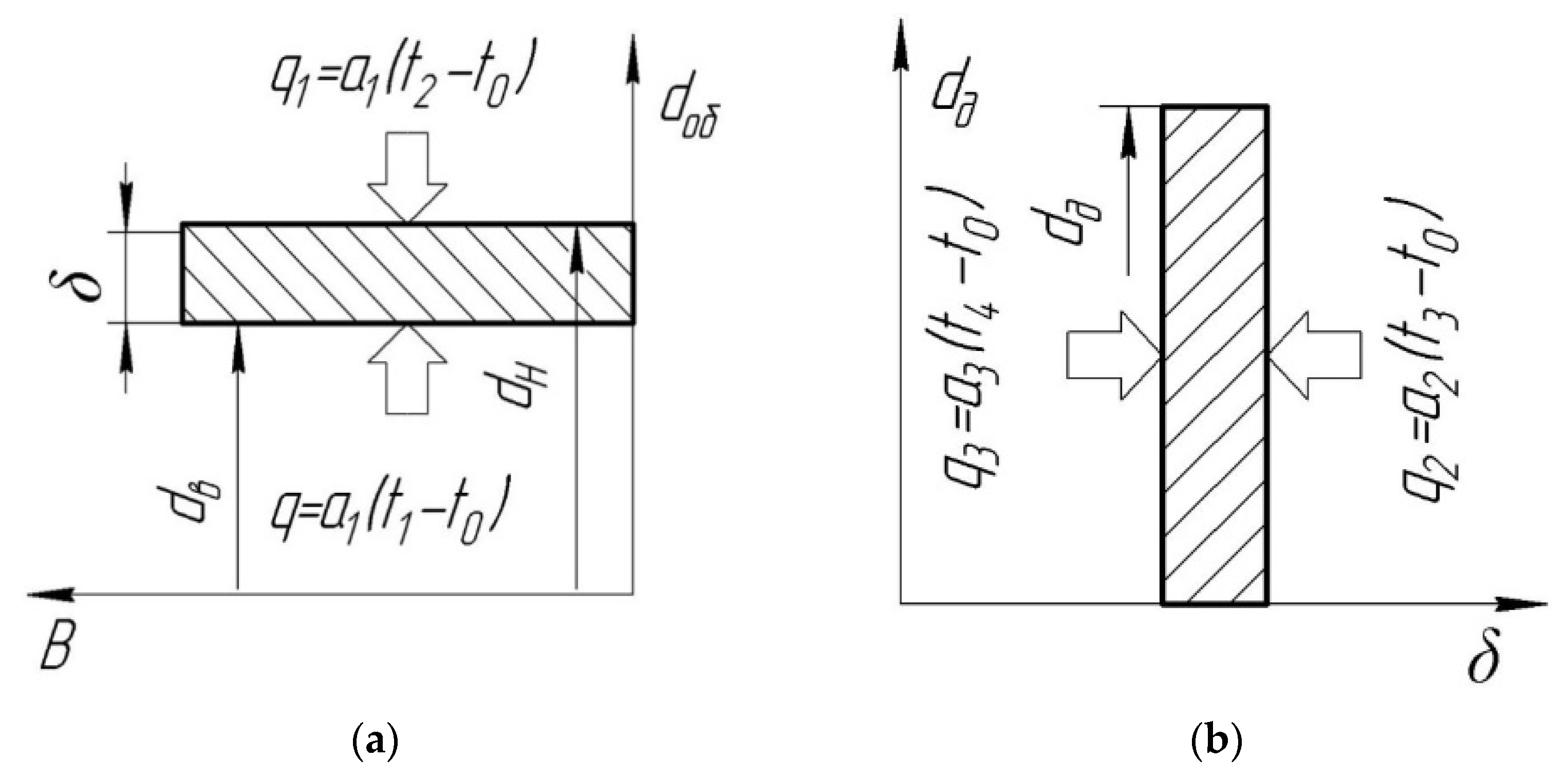
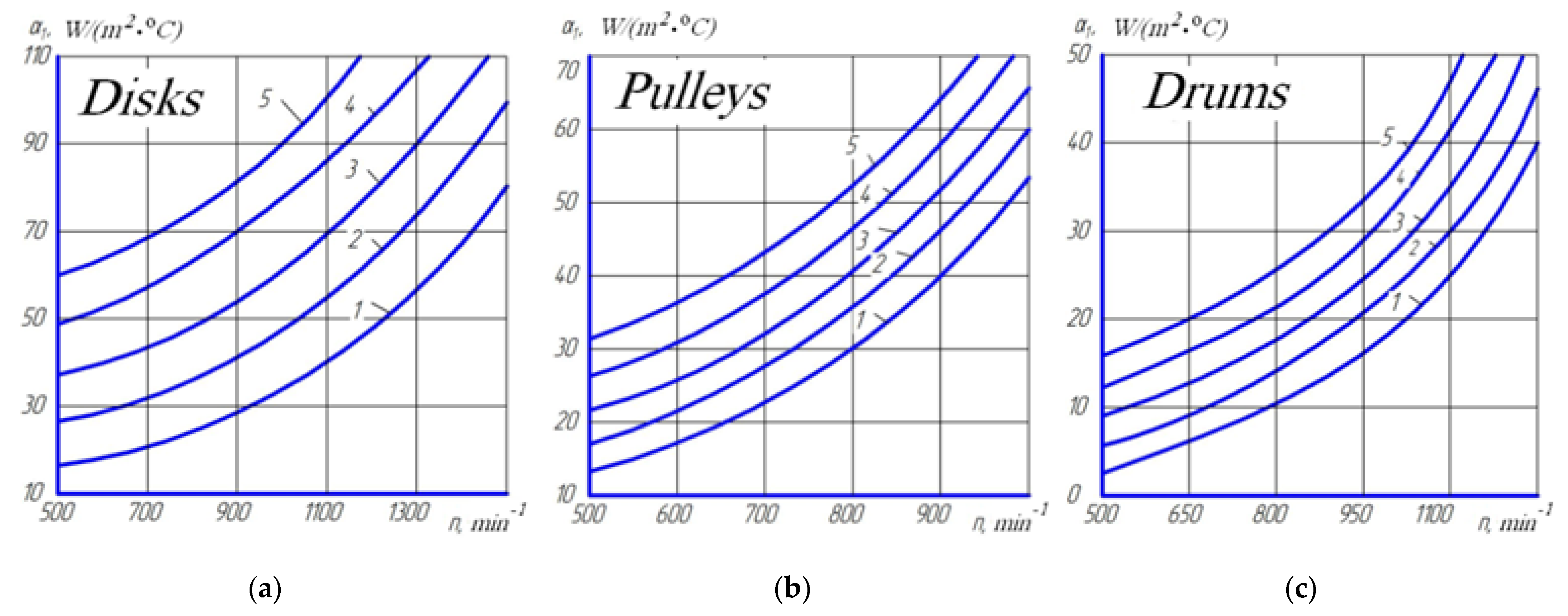
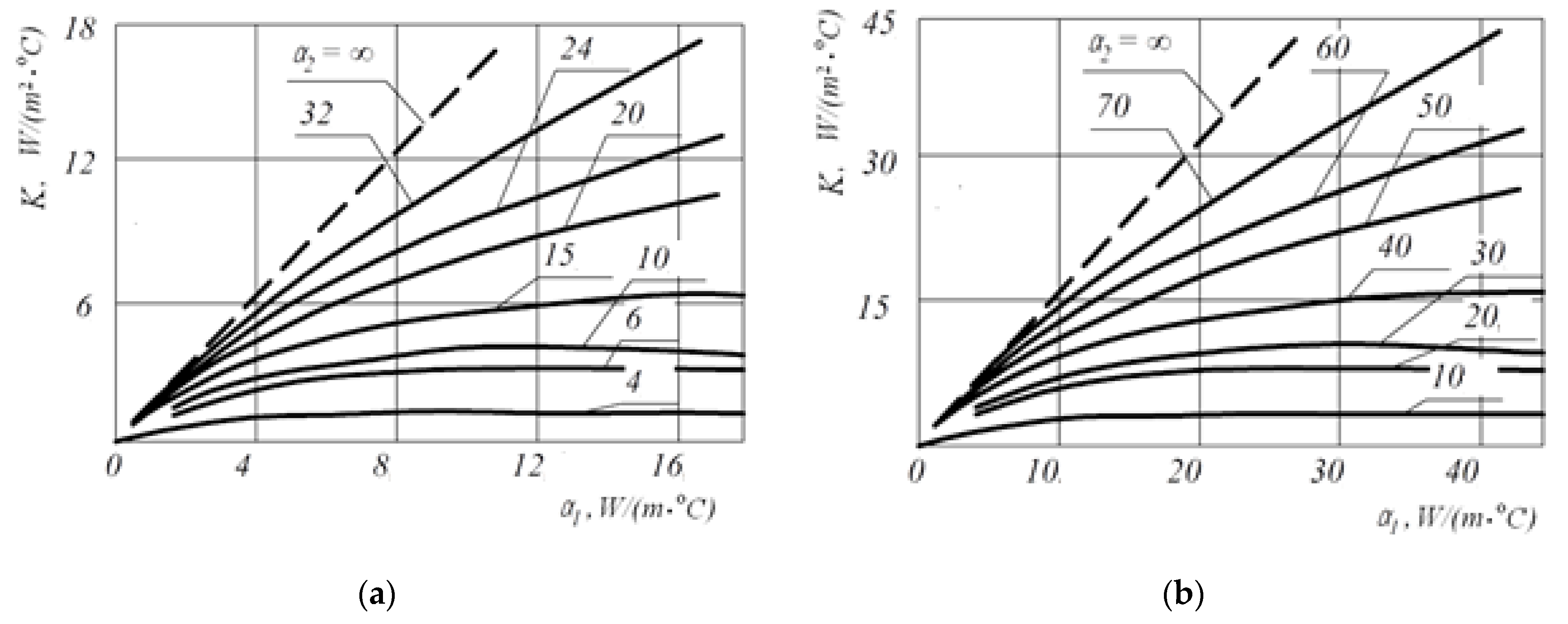
		Dependencies
Type of boundary condition	I-st	The intensity of the heat flux from the outside into the body is given ($q_v$)
		${\left.-\lambda \frac{\partial t_n}{\partial x}\right|}_{x=+0}=q_v$	(3)
	II-nd	The body is in contact with another body that has different thermophysical characteristics
		${\left.t_{n1}\right|}_{x=+0}={\left.t_{n2}\right|}_{x=-0}$	(4)
	III-rd	The body’s surface temperature is known ($t_s$)
	IV-th	The heat flux coming from the washing medium is directly proportional to the difference in temperature between the surface of the body and the medium, multiplied by the heat transfer coefficient
		${\left.-\lambda \frac{\partial t_n}{\partial x}\right|}_{x=+0}=\alpha \left(t_n-t_c\right)$	(5)

a list of boundary conditions is presented for the metal-polymer friction pairs of brakes, where $t_{n1}$, $t_{n2}$ are surface temperatures of the friction pair. The rest of the conventions are given in

Table 2. Complex heat exchange between the body and environment.

No.	Dependencies and Decoding of Their Parameters
1	Heat transfer of conduits occurs according to the Fourier law: the heat flux density $q$ is directly proportional to the temperature gradient, i.e.,
	$q=-\lambda gradt=-\lambda n_0\frac{\partial t}{\partial n}$	(6)
	where: $\lambda$ is the coefficient of thermal conductivity of the material; $n_0$ is unit vector directed along the normal direction of increasing temperature; $\frac{\partial t}{\partial n}$ is the derivative of the temperature along the normal direction; $gradt$= $n_0\frac{\partial t}{\partial n}$ is the temperature gradient.
2	Convective heat transfer between the surface $A$ of a solid and the surrounding liquid or gaseous medium obeys the Newton-Richmann law:
	$q={\alpha }_{ic}\left(t_i-t_c\right)A_i$	(7)
	where: q is the heat flux from the surface of the solid to the medium; $A_i$ is heat exchange surface area; ${\alpha }_{ic}$ is the heat transfer coefficient between the body’s surface and the environment; $t_i$ and $t_c$ are the temperatures of the surface of the body and the environment.
3	Heat transfer by radiation is determined on the basis of the laws of thermal radiation and has the form:
	$q={\epsilon }_{nij}{C}_0\left[{\left(T_i/100\right)}^4-{\left(T_j/100\right)}^4\right]A_i{\varphi }_{ij}$	(8)
	where: ${\epsilon }_{nij}$ is the reduced emissivity of bodies i and j; ${\varphi }_{ij}$ is the coefficient of irradiation of the i-th body by the j-th; $T_i$ and $T_j$ are values of the absolute temperatures of bodies i and j; $C_0$ is the emissivity of an absolutely black body, equal to 5.67 W/(m2 ∙ K4).
	$\frac{C_0}{C_1}=\frac{A_h}{A_c}$	(9)
	where: $C_1$ is the emissivity of the polished surface in W/(m2 ∙ K4); $A_h$ and $A_c$ are heated and cooled body surface areas in m2.
4	The total thermal resistance R or the total thermal conductivity σ0 are equal to
	$\left.\begin{array}{c}\frac{1}{R_0}=\frac{1}{R_T}+\frac{1}{R_K}+\frac{1}{R_p}\\ {\sigma }_0={\sigma }_T+{\sigma }_K+{\sigma }_p\end{array}\right\}$	(10)
	where $R_T$, $R_K$, $R_p$ are the thermal resistance of heat exchanges by thermal conductivity, convection and radiation. Note that the addition of three parallel-connected conductivities is justified by the law of the conservation of energy. If concerning thermal coefficients, then such an addition in the general case would be unreasonable.

[23]. Surprisingly in Table 1 there are no boundary conditions for radiative heat transfer of a metallic friction element.

The relationship between the intensity of heat transfer by conduction and convection varies within the boundary layer [25]. At the surface, heat transfer takes place solely due to the effect of thermal conductivity and when the speed of air movement is zero. Then, the heat flux is determined by relation (7) [23].

With the distance from the working surface of the pulley rim, the relative role of convection increases. Within the boundary layer, the heat transfer processes caused by heat conduction and convection are characterized by comparable intensities [23,25]. No exo- or endothermic reactions take place in the boundary thermal layer.

Around the non-working surface of the brake drum rim, mono-circular airflow does not disturb along the thermal boundary layer (Figure 3a). Conversely, the circular flow of vortices of upper and lower airflows increases and decreases the velocity, creating a positive gradient and destroying the thermal boundary layer on the working surface of the brake pulley rim (Figure 3b).

3.2. Combined Action of the Convection Fields from Washing Air and Thermal Conductivity of Metal Friction Elements of Brakes

In the processes of heat transfer by conduction, the thermal resistance $\frac{\delta }{\lambda }$ across the thickness of a solid-disc plays an important role (Figure 4a,b).

The design and weight parameters of self-ventilated discs of disc-shoe brakes (SIME, France) are illustrated in [23].

Let us dwell on the rim of a metal friction element of braking devices, which for a disc-shoe brake of a vehicle is represented as a vertical flat wall.

Let us consider as an example a vertical flat wall with a friction belt of a left half-disc of a self-ventilated disc. The heat transfer coefficient is given by Formula (1), where ${\alpha }_1$, ${\alpha }_2$ are the coefficients of the heat transfer from the working and inner surfaces of the half-disc, and $\lambda$ is the coefficient of the thermal conductivity of the half-disc material.

From Formula (1) it follows that an increase in $K$ can be achieved due to an increase in any of the three thermal resistances $\frac{1}{{\alpha }_1}$, $\frac{1}{{\alpha }_2}$, and $\frac{\delta }{\lambda }$, [26,27,28].

Consider the influence of the internal thermal resistance $\frac{\delta }{\lambda }$ on the value of the heat transfer coefficient. Since the choice of the material of the half-disc is determined by the specification for this material, the thermal conductivity $\lambda$ is a constant value. Thus, a reduction in the transit time of the heat flux (at ${\alpha }_1=const.$, ${\alpha }_2=const.$) is possible only due to a decrease in the wall thickness $\delta$. However, the possibility of reducing $\delta$ is very limited, as is related to its strength properties. A better result can be achieved by changing the heat transfer coefficients. Taking $\frac{\delta }{\lambda }\to 0$, Formula (1) takes the form [26]:

$$K={\left(\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}\right)}^{-1}.$$

(11)

The above formula can be transformed to the form:

$$K=\frac{{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2}.$$

(12)

It follows that as ${\alpha }_2\to \infty$ then $K\to {\alpha }_1$ and vice versa, as ${\alpha }_1\to \infty$ then $K\to {\alpha }_2$. Thus, the higher limit value of the heat transfer coefficient should not exceed the value of the smallest of the heat transfer coefficients [27].

Let us denote that $\frac{{\alpha }_2}{{\alpha }_1}=K_{\alpha },$ then ${\alpha }_2=K_{\alpha }{\alpha }_1$ and Formula (12) is transformed to:

$$K={\alpha }_1\frac{K_{\alpha }}{1+K_{\alpha }}.$$

(13)

Increasing ${\alpha }_2$ by a factor of $K_{\alpha 2}$ in the form ${\alpha }_2^{\prime }$ = ${\alpha }_2{K}_{\alpha 2}=K_{\alpha }{\alpha }_1{K}_{\alpha 2}$, where $K_{\alpha 2}>1$ the value of the heat transfer coefficient takes the form [24,25,28]:

$$K^{\prime }={\alpha }_1\frac{K_{\alpha }{K}_{\alpha 2}}{1+K_{\alpha }{K}_{\alpha 2}}.$$

(14)

Finally, it can be written that:

$$\frac{K^{\prime }}{K}=\frac{K_{\alpha 2}+K_{\alpha }{K}_{\alpha 2}}{1+K_{\alpha }{K}_{\alpha 2}}=1+\frac{K_{\alpha 2}-1}{K_{\alpha }{K}_{\alpha 2}+1}=1+\epsilon .$$

(15)

where $\epsilon =\left(K_{\alpha 2}-1\right)/\left(K_{\alpha }{K}_{\alpha 2}+1\right).$

For example, when $K_{\alpha }=100$,${\alpha }_2$ is doubled, then $K_{\alpha 2}=2$, and $\epsilon \approx 0.5\%$. This proves that the value of $\epsilon$ is small.

3.3. Combined Action of Convection Fields from Washing Air and Thermal Conductivity of Metal Friction Elements of Brakes

This section presents the relationships necessary to understand the combined action of convection fields from washing air and thermal conductivity of metal friction elements of brakes. These main relations will be quoted from [24,25].

The concept of the “heat transfer coefficient of a rotating metal friction element” ${\alpha }_{\Sigma }\left(\tau \right)$ introduced in [24,29,30,31,32,33,34,35] make it possible to describe the processes of heat transfer. After performing a number of transformations and taking into account the empirical formula α = 7.14υ^0.78 dependence for ${\alpha }_{\Sigma }\left(\tau \right)$ takes the form:

$$\frac{1.23{\upsilon }^{0.78}}{A}{{\displaystyle \int }}_{A}0.5D^{0.78}dA=g$$

(16)

where:

υ—speed of movement of the washing medium relative to the cooled surface of the metal friction element,

D—diameter of the element,

$g$—coefficient dependent on the geometry of the metal friction element.

Formula (16) can also be presented in form:

$${\alpha }_{\Sigma }\left(n\right)=g{n}^{0.78}$$

(17)

where:

n—rotational speed of the metal friction element.

The results of calculations based on relation (17) are shown in Figure 5a–c for various diameters of metal friction elements of braking devices.

As pointed out in [24,35] it can be observed that the heat transfer coefficient for various metal friction elements increases as a result of increasing matte and polished areas, friction radii and rotational speed, as well as washing surfaces with moist air and water in severe weather.

After using the experimental data on the energy loading of the metal friction elements of brake devices, establishing the relationship between the criteria in Equation (16), and taking into account the test condition ${\alpha }_2/K$, one receives:

$${\alpha }_2=0.75K{\left(\frac{{\alpha }_{1}D}{{\lambda }_2}\right)}^{0.5}{\left(\frac{\upsilon D}{a}\right)}^{0.25}{\left(\frac{\upsilon \rho c_p}{{\lambda }_2}\right)}^{0.1}$$

(18)

where:

$a$—coefficient of thermal diffusivity,

$\rho$—air density,

$c_p$—heat capacity of air at $p=const.$

In Figure 6a,b shows the graphical dependence of $K=f\left({\alpha }_2,{\alpha }_2\right)$ described by Formula (18).

The graphs show that K increases swiftly as ${\alpha }_1$ increases, until ${\alpha }_1$ and ${\alpha }_2$ become approximately equal. With a further increase in ${\alpha }_1$, the increase of K slows down and then almost stops. Thus, at ${\alpha }_1\ll {\alpha }_2$, an increase in ${\alpha }_1$ is required to increase $K$, which is equivalent to a decrease in thermal resistance $\frac{1}{{\alpha }_1}$. Once ${\alpha }_1\approx {\alpha }_2$ is reached, any of the heat transfer coefficients can be increased to enhance heat transfer.

4. Conclusions

The combined effect of heat conduction, radiation of free and forced convection due to the presence of associated processes, phenomena and transfer effects, complex heat transfer is much more complex than its components listed above, which greatly complicates its analytical and experimental study. Despite these circumstances, the following can be stated:

(i)

in the given relationship for determining the heat transfer coefficient (K), there are two terms related to the thermal coefficient of heat transfer resistance, which include the thermal coefficient of radiation resistance;

(ii)

a vacuum of 10⁻³ mm Hg is necessary to separate convection from radiation in air;

(iii)

contradictory data on the values of heat transfer coefficients used by various researchers suggest that they have a fictitious meaning;

(iv)

regulators of heat exchange processes in the air K₂ and K always differ significantly from each other.

The novelty of the work is as follows:

• metal friction elements of types of brakes in the design scheme are presented in the form of a plate;
• non-classical boundary conditions are given, but are modified;
• it has been established that the main type of heat transfer is conductive, and the rest depend on the energy load of the metal friction element;

Thus, the assessment of conductive and convective heat transfer in friction pairs of brake devices has been made.