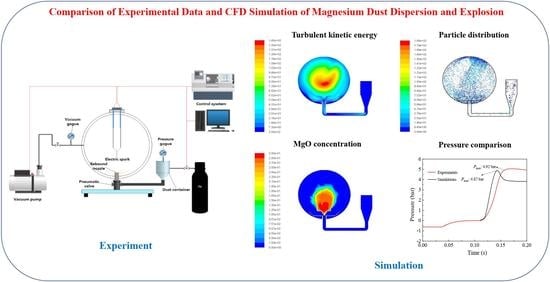
Numerical Simulation of Magnesium Dust Dispersion and Explosion in 20 L Apparatus via an Euler–Lagrange Method
Abstract
:1. Introduction
2. Materials and Methods
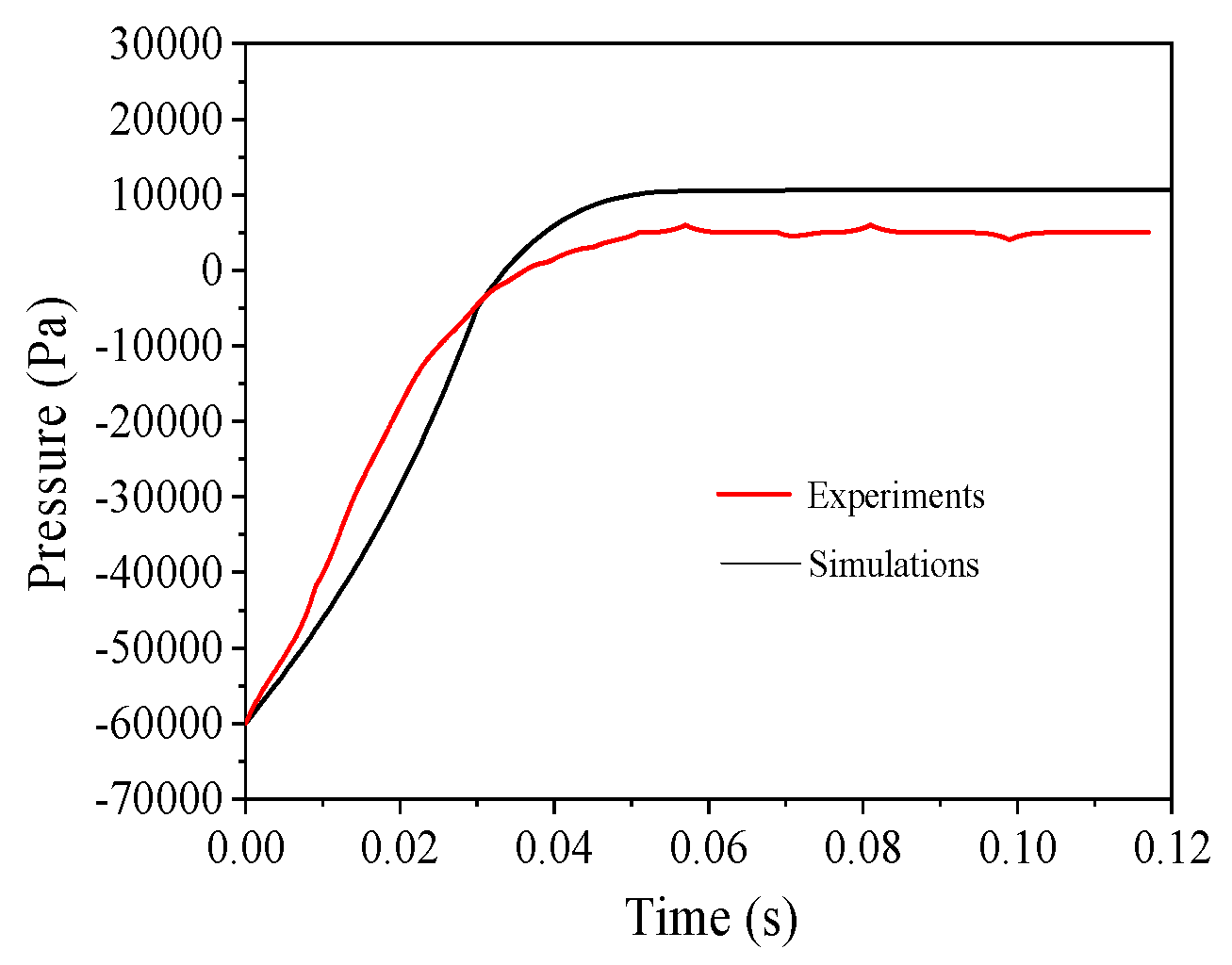
2.1. Explosion Experiments via 20 L Apparatus
2.2. Geometric Model
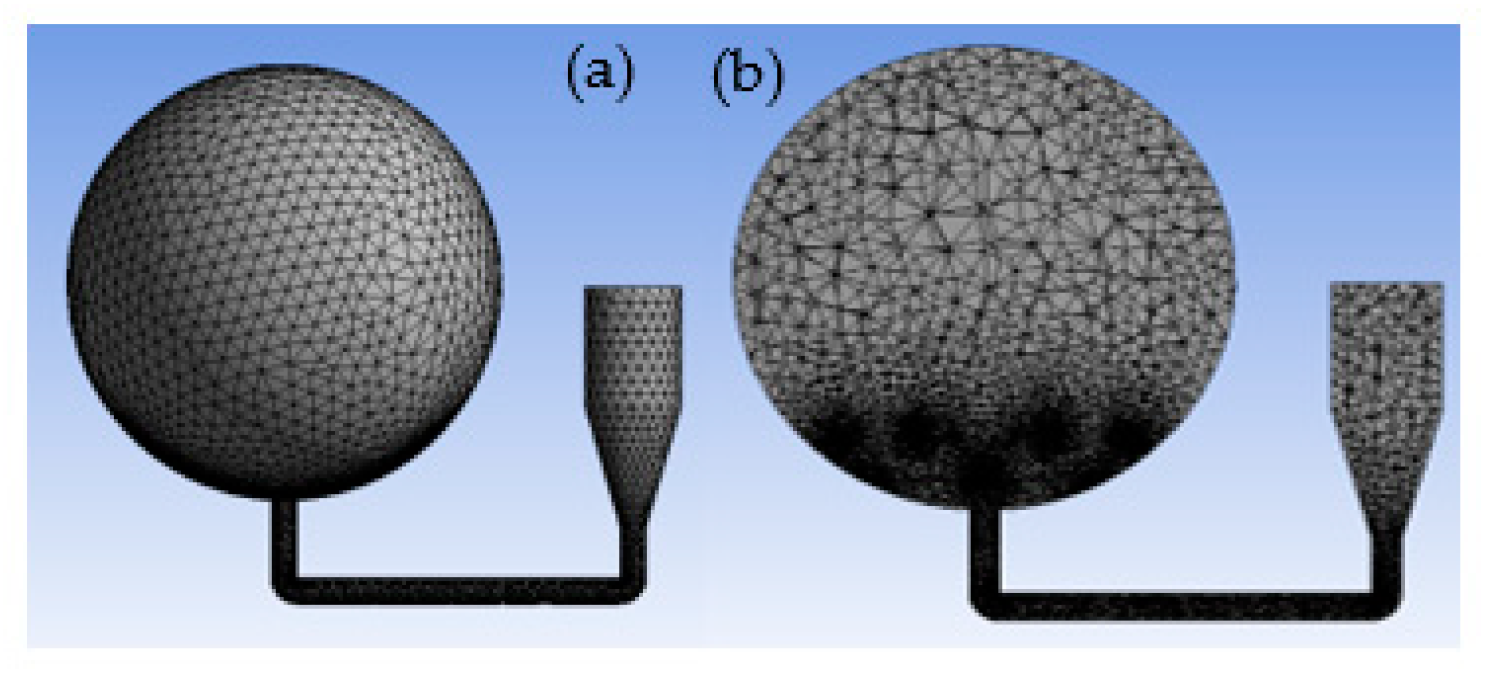
2.3. Meshing
2.4. Control Equation and Numerical Method
2.4.1. Gas-Phase Model
2.4.2. K-ε Turbulence Model
2.4.3. Particle-Phase Model
2.4.4. Species Transport Model
- (1)
- Mg particles were spherical and regular in shape;
- (2)
- The initial pressure of the 20 L apparatus and of the dust bin were −0.6 barg and 20 barg, respectively;
- (3)
- Initial temperature was set to 298 K;
- (4)
- All boundary condition functioned as the wall without slide;
- (5)
- Semi-Implicit Method for Pressure Linked Equations, SIMPLE, was developed for solving discrete process.
3. Results
3.1. Grid Sensitivity Studies
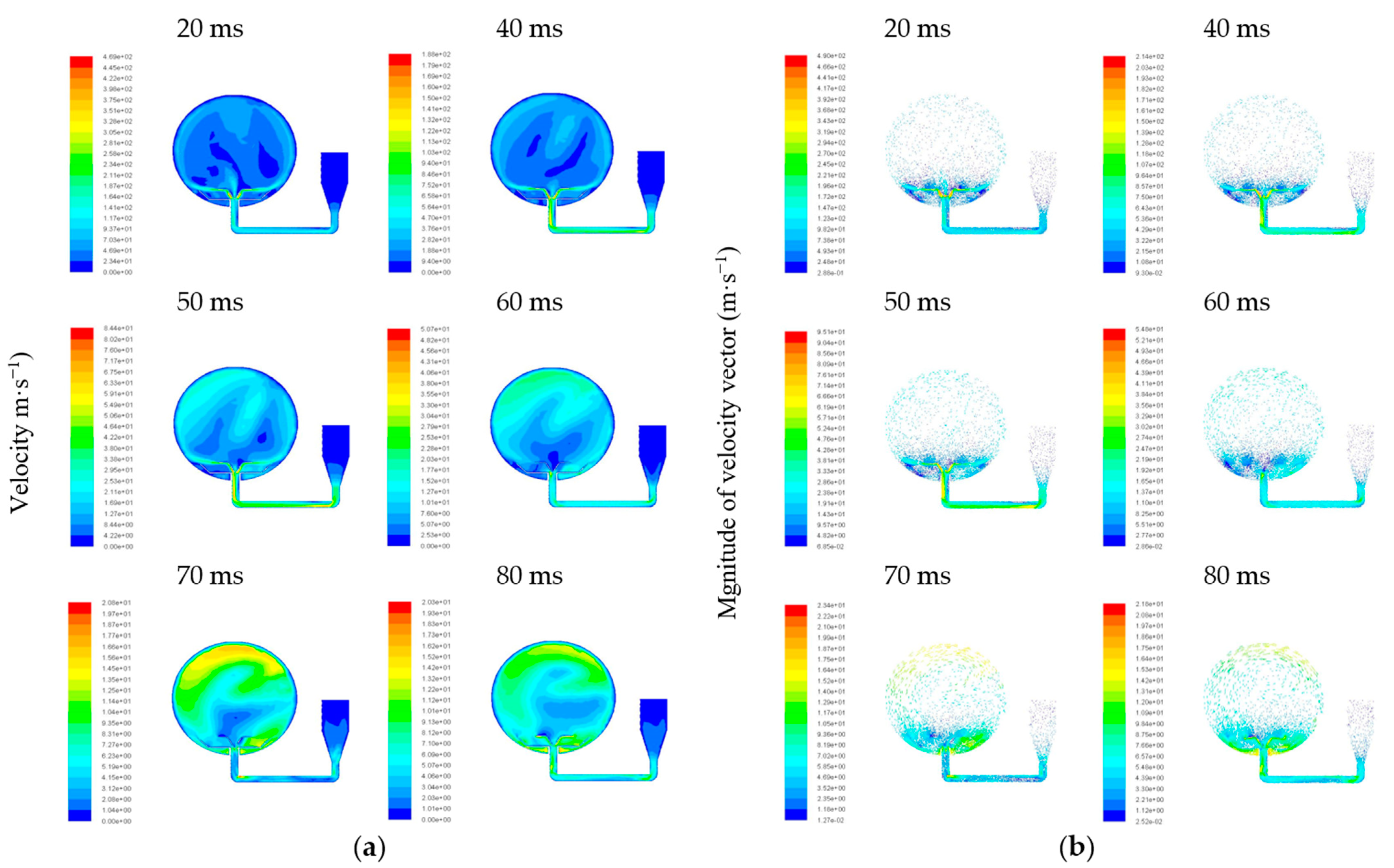
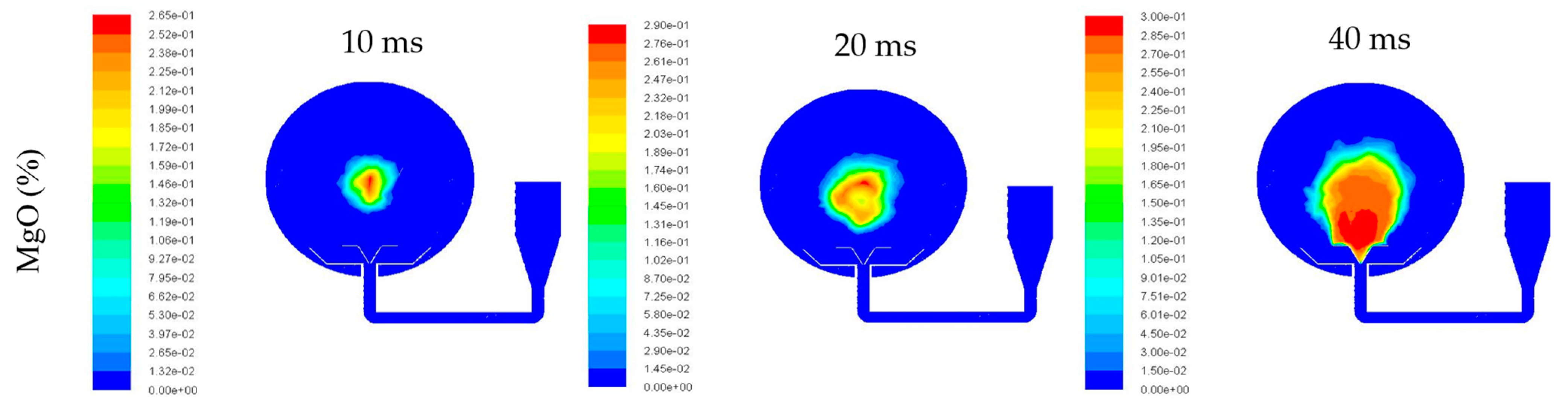
3.2. Dispersion Simulation of Dust–Air Mixtures
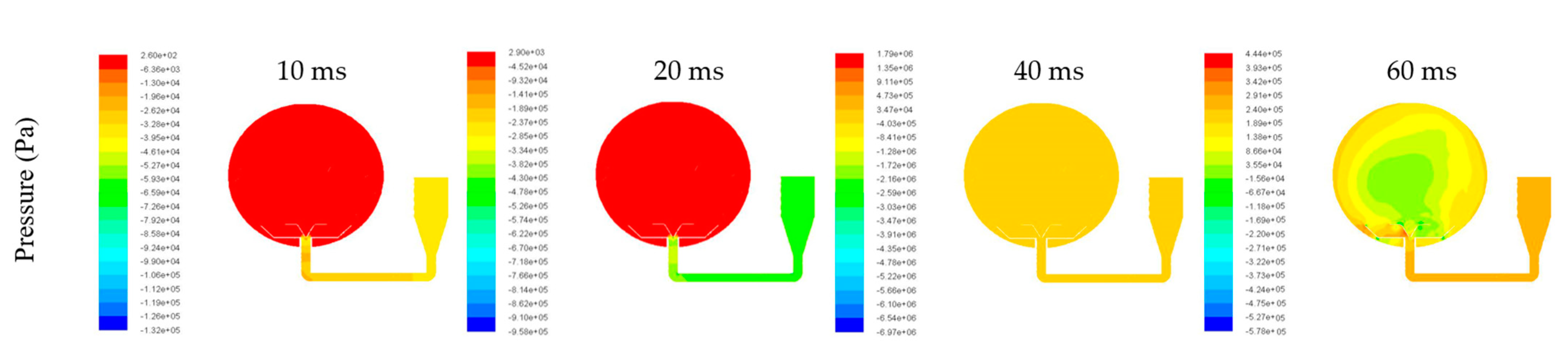
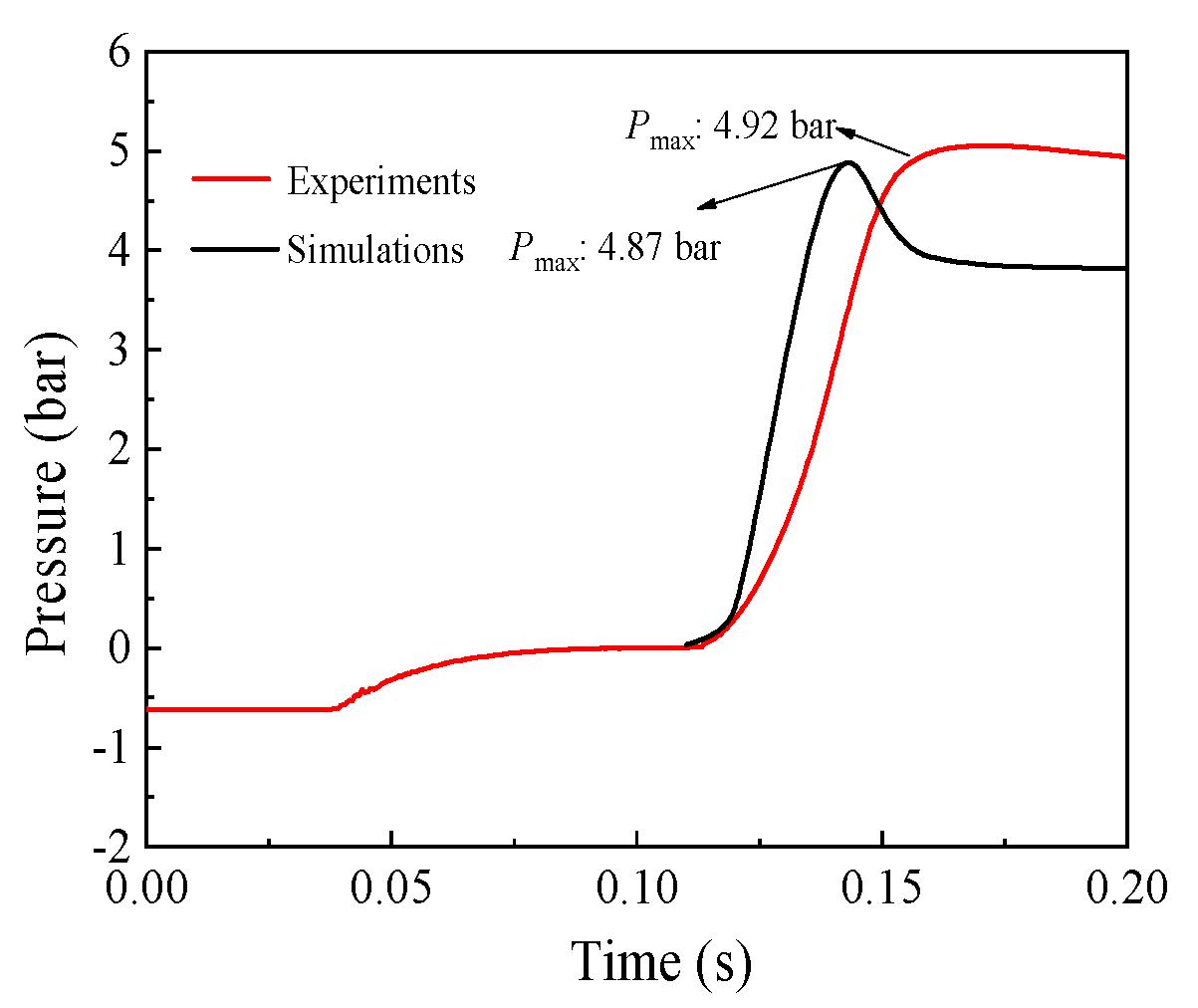
3.3. Explosion Simulation of Dust–Air Mixture
4. Conclusions
- (1)
- When gas and particles came into the sphere, the pressure and mass differences caused them to move downwards, and then the vortex formed. When delay ignition time reached 60 ms, the particles were evenly distributed in the sphere. Therefore, 60 ms is the optimum delay ignition time for the Mg/air explosion. This is in line with the delay ignition time as suggested in the ASTM E1226 method.
- (2)
- The explosion simulation indicated that the explosion pressure profile went through an increase-highest-decrease trend. Moreover, the simulation favorably agreed with the experimental data, and the relative error was approximately 1.02%. Therefore, the developed model is reliable for further investigating the explosion mechanism of the Mg/Air mixture.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, F.; Zhao, P.; Niu, M.; Maddy, J. The survey of key technologies in hydrogen energy storage. Int. J. Hydrogen Energy 2016, 41, 14535–14552. [Google Scholar] [CrossRef]
- Guo, H.; Yang, H.H. Current status and future prospect of research on solid-state hydrogen storage material. New Chem. Mater. 2016, 44, 19–21. [Google Scholar]
- Yang, M.; Wang, S.; Zhang, Y.; Han, B.; Wu, J.; Cheng, H. Current status and future prospects of research on hydrogen storage materials. J. Chin. Ceram. Soc. 2011, 39, 1053–1060. [Google Scholar]
- Li, Y.; Bi, M.; Li, B.; Zhou, Y.; Gao, W. Effects of hydrogen and initial pressure on flame characteristics and explosion pressure of methane/hydrogen fuels. Fuel 2018, 233, 269–282. [Google Scholar] [CrossRef]
- Zheng, X.; Xu, K.; Wang, Y.; Wang, Q. Hydrogen inhibition method for preventing hydrogen explosion accident in wet dust removal systems. Int. J. Hydrogen Energy 2019, 44, 17195–17201. [Google Scholar] [CrossRef]
- Salzano, E.; Cammarota, F.; Benedetto, A.D.; Sarli, V.D. Explosion behavior of hydrogen–methane/air mixtures. J. Loss Prevent. Proc. 2012, 25, 443–447. [Google Scholar] [CrossRef]
- Potapov, S.N.; Gvozdkov, I.A.; Belyaev, V.A.; Verbetsky, V.N.; Mitrokhin, S.V. Magnesium hydride based hydrogen chemical source: Development and application perspectives. Int. J. Hydrogen Energy 2019, 44, 28578–28585. [Google Scholar] [CrossRef]
- Schlapbach, L.; Züttel, A. Hydrogen-storage materials for Mobile Applications. Nature 2001, 414, 353–358. [Google Scholar] [CrossRef]
- Chen, J.; Hu, S.Q.; Hu, L.S.; Ren, R.; Huang, F. Experimental study on minimum ignition temperature and suppression technology of magnesium dust cloud. Sci. Technol. Eng. 2015, 15, 96–100. [Google Scholar]
- Wei, J.; Wen, L.Q. Numerical simulation of explosion characteristics of gas and coal dust mixture. J. North Univ. China 2015, 36, 208–213. [Google Scholar]
- Li, R.Z. Numerical simulation of coal dust explosion induced by gas explosion. Explos. Shock Waves 2010, 30, 529–534. [Google Scholar]
- Tsai, Y.T.; Ho, S.C.; Huang, A.C.; Shu, C.M. Potential explosion hazard of polyester resin dust formed from a granulation process: Limiting oxygen concentration with different pressures. Appl. Therm. Eng. 2018, 135, 74–82. [Google Scholar] [CrossRef]
- Tsai, Y.T.; Yang, Y.; Huang, H.C.; Shu, C.M. Inhibitory effects of three chemical dust suppressants on nitrocellulose dust cloud explosion. AIChE J. 2020, 66, e16888. [Google Scholar] [CrossRef]
- Tsai, Y.; Huang, G.; Zhao, J.; Shu, C. Dust cloud explosion characteristics and mechanisms in MgH2-based hydrogen storage materials. AIChE J. 2021, 67, e17302. [Google Scholar] [CrossRef]
- Benedetto, A.D.; Russo, P.; Sanchirico, R.; Sarli, V.D. CFD simulations of turbulent fluid flow and dust dispersion in the 20 liter explosion vessel. AIChE J. 2013, 59, 2485–2496. [Google Scholar] [CrossRef]
- Sarli, V.D.; Russo, P.; Sanchirico, R.; Benedetto, A.D. CFD simulations of dust dispersion in the 20 L vessel: Effect of nominal dust concentration. J. Loss Prevent. Proc. 2014, 27, 8–12. [Google Scholar] [CrossRef]
- Sarli, V.D.; Russo, P.; Sanchirico, R.; Benedetto, A.D. CFD simulations of the effect of dust diameter on the dispersion in the 20 L bomb. Chem. Eng. Tran. 2013, 31, 727–732. [Google Scholar]
- Portarapillo, M.; Sarli, V.D.; Sanchirico, R.; Benedetto, A.D. CFD simulation of the dispersion of binary dust mixtures in the 20 L vessel. J. Loss Prevent. Proc. 2020, 67, 104231. [Google Scholar] [CrossRef]
- Sanchirico, R.; Sarli, V.D.; Russo, P.; Benedetto, A.D. Effect of the nozzle type on the integrity of dust particles in standard explosion tests. Powder Technol. 2015, 279, 203–208. [Google Scholar] [CrossRef]
- Vizcaya, D.; Pinilla, A.; Amín, M.; Ratkovich, N.; Munoz, F.; Murillo, C.; Bardin-Monnier, N.; Dufaud, O. CFD as an approach to understand flammable dust 20 L standard test: Effect of the ignition time on the fluid flow. AIChE J. 2018, 64, 42–54. [Google Scholar] [CrossRef]
- Li, H.; Deng, J.; Chen, X.; Shu, C.M.; Kuo, C.H.; Hu, X. Influence of ignition delay on explosion severities of the methane–coal particle hybrid mixture at elevated injection pressures. Powder Technol. 2020, 367, 860–876. [Google Scholar] [CrossRef]
- Li, H.; Chen, X.; Deng, J.; Shu, C.M.; Kuo, C.H.; Yu, Y.; Hu, X. CFD analysis and experimental study on the effect of oxygen level, particle size, and dust concentration on the flame evolution characteristics and explosion severity of cornstarch dust cloud deflagration in a spherical chamber. Powder Technol. 2020, 372, 585–599. [Google Scholar] [CrossRef]
- Murillo, C.; Bardin-Monnier, N.; Blanchard, C.; Funfschilling, D.; Munoz, F.; Ratkovich, N.; Vizcaya, D.; Dufaud, O. CFD to improve the repeatability and accuracy of dust explosion tests in the 20-liters sphere. Chem. Eng. Tran. 2016, 48, 115–120. [Google Scholar]
- Tsai, Y.-T.; Fu, T.; Zhou, Q. Explosion characteristics and suppression of hybrid Mg/H2 mixtures. Int. J. Hydrogen Energy 2021, 46, 38934. [Google Scholar] [CrossRef]
- Kashireninov, O.E.; Kuznetsov, V.A.; Manelis, G.B. Kinetics of alkaline-earth atoms reactions with molecular oxygen. AIAA J. 1977, 15, 860–876. [Google Scholar] [CrossRef]
- Liu, M.; Yang, M.; Chen, M.; Yu, D.; Zheng, J.; Chang, J.; Wang, X.; Ji, C.; Wei, Y. Numerical optimization of membrane module design and operation for a full-scale submerged MBR by computational fluid dynamics. Bioresour. Technol. 2018, 269, 300–308. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Theory Guide; Release-15.0; ANSYS Inc.: Canonsburg, PA, USA, 2015; Volume 15317, pp. 1–759. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 1035. [Google Scholar] [CrossRef]
- Li, H.; Deng, J.; Shu, C.M.; Kuo, C.H.; Yu, Y.; Hu, X. Flame behaviours and deflagration severities of aluminium powder–air mixture in a 20-L sphere: Computational fluid dynamics modelling and experimental validation. Fuel 2020, 276, 118028. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Yu, J.; Lu, L.; Gao, X.; Xu, Y.; Shahnam, M.; Rogers, W.A. Coupling reduced-order modeling and coarse-grained CFD-DEM to accelerate coal gasifier simulation and optimization. AIChE J. 2021, 67, e17030. [Google Scholar] [CrossRef]
- Xu, T.; Chen, Q.; Zhang, B.; Lu, S.; Mo, D.; Zhang, Z.; Gao, X. Effects of electric field on micro-scale flame properties of biobutanol fuel. Sci. Rep. 2016, 6, 32938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
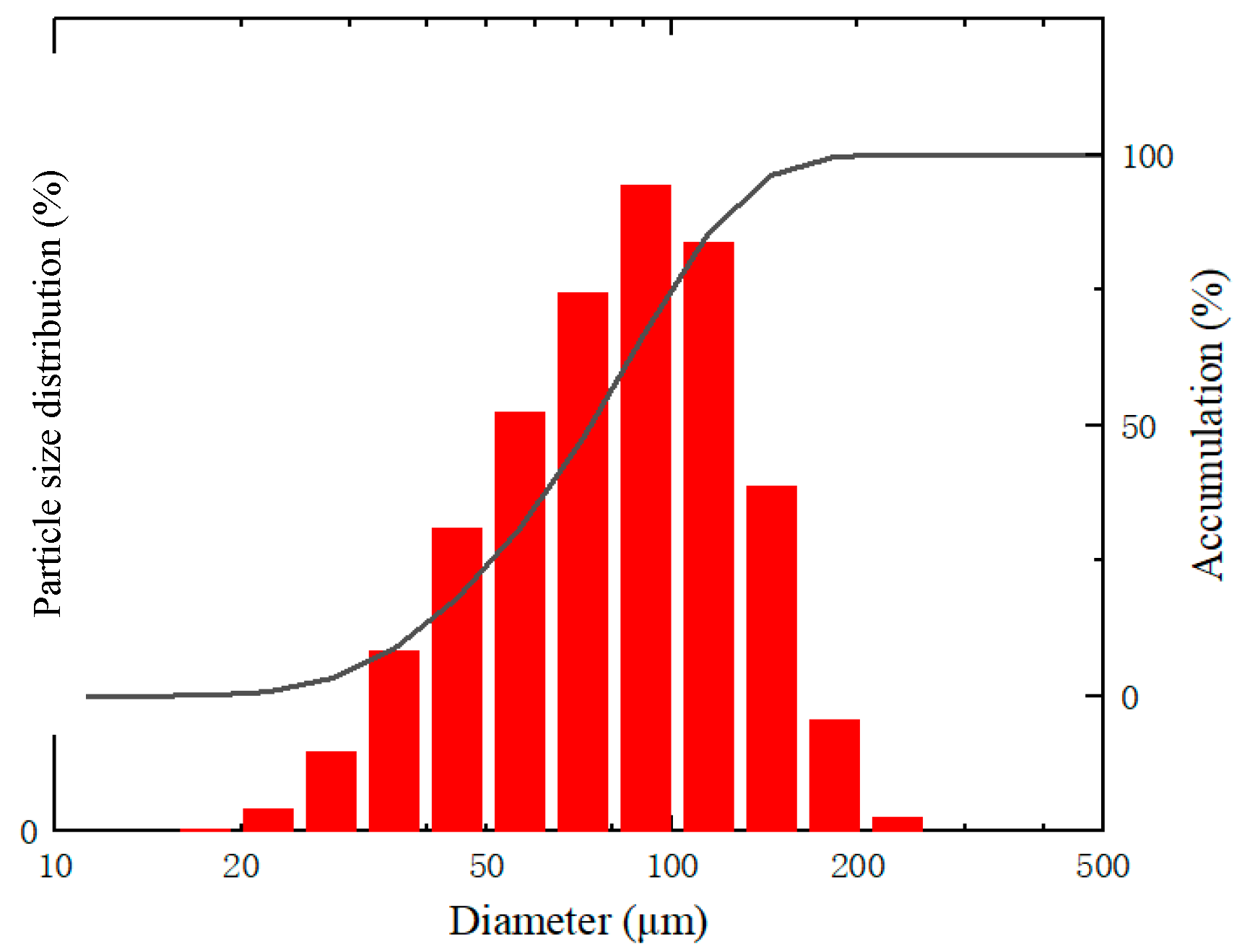
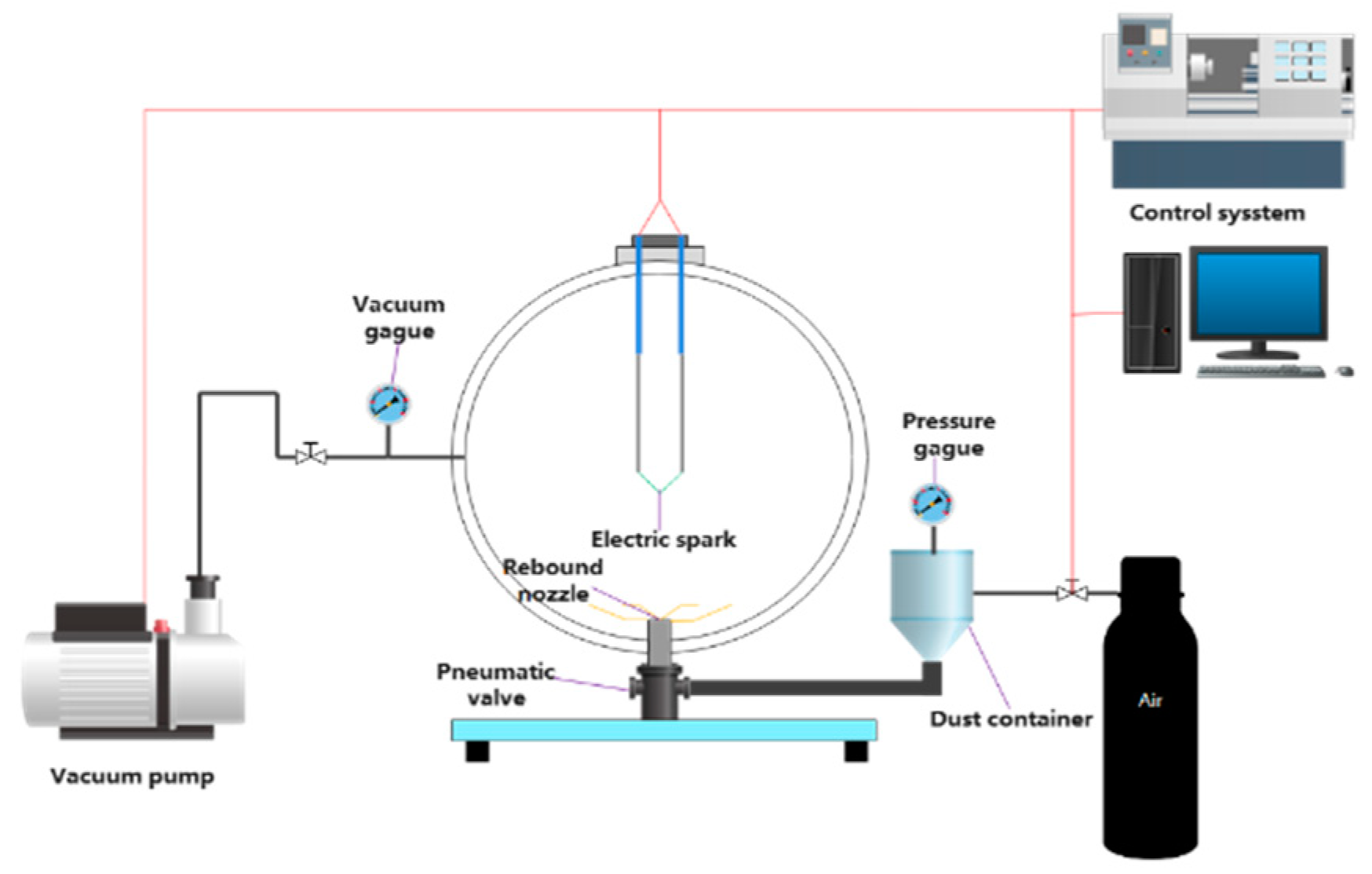
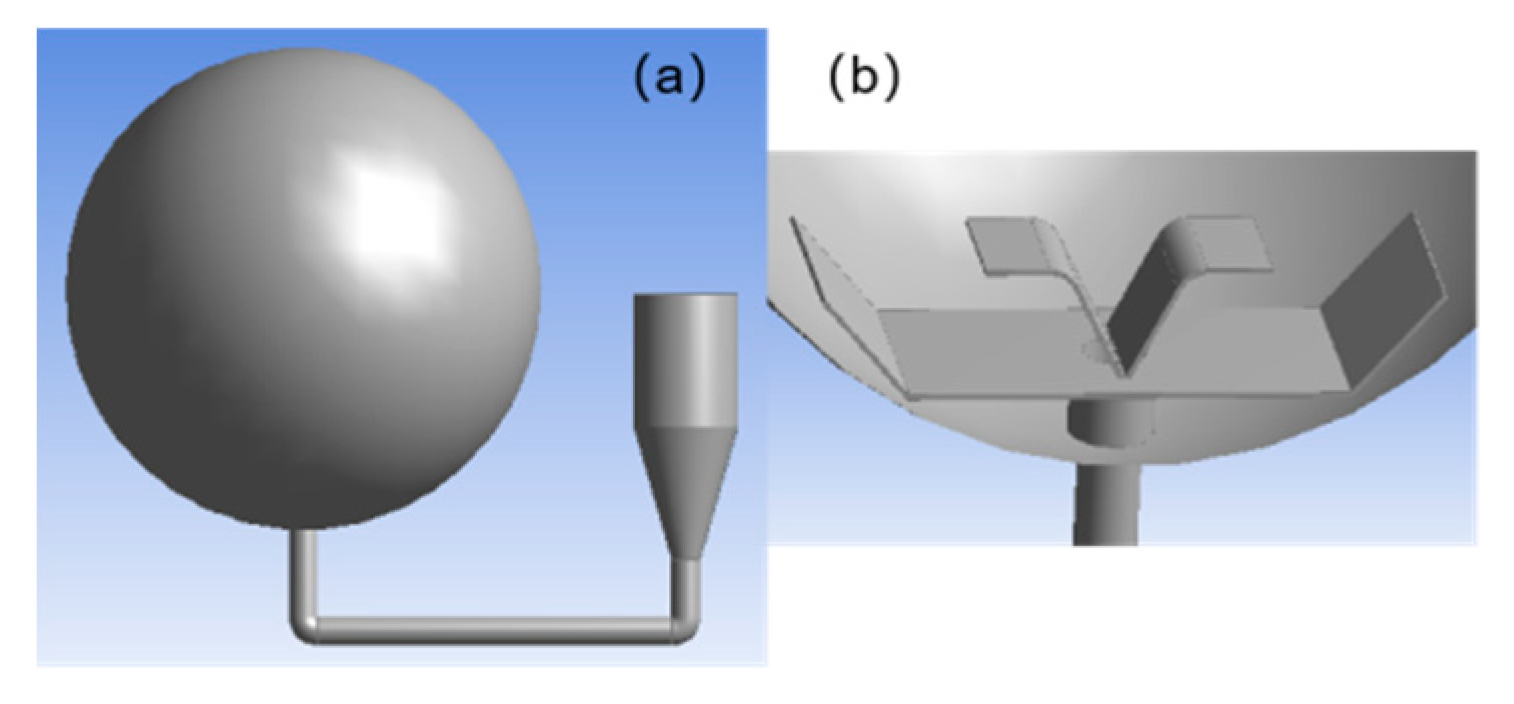

| Parameter | Value | Unit |
|---|---|---|
| Particle diameter | 75 | μm |
| Particle density | 1738 | kg/m3 |
| Particle dynamic viscosity | 1.72 × 10−5 | P·s |
| Gas density | 1.29 | kg/m3 |
| Gas dynamic viscosity | 1.79 × 10−5 | P·s |
| Apparent activation energy (E) | 16.0 | kcal/mol |
| Pre-exponential factor (A) | 2.1 × 108 | m3/mol·s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, T.; Tsai, Y.-T.; Zhou, Q. Numerical Simulation of Magnesium Dust Dispersion and Explosion in 20 L Apparatus via an Euler–Lagrange Method. Energies 2022, 15, 402. https://doi.org/10.3390/en15020402
Fu T, Tsai Y-T, Zhou Q. Numerical Simulation of Magnesium Dust Dispersion and Explosion in 20 L Apparatus via an Euler–Lagrange Method. Energies. 2022; 15(2):402. https://doi.org/10.3390/en15020402
Chicago/Turabian StyleFu, Tao, Yun-Ting Tsai, and Qiang Zhou. 2022. "Numerical Simulation of Magnesium Dust Dispersion and Explosion in 20 L Apparatus via an Euler–Lagrange Method" Energies 15, no. 2: 402. https://doi.org/10.3390/en15020402
APA StyleFu, T., Tsai, Y.-T., & Zhou, Q. (2022). Numerical Simulation of Magnesium Dust Dispersion and Explosion in 20 L Apparatus via an Euler–Lagrange Method. Energies, 15(2), 402. https://doi.org/10.3390/en15020402