Improved-Efficacy EM-Based Antenna Miniaturization by Multi-Fidelity Simulations and Objective Function Adaptation
Abstract
:1. Introduction
2. Accelerated Antenna Miniaturization by Model Fidelity and Constraint Management
2.1. EM-Based Antenna Miniaturization with Penalty Functions
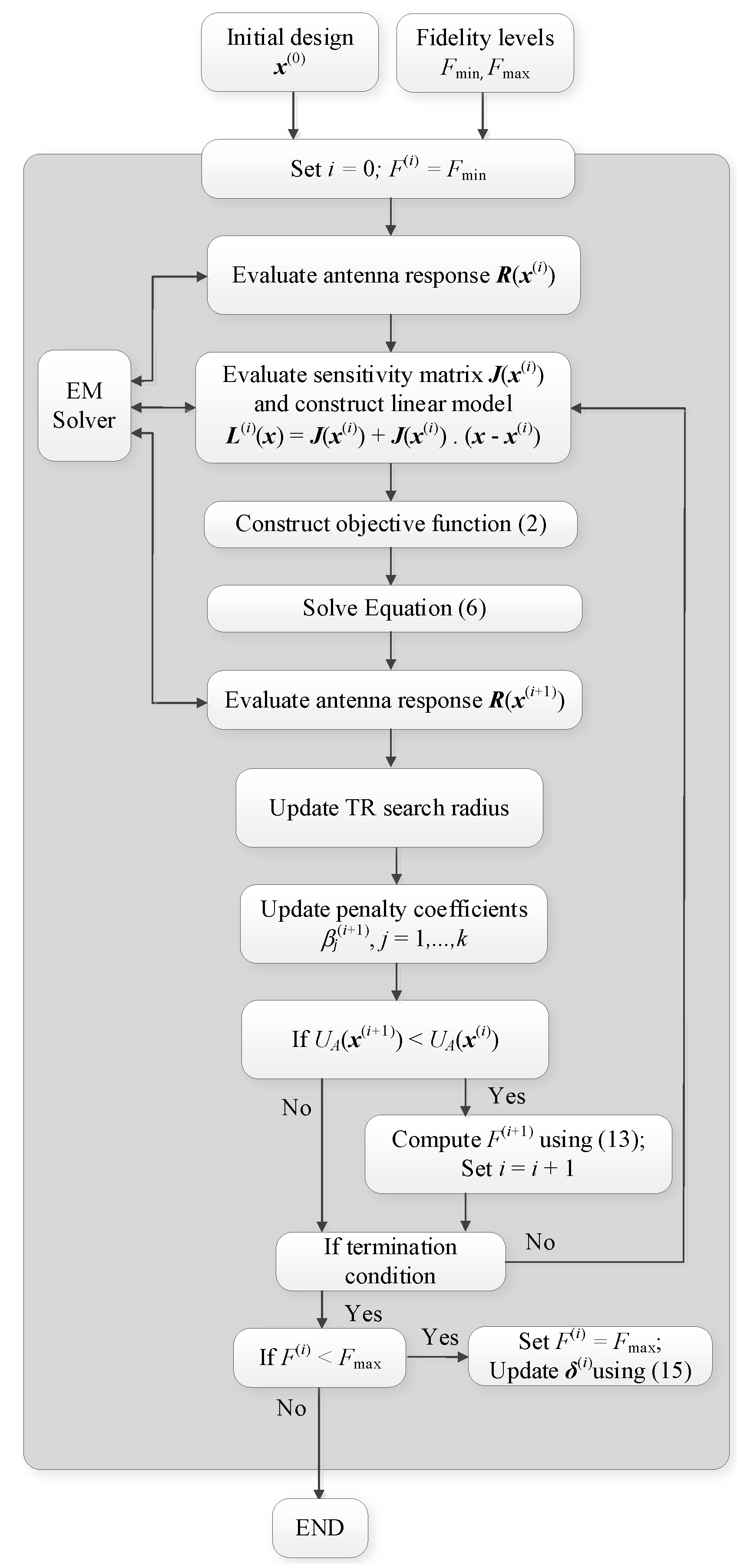
2.2. Trust-Region Gradient-Based Algorithm
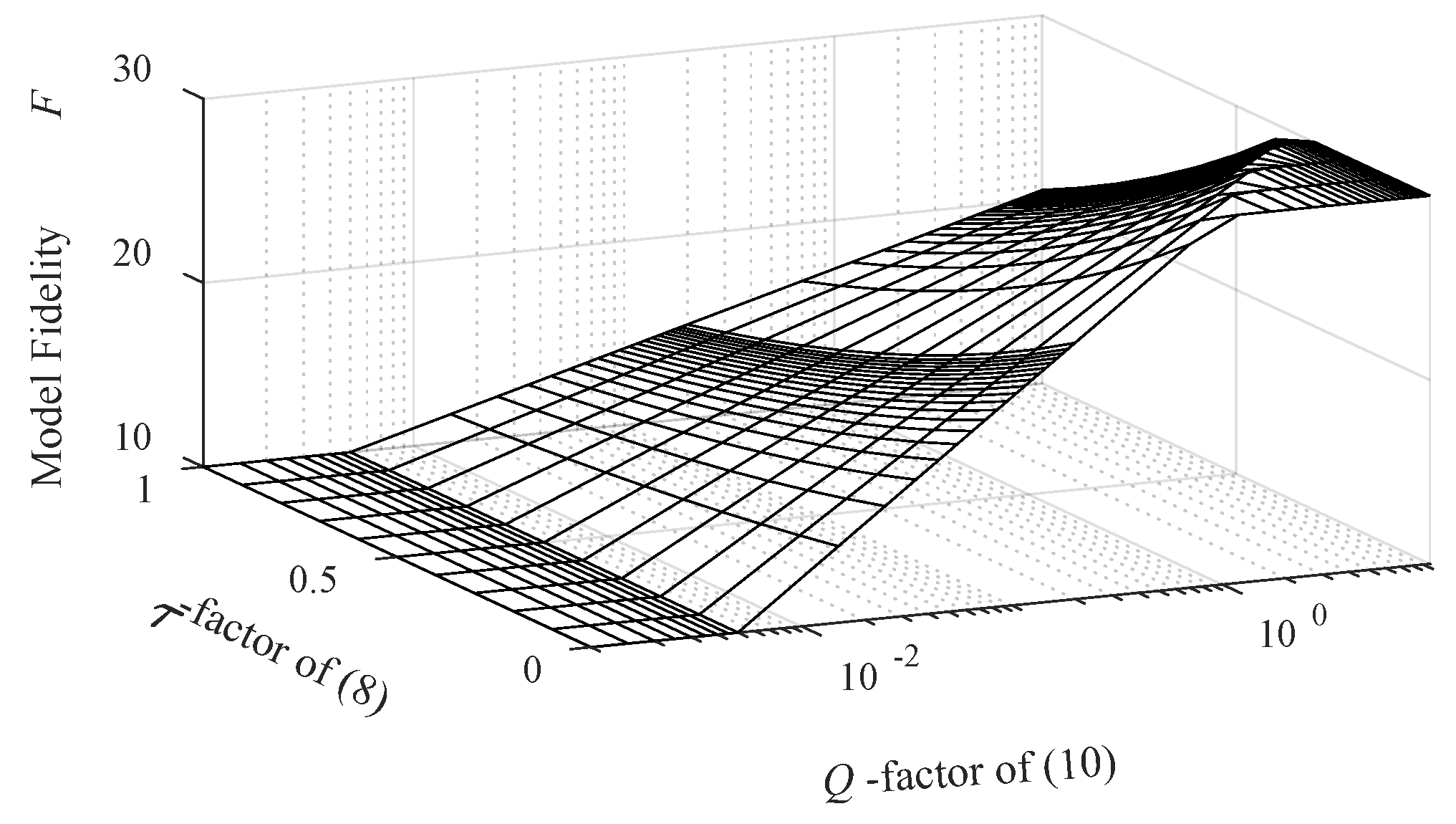
2.3. EM-Based Antenna Miniaturization and Adaptive Penalty Coefficients
- if x(i+1) produced in the ith iteration of (5) is infeasible from the point of view of the jth constraint but constraint violation is improved by at least Δj w.r.t x(i), ¦Âj is kept intact;
- if x(i+1) is feasible w.r.t. the jth constraint, βj is reduced;
- if x(i+1) is infeasible w.r.t the jth constraint and there is either insufficient improvement or no improvement in the constraint violation, βj is increased.
2.4. Multi-Fidelity EM Simulation Models
2.5. Constraint–Convergence-Based Model Management
- Fidelity level is set to the lowest value Fmin in the early stages of the optimization process (away from convergence). The decision is made regardless of the feasibility status of the solution. This permits a cost-efficient initial search within the design space;
- Fidelity is set to the highest value Fmax upon convergence. This allows to ensure reliability of the final solution;
- Fidelity selection in the transition phase, either from infeasible to feasible, or approaching convergence, is based upon both the feasibility status of the solution (to be formulated later), and the convergence status of the procedure;
- The fidelity is selected from a continuous range of F-values, which improves the stability of the procedure. In particular, it allows for a smooth transition between model fidelities throughout the optimization process.
2.6. Proposed Miniaturization Procedure
- δth—a threshold used to initiate an increase in the model fidelity (cf. Section 2.5);
- M—sufficient constraint violation improvement factor (cf. Section 3.3);
- Mδ—a multiplication factor used to increase the TR search radius in (15) (upon convergence);
- τcj—constraint violation normalization factors in (8).
3. Verification Examples
3.1. Benchmark Antenna Structures
- A monopole antenna with L-shaped ground plane stub [57], Antenna I;
- A monopole antenna with a radiator slot and modified ground plane [58], Antenna II;
- A monopole antenna with two radiator slots and elliptical ground plane slit [59], Antenna III;
- A stacked circular polarization antenna with circular and annular slots [60], Antenna IV;
- A stacked circular polarization antenna with a cross-shaped radiator slot [61], Antenna V.
3.2. Experimental Setup
3.3. Result
3.4. Discussion
- The proposed variable-fidelity procedure allows for a considerable acceleration of the miniaturization process as compared to the single-fidelity adaptive penalty function approach, by about 28 to 53 percent and by 43 percent on average.
- The designs rendered by the proposed procedure are of a quality comparable to that produced by the single-fidelity procedure, both in terms of constraint satisfaction and achievable size reduction rates. For Antennas I–V, all constraint violations are kept at the same level of 0.0 dB, whereas the achieved antenna footprint area is smaller by 9 mm2, larger by 8 mm2, larger by 1 mm2, degraded by 25 mm2, and smaller by about 5 mm2, respectively. In practical terms, these differences can be considered minor.
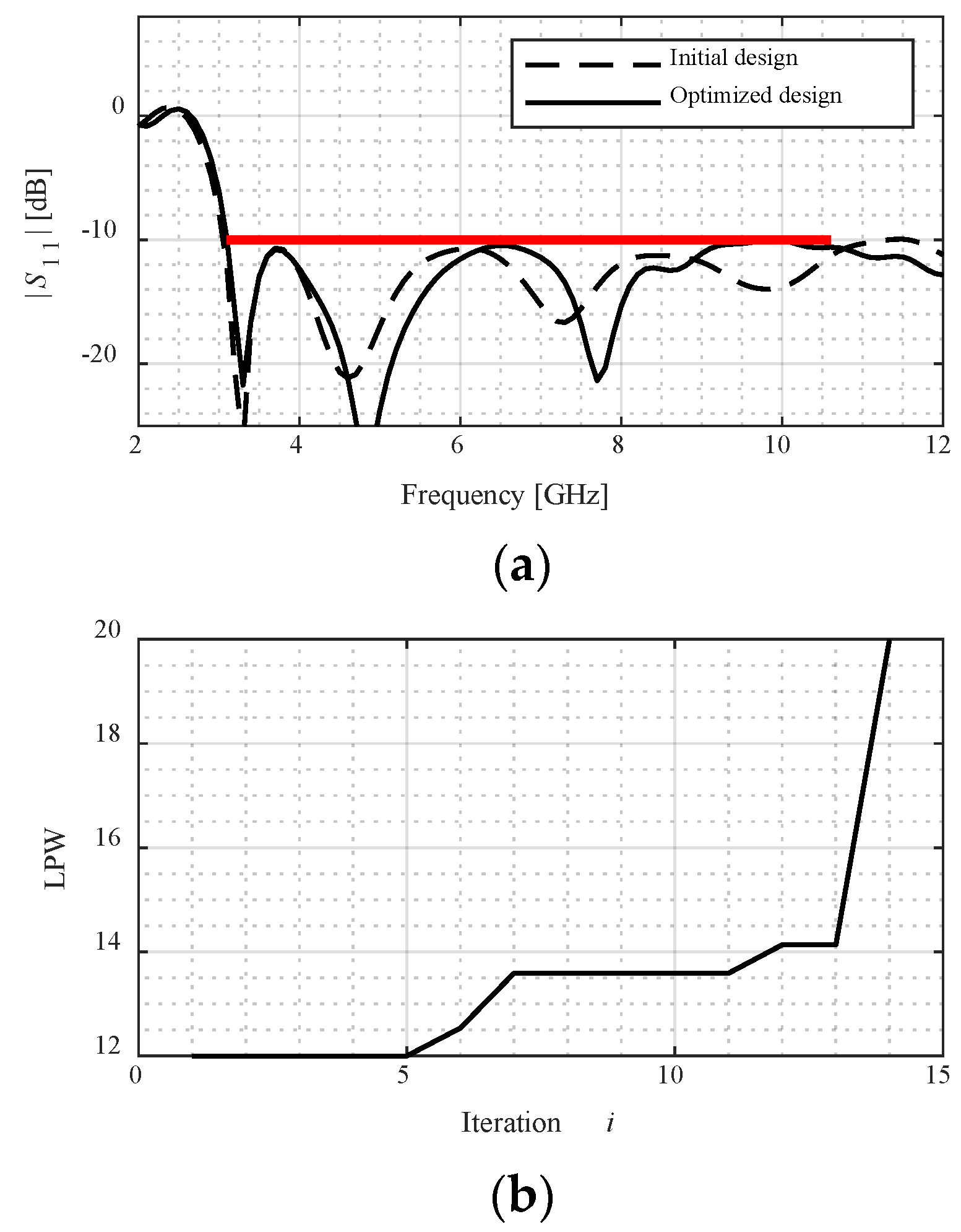
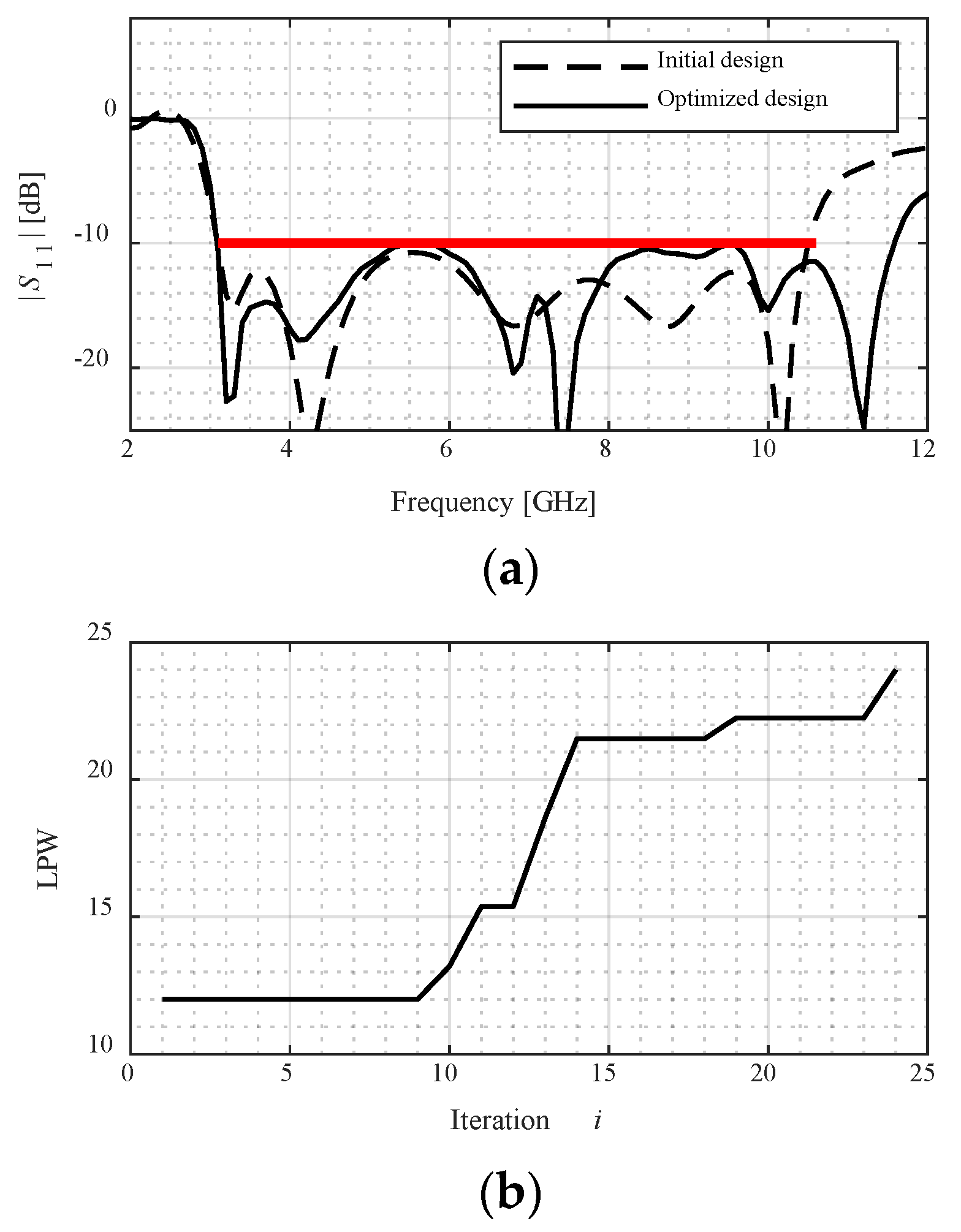
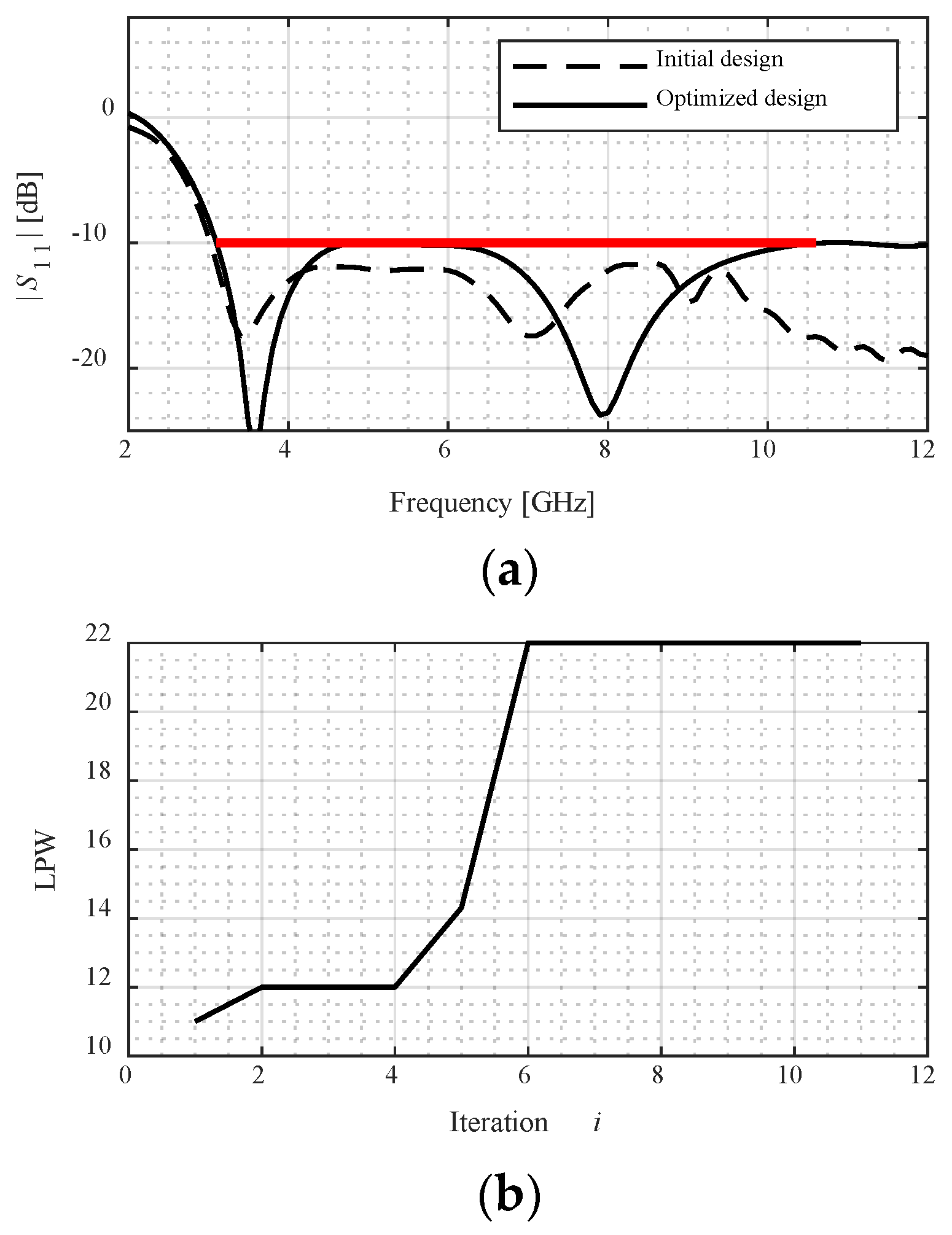
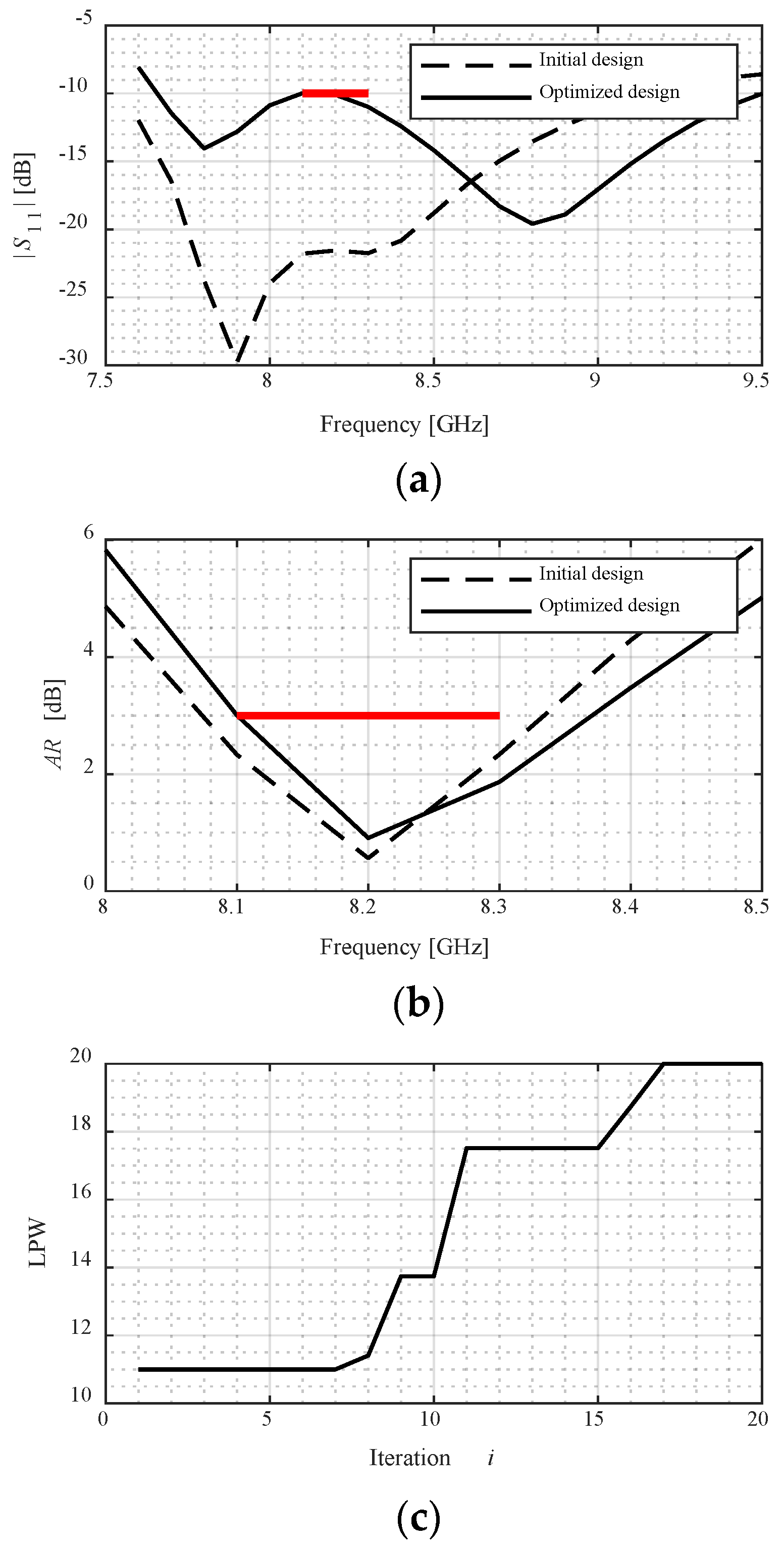
- The reliability of the miniaturization process is ensured by conducting the final iterations of the optimization process at the level of a high-fidelity model, which gives an accurate account of antenna characteristics. This can be observed in the plots showing the evolution of the model fidelity, as included in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. As can be observed in Figure 7, the initial design is allocated in the feasible region to demonstrate the margin for size reduction. It can be seen that the design moves towards the boundary of the feasible region as the final allocation of the optimized design, at which the reflection constraint is active. Figure 7b shows the evolution of the model fidelity across the iterations of the optimization process. It is set to the lowest value in the first few iterations, as the algorithm is away from convergence. There is a gradual increase in the model fidelity between iterations 5 and 13, corresponding to the transition phase either from infeasible to feasible, or due to approaching convergence. This increase is based on the feasibility and the convergence status of the optimization process as formulated in (13). The model fidelity is set to the highest level at the last iteration of the optimization process, when approaching convergence.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Le, T.T.; Yun, T.-Y. Miniaturization of a dual band wearable antenna for dual-band WBAN applications. IEEE Trans. Antennas Propag. 2020, 19, 1452–1456. [Google Scholar] [CrossRef]
- Agneessens, S.; Rogier, H. Compact half diamond dual-band textile HMSIW on-body antenna. IEEE Trans. Antennas Propag. 2014, 62, 2374–2381. [Google Scholar] [CrossRef] [Green Version]
- Abbosh, A.M. Miniaturized microstrip-fed tapered-slot antenna with altrawideband performance. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 690–692. [Google Scholar] [CrossRef] [Green Version]
- Abbosh, A.M. Miniaturization of planar ultrawideband antenna via corrugation. IEEE Antennas Wirel. Propag. Lett. 2008, 7, 685–688. [Google Scholar] [CrossRef]
- Arif, A.; Zubair, M.; Ali, M.; Khan, M.U.; Mehmood, M.Q. A compact, low-profile fractal antenna for wearable on-bode WBAN applications. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 981–985. [Google Scholar] [CrossRef]
- Yand, Y.; Zhao, Z.; Ding, X.; Nie, Z.; Liu, Q. Compact UWB slot antenna utilizing travelling-wave mode based on slitline transitions. IEEE Trans. Antennas Propag. 2019, 67, 140–150. [Google Scholar]
- Dong, J.; Qin, W.; Wang, M. Fast multi-objective optimization of multi-parameter antenna structures based on improved BPNN surrogate model. IEEE Access 2019, 7, 77692–77701. [Google Scholar] [CrossRef]
- Lee, K.; Sung, H.; Park, E.; Lee, I. Joint optimization for one and two-way MIMO AF multiple relay systems. IEEE Trans. Wirel. Commun. 2010, 9, 3671–3681. [Google Scholar] [CrossRef]
- Tomasson, J.A.; Koziel, S.; Pietrenko Dabrowska, A. Quasi-global optimization of antenna structures using principal components and affine subspace-spanned surrogates. IEEE Access 2020, 8, 50078–50084. [Google Scholar] [CrossRef]
- Al-Azza, A.A.; Al-Jodah, A.A. Spider monkey optimization: A novel technique for antenna optimization. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1016–1019. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P. Multiobjective particle swarm optimization to design a time-delay equalizer metasurface for an electromagnetic band-gap resonator antenna. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 912–915. [Google Scholar] [CrossRef]
- Goudos, S.K.; Siakavara, K.; Samaras, T.; Vafiadis, E.E.; Sahalos, J.N. Self-adaptive differential evolution applied to real-valued antenna and microwave design problems. IEEE Trans. Antennas Propag. 2011, 59, 1286–1298. [Google Scholar] [CrossRef]
- Koziel, S. Computationally efficient multi-fidelity multi-grid design optimization of microwave structures. Appl. Comp. Electromagn. Soc. J. 2010, 25, 578–586. [Google Scholar]
- Ohira, M.; Miura, A.; Taromaru, M.; Ueba, M. Efficient gain optimization techniques for azimuth beam/null steering of inverted-F multiport parasitic array radiator (MuPAR) antenna. IEEE Trans. Ant. Propag. 2012, 60, 1352–1361. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.S.; Wang, B.Z. Efficient gradient-based optimization of pixel antenna with large-scale connections. IET Microw. Ant. Propag. 2018, 12, 385–389. [Google Scholar] [CrossRef]
- Kalantari, L.S.; Bakr, M.H. Wideband cloaking of objects with arbitrary shapes exploiting adjoint sensitivities. IEEE Trans. Antennas Propag. 2016, 64, 1963–1968. [Google Scholar] [CrossRef]
- Paronneau, O. Optimal Shape Design for Elliptic Systems; Springer: Berlin/Heidelberg, Germany, 1982; Volume 3, pp. 42–66. [Google Scholar]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef] [Green Version]
- El Sabbagh, M.A.; Bakr, M.H.; Nilolova, N.K. Sensitivity analysis of the scattering parameters of microwave filters using the adjoint network method. Int. J. RF Microw. CAE 2006, 16, 569–606. [Google Scholar] [CrossRef]
- Papadimitriou, D.; Giannakoglou, K. Aerodynamic shape optimization using first and second order adjoint and direct approaches. Arch. Comput. Methods Eng. 2008, 15, 447–488. [Google Scholar] [CrossRef]
- Toivann, J.I.; Mäkinen, R.A.E.; Järvenpää, S.; Ylä-Oijala, P.; Rahola, J. Electromagnetic sensitivity analysis and shape optimization using method of moments and automatic differentiation. IEEE Trans. Antennas Propag. 2009, 57, 168–175. [Google Scholar] [CrossRef]
- Director, S.; Rohrer, R. The generalized adjoint network and network sensitivities. IEEE Trans. Circuit Theory 1969, 16, 318–323. [Google Scholar] [CrossRef]
- Easum, J.A.; Nagar, J.; Werner, P.L.; Werner, D.H. Efficient multi-objective antenna optimization with tolerance analysis through the use of surrogate models. IEEE Trans. Ant. Propag. 2018, 66, 6706–6715. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Chen, H.; Palma, M.S.; Zhu, M. Lessons learned using a physics based macro model for analysis of radio wave propagation in wireless transmission. IEEE Trans. Antennas Propag. 2019, 67, 2150–2157. [Google Scholar] [CrossRef]
- Alzahed, A.M.; Mikki, S.M.; Antar, Y.M.M. Nonlinear mutual coupling compensation operator design using a novel electromagnetic machine learning paradigm. IEEE Ant. Wirel. Propag. Lett 2019, 18, 861–865. [Google Scholar] [CrossRef]
- Hassan, A.K.S.O.; Etman, A.S.; Soliman, E.A. Optimization of a novel nano antenna with two radiation modes using kriging surrogate models. IEEE Photonics J. 2018, 10, 4800807. [Google Scholar] [CrossRef]
- Rawat, A.; Yadav, R.N.; Shrivastava, S.C. Neural network applications in smart antenna arrays: A review. AEU Int. J. Elec. Commun. 2012, 66, 903–912. [Google Scholar] [CrossRef]
- Cai, J.; King, J.; Yu, C.; Liu, J.; Sun, L. Support vector regression-based behavioral modeling technique for RF power transistors. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 428–430. [Google Scholar] [CrossRef]
- Van Der Herten, J.; Couckuyt, I.; Deschrijver, D.; Dhaene, T. A fuzzy hybrid sequential design strategy for global surrogate modeling of high-dimensional computer experiments. SIAM J. Sci. Comput. 2015, 32, A1020–A1039. [Google Scholar]
- Rayas-Sánchez, J.E.; Chávez-Hurtado, J.L.; Brito-Brito, Z. Optimization of full-wave EM models by low-order low-dimension polynomial surrogate functionals. Int. J. Numer. Model. Electron. Netw. Devices Fields 2015, 30, e2094. [Google Scholar] [CrossRef]
- Bandler, J.W.; Cheng, Q.S.; Dakroury, S.A.; Mohamed, A.S.; Bakr, M.H.; Madsen, K.; Sondergaard, J. Space mapping: The state of the art. IEEE Trans. Microw. Theory Tech. 2004, 52, 337–361. [Google Scholar] [CrossRef]
- Robinson, T.D.; Eldred, M.S.; Willcox, K.E.; Haimes, R. Surrogate-based optimization using multifidelity models with variable parameterization and corrected space mapping. AIAA J. 2008, 46, 2814–2822. [Google Scholar] [CrossRef] [Green Version]
- Echeverria, D.; Hemker, P.W. Space mapping and defect correction. Comput. Methods Appl. Math. 2005, 5, 107–136. [Google Scholar] [CrossRef]
- Manchec, A.; Quendo, C.; Favennec, J.-F.; Rius, E.; Person, C. Synthesis of capacitive-coupled dual-behavior resonator (CCDBR) filters. IEEE Trans. Microw. Theory Tech. 2006, 54, 2346–2355. [Google Scholar] [CrossRef]
- Feng, F.; Zhang, J.; Zhang, W.; Zhao, Z.; Jin, J.; Zhang, Q.J. Coarse-and fine-mesh space mapping for EM optimization incorporating mesh deformation. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 510–512. [Google Scholar] [CrossRef]
- Zhou, R.; Sun, J.; Wei, S.; Wang, J. Synthesis of conformal array antenna for hypersonic platform SAR using modified particle swarm optimization. IET Radar Sonar Navigat. 2017, 11, 1235–1242. [Google Scholar] [CrossRef]
- Greda, L.A.; Winterstein, A.; Lemes, D.L.; Heckler, M.V.T. Beamsteering and beamshaping using a linear antenna array based on particle swarm optimization. IEEE Access 2019, 7, 11562–141573. [Google Scholar] [CrossRef]
- Aoad, M.; Simsek, M.; Aydin, Z. Development of knowledge based response correction for a reconfigurable N-shaped microstrip antenna design. In Proceedings of the 2015 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Ottawa, ON, Canada, 11–14 August 2015; pp. 1–3. [Google Scholar]
- Koziel, S.; Ogurtsov, S.; Cheng, Q.S.; Bandler, J.W. Rapid EM-based microwave design optimization exploiting shape-preserving response prediction and adjoint sensitivities. IET Microw. Ant. Propag. 2014, 8, 775–781. [Google Scholar] [CrossRef]
- Rayas-Sánchez, J.E. Power in simplicity with ASM: Tracing the aggressive space mapping algorithm over two decades of development and engineering applications. IEEE Microw. Mag 2016, 17, 64–76. [Google Scholar] [CrossRef]
- Cervantes-González, J.C.; Rayas-Sánchez, J.E.; López, C.A.; Camacho-Pérez, J.R.; Brito-Brito, Z.; Chávez-Hurtado, J.L. Space mapping optimization of handset antennas considering EM effects of mobile phone components and human body. Int. J. RF Microw. CAE 2016, 26, 121–128. [Google Scholar] [CrossRef]
- De Villiers, D.I.L.; Couckuyt, I.; Dhaene, T. Multi-objective optimization of reflector antennas using Kriging and probability of improvement. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 985–986. [Google Scholar]
- Bandler, J.W.; Cheng, Q.S.; Georgieva, N.; Ismail, M.A. Implicit space mapping EM-based modeling and design exploiting preassigned parameters. In Proceedings of the 2002 IEEE MTT-S International Microwave Symposium Digest (Cat. No.02CH37278), Seattle, WA, USA, 2–7 June 2002; pp. 713–716. [Google Scholar]
- Aoad, A.; Simsek, M.; Aydin, Z. Knowledge based response correction method for design of reconfigurable N-shaped microstrip patch antenna using inverse ANNs. Int. J. Numer. Model Electron. Netw. Devices Fields 2015, 30, e2129. [Google Scholar] [CrossRef]
- Diehl, M.; Walther, A.; Georg Bock, H.; Kostina, E. An adjoint-based SQP algorithm with quasi-Newton Jacobin updates for iequality constrained optimization. Opt. Methods Softw. 2009, 25, 531–552. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Expedited feature-based quasi-global optimization of multi-band antenna input characteristics with jacobian variability tracking. IEEE Access 2020, 8, 83907–83915. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Reduced-cost electromagnetic-driven optimization of antenna structures by means of trust-region gradient-search with sparse Jacobian updates. IET Microw. Ant. Propag. 2019, 13, 1646–1652. [Google Scholar] [CrossRef]
- Koziel, S.; Ogurtsov, S. Multi-level design optimization of microwave structures with automated model fidelity adjustment. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013. [Google Scholar]
- Koziel, S. Objective relaxation algorithm for reliable simulation-driven size reduction of antenna structure. IEEE Ant. Wirel. Propag. Lett. 2017, 16, 1949–1952. [Google Scholar] [CrossRef]
- Mahrokh, M.; Koziel, S. Optimization-based antenna miniaturization using adaptively adjusted penalty factors. Electronics 2021, 10, 1751. [Google Scholar] [CrossRef]
- Mahrokh, M.; Koziel, S. Explicit size-reduction of circularly polarized antennas through constrained optimization with penalty factor adjustment. IEEE Access 2021, 9, 132390–132396. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Accelerated gradient-based optimization of antenna structures using multi-fidelity simulations and convergence-based model management scheme. IEEE Trans. Ant. Propag. 2021, 69, 8778–8789. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. Trust Region Methods; MPS-SIAM Series on Optimization; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Koziel, S.; Ogurtsov, S. Model management for cost-efficient surrogate-based optimization of antennas using variable-fidelity electromagnetic simulations. IET Microw. Ant. Propag. 2012, 6, 1643–1650. [Google Scholar] [CrossRef]
- Sendrea, R.E.; Zekios, C.L.; Georgakopoulos, S.V. A multi-fidelity surrogate optimization method based on analytical models. In Proceedings of the 2021 IEEE MTT-S International Microwave Symposium (IMS), Atlanta, GA, USA, 7–25 June 2021; pp. 70–73. [Google Scholar]
- Xiao, L.; Shao, W.; Ding, X.; Wang, B. Dynamic adjustment kernel extreme learning machine for microwave component design. IEEE Trans. Microw. Theory Tech. 2018, 66, 4452–4461. [Google Scholar] [CrossRef]
- Koziel, S.; Bekasiewicz, A. Comprehensive comparison of compact UWB antenna performance by means of multi-objective optimization. IEEE Trans. Ant. Propag. 2017, 65, 3427–3436. [Google Scholar] [CrossRef]
- Alsath, M.G.N.; Kanagasabai, M. Compact UWB monopole antenna for automotive communications. IEEE Trans. Antennas Propag. 2015, 63, 4204–4208. [Google Scholar] [CrossRef]
- Haq, M.A.; Koziel, S. Simulation-based optimization for rigorous assessment of ground plane modifications in compact UWB antenna design. Int. J. RF Microw. Comput. Aided Eng. 2018, 28, e21204. [Google Scholar] [CrossRef]
- Kumar, B.P.; Kumar, C.; Guha, D. A new design approach to improve the circular polarization characteristics of a microstrip antenna. In Proceedings of the 2018 IEEE Indian Conference on Antennas and Propogation (InCAP), Hyderabad, India, 16–19 December 2018; pp. 1–2. [Google Scholar]
- Malekabadi, S.A.; Attari, A.R.; Mirsalehi, M.M. Compact broadband circular polarized microstrip antenna with wideband axial-ratio bandwidth. In Proceedings of the 2008 International Symposium on Telecommunications, Tehran, Iran, 27–28 August 2008; pp. 106–109. [Google Scholar]
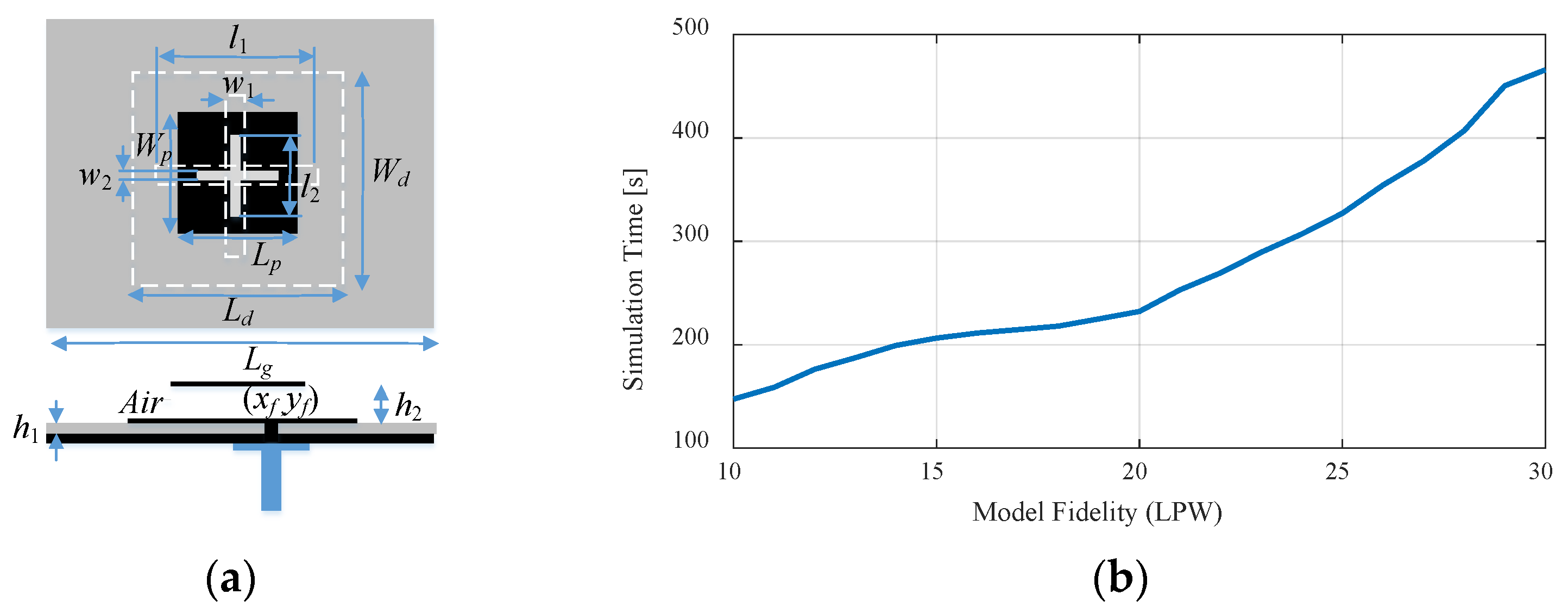






| Antenna I [57] | Antenna II [58] | Antenna III [59] | Antenna IV [60] | Antenna V [61] | |
|---|---|---|---|---|---|
| Substrate I | RF-35 (εr = 3.5 h = 0.762 mm) | RF-35 (εr = 3.5 h = 0.762 mm) | FR4 (εr = 4.3 h = 1.55 mm) | Arlon AD250 (εr = 2.5 h = 3.8 mm) | Arlon (εr = 2.2 h = 1.575 mm) |
| Substrate II | − | − | − | Air (εr = 1.08, h = 2 mm) | Air (εr = 1, h = 3.8 mm) |
| Designable parameters (mm) | x = [L0 g a l1 l2 w1 o]T | x = [L0 dR R rrel dL dw Lg L1 R1 dr crel]T | x = [Lg L0 Ls Ws d dL ds dWs dW a b]T | x = [r g Lg d ρ Ls α x1] | x = [xf yf l1 l2 Wp Wd Lp Ld w2 w1 Lg] |
| Other parameters (dB) | w0 = 2o + a, wf = 1.7 | w0 = 1.7 | W0 = 3 | − | − |
| Target operating bandwidth | 3.1 GHz to 10.6 GHz | 3.1 GHz to 10.6 GHz | 3.1 GHz to 10.6 GHz | 8.1 GHz to 8.3 GHz | 5.36 GHz to 5.9 GHz |
| Design constraints | |S11| ≤ −10 dB | |S11| ≤ −10 dB | |S11| ≤ −10 dB | |S11| ≤ −10 dB, AR ≤ 3 dB | |S11| ≤ −10 dB, AR ≤ 3 dB |
| Initial design (mm) | x = [20.23 18.62 9.23 6.67 5.64 3.84 2.29] | x = [8.74 0.66 4.59 0.75 4.75 1.84 10.00 5.94 3.67 0.49 0.79] | x = [8.53 12.35 9.68 0.33 3.90 1.72 1.04 1.48 1.95 0.37 0.57] | x = [1.58 0.48 21.7 12.46 3.40 9.40 52.40 1.52] | x = [4.16 3.09 8.26 12.08 17.23 12.93 17.70 15.96 1.15 0.89 26.04] |
| Benchmark Antenna Structure | Model Fidelity [Fmin Fmax] | Simulation Time [TFmin TFmax] [s] |
|---|---|---|
| Antenna I | [1130] | [145 466] |
| Antenna II | [12 20] | [49 124] |
| Antenna III | [10 24] | [31 164] |
| Antenna IV | [11 20] | [38 219] |
| Antenna V | [11 22] | [82 236] |
| Performance Figures | Antenna I | Antenna II | Antenna III | Antenna IV | Antenna V | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Adaptive β | This Work 4 | Adaptive β | This Work | Adaptive β | This Work | Adaptive β | This Work | Adaptive β | This Work | ||
| Area A (mm2) | 293 | 284 | 207 | 215 | 176 | 177 | 590 | 615 | 372.7 | 368 | |
| Constraint violation ζS11 1 (dB) | 0.08 | 0.04 | 0.02 | 0 | 0.06 | 0 | 0 | 0 | 0 | 0.02 | |
| Constraint violation ζAR 2 (dB) | _ | _ | _ | _ | _ | _ | 0.07 | 0.01 | 0 | 0 | |
| CPU Time | Absolute (h) | 6.5 | 4.7 | 6.8 | 3.2 | 12.3 | 7.2 | 13.9 | 6.6 | 8.8 | 4.7 |
| Relative to Rf 3 | 144 | 104 | 150 | 70 | 2.4 | 119 | 108 | 51 | 135 | 72 | |
| Saving (%) | _ | 28 | _ | 53 | _ | 33 | _ | 53 | _ | 47 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahrokh, M.; Koziel, S. Improved-Efficacy EM-Based Antenna Miniaturization by Multi-Fidelity Simulations and Objective Function Adaptation. Energies 2022, 15, 403. https://doi.org/10.3390/en15020403
Mahrokh M, Koziel S. Improved-Efficacy EM-Based Antenna Miniaturization by Multi-Fidelity Simulations and Objective Function Adaptation. Energies. 2022; 15(2):403. https://doi.org/10.3390/en15020403
Chicago/Turabian StyleMahrokh, Marzieh, and Slawomir Koziel. 2022. "Improved-Efficacy EM-Based Antenna Miniaturization by Multi-Fidelity Simulations and Objective Function Adaptation" Energies 15, no. 2: 403. https://doi.org/10.3390/en15020403
APA StyleMahrokh, M., & Koziel, S. (2022). Improved-Efficacy EM-Based Antenna Miniaturization by Multi-Fidelity Simulations and Objective Function Adaptation. Energies, 15(2), 403. https://doi.org/10.3390/en15020403







