Understanding Power Market Dynamics by Reflecting Market Interrelations and Flexibility-Oriented Bidding Strategies

Abstract

Power markets are becoming increasingly complex as they move towards (i) integrating higher amounts of variable renewable energy, (ii) shorter trading intervals and lead times, (iii) stronger interdependencies between related markets, and (iv) increasing energy system integration. For designing them appropriately, an enhanced understanding of the dynamics in interrelated short-term physical power and energy markets is required, which can be supported by market simulations. In this paper, we present an agent-based power market simulation model with rule-based bidding strategies that addresses the above-mentioned challenges, and represents market participants individually with a high level of technical detail. By allowing agents to participate in several interrelated markets, such as the energy-only market, a procurement platform for control reserve and a local heat market representing district heating systems, cross-market opportunity costs are well reflected. With this approach, we were able to reproduce EPEX SPOT market outcomes for the German bidding zone with a high level of accuracy (mean absolute percentage error of 8 €/MWh for the years 2016–2019). We were also able to model negative market prices at the energy-only market realistically, and observed that the occurrence of negative prices differs among data inputs used. The simulation model provides a useful tool for investigating different short-term physical power/energy market structures and designs in the future. The modular structure also enables extension to further related markets, such as fuel, CO${}_2$, or derivative markets.

1. Introduction

Power markets are constantly evolving to respond effectively to the changing needs of the energy system. Increasing amounts of power generation from variable renewable energy (VRE) sources significantly impact power market performance, and today’s market design requires changes to support efficient operations in a future system with even higher renewable energy shares, and to provide incentives to attract flexibility provision to the system [1]. Power markets nowadays allow for short-term trading in fine-grained time intervals, which better supports reactions to updated renewable generation forecasts, up to closely before delivery time. Along with the development of energy-only markets, they are linked with markets for control reserves that are also characterized by shorter-term market clearing in smaller time intervals. Given market interrelations, opportunity costs from one market influence bidding strategies on other markets, which impacts the market dynamics. Moreover, energy systems outside the power sector, such as heat supply and electric mobility, will also have an increased influence on power markets, additionally increasing their complexity and interrelations.

Due to the system criticality of electricity markets and the constant need for adaptations of market designs, appropriate tools for their analysis are needed. In energy system modeling, optimization models prevail, which typically do not model market interrelations and the dynamics resulting from bidding strategies in detail. Therefore, they are less suitable for realistically modeling power market outcomes, and therefore also have only limited capabilities of analyzing power market designs. Simulation models, in contrast, provide the flexibility to model specific markets in high levels of detail, without prohibitively increasing the computational complexity of the model. Agent-based models in particular allow for representing the market participant’s perspective and meaningful bidding strategies under consideration of opportunity costs from participation in several interrelated markets. This agent perspective increases the understanding of such systems and reduces risks and uncertainties [2,3].

This work introduces the flexibility-oriented Agent-Based Laboratory for Electricity Market Analysis flexABLE as an open-source model that allows for detailed analysis of power market dynamics, addressing the above-mentioned challenges and research requirements. It models electricity markets using a bottom-up approach and has a high level of detail on relevant technical parameters. The primary results of the model are the electricity prices on the energy-only market (day-ahead/intraday market), and the operation plans of different power generation units. The contributions to the research community are as follows:

• An open-source agent-based Python framework that allows the user to set up market configurations easily.
• A novel approach of including multiple interrelated markets, allowing better understanding of agents’ behavior in such complex environment. The three default market configurations cover an energy-only, control reserve (covering capacity and energy market schemes) and district heat markets.
• A modular structure that allows users to develop and implement new classes (sub-classes) and units.
• Low system requirements due to iterative design (All simulations presented in Section 4 were performed using an Intel(R) Core(TM) i5-7300U CPU 2.60 GHz, 12 GB RAM computer. The simulation of a complete year required 20 min). The iterative design also allows modeling any period of interest, which can range from a few weeks to several consecutive years.

The ability to model multiple interrelated markets helps increase the realism of the model. Agents can formulate multiple bids, classified as inflexible and flexible bids, which is particularly relevant for thermal power plants. The inflexible bids represent the minimum amount of power the agent must deliver either for technical restrictions or for its commitment to other markets, and the price of such bid is set so that it reflects the avoided cost of shutting down a units or of not being able to meet commitments made on other markets. Modeling the market in this way means some agents formulate negative bids, leading to negative market prices at times where residual demand is low.

The outcomes of the flexABLE model can be used to answer economic questions, e.g., questions related to the effects of market design changes, or also system changes such as effects of a phase-out of conventional power generation technologies. The model can also be used to tackle technical questions, due to the ability to model different market participants with a high level of technical details.

The paper proceeds as follows: Section 2 briefly compares different energy systems modeling paradigms and reviews similar models. Section 3 describes the flexABLE framework architecture and the bidding strategies. Section 4 describes the scenarios used to validate the models and discusses the results, and Section 5 finally provides the conclusions.

2. Related Work

A variety of models can be found in the literature that help analyzing energy systems. Pfenninger et al. [4] identify four paradigms of energy system models, which are (1) energy system optimization models, (2) energy systems simulation models, (3) power systems and electricity market models, and (4) qualitative and mixed-methods scenarios. They further distinguish between two methods and purpose pairs, i.e., simulation/forecast, and optimization/scenario. Within these categories, the approach of this work would be classified as the third paradigm, i.e., power systems and electricity market model. While our simulation model can be used for forecasting, the purpose is rather to explore possible market outcomes if the market structures or market designs are altered. In that sense, it is best used for “what-if” predictions rather than for forecasting.

With a stricter focus on electricity market modeling, Ventosa et al. [5] propose a classification scheme that elaborates on the mathematical structure of the models, with the three main trends of (1) optimization models, (2) equilibrium models, and (3) simulation models. Within the last category, a further distinction is made between equilibrium simulation models and agent-based simulation models. This work would rather constitute the last of the named types.

In power system analysis, optimization models are the most popular. The majority of these models are expressed as linear programming problems. Some also include integer and binary variables for, e.g., defining a plant’s on/off state or for formulating minimum power constraints, which then makes them mixed-integer linear programming problems. While these models are powerful in determining not only the cost-optimal short-term dispatch under given constraints, but also longer-term investment decisions; they are typically not designed—and not adequate—for analyzing power markets in detail. The system marginal cost given by the shadow variable of the energy balance equation can be taken as an indication for power price levels, which neglects many aspects typical for real-world markets, such as bidding behavior or interactions between related markets.

Equilibrium models reflect the competition between multiple agents. The individual agents set their supply and demand behavior by optimizing their utility, profit, or cost objectives [6]. In equilibrium models, the system is defined as a set of mathematical (algebraic or differential) equations.

In such complex systems as interrelated power markets, the formulation and solution for mathematical problems are hard to find [7], which encouraged the emergence of simulations. Simulation models are usually built modularly rather than in a rigid mathematical formulation [8]. This approach provides the flexibility of implementing the agents’ strategic behavior [5]. The modularity of simulation models also allows the modelers to incorporate multiple approaches to the model to gain better insights, bridging the gaps between bottom-up and top-down approaches [7,9]. The need for such hybrid simulation models emerged from the structural incapability of standard macroeconomic models of representing major and complex technical details of the energy systems. Instead, macroeconomic models offer an aggregate mathematical representation [9,10].

The boundaries between the energy system modeling approaches are rather “fluid” instead of rigid [4]. A particular model can be positioned anywhere along the continuous scale between the extremities, depending on the model’s purpose. Due to the large number of available models, the authors have restricted this review to those related approaches that deliver comparable output to the simulation model presented in this work, although they might have different purposes. A summary and comparison of those models is presented in

Table 1. Energy system models and frameworks with similar research scope to flexABLE.

Model	Approach	Dispatch	Sectors	Spatial Resolution	Temporal Resolution	Reserves	Network	Open-Source	Reference
Dispa-Set	Optimization	Unit	Electricity, heat	Country	Hour	✓	Cross-border	✓	[11]
ELMOD	Optimization	Unit	Electricity, heat	Transmission network node	Hour	✓	DC-OPF	✓	[12]
PyPSA	Optimization	Unit	Cross-sectoral	Nodal	Hour	–	DC-OPF, LPF	✓	[13]
Oemof	Optimization	Unit	Cross-sectoral	Nodal	Hour	–	Transport model	✓	[14]
EMMA	Optimization	Type	Electricity	Country (North-Western Europe)	Hour	Minimum spinning reserve constraint	Cross-boder trades (ATC)	✓	[15]
Renpass	Optimization	Type	Electricity	Germany: 21 regions other countries: country	Hour	–	net transfer capacities	✓	[16]
PowerFlex	Optimization	Unit	Electricity, heat	Transmission network node	Hour	✓ (as baseload)	DC-OPF	–	[17]
E2M2	Optimization	Unit	Electricity, heat	Country	Hour	✓	–	–	[18]
REMix	Optimization	Type	Electricity, heat	Nodal	Hour	–	DC-OPF	–	[19]
AMIRIS	Simulation	Type	Electricity	Federal states (Germany)	15 min	–	–	–	[20]
GAPEX	Simulation	Genco agents	Electricity	Power exchange markets		–	Net transfer capacities	–	[21]
flexABLE	Simulation	Unit	Electricity, heat	Nodal	15 min	✓	Linked to PyPSA	✓

.

As shown in this table, the temporal resolution of most reviewed models is one hour. While the hourly resolution is sufficiently detailed for capacity expansion models, it falls short of representing today’s power markets, which offer trading intervals down to the 15-min level. Another important feature for detailed electricity system models is a high spatial resolution and the representation of grid constraints. Many reviewed models incorporate grid constraints through direct current optimal power flow (DC-OPF) approximations of transmission systems. The flexABLE model does not have its own grid representation but can be linked to PyPSA [13] for calculating necessary re-dispatch measures when lines are overloaded.

Optimization models are common when calculating dispatch plans; the output of these models varies according to the defined objective function and constraints, such as Dispa-SET model [11] developed within the Joint Research Centre, focuses on balancing and flexibility problems in European grids. The model solves a linear optimization problem (LP) to minimize operational costs. The model produces hourly unit-wise dispatch plans for multiple European countries. The power plants’ technical constraints, such as minimum power and ramping limits, are taken into consideration. The short-run marginal cost of the different units is calculated depending on the fuel costs provided. A markup is added to consider ramping, startup, and shutdown costs.

A similar approach is followed in the ELMOD model family [12], but with a more detailed representation of the European transmission network. Currently, four submodels have emerged from ELMOD, introducing extra constraints to answer different research questions, such as the impacts of wind generation uncertainty [22], or the multi-period investments covering multiple sectors [23].

Building modular frameworks could also be noticed in models such as PyPSA [13] and Oemof [14]. Both of these models offer an easy framework for the user to implement their own multi-sectoral scenarios. The frameworks also provide the user with the flexibility of defining the spatial and temporal resolution for their simulations. Similar to Dispa-SET and ELMOD, those models use the short-run marginal cost with an added markup to model different technical constraints. This approach fulfills the purpose of these models to optimize dispatch plans with minimal cost objectives. Still, it does not reflect the agents’ competition for self-profit maximization.

The authors in [24] introduced a generalized Nash equilibrium model to represent the effects of coordination between different transmission network operators. A similar approach has been used in different energy markets to describe the competition of the various agents. MultiMOD [20] represents the large-scale supply and demand for fossil fuels and renewable energy sources. The model is formulated as a dynamic generalized Nash equilibrium.

Although equilibrium model implementation has been repeatedly researched and proposed for electricity market modeling, we did not identify frameworks/models with comparable output to the model introduced by this paper. Equilibrium models typically answer questions related to agents’ strategic behavior or policy introduction. The model presented in [25] analyzes the market power exerted by different market agents while characterizing their bidding strategies by conjectured price response. The authors of [26] propose a method to model electricity markets as single-level equilibrium problems while still identifying equilibria similar to those obtained using bi-level problems. It was also indicated that equilibrium models help comprehend the market participant’s behavior rather than being an offering/bidding tool for producers/consumers [26]. The authors of [27] identify a supply function equilibrium (SFE) model that can be applied to a multiple-period situation. It was also shown that actual market prices can be well simulated by SFE models given certain assumptions [27,28].

The complexity of equilibrium models encourages the implementation of agent and heuristic models. The drawback of such models is that the underlying mathematical foundation is not well developed [28], explaining the trend of implementing hybrid models. Their main structure is a discrete event object-oriented simulation model. However, the different agents (components) could still use optimization or game-theoretic methods for internal calculations.

AMIRIS [21] focuses on the regulatory framework’s impact on renewable energy resources and storage units development in a market. Therefore, the model’s main output is the dispatch plans of renewable energy resources and storage units, the income and expenses of involved agents, and support schemes’ costs. The model has 15 min time resolution and is JAVA based, and the renewable energy agents are modeled in a more detailed manner than thermal power plants. AMIRIS itself is not open-source, but the framework upon which it is based was published under Apache License [29].

GAPEX framework [30] allows the users to study the dynamic performance of electricity markets. The framework was implemented in Matlab using the object-oriented programming capabilities to allow for representing different components. The framework was used to simulate the Italian electricity market, with accurate results [30]. No information was found about the availability of the framework; nonetheless, the availability is further affected by Matlab being proprietary software.

AMES [31] is an agent-based model that offers users a framework to model wholesale power markets along with transmission networks. The framework was developed in 2009 to simulate and research wholesale markets that follow the U.S. Federal Energy Regulatory Commission (FERC) design [32]. The model is available as open-source software under GNU General Public License (GPL). Most parts were developed in Java programming language.

EMCAS [33] and PowerACE [34] are also agent-based models that focus on answering questions related to distributed decision-making in electricity markets and market design. These models were used in multiple projects but are not offered as open-source (currently).

3. Materials and Methods

The model presented in this work is a simulation framework implemented as an object-oriented Python program. Its architecture and the interaction of the market participants are described in Section 3.1. Section 3.2 describes the bidding strategies applied by each agent as a basis for the market outcome.

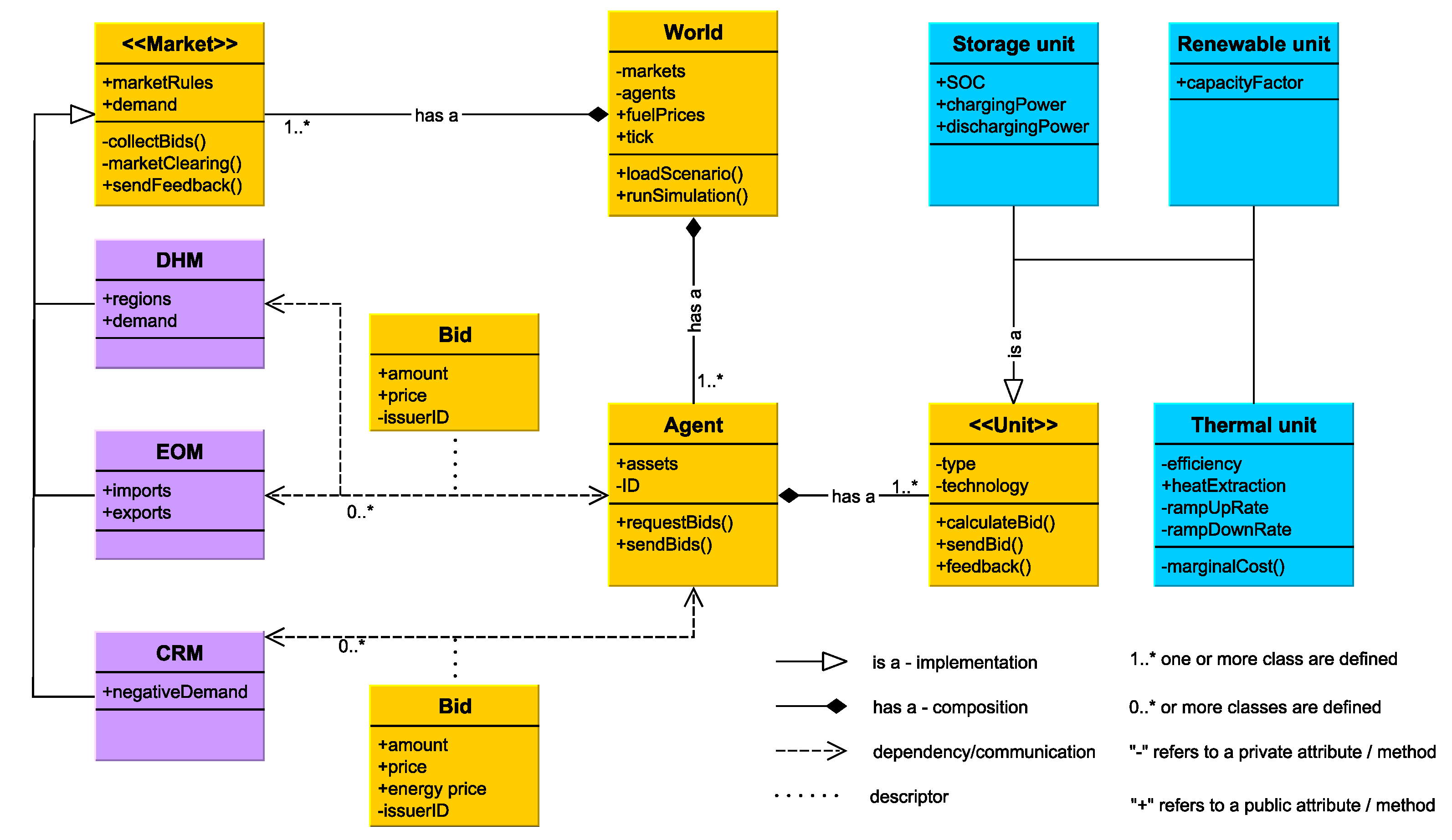
3.1. Model Architecture

Following an object-oriented paradigm, all market participants and other objects are implemented as classes, each defining the most relative attributes and functions. This enables the modeler to populate a scenario with multiple markets and generation units by only setting the individual attributes. This modularity allows for representing numerous different market setups, reflecting regional characteristics. The sample implementation presented in this paper is adapted to the market design in the German bidding zone. The following common classes are defined in flexABLE:

• The World class serves as a container for all other components and functions that control the simulation.
• The Market class simulates a market operator, and contains functions for bid collection and market clearing. The attributes of the class also specify properties such as gate closure times or minimum bid sizes. This class currently has three instances for representing different markets: the energy-only market, the control reserve market, and a district heat market.
• The Unit class is a generic class representing any generation unit. It can be instantiated as a thermal power plant, a VRE power plant, or a storage unit.
• The Agent class represents the market participants, who are generation companies (GenCos). The agent class has access to all the assets (from the Unit class) owned by the company, and it manages the bid formulation and can also perform portfolio optimization if one GenCo owns several assets.
• The Bid class represents the communication method between the different classes. The agent (GenCo) collects bids formulated from its assets and sends them to the respective market instances. The markets will send the feedback to the bid issuer, containing the information on whether the bid was accepted, rejected, or partially accepted.

In Figure 1, the interaction between the instances of the classes can be seen. The Agent class organizes the communication between the markets and the assets (of the Unit class). As a response to a call for bids sent by the market, the agent first collects the bids from its different assets and then transfers them to the respective markets.

The energy-only market (EOM) is the main electricity market, and is implemented similar to real-world markets such as the European EPEX SPOT [35]. It constitutes an abstract market that has similarities with both intraday continuous trading, as the trading interval is 15 min and delivery happens shortly after trading, and with the day-ahead market, as all bids are collected and cleared in an auction. The total demand added to this instance is equal to the total energy consumption in Germany. When all bids are collected, the market is cleared based on a uniform-price auction rule. The lowest supply bids are accepted first until the supply meets demand, or no more supply is available. After the market is cleared, the spot price is paid to all successful suppliers regardless of their submitted bid price.

The control reserve market (CRM) represents an abstract control reserve market that has compromise features of automated and manually activated frequency restoration reserve (aFRR and mFRR) markets. Both positive and negative reserve capacities can be offered and traded. CRM bids consist of both a capacity price and an energy price, along with the power offered over the whole bidding period, which is four hours each. For the reserve capacity, the market is cleared by accepting the lowest capacity price first, whereas when the balance energy is called for, market clearing happens with respect to the energy bid prices. In contrast to the EOM, the CRM follows the pay-as-bid settlement rule, where each supplier is paid its capacity or energy bid price. While the CRM capacity is cleared every four hours, energy procurement is cleared per 15 min interval.

The district heat market (DHM) is a regional market in which trades are restricted to plants located in the region. Every asset therefore has geographical parameters representing its location. Coal or gas-fired combined heat-and-power plants can offer heat as a coupled product along with their power generation. Here, similar to EOM, the agents can submit their supply and demand bids, and the central unit provides the local district heat demand bids. District heat market regions can be defined flexibly, and power plants located in these regions can then connect to the heat network. As the EOM, the DHM also operates in 15 min intervals.

An agent can have multiple assets (of the class Unit) of either one of the three types shown in blue in Figure 1. These types are thermal power plants, VRE power plants, and storage units. Each of these types of assets has its own set of techno-economic parameters that are essential for the correct operation modeling and bid formulation, such as: rated power (for thermal and VRE plants), ramp rates, startup or shut-down costs, fuel type, and heat extraction capability (for thermal power plants); time-varying capacity factor (for VRE plants), charging and discharging power, storage capacity and efficiency (for storage units).

In each simulation time step, the markets are executed sequentially, in the order that is depicted in Figure 2. An agent can make a bid for each generation unit that it owns, as long as the plant is technically able to deliver the respective product. This means that all units pre-qualified for control reserve can submit bids to the control reserve market, and all combined heat and power unites can bid for district heat delivery. The information on whether or not a plant can deliver a product is specified in the input database for each unit. The agent’s individual market outcome determines the possible bids in subsequent markets in the sequence. Using this procedure, the market outcomes as a whole decide what part of the plant’s capacity is allocated to which product.

At the beginning of the sequence, the agents assess the current operational state of their units and derive the possible operation for the next time step. Relevant parameters are, e.g., the current shut-down time for a thermal power plant (once shut down, the plant needs to stay off for a minimum duration), or the current state of charge for storage units. The agents then formulate and submit their capacity bids to the CRM, following the approach explained later in Section 3.2. After receiving feedback from the CRM, agents with assets capable of delivering heat to the district heat network participate in the DHM market by submitting their bids. The order of markets is important, since the information from both the CRM and DHM is required to determine the flexible and inflexible capacity of each unit. The agents then participate in the EOM by submitting their inflexible and flexible bids. The calls for balance energy are done at the end of each simulation step, and finally the operational plan is determined for each unit on the basis of the market success.

The model is designed for the analysis of one bidding zone, following the zonal market model currently implemented in Europe [36]. However, imports and exports to and from that market zone are also accounted for. For the back-casting scenarios, this was done through exogenous time series of actual cross-border exchanges (commercial flows), which are directly added as supply and demand bids to the EOM. When modeling future scenarios, neighboring countries could also be modeled in the form of simple merit-order models that are linked to the market zone under study. This requires knowledge of the transfer capacities between countries in each time step, which is an interesting research topic on its own [37].

3.2. Bidding Strategies

Bids are formulated separately for each asset and for each market based on the asset’s techno-economic parameters, the current operational state and bidding strategy. Currently, bidding strategies are fixed implementations of if-else rules. However, modules that allow for strategic bids formulated through machine learning are currently under development. This section presents the bidding strategies for thermal power plants and energy storage units. The bidding strategies formulated here have similarly been presented in [38].

3.2.1. Variable Renewable Energy Power Plants

VRE plants simply offer all their available capacity of the next time step (i.e., the product of capacity factor and rated capacity) to the EOM as a price-independent bid, which ensures that they are always placed first in the merit order and their capacities are always cleared. Technically, this is implemented as a bid price of $-500$ EUR, the lowest possible price.

For research questions related to analyzing the effects of VRE participation in the control reserve market, or analyzing strategic VRE bidding, other bidding strategies could also be implemented. Passive price-independent bids are the default used here, as current VRE support schemes do not provide incentives to bid differently.

3.2.2. Thermal Power Plants

Thermal power plants (denoted by superscript TPP) can participate in all three markets CRM, EOM, and DHM (in the latter only if heat extraction is possible). First bids are formulated for the CRM. For this, each thermal power plant calculates its available control reserve capacities (Equations (1) and (2)), and based on the variable operating cost of Equation (3), the corresponding capacity (Equations (4) and (5)) and energy bid prices (Equations (6) and (7)).

A bid is placed for the entire reserve procurement time interval $\tau$, which is a four hour block. In contrast, the time step t refers to the trading interval at the EOM and DHM, and is 15 min, so $1\tau =16t$. The available positive and negative reserve capacity, defined in Equations (1) and (2), respectively, is restricted by the plant’s power output in the previous time step, $P_{t-1}^{\mathrm{TPP}}$, and the thus remaining headroom for ramping up or down until the rated capacity $P^{\mathrm{TPP},\max }$ or the minimum power output $P^{\mathrm{TPP},\min }$ is reached, or by the maximum ramp-up $P_{\mathrm{CRM}}^{\mathrm{TPP},\mathrm{ru}}$ or ramp-down $P_{\mathrm{CRM}}^{\mathrm{TPP},\mathrm{rd}}$ power achievable within five minutes, as prescribed for aFRR. For better readability, no index for the asset is given, although each bid is formulated individually per asset.

$$P_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{pos}}=min\left(P^{\mathrm{TPP},\max }-P_{el,t-1}^{\mathrm{TPP}};P_{\mathrm{CRM}}^{\mathrm{TPP},\mathrm{ru}}\right)$$

(1)

$$P_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{neg}}=min\left(P_{el,t-1}^{\mathrm{TPP}}-P^{\mathrm{TPP},\min };P_{\mathrm{CRM}}^{\mathrm{TPP},\mathrm{rd}}\right)$$

(2)

The control reserve capacity price is defined by the forgone contribution margin $c{m}_{\mathrm{EOM}}^{\mathrm{TPP}}$ of not being able to offer the same capacity at the EOM (opportunity cost). It is calculated by Equation (3) as the difference between the forecast EOM clearing price $M^{\mathrm{PFC}}$ and the power plant-specific marginal generation cost $m{c}^{\mathrm{TPP}}$ summed over all (here 16) time steps of the CRM clearing interval. The marginal cost is time-specific, as the applicable fuel and CO${}_2$ emission costs depend on the plant’s efficiency, which in turn is a function of the current output level (higher efficiency close to full load, and lower efficiency at partial load) [39]. A price forward curve, which is calculated as with a simplified merit order model ahead of the simulation run, is used as an EOM price forecast:

$$c{m}_{\mathrm{EOM},\tau }^{\mathrm{TPP}}=\sum _{t\in \tau }{M}_t^{\mathrm{PFC}}-m{c}_t^{\mathrm{TPP}}$$

(3)

The bid price for positive reserve capacity $c{p}_{\mathrm{CRM}}^{\mathrm{TPP},\mathrm{pos}}$, defined in Equation (4), is set equal to $c{m}_{\mathrm{EOM}}^{\mathrm{TPP}}$ if the expected contribution margin is greater than zero, so the price represents the opportunity cost of participating in the CRM. Otherwise, it is the absolute value of the expected loss, per unit of reserve capacity offered that occurs on the EOM market due to keeping the power plant operational at the minimum output.

The negative reserve capacity bid price $c{p}_{\mathrm{CRM}}^{\mathrm{TPP},\mathrm{neg}}$, defined in Equation (5), is zero when $c{m}_{\mathrm{EOM}}^{\mathrm{TPP}}$ is positive, since reducing the power output does not lead to additional cost. Otherwise, the losses from running at a level that is by the offered capacity higher than the minimum output, and selling the output at the EOM is set as the bid price.

These bid price settings ensure that either opportunity or actual costs from keeping the plant running under unfavorable EOM market conditions are compensated if the bid is successful:

$$c{p}_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{pos}}=\left\{\begin{array}{cc}c{m}_{\mathrm{EOM},\tau }^{\mathrm{TPP}}\hfill & \mathrm{if}c{m}_{\mathrm{EOM},\tau }^{\mathrm{TPP}}\ge 0\hfill \\ \frac{\left|c{m}_{\mathrm{EOM},\tau }^{\mathrm{TPP}}\right|·P^{\mathrm{TPP},\min }}{P_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{pos}}}\hfill & \mathrm{else}\hfill \end{array}\right.$$

(4)

$$c{p}_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{neg}}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}c{m}_{\mathrm{EOM},\tau }^{\mathrm{TPP}}\ge 0\hfill \\ \\ \frac{\left|c{m}_{\mathrm{EOM},\tau }^{\mathrm{TPP}}\right|·(P_{el}^{\mathrm{TPP},\min }+P_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{neg}})}{P_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{neg}}}\hfill & \mathrm{else}\hfill \end{array}\right.$$

(5)

The balance energy delivery price $e{p}_{\mathrm{CRM}}^{\mathrm{TPP}}$ for the positive (Equation (6)) and negative (Equation (7)) reserves is the marginal cost of the power plant with positive and negative sign, respectively. Thus, it simply reflects actual costs or savings from providing balance energy and does not yield any profits:

$$e{p}_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{pos}}=m{c}_t^{\mathrm{TPP}}$$

(6)

$$e{p}_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{neg}}=-m{c}_t^{\mathrm{TPP}}$$

(7)

Market clearing at the CRM is done on the basis of all submitted bids, and each power plant receives as feedback the confirmed positive $P_{\mathrm{CRM}}^{\mathrm{TPP},\mathrm{pos},\mathrm{con}}$ and negative $P_{\mathrm{CRM}}^{\mathrm{TPP},\mathrm{neg},\mathrm{con}}$ reserve capacity, which it must keep available during the time interval $\tau$.

Next, bids are formulated for the DHM. Only thermal power plants capable of heat extraction can participate. Depending on the power plant’s location, heat can either be extracted from the primary heat-power process (hpp) and sold as ($P^{TPP,hpp}$) or generated by auxiliary firing located on-site ($P^{TPP,auxFi}$). Using the simplified heat-to-power ratio curves described by [40], the theoretical (theo) heat extraction from steam power plants (spp) and open-cycle gas turbines (ocgt) is calculated using Equations (8) and (9), respectively:

$$P_{dhm,theo,t}^{TPP,hpp,spp}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le P_{el,t-1}<P^{TPP,min}\hfill \\ 2·P_{el,t-1}\hfill & \mathrm{if}{P}^{TPP,min}\le P_{el,t-1}<0.6·P^{TPP,max}\hfill \\ 1.2·P_{el,t-1}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

$$P_{dhm,theo,t}^{TPP,hpp,ocgt}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}0\le P_{el,t-1}<P^{TPP,min}\hfill \\ 2·P_{el,t-1}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(9)

The maximum heat extraction at the power plant location ($P_{dh}^{TPP,max}$) limits the heat that can possibly be extracted (poss), as shown in Equation (10):

$$P_{dhm,poss,t}^{TPP,hpp}=min(P_{dh}^{TPP,max};P_{dhm,theo,t}^{TPP,hpp})$$

(10)

The maximum possible heat output by auxiliary firing is also dependent on the maximum district heat extraction at the power plant site and is calculated from the difference between the already extracted heat at the site and the maximum possible extraction, as shown in Equation (11):

$$P_{dhm,t}^{TPP,auxFi}=P_{dh,t}^{TPP,max}-P_{dhm,theo,t}^{TPP,hpp}$$

(11)

The cost of heat extraction from the heat-power process is equivalent to the marginal costs of electricity generation multiplied by the power loss ratio ($\beta$) due to heat extraction (cf. ([41], p. 295)), as given in Equation (12):

$$h{p}_{dhm,t}^{TPP,hpp}=m{c}_t^{TPP}·\beta$$

(12)

The power loss ratio depends on the type of power plant and the ratio of generated power to the decoupled heat. For auxiliary firing, it is assumed that gas boilers provide the required heat; therefore, the bid prices are calculated as shown in Equation (13):

$$h{p}_{dhm,t}^{TPP,aux}=\frac{p_{ng,t}}{{\eta }_{boiler}}$$

(13)

Next, the bids are formulated for the EOM. Thermal power plants formulate two separate bids to the EOM which are related to the flexible and inflexible parts of their capacity, respectively. This allows the plant operators to offer a low or even negative price for the part of the plant’s capacity that should stay operational to avoid shut-down and startup costs during times of high renewable feed-in or low demand. Simultaneously, flexible parts of the plant’s capacity can be offered at a higher price.

The calculation of the inflexible capacity $P_{\mathrm{EOM}}^{\mathrm{TPP},\mathrm{inflex}}$ is given in Equation (14), where $P_{\mathrm{EOM}}^{\mathrm{TPP},\mathrm{rd}}$ is the power that can be ramped down within a 15 min interval; if negative FRR was successfully sold at the CRM, parts for the ramp down capability need to remain available for this service. This equation describes the power plant’s lowest possible power output in the next step that avoids a shut-down:

$$P_{\mathrm{EOM},t}^{\mathrm{TPP},\mathrm{inflex}}=max\left(P_{el,t-1}^{\mathrm{TPP}}-P_{\mathrm{EOM}}^{\mathrm{TPP},\mathrm{rd}};P_{el}^{\mathrm{TPP},\min }\right)+P_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{neg},\mathrm{con}}$$

(14)

The energy price for the inflexible capacity $e{p}_{\mathrm{EOM}}^{\mathrm{TPP},\mathrm{inflex}}$ is calculated according to Equation (15). The second term in the equation considers the technology-specific shut-down and startup cost, $c^{\mathrm{TPP},\mathrm{su}}$, $c^{\mathrm{TPP},\mathrm{sd}}$, and the average operation duration of the power plant, $d^{\mathrm{TPP},\mathrm{op}}$. This specifies the amount of money that the power plant operator would prefer to pay per unit of energy to stay operational and avoid shut-down and subsequent startup costs. The third term represents the revenue procured from the DHM per power unit of inflexible bid amount. This would represent the forgone opportunity for the agent if they could not participate in the DHM. Such bid formulation for an inflexible capacity can entail negative bid prices, so in times of low residual demand, negative market clearing prices can also occur:

$$e{p}_{\mathrm{EOM},t}^{\mathrm{TPP},\mathrm{inflex}}=m{c}_t^{\mathrm{TPP}}-\left(\frac{\left(c^{\mathrm{TPP},\mathrm{sd}}+c^{\mathrm{TPP},\mathrm{su}}\right)}{d_t^{\mathrm{TPP},\mathrm{op}}}\right)-\left(\frac{\left(P_{dhm,t}^{\mathrm{TPP},\mathrm{hpp}}+P_{dhm,t}^{\mathrm{TPP},\mathrm{auxFi}}\right)·\left(\frac{p_{ng}}{{\eta }_{boiler}}\right)}{P_{eom,t}^{\mathrm{TPP},\mathrm{inflex}}}\right)$$

(15)

The available flexible capacity $P_{\mathrm{EOM}}^{\mathrm{TPP},\mathrm{flex}}$ is calculated using Equation (16), where $P_{\mathrm{EOM}}^{\mathrm{TPP},\mathrm{ru}}$ represents the ramp-up speed within a 15 min interval. This calculation assures that the power plant bids its current maximum feasible capacity, in addition to the inflexible capacity, while securing the positive reserve capacity:

$$P_{\mathrm{EOM},t}^{\mathrm{TPP},\mathrm{flex}}=min\left(P_{el,t-1}^{\mathrm{TPP}}+P_{\mathrm{EOM}}^{\mathrm{TPP},\mathrm{ru}};P_{el}^{\mathrm{TPP},\max }\right)-P_{\mathrm{CRM},\tau }^{\mathrm{TPP},\mathrm{pos},\mathrm{con}}-P_{\mathrm{EOM},t}^{\mathrm{TPP},\mathrm{inflex}}$$

(16)

The flexible bid price $e{p}_{\mathrm{EOM}}^{\mathrm{TPP},\mathrm{flex}}$, defined in Equation (17), is set equal to the marginal operating costs, so that the power plant avoids losses in case the bid is successful and can earn a contribution margin if the market-clearing price is greater than the marginal cost:

$$e{p}_{\mathrm{EOM},t}^{\mathrm{TPP},\mathrm{flex}}=m{c}_t^{\mathrm{TPP}}$$

(17)

Note that energy is traded at the EOM, not power. Thus, ultimately, the power values are converted from power to energy given the time interval and assuming linear ramps between capacity levels at times t and $t-1$.

3.2.3. Energy Storage Units

Energy storage units can be pumped-hydro storage plants, batteries or any other type of storage unit. In flexABLE, such units participate in both EOM and CRM. There are several reasons for different bidding strategies for storage units. First, marginal operating cost is insignificant, while it plays an important role in price formulation of a thermal power plant. Second, in the current implementation, the storage units target to operate in a grid friendly manner instead of maximizing their profit. Thus, the storage units provide energy when it is deficient, and buys when it is abundant. Third, storage units have a limited capacity for charging and discharging, which is particularly important for CRM bids, where a reserve capacity must be available at any time during the market interval if accepted.

The positive and negative reserve for the CRM is defined according to Equations (18) and (19):

$$P_{\mathrm{CRM},t}^{\mathrm{ES},\mathrm{pos}}=min\left[\left(\frac{{\mathrm{SOC}}_t-{\mathrm{SOC}}^{\min }}{\Delta t}\right){\eta }^{dis};P^{\mathrm{ES},\max .\mathrm{dis}}\right]$$

(18)

$$P_{\mathrm{CRM},t}^{\mathrm{ES},\mathrm{neg}}=min\left[\left(\frac{{\mathrm{SOC}}^{\max }-{\mathrm{SOC}}_t}{\Delta t}\right)/{\eta }^{ch};P^{\mathrm{ES},\max .\mathrm{ch}}\right]$$

(19)

The capacity price for the positive control reserve is defined similarly to the thermal power plants as a foregone contribution margin at the EOM, and the energy price is set equal to the value of the energy stored, given the past EOM prices. For the negative reserve capacity, both capacity and energy prices are set to zero since charging does not lead to additional costs.

At the EOM, energy storage units can submit bids for both supply and demand. The supply bid, given in Equation (20), depends on the current state of charge (SOC), minimal SOC (both in MWh), accepted positive CRM reserve capacity, discharging efficiency ${\eta }^{dis}$, and maximum discharge power $P^{\mathrm{ES},\max .\mathrm{dis}}$. The demand bid, in turn, depends on the current and maximum SOC, confirmed negative reserve capacity, charging efficiency ${\eta }^{ch}$, and maximum charge power $P^{\mathrm{ES},\max .\mathrm{ch}}$ (Equation (21)):

$$P_{\mathrm{EOM},t}^{\mathrm{ES},\sup }=min\left[\left(\frac{{\mathrm{SOC}}_t-{\mathrm{SOC}}^{\min }}{\Delta t}-P_{\mathrm{CRM},\tau }^{\mathrm{ES},\mathrm{pos},\mathrm{con}}\right){\eta }^{dis};P_{el}^{\mathrm{ES},\max .\mathrm{dis}}\right]$$

(20)

$$P_{\mathrm{EOM},t}^{\mathrm{ES},\mathrm{dem}}=min\left[\left(\frac{{\mathrm{SOC}}^{\max }-{\mathrm{SOC}}_t}{\Delta t}-P_{\mathrm{CRM},\tau ,i}^{\mathrm{ES},\mathrm{neg},\mathrm{con}}\right)/{\eta }^{ch};P_{el}^{\mathrm{ES},\max .\mathrm{ch}}\right]$$

(21)

For the decision to submit a supply or a demand bid, the predicted electricity price $M_t^{\mathrm{PFC}}$ is compared to the average price over the upcoming n time intervals, $e{p}_{\mathrm{EOM},t}^{\mathrm{av}}$, as defined in Equation (22). The default time horizon for this evaluation is one day, i.e., $n=96$ time steps:

$$e{p}_{\mathrm{EOM},t}^{\mathrm{av}}=\frac{1}{n}\sum _{j=1}^n{M}_{t+j}^{\mathrm{PFC}}$$

(22)

If the current predicted electricity price is greater than the current average price, indicating a rising need for energy, the storage units submit a supply bid. Alternatively, if the market price is below the average price, the storage units submit a demand bid (Equation (23)):

$$P_{\mathrm{EOM},t,i}^{\mathrm{ES}}=\left\{\begin{array}{cc}{P}_{\mathrm{EOM},t,i}^{\mathrm{ES},\sup }\hfill & \mathrm{if}{M}_t^{\mathrm{PFC}}\ge e{p}_{\mathrm{EOM},t}^{\mathrm{av}}\hfill \\ \hfill & \\ P_{\mathrm{EOM},t,i}^{\mathrm{ES},\mathrm{dem}}\hfill & else\hfill \end{array}\right.$$

(23)

In both cases, the bid price, defined in Equation (24), is set to the forecast average price:

$$e{p}_{\mathrm{EOM},t}^{\mathrm{ES}}=e{p}_{\mathrm{EOM},t}^{\mathrm{av}}$$

(24)

4. Results

This work aims to validate the model against real-world data. The validation is not only done for one illustrative year, but for four consecutive years that have quite different (renewable) generation, demand, and price characteristics. If the model can correctly represent the past, it can be used for scenario exploration of future energy scenarios.

In order to test and validate the model and the proposed bidding strategies, simulations for the German bidding zone for 2016–2019 were performed. Section 4.1 presents the input data and the sources used. The results of the simulations and their evaluation are described in Section 4.2.

4.1. Input Data

An essential part of modeling and analyzing power markets is the collection and preparation of input data. For the validation scenarios defined in this paper, data were collected from different publicly available sources, as seen in

Table 2. Data sources used for the validation.

Type	Data Description	Resolution Temporal, Spatial	Reference
Fuel and CO${}_2$ prices	Gas prices CO${}_2$ EU-ETS certificates Other energy carriers	15 min, country-wise daily, country-wise 15 min, country-wise	[42] [43] [44]
Agents	Thermal power plants VRE power plants Storage units	-, unit-wise 15 min, country-wise -, unit-wise	[45,46,47] [48,49,50,51] [47,52]
Demand	Heat demand Weather data Inelastic demand Control reserve demand	15 min, 16 regions hourly, 16 stations 15 min, 1 region 15 min, country-wise	[53] [54] [48] [55]
Imports and exports	Scheduled commercial exchanges	15 min, country-wise	[48]

.

4.1.1. Fuel and CO${}_2$ Prices

A significant parameter in calculating the short-run marginal costs (SRMC) of thermal power plants is fuel and CO${}_2$ prices. These must be available in high temporal resolution. As an illustration, the large price differences for CO${}_2$ certificates in Europe are shown in Figure 3. Daily CO${}_2$ prices were used for validation simulations.

Daily fuel prices were also used in the SRMC calculation. Uniform transport costs of 10 EUR/t were assumed for hard coal, following [40]. In addition, gas prices were assumed to be uniform across the bidding zone. They were taken from the NetConnet Germany (NCG) hub.

4.1.2. Thermal Power Plant Parameters

The power plant list from [40] was used as the basis for the validation simulations. In his work, Künzel derived a power plant list from the World Electric Power Plants Database [45]. Missing data were filled from other available open-source datasets, such as the power plant list provided by the German environment agency (UBA) [46], and the federal network agency (BNetzA) [47]. The BNetzA power plant list was primarily used to vary the installed capacities between the different simulation years.

4.1.3. VRE Installed Capacities and Capacity Factors

Since VRE plants do not follow individual bidding strategies, one VRE plant per type (solar PV, wind on-shore and wind-offshore) was used to represent each technology in Germany. This was done to minimize the computational burden in the simulations. The actual generation time series were obtained from ENTSO-E [48]. Additionally, time series obtained from the reanalysis data source renewables.ninja was used [50,51]. The difference between both data sources is discussed in Section 4.2.

4.1.4. Storage Units

In this work, only pumped-hydro storage units were considered. Installed capacities were obtained from [52] and BNetzA [47]. Storage units with an installed capacity of less than 4 MW were not included, since they are incapable of providing the minimum offer amount of 1 MWh in a single quarter-hour. It was also assumed that all storage units had an initial state of charge equal to 50% of their maximum capacity.

4.1.5. Electricity and Control Reserve Demand

Although the model can handle price-elastic demand bids, the scope of this work is limited to a price-inelastic demand. The time series for Germany’s electrical consumption was obtained from the ENTSO-E transparency platform [48]. Since no network was investigated, a single column representing the total consumption was used.

For the control reserve market, aFRR and mFRR reserve data were obtained from the regelleistung.net data center [55], which is a joint platform for all German (and neighboring) transmission system operators. The data represent both reserved capacities and the called energy with 15 min resolution.

4.1.6. Heat Demand

In the German bidding zone, district heat markets play an essential role in deciding the economic feasibility for combined heat-and-power power plants. Therefore, it is crucial to represent this sector as accurately as possible. In our validation simulations, each federal state in Germany was modeled as a separate district heat region, allowing only power plants in that state to serve the demand. The heat demand profiles were built using the methods suggested by Koch et al. [56], which implements the formula developed by Hellwig [57]. The formula calculates heat consumption as a function of ambient temperature, which was used to produce quarter-hourly demand profiles using weather data. The formula is also used to create separate profiles for industrial, commercial and residential sectors. Weather data were obtained from the German Meteorological Service data center [54], of which temperature profiles of reference stations per region were used.

4.1.7. Cross-Border Exchange

For the import and export data, time series of scheduled commercial exchanges obtained from the ENTSO-E transparency platform was used [48]. Since the validation simulations do not have a network representation, cross-border exchange time series were used as exogenous input to the model.

4.2. Modeled Prices and Generation Profiles

The main output of the model discussed here is time series of 15 min electricity prices at the energy-only market and the aggregate dispatch plans. As mentioned in Section 3, EOM is a stylized representation of the day-ahead and intraday markets where the total demand volume is traded.

At EPEX SPOT, the day-ahead auction trades hourly bids, which would not be directly comparable to the model result. The trading volumes in day-ahead markets are larger than those at the intraday market (This could be seen from the EPEX SPOT annual report https://www.EPEXSPOT.com/sites/default/files/sites/annual-report-2020/, accessed on 23 December 2021). Therefore, the model results were resampled to an hourly time resolution. For the dispatch plans, the actual total generation per technology is compared to the simulated generation per technology. A unit-wise comparison of actual versus simulated generation would theoretically be possible too. However, as the real operation of a plant is also affected by non-market decisions and parameters, such as re-dispatch measures or planned and unplanned outages, such a comparison would be less insightful.

The simulated and actual historical market clearing prices from EPEX SPOT are shown in Figure 4 (An interactive plot with zoom functions can be found at https://flexable.energy/, accessed on 23 December 2021). The mean absolute error (MAE) and root mean squared error (RMSE) metrics were used to evaluate the quality of the obtained results. The calculated values are summarized in

Table 3. Error metrics and obtained values for different simulation years.

Simulation Period	MAE in €/MWh	RMSE in €/MWh
Year 2016	6.54	8.83
Year 2017	9.44	13.01
Year 2018	8.88	11.69
Year 2019	6.69	10.91
Total period	7.89	11.21

. The MAE measures the average magnitude of error of each point considering only the absolute value, so positive and negative values do not cancel each other out. The MAE could be calculated using Equation (25):

$$MAE=(\frac{1}{n})\sum _{i=1}^n\left|y_i-x_i\right|$$

(25)

The RMSE uses a quadratic scoring rule for errors; the forecasted values and corresponding observations are squared and then averaged. Thus, relatively higher scores are given to larger errors. The root of the squared error is usually taken to make sure that the error is expressed using the same unit as the data. The RMSE could be calculated using Equation (26):

$$RMSE=\sqrt{(\frac{1}{n})\sum _{i=1}^n{(y_i-x_i)}^2}$$

(26)

Compared to other electricity market simulation models for the German market zone, the obtained results are excellent. Genoese [58] reports a MAE of 17.3 €/MWh for an agent-based simulation of the German market in 2005. The same study also reports on a comparison with non-published results from a fundamental model described by Brand et al. [59] and Möst et al. [60], with an MAE of 17.7 €/MWh and 13.7 €/MWh, respectively, for the simulation year 2005. These findings are not directly comparable, as many aspects of the market have changed since then. For example, no negative prices occurred before 2008 in the German market. In addition, the VRE share in generation was much lower 2005 than it is today. Thus, even with increased market complexity, the simulated market results had a lower error than the other reported models. In addition, it is capable of modeling negative prices, which is not true for many other models in the literature.

To further analyze the data, weekly averaged values were compared. The weekly pattern of EPEX SPOT prices for the simulation period 2016–2019 and simulation results can be seen in Figure 5a. The data were also split into summer and winter periods (Summer defined as the period starting with spring equinox and ending by autumnal equinox), and the results are depicted in Figure 5b,c. It can be observed that the error during summer is higher than in the winter period. A reason for such deviation could be the availability of power plants since it was assumed that power plants are always available, and maintenance periods were not included in these scenarios. When looking at the data on plant availabilities, it becomes apparent that lignite, nuclear, and hard coal power plant capacities were less available in the summer period compared to the winter of the same years (Data on power plant availability is published at https://www.eex-transparency.com/power/de/production/capacity, accessed on 23 December 2021). This could explain the high price peaks not being met in the simulations.

From Figure 5, it can be seen that the model results are close to the mean actual data, but the peaks, both positive and negative, are less pronounced in the simulation results. One error that could explain under-representation of negative peaks is the VRE generation data used. A comparison of the hourly VRE generation time series reported by ENTSO-E with generation estimations done by renewables.ninja (accessed on 23 December 2021) shows clear differences. While renewable.ninja provides capacity factors based on weather reanalysis data and assumed plant characteristics, ENTSO-E provides measured generation in-feeds (after curtailment, if applicable, and given planned or unplanned plant outages). As forecast generation before curtailment and outages is a more relevant basis for the bids placed in the markets, we performed the simulations again with renewable.ninja data [50,51]. Figure 6 shows the results of this comparison.

It can be seen that the negative prices were better modeled with data obtained from renewable.ninja (accessed on 20 April 2021) (MAE is 5.51 €/MWh and RMSE was 7.9 €/MWh). This could be due to generation being curtailed due to congestion management measures, which leads to lower values of VRE generation in the ENTSO-E time series than in the reanalysis-based time series. Figure 7 shows the week 32 of 2019, where this effect can be seen clearly.

Although using alternative renewable generation data resulted in better estimations, the positive price peaks are still not accurately modeled. The availability of power plants and reserved capacities data was not used in these simulations, which meant higher capacities were modeled than reality, which could lower prices in positive peaks as explained earlier. This could also cause higher more flexible offers in the simulations, increasing the prices in negative peaks. In the second half of the year 2018, about 1.5 GW of thermal capacity were decommissioned (1.25 GW nuclear and about 230 MW of lignite power plants), explaining the higher error in that period in comparison with results of the half-year before and after. Another major factor that was not considered in these simulations was the price elasticity of demand, since only inelastic demand was modeled.

To further validate the model and to check the effect of the unavailability of power plants, the generation per energy carrier type was compared between historical data (obtained from [48]) and model results. The annual generation for 2019 is presented in Figure 8.

Figure 8a shows the total generation of each technology in TWh during 2019. All renewable generation quantities match exactly, since they were used as model-exogenous time series. It can also be seen that total simulated energy is higher than actual data, since 10 TWh of energy was classified as “other conventional” in the source data (and was neglected in the simulation). Despite this, simulation results match reality very closely. The largest difference is observed in lignite, which supports the assumption that the availability of lignite-fired power plants plays an important role in the real-world market.

5. Conclusions and Outlook

In this work, a framework for modeling European electricity markets was presented. It can reproduce electricity market prices realistically, thus facilitating market design analysis. As a simulation models or more specifically an agent-based simulation representing individual market participants and their bidding strategies on the markets, it offers both the methodological flexibility to account for real-world market design features and the necessary level of detail and realism to provide high-quality reconstruction of actual market results. The flexABLE allows for easily implementing different market setups modularly, thus providing higher flexibility in investigating market designs. To showcase the framework’s capability, three different markets were investigated, i.e., the energy-only market, a control reserve market, and a district heating market, to represent the German bidding zone. We were able to reproduce actual market results in the energy-only market not only in one representative year, but in a period of four consecutive years with different supply and demand situations. The level of realism obtained was high, and even negative prices were modeled with high precision.

One distinguishing feature of the presented model is that it markets interrelations through individual bidding strategies at each market. In the German case study, the inclusion of the district heat market turned out to be decisive for negative prices to occur as many power plants had strong incentives to keep their plant in operation even in times of low residual demand, to avoid shut-down and consecutive startup costs when entering again into the market.

The presented model is provided open-source, and all input data used are publicly available. This is essential for ensuring reproducibility and allowing other researchers to use the model as well. The results have shown that the model can reproduce average prices for the day-ahead market with a mean absolute error on the order of 8 €/MWh. Negative and positive price peaks were less pronounced in the simulation results than in reality. Using alternative input data sources, such as renewable generation based on reanalysis data rather than actual generation data, better represented the negative peaks. By splitting the results into winter and summer periods, it was noticed that positive peaks deviated more strongly during summer. This could be due to the lower lignite power plant availability during summer due to maintenance or other technical reasons. Modeling plant availability appropriately turned out to be a substantial challenge, since available data do not support an easy matching of power plant unit names to existing unit lists. Including unit availability information was left for future work. Comparing the actual and simulated generation per type can further strengthen the assumption that positive peak errors might be due to plant availability.

Integrating a network model into the market model is essential to develop it further. The current implementation has already established a link to a network representation using PyPSA. This allows the model to replace exogenous time series of VRE actual generation and cross-border power exchanges. Re-dispatch and other corrective measures should also be modeled endogenously with a network model integrated into the market model as part of future work. Another promising extension of the model for future work would be to consider other types of markets that are interrelated with the EOM, CRM, and heat supply. Interesting candidates are additional flexibility products delivered from the same units modeled here (for, e.g., congestion management, re-dispatch or other services). Alternatively, markets for other products related to energy are worth considering, such as fuels (natural gas, coal), CO${}_2$ emission certificates or long-term contracts and derivatives. Finally, interrelations to product markets in integrated energy systems, such as hydrogen, are also interesting applications of the model within future work.