Quasi-Analytical Calculation of Frequency-Dependent Resistance of Rectangular Conductors Considering the Edge Effect
Abstract
:1. Introduction
- Recalculating the two-dimensional analytical ac resistance of single rectangular conductors.
- Reducing the inaccuracy of two-dimensional analytical methods.
- Being simple for engineering applications.
- Being applicable to any rectangular thickness (from square to very thin conductors).
2. Ac Resistance of an Isolated Conductor
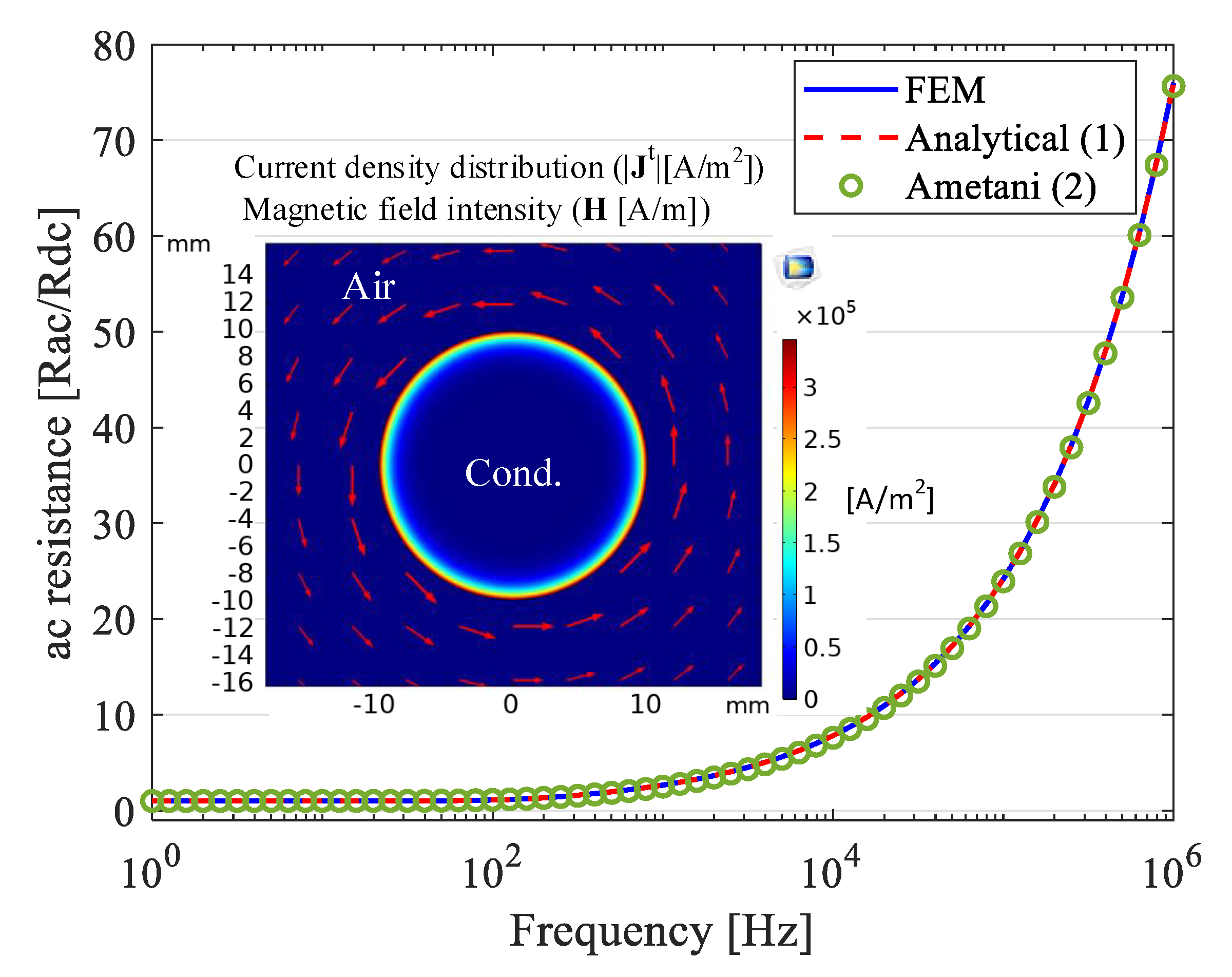
2.1. Circular Conductor
2.2. Ametani’s Approach
2.3. One-Dimensional Calculation
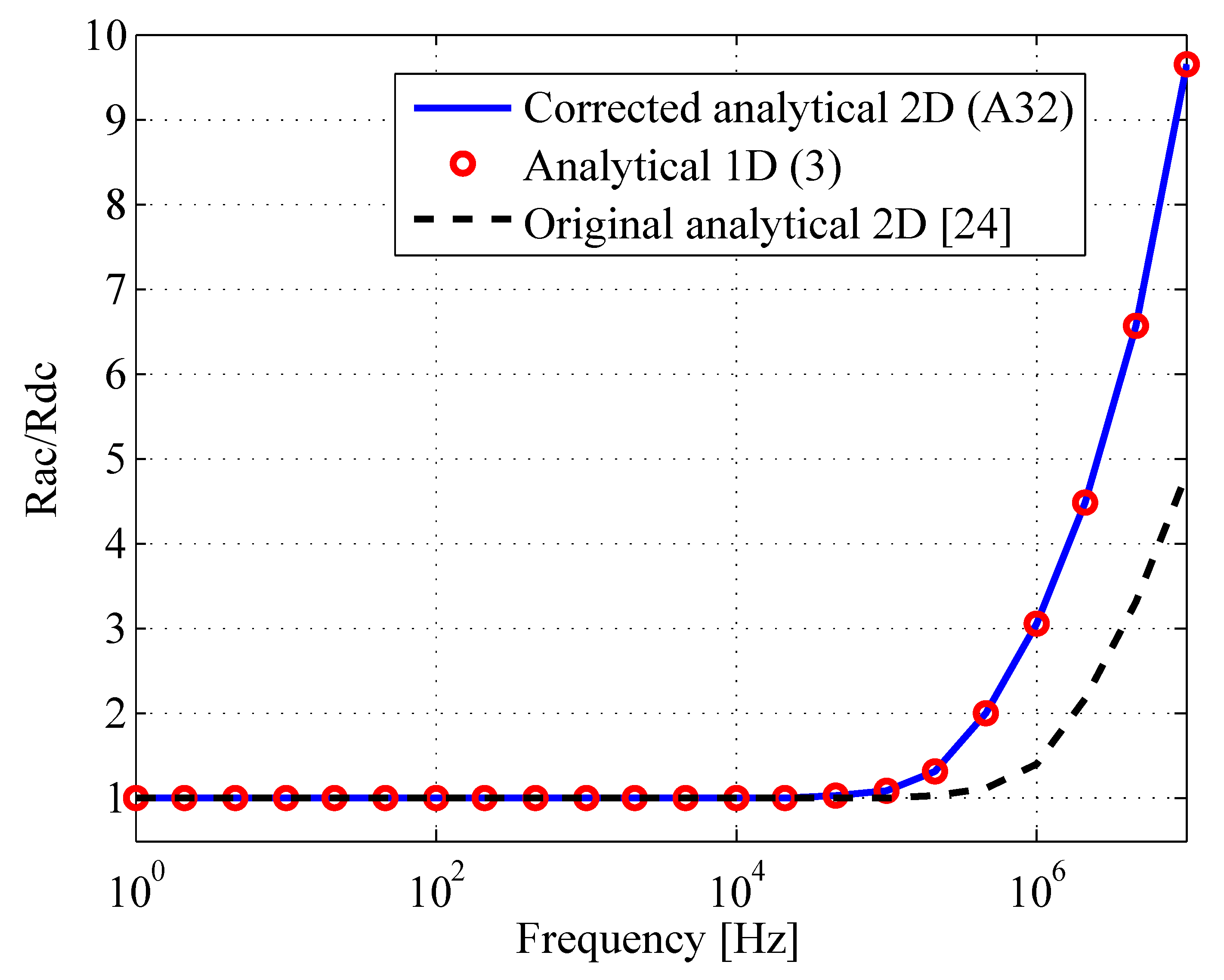
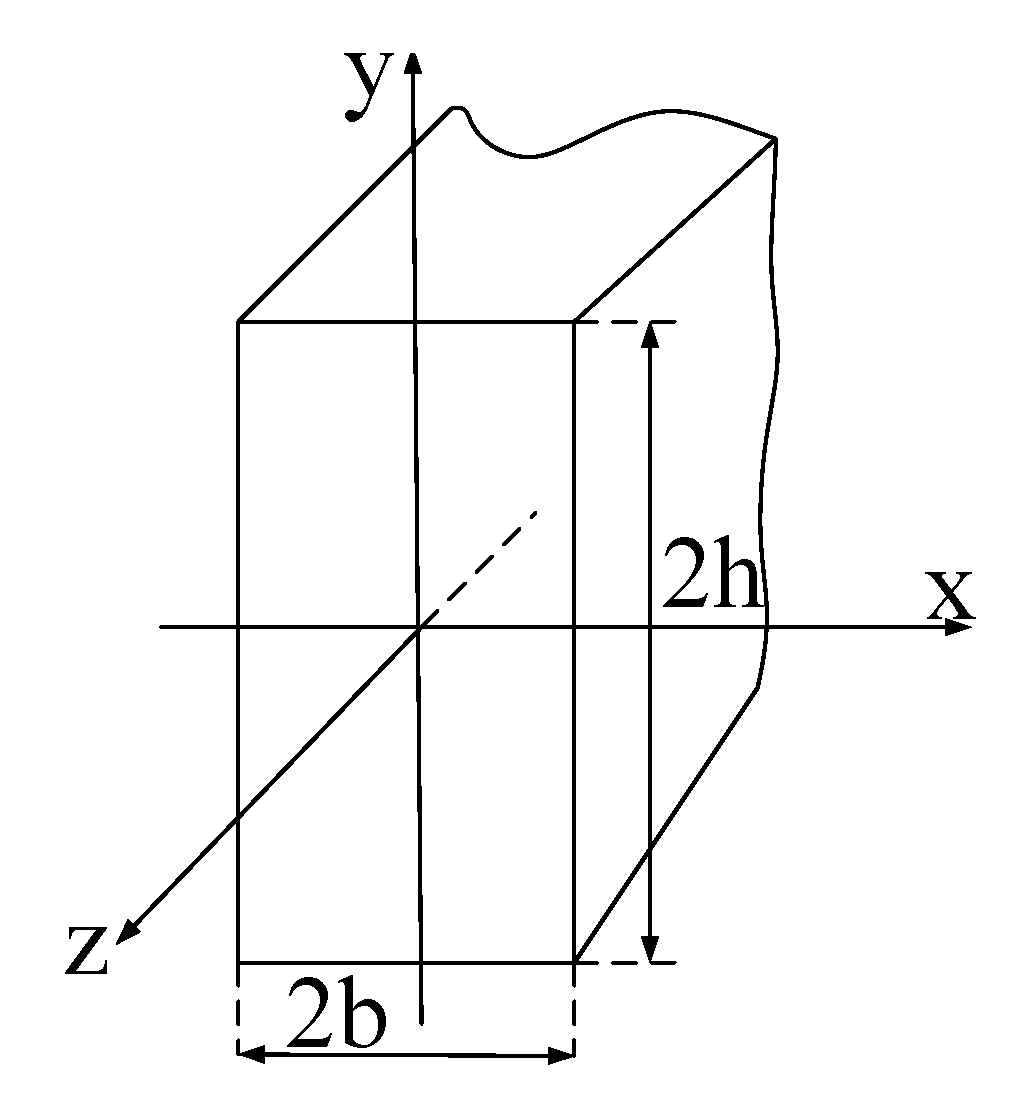
2.4. Two-Dimensional Calculation
2.5. Finite Element Method (FEM) Approach
3. Results of ac Resistance Calculation
3.1. Circular Conductor
3.2. Foil Type Transformer
3.3. Square Conductor
3.4. Effect of Thickness on Accuracy
4. Proposed Quasi-Analytical Method for Accurate Calculation of for Rectangular Conductors
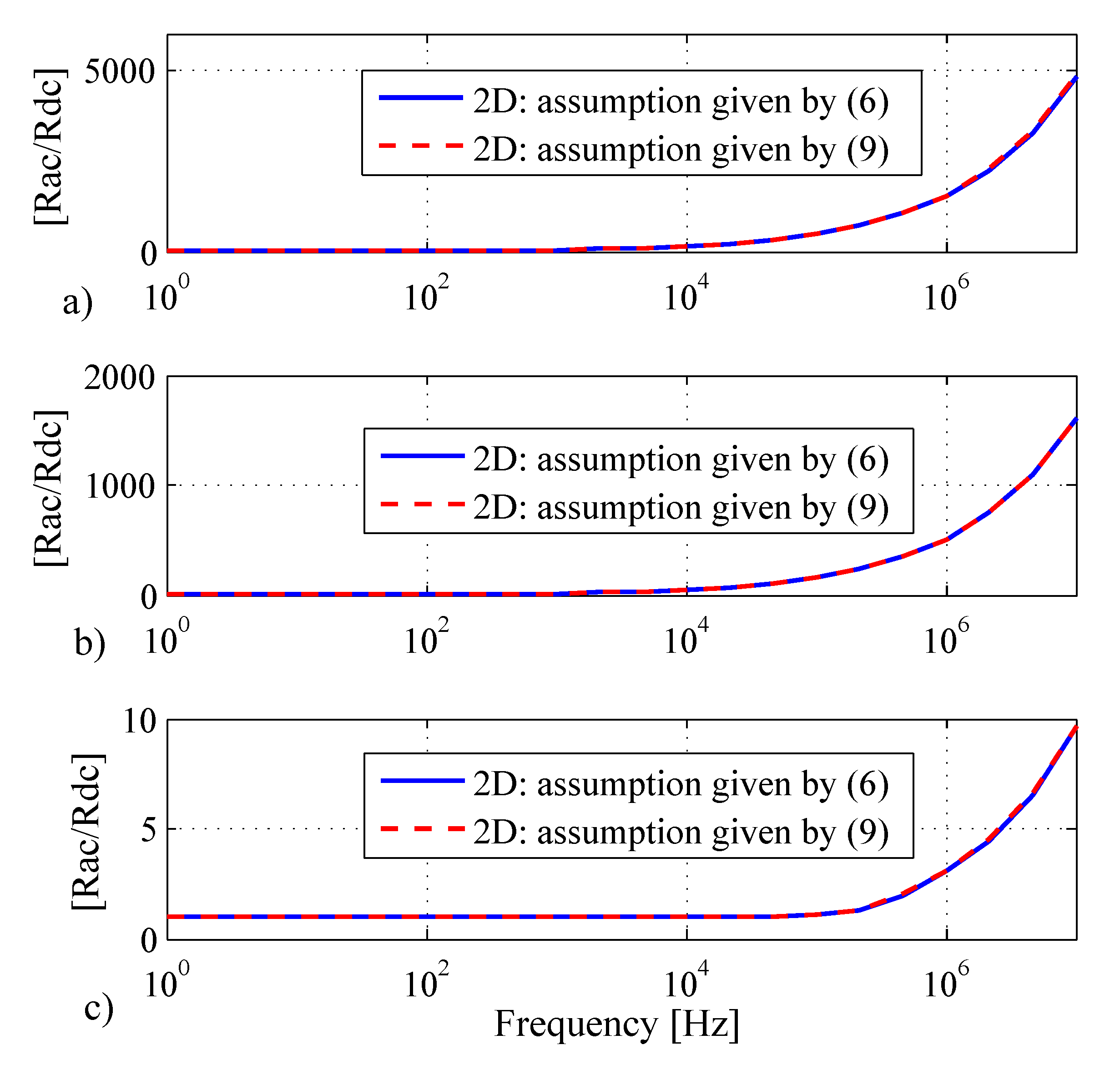
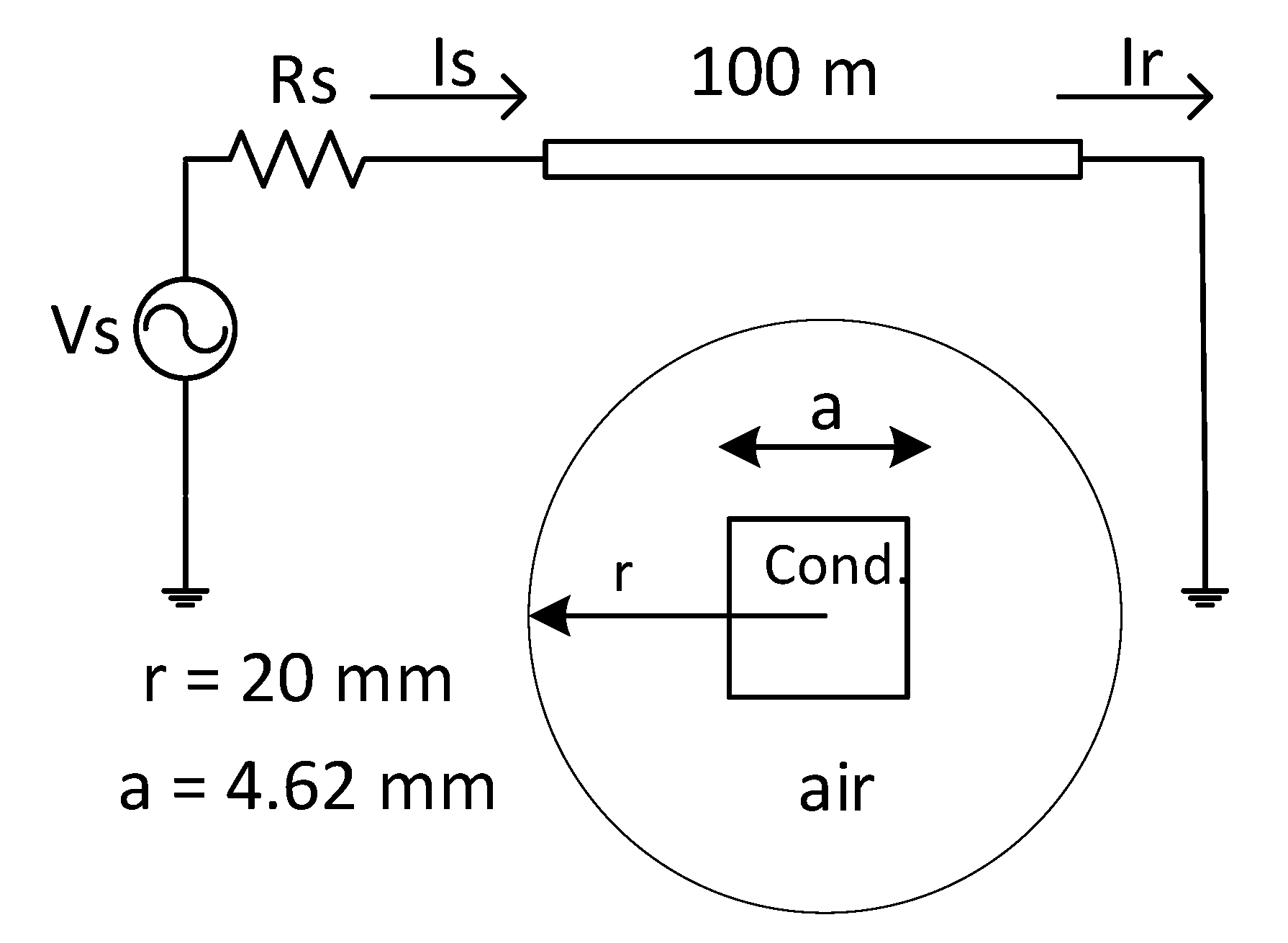
- Case 1: mm, , and S/m.
- Case 2: mm, , and S/m.
- Case 3: mm, , and [40].
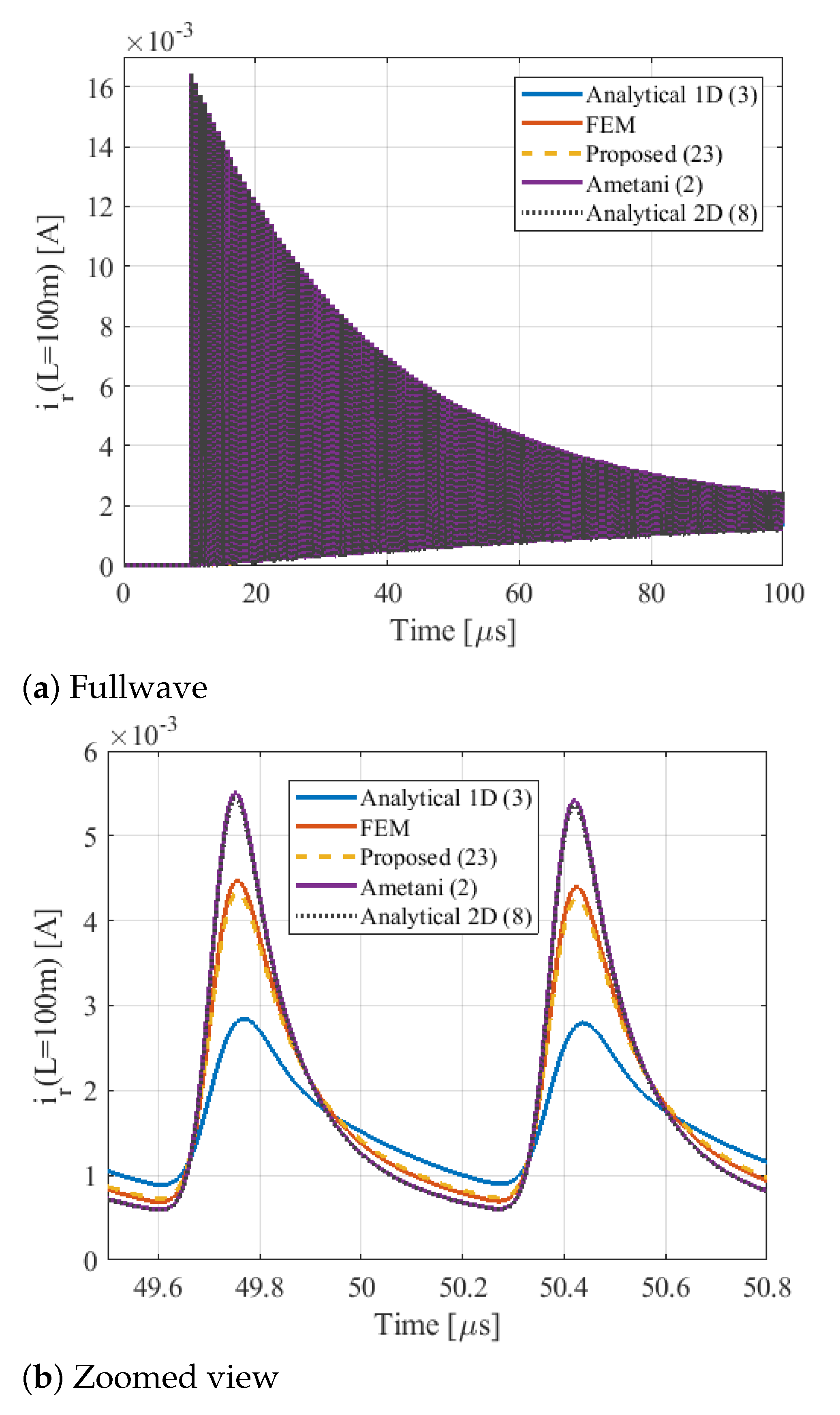
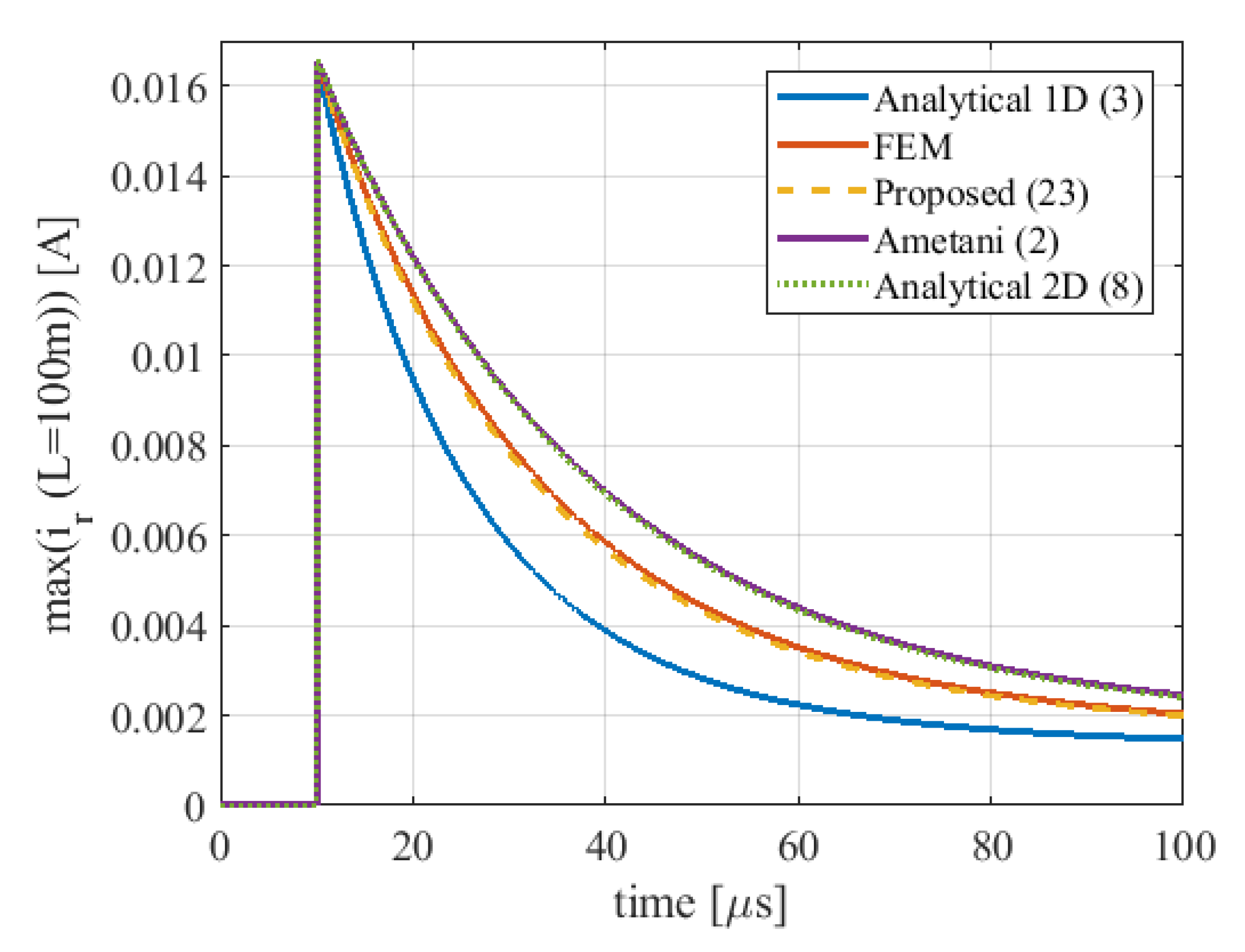
5. Transient Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Two-Dimensional Analytical Calculations of The Ac Resistance of Rectangular Conductors
Appendix A.1. Calculation of Current Density Distribution
Appendix A.2. Ac Resistance Calculation
References
- Shintemirov, A.; Tang, W.H.; Wu, Q.H. A hybrid winding model of disc-type power transformers for frequency response analysis. IEEE Trans. Power Deliv. 2009, 24, 730–739. [Google Scholar] [CrossRef]
- Mitchell, S.D.; Welsh, J.S. Modeling power transformers to support the interpretation of frequency-response analysis. IEEE Trans. Power Deliv. 2011, 26, 2705–2717. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Y.; Li, H.; Lin, F. Diagnosis of transformer winding faults based on FEM simulation and on-site experiments. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3752–3760. [Google Scholar] [CrossRef]
- Bigdeli, M.; Siano, P.; Alhelou, H.H. Intelligent classifiers in distinguishing transformer faults using frequency response analysis. IEEE Access 2021, 9, 13981–13991. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Pourhossein, K.; Mohammadi-Ivatloo, B.; Mohammadi, F. Locating inter-turn faults in transformer windings using isometric feature mapping of frequency response traces. IEEE Trans. Ind. Inform. 2021, 17, 6962–6970. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Moayyed, H.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B.; Aguiar, A.P. Turn-to-turn short circuit fault localization in transformer winding via image processing and deep learning method. IEEE Trans. Ind. Inform. 2021, 3203, 1–10. [Google Scholar] [CrossRef]
- Abu-Siada, A.; Mosaad, M.I.; Kim, D.; El-Naggar, M.F. Estimating power transformer high frequency model parameters using frequency response analysis. IEEE Trans. Power Deliv. 2020, 35, 1267–1277. [Google Scholar] [CrossRef]
- Electrical Transient Interaction between Transformers and the Power System—Part 1: Expertise. Available online: http://xmlopez.webs.uvigo.es/Html/Info/2014ElectricalTransientsPart1Expertise.pdf (accessed on 15 November 2021).
- Fuhr, J.; Haessig, M.; Boss, P.; Tschudi, D.; King, R.A. Detection and location of internal defects in the insulation of power transformers. IEEE Trans. Electr. Insul. 1993, 28, 1057–1067. [Google Scholar] [CrossRef]
- Jafari, A.M.; Akbari, A. Partial discharge localization in transformer windings using multi-conductor transmission line model. Electr. Power Syst. Res. 2008, 78, 1028–1037. [Google Scholar] [CrossRef]
- Naderi, M.S.; Vakilian, M.; Blackburn, T.R.; Phung, B.T.; Naderi, M.S.; Nasiri, A. A hybrid transformer model for determination of partial discharge location in transformer winding. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 436–443. [Google Scholar] [CrossRef]
- Akbari, A.; Werle, P.; Borsi, H.; Gockenbach, E. Transfer function-based partial discharge localization in power transformers: A feasibility study. IEEE Electr. Insul. Mag. 2002, 18, 22–32. [Google Scholar] [CrossRef]
- Bjerkan, E.; Høidalen, H.K. High frequency FEM-based power transformer modeling: Investigation of internal stresses due to network-initiated overvoltages. Electr. Power Syst. Res. 2007, 77, 1483–1489. [Google Scholar] [CrossRef]
- Gunawardana, M.; Fattal, F.; Kordi, B. Very fast transient analysis of transformer winding using axial multiconductor transmission line theory and finite element method. IEEE Trans. Power Deliv. 2019, 34, 1948–1956. [Google Scholar] [CrossRef]
- Kane, M.M.; Kulkarni, S.V. MTL-based analysis to distinguish high-frequency behavior of interleaved windings in power transformers. IEEE Trans. Power Deliv. 2013, 28, 2291–2299. [Google Scholar] [CrossRef]
- Stoyanov, L.; Lazarov, V.; Zarkov, Z.; Popov, E. Influence of skin effect on stator windings resistance of AC machines for electric drives. In Proceedings of the 2019 16th Conference on Electrical Machines, Drives and Power Systems (ELMA), Varna, Bulgaria, 6–8 June 2019; pp. 1–6. [Google Scholar]
- Gerling, D. Approximate analytical calculation of the skin effect in rectangular wires. In Proceedings of the 2009 International Conference on Electrical Machines and Systems, Tokyo, Japan, 15–18 November 2009; pp. 1–6. [Google Scholar]
- Morisco, D.P.; Kurz, S.; Rapp, H.; Möckel, A. A hybrid modeling approach for current diffusion in rectangular conductors. IEEE Trans. Magn. 2019, 55, 1–11. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Mao, L.; Zhang, Y. A Simple Analytical Technique for Evaluating the 2-D Conductive Losses in Isolated Rectangular Conductor. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1245–1249. [Google Scholar]
- Barbini, N.; Colavitto, A.; Vicenzutti, A.; Contin, A.; Sulligoi, G. High Frequency Modeling of Foil Type Transformers for Shipboard Power Electronic Power Distribution Systems. In Proceedings of the 2019 AEIT International Annual Conference (AEIT), Florence, Italy, 18–20 September 2019; pp. 1–6. [Google Scholar]
- De León, F.; Gómez, P.; Martinez-Velasco, J.A.; Rioual, M. Transformers. In Power System Transients: Parameter Determination; Martinez-Velasco, J.A., Ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 177–250. [Google Scholar]
- Lammeraner, J.; Stafl, M. Eddy Currents; Iliffe Books Ltd.: London, UK, 1966. [Google Scholar]
- Stoll, R.L. The Analysis of Eddy Currents; Oxford University Press: Oxford, UK, 1974. [Google Scholar]
- De Leon, F.; Semlyen, A. Time domain modeling of eddy current effects for transformer transients. IEEE Trans. Power Deliv. 1993, 8, 271–280. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, J.A. Improved analytical modeling of conductive losses in magnetic components. IEEE Trans. Power Electron. 1994, 9, 127–131. [Google Scholar] [CrossRef]
- Perry, M.P. Multiple layer series connected winding design for minimum losses. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 116–123. [Google Scholar] [CrossRef]
- Dowell, P. Effects of eddy currents in transformer windings. Proc. Inst. Electr. Eng. 1966, 113, 1387–1394. [Google Scholar] [CrossRef]
- Islam, M.S.; Husain, I.; Ahmed, A.; Sathyan, A. Asymmetric bar winding for high-speed traction electric machines. IEEE Trans. Transp. Electrif. 2020, 6, 3–15. [Google Scholar] [CrossRef]
- Pyrhönen, J.; Jokinen, T.; Hrabovcová, V. Design of Rotating Electrical Machines, 2nd ed.; Wiley: Chichester, UK, 2014. [Google Scholar]
- Ametani, A.; Fuse, I. Approximate method for calculating impedance of multiconductor with arbitrary cross-section. Electr. Eng. Jpn. 1991, 111-B, 896–902. [Google Scholar] [CrossRef]
- Ametani, A.; Ohno, T. Transmission Line Theories for the Analysis of Electromagnetic Transients in Coil Windings. In Electromagnetic Transients in Transformer and Rotating Machine Windings; Su, Q., Ed.; IGI Global: Hershey, PA, USA, 2013; pp. 1–44. [Google Scholar]
- Asada, T.; Baba, Y.; Nagaoka, N.; Ametani, A.; Mahseredjian, J.; Yamamoto, K. A study on basic characteristics of the proximity effect on conductors. IEEE Trans. Power Deliv. 2017, 32, 1790–1799. [Google Scholar] [CrossRef]
- Schelkunoff, S.A. The electromagnetic theory of coaxial transmission lines and cylindrical shields. Bell Syst. Tech. J. 1934, 13, 532–579. [Google Scholar] [CrossRef]
- IEC 60287-1-1; Electric Cables—Calculation of Current Rating—Part 1: Current Rating Equations (100% Load Factor) and Calculation of Losses—Section 1: General. International Electrotechnical Commission: Geneva, Switzerland, 2001.
- Riba, J.R. Analysis of formulas to calculate the AC resistance of different conductors configurations. Electr. Power Syst. Res. 2015, 127, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Liang, G.; Sun, H.; Zhang, X.; Cui, X. Modeling of transformer windings under very fast transient overvoltages. IEEE Trans. Electromagn. Compat. 2006, 48, 621–627. [Google Scholar] [CrossRef]
- De Leon, F.; Semlyen, A. Detailed modeling of eddy current effects for transformer transients. IEEE Trans. Power Deliv. 1994, 9, 1143–1150. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Tang, W.H.; Ji, T.Y.; Wu, Q.H. Finite-element modeling for analysis of radial deformations within transformer windings. IEEE Trans. Power Deliv. 2014, 29, 2297–2305. [Google Scholar] [CrossRef]
- Costache, G.I. Finite element method applied to skin-effect Problems in strip transmission lines. IEEE Trans. Microw. Theory Tech. 1987, 35, 1009–1013. [Google Scholar] [CrossRef]
- Tsuk, M.; Kong, J. A hybrid method for the calculation of the resistance and inductance of transmission lines with arbitrary cross sections. IEEE Trans. Microw. Theory Tech. 1991, 39, 1338–1347. [Google Scholar] [CrossRef]
- Antonini, G.; Orlandi, A.; Paul, C.R. Internal impedance of conductors of rectangular cross section. IEEE Trans. Microw. Theory Tech. 1999, 47, 979–985. [Google Scholar] [CrossRef]
- Preis, K.; Renhart, W.; Rabel, A.; Bíró, O. Transient behavior of large transformer windings taking capacitances and eddy currents into account. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Goddard, K.F.; Roy, A.A.; Sykulski, J.K. Inductance and resistance calculations for a pair of rectangular conductors. IEE Proc. Sci. Meas. Technol. 2005, 152, 73–78. [Google Scholar] [CrossRef] [Green Version]
- Warne, L.K. Eddy current power dissipation at sharp corners: Rectangular conductor examples. Electromagnetics 1995, 15, 273–290. [Google Scholar] [CrossRef]
- Tabei, B.; Ametani, A.; Gole, A.M.; Kordi, B. A Study on AC Resistance Calculation of Single Rectangular Conductors. In Proceedings of the Annual IEEE Canada Electrical Power and Energy Conference (EPEC2021), Toronto, ON, Canada, 22–31 October 2021; pp. 1–4. [Google Scholar]
- Harrington, R.F. Time-Harmonic Electromagnetic Fields; IEEE Press: Piscataway, NJ, USA, 2001. [Google Scholar]
- Larsson, J. Electromagnetics from a quasistatic perspective. Am. J. Phys. 2007, 75, 230–239. [Google Scholar] [CrossRef] [Green Version]
- Tabei, B.; Ametani, A.; Gole, A.M.; Kordi, B. Study of Skin and Proximity Effects of Conductors for MTL-Based Modeling of Power Transformers Using FEM. In Proceedings of the 2020 IEEE Power Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Chapra, S.C. Applied Numerical Methodes with MATLAB for Engineers and Scientists; MC Graw Hill: Natick, MA, USA, 2012. [Google Scholar]
- Paul, C.R. Analysis of Multiconductor Transmission Lines, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kordi, B.; LoVetri, J.; Bridges, G. Finite-difference analysis of dispersive transmission lines within a circuit simulator. IEEE Trans. Power Deliv. 2006, 21, 234–242. [Google Scholar] [CrossRef]
- Hillen, T.; Leonard, I.E.; Roessel, H.V. Partial Differential Equations, Theory and Completely Solved Equations; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabei, B.; Ametani, A.; Gole, A.M.; Kordi, B. Quasi-Analytical Calculation of Frequency-Dependent Resistance of Rectangular Conductors Considering the Edge Effect. Energies 2022, 15, 503. https://doi.org/10.3390/en15020503
Tabei B, Ametani A, Gole AM, Kordi B. Quasi-Analytical Calculation of Frequency-Dependent Resistance of Rectangular Conductors Considering the Edge Effect. Energies. 2022; 15(2):503. https://doi.org/10.3390/en15020503
Chicago/Turabian StyleTabei, Barzan, Akihiro Ametani, Aniruddha M. Gole, and Behzad Kordi. 2022. "Quasi-Analytical Calculation of Frequency-Dependent Resistance of Rectangular Conductors Considering the Edge Effect" Energies 15, no. 2: 503. https://doi.org/10.3390/en15020503
APA StyleTabei, B., Ametani, A., Gole, A. M., & Kordi, B. (2022). Quasi-Analytical Calculation of Frequency-Dependent Resistance of Rectangular Conductors Considering the Edge Effect. Energies, 15(2), 503. https://doi.org/10.3390/en15020503







