Multiobjective Optimal Control of Wind Turbines: A Survey on Methods and Recommendations for the Implementation
Abstract
:1. Introduction
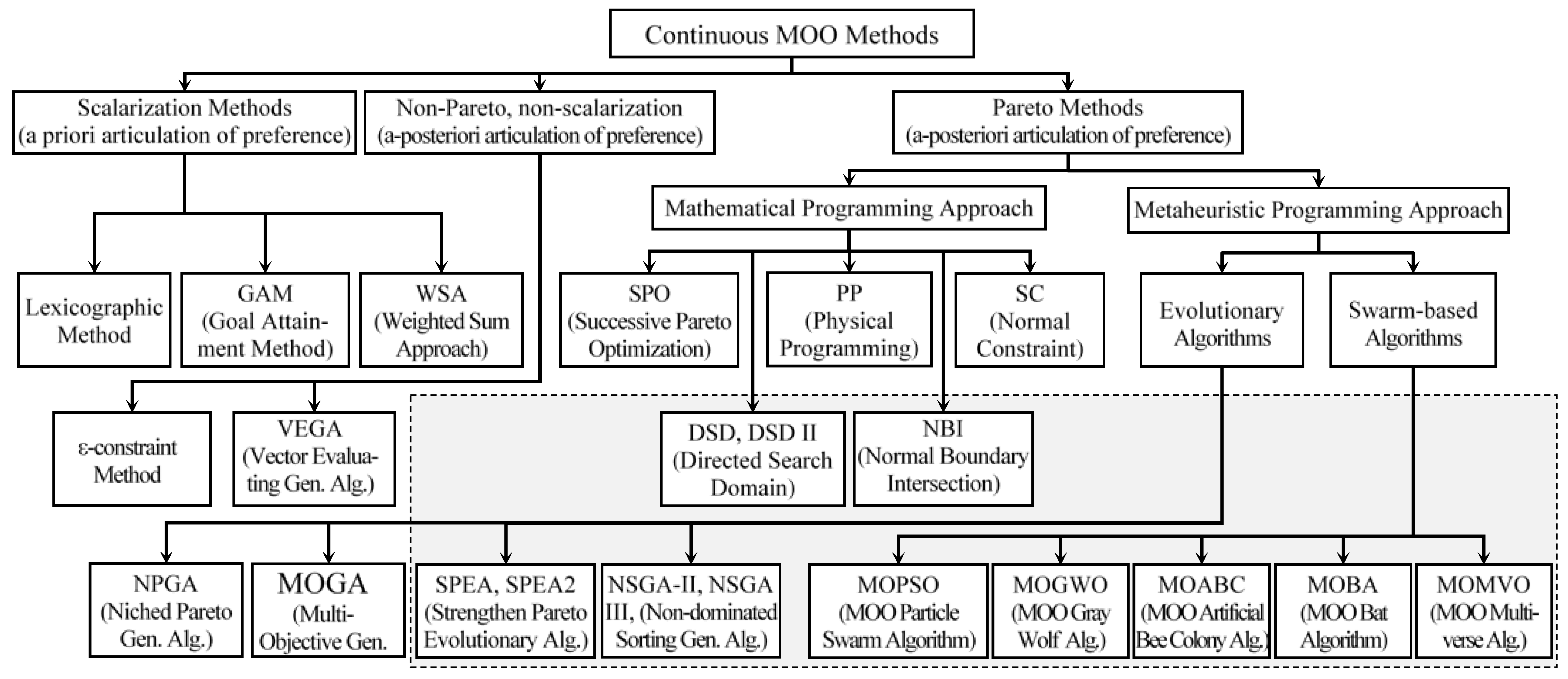
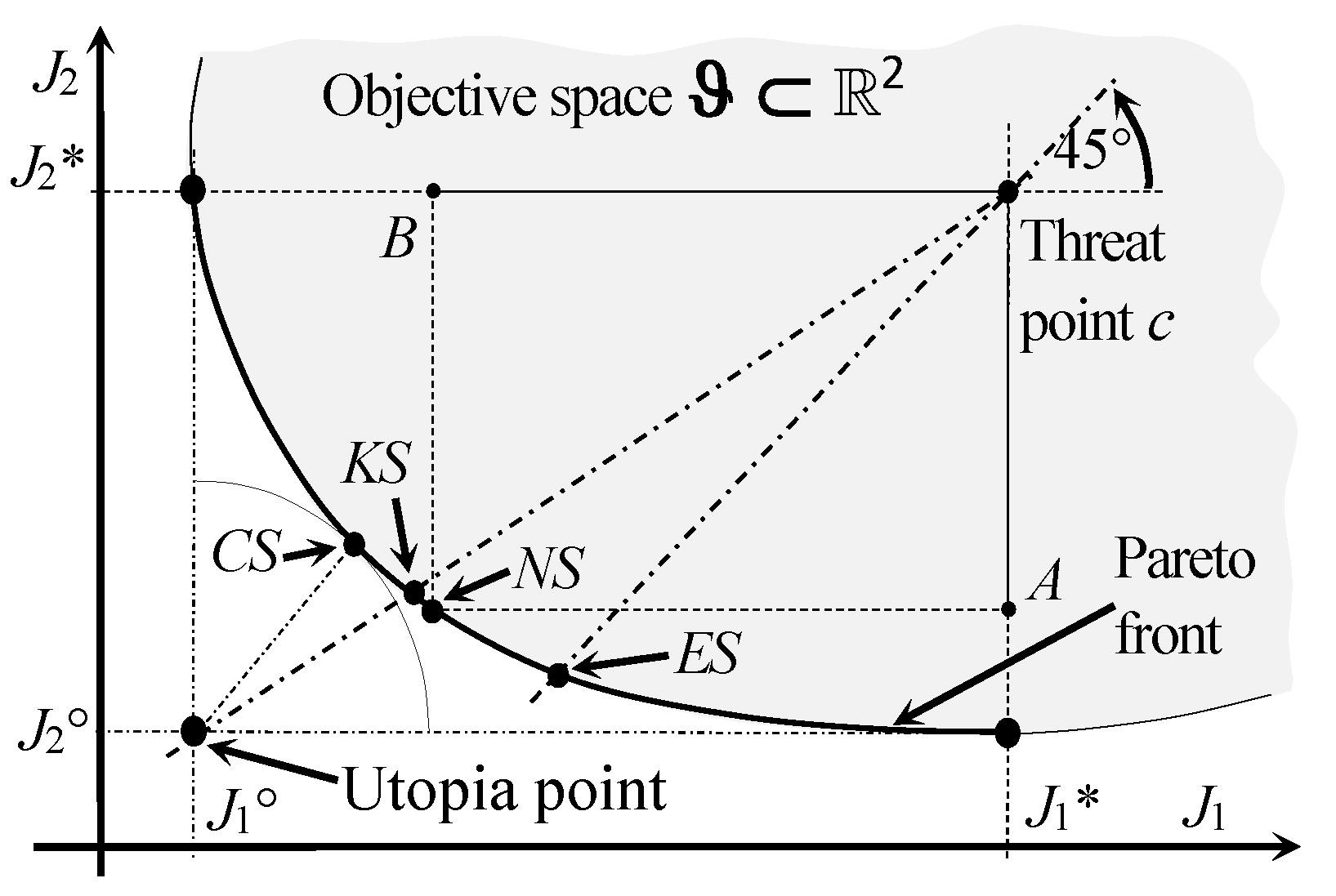
2. Some Fundamentals on Multiobjective Optimization
2.1. Definitions
| to find | α = [α1 … α np]T or u = [u1 … ul]T, |
| optimizing | J(u,α) = [J1(u,α) … Jnf(u,α)]T |
| with respect to | α or to u |
| subject to | gi(u,α) ≤ 0 and hj(u,α) = 0, |
| for | i = 1, …, ng, j = 1, …, nh, |
2.2. Methods Founded on the Mathematical Programming
2.3. Methods Founded on the Metaheuristic Programming
2.4. Methods for Bilevel Multiobjective Optimization Problems
2.5. Selecting Methods for the Application
3. Objective Functions for MOO Control Problems
3.1. Typical Performance Indices
3.2. Performance Indices for Time-Limited Problems
3.3. Performance Indices Formulated Using Fractional Order Calculus
3.4. Objective Functions for Specific Applications
4. Evaluation of Objective Functions
4.1. Evaluation of Objective Functions Based on Dynamic Models
4.2. Evaluation Based on Simulation Data
5. Decision-Making
5.1. Approach Using Additional Control Criteria
5.2. Approach Using a Compromise between the Criteria
6. Application Study
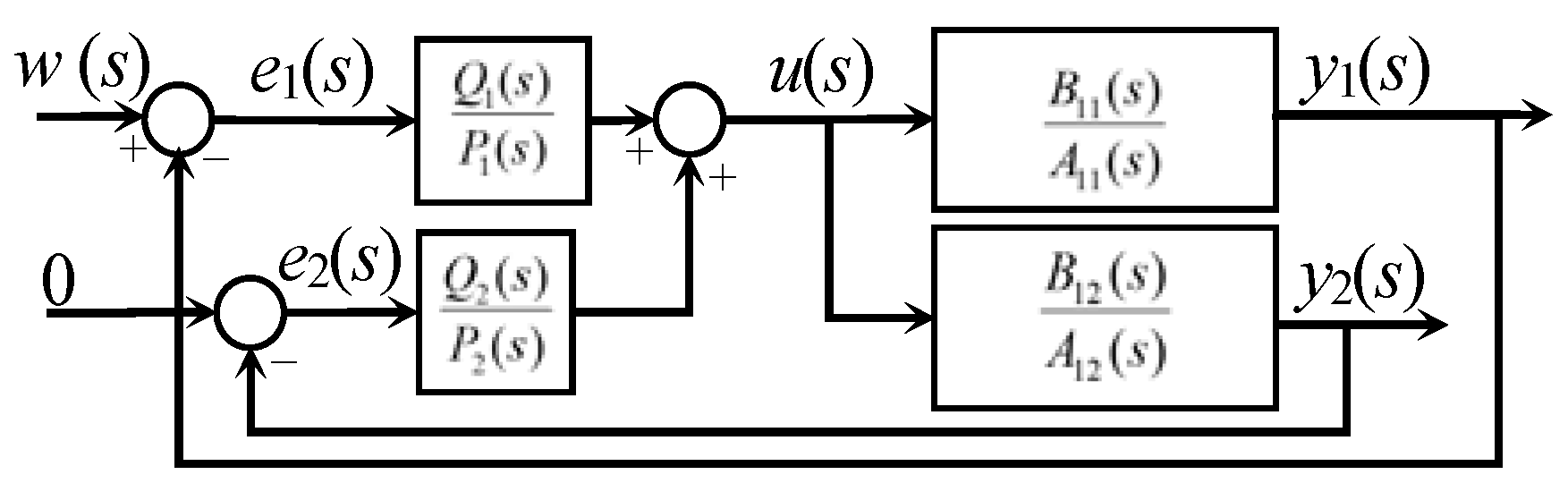
6.1. Description of the Application and the Control Problem
6.2. Simplified Model of the System
6.3. Mechanization of the Optimization Procedure
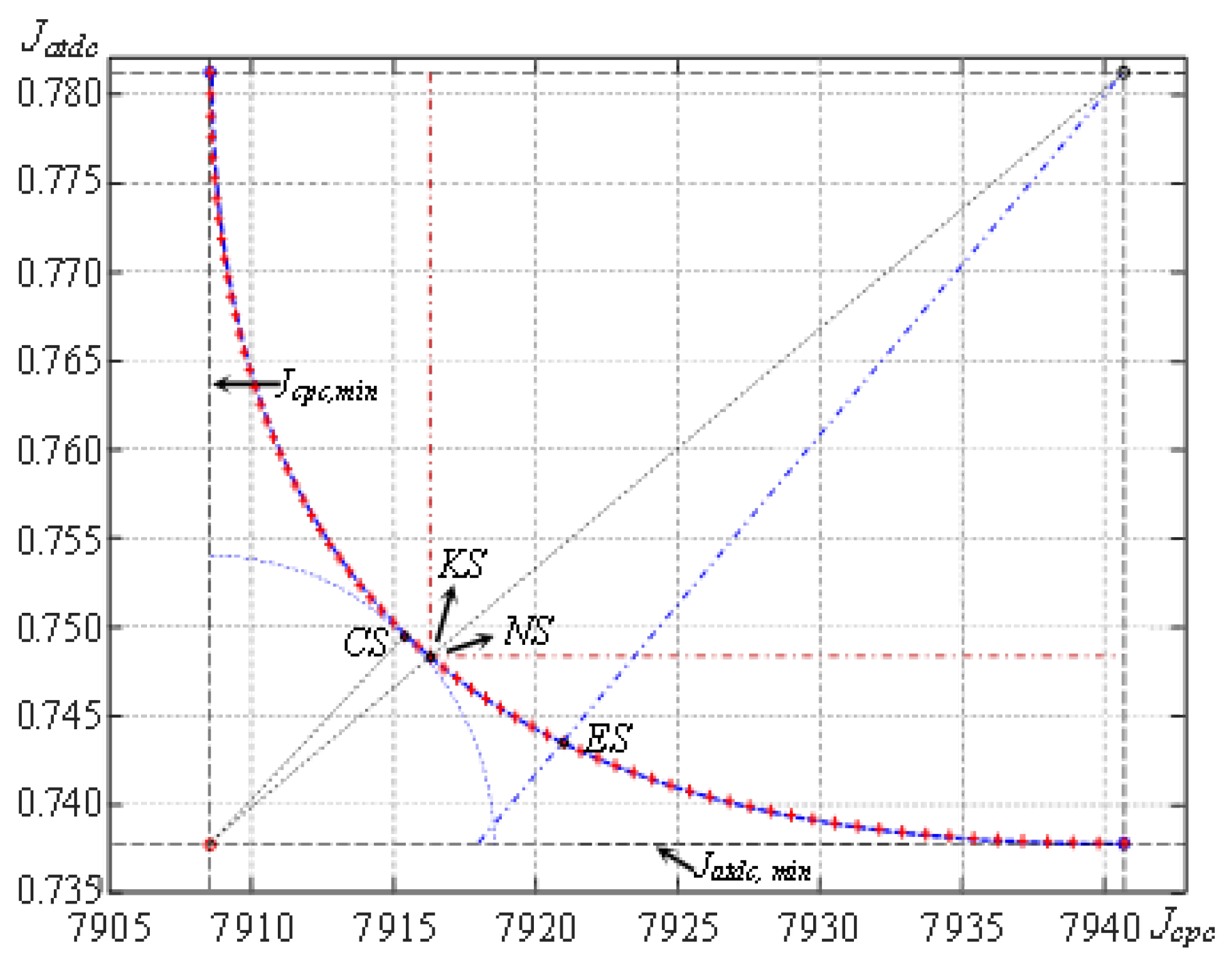
7. Optimization Results
7.1. Evaluation Procedure for the MOO Algorithms
7.2. Assessment of Results
7.3. Important Issues Emerging from Practical Experience
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, G.P.; Yang, J.B.; Whidborne, J.F. Multiobjective Optimisation and Control; Research Studies Press Ltd.: Exeter, UK, 2003. [Google Scholar]
- Gambier, A.; Badreddin, E. Multi-objective optimal control: An overview. In Proceedings of the IEEE Conference on Control Applications, Singapore, 1–3 October 2007; pp. 170–175. [Google Scholar]
- Gambier, A. MPC and PID control based on multi-objective optimization. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 2886–2891. [Google Scholar]
- Gambier, A.; Jipp, M. Multi-objective optimal control: An introduction. In Proceedings of the Asian Control Conference, Kaohsiung, Taiwan, 15–18 May 2011; pp. 1084–1089. [Google Scholar]
- Reynoso-Meza, G.; Ferragud, X.B.; Saez, J.S.; Durá, J.M.H. Controller Tuning with Evolutionary Multiobjective Optimization: A Holistic Multiobjective Optimization Design Procedure, 1st ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Peitz, S.; Dellnitz, M. A survey of recent trends in multiobjective optimal control—Surrogate models, feedback control and objective reduction. Math. Comput. Appl. 2018, 23, 30. [Google Scholar] [CrossRef] [Green Version]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Eichfelder, G. Multiobjective bilevel optimization. Math. Program. 2010, 123, 419–449. [Google Scholar] [CrossRef]
- Liang, J.Z.; Miikkulainen, R. Evolutionary bilevel optimization for complex control tasks. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 871–878. [Google Scholar]
- Gambier, A. Multiobjective Optimal Control: Algorithms, Approaches and Advice for the Application. In Proceedings of the 2020 International Automatic Control Conference, Hsinchu, Taiwan, 4–7 November 2020; pp. 1–7. [Google Scholar]
- Pareto, V. Manuale di Economia Politica; Societa Editrice Libraria: Milan, Italy, 1906; (Translated into English by A. S. Schwier as Manual of Political Economy, Macmillan, New York, 1971). [Google Scholar]
- Miettinen, K.M. Nonlinear Multiobjective Optimization, 4th ed.; Kluwer Academic Publishers: New York, NY, USA, 2004. [Google Scholar]
- de Weck, O.L. Multiobjective optimization: History and promise. In Proceedings of the 3rd China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kanazawa, Japan, 30 October–2 November 2004; pp. 1–14. [Google Scholar]
- Das, I.; Dennis, J.E. Normal-Boundary Intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Coello, C.A.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on the Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; pp. 1051–1056. [Google Scholar]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; Research Report; Swiss Federal Institute of Technology (ETH): Zurich, Switzerland, 2001. [Google Scholar]
- Motta, R.S.; Afonso, S.M.; Lyra, P.R. A modified NBI and NC method for the solution of N-multiobjective optimization problems. Struct. Multidiscip. Optim. 2012, 46, 239–259. [Google Scholar] [CrossRef]
- Erfani, T.; Utyuzhnikov, S.V. Directed Search Domain: A Method for even generation of Pareto frontier in multiobjective optimization. J. Eng. Optim. 2010, 43, 1–17. [Google Scholar] [CrossRef]
- Angus, D.; Woodward, C. Multiple objective ant colony optimisation. Swarm Intell. 2009, 3, 69–85. [Google Scholar] [CrossRef]
- Akbari, R.; Hedayatzadeh, R.; Ziarati, K.; Hassanizadeh, B. A multi-objective artificial bee colony algorithm. Swarm Evol. Comput. 2012, 2, 39–52. [Google Scholar] [CrossRef]
- Yang, X.S. Bat algorithm for multi-objective optimisation. Int. J. Bio-Inspired Comput. 2011, 3, 267–274. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with Box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.d.S. Multi-objective grey wolf optimizer: A novel algorithm for multicriterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Mirjalili, S.Z.; Saremi, S.; Trivedi, I.N. Optimization of problems with multiple objectives using the multi-verse optimization algorithm. Knowl.-Based Syst. 2017, 134, 50–71. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-objective ant lion optimizer: A multi-objective optimization algorithm for solving engineering problems. Appl. Intell. 2017, 46, 79–95. [Google Scholar] [CrossRef]
- Messac, A.; Mattson, C. Normal constraint method with guarantee of even representation of complete Pareto frontier. AIAA J. 2004, 42, 2101–2111. [Google Scholar] [CrossRef] [Green Version]
- Messac, A. Physical programming: Effective optimization for computational de sign. AIAA J. 1996, 34, 149–158. [Google Scholar] [CrossRef]
- Mueller-Gritschneder, D.; Graeb, H.; Schlichtmann, U. A successive approach to compute the bounded Pareto front of practical multiobjective optimization problems. SIAM J. Optim. 2009, 20, 915–934. [Google Scholar] [CrossRef]
- Kunkle, D. A Summary and Comparison of MOEA Algorithms; Research Report; College of Computer and Information Science Northeastern University: Boston, MA, USA, 2005. [Google Scholar]
- Grimme, C.; Schmitt, K. Inside a predator-prey model for multiobjective optimization: A second study. In Proceedings of the Genetic and Evolutionary Computation Conference, Seattle, WA, USA, 8–12 July 2006; pp. 707–714. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls, 1st ed.; Springer: London, UK, 2010. [Google Scholar]
- Das, S.; Pan, I.; Halder, K.; Das, S.; Gupta, A. LQR based improved discrete PID controller design via optimum selection of weighting matrices using fractional order integral performance index. Appl. Math. Model. 2013, 37, 4253–4268. [Google Scholar] [CrossRef]
- Gambier, A. Evolutionary multiobjective optimization with fractional order integral objectives for the pitch control system design of wind turbines. IFAC-PapersOnLine 2019, 52, 274–279. [Google Scholar] [CrossRef]
- Romero, M.; de Madrid, A.P.; Vinagre, B.M. Arbitrary real-order cost functions for signals and systems. Signal Process. 2011, 91, 372–378. [Google Scholar] [CrossRef]
- Ortigueira, M.; Machado, J. Fractional definite integral. Fractal Fract. 2017, 1, 2. [Google Scholar] [CrossRef] [Green Version]
- Valério, D.; Sá da Costa, J. Ninteger: A non-integer control toolbox for MatLab. In Proceedings of the First IFAC Workshop on Fractional Differentiation and Applications, Bordeaux, France, 19–21 July 2004; pp. 208–213. [Google Scholar]
- Xue, D. FOTF toolbox for fractional-order control systems. In Volume 6 Applications in Control; Petráš, I., Ed.; De Gruyter: Berlin, Germany, 2019; Volume 6, pp. 237–266. [Google Scholar]
- Alamir, M.; Collet, D.; Di Domenico, D.; Sabiron, G. A fatigue-oriented cost function for optimal individual pitch control of wind turbines. IFAC-PapersOnLine 2020, 52, 12632–12637. [Google Scholar]
- Gambier, A. Optimal PID controller design using multiobjective normal boundary intersection technique. In Proceedings of the 7th Asian Control Conference, Hong Kong, China, 27–29 August 2009; pp. 1369–1374. [Google Scholar]
- Åström, K. Introduction to Stochastic Control Theory; Academic Press: London, UK, 1970. [Google Scholar]
- Akhtar, T.; Shoemaker, C.A. Efficient Multi-Objective Optimization through Population-Based Parallel Surrogate Search; Research Report; National University of Singapore: Singapore, 2019. [Google Scholar]
- Wellenreuther, A.; Gambier, A.; Badreddin, E. Application of a game-theoretic multi-loop control system design with robust performance. IFAC Proc. Vol. 2008, 41, 10039–10044. [Google Scholar] [CrossRef]
- Gatti, N.; Amigoni, F. An approximate Pareto optimal cooperative negotiation model for multiple continuous dependent issues. In Proceedings of the 2005 IEEE/WIC/ACM International Conference on Intelligent Agent Technology, Compiègne, France, 19–22 October 2005; pp. 565–571. [Google Scholar]
- Thomson, W. Cooperative models of bargaining. In Handbook of Game Theory with Economic 2; Aumann, R.J., Hart, S., Eds.; Elsevier: Oxford, UK, 1994; pp. 1237–1284. [Google Scholar]
- Gambier, A. Simultaneous design of pitch control and active tower damping of a wind turbine by using multi-objective optimization. In Proceedings of the 1st IEEE Conference on Control Technology and Applications, Kohala Coast, HI, USA, 27–30 August 2017; pp. 1679–1684. [Google Scholar]
- Gambier, A.; Nazaruddin, Y. Collective pitch control with active tower damping of a wind turbine by using a nonlinear PID approach. IFAC–PapersOnLine 2018, 51, 238–243. [Google Scholar] [CrossRef]
- Ashuri, T.; Martins, J.R.R.; Zaaijer, M.B.; van Kuik, G.A.M.; van Bussel, G.J.W. Aeroservoelastic design definition of a 20 MW common research wind turbine model. Wind Energy 2016, 19, 2071–2087. [Google Scholar] [CrossRef]
- Gambier, A.; Meng, F. Control system design for a 20 MW reference wind turbine. In Proceedings of the 3rd. IEEE Conference on Control Technology and Application, Hong Kong, China, 19–21 August 2019; pp. 258–263. [Google Scholar]
- Zhuang, M.; Atherton, D.P. Tuning PID controllers with integral performance criteria. In Proceedings of the IEE Conference on Control 91, Edinburgh, UK, 25–28 March 1991; pp. 481–486. [Google Scholar]
- Wan, K.C.; Sreeram, V. Solution of bilinear matrix equation using Astrom-Jury-Agniel algorithm. IEE Proc. Part-D Control Theory Appl. 1995, 142, 603–610. [Google Scholar] [CrossRef]
- Riquelme, N.; von Lücken, C.; Baran, B. Performance metrics in multi-objective optimization. In Proceedings of the 2015 Latin American Computing Conference, Arequipa, Peru, 19–23 October 2015; pp. 1–11. [Google Scholar]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Grunert da Fonseca, V. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef] [Green Version]
- Coello Coello, C.A.; Cortés, N. Solving multiobjective optimization problems using an artificial immune system. Genet. Program. Evol. Mach. 2005, 6, 163–190. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. J. 2000, 8, 125–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Parameter | Variable | Values | Units |
|---|---|---|---|
| Rated power | P0 | 20 × 106 | W |
| Rated rotor speed | ωr0 | 0.7494 | rad/s |
| Rotor mass moment of inertia | Jr | 2919659264.0 | kg m2 |
| Generator mass moment of inertia | Jg | 7248.32 | kg m2 |
| Equivalent shaft damping | Ddt | 4.97 × 107 | Nm/rad |
| Equivalent shaft stiffness | Kdt | 6.94 × 109 | Nm/(rad/s) |
| Damping ratio of the drivetrain | ζdt | 5 | % |
| Mass of tower | mt | 1782947.0 | kg |
| First in-plane blade frequency | ft | 0.1561 | Hz |
| Damping ratio of the tower | ζt | 5 | % |
| Equivalent tower stiffness | Kt | 4 π2 ft2 mt | Nm/(m/s) |
| Equivalent tower damping | Dt | Nm/rad | |
| Gearbox ratio | nx | 164 | -- |
| Generator efficiency | ηg | 94.4 | % |
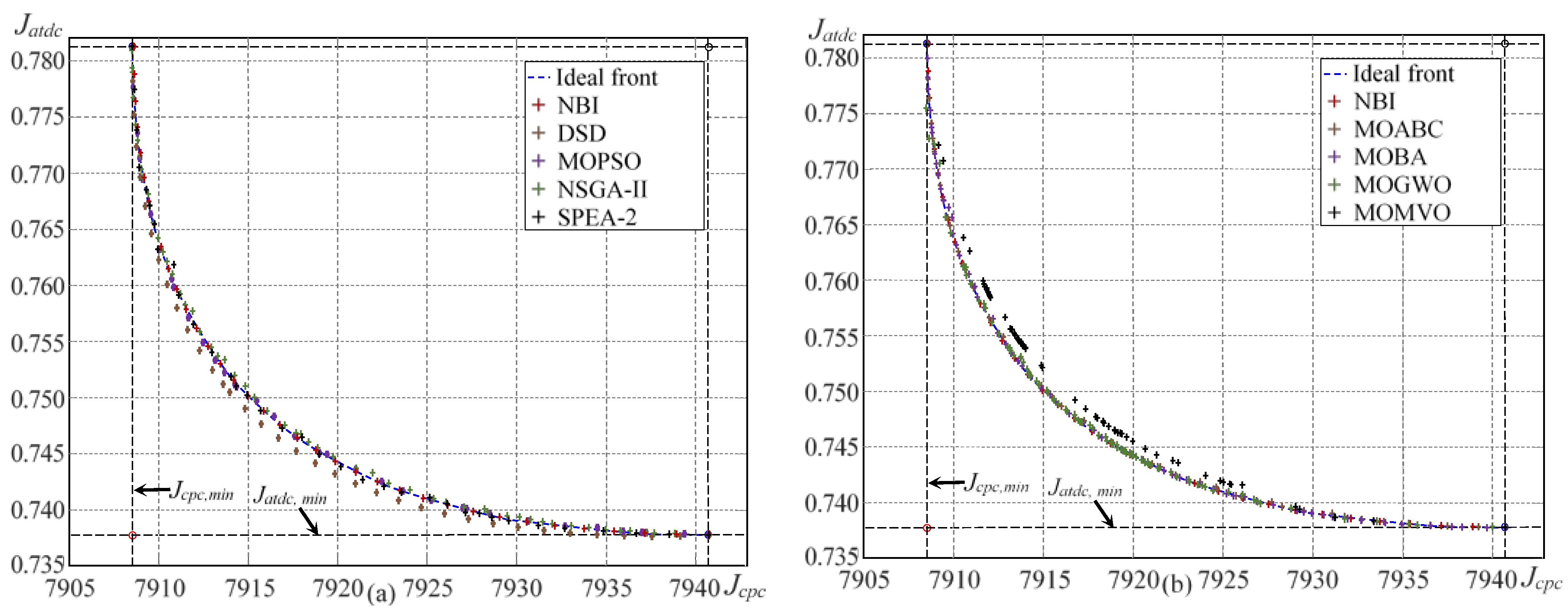
| Algorithm | Time [s] | Evaluations | IGD | SP | Epsilon |
|---|---|---|---|---|---|
| DSD | 3.2080 | 1200 | 0.1420 | 0.0531 | 0.0048 |
| MOABC | 14.7438 | 20243 | 0.0349 | 0.0137 | 2.7589 × 10−4 |
| MOBA | 6.9250 | 14070 | 0.0097 | 0.0031 | 2.0520 × 10−4 |
| MOGWO | 7.0332 | 14070 | 0.0562 | 0.0170 | 2.2919 × 10−4 |
| MOMVO | 11.0681 | 40000 | 0.1444 | 0.0146 | 1.3056 × 10−4 |
| MOPSO | 4.4882 | 14280 | 0.0196 | 0.0064 | 7.5852 × 10−5 |
| NBI | 1.9437 | 4134 | 0.0077 | 0.0025 | 6.8926 × 10−5 |
| NSGA-II | 2.9186 | 1200 | 0.0175 | 0.0056 | 3.1163 × 10−4 |
| SPEA-2 | 4.6237 | 14000 | 0.0108 | 0.0036 | 3.4632 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gambier, A. Multiobjective Optimal Control of Wind Turbines: A Survey on Methods and Recommendations for the Implementation. Energies 2022, 15, 567. https://doi.org/10.3390/en15020567
Gambier A. Multiobjective Optimal Control of Wind Turbines: A Survey on Methods and Recommendations for the Implementation. Energies. 2022; 15(2):567. https://doi.org/10.3390/en15020567
Chicago/Turabian StyleGambier, Adrian. 2022. "Multiobjective Optimal Control of Wind Turbines: A Survey on Methods and Recommendations for the Implementation" Energies 15, no. 2: 567. https://doi.org/10.3390/en15020567
APA StyleGambier, A. (2022). Multiobjective Optimal Control of Wind Turbines: A Survey on Methods and Recommendations for the Implementation. Energies, 15(2), 567. https://doi.org/10.3390/en15020567





