Numerical Investigation of Jet Control Using Two Pulsed Jets under Different Amplitudes
Abstract
:1. Introduction
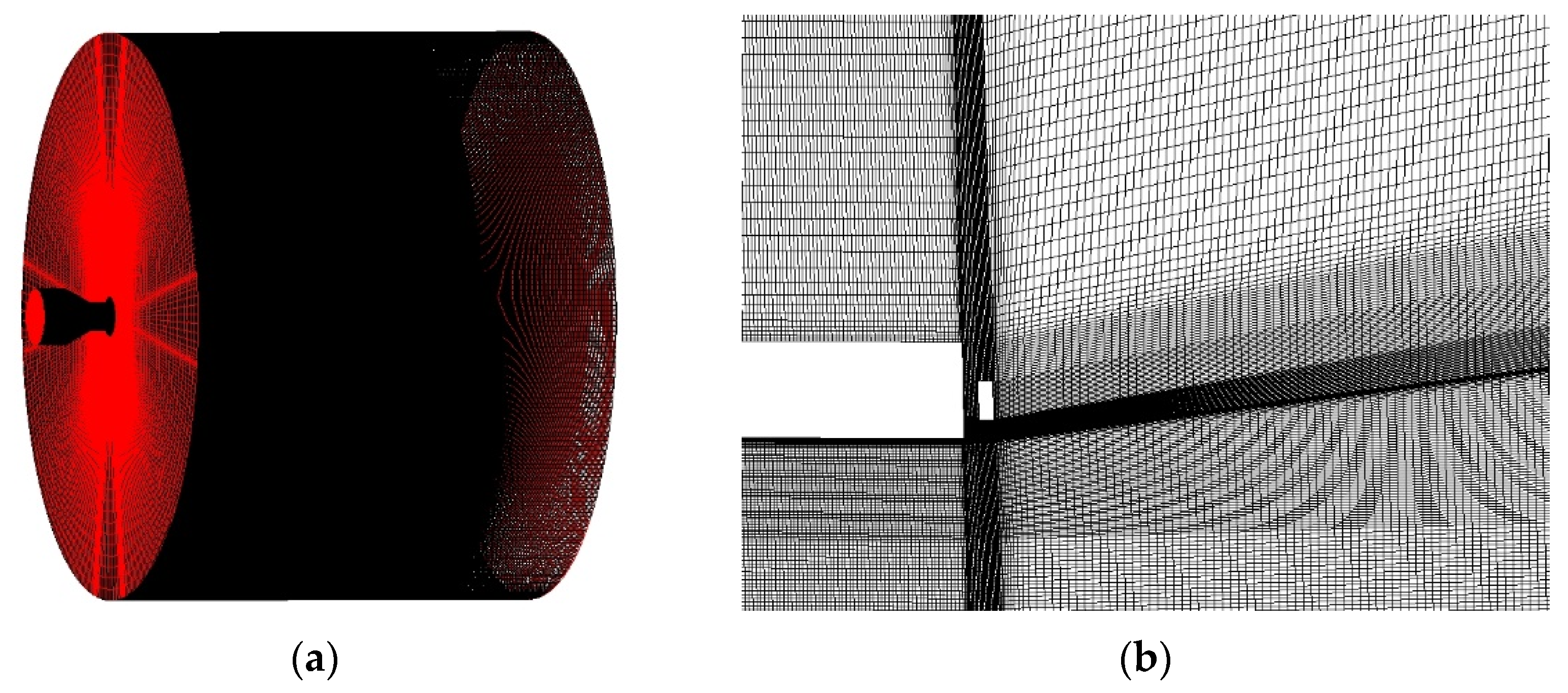
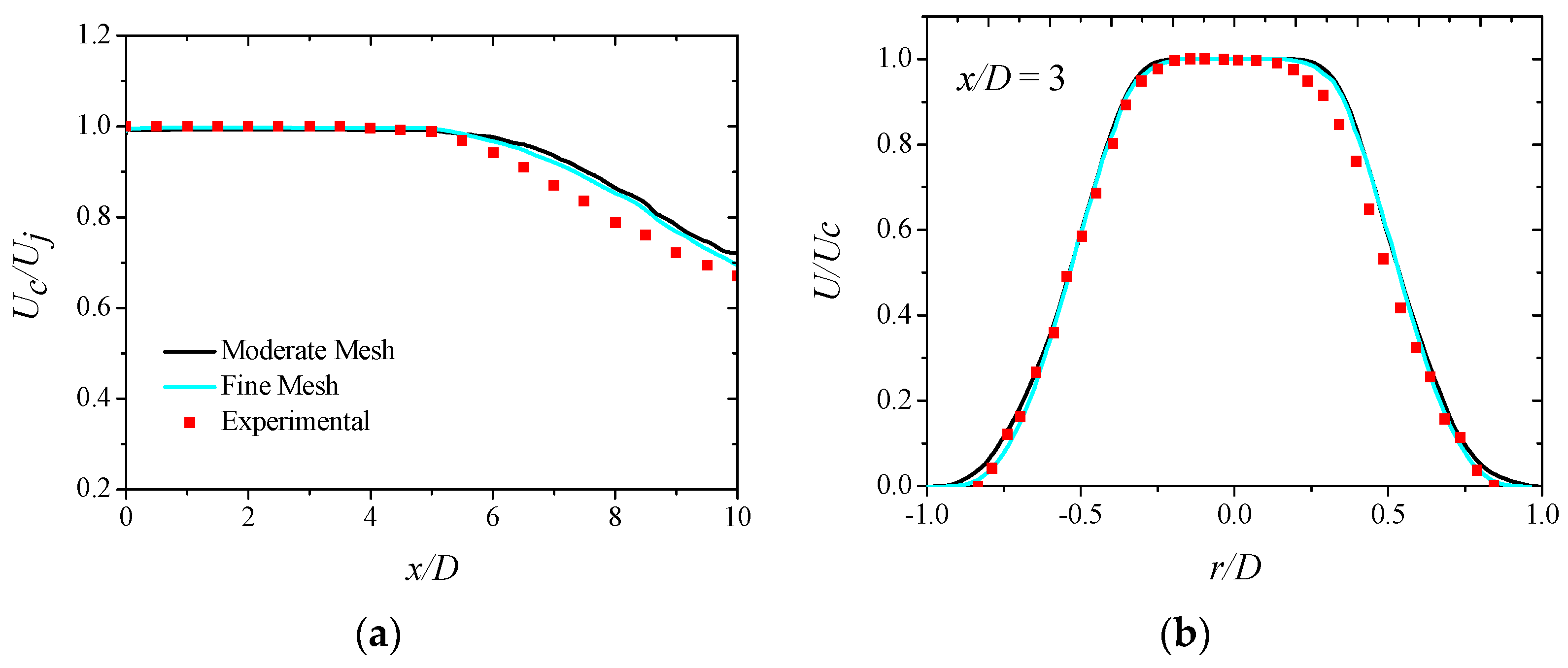
2. Computational Setup
3. Results and Discussion
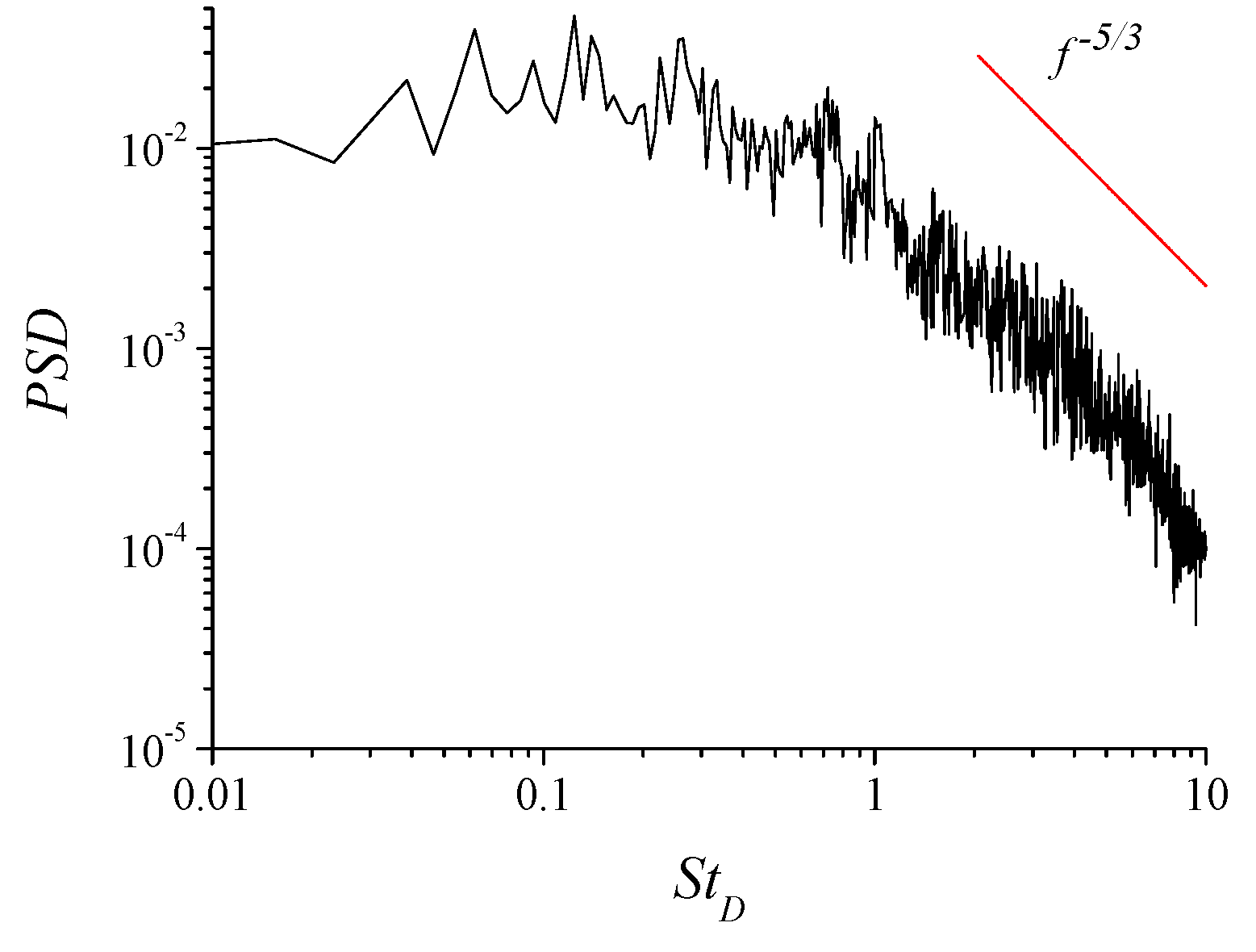
3.1. No Control
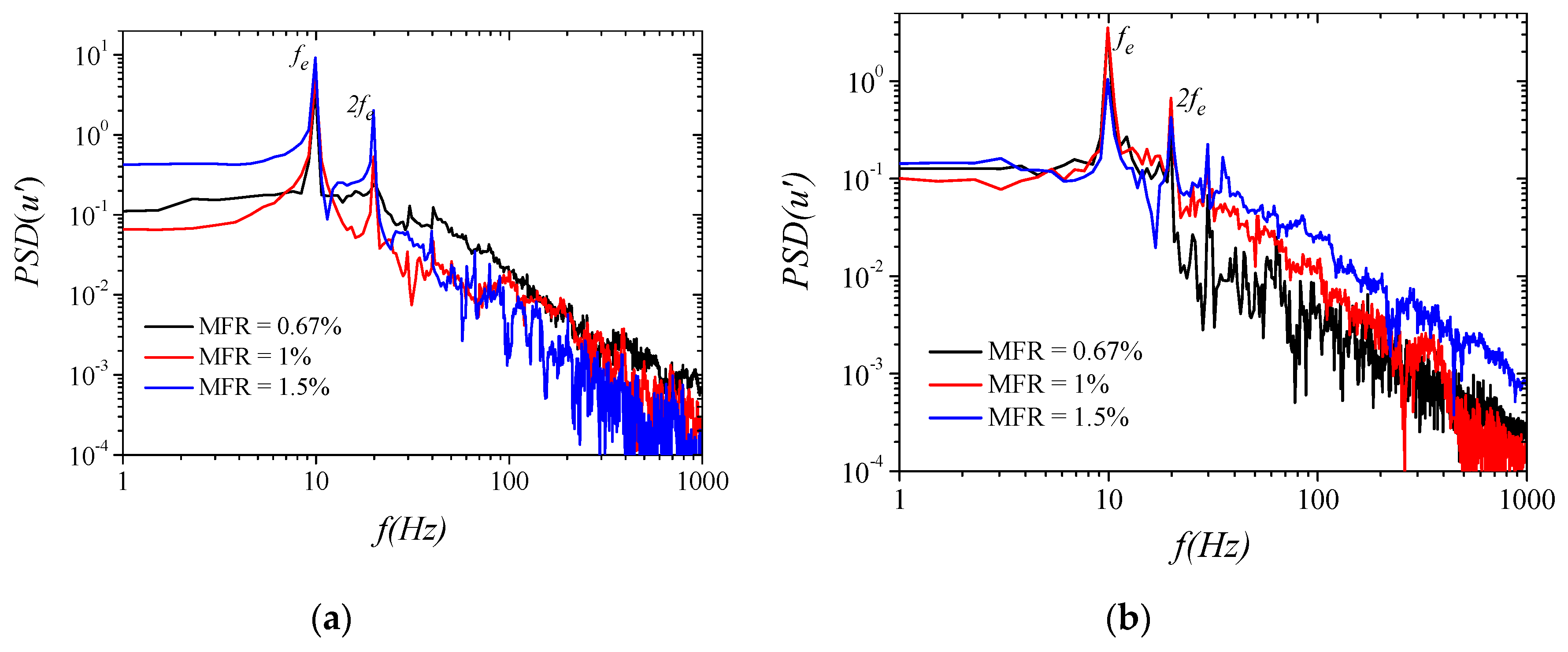
3.2. Forcing at Different Amplitudes
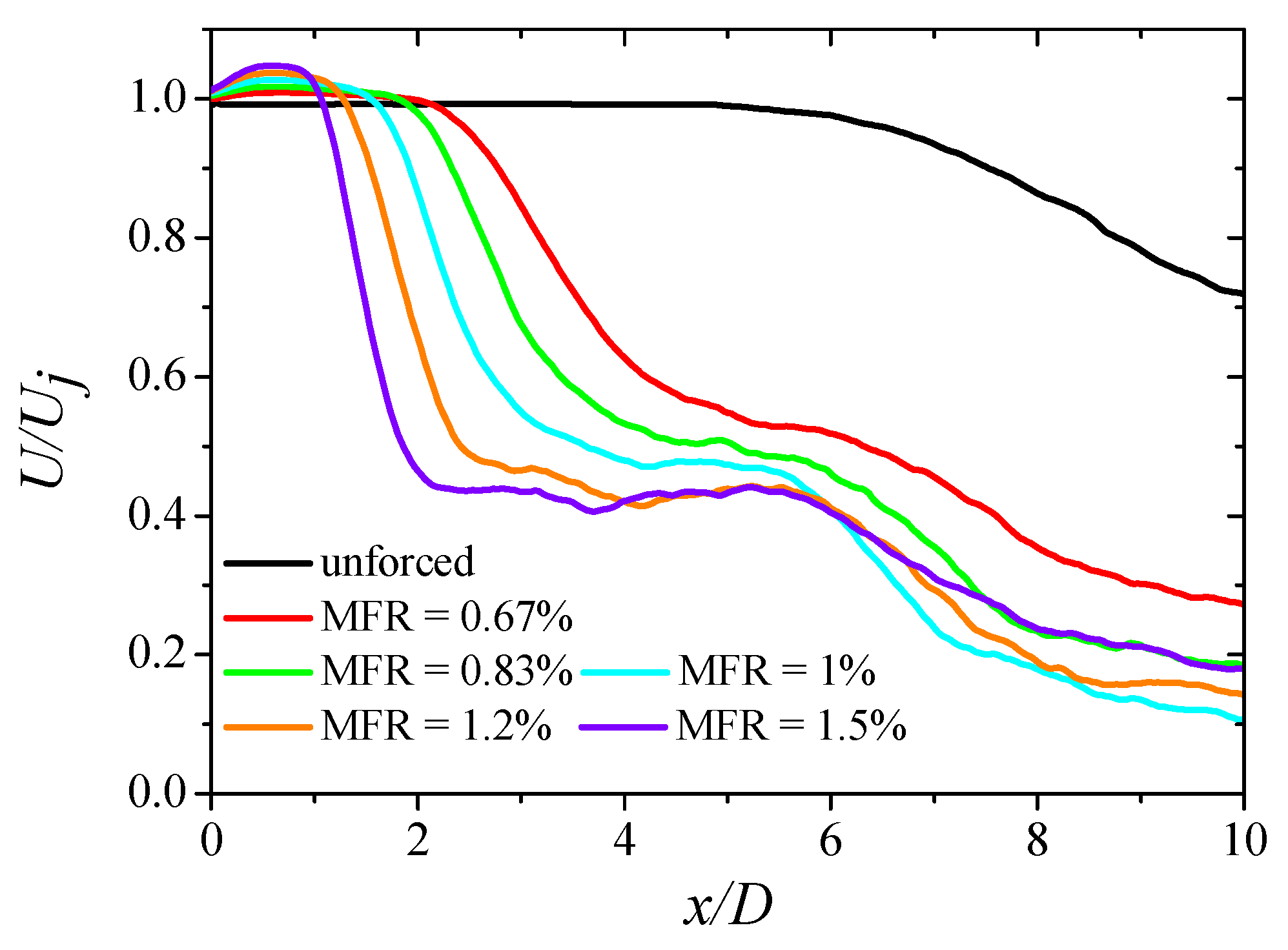
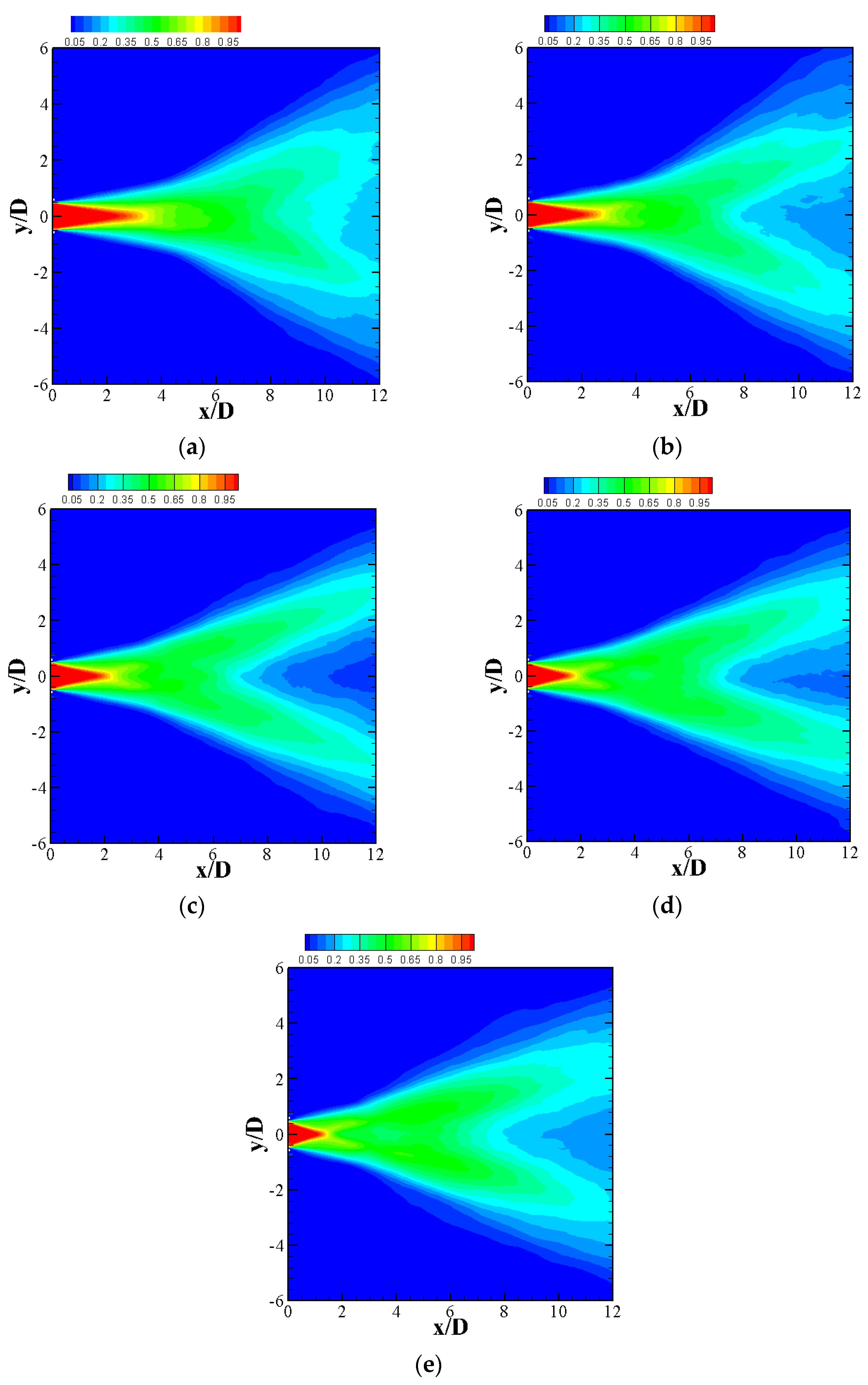
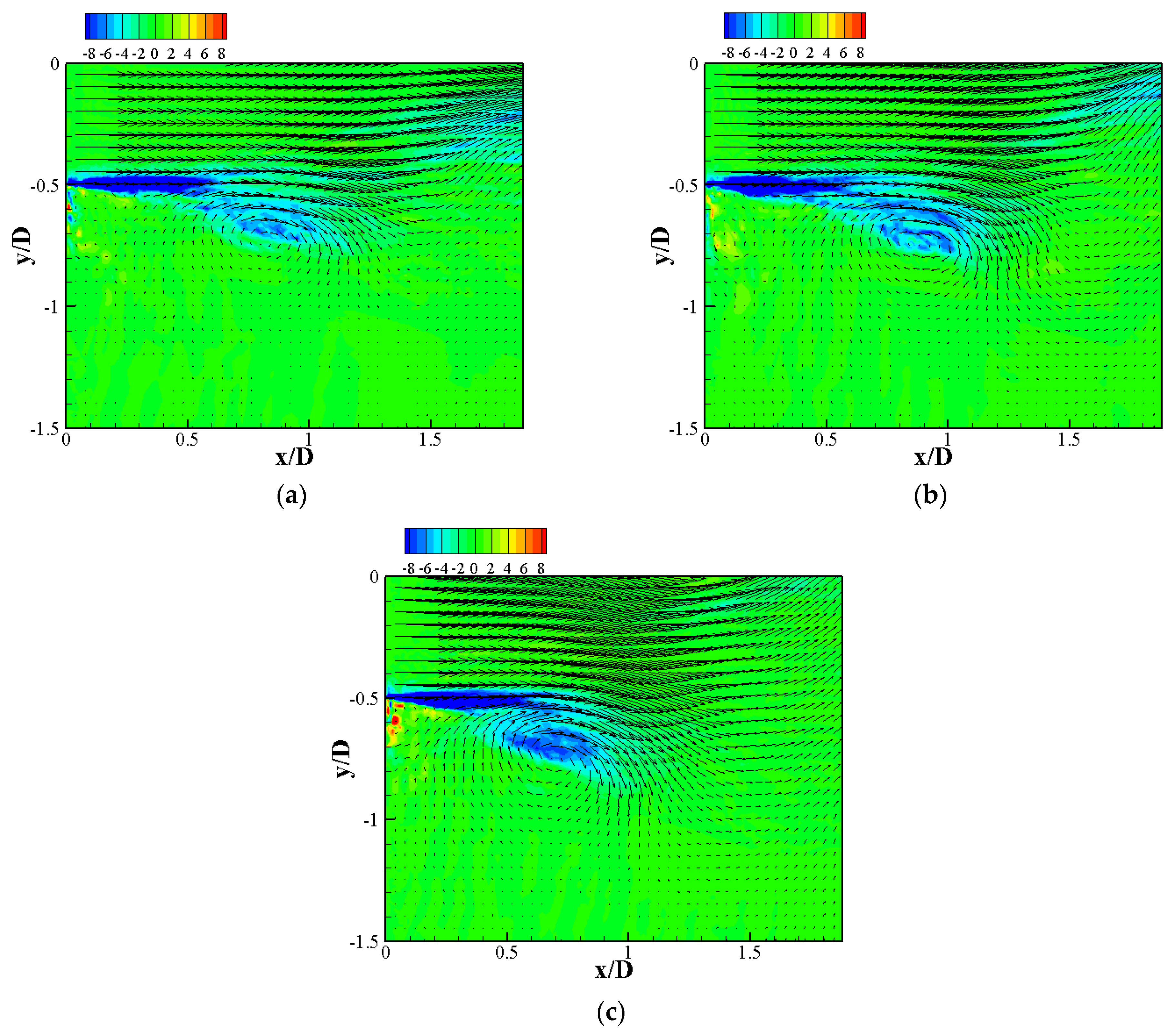
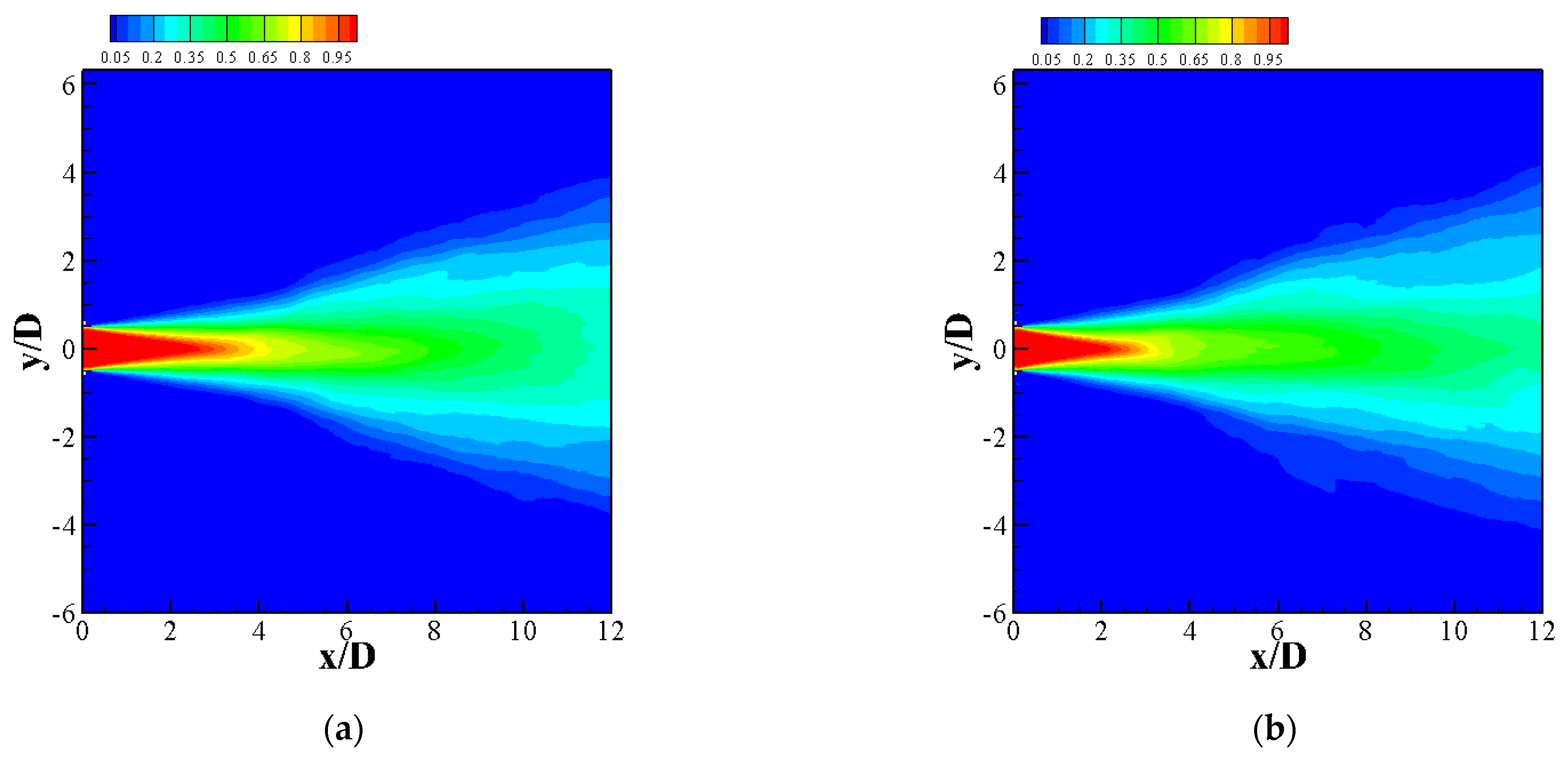
3.2.1. Effect on Mean Flow Field
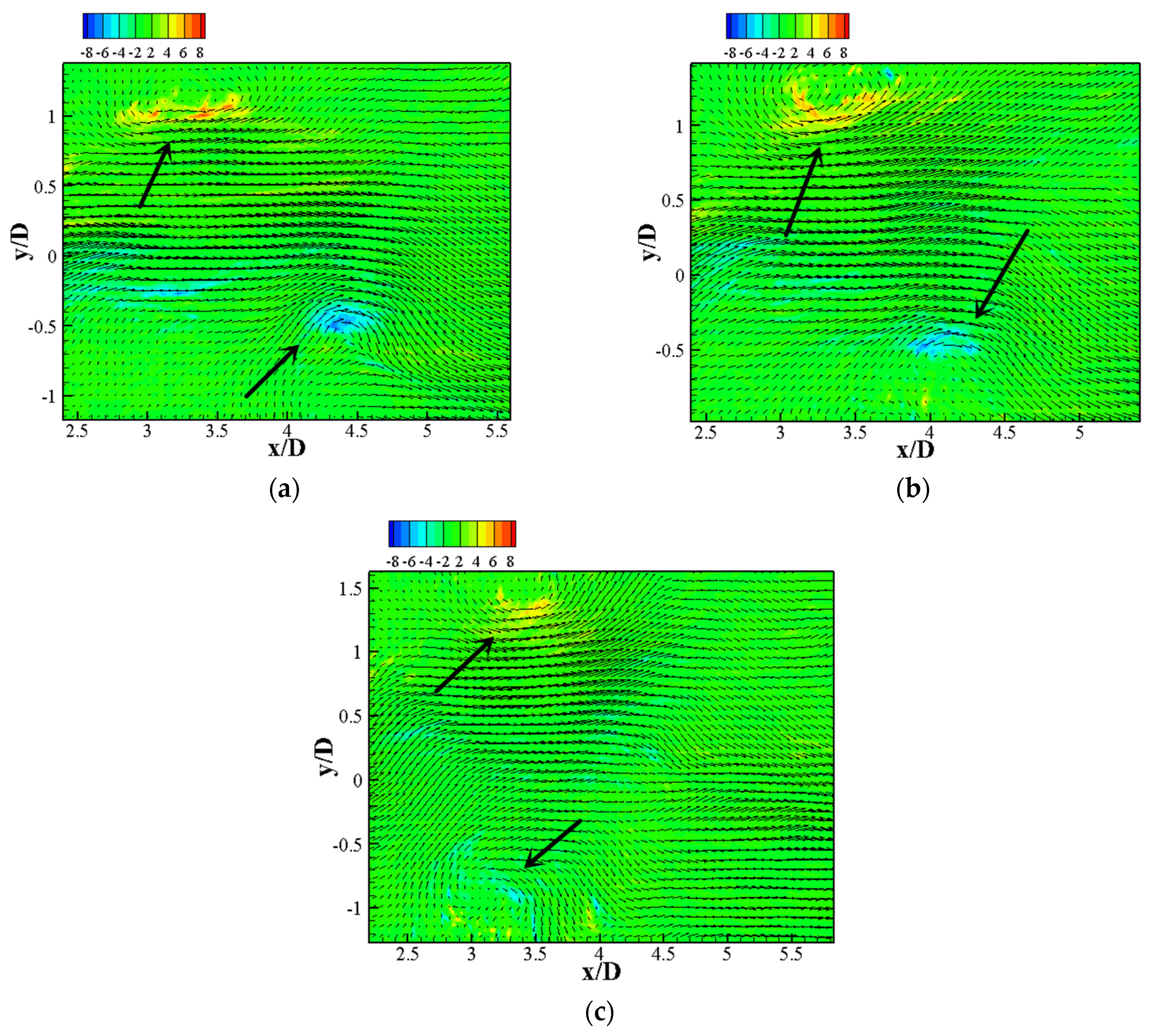
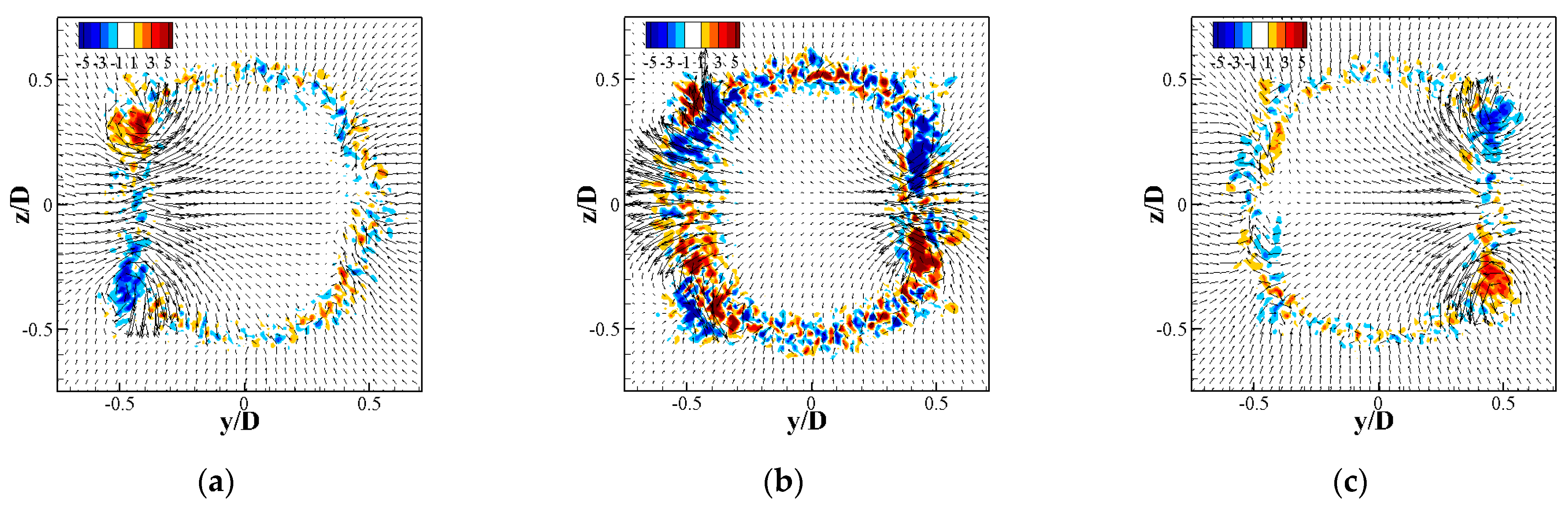
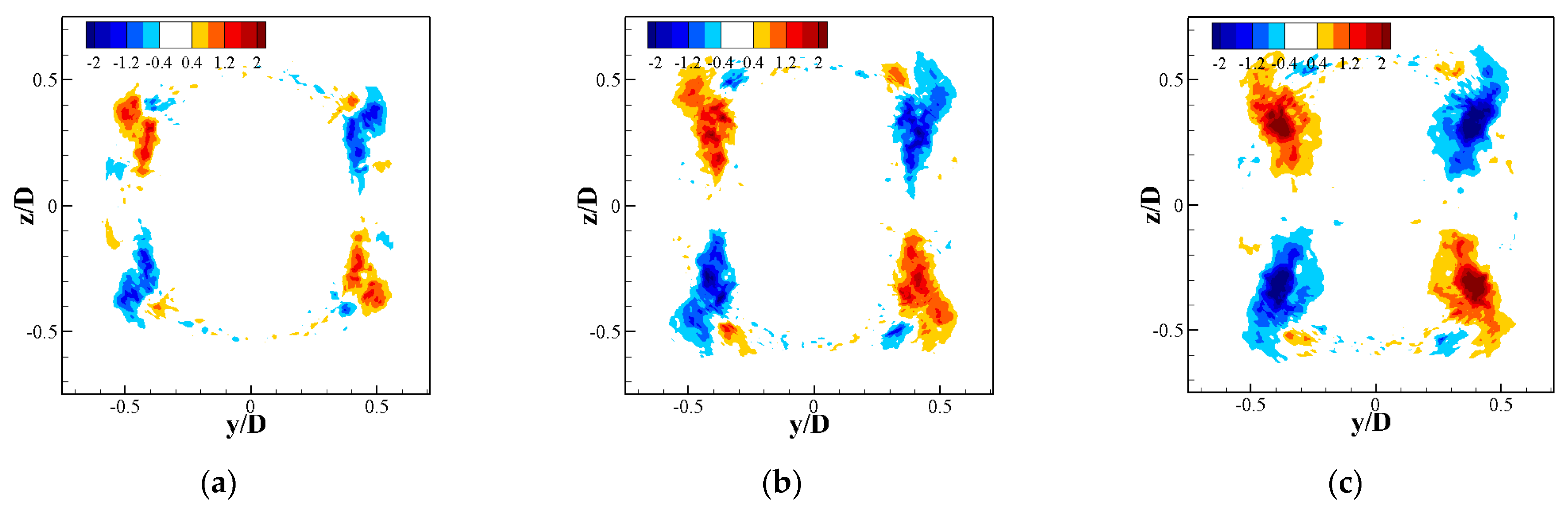
3.2.2. Effect on Azimuthal Structures
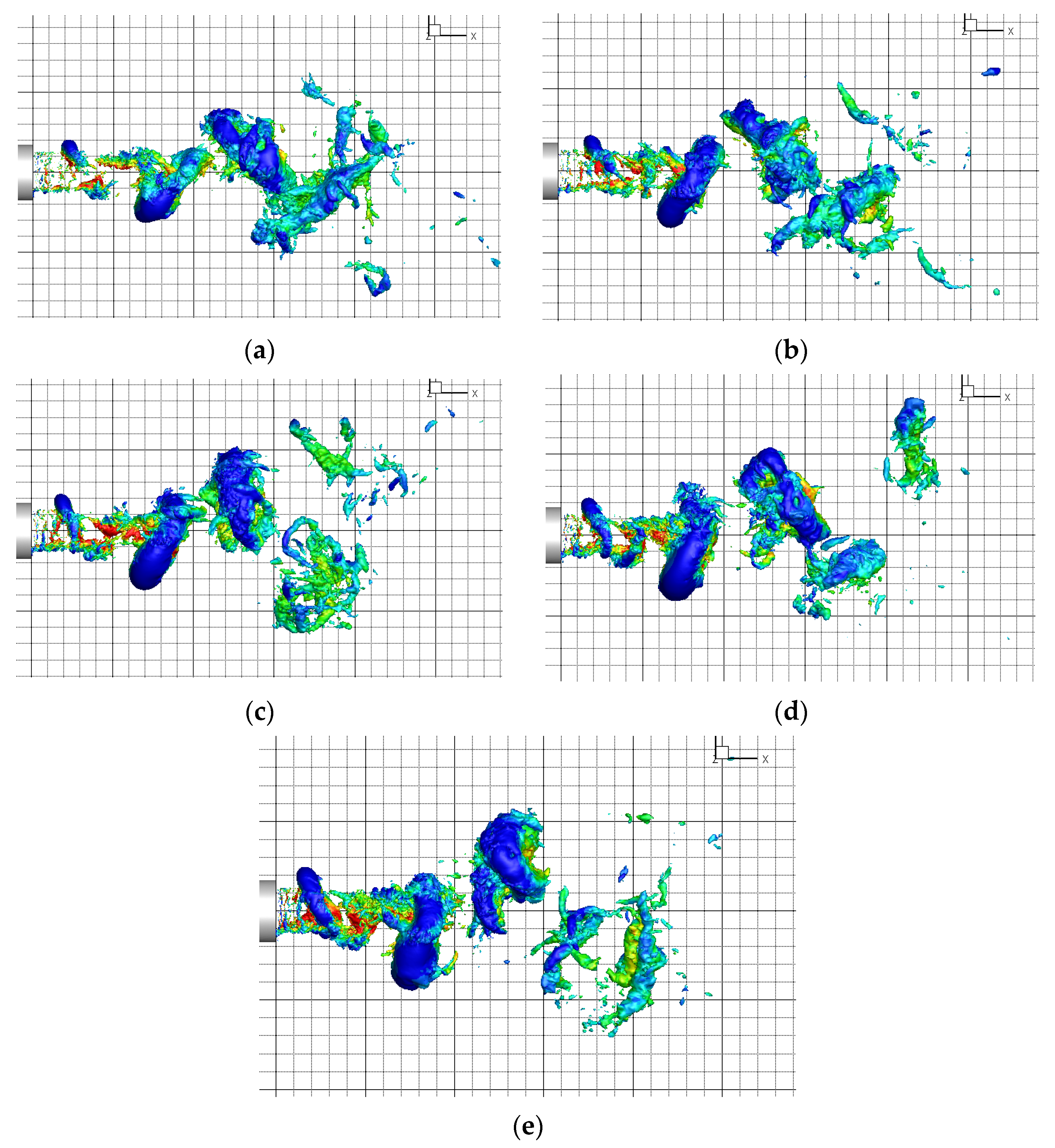
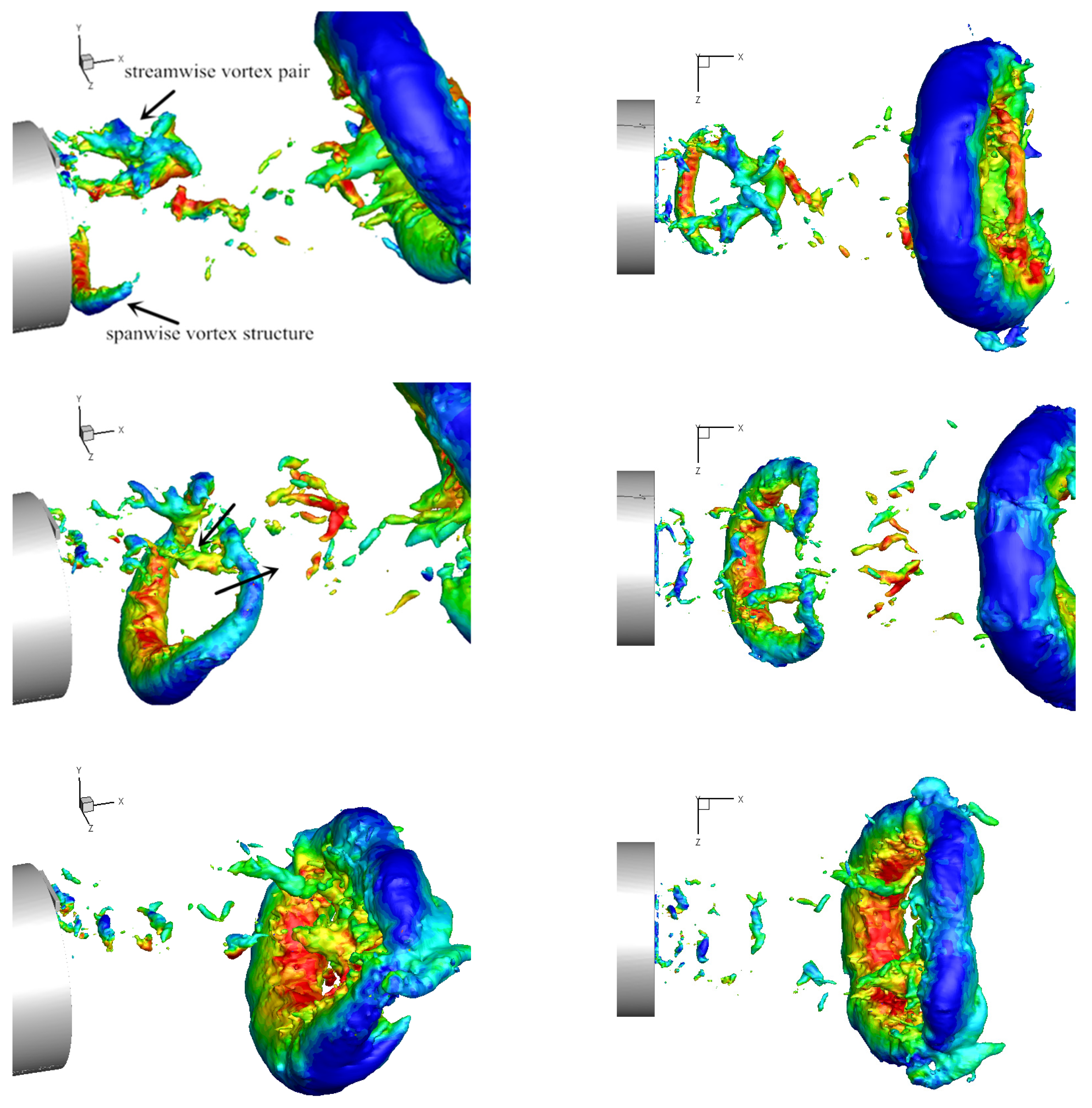
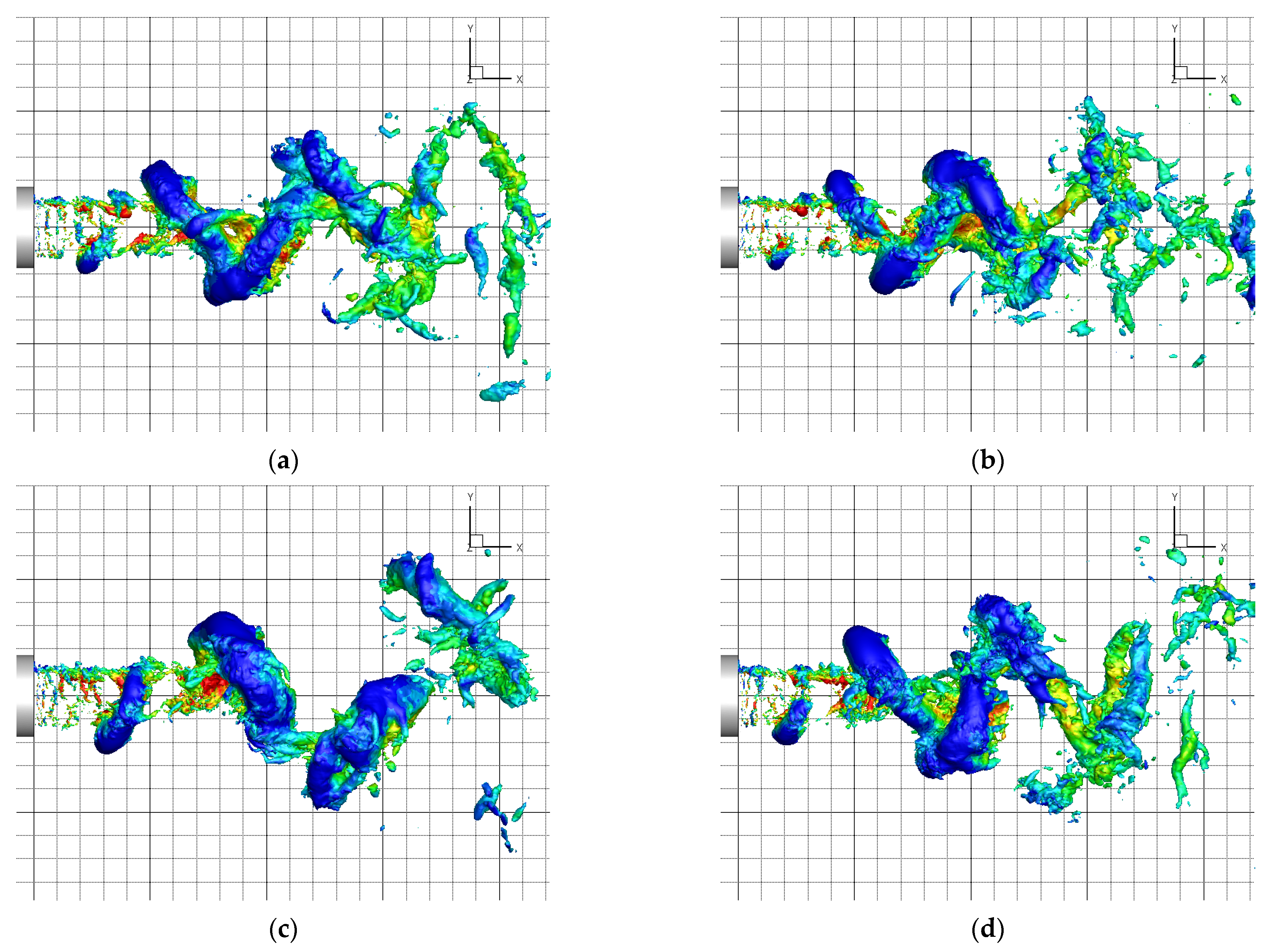
3.2.3. Effect on Streamwise Structures
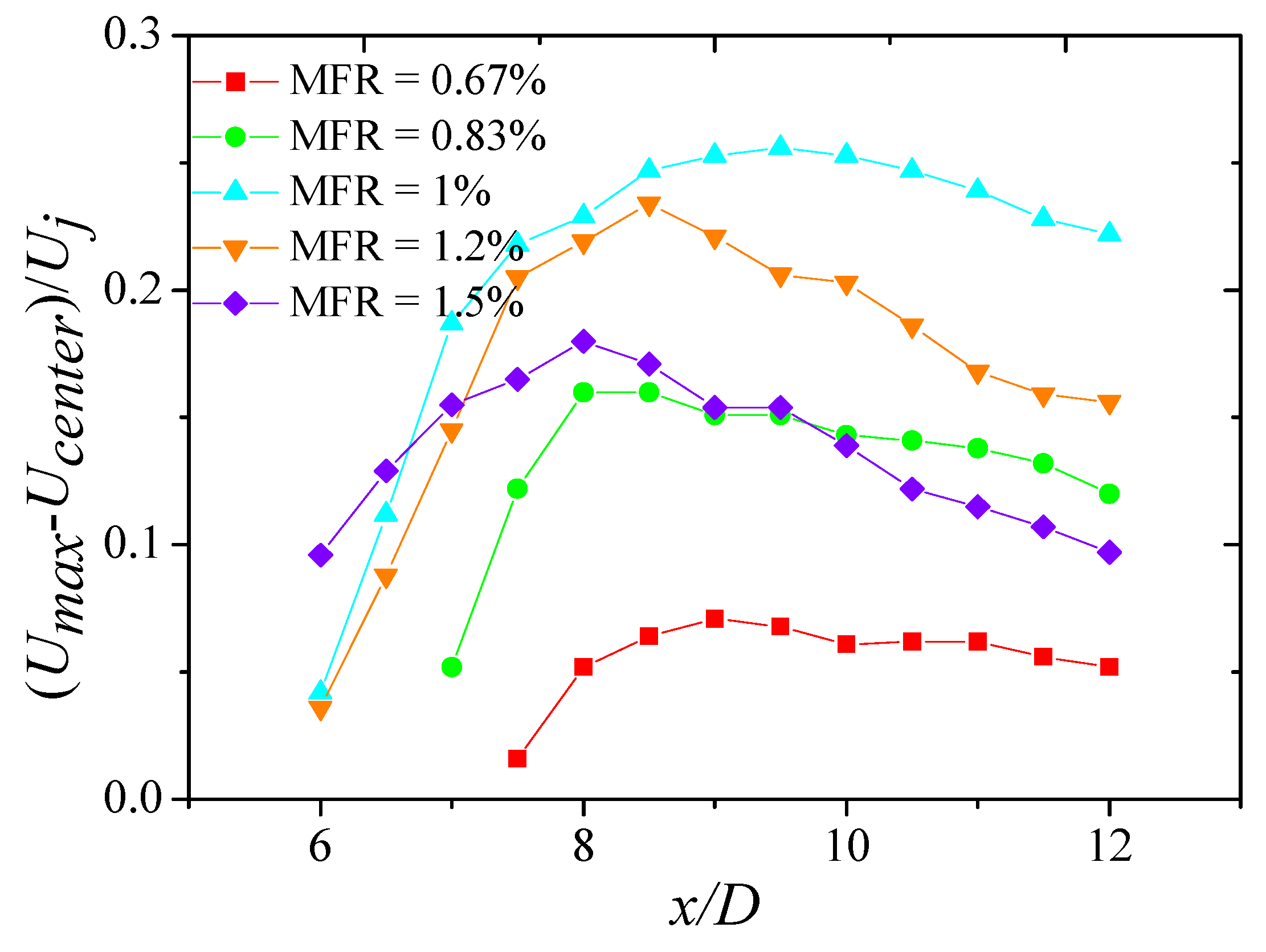
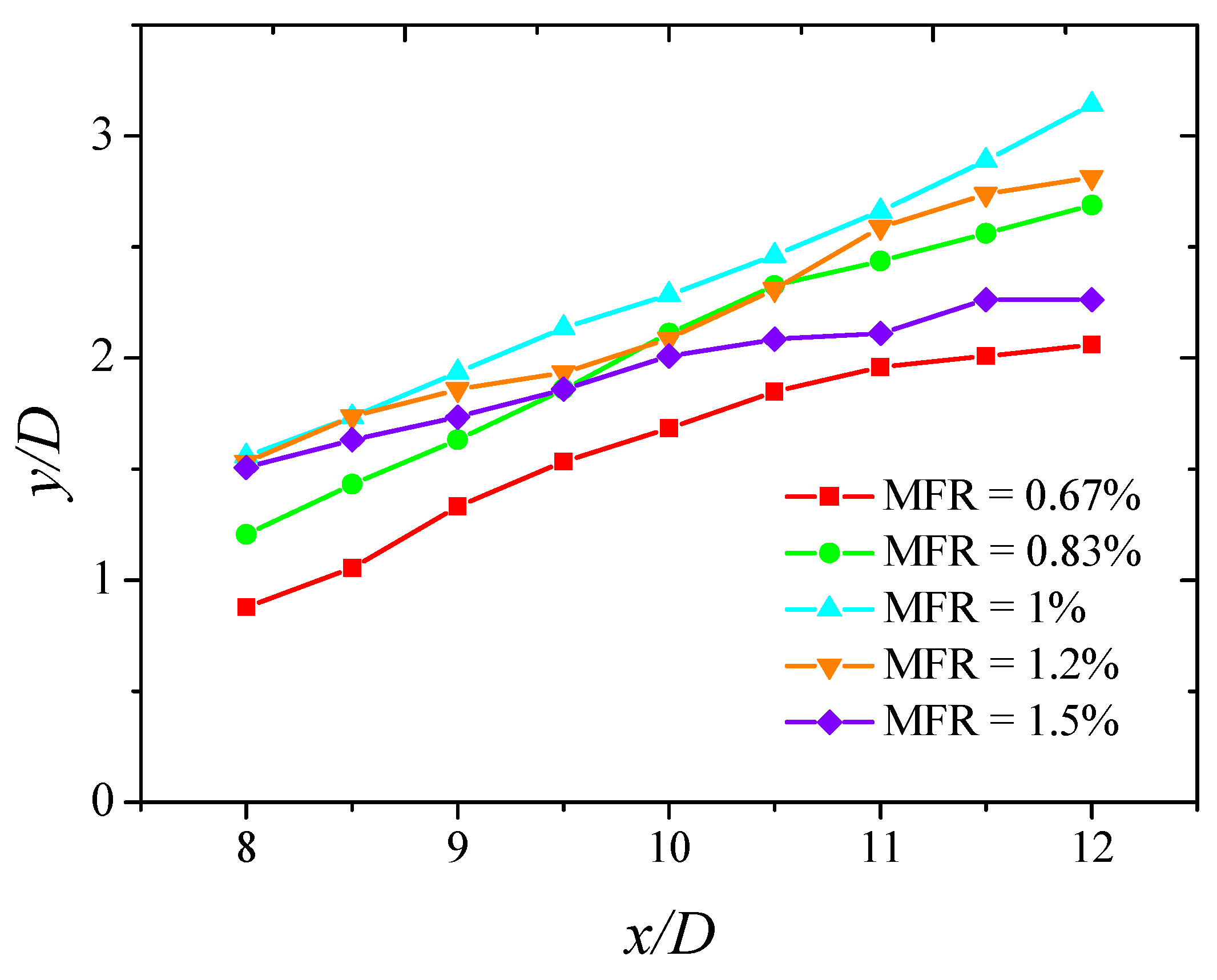
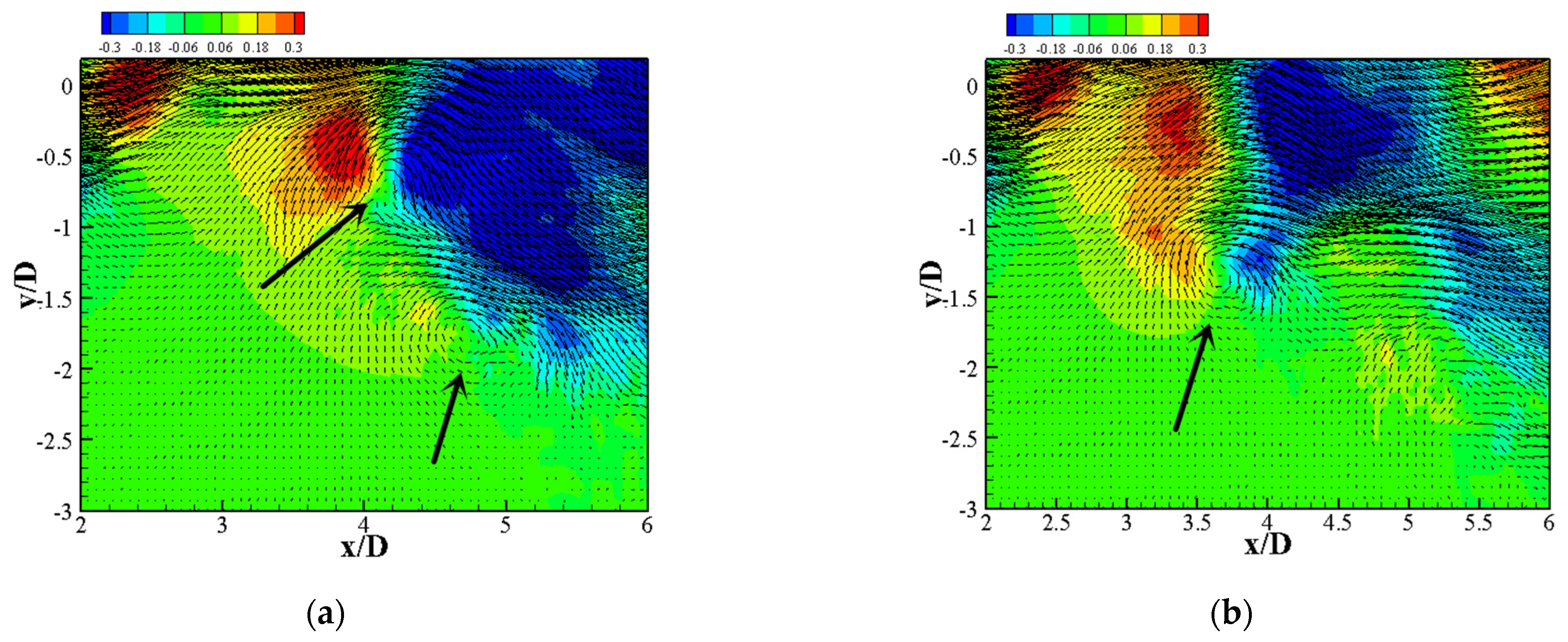
3.2.4. Mutual Interaction
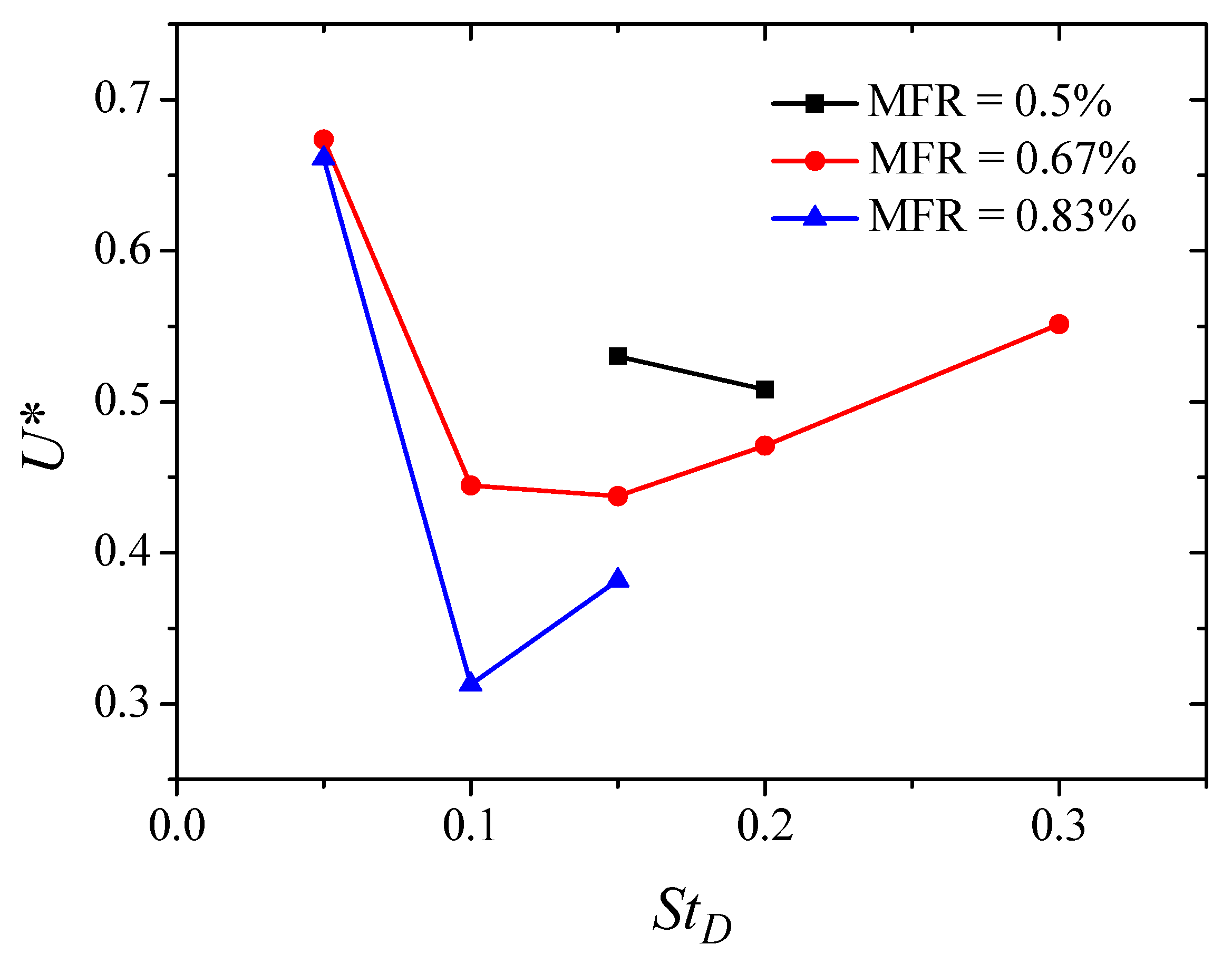
3.3. Coupling Effect of the Forcing Frequency and Amplitude
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| MFR | Mass flow ratio |
| CVP | Counter-rotating vortex pair |
| fa | Axial frequency, Hz |
| fh | Helical frequency, Hz |
| St | Strouhal number |
| LES | Large-eddy simulation |
| u | Velocity, m/s |
| ρ | Density, kg/m3 |
| p | Pressure, pascal |
| ν | Viscosity, m2/s |
| τij | Subgird stress tensor |
| νT | Subgrid eddy viscosity, m2/s |
| Δ | Filter width |
| ksgs | Subgrid kinetic energy |
| Filtered strain rate tensor | |
| ε | Dissipation rate |
| D | Nozzle exit diameter |
| y+ | Wall Y plus |
| Uj | Bulk velocity, m/s |
| Uc | Time-averaged streamwise velocity, m/s |
| H | Shape factor |
| θ | Momentum thickness |
| U | Mean streamwise velocity, m/s |
| PSD | Power spectral density |
| U* | Velocity decay metric |
| POD | Proper orthogonal decomposition |
| fe | Forcing frequency, Hz |
References
- Banken, G.J.; Cornette, W.M.; Gleason, K.M. Investigation of infrared characteristics of three generic nozzle concepts. In Proceedings of the 16th AIAA/SAE/ASME Joint Propulsion Conference, Hartford, CT, USA, 30 June–2 July 1980; p. AIAA-80-1160. [Google Scholar]
- Castelain, T.; Sunyach, M.; Juvé, D.; Béra, J.C. Jet-Noise Reduction by Impinging Microjets: An Acoustic Investigation Testing Microjet Parameters. AIAA J. 2008, 46, 1081–1087. [Google Scholar] [CrossRef] [Green Version]
- Behrouzi, P.; McGuirk, J.J. Flow Control of Jet Mixing Using a Pulsed Fluid Tab Nozzle. In Proceedings of the 3rd AIAA Flow Control Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Cattafesta, L.N.; Sheplak, M. Actuators for Active Flow Control. Annu. Rev. Fluid Mech. 2011, 43, 247–272. [Google Scholar] [CrossRef] [Green Version]
- Crow, S.C.; Champagne, F.H. Orderly structure in jet turbulence. J. Fluid Mech. 1971, 48, 547–591. [Google Scholar] [CrossRef]
- Liepmann, D.; Gharib, M. The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 1992, 245, 643–668. [Google Scholar] [CrossRef] [Green Version]
- Zaman, K.B.M.Q.; Hussain, A.K.M.F. Vortex pairing in a circular jet under controlled excitation. Part 1: General jet response. J. Fluid Mech. 1980, 101, 449–491. [Google Scholar]
- Tamburello, D.A.; Amitay, M. Active control of a free jet using a synthetic jet. Int. J. Heat Fluid Flow 2008, 29, 967–984. [Google Scholar] [CrossRef]
- Ioannou, V.; Laizet, S. Numerical investigation of plasma-controlled turbulent jets for mixing enhancement. Int. J. Heat Fluid Flow 2018, 70, 193–205. [Google Scholar] [CrossRef]
- Kamran, M.A.; McGuirk, J.J. Unsteady Predictions of Mixing Enhancement with Steady and Pulsed Control Jets. AIAA J. 2015, 53, 1262–1276. [Google Scholar] [CrossRef] [Green Version]
- Parekh, D.E.; Kibens, V.; Glezer, A.; Wiltse, J.M.; Smith, D.M. Innovative Jet Flow Control: Mixing Enhancement Experiments. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996; AIAA: Reston, VA, USA, 1996; p. 308. [Google Scholar]
- New, T.H.; Tay, W.L. Effects of cross-stream radial injections on a round jet. J. Turbul. 2006, 7, N57. [Google Scholar] [CrossRef]
- Wickersham, P. Jet Mixing Enhancement by high amplitude pulsed fluidic actuation. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2007. [Google Scholar]
- Yang, H.; Zhou, Y. Axisymmetric jet manipulated using two unsteady minijets. J. Fluid Mech. 2016, 808, 362–396. [Google Scholar] [CrossRef]
- Perumal, A.K.; Zhou, Y. Parametric study and scaling of jet manipulation using an unsteady minijet. J. Fluid Mech. 2018, 848, 592–630. [Google Scholar] [CrossRef]
- Reynolds, W.C.; Parekh, D.E.; Juvet, P.J.D.; Lee, M.J.D. Bifurcating and blooming jets. Annu. Rev. Fluid Mech. 2003, 35, 295–315. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Reynolds, W.C. Bifurcating and blooming jets at high Reynolds number. In Proceedings of the 5th Symposium on Turbulent Shear Flows, New York, NY, USA, 7–9 August 1985. [Google Scholar]
- Danaila, L.; Boersma, B.J. Direct numerical simulation of bifurcating jets. Phys. Fluids 2000, 12, 1255. [Google Scholar] [CrossRef]
- Da Silva, C.B.; Métais, O. Vortex control of bifurcating jets: A numerical study. Phys. Fluids 2002, 14, 3798. [Google Scholar] [CrossRef]
- Kong, B.; Li, T.; Qitai, E. Large eddy simulation of turbulent jet controlled by two pulsed jets: Effect of forcing frequency. Aerosp. Sci. Technol. 2019, 89, 356–369. [Google Scholar] [CrossRef]
- Kim, W.W.; Menon, S. A new dynamic one-equation subgrid-scale model for large eddy simulations. In Proceedings of the 33rd Aerospace Science Meeting and Exhibition, Reno, NV, USA, 9–12 January 1995. [Google Scholar]
- Fureby, C.; Tabor, G.; Weller, H.; Gosman, A.D. A Comparative Study of Sub Grid Scale Models in Homogeneous Isotropic Turbulence. Phys. Fluids 1997, 9, 1416–1429. [Google Scholar] [CrossRef]
- Fureby, C.; Gosman, A.D.; Tabor, G.; Weller, H.G.; Sandham, N.; Wolfshtein, M. Large Eddy Simulation of Turbulent Channel Flows. 1997. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.45.5126&rep=rep1&type=pdf (accessed on 27 December 2021).
- Husain, Z.D.; Hussain, A.K.M.F. 1979 Axisymmetric mixing layer: Influence of the initial and boundary conditions. AIAA J. 1979, 17, 48–55. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Influence of nozzle-exit boundary-layer conditions on the flow and acoustic fields of initially laminar jets. J. Fluid Mech. 2010, 663, 507–538. [Google Scholar] [CrossRef] [Green Version]
- Tyliszczak, A.; Geurts, B.J. Parametric Analysis of Excited Round Jets–Numerical Study. Flow Turbul. Combust 2014, 93, 221–247. [Google Scholar] [CrossRef] [Green Version]
- Parekh, D.E.; Reynolds, D.E.; Mungal, M.G. Bifurcation of round air jets by dual-mode acoustic excitation. In Proceedings of the 25th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 12–15 January 1987. [Google Scholar]
- Suzuki HKasagi, N.; Suzuki, Y. Active control of an axisymmetric jet with distributed electromagnetic flap actuators. Exp. Fluids 2004, 36, 498–509. [Google Scholar] [CrossRef]
- New, T.H.; Tay, W.L. Cross-Stream Radial Fluid Injection into a Round Jet. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar]
- Grinstein, F.F.; Gutmark, E.J.; Parr, T.P.; Hanson-Parr, D.M.; Obeysekare, U. Streamwise and spanwise vortex interaction in an axisymmetric jet. A computational and experimental study. Phys. Fluids 1996, 8, 1515. [Google Scholar] [CrossRef]
- Gohil, T.B.; Saha, A.K.; Muralidhar, K. Direct numerical simulation of free and forced square jets. Int. J. Heat Fluid Flow 2015, 52, 169–184. [Google Scholar] [CrossRef]

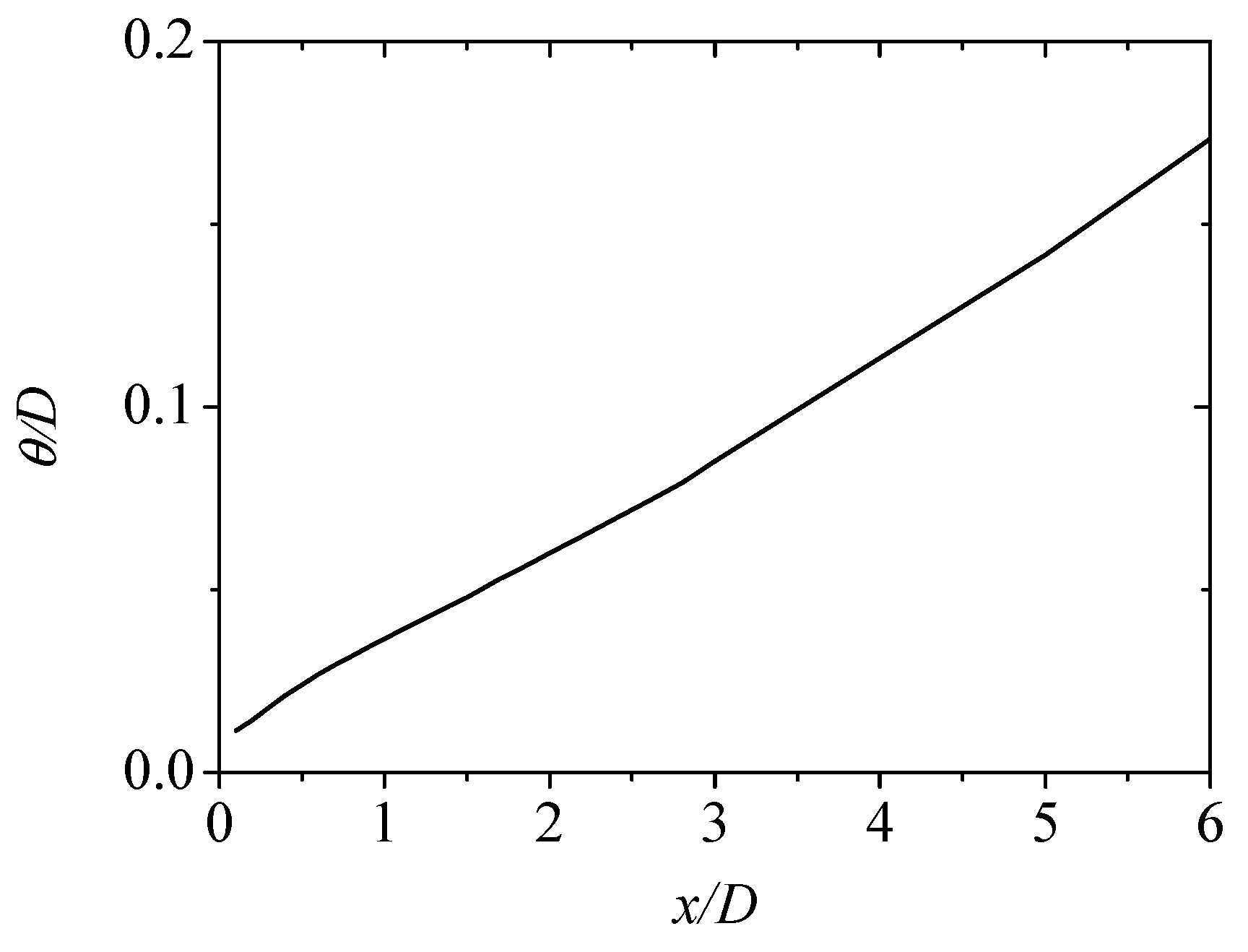



| MFR% | 0.67 | 0.83 | 1 | 1.2 | 1.5 |
| α° | 16.45 | 20.34 | 21.59 | 17.76 | 10.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eri, Q.; Ding, W.; Kong, B. Numerical Investigation of Jet Control Using Two Pulsed Jets under Different Amplitudes. Energies 2022, 15, 640. https://doi.org/10.3390/en15020640
Eri Q, Ding W, Kong B. Numerical Investigation of Jet Control Using Two Pulsed Jets under Different Amplitudes. Energies. 2022; 15(2):640. https://doi.org/10.3390/en15020640
Chicago/Turabian StyleEri, Qitai, Wenhao Ding, and Bo Kong. 2022. "Numerical Investigation of Jet Control Using Two Pulsed Jets under Different Amplitudes" Energies 15, no. 2: 640. https://doi.org/10.3390/en15020640





