Automated QFT-Based PI Tuning for Speed Control of SynRM Drive with Analytical Selection of QFT Control Specifications
Abstract
:1. Introduction
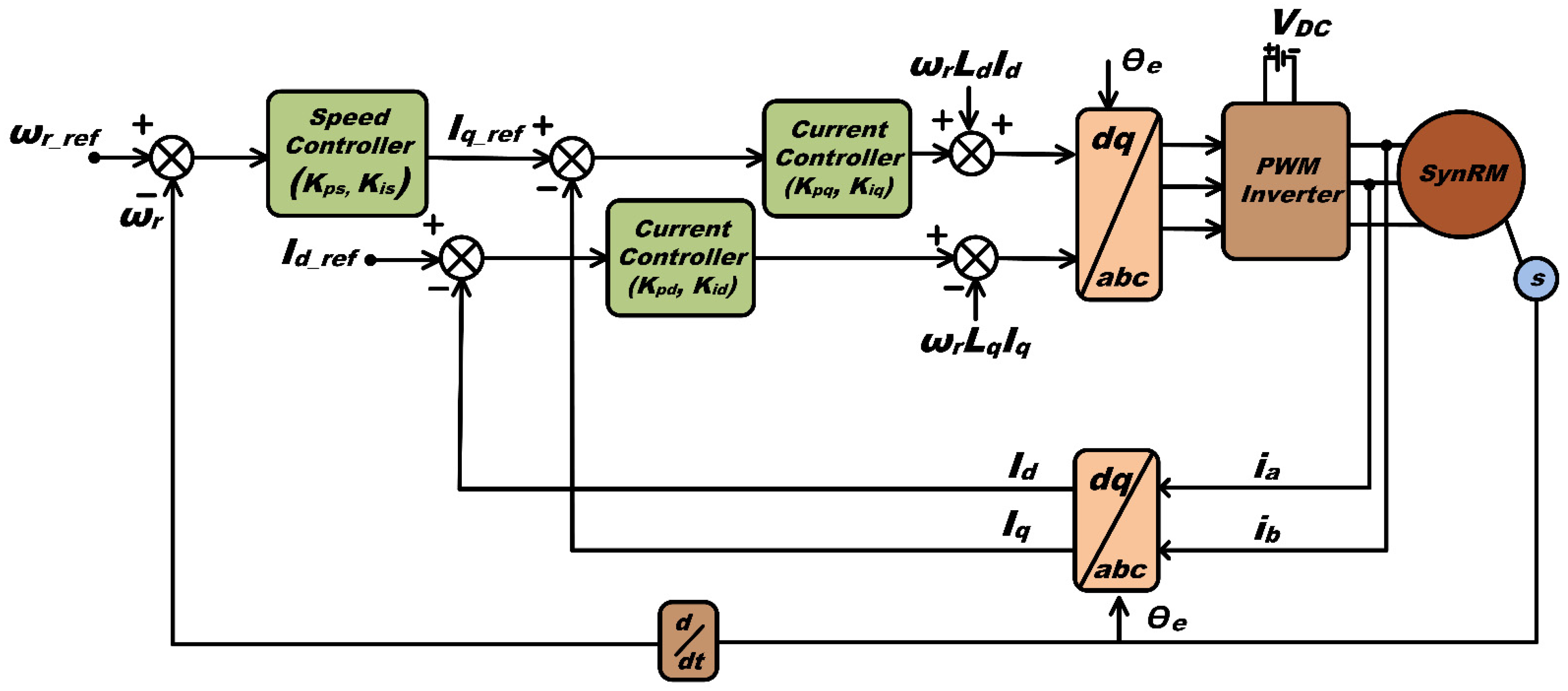
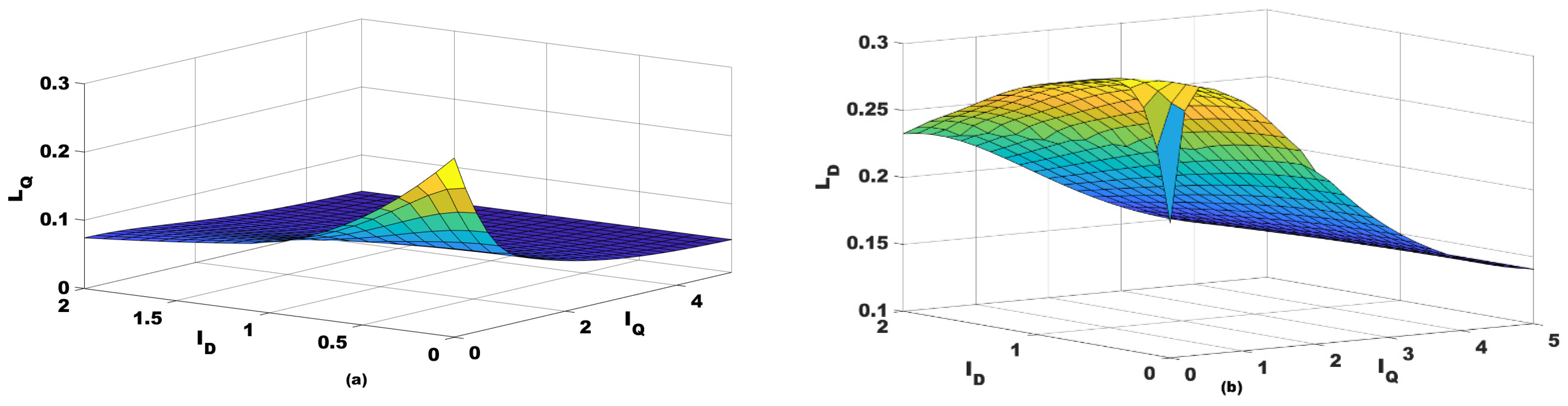
2. Mathematical Modeling of SynRM in FOC Frame
3. QFT Method and FPA Algorithm
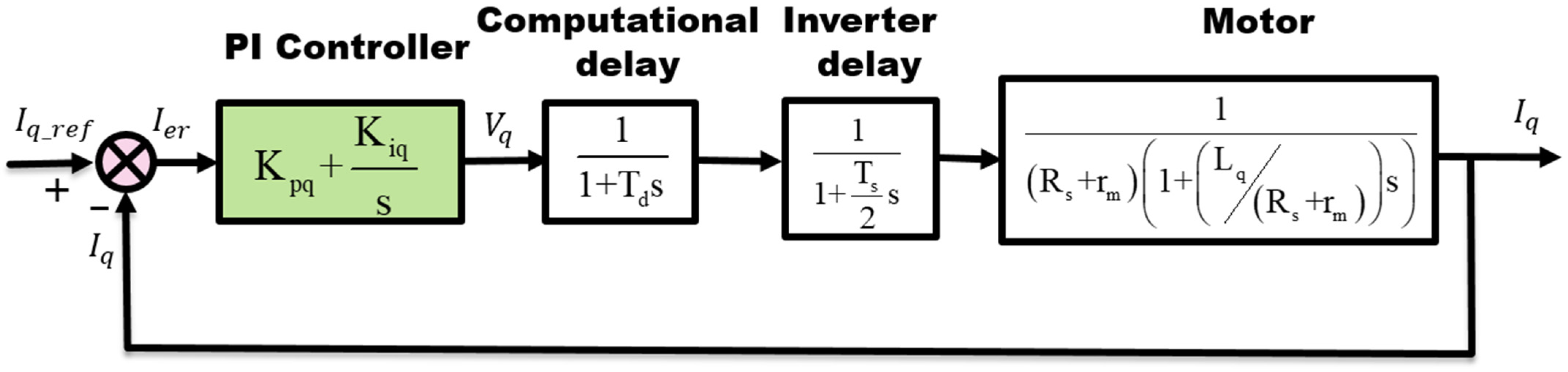
3.1. QFT Method for PI Tuning
- For a given plant (G(s)), specify the performance indices of the closed-loop control system for the required closed-loop stability and tracking performance [29].
- Describe the transfer function of the nominal model along with the uncertainties, such as the parametric variations and unmodeled dynamics. This illustration provides a set of multiple plants along with the nominal plant.
- Draw the templates by plotting the set of multiple plants in a gain vs. phase plot at the specified discrete frequency set. These templates are useful for observing the variations in phase and magnitude of the transfer function caused by the uncertainties in the plant [30].
- Plot the QFT bounds for all of the controller specifications mentioned in step 1 and draw the intersection of all these bounds in a Nichols chart so that it can represent the worst-case scenario for the set of multiple plants.
- Perform the loop shaping by adding the PI controller (C(s)) to G(s), such that the open loop, L(s) (=G(s)C(s)), should satisfy all bounds plotted for the worst-case scenario in step 4.
- Once the L(s) satisfies all the bounds on the Nichols chart, derive the PI controller from L(s) through L(s)/G(s) [31].
3.2. Flower Pollination Algorithm
- The pollens (as solutions) are uniformly distributed in the search space at the initial iteration. Before the initiation of each iteration, a random value is assigned to the switching probability variable (ρ). Variable ρ is the decision variable for switching the algorithm between the local and global search for a given pollen.
- If pollen is selected for the global search, the algorithm first calculates the strength of pollination using the Levy distribution function for the long flight distances as follows:where the step variable is the domain over which the Levy distribution function is defined and is used to calculate the final value of L, the Levy flight step size. Thus, the update to the pollen’s position (i.e., solution), in a global search, can be represented as:where is ith solution (pollen) at iteration k and is the best solution among all pollens until the kth iteration.
- If a pollen is selected for the local search, the update step for flower constancy, ε, is selected for each solution from a uniform distribution in the interval [0, 1] and the updated solution is given as below:where the jth and lth solutions are chosen randomly from the available n solutions.
- After the update of the pollens, from Equation (9) or (10), the fitness function is evaluated to select the best solution for next iteration, and the next iteration starts again from step 1.
4. Selection of Control Specifications for QFT Method
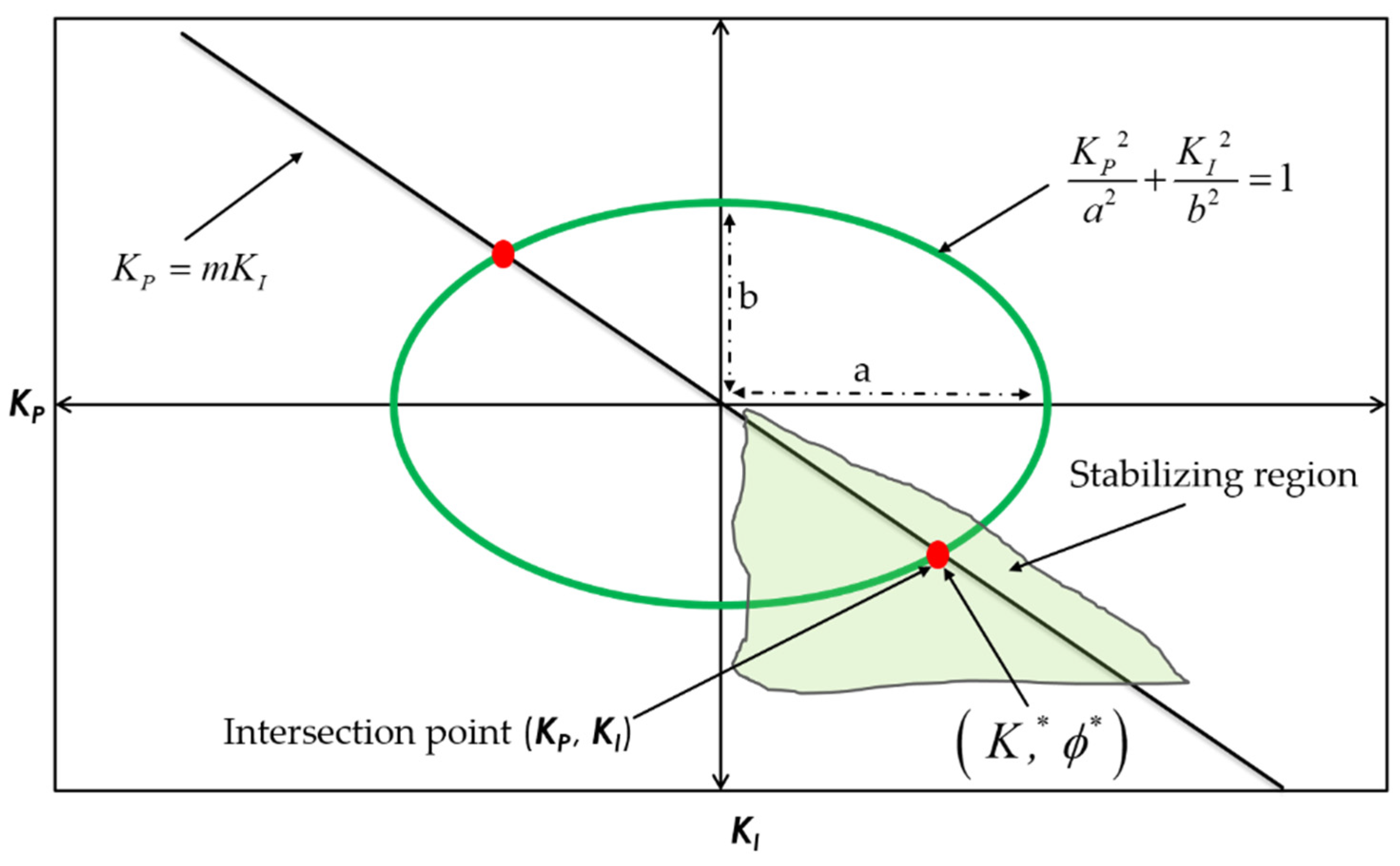
4.1. Selection of Robust Stability and Performance Specifications
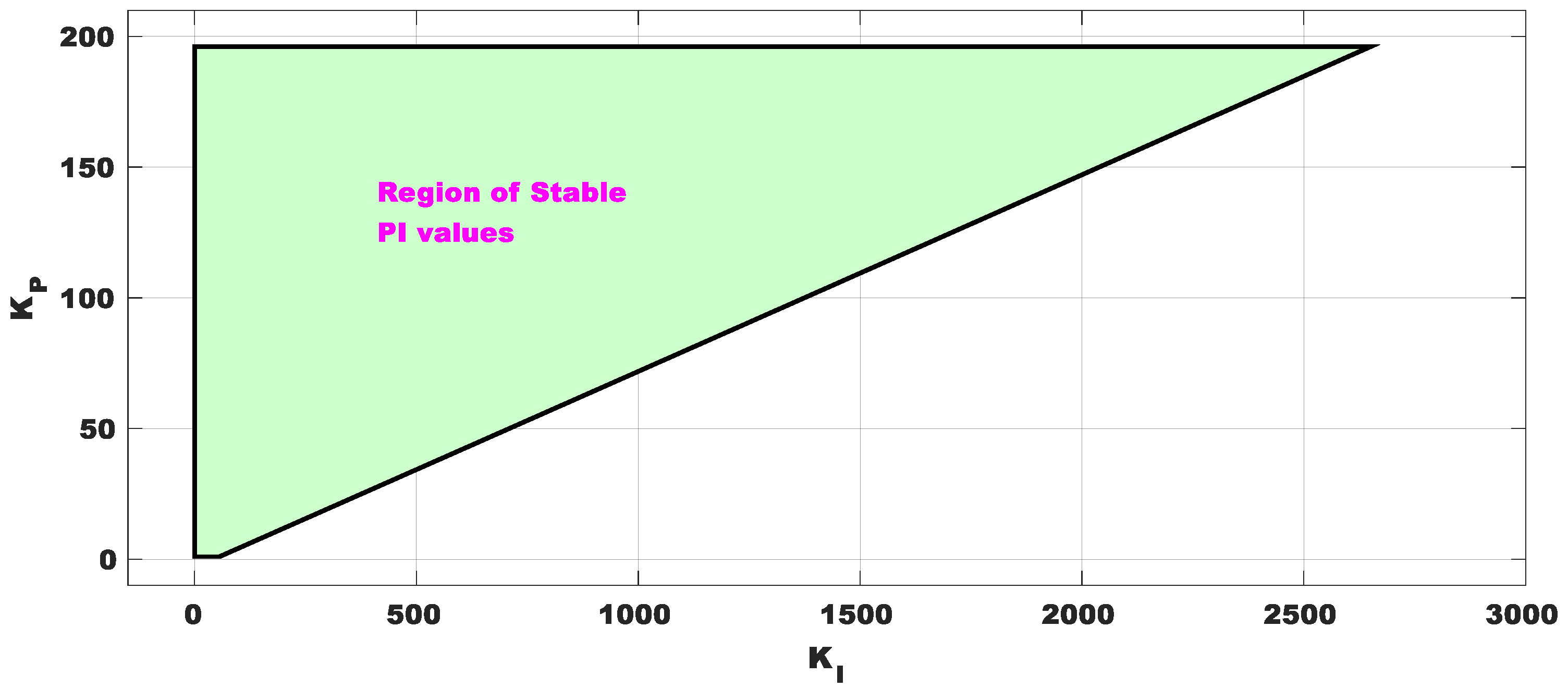
4.2. Selection of Intial Search Space for FPA Algoirthm
5. Automatic Loop Shaping QFT Using FPA for PI Design
- Define the discrete set of frequency points at which the QFT design procedure is conducted. For the current case, 12 discrete frequency values are chosen in the range of [1 rad/s, 31,416 rad/s].
- To define robust stability, the limit to the closed-loop transfer function, εs, is selected from the P.M. value, i.e., 80° as shown below:
- The sensitivity function weight Ws is chosen as shown in Equation (17) for a maximum sensitivity (Ms) set to 1.2 and B.W. = 350 rad/s:
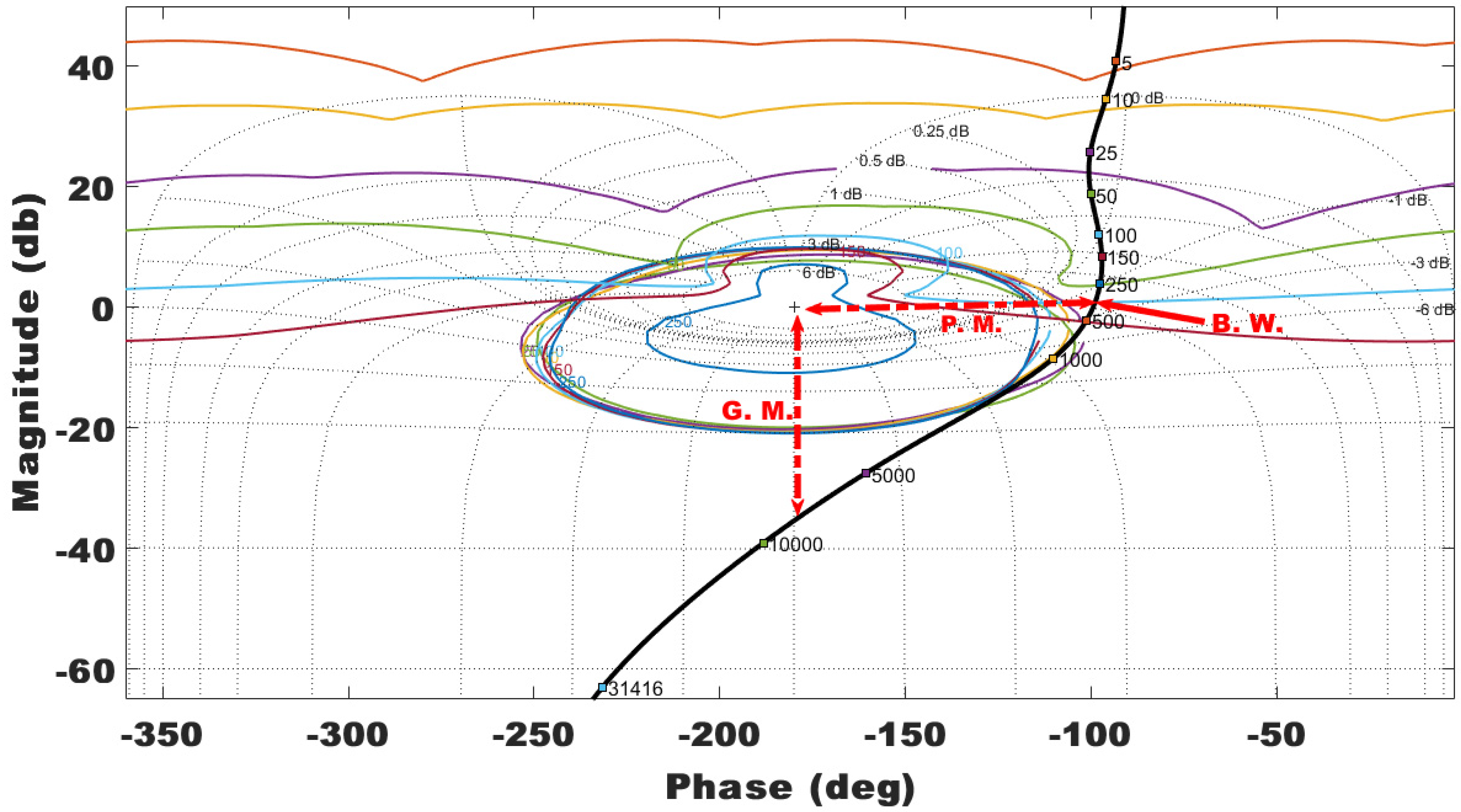
- All closed-loop specifications and plant uncertainties are plotted in the Nichols chart as bounds for the worst-case scenario. Thus, the loop shaping need to be performed to satisfy these bounds at all frequencies.
- The automatic loop shaping is performed by initializing the search space with the range of PI values selected in Section 4.2. The other parameters used in the FPA algorithm are shown in Table 2.
- The multi-component objective function has been used for automatic loop shaping. The fitness function used in Equation (18) is formulated to minimize the distance between the L(s) and QFT bounds, and hence the magnitude of PI gains, as given below:where α is the weighting coefficient with a value of 0.5 to give equal priority in the objective function.
- The synthesized PI controller for Q-axis current regulation is given by Equation (19) and its loop shaping on the Nichols chart to satisfy QFT bounds is shown in Figure 8:From the figure, it is evident that with only two gain variables, the loop shaping is tightly performed at each discrete frequency. The P.M., G.M., and B.W. for even the worst-case scenario are 82°, 36.58 dB, and 386 rad/s, respectively. This ensures that the design procedure not only systematically chooses the control specifications to force the PI controller performance to its bottleneck, but it also ensures that the synthesized controller absolutely satisfies the chosen control specifications in the design procedure.
- The PI controllers for the D-axis current loop and the outer speed loop are synthesized using a similar procedure, and are presented as given in Equations (20) and (21), respectively:The synthesized PI controllers are discretized using the forward Euler method before being implemented in the MATLAB/Simulink simulation environment.
6. Results and Discussions
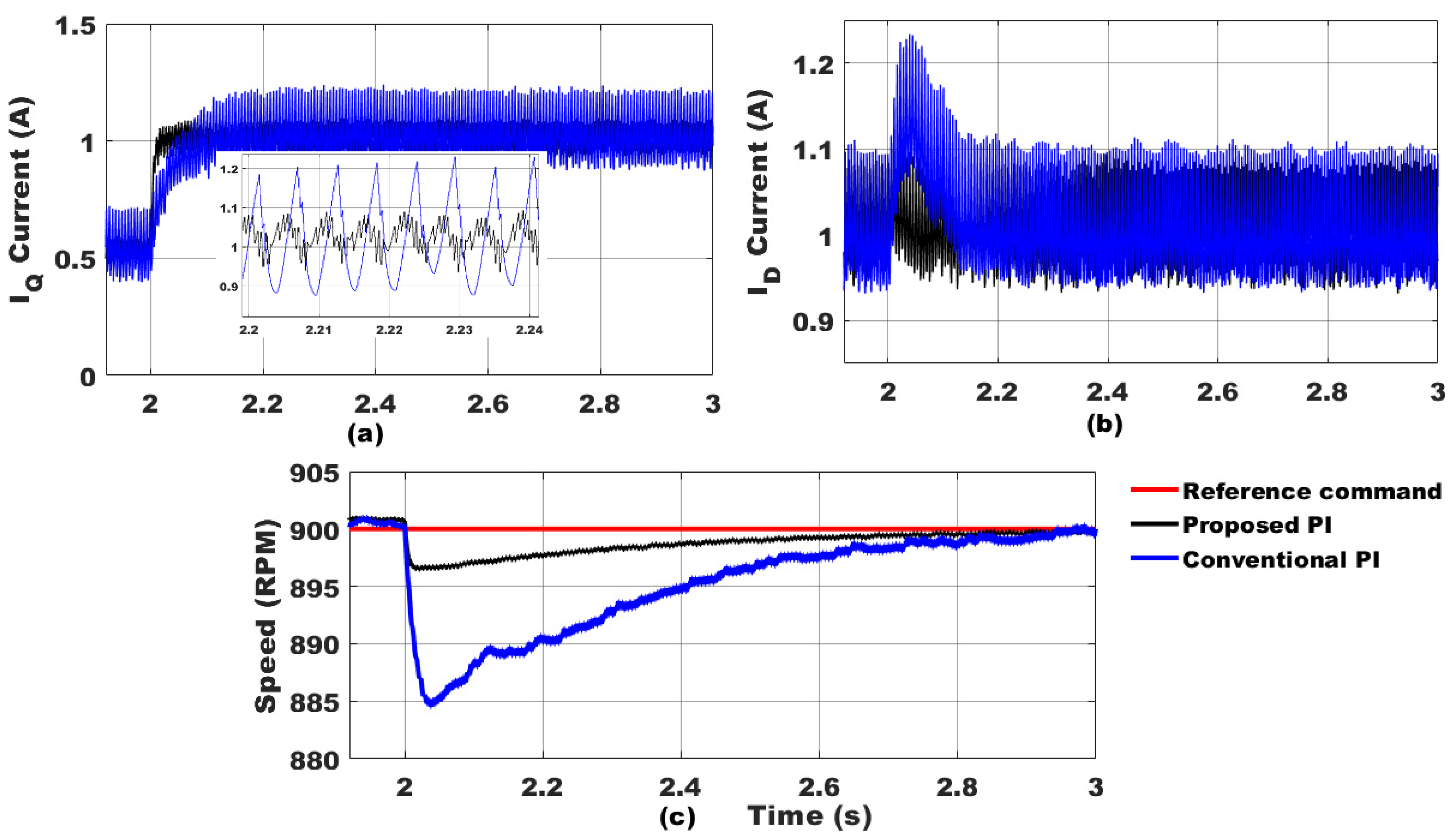
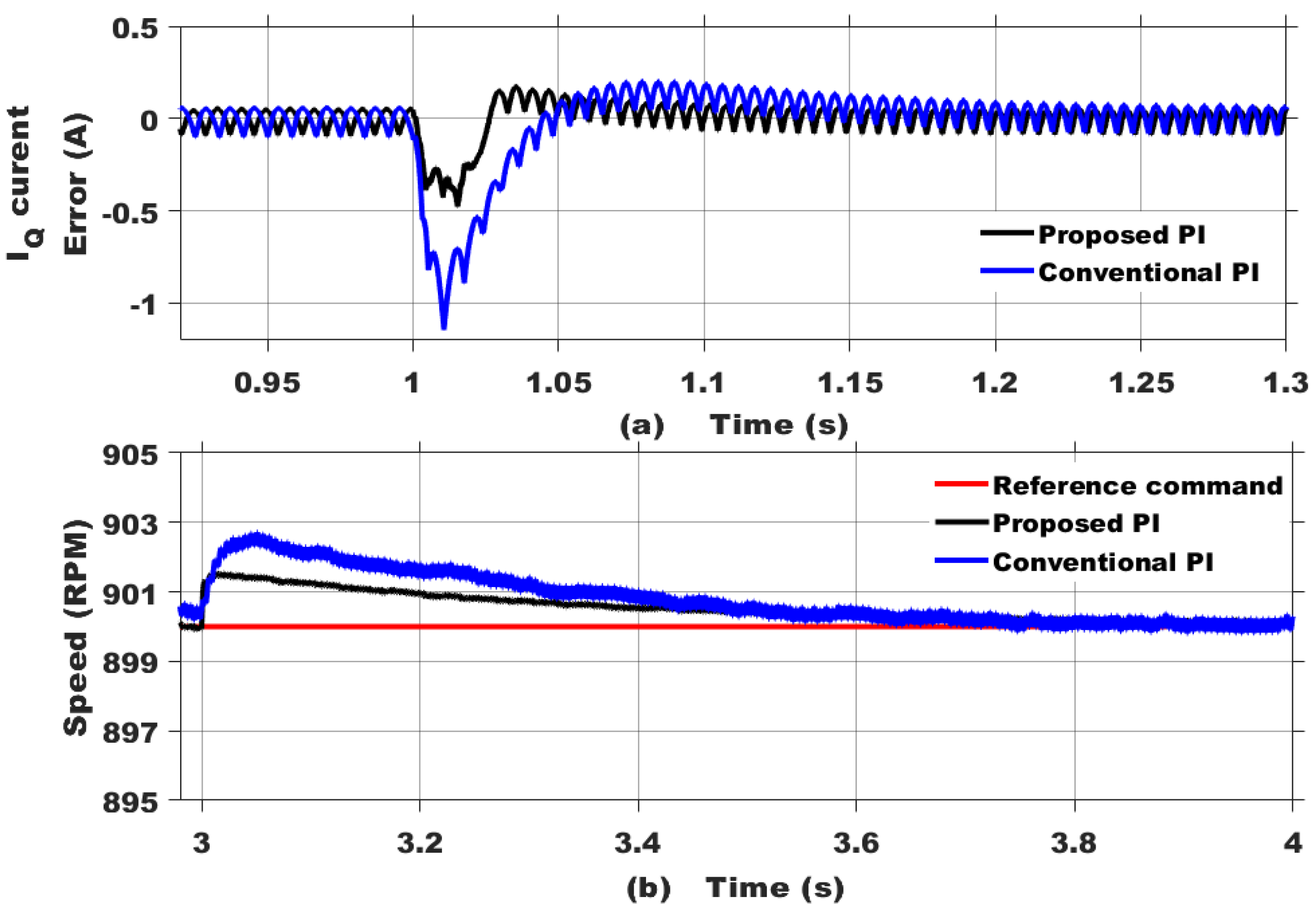
6.1. Robust Regulatory Performance
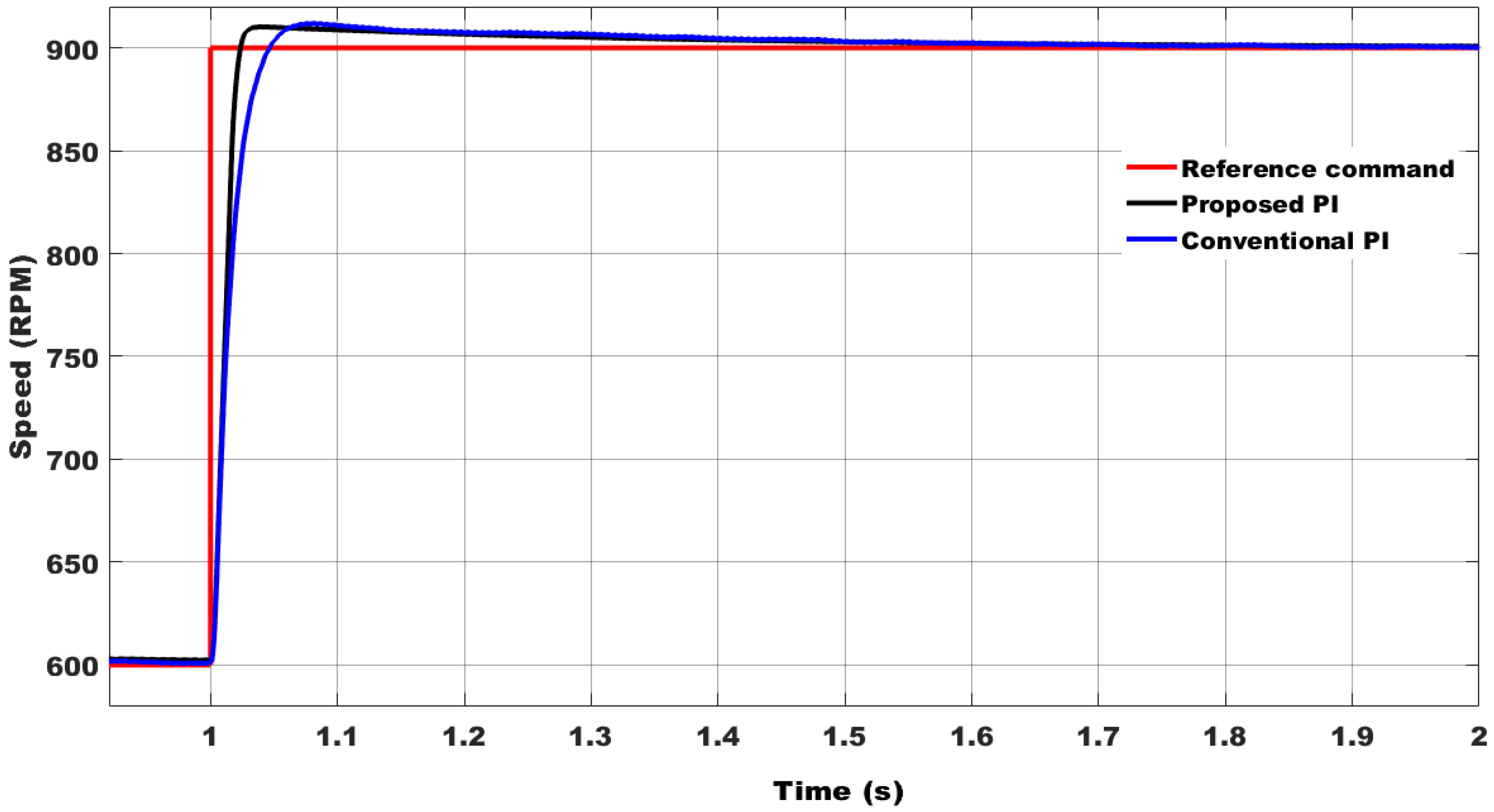
6.2. Robust Tracking Performance
6.3. Robust Performance to the Parametric Variations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ozcelik, N.G.; Dogru, U.E.; Imeryuz, M.; Ergene, L.T. Synchronous Reluctance Motor vs. Induction Motor at Low-Power Industrial Applications: Design and Comparison. Energies 2019, 12, 2190. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, F.; Ukil, A. Comparative performance analysis of induction & synchronous reluctance motors in chiller systems for energy efficient buildings. IEEE Trans. Ind. Informat. 2019, 15, 4384–4393. [Google Scholar]
- Zhu, Z.Q.; Chu, W.Q.; Guan, Y. Quantitative comparison of electromagnetic performance of electrical machines for HEVs/EVs. CES Trans. Electr. Mach. Syst. 2017, 1, 37–47. [Google Scholar] [CrossRef]
- Goman, V.; Prakht, V.; Kazakbaev, V.; Dmitrievskii, V. Comparative Study of Energy Consumption and CO2 Emissions of Variable-Speed Electric Drives with Induction and Synchronous Reluctance Motors in Pump Units. Mathematics 2021, 9, 2679. [Google Scholar] [CrossRef]
- Cai, S.; Jin, M.-J.; Hao, H.; Shen, J.-X.A. Comparative study on synchronous reluctance and PM machines. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 607–623. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Carraro, E.; Castiello, M.; Fornasiero, E. Electric vehicle traction based on synchronous reluctance motors. IEEE Trans. Ind. Appl. 2016, 52, 4762–4769. [Google Scholar] [CrossRef]
- Zhao, Y.; Ren, L.; Liao, Z.; Lin, G. A Novel Model Predictive Direct Torque Control Method for Improving Steady-State Performance of the Synchronous Reluctance Motor. Energies 2021, 14, 2256. [Google Scholar] [CrossRef]
- Boldea, I.; Fu, Z.; Nasar, S. Torque vector control (TVC) of axially-laminated anisotropic (ALA) rotor reluctance synchronous motors. Electr. Mach. Power Syst. 1991, 19, 381–398. [Google Scholar] [CrossRef]
- Matsuo, T.; Lipo, T. Field Oriented Control of Synchronous Reluctance Machine. In Proceedings of the 24th Annual IEEE Power Electronics Specialists Conference, Seattle, WA, USA, 20–24 June 1993; pp. 425–431. [Google Scholar]
- Chikhi, A.; Djarallah, M.; Chikhi, K. A comparative study of field-oriented control and direct-torque control of induction motors using an adaptive flux observer. Serb. J. Electr. Eng. 2010, 7, 41–55. [Google Scholar] [CrossRef]
- Rashad, E.; Radwan, T.; Rahman, M. A Maximum Torque Per Ampere Vector Control Strategy for Synchronous Reluctance Motors Considering Saturation and Iron Losse. In Proceedings of the 2004 IEEE Industry Applications Conference (39th IAS Annual Meeting), Seattle, WA, USA, 3–7 October 2004; Volume 4, pp. 2411–2417. [Google Scholar]
- Hackl, C.M.; Kamper, M.J.; Kullick, J.; Mitchell, J. Current Control of Reluctance Synchronous Machines with Online Adjustment of the Controller Parameters. In Proceedings of the IEEE 25th International Symposium on Industrial Electronics (ISIE), Santa Clara, CA, USA, 8–10 June 2016; pp. 153–160. [Google Scholar]
- Lin, F.; Huang, M.; Chen, S.; Hsu, C. Intelligent Maximum Torque per Ampere Tracking Control of Synchronous Reluctance Motor Using Recurrent Legendre Fuzzy Neural Network. IEEE Trans. Power Electron. 2019, 34, 12080–12094. [Google Scholar] [CrossRef]
- Ramon, V.; Antonio, V. PID Control in the Third Millennium: Lessons Learned and New Approaches; Springer: New York, NY, USA, 2012. [Google Scholar]
- Sanz, M.G. Robust Control Engineering: Practical QFT Solutions, 1st ed.; CRC, Taylor & Francis Group: Boca Raton, FL, USA, 2021; pp. 17–78. [Google Scholar]
- Rigatos, G.; Siano, P.; Wira, P.; Hamida, M. An H-infinity approach to optimal control of doubly-fed reluctance machines. IFAC-PapersOnLine 2016, 49, 116–122. [Google Scholar] [CrossRef]
- Nitish, K.; Shiv, N. Automatic Loop Shaping of Robust QFT Controller for Permanent Magnet Stepper Motor using Flower Pollination Algorithm. Int. J. Control Theory Appl. 2016, 9, 85–94. [Google Scholar]
- Lucas, C.; Shanehchi, M.M.; Asadi, P.; Rad, P.M. A Robust Speed Controller for Switched Reluctance Motor with Nonlinear QFT Design Approach. In Proceedings of the Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy, Rome, Italy, 8–12 October 2000; pp. 1573–1577. [Google Scholar]
- Xu, Q.; Huang, J.; Li, H. Gravitational search algorithm-based fractional order QFT control scheme for PMSM. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 4442–4445. [Google Scholar]
- Luis, I.; Pedro, P.; Arturo, M. Robust QFT-based control of DTC-speed loop of an induction motor under different load conditions. IFAC-PapersOnLine 2015, 48, 2429–2434. [Google Scholar]
- Kilthau, A.; Pacas, J.M. Appropriate Models for the Control of the Synchronous Reluctance Machine. In Proceedings of the 37th IAS Annual Meeting Industry Applications Conference, Pittsburgh, PA, USA, 13–18 October 2002; Volume 4, pp. 2289–2295. [Google Scholar]
- Liu, T.H.; Ming-Tsan, U.N. A fuzzy sliding-mode controller design for a synchronous reluctance motor drive. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1065–1076. [Google Scholar]
- Senjyu, T.; Kinjo, K.; Urasaki, N.; Uezato, K. Sensorless Control of Synchronous Reluctance Motors Considering the Stator Iron Loss with Extended Kalman Filter. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 15–19 June 2003; Volume 7445, pp. 403–408. [Google Scholar] [CrossRef]
- Dalibor, I.; Amor, C.; Bojan, Š.; Andrej, S. Robust tracking system design for a synchronous reluctance motor—SynRM based on a new modified bat optimization algorithm algorithm. Appl. Soft Comput. 2018, 69, 568–584. [Google Scholar]
- Lin, C. Adaptive recurrent fuzzy neural network control for synchronous reluctance motor servo drive. IEE Proc. Electr. Power Appl. 2004, 151, 711–724. [Google Scholar] [CrossRef]
- Yahia, K.; Matos, D.; Estima, J.O.; Cardoso, A.J.M. Modeling Synchronous Reluctance Motors including Saturation, Iron Losses and Mechanical Losses. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 18–20 June 2014; pp. 601–606. [Google Scholar]
- Horowitz, I. Synthesis of Feedback Systems; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Garcia-Sanz, M.; Houpis, C.H. Part I: QFT Control, Part II: Wind Turbine Design and Control. In Wind Energy Systems: Control Engineering Design; A CRC Press Book; Taylor & Francis Group: Boca Raton, FL, USA, 2012. [Google Scholar]
- Longdon, L.; East, D.J. A simple geometrical technique for determining loop frequency bounds which achieve prescribed sensitivity specifications. Int. J. Control 1978, 30, 153–158. [Google Scholar] [CrossRef]
- Ballance, D.J.; Hughes, G. A Survey of Template Generation Methods for Quantitative Feedback Theory. In Proceedings of the UKACC International Conference on Control, Exeter, UK, 2–5 September 1996; pp. 172–174. [Google Scholar]
- Garcia-Sanz, M.; Brugarolas, M.J.; Eguinoa, I. Quantitative Analysis of Controller Fragility in the Frequency Domain. In Proceedings of the UKACC 23rd IASTED International Symposium on Modelling, Identiication and Control, Grindelwald, Switzerland, 23–25 February 2004. [Google Scholar]
- Yang, X.-S. Flower Pollination Algorithm for Global Optimization. In Unconventional Computation and Natural Computation 2012; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7445, pp. 240–249. [Google Scholar]
- Valenti, C. Microchip, AN937, Implementing a PID Controller Using a PIC18 MCU. Available online: https://ww1.microchip.com/downloads/en/AppNotes/00937a.pdf (accessed on 14 October 2021).
- Wang, Q.G.; Fung, H.W.; Zhang, Y. PID tuning with exact gain and phase margins. ISA Trans. 1999, 38, 243–249. [Google Scholar] [CrossRef]




| Parameter | Nominal Value | Range of QFT Bounds |
|---|---|---|
| Rs (Stator resistance) | 3.22 Ω | [3, 4] Ω |
| Krm (Iron loss constant) | 10 mΩ/(rad/s) | [5, 15] mΩ/(rad/s) |
| Lq (Q-axis inductance) | 120 mH | [50, 250] mH |
| Ld (D-axis inductance) | 280 mH | [120, 300] mH |
| Krτ (equivalent reluctance torque constant) | 0.96 H.V | [−1.04, 2] H.V |
| Speed | 600 min−1 | N.A.1. |
| Torque | 0.1 Nm | N.A.1. |
| Voltage | 200 V | N.A.1. |
| Current | 1 A | N.A.1. |
| Parameters | Value |
|---|---|
| Switching probability variable (ρ) | 0.8 |
| Size of Population (n) | 50 |
| variable | 1.5 |
| Step size in Levy flight function (step) | 0.01 |
| No. of iteration | 100 |
| Pollen vector (X) | [KP, KI]T |
| Parameters | Value |
|---|---|
| Pole pairs (PP) | 2 |
| Inertia constant (J) | 1.85 × 10−3 Kg.m2 |
| Computational delay for current loop (Td) 1 | 0.3 ms |
| Inverter delay (Tsw) | 0.1 ms |
| Computational delay for speed loop (Twd) 1 | 0.3 ms |
| Simulation sampling time (Ts) | 5 μs |
| Switching frequency (fsw) | 10 kHZ |
| Type of Transient | Proposed PI Design | Conventional PI Design |
|---|---|---|
| Load torque change | 1.32 | 4.955 |
| Reference speed change | 6.82 | 8.218 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poola, R.; Hanamoto, T. Automated QFT-Based PI Tuning for Speed Control of SynRM Drive with Analytical Selection of QFT Control Specifications. Energies 2022, 15, 642. https://doi.org/10.3390/en15020642
Poola R, Hanamoto T. Automated QFT-Based PI Tuning for Speed Control of SynRM Drive with Analytical Selection of QFT Control Specifications. Energies. 2022; 15(2):642. https://doi.org/10.3390/en15020642
Chicago/Turabian StylePoola, Rajesh, and Tsuyoshi Hanamoto. 2022. "Automated QFT-Based PI Tuning for Speed Control of SynRM Drive with Analytical Selection of QFT Control Specifications" Energies 15, no. 2: 642. https://doi.org/10.3390/en15020642
APA StylePoola, R., & Hanamoto, T. (2022). Automated QFT-Based PI Tuning for Speed Control of SynRM Drive with Analytical Selection of QFT Control Specifications. Energies, 15(2), 642. https://doi.org/10.3390/en15020642







