A Quantile Regression Random Forest-Based Short-Term Load Probabilistic Forecasting Method
Abstract
:1. Introduction
- (1)
- The use of a single deep neural network leads to some limitations of the prediction model, and the prediction performance is difficult to improve.
- (2)
- Most of the load point forecasting based on DNN is converted to probabilistic forecasting by linear methods; hence, it is difficult to analyze the nonlinear relationship between load point forecasting results and load probabilistic forecasting results.
- (1)
- For the missing values and outliers of the actual load data, missing data filling and outlier correction technology are used to process the load dataset. Through analyzing the features of short-term power load, the original load series is decomposed by EMD. Then, those load decomposition components are converted into two-dimensional matrices, which are subsequently used as the input of CNN to effectively assist the model to learn local implicit features from the load series with different timescales. Moreover, the similar daily load selection algorithm is used to select the similar daily load as the input of point prediction and probabilistic prediction models to generate additional effective features. The continuous features and discrete features in the dataset are standardized by different standardization approaches. The preprocessed features are used as the input of the model proposed in this paper.
- (2)
- To solve the feature extraction problem of short-term power load point prediction, this paper combines the EMD method with a CNN-LSTM [11] combined model and proposes three short-term load point prediction models based on multi-mode DNN: a point prediction model based on Visual Geometry Group networks (VGGNet) [12] and LSTM [13], a point prediction model based on residual neural networks (ResNet) [14] and LSTM, and a point prediction model based on Inception and LSTM. Specifically, those three short-term load point prediction models adapt VGGNet, ResNet, and Inception subnets to extract spatial features hidden in a two-dimensional load EMD component matrix. Subsequently, the spatial features, load data, and load price are input into the LSTM subnetwork as temporal information. Long-term dependencies between data are captured through the LSTM subnets to estimate the load value for the next hour. Therefore, the three proposed point prediction models can extract multimodal spatial–temporal features with more hidden information.
- (3)
- With regard to the problem of being unable to quantify the uncertainty of load forecasting, this paper puts forward a short-term load probabilistic forecasting method based on random forests with quantile regression. The proposed method uses the three multimodal DNN based point prediction models mentioned above and a similar day load selection algorithm to extract the hidden features of the original data, and then get the representative to extract the features from the prediction of the transition point. Random forest with quantile regression is used to predict short-term power load probability in the form of loci according to transition point prediction results. In order to verify the reliability and effectiveness of the method proposed, the quantile score and Winkler score are used to evaluate the comprehensive index of the probabilistic forecasting result on the actual load of the Singapore electricity market. The analysis indicates that the short-term load probabilistic forecasting method proposed in this paper has higher accuracy and reliability than other baseline approaches.
2. Methodology
2.1. Convolutional Neural Network
- (1)
- VGGNet
- (2)
- GoogLeNet
- (3)
- ResNet
2.2. Long Short-Term Memory
2.3. Quantile Regression
2.4. Quantile Regression Random Forest
3. Implementation
3.1. Data Preparation
- (1)
- Data standardization and transformation
- (2)
- EMD
- (1)
- The difference between the number of extreme points and zero-crossing points is not more than 1;
- (2)
- The average of the upper envelope and the lower envelope must be zero.
- (1)
- Identify all local maxima and minima in a given timeseries ;
- (2)
- According to local extremum, upper envelope and lower envelope are generated by cubic spline interpolation;
- (3)
- Calculate the average sequence of the two envelopes:
- (4)
- Calculate the difference between the initial data and the mean:
- (5)
- Check to see whether it meets the two required properties of the eigenmode function mentioned above:
- (6)
- Take as the new initial time series , and return to step (1). The process terminates when the trend of the final residuals is monotonous.
- (3)
- Similar day load selection
- (1)
- Starting from the historical day nearest to the day i to be predicted, the similarity value between the day to be predicted and the historical day j is reversely calculated daily according to Equations (19) and (20);
- (2)
- Select D days with the highest similarity to the day i to be predicted in the recent N days as its similarity day.
3.2. Point Forecasting Model
- (1)
- Point forecasting model based on VGGNet and LSTM
- (2)
- Point forecasting model based on Inception and LSTM
- (3)
- Point forecasting model based on ResNet and LSTM
3.3. Probabilistic Forecasting Method Based on Quantile Regression Random Forest
4. Numerical Simulations
4.1. Evaluation Indicators
- (1)
- Quantity Score
- (2)
- Winkler Score
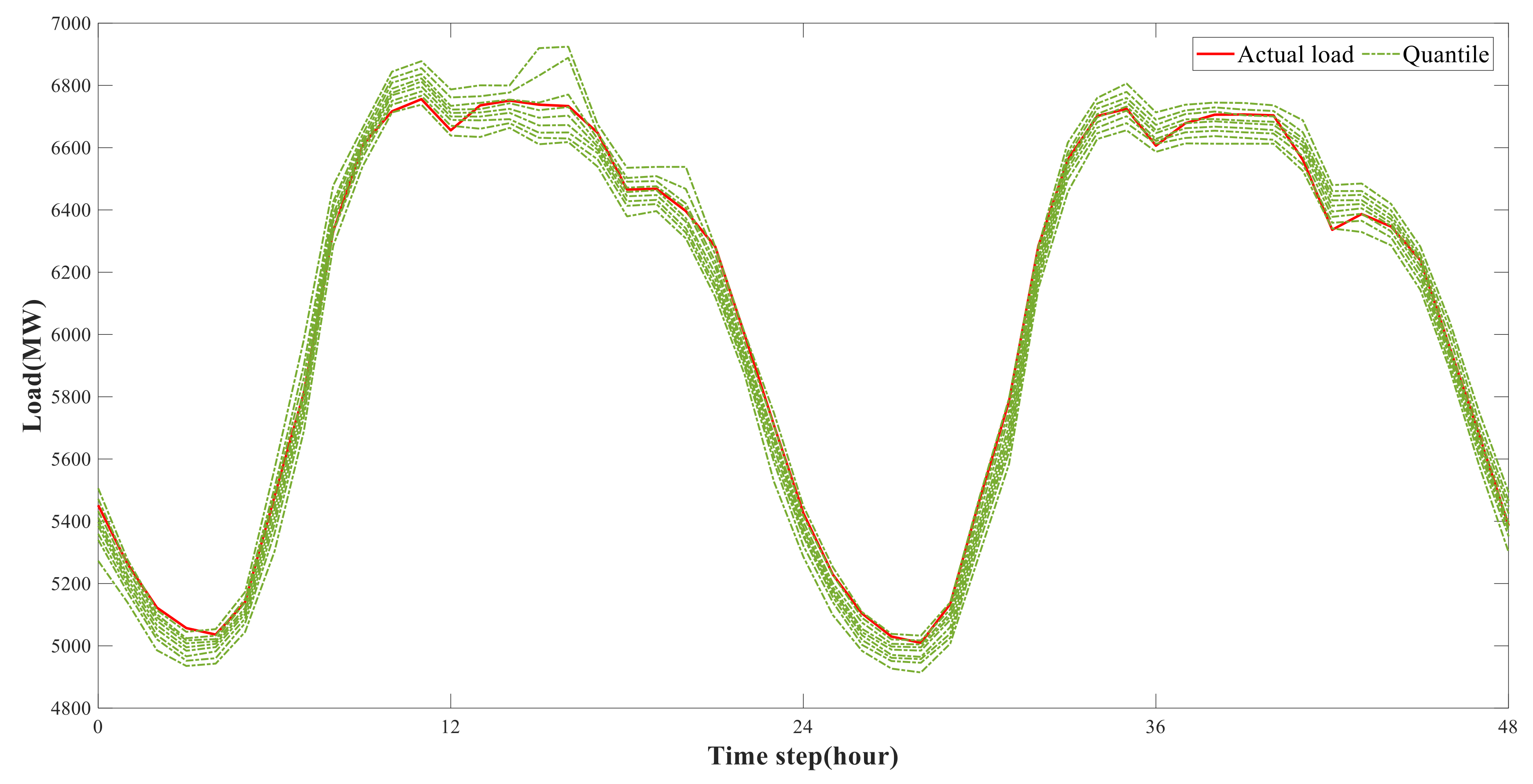
4.2. Forecasting Results and Analysis
- (1)
- Comparison method 1: quantile gradient enhanced regression tree. This method uses a quantile gradient enhanced regression tree to directly predict short-term load probability. The input features are historical load data and related factors, and the output is the quantile of load.
- (2)
- Comparison method 2: quantile regression random forest. The quantile regression random forest was briefly introduced in Section 4.1. This method uses quantile regression random forest to directly predict short-term load probability, and the input features are historical load data and related factors.
- (3)
- Comparison method 3: probabilistic forecasting method based on prediction residual modeling. Firstly, it uses historical load data and related factors to realize a point prediction and obtain the result. Then, the result is used as an additional input feature to describe the conditional distribution of residuals on the point prediction. Finally, the point prediction is combined with the conditional distribution of residuals to obtain the final load probabilistic forecasting result.
5. Conclusions
- (1)
- Although LSTM has a strong performance in processing timeseries modeling tasks, its parameters still have some room for optimization. In order to reduce the computation and time consumption of model training and improve computing efficiency, it should be considered to reduce the parameters while keeping the prediction accuracy unchanged.
- (2)
- In this paper, only historical load, historical load prices, month, week, holiday, and hour information are used to predict the probability of short-term power load. However, in practice, the influencing factors of power load are complicated, and the accurate prediction of short-term power load may not be achieved only by relying on the above features. Therefore, subsequent research needs to consider the influence of other factors on power load such as temperature, humidity, regional economy, and environment, so as to improve the accuracy of short-term load forecasting.
- (3)
- The data used in this paper only correspond to the Singapore National Electricity Market. In future research, different power load datasets can be selected to train and verify the proposed model and method, as well as optimize it to enhance its generalization ability. In addition, it is also necessary to classify the types of electricity users, such as residential, industrial, and commercial, and construct load probabilistic forecasting models for all types of users according to the differences in the behavior characteristics of each type, so as to provide suggestions for personalized electricity sales services.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kang, C.; Wang, Y.; Xue, Y.; Mu, G.; Liao, R. Big Data Analytics in China’s Electric Power Industry: Modern Information, Communication Technologies, and Millions of Smart Meters. IEEE Power Energy Mag. 2018, 16, 54–65. [Google Scholar] [CrossRef]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Kang, C.; Xia, Q.; Liu, M. Load Forecasting of Power System; China Electric Power Press: Beijing, China, 2007. [Google Scholar]
- Li, Z.; Ding, J.; Wu, D.; Wen, F. Integrated extreme learning machine method for power load interval prediction. J. North China Electr. Power Univ. (Nat. Sci. Ed.) 2014, 41, 78–88. [Google Scholar]
- Vossen, J.; Feron, B.; Monti, A. Probabilistic forecasting of household electrical load using artificial neural networks. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, Idaho, 23–28 June 2018; pp. 1–6. [Google Scholar]
- Zhang, J.; Wang, Y.; Sun, M.; Zhang, N.; Kang, C. Constructing probabilistic load forecast from multiple point forecasts: A bootstrap based approach. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 184–189. [Google Scholar]
- Wang, Y.; Gan, D.; Sun, M.; Zhang, N.; Lu, Z.; Kang, C. Probabilistic individual load forecasting using pinball loss guided LSTM. Appl. Energy 2019, 235, 10–20. [Google Scholar]
- Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-term load forecasting with deep residual networks. IEEE Trans. Smart Grid 2018, 10, 3943–3952. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Quan, H.; Srinivasan, D. An improved quantile regression neural network for probabilistic load forecasting. IEEE Trans. Smart Grid 2018, 10, 4425–4434. [Google Scholar] [CrossRef]
- Fan, Y.; Fang, F.; Wang, X. Probability forecasting for short-term electricity load based on LSTM. In Proceedings of the 2019 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Beijing, China, 15–17 August 2019; pp. 516–522. [Google Scholar]
- Song, X.; Yang, F.; Wang, D.; Tsui, K.-L. Combined CNN-LSTM network for state-of-charge estimation of lithium-ion batteries. IEEE Access 2019, 7, 88894–88902. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comp. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Wei, L.; Yangqing, J.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Liu, B.; Nowotarski, J.; Hong, T.; Weron, R. Probabilistic load forecasting via quantile regression averaging on sister Forecasts. IEEE Trans. Smart Grid 2015, 8, 730–737. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 15, 33–50. [Google Scholar] [CrossRef]
- Zhukov, A.; Sidorov, D.N.; Foley, A.M. Random forest based approach for concept drift handling. Commun. Comp. Inf. Sci. 2017. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Meinshausen, N.; Ridgeway, G. Quantile Regression Forests. J. Mach. Learn. Res. 2006, 7, 984–987. [Google Scholar]
- Kurbatsky, V.; Sidorov, D.N.; Spiryaev, V.A.; Tomin, N.V. Forecasting nonstationary time series based on Hilbert—Huang transform and machine learning. Autom. Remote Control 2014, 75, 922–934. [Google Scholar] [CrossRef]
- Kurbatskii, V.; Sidorov, D.N.; Spiryaev, V.A.; Tomin, V.N. On the neural network approach for forecasting of nonstationary time series on the basis of the hilbert-huang transform. Autom. Remote Control. 2011, 72, 1405–1414. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), SanDiego, MA, USA, 7–9 May 2015. [Google Scholar]
- Wang, Y.; Zhang, N.; Tan, Y.; Hong, T.; Kirschen, D.S.; Kang, C. Combining probabilistic load forecasts. IEEE Trans. Smart Grid 2018, 10, 3664–3674. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Quan, H.; Srinivasan, D. Parallel and reliable probabilistic load forecasting via quantile regression forest and quantile determination. Energy 2018, 160, 810–819. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Zhang, N.; Wang, Y. Conditional residual modeling for probabilistic load forecasting. IEEE Trans. Power Syst. 2018, 33, 7327–7330. [Google Scholar] [CrossRef]
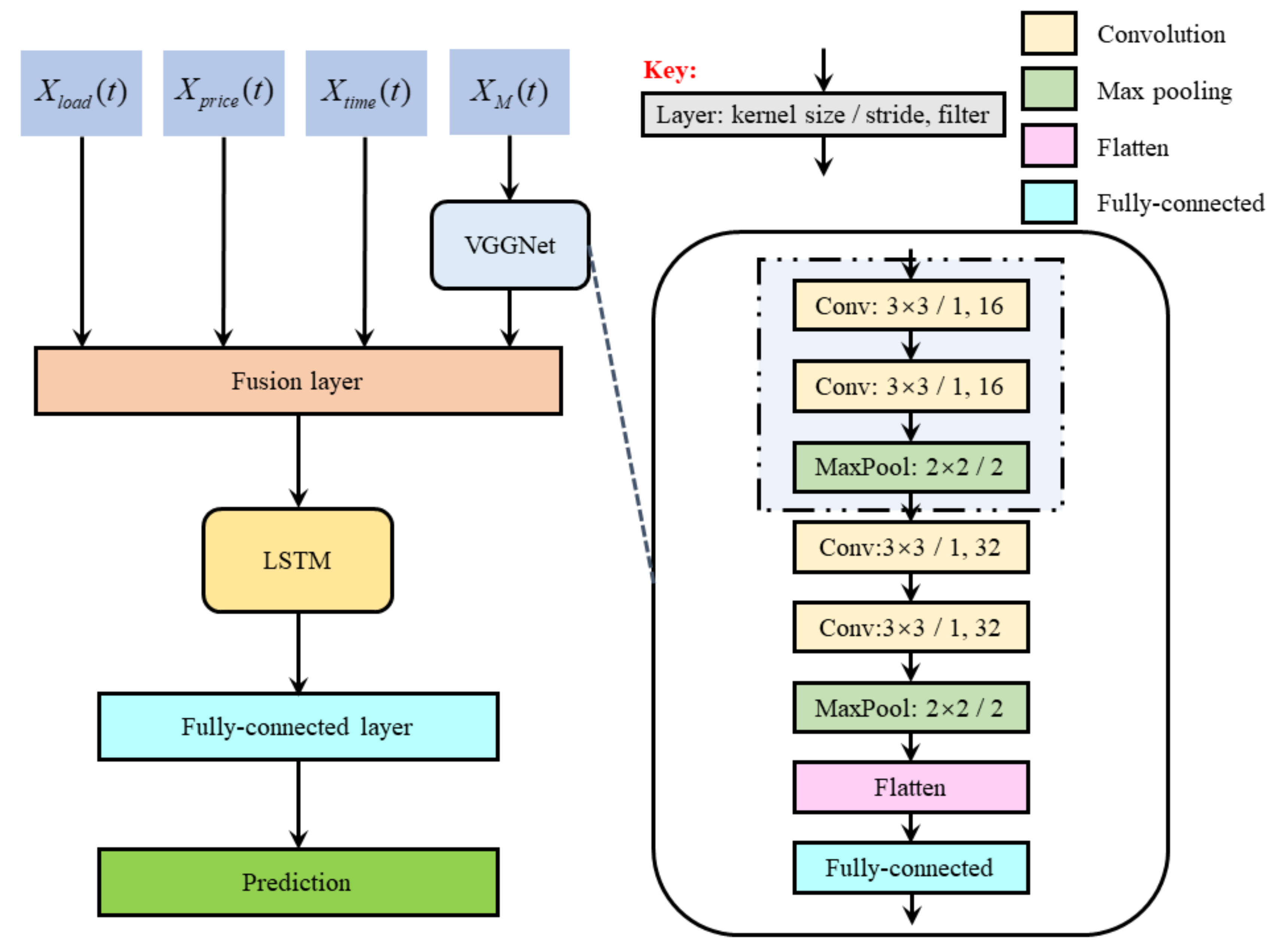


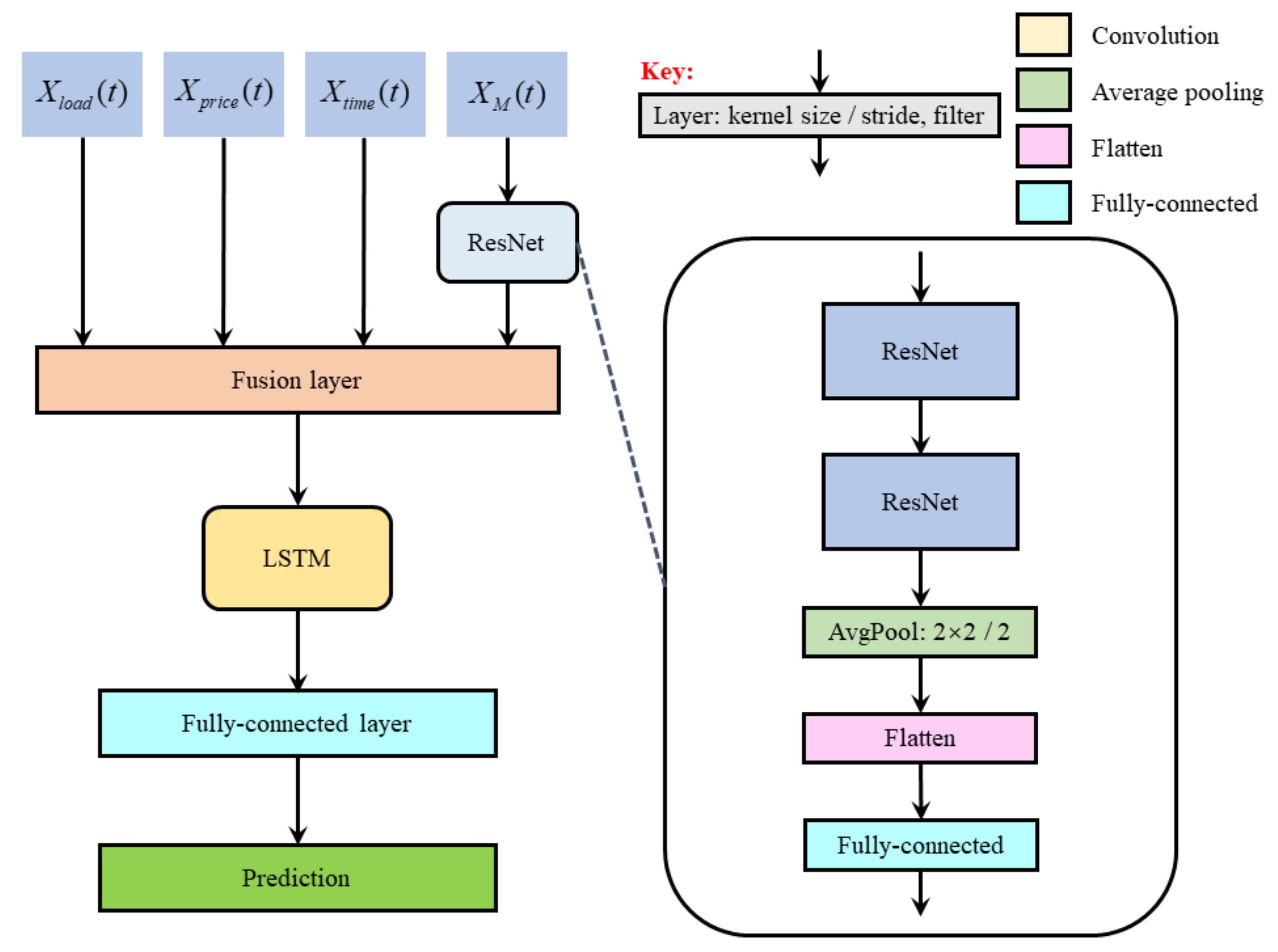



| Variable | Size | Description |
|---|---|---|
| (1,379) | Input vector containing the load and the electricity price information 168 h before , and the time information of the hour, week, month, and holiday at . | |
| (1,344) | Input load influencing factors vector at . | |
| (1,1) | Output forecasting results obtained by the point forecasting sub-model based on VGGNet and LSTM in the feature extraction layer at . | |
| (1,1) | Output forecasting results obtained by the point forecasting sub-model based on Inception and LSTM in the feature extraction layer at . | |
| (1,1) | Output forecasting results obtained by the point forecasting sub-model based on ResNet and LSTM in feature extraction layer at . | |
| (1,4) | Output vector of the forecasting results obtained by the similar day load selection sub-model at . |
| Method | Avg.QS | Avg.WS |
|---|---|---|
| Comparison method 1 | 31.09 | 237.60 |
| Comparison method 2 | 30.37 | 233.18 |
| Comparison method 3 | 27.26 | 198.72 |
| The proposed method | 24.44 | 185.80 |
| Method | α = 20% | α = 40% | α = 60% | α = 80% |
|---|---|---|---|---|
| Comparison method 1 | 599.85 | 296.87 | 237.60 | 247.76 |
| Comparison method 2 | 601.90 | 282.84 | 233.18 | 269.12 |
| Comparison method 3 | 583.45 | 275.05 | 198.72 | 199.91 |
| The proposed method | 503.75 | 238.58 | 185.80 | 204.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, S.; Peng, L.; Zhao, J.; Li, J.; Kong, Z. A Quantile Regression Random Forest-Based Short-Term Load Probabilistic Forecasting Method. Energies 2022, 15, 663. https://doi.org/10.3390/en15020663
Dang S, Peng L, Zhao J, Li J, Kong Z. A Quantile Regression Random Forest-Based Short-Term Load Probabilistic Forecasting Method. Energies. 2022; 15(2):663. https://doi.org/10.3390/en15020663
Chicago/Turabian StyleDang, Sanlei, Long Peng, Jingming Zhao, Jiajie Li, and Zhengmin Kong. 2022. "A Quantile Regression Random Forest-Based Short-Term Load Probabilistic Forecasting Method" Energies 15, no. 2: 663. https://doi.org/10.3390/en15020663
APA StyleDang, S., Peng, L., Zhao, J., Li, J., & Kong, Z. (2022). A Quantile Regression Random Forest-Based Short-Term Load Probabilistic Forecasting Method. Energies, 15(2), 663. https://doi.org/10.3390/en15020663







