A Novel Model for Wind Turbines on Trains †
Abstract
:1. Introduction
- The power generated by the wind turbines must be calculated as a function of time for each second of wind turbine exposure and be subject to real-time analysis. The power () carried by the wind of density (), which moves at a velocity () in relation to the surface area () covered by the wind turbine blades, is:
- Attaching wind turbines to the exterior of trains negatively alters the train’s aerodynamics. The increased surface area will cause increased drag on the train. The train will be continuously slowed and its performance will be degraded.
- To operate at normal speeds with an attached wind turbine, a train would have to consume more energy to overcome the drag. While the train is decelerating, however, the additional drag serves as a merit to the train’s stoppage.
- There is potential to generate energy when the train has come to a complete stop because there may be residual turbine rotation [13]. If the ambient wind speeds meet the operational speed required by the turbines, then energy can be generated for the duration of the stop.
1.1. Literature Review
1.2. Hypothesis
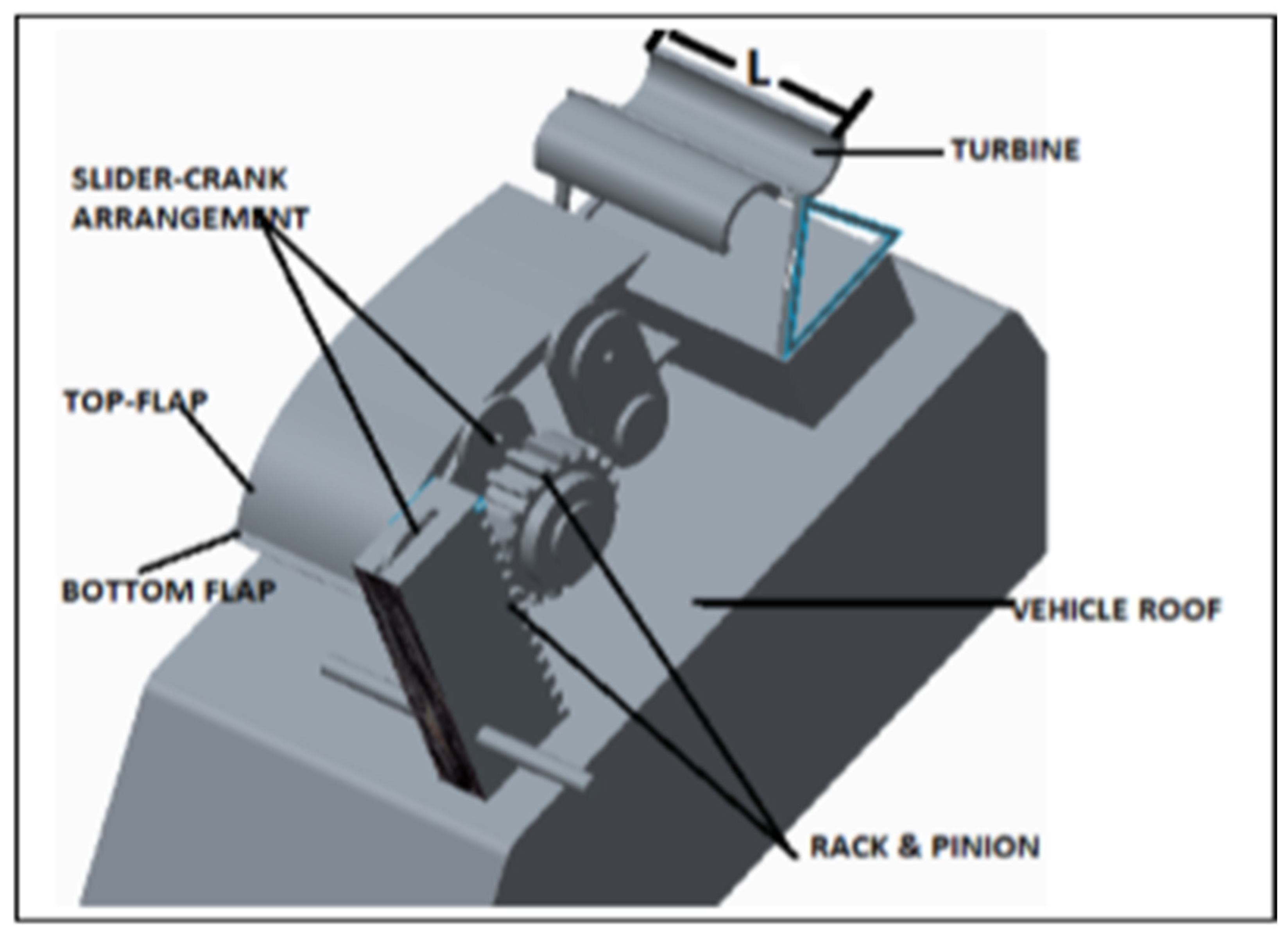
2. Materials and Methods
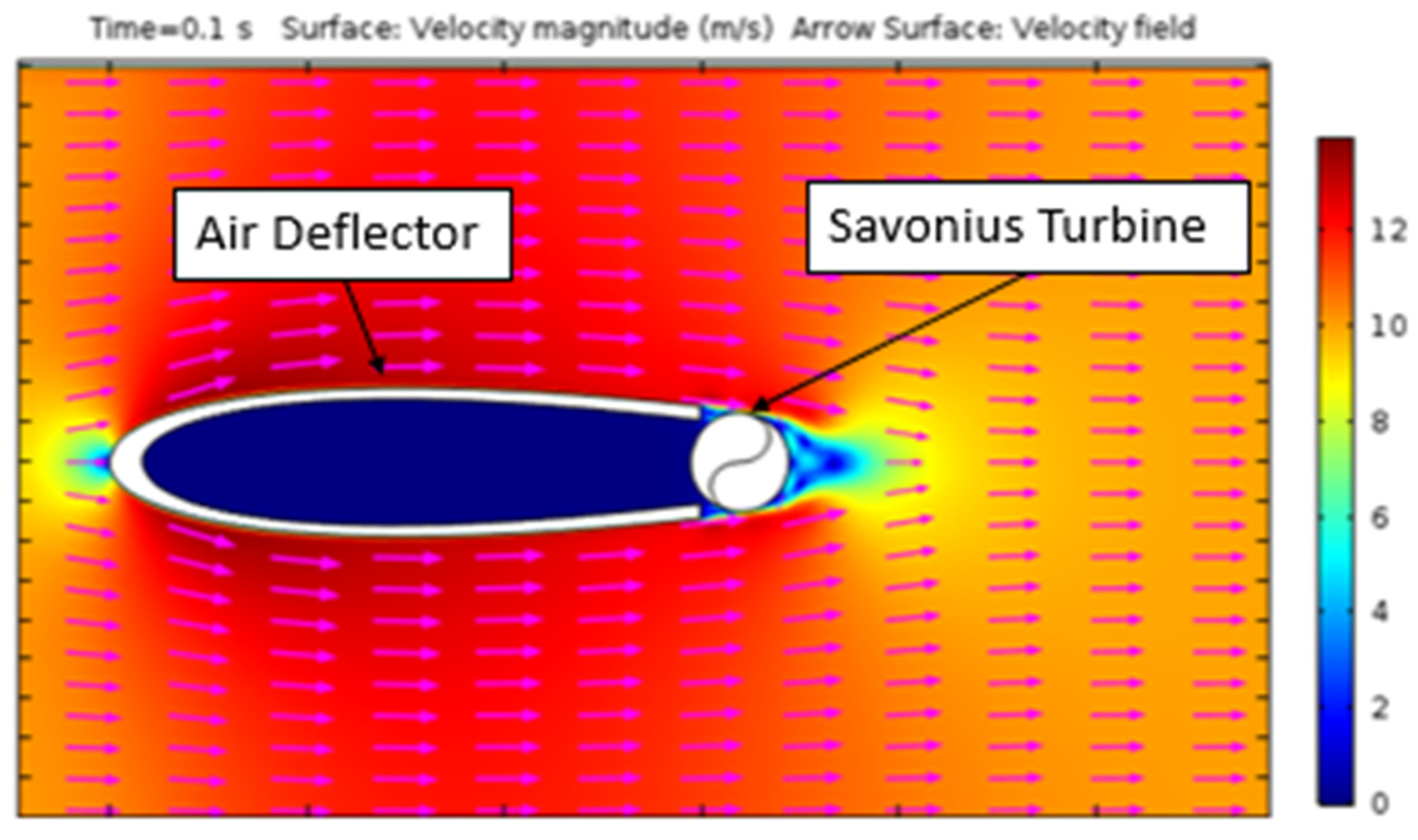
2.1. Drag Force Simulation
2.2. Mathematical Model
2.3. Dataset Sample
2.4. Power Simulation
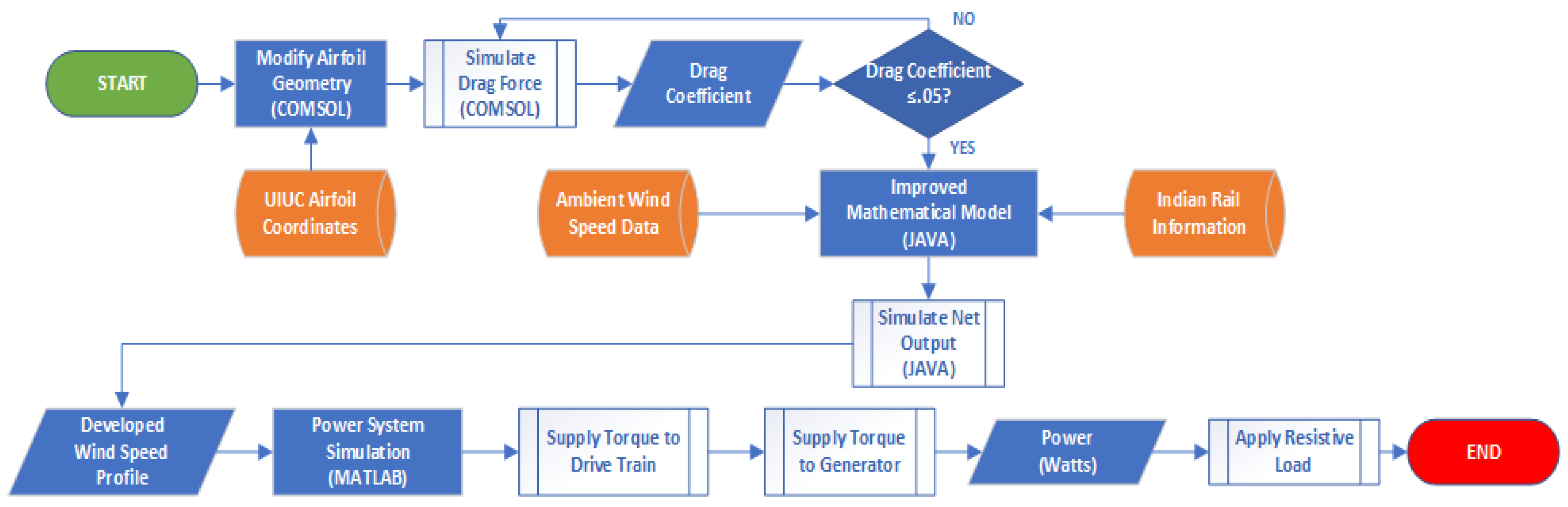
2.5. Improved Modeling Process
- Verification of the drag coefficient assumptions made about the airfoil and wind turbine using CFD software (COMSOL).
- Incorporation of real wind speed data for the geographical area of the case study.
- Incorporation of real train dimensions, speeds, stop durations, stop frequencies, and travel distance.
- Programmatic mathematical modeling of the energy output over time.
- MATLAB simulation of the energy output connected to a real power system to assess power quality.
3. Results and Discussion
3.1. Mathematical Model Results
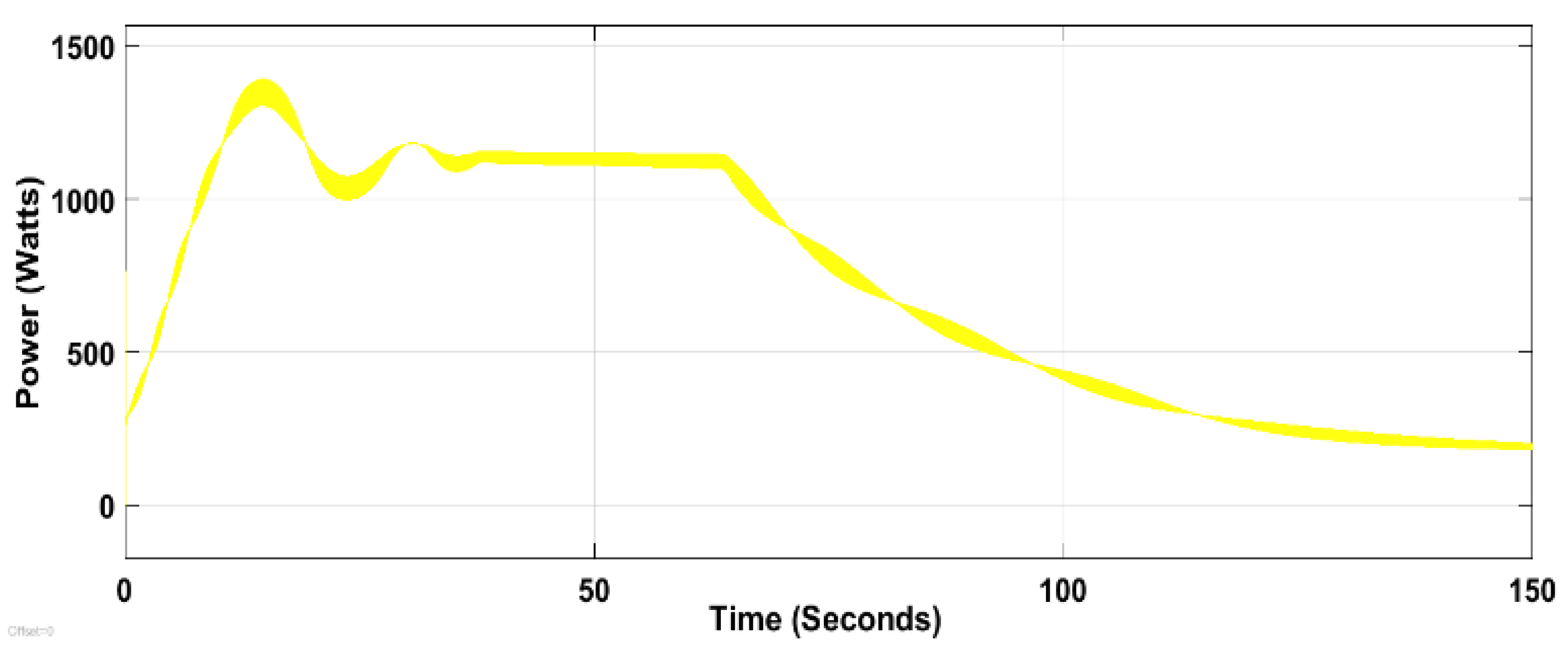
3.2. Power Simulation Results
3.3. Discussion
3.4. Recommendations for Future Research
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Prentiss, M. Energy Revolution; The Belknapp Press of Harvard University Press: Cmbridge, MA, USA; London, UK, 2015; pp. 1–20. [Google Scholar]
- Li, Y.; Qiang, S.; Liao, H.; Xu, Y.L. Wind tunnel test with moving vehicle model for aerodynamic forces of vehicle-bridge systems under cross wind. Presented at the Seventh Asia-Pacific Conference on Wind Engineering, Taipei, Taiwan, 8–12 November 2009. [Google Scholar]
- Cheli, F.; Rocchi, D.; Schito, P.; Tomasini, G. Steady and moving high-speed train crosswind simulations. Comparison with wind-tunnel tests. Presented at the World Congress on Railway Research, Lille, France, 22–26 May 2011; pp. 1–12. [Google Scholar]
- Rekhi, B.S. A Method for Generating Electricity by Capturing wind Induced by Moving Vehicles and a System Therefor. July 2009. Available online: https://patents.google.com/patent/WO2009093265A2/en (accessed on 2 September 2022).
- Prakash, B.; Rahul, A.; Abhijit, D.; Vikrant, D.; Sachin, P.V. Review on Wind Power Generation Through Running Trains. Int. Eng. Res. J. 2016, 2, 519–523. [Google Scholar]
- Aditya, K.V.; Sharma, K. Generation of Electricity through air pressure of running trains. Presented at the 55th IRF International Conference, Pune, India, 22 May 2016. [Google Scholar]
- Bharathi, S.; Balaji, G.; Saravanan, V.A.; Suresh, S. A Method for Generating Electricity by Fast Moving Vehicles. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2012; pp. 2177–2182. [Google Scholar]
- Joshi, S.; Mathur, A.; Jain, A.; Gupta, S.; Jani, N.; Chhabra, B. Generation of Electricity using Wind Energy Produced due to the Motion of Trains. J. Energy Technol. Policy 2012, 2, 19–20. [Google Scholar]
- Chaitanya, P.B.; Gowtham, G. Electricity through Train. J. Electr. Electron. Eng. 2015, 10, 1–6. [Google Scholar]
- Asif, H.; Asrar, H. Parametric Study of Turbine Mounted on Train for Electricity Generation. Int. Res. J. Eng. Technol. 2018, 5, 1783–1786. [Google Scholar]
- Reddy, K.K.; Praveenkumar, K.; Mark, M.P.D. Generating Electricity Through Fast Moving Vehicles; Mahatma Gandhi Institute of Technology: Telangana, India, 2016. [Google Scholar]
- Hyman, M.; Ali, M.H. Improved Modelling for Wind Turbines on Trains,” Paper ID: 2019ISGT0216. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference, Washington, DC, USA, 17–20 February 2019. [Google Scholar]
- Chen, A. Metro Explores New Green Energy Options: Placing a Wind Turbine in a Subway Tunnel. 2014. Available online: http://thesource.metro.net/2014/03/31/metro-explores-new-green-energy/ (accessed on 2 September 2022).
- Tupe, S.M.; Chavan, D.P.; Avhad, C.P.; Pathak, A.K. Power Generation Through Wind Created by Moving Train. J. Adv. Res. Innov. Ideas Educ. 2016, 2, 852–855. [Google Scholar]
- Indian Rail Info: A Busy Junction for Travellers and Rail Enthusiasts. Available online: https://indiarailinfo.com (accessed on 2 September 2022).
- Abbas, M.A.; Anwar, M.; Rana, M.R. Electricity Generation by Fast Moving Vehicles using Wind Turbine (Metro Rail). In Proceedings of the 2021 1st International Conference on Power Electronics and Energy (ICPEE), Bhubaneswar, India, 2–3 January 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Sekhar, Y.R.; Natarajan, M.; Chiranjeevi, C.; Sukanta, R.; Yugandhar, P. Experimental Study on Vertical Axis Wind Turbine to Harness Wind Power from Rapidly Moving Railway Locomotives. In Theoretical, Computational, and Experimental Solutions to Thermo-Fluid Systems; Springer: Singapore, 2021; p. 445. [Google Scholar]
- Kebede, A.B.; Worku, G.B.; Maru, A.T. A Novel Train Roof-Top Wind Energy Conversion System. Int. J. Eng. Res. Afr. 2022, 61, 165–194. [Google Scholar] [CrossRef]
- Dwivedi, R.; Upadhyay, K.; Kumar, A.K.; Kumar, S.A. Proposed Model for the Wind Energy Harnessing System in Trains. Int. J. Appl. Eng. Technol. 2011, 1, 119–126. [Google Scholar]
- Wankhede, V.; Khedkar, D.A.; Limaje, T.A.; Khedkar, D.S.; Mahajan, V.D. A Model for Electricity Generation by Fast Moving Vehicle. Int. J. Science Adv. Res. Technol. 2016, 2, 25–29. [Google Scholar]
- Sindhuja, B. A proposal for implementation of wind energy harvesting system in trains. In Proceedings of the 2014 International Conference on Control, Instrumentation, Energy and Communication (CIEC), Calcutta, India, 31 January–2 February 2014; pp. 696–702. [Google Scholar]
- Chilugodu, N.; Yoon, Y.J.; Chua, K.S.; Datta, D.; Baek, J.D.; Park, T.; Park, W.T. Simulation of train induced forced wind draft for generating electrical power from Vertical Axis Wind Turbine (VAWT). Int. J. Precis. Eng. Manuf. 2012, 13, 1177–1181. [Google Scholar] [CrossRef]
- Kumar, N.; Sharma, V.K. Production of electricity by using turbine mounted on train. Int. J. Concept. Electr. Electron. Eng. 2013, 1, 32–35. [Google Scholar]
- Mahendran, I.; Krishnaprasanth, B.; Gandhimathi, R.; Elakiya, S. A Novel Method to Generate Electricity Using Fast Moving Vehicles Train. Int. J. Res. Appl. Sci. Eng. Technol. 2016, 4, 292–296. [Google Scholar]
- Joshi, A.Y.; Channiwala, S.A. Efficient Generation of Wind Power from Fast-Moving Heavy Vehicles during Deceleration. Int. J. Eng. Res. Technol. (IJERT) 2016, 5, 135–140. [Google Scholar]
- Aymane, D.N.S.E.; Darhmaoui, H. Savonius Vertical Wind Turbine: Design, Simulation, and Physical Testing; School of Science and Engineering: Ifran, Morocco, May 2017. [Google Scholar]
- No. 2011/CEDO/SD/17/O; Standard Schedule of Dimensions. Government of India, Ministry of Railways: New Delhi, India, 21 January 2013.
- Nimvari, M.E.; Fatahian, H.; Fatahian, E. Performance improvement of a Savonius vertical axis wind turbine using a porous deflector. Energy Convers. Manag. 2020, 220, 113062. [Google Scholar] [CrossRef]
- Mauro, S.; Brusca, S.; Lanzafame, R.; Messina, M. CFD modeling of a ducted Savonius wind turbine for the evaluation of the blockage effects on rotor performance. Renew. Energy 2019, 141, 28–39. [Google Scholar] [CrossRef]
- Bethi, R.V.; Laws, P.; Kumar, P.; Mitra, S. Modified Savonius wind turbine for harvesting wind energy from trains moving in tunnels. Renew. Energy 2019, 135, 1056–1063. [Google Scholar] [CrossRef]
- Tjahjana, D.D.; Hadi, S.; Wicaksono, Y.A.; Kurniawati, D.M.; Fahrudin, F.; Utomo, I.S.; Cahyono, S.I.; Prasetyo, A. Study on performance improvement of the Savonius wind turbine for Urban Power System with Omni-Directional Guide Vane (ODGV). J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 55, 126–135. [Google Scholar]
- Bai, H.L.; Chan, C.M.; Zhu, X.M.; Li, K.M. A numerical study on the performance of a Savonius-type vertical-axis wind turbine in a confined long channel. Renew. Energy 2019, 139, 102–109. [Google Scholar] [CrossRef]
- Chan, C.M.; Bai, H.L.; He, D.Q. Blade shape optimization of the Savonius wind turbine using a genetic algorithm. Appl. Energy 2018, 213, 148–157. [Google Scholar] [CrossRef]
- Ahmed, M.; Sharma, S. An investigation on the aerodynamics of a symmetrical airfoil in ground effect. Exp. Therm. Fluid Sci. 2005, 29, 633–647. [Google Scholar] [CrossRef]
- Ali, M.H. Wind Energy Systems: Solutions for Power Quality and Stabilization; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-1-4398-5614-7. [Google Scholar]
- Wind Finder–Wind, Waves and Weather. Available online: https://www.windfinder.com/#9/29.9679/77.5452 (accessed on 1 September 2022).
- Hansen, A.D.; Michalke, G. Modelling and control of variable-speed multi-pole permanent magnet synchronous generator wind turbine. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2008, 11, 537–554. [Google Scholar] [CrossRef]
- Wong, K.H.; Chong, W.T.; Poh, S.C.; Shiah, Y.-C.; Sukiman, N.L.; Wang, C.-T. 3D CFD simulation and parametric study of a flat plate deflector for vertical axis wind turbine. Renew. Energy 2018, 129, 32–55. [Google Scholar] [CrossRef]

| Origin City | Train # | Time (s) | Stops | Average Velocity (m/s) | Carts |
|---|---|---|---|---|---|
| Ahmedabad | 54,805 | 84,000 | 87 | 7.50 | 12 |
| Bareilly | 14,236 | 56,700 | 42 | 9.70 | 15 |
| Beas | 4,918 | 24,000 | 6 | 12.0 | 20 |
| Dindigul | 56,822 | 21,600 | 20 | 10.0 | 15 |
| Gaya | 53,215 | 10,800 | 27 | 8.60 | 14 |
| Nagpur | 51,286 | 36,300 | 45 | 10.8 | 14 |
| New Delhi | 12,952 | 57,000 | 6 | 24.3 | 18 |
| Rewari | 54,784 | 41,100 | 58 | 10.3 | 10 |
| Visakhapatnam | 57,255 | 38,100 | 54 | 9.20 | 13 |
| Origin City | Net Output (KJ) | |
|---|---|---|
| Existing Model | Proposed Model | |
| Ahmedabad | −485 | 1562 |
| Bareilly | −850 | 1945 |
| Beas | −1015 | −544 |
| Dindigul | −255 | 1306 |
| Gaya | 120 | 893 |
| Nagpur | -371 | 3311 |
| New Delhi | −23,882 | −13,097 |
| Rewari | −520 | 2073 |
| Visakhapatnam | −142 | 3374 |
| Parameters | Train Name (Number) | |||
|---|---|---|---|---|
| Gujarat (19033) | Delhi (54033) | New Delhi (12952) | Jabalpur (01704) | |
| Average Velocity (m/s) | 13.07 | 8.90 | 24.3 | 14.0 |
| Time (s) | 22,800 | 18,000 | 57,000 | 82,800 |
| Stops | 25 | 27 | 6 | 19 |
| Turbines | 19 | 9 | 18 | 19 |
| E (kJ) | 296 | 129 | 278 | 244 |
| E1 (kJ) | 3.3 | 5.5 | 0.8 | 1.7 |
| E2 (kJ) | 77 | 22 | 1001 | 460 |
| E3 (kJ) | 25 | 27 | 6 | 19 |
| E4 (kJ) | 3.4 | 12 | 2.9 | 2.6 |
| Enet (kJ) | 194 | 87 | −727 | −233 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyman, M.; Ali, M.H. A Novel Model for Wind Turbines on Trains. Energies 2022, 15, 7629. https://doi.org/10.3390/en15207629
Hyman M, Ali MH. A Novel Model for Wind Turbines on Trains. Energies. 2022; 15(20):7629. https://doi.org/10.3390/en15207629
Chicago/Turabian StyleHyman, Mario, and Mohd Hasan Ali. 2022. "A Novel Model for Wind Turbines on Trains" Energies 15, no. 20: 7629. https://doi.org/10.3390/en15207629
APA StyleHyman, M., & Ali, M. H. (2022). A Novel Model for Wind Turbines on Trains. Energies, 15(20), 7629. https://doi.org/10.3390/en15207629







