3SSC-A-Based Step-Down DC–DC Converters: Analysis, Design and Experimental Validation

Abstract

This paper proposes two non-isolated step-down DC–DC converters based on the type-A three-state switching cell (3SSC-A), resulting in an alternative to the buck and buck-boost classical converters, respectively. The proposed topologies are part of a group of unexplored converters that employ the 3SSC-A, which has the advantages of 3SSC-based converters, such as high power density, reduced current stress on the semiconductors and suitable thermal loss distribution. In this regard, a complete static analysis is performed, including a detailed study of all semiconductor voltage and current efforts and developing loss models for each one. Moreover, by using simulation models, AC sweep analyses validate the dynamic frequency response of each converter’s small-signal models, and PI-based output–voltage closed-loop controllers are duly designed. Finally, the topologies are experimentally validated through the implementation of adequately designed prototypes, achieving efficiency values greater than 91% under several output power rates varying from 50% to 100%.

1. Introduction

The demand for step-down DC–DC converters with high power density, high efficiency, lower cost, and volume has progressively increased [1]. In this scenario, the development of these structures has been driven mainly by the evolution of electric and hybrid vehicles [2,3], electric aircraft [4], the implementation of smart grids [5], and application in equipment such as voltage regulator modules for microprocessors and data centers [6,7], battery chargers [8] and light-emitting diode lamps [9,10]. Although the classic step-down converters have a relatively simple structure and control system, in higher power processing applications, there is a significant current ripple, an increase in semiconductor conduction and switching losses, and a consequent reduction in the overall efficiency of the topology. In this context, researchers have focused on proposing alternatives to overcome the limitations of classic step-down converters, working mainly on the development of non-isolated architectures that, compared to isolated topologies, have the advantage of having higher power density, greater ease of adaptation to different loads and greater efficiency [11].

Therefore, the interleaved buck converters have been applied for point-of-load (POL), operating normally in hard-switching at low voltage and high current. These converters feature high power density and efficiency, fast transient response, reduced cost, and high reliability. Such advantages result from reducing the components’ current stress and cancelling current ripple in input EMI and output filters [12,13,14].

Despite the advantages mentioned, interleaved buck converters have high sensitivity to the phase errors present in interleaving control, which causes the current imbalance in the converter phases, resulting in the non-elimination of the current fundamental component from the switched operation and in the increase of the volume of the EMI filters. Closed-loop interleaving control can ensure current balance, but it requires that the compensators control the currents of each phase, increasing the control system’s complexity and the converter cost [13,14,15,16]. In open-loop interleaving control, the compensator regulates the current in one phase, and the same duty cycle and frequency control the other phase. This implementation is simpler, but small parametric variations between the circuit components, including those resulting from the layout design, cause imbalanced average currents in the phases [16].

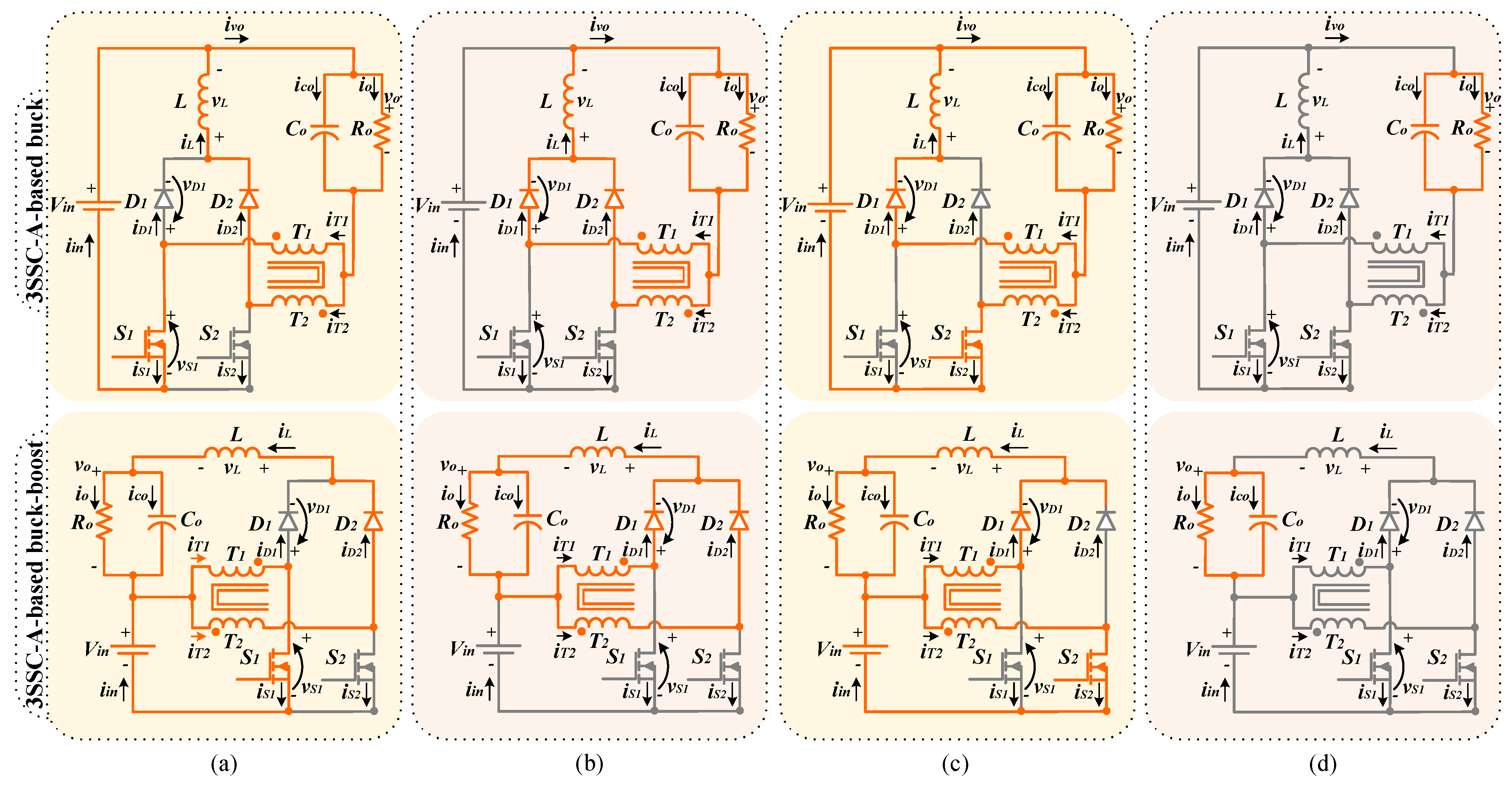
Similar to interleaving solutions, the three-state switching cell (3SSC) was introduced in [17], being an interesting solution for increasing power density with a high-efficiency level and without the need for special control strategies. Since the 3SSC was proposed, a variety of topologies for DC–DC, AC–DC, and DC–AC converters have been presented in the literature [18,19,20,21,22]. All of these approaches present interesting advantages inherent to the application of the 3SSC, i.e., reduction of weight and volume of the filter elements, current stress division between the semiconductors, and distribution of the losses, providing the reduction of the heat-sinks size [23,24,25]. Although the 3SSC uses a high-frequency autotransformer, its dimensions are compact because that element operates in two quadrants of the B-H curve [26]. Furthermore, the operation of the autotransformer naturally doubles the frequency of the inductor current ripple and still ensures that the interleaved currents may be equalized without the need of an active balancer, which does not occur in the classic interleaved converter [22].

It is noteworthy that most of the applications with 3SSC mainly use the type-B cell (3SSC-B) topology [27]. It could be associated with the fact that the 3SSC-B-based buck, boost, and buck-boost converters have a static gain identical to the classic non-isolated converters in the whole range of duty cycle when they operate in continuous conduction mode (CCM).

Therefore, taking into account the reduced amount of research that employs the 3SSC-A and the advantages inherent to the 3SCC applications, this paper contributes to the detailed development and the experimental validation of the 3SSC-A-based buck and buck-boost converters, both operating as step-down DC–DC converters.

In this way, completing the initial study presented by the authors in [28], the proposed research fills a gap related to the exploration and implementation of the 3SSC-A-based DC–DC converters with the following contributions:

• A generalized and detailed static analysis of 3SSC-A-based buck and buck-boost DC–DC converters, including highlights of discontinuous conduction mode (DCM) and critical conduction mode (CRM).
• A complete theoretical and experimental validation of the loss model for both proposed structures, including a study of voltage and current stresses in semiconductors.
• Development and validation of small-signal equivalent models and verification of the dynamic response of the closed-loop control scheme by simulation results.
• A detailed experimental validation by implementing prototypes for each proposed converter, operating under several power rangers at the load side.

This paper is organized as follows: Section 2 describes the analysis of the converters, including loss models, dynamic models, and control systems design. Section 3 presents the experimental validations, which is followed by the final considerations.

2. The 3SSC-A-Based Buck and Buck-Boost: Static Analysis

Figure 1 illustrates the 3SSC-A-based buck and buck-boost converters, which consist of an autotransformer with two windings ($T_1$, $T_2$), two switches ($S_1$, $S_2$), two diodes ($D_1$, $D_2$), one inductor (L), and one output capacitor ($C_o$) connected in parallel with the equivalent load ($R_o$). Similar to the 3SSC-A-based boost converter presented in [28], the 3SSC-A-based step-down topologies do not operate with a duty cycle equal to or greater than 0.5, as an overlap between the pulses will cause a short circuit between the autotransformer terminals through switches $S_1$ and $S_2$. Additionally, in this section, to analyze the operating principle of the converters, it is considered that both operate in a steady state and all components are ideal.

2.1. Operation Principle

The operation principle study of the 3SSC-A-based buck and buck-boost converters is accomplished under CCM, DCM and CRM, with the help of Figure 1, Figure 2 and Figure 3. $V_{G{S}_{1,2}}$ are the gating signals for $S_1$ and $S_2$, which are 180${}^{\circ }$ phase shifted. $i_{in}\left(t\right)$ is the input current. $i_{S_1}\left(t\right)$ and $i_{D_1}\left(t\right)$ are the currents in switch $S_1$ and diode $D_1$, respectively. $i_L\left(t\right)$ and $v_L\left(t\right)$ represent the current and voltage in the inductor. $v_{S_1}\left(t\right)$ and $v_{D_1}\left(t\right)$ are the voltages on switch $S_1$ and diode $D_1$, respectively. In addition, $i_o\left(t\right)$ is the load current and $i_{C_o}\left(t\right)$ is the current in the capacitor. It is noteworthy that the waveforms in Figure 2 and Figure 3 are not on the same scale.

2.1.1. CCM

The equivalent circuit stages in CCM and the main theoretical waveforms, defined according to four operation stages, are shown in Figure 1a–c, Figure 2a and Figure 2b, respectively.

First Stage ($t_0<t<t_1$)

As shown in Figure 1a, during the first stage, the switch $S_1$ and diode $D_2$ are conducting. At this instant, the inductor L is storing energy. As the turns ratio of the autotransformer is unitary, this implies the proper balance of currents and voltages in its windings. For the 3SSC-A-based buck converter, the voltage on the windings $T_1$ and $T_2$ are equal to $V_{in}-V_o$. Meanwhile, for the 3SSC-A-based buck-boost structure, the voltage on the windings $T_1$ and $T_2$ are equal to $-V_{in}$.

Second Stage ($t_1<t<t_2$)

As shown in Figure 1b, the second stage for both converters is characterized by the commutation of the diode $D_1$ to state on, while diode $D_2$ remains turned on. $S_1$ is turned off, and $S_2$ remains turned off. At this instant, the inductor L supplies energy to the load. Due to the short circuit between the terminals of windings $T_1$ and $T_2$, the magnetic flux in the autotransformer core is null.

Third Stage ($t_2<t<t_3$)

The third stage is similar to the first stage, where the switch $S_2$ is turned on, and $S_1$ remains turned off. The diode $D_1$ remains turned on and $D_2$ is turned off. The equivalent circuits to the converters are shown in Figure 1c.

Fourth Stage ($t_3<t<T_s$)

This stage is identical to the second stage, as shown in Figure 1b, where the current through the inductor L flows through the diodes $D_1$, $D_2$, and the autotransformer windings.

According to the waveforms presented in Figure 2a,b, it is verified that the current in the inductor does not become zero in any operating stage, thus characterizing the CCM. Although the operating principle of the converters is similar, the arrangement of the elements in each structure changes the maximum voltage stress to which the semiconductors are subjected. In the 3SSC-A-based buck converter, the maximum voltage blocking of the semiconductors has a module equal to $2(V_{in}-V_o)$. Meanwhile, for the 3SSC-A-based buck-boost structure, the maximum voltage stress in the semiconductors has a module equal to $2V_{in}$.

2.1.2. DCM

In this operating mode, the converters have six operating steps, with the respectively equivalent waveforms shown in Figure 3a,b. Some of the operation stages in DCM are equivalent to the CCM, and these will not be described in detail.

First Stage ($t_0<t<t_1$)

This stage is identical to the first stage in CCM.

Second Stage ($t_1<t<t_2$)

This stage is identical to the second stage when the converters are operating in CCM.

Third Stage ($t_2<t<t_3$)

As shown in Figure 1d, in this stage, the current in the inductor becomes zero, the switches remain turned off, and diodes are turned off. Thus, only the output capacitor $C_o$ supplies energy to the load.

Fourth Stage ($t_3<t<t_4$)

This operation stage is identical to the third stage of the CCM.

Fifth Stage ($t_4<t<t_5$)

This operation stage is identical to the fourth stage of the CCM.

Sixth Stage ($t_5<t<T_s$)

This stage of operation is identical to the third stage of the DCM.

In Figure 3a,b, it is verified that the current in the inductor is null during the third and sixth operation stages, characterizing the DCM. Additionally, in this operating mode, the semiconductors of the respective converters are subjected to the same voltage stresses presented in the CCM.

2.1.3. CRM

In this mode, maintaining the 180-degree delay, each switch is turned on at the exact moment when the current in the inductor becomes null, causing the current increases again. The inductor current becomes null every half-time, so the minimum current $I_m$ is equal to zero, and the current ripple $\Delta I_L$ in the inductor is equal to its maximum current $I_M$. The first and second operation stages in CRM are equivalent to the first and second stages in DCM, respectively.

2.1.4. Output Characteristic of the Converters

The static gain expressions for the converters operating in CCM, DCM, and CRM are presented in

Table 1. Static Gain.

Static Gain	3SSC-A-Based Buck	3SSC-A-Based Buck-Boost
$G_{v_{CCM}}$	${\displaystyle \frac{2D}{1+2D}}$	${\displaystyle 2D}$
$G_{v_{DCM}}$	${\displaystyle \frac{D^2}{\gamma +D^2}}$	${\displaystyle \frac{D^2}{\gamma +2D^2}}$
$G_{v_{CRM}}$	${\displaystyle \frac{1}{1+\frac{1}{\left(\frac{1}{2}\pm 2\sqrt{\frac{1}{16}-\gamma }\right)}}}$	${\displaystyle \frac{1}{2}\pm 2\sqrt{\frac{1}{16}-\gamma }}$

.

Here, $I_o$ is the average output current, $f_s$ is the switching frequency, D is the duty cycle, and $\gamma$ represents the normalized output current, defined in (1).

$$\gamma =\frac{L{I}_o{f}_s}{V_{in}}$$

(1)

From the equations in Table 1, the static gain curves of the proposed converters are presented in Figure 4. Analogously to the classic buck and buck-boost converters, the output voltage of the converters under analysis is also a function of the load current in DCM. For the 3SSC-A-based buck converter, the maximum static gain in CRM occurs at $\gamma$ = 0.0625 and D = 0.25. In contrast, for the classic buck converter, the maximum static gain in CRM is verified when $\gamma$ = 0.25 and D = 0.5. So, this implies that the CCM region is wider for the 3SSC-A-based buck structure, so the inductance becomes 1/4 of that required for the classic buck converter for the same operating point.

Making the same analogy with the 3SSC-A-based buck-boost converter, the maximum static gain in CRM also occurs at $\gamma$ = 0.0625 and D = 0.25. Whereas, for the classic buck-boost converter, the maximum static gain in CRM is verified when $\gamma$ = 0.125 and D = 0.5. Therefore, the CCM region is also wider for the 3SSC-A-based buck-boost structure, requiring only half the inductance required by the classic buck-boost converter. Additionally, contrasting the two proposed topologies, it is verified that the CCM region is larger for the 3SSC-A-based buck-boost converter, with maximum voltage gain equal to unity, while the 3SSC-A-based buck structure reaches only half.

2.1.5. Filter Elements

From the steady-state analysis presented earlier, applying Kirchhoff’s voltage law to the equivalent circuits of Figure 1a, the equation relating the duty cycle and the current ripple $\Delta I_L$ in the inductors is obtained and exhibited in the following expressions for the 3SSC-A-based buck and buck-boost converters:

$$\Delta I_L=\frac{(1-2D)V_o}{2L{f}_S}$$

(2)

The normalized current ripple $\overline{\Delta I_L}$ for the 3SSC-A-based buck and buck-boost converters is given by Equations (3) and (4), respectively. These expressions are plotted in Figure 5, where it can be seen that the maximum value for the 3SSC-A-based buck converter occurs at D = 0.25, while for the 3SSC-A-based buck-boost structure, it occurs at D = 0.2072.

$${\overline{\Delta I_L}}_{3SSCA-buck}=\frac{L{f}_S\Delta I_L}{V_{in}}=\frac{(1-2D)D}{(1+2D)}$$

(3)

$${\overline{\Delta I_L}}_{3SSCA-buck-boost}=\frac{L{f}_S\Delta I_L}{V_{in}}=(1-2D)D$$

(4)

Compared to the 3SSC-A-based buck-boost converter, the 3SSC-A-based buck structure shows lower overall inductor current ripple; consequently, considering the same operating point, it will result in lower inductor losses.

The inductance L for the two converters is determined by reorganizing (2), according to (5).

$$L=\frac{(1-2D)V_o}{2\Delta I_L{f}_S}$$

(5)

The critical inductance $L_{crit}$ that corresponds to the threshold value of inductance between CCM and DCM is described in (6). From Figure 4, for both converters, the threshold value of $\gamma$ is 0.0625, and the critical inductance is calculated by replacing this value in (1).

$$L_{crit}=\frac{V_{in}}{{\gamma }_{thr}{I}_o{f}_s}=\frac{V_{in}}{16I_o{f}_s}$$

(6)

By using the voltage ripple equation, the value of output capacitor $C_o$ can be obtained as follows:

$$C_{o_{3SSCAbuck}}⩾D\left(\frac{1-2D}{1+2D}\right)\frac{P_o}{V_o\Delta V_o{f}_S}$$

(7)

$$C_{o_{3SSCA-buck-boost}}⩾\frac{(1-2D)}{32}\frac{V_o}{L{f}_S^2\Delta V_o}$$

(8)

where $\Delta V_o$ is the voltage ripple of the capacitor.

2.2. Autotransformer Design

For the autotransformer design procedure, the same methodology presented in [28] is considered, starting with an equation that defines the core product $A_e{A}_w$ as a function of the electromagnetic parameters of the converter.

2.3. Component Voltage and Current Stresses in CCM

Table 2. Average and RMS components currents for 3SSC-A-based buck and buck-boost converters.

Parameter	3SSC-A-Based Buck	3SSC-A-Based Buck-Boost
RMS value of $T_1$-$T_2$ current ($I_{Trms}$)	$\sqrt{\frac{1}{12}(1+6D)\left(\frac{\Delta {I_L}^2}{4}+3{\left(\frac{I_o}{1+2D}\right)}^2\right)}$	$\sqrt{\frac{1}{12}(1+6D)\left(3I_o^2+\frac{\Delta {I_L}^2}{4}\right)}$
Avg value of $T_1$-$T_2$ current ($I_{Tavg}$)	${\displaystyle \frac{I_o}{2}}$	${\displaystyle \frac{(1+2D)I_o}{2}}$
RMS value of L current ($I_{Lrms}$)	${\displaystyle \sqrt{{\left(\frac{I_o}{1+2D}\right)}^2+\frac{\Delta {I_L}^2}{12}}}$	${\displaystyle \sqrt{I_o^2+\frac{\Delta {I_L}^2}{12}}}$
Avg value of L current ($I_{Lrms}$)	${\displaystyle \frac{I_o}{(1+2D)}}$	${\displaystyle I_o}$
RMS value of $C_o$ current ($I_{Crms}$)	${\displaystyle \sqrt{2D(1-2D)I_L^2+(1+6D)\frac{\Delta I_L^2}{12}}}$	${\displaystyle \sqrt{\frac{\Delta {I_L}^2}{12}}}$

summarizes the current efforts on the magnetic components and on the capacitor of the proposed converters.

Table 3. Voltage Stress across Semiconductors.

Parameter	3SSC-A-Based Buck	3SSC-A-Based Buck-Boost
Maximum Voltage in $S_1$-$S_2$ $\left(V_{S_{\left(max\right)}}\right)$	$2(V_{in}-V_o)$	$2V_{in}$
Maximum Voltage in $D_1$-$D_2$ $\left(V_{D_{\left(max\right)}}\right)$	$-2(V_{in}-V_o)$	$-2V_{in}$

summarizes the maximum voltage stress across all power semiconductors during a period of operation of the 3SSC-A-based buck and buck-boost converters.

From the perspective of equivalent operating points, comparing the topologies proposed in Table 3, it can be seen that the semiconductors of the 3SSC-A-based buck-boost converter are subject to higher voltage stress. The average and RMS values of the switches and diodes currents are shown in

Table 4. Average and RMS Semiconductors Currents for 3SSC-A-based Buck and Buck-Boost converters.

Parameter	3SSC-A-Based Buck	3SSC-A-Based Buck-Boost
RMS value of $S_1$-$S_2$ current ($I_{S_{rms}}$)	${\displaystyle \sqrt{D\left({\left(\frac{I_o}{1+2D}\right)}^2+\frac{\Delta I_L^2}{12}\right)}}$	${\displaystyle \sqrt{D\left(I_o^2+\frac{\Delta I_L^2}{12}\right)}}$
Avg value of $S_1$-$S_2$ current ($I_{S_{avg}}$)	${\displaystyle \frac{D{I}_o}{1+2D}}$	${\displaystyle D{I}_o}$
RMS value of $D_1$-$D_2$ current ($I_{D_{rms}}$)	${\displaystyle \sqrt{\frac{1}{12}(1+2D)\left(3{\left(\frac{I_o}{1+2D}\right)}^2+\frac{\Delta I_L^2}{4}\right)}}$	${\displaystyle \sqrt{\frac{1}{12}(1+2D)\left(3I_o^2+\frac{\Delta I_L^2}{12}\right)}}$
Avg value of $D_1$-$D_2$ current ($I_{D_{avg}}$)	${\displaystyle \frac{I_o}{2(1+2D)}}$	${\displaystyle \frac{I_o}{2}}$

.

2.4. Power Losses

The power losses in the proposed converters can be divided into five main groups: (I) conduction ($P_{S_{\left(cond\right)}}$) and switching ($P_{S_{\left(sw\right)}}$) losses in the switches, (II) conduction ($P_{D_{\left(cond\right)}}$) and reverse recovery ($P_{D_{\left(sw\right)}}$) losses in the diodes, (III) ohmic ($P_{Tcopper}$) and core losses ($P_{Tcore}$) in the autotranformer, (IV) ohmic ($P_{Lcopper}$) and core losses ($P_{Lcore}$) in the inductor and (V) capacitor losses ($P_C$). Such losses are described following the methodology presented in [28]; therefore, the set of equations to calculate the theoretical losses of the converters is given by:

$$P_{S_{\left(cond\right)}}=V_{C{E}_{\left(sat\right)}}{I}_{S_{AVG}}$$

(9)

$$P_{S_{\left(sw\right)}}=\frac{f_s}{2}{V}_{{CE}_{\left(max\right)}}{I}_{S_{peak}}(t_{on}+t_{off})$$

(10)

$$P_{D_{\left(cond\right)}}=V_F{I}_{D_{AVG}}+R_D{I}_{D_{RMS}}^2$$

(11)

$$P_{D_{\left(sw\right)}}=\frac{f_s}{2}{t}_{rr}{I}_r{V}_{D\left(max\right)}$$

(12)

$$P_{Tcopper}=\frac{2{\rho }_{cu}{l}_{wdg}{I}_{T_{RMS}}^2}{n{A}_{cu}}$$

(13)

$$P_{Tcore}=P_{Lcore}=4^{\alpha }k{\left(2f_s\right)}^{\alpha }{B}_{pk}^{\beta }{M}_{core}$$

(14)

$$P_{Lcopper}=\frac{{\rho }_{cu}{l}_{wdg}{I}_{L_{RMS}}^2}{n{A}_{cu}}$$

(15)

$$P_C=I_{C_{RMS}}^{2}ESR$$

(16)

where these losses are calculated by using the following variables: peak of the current switch ($I_{S_{peak}}$), collector–emitter saturation voltage ($V_{{CE}_{\left(sat\right)}}$), turn-on ($t_{on}$) and turn-off ($t_{on}$) switching times, forward voltage ($V_F$), dynamic resistance ($R_D$), reverse recovery time ($t_{rr}$), maximum instantaneous reverse current ($I_r$), copper resistivity constant (${\rho }_{cu}$), length of winding ($l_{wdg}$), number of litz wires (n), core cross-sectional ($A_{cu}$), equivalent series resistance ($ESR$), core mass ($M_{core}$) and half of the peak AC flux density ($B_{pk}$). In addition, for the magnetic losses, k, $\alpha$, and $\beta$ are extracted from the core losses per volume unit based on the value of flux density and frequency from the datasheet provided by the manufacturer.

2.5. Transfer Function and Control Design

For the analysis of the dynamic characteristics of the proposed converters, aiming at the implementation of the linear control techniques, the AC modeling approach proposed by [29] was applied. Considering the CCM operation stages presented in Section 2.1.1, the output voltage and the inductor current are denoted together by the state vector $x\left(t\right)=[i_L\left(t\right)$$v_o\left(t\right)]$. Therefore, from the temporal dynamics of the 3SSC-A-based buck structure, (17) and (18) are obtained.

$$\frac{dx\left(t\right)}{dt}=\left[\begin{array}{cc}0& -\frac{2}{L}\\ \frac{2}{C_o}& -\frac{1}{R_o{C}_o}\end{array}\right]x\left(t\right)+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}\left(t\right)$$

(17)

during $t_0<t<t_1$ and $t_2<t<t_3$.

$$\frac{dx\left(t\right)}{dt}=\left[\begin{array}{cc}0& -\frac{1}{L}\\ \frac{1}{C_o}& -\frac{1}{R_o{C}_o}\end{array}\right]x\left(t\right)+\left[\begin{array}{c}0\\ 0\end{array}\right]v_{in}\left(t\right)$$

(18)

during $t_1<t<t_2$ and $t_3<t<T_s$.

Likewise, from the temporal dynamics of the 3SSC-A-based buck-boost converter, (19) and (20) are obtained.

$$\frac{dx\left(t\right)}{dt}=\left[\begin{array}{cc}0& -\frac{1}{L}\\ \frac{1}{C_o}& -\frac{1}{R_o{C}_o}\end{array}\right]x\left(t\right)+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}\left(t\right)$$

(19)

during $t_0<t<t_1$ and $t_2<t<t_3$.

$$\frac{dx\left(t\right)}{dt}=\left[\begin{array}{cc}0& -\frac{1}{L}\\ \frac{1}{C_o}& -\frac{1}{R_o{C}_o}\end{array}\right]x\left(t\right)+\left[\begin{array}{c}0\\ 0\end{array}\right]v_{in}\left(t\right)$$

(20)

during $t_1<t<t_2$ and $t_3<t<T_s$.

For (17)–(20), by applying the state-space average modelling method, and considering $D^{\prime }=(0.5-D)$, matrix A, B and C are obtained for each proposed converter as follows:

• 3SSC-A-based buck:

  $$\mathbf{A}=\left[\begin{array}{cc}0& \frac{1+2D}{L}\\ \frac{1+2D}{C_o}& -\frac{1}{R_o{C}_o}\end{array}\right];\mathbf{B},=\left[\begin{array}{c}\frac{2D}{L}\\ 0\end{array}\right];\mathbf{C}=\left[\begin{array}{cc}0& 1\end{array}\right]$$

  (21)
• 3SSC-A-based buck-boost:

  $$\mathbf{A}=\left[\begin{array}{cc}0& -\frac{1}{L}\\ \frac{1}{C_o}& -\frac{1}{R_o{C}_o}\end{array}\right];\mathbf{B}=\left[\begin{array}{c}\frac{2D}{L}\\ 0\end{array}\right];\mathbf{C}=\left[\begin{array}{cc}0& 1\end{array}\right]$$

  (22)

Thus, using the small-signal perturbations and linearizing around the equilibrium point, the small-signal AC equivalent circuit of the converters was obtained, as shown in Figure 6. From this circuit, the control-to-output transfer function of the converters is obtained and described by (23) and (24), whose validation by the AC sweep analysis performed in the PSIM software (UNESP, Ilha Solteira, Brazil) is shown in Figure 7a and Figure 8a.

$$G_{v{d}_{buck}}\left(s\right)=\frac{V_o}{(1+2D)D}·\frac{1+s\frac{2DL}{{(1+2D)}^2{R}_o}}{s^2\frac{C_{o}L}{{(1+2D)}^2}+s\frac{L}{{(1+2D)}^2{R}_o}+1}$$

(23)

$$G_{v{d}_{buck-boost}}\left(s\right)=\frac{2V_{in}}{s^{2}L{C}_o+s\frac{L}{R_o}+1}$$

(24)

Analyzing the transfer function $G_{vd}\left(s\right)$ of the 3SSC-A-based buck converter, we can see the presence of two poles and a zero, all in the left-half plane, characterizing a system of minimum phase. Unlike the $G_{vd}\left(s\right)$ transfer functions of the classic buck and 3SSC-B-based buck converters, the presence of the zero in the 3SSC-A-based buck structure equation promotes a phase advance, making the step response of the less oscillatory system. Additionally, the absence of right-half-plane (RHP) zeros allows the controller design for the 3SSC-A-based buck converter to be simplified, making it possible to obtain a satisfactory dynamic response without needing additional control loop implementation.

The transfer function $G_{vd}\left(s\right)$ of the 3SSC-A-based buck-boost structure is identical to that of the 3SSC-A-based boost [28] topology, thus presenting the characteristic of a minimum phase system due to the absence of right-half-plane zeros. In this way, as mentioned for the 3SSC-A-based buck converter, the implementation of the control design for the 3SSC-A-based buck-boost structure also becomes simplified. Additionally, it is observed that the 3SSC-A-based buck-boost topology has dynamic characteristics that differ from the classic buck-boost and 3SSC-B buck-boost converters [30]. However, the dynamic response is similar to that presented by the classical buck structure operating in CCM, which is mathematically proven by the transfer function expressed in (24).

With the voltage loop transfer functions obtained, the voltage compensators were designed to guarantee satisfactory stability margins both in terms of gain and phase. Thus, using the design specifications in

Table 5. Design specifications.

Parameter	3SSC-A-Based Buck		3SSC-A-Based Buck-Boost
Input Voltage ($V_{in}$)	180 V		180 V
Output Voltage ($V_o$)	48 V		96 V
Output Power ($P_o$)	300 W		600 W
Switching Frequency ($f_s$)	50 kHz		50 kHz
Current Ripple ($\Delta I_L$)	0.15$I_o$		0.15$I_o$
Voltage Ripple ($\Delta V_o$)	0.065$V_o$		0.0055$V_o$
Inductor (L)	L = 444.3 µH, core NEE-42/21/15-IP12 by Thornton, N = 41 turns − 7 × AWG25	$\alpha$ =1.32, $\beta$ = 2.17, k = $3.67·{10}^{-16}$, $B_{pk}$ = 206 G, $M_{core}$ = 88 g, ${\rho }_{cu}=1.67·{10}^{-8}{\Omega }$m, $l_{wdg}$ = 22.71 m, n = 7, $A_{cu}=1.63·{10}^{-7}$ m${}^2$	L = 477.9 µH, core NEE-55/28/21-IP12 by Thornton, N = 31 turns − 11 × AWG26	$\alpha$ = 1.32, $\beta$ = 2.17, k = $3.67·{10}^{-16}$, $B_{pk}$ = 400 G, $M_{core}$ = 218 g, ${\rho }_{cu}=1.67·{10}^{-8}{\Omega }$m, $l_{wdg}$ = 23.68 m, n = 11, $A_{cu}=1.28·{10}^{-7}$ m${}^2$
Capacitor ($C_o$)	$C_o$ = 4.7 $\mathsf{\mu }$F/630 V, metal polyester film capacitor	$ERS$ = 1.5 m${\Omega }$	$C_o$ = 2.2 $\mathsf{\mu }$F/630 V, metal polyester film capacitor	$ERS$ = 3.3 m${\Omega }$
Load ($R_o$)	7.68 ${\Omega }$		15.36 ${\Omega }$
Autotransformer (T)	$N_p/N_s=1$, core NEE-42/21/20-IP12 by Thornton, N = 19 turns − 6 × AWG26	$\alpha$ = 1.32, $\beta$ = 2.17, $k=3.67·{10}^{-16},B_{pk}$ = 75 G, $M_{core}$ = 112 g, ${\rho }_{cu}=1.67·{10}^{-8}{\Omega }$m, $l_{wdg}$ = 12.23 m, n = 6, $A_{cu}=1.28·{10}^{-7}$ m${}^2$	$N_p/N_s=1$, core NEE-55/28/21-IP12 by Thornton, N = 19 turns − 9 × AWG26	$\alpha$ = 1.32, $\beta$ = 2.17, $k=3.67·{10}^{-16},B_{pk}$ = 125 G, $M_{core}$ = 218 g, ${\rho }_{cu}=1.67·{10}^{-8}{\Omega }$m, $l_{wdg}$ = 14.52 m, n = 9, $A_{cu}=1.28·{10}^{-7}$ m${}^2$
Switches $S_1$–$S_2$	IGBT FGH20N60SFD, $I_C$ = 20 A, $V_{CE}$ = 600 V, by FAIRCHILD	$t_{on}$ = 29 ns, $t_{off}$ = 114 ns, $I_{S_{peak}}$ = 4.93 A, $V_{{CE}_{\left(sat\right)}}=2.4$ V, $V_{{CE}_{\left(max\right)}}=132$ V	IGBT FGH20N60SFD, $I_C$ = 20 A, $V_{CE}$ = 600 V, by FAIRCHILD	$t_{on}$ = 29 ns, $t_{off}$ = 114 ns, $I_{S_{peak}}$ = 6.72 A, $V_{{CE}_{\left(sat\right)}}=2.4$ V, $V_{{CE}_{\left(max\right)}}=180$ V,
Diodes $D_1$–$D_2$	$V_R$ = 600 V, $I_F$ = 14.5 A, $V_F$ = 1.5 V, by CREE	$R_D=55$ m${\Omega }$, $t_{rr}$ = 9.8 ns, $I_r$ = 50 $\mathsf{\mu }$A	$V_R$ = 600 V, $I_F$ = 14.5 A, $V_F$ = 1.5 V, by CREE	$R_D=$ 55 m${\Omega }$, $t_{rr}$ = 9.8 ns, $I_r$ = 50 $\mathsf{\mu }$A

, the frequency analysis for each $G_{vd}H$ are illustrated in Figure 7b and Figure 8b (blue curve), which include the sensor gains $H=5.21\times {10}^{-2}$ V/V and $H=26\times {10}^{-3}$ V/V, respectively. To regulate the output voltage of the converters, a voltage control loop was implemented by using PI controllers, which were tuned according to the conventional criteria of phase and gain margin ($0.25f_s\le f_c\le 10f_s$ and $45\le PM\le 90$) to provide a good response with adequate output voltage overshoot and ensures the stability of the converters during the load step. For the 3SSC-A-based buck converter, as shown in Figure 7b (orange curve), the PI controller was designed with proportional gain $K_p$ = 0.08 and integral gain $K_i$ = 2223, resulting in a voltage control loop with a frequency of 5 kHz crossover and 57${}^{\circ }$ phase margin. Meanwhile, for the 3SSC-A-based buck-boost structure, as shown in Figure 8b (orange curve), a PI controller with $K_p$ = 0.095 and $K_i$ = 1399 was implemented, obtaining a voltage control loop with frequency crossover and phase margin of 5 kHz and 62${}^{\circ }$, respectively.

2.6. Comparison with Classic Topologies

Table 6. Comparison among 3SSC-A-based step-down DC–DC converters and the classical topologies in CCM.

Parameter	Classic Buck	Classic Buck Buck-Boost	3SSC-A-Based Buck	3SSC-A-Based Buck-Boost
Static gain	D	$\frac{D}{1-D}$	$\frac{2D}{1+2D}$	$2D$
Voltage stress on the switches	$V_o$	$V_{in}+V_o$	$2(V_{in}-V_o)$	$2V_{in}$
# Switches	1	1	2	2
# Diodes	1	1	2	2
Autotransformer	-	-	1	1
# Capacitors	1	1	1	1
# Inductors	1	1	1	1
Ripple frequency of $i_L$	$f_s$	$f_s$	$2f_s$	$2f_s$
Ripple frequency of $i_{C_o}$	$f_s$	$f_s$	$2f_s$	$2f_s$
Duty cycle range	$0<D<1$	$0<D<0.5$ *	$0<D<0.5$	$0<D<0.5$

* Duty cycle limited to the step-down operation.

compares the proposed step-down converters and the classic topologies. Unlike classical converters, 3SSC-A-based step-down converters have a three-state switching cell arrangement, resulting in more components. However, this configuration allows proper current sharing between the semiconductors, reducing current efforts and power losses and increasing power processing capacity. Another interesting aspect is the reduced size of energy storage elements in the proposed converters, since these components operate with twice the switching frequency, contributing to the decrease in weight and volume of the structures. Furthermore, even at higher power levels, this feature allows using only film capacitors, which is convenient as they have a longer lifespan, contrasting with the classical topologies that often rely on electrolytic capacitors.

The static gain of the 3SSC-A-based buck converter has non-linear characteristics and is limited to half the input voltage, differing from the gain of the classical buck structure. In contrast, the 3SSC-A-based buck-boost topology has a linear static gain with a maximum value of unity. Regarding voltage stresses, 3SSC-A-based step-down converters present higher voltage stress on switches. On the other hand, the switches are in the same reference and in the common point of the source, which can provide simpler control circuits (non-isolated drivers).

In addition to the characteristics presented in Table 6, the minimum phase system property given by the transfer function $G_{vd}\left(s\right)$ of the 3SSC-A-based step-down converters is unlike the transfer function $G_{vd}\left(s\right)$ of the buck structure-boost classic, which features a zero right-half-plane. In this way, the controller design for 3SSC-A-based step-down topologies becomes simplified, making it possible to obtain a satisfactory dynamic response without needing an additional control loop.

3. Experimental Results

The two proposed converters were designed according to the specifications presented in Table 5, following the design methodology developed in CCM. The experimental set-up implemented for carrying out the laboratory tests is shown in Figure 9, with details for the power circuit of the converters.

The main experimental waveforms of the 3SSC-A-based buck converter are shown in Figure 10. Figure 10a shows the waveforms of the control signals from switches $S_1$ and $S_2$, current $i_{S1}$ and voltage $v_{S1}$. These results indicate that the converter operates with D = 0.18 without overlapping the switches’ command signals. Furthermore, it can be verified that the maximum voltage $v_{S1}$ on the switches is approximately 264 V, which can allow the implementation of components with voltage $V_{CE}$ in the range of 300 V. The current $i_{S1}$ grows linearly up to 5 A. Complementarily, Figure 10b presents the waveforms of voltage and current stress in switches $S_1$ and $S_2$. It is observed that the switches do not conduct simultaneously, evidencing a delay of 180${}^{\circ }$ between the control signals. As with the 3SSCA-based boost topology, the resonance between the leakage inductance of the autotransformer and the collector-emitter capacitance of the IGBT causes the current peaks observed in the currents $i_{S1}$ and $i_{S2}$ during the switching turn-on. However, these peaks were minimized with snubber RLD circuits, mitigating the voltage peaks in the switches.

In Figure 10c, voltage $v_{D1}$, currents $i_L$, current id1 and current $i_{S1}$ are shown. The diodes’ voltage stress is around −264 V, which confirms the theoretical analysis. Analyzing the currents $i_{S1}$ and $i_{D1}$, it is verified that the switch $S_1$ and the diode $D_1$ operate in a complementary way, evidencing that they do not conduct simultaneously. In addition, observing the waveform of the current $i_L$, it is verified that the converter operates in CCM, with a current ripple at 100 kHz, that is, twice the switching frequency of the switches with an average value of 4.6 A. Additionally, it can be seen that diodes $D_1$ and $D_2$ conduct simultaneously when the current $i_L$ decreases linearly, that is, the current through each diode is equivalent to half the inductor current at this instant, with an average value of 2.3 A. Therefore, due to the characteristic of 3SSC, the division of current efforts between these semiconductors naturally occurs.

Figure 10d shows the waveforms of input current $i_{in}$, current $i_L$ and voltages $V_{in}$ and $V_o$. These results demonstrate the characteristic of the converter operating as a voltage step-down, with an average output voltage $V_o$ at 48 V, according to the desired voltage gain. Similar to the classic buck converter, the 3SSC-A-based buck structure generates a pulsating ripple current $i_{in}$ with high $d_i$/$d_t$. In addition, the voltage $V_o$, and the currents $i_L$ and $i_{in}$ present a ripple corresponding to twice the switching frequency of the switches, an intrinsic characteristic of the three-state switching cell, which allows the reduction of weight and volume of the energy storage elements of this structure.

In the same way as the one presented for the 3SSC-A-based buck converter, Figure 11 illustrates the main results obtained during the experimental validation of the 3SSC-A-based buck-boost structure. The waveforms of control signals from switches $S_1$ and $S_2$, voltage $v_{S1}$ and current $i_{S1}$ are shown in Figure 11a. Observing the gate pulses, it is verified that the converter operates without overlapping the command signals, with D = 0.27. The $v_{S1}$ voltage stress on switch $S_1$ is 360V, which is higher than that presented by the 3SSC-A-based buck converter. In a complementary way, Figure 11b illustrates the current and voltage stress in switches $S_1$ and $S_2$, demonstrating that these semiconductors do not remain in conduction simultaneously, with the 180${}^{\circ }$ delay between the command signals being evident. As in the 3SSC-A-based boost and 3SSC-A-based buck topologies, the interaction between the leakage inductance of the autotransformer and the collector–emitter capacitance of the IGBT results in current peaks observed in currents $i_{S1}$ and $i_{S2}$ during the activation of switches, which is a characteristic of the 3SSC-A in these configurations. However, these peaks were also reduced in the 3SSC-A-based buck-boost structure by introducing RLD snubber circuits.

The waveforms of voltage $v_{D1}$, current $i_L$ and currents $i_{D1}$ and $i_S$ are illustrated in Figure 11c. The diodes are subjected to voltage stress equivalent to twice the voltage $V_{in}$, that is, −360 V. Analyzing the currents $i_{S1}$ and $i_{D1}$, it is verified that switch $S_1$ and diode $D_1$ do not operate simultaneously, evidencing the complementary operation between these semiconductors. In addition, the current $i_L$ has a ripple frequency equivalent to 100 kHz, that is, twice the switching frequency, with an average value of 6.25 A, and its format indicates that the converter operates in CCM. Additionally, as in other 3SSC-A-based converters, it is verified that diodes $D_1$ and $D_2$ conduct simultaneously when the switches are off, with the current through each of these semiconductors corresponding to half the current $i_L$, with a value average of 3.1 A; therefore, there is a division of the current stresses.

The waveforms of voltage $V_{in}$, voltage $V_o$, current $i_L$ and input current $i_{in}$ are shown in Figure 11d. These results confirm the step-down characteristic of the converter, with $V_o$ at 96 V. Analogously to the classical buck-boost and 3SSC-A-based buck structures, the current $i_{in}$ of the 3SSC-A-based buck-boost converter also shows a pulsating ripple with high $d_i$/$d_t$. However, in contrast to the classic buck-boost converter, the 3SSC-A-based buck-boost structure has an inductor connected to the output, presenting reduced current ripple, as can be seen in $i_L$, which considerably decreases the RMS current in the output capacitor. Additionally, still, through Figure 11d, it can be seen that both currents $i_L$ and $i_{in}$, as well as voltage $V_o$ present ripple equivalent to twice the switching frequency, which allows weight reduction and volume of energy storage elements.

Figure 12 presents the closed-loop operation of the converters. As can be seen in the experimental results of the 3SSC-A-based buck converter in Figure 12a, the output voltage remains at 48 V for the load steps from 100% power to 50% and from 50% to 100%. Similarly, the same load percentage variation was applied to the 3SSC-A-based buck-boost structure, its dynamic response being shown in Figure 12b, and it can be verified that the output bus is maintained at 96 V.

According to the theoretical model described in Section 2.4 and the parameters in Table 5 and

Table 7. Power losses per component.

Component	3SSC-A-Based Buck	3SSC-A-Based Buck-Boost
Switches ($S_1$-$S_2$)	8.65 W	16.65 W
Diodes ($D_1$-$D_2$)	7.66 W	11.02 W
Autotransformer (T)	5.86 W	10.76 W
Inductor (L)	7.1 W	11.88 W
Capacitor ($C_o$)	7.5 mW	0.23 mW
Total	29.3 W	50.3 W

, Figure 13 presents the distribution of power losses in converters operating at full load. The total power losses for the 3SSC-A-based buck and 3SSC-A-based buck-boost topologies are approximately 29.3 W and 50.3 W, with a theoretical efficiency of about 91.1% and 92.3%, respectively. It can be observed that in both converters, even with different operating points, the losses in the switches are dominant, contributing to a higher percentage of the total losses. In addition, the converter capacitors’ power loss is highly reduced compared to the other elements.

The efficiency of the experimental prototypes was evaluated in a load range from 16.67% to 100% of the rated load. Figure 14 presents the normalized practical efficiency of the proposed converters. Both prototypes present performance superior to 85% in the entire defined power range, highlighting, at rated load, the efficiency of approximately 91% for the 3SSC-A-based buck converter and 92% for the 3SSC-A-based buck-boost structure. In contrast to Figure 13, the measured losses at nominal power are practically identical to the calculated losses. Therefore, there is an experimental validation of the theoretical losses model.

A thermal image of the converters operating at full load is shown in Figure 15. This result also validates the characterization of losses shown in Figure 13, proving the distribution of thermal losses between the components caused by the division of current efforts between the semiconductors and, consequently, validating the potential benefits of the application of 3SSC-A in terms of improving the thermal performance in power processing.

4. Conclusions

In this paper, two unexplored topologies based on 3SSC-A for step-down applications were thoroughly analyzed, implemented and experimentally verified. According to the experimental validations, the proposed converters present several advantages compared with the classical topologies, such as reducing current stress between the semiconductors, distribution of power losses between these components, and reducing heat sinks. In addition, the energy storage elements of these topologies operate at twice the switching frequency, allowing weight and volume reduction and, consequently, increased power density. The 3SSC-A-based buck-boost structure presents less current ripple at the load side since the inductor is directly coupled to the output, reducing the RMS current over the capacitor. However, the 3SSC-A-based buck converter presents less voltage stress over the semiconductors. Furthermore, the 3SSC-A-based buck converter has a maximum static gain of half the input voltage, while the theoretical maximum static gain of the 3SSC-A-based buck-boost topology equals the input voltage.

Detailing the loss distribution effects, one can note that the losses in the inductors and autotransformers are very close for the two converters. Table 2 indicates that the current stresses on these magnetic elements are higher for the 3SCC-A-based buck-boost converter, which would result in a relative increase in copper losses. However, the design specifications presented in Table 5 indicate that the inductor and autotransformer winding resistances are lower for the 3SCC-A-based buck-boost converter, which justifies the balance of this losses portion between the two topologies. The losses proportion in the switches is slightly higher for the 3SCC-A-based buck-boost converter due to the higher relative current stresses indicated in Table 4.

Therefore, the power loss characterization of the proposed converters allowed us to conclude that the switches contribute significantly to the power losses of the 3SSC-A converters. Moreover, although the converters were projected at different operating points, both presented a similar power loss distribution with high efficiency, which was around 91% for the 3SSC-A-based buck converter and 92% for the 3SSC-A-based buck-boost converter. Thus, it is up to the designer to analyze the figures of merit of each converter as a starting point for selecting the most suitable topology for a specific application.