Inertia Estimation of Synchronous Devices: Review of Available Techniques and Comparative Assessment of Conventional Measurement-Based Approaches

Abstract

The increasing deployment of renewable energy sources (RESs) reduces the inertia levels of modern power systems, raising frequency stability issues. Therefore, it becomes crucial, for power-system operators, to monitor system inertia, in order to activate proper preventive remedial actions in a timely way, ensuring, this way, the reliable and secure operation of the power system. This paper presents a brief review of available techniques for inertia estimation of synchronous devices. Additionally, a comparative assessment of conventional measurement-based inertia-estimation techniques is performed. In particular, five conventional inertia-estimation techniques are considered and examined. The distinct features of each method are presented and discussed. The effect of several parameters on the accuracy of the examined methods is evaluated via Monte Carlo analysis. The performance of the examined methods is evaluated using dynamic responses, obtained via RMS simulations, conducted on the IEEE 9 bus test system. Based on the conducted analysis, recommendations to enhance the accuracy of the examined techniques are proposed.

1. Introduction

Sufficient inertia levels are of crucial importance for the secure and reliable operation of power systems [1,2]. In traditional power systems, inertia is provided by the rotating masses of the installed synchronous generators (SGs) [3]. However, recently, due to environmental concerns, fossil-fueled SGs have been decommissioned and the power-system industry has shifted towards generating electricity from renewable energy sources (RESs) [4].

Indeed, nowadays, the global share of RESs in the power system is constantly increasing [5]. In several regions around the globe, such as Texas, Ireland, Tasmania, Hawaii, and South Australia, 50% to 60% of the local energy needs are covered, during specific time periods of the day, by RESs [6,7]. According to [8], by 2025, power generation from RESs will cover at least 50% of the instantaneous demand in 22 European countries. This percentage will reach up to 100% for countries such as Denmark, Greece, Germany, Ireland, Netherlands, and Portugal. The Australian Energy Market Operator has ambitious plans to achieve a full decarbonized power system in the next few years [9]. The European Union and India target at least 40% of RESs in their overall energy mix by 2030 [10,11]. Therefore, it is clear that future power systems will be dominated by RESs [6].

However, RESs are connected to the utility grid via power electronic converters [12]. Consequently, they are mechanically decoupled from grid frequency and, thus, they cannot automatically provide inertia to the power system [2,13]. This shift towards converter-interfaced generation progressively reduces the overall inertia levels [14], modifying power-system dynamics, and also raising frequency stability issues [15,16]. Indeed, fast-frequency dynamics are more prevalent in low-inertia power systems [17]. Therefore, during frequency events, a high rate of change of frequency (RoCoF) values and frequency deviations are expected [3]. These high RoCoF values, which in the near future may exceed 3 Hz/s [18], can trigger special protection systems, over- and under-frequency relays, and load shedding schemes, thus leading to cascaded outages and, even worse, to total blackouts [19,20,21]. Additionally, it is worth noting that the intermittent nature of RESs constitutes power-system inertia levels variable during the day [22,23], thus posing further challenges to system operators, concerning the frequency control of modern power systems [3].

To deal with the above-mentioned challenges, inertial control functionalities are nowadays embedded to RESs [24,25,26]. Additionally, wide-area monitoring applications have been developed to estimate, close to real time, the overall system inertia [27,28,29,30]. Using the information of inertia level, system operators can activate appropriate preventive remedial actions, such as the deployment of synchronous condensers [31,32] and/or the dispatch of controllable RESs [33], ensuring, this way, the overall system stability [34].

Due to the importance of accurate inertia estimation for the secure operation of low-inertia powers systems, the relevant research is an ongoing field of study. Indeed, several research efforts were dedicated to the development of efficient inertia-estimation techniques, during the last few years. Thus, a large number of research papers is already available in the archived literature and several review papers can be found regarding this topic [1,2,5,11,35]. Nevertheless, what is currently missing from the existing literature is a systematic evaluation of the performance of the most well-established inertia-estimation techniques. This evaluation will demonstrate the accuracy capabilities of the existing methods, setting also a framework for the objective assessment of new techniques that may be developed in the near future. Towards this objective, in this paper, a comparative assessment of the most prevalent measurement-based inertia-estimation techniques is performed. The contributions of the paper can be summarized as follows:

• A literature review is initially conducted, aiming to provide a comprehensive overview of the existing inertia-estimation techniques. Special emphasis is placed on the analysis of measurement-based approaches, since they can be easily implemented for wide-area monitoring applications [36].
• The performance of the most prevalent measurement-based inertia-estimation techniques is systematically evaluated.
• The effect of several factors, on the accuracy of the examined methods, is evaluated via Monte Carlo (MC) analysis.
• Guidelines and recommendations to enhance the accuracy of the examined techniques are proposed.

The rest of the paper is organized as follows: Section 2 provides the definitions of power-system inertia. In Section 3, a comprehensive review of the existing inertia-estimation techniques is presented. Section 4 provides the theoretical background for the implementation of the most prevalent measurement-based inertia-estimation techniques, those tested in this paper. In Section 5, a comparative assessment of the examined methods is conducted. Guidelines and recommendations to enhance the accuracy of the examined techniques are proposed in Section 6. Section 7 summarizes the key findings and concludes the paper.

2. Power-System Inertia: Fundamental Concepts and Definitions

This section provides definitions concerning physical inertia, inertia time constant, and overall power-system inertia.

2.1. Inertia Definition

Inertia can be defined as the resistance of a rotating body to a change in its state of motion [1,12]. In the context of traditional power systems, inertia can be defined as the resistance of the rotating masses of SGs to a change in their speed [2]. It can be also perceived as the resistance (in the form of energy exchange), to counteract power-system-frequency changes, resulting from power imbalances in generation and load demand [1].

2.2. Inertia Time Constant

The kinetic energy ($E_k$) stored in the rotating mass of an SG is defined at the nominal frequency ($f_n$) as:

$$E_k=\frac{1}{2}J{\omega }_n^2$$

(1)

In the above notation, J is the moment of inertia of the SG (measured in $\mathrm{k}\mathrm{g}·{\mathrm{m}}^2$) and ${\omega }_n=2\pi f_n$ is the synchronous rotational speed (in $\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$).

The inertia time constant of a synchronous machine is defined as the stored kinetic energy, given by (1), divided by the rated apparent power ($S_n$ in MVA) of the machine. Mathematically, the inertia time constant (H) is expressed as follows:

$$H=\frac{J·{\omega }^2}{2·S_n}.$$

(2)

H reflects the maximum time (in seconds) that an SG can infeed, with its rated active power, the power system without any additional mechanical power input until it becomes completely still [37]. H lies on the range between 2 s and 10 s, depending on the type and size of the machine [12,37]. Generally, for a given type of SG, the larger the rated power of the machine, the larger the inertia constant is [2]. Typical/mean values for coal-fired, gas-fired, nuclear, and hydraulic SGs are 3.5 s, 5 s, 4 s, and 3 s, respectively [38].

2.3. The Swing Equation

Under small frequency variations, the rotor dynamics of an SG can be described using the following form of the swing equation [13,39]:

$$2·H·\frac{\mathrm{d}\Delta \omega \left(t\right)}{\mathrm{d}t}={\Delta }_{p_m}\left(t\right)-{\Delta }_{p_e}\left(t\right)-D·\Delta \omega \left(t\right).$$

(3)

Here, $\Delta \omega$ is the difference between the synchronous and the actual rotational speed of the rotor in p.u. and ${\Delta }_{p_m}$ and ${\Delta }_{p_e}$ denote the change in the mechanical and electric power in p.u., respectively. D is the damping coefficient of the machine, expressed also in p.u.

Immediately after a disturbance, the mechanical power is considered constant [13,40], i.e., ${\Delta }_{p_m}$ = 0. Additionally, the rotor speed deviation, $\Delta \omega$, can be represented by the rotor frequency deviation ($\Delta f_r$), which can be approximated as $\Delta f_r\approx \Delta f$ [13,39]. Here, $\Delta f$ represents the frequency deviation at the connection bus of the SG. Based on the above, the swing equation of (3) can be rewritten as:

$$2·H·\frac{\mathrm{d}\Delta f\left(t\right)}{\mathrm{d}t}=-{\Delta }_{p_e}\left(t\right)-D·\Delta f\left(t\right).$$

(4)

By applying the Laplace transform on both sides of (4), the following transfer function derives:

$$\frac{\Delta f\left(s\right)}{{\Delta }_{p_e}\left(s\right)}=-\frac{1/2H}{s+D/2H}$$

(5)

Here, $\Delta f\left(s\right)$ and ${\Delta }_{p_e}\left(s\right)$ denote the bus frequency and active power deviations in the Laplace domain, respectively.

At this point, it is worth noting that the value of the damping term in (3) and (4) is rather small (it generally varies between 1% and 3% across different power systems [1]). Thus, in many publications, the damping term is completely neglected and the swing equation is further simplified, as shown below:

$$2·H·\frac{\mathrm{d}\Delta f\left(t\right)}{\mathrm{d}t}=-{\Delta }_{p_e}\left(t\right).$$

(6)

2.4. Overall Power-System Inertia

The swing equation, (4), can be generalized to describe frequency dynamics of multi-machine power systems, by adopting the concept of center of inertia (CoI) [41,42,43,44]. In this case, all SGs of the examined region are aggregated into an equivalent unit and (4) is re-written as [2]:

$$2·H_{sys}·\frac{\mathrm{d}\Delta f_{sys}\left(t\right)}{\mathrm{d}t}={\Delta }_{p_{m,sys}}\left(t\right)-{\Delta }_{p_{e,sys}}\left(t\right)-D_{sys}·\Delta f_{sys}\left(t\right).$$

(7)

In the above notation, ${\Delta }_{p_{m,sys}}$ and ${\Delta }_{p_{e,sys}}$ denote the total mechanical power change and the total electric power change of all interconnected SGs, respectively. $D_{sys}$ is the overall damping factor of the system. $H_{sys}$ is the inertia constant of the entire power system, defined according to (8), [41]; $f_{sys}$ is the CoI frequency and it is formally defined as shown in (9), [41].

$$H_{sys}=\frac{{\sum }_{i=1}^N{H}_i·S_i}{{\sum }_{i=1}^N{S}_i}$$

(8)

$$f_{sys}=\frac{{\sum }_{i=1}^N{H}_i·S_i·f_i}{{\sum }_{i=1}^N{H}_i·S_i}$$

(9)

Here, N is the total number of SGs connected to the examined power system. $H_i$, $S_i$, and $f_i$ are the inertia constant, rated apparent power, and frequency of the i-th SG, respectively.

3. Inertia Estimation: Review of Available Techniques

Inertia-estimation techniques can be classified into two main categories [2]: (i) model-based and (ii) measurement-based approaches. In the former, inertia time constants are derived using the following two-step approach [35]: Initially, a white- or grey-box equivalent representation of the examined system is constructed. Note that the inertia constant is a parameter of this equivalent model. Subsequently, the equivalent-model parameters, and, thus, the inertia constant, are estimated using optimization techniques and system measurements/responses, obtained from phasor measurement units (PMUs). On the other hand, measurement-based methods do not require information concerning the underlying dynamic properties of the examined power system, e.g., an equivalent representation of the examined system. In fact, measurement-based approaches use either artificial intelligence (AI) methods or combine the swing equation with processed PMU measurements of frequency and active power in order to provide inertia estimates [2].

A comprehensive review of model-based and measurement-based methods is presented in Section 3.1 and Section 3.2, respectively.

3.1. Model-Based Inertia-Estimation Techniques

In [45,46,47,48,49,50,51,52], methods to identify parameters of single SGs are proposed. These methods assume that the model of the examined SG is a-priori known. The unknown model parameters are estimated using measured responses of the examined system. This type of method can be classified either based on the type of the machine model used or based on the adopted parameter estimation technique [45]. In [47,49], the classic model is used. The transient model is adopted in [46,51], while the subtransient model is employed in [45,48]. Techniques based on nonlinear optimization are developed in [45,46]; a heuristic method, based on genetic algorithms, is proposed in [48] and Kalman filtering approaches are proposed in [49,50,51,52]. Model-based inertia estimation is also performed in [53,54,55]. These methods require only the network admittance matrix in order to perform satisfactorily.

Model-based methods have also been developed to estimate the contribution of distribution systems and virtual power plants to the overall power-system inertia [56,57,58,59,60]. For instance, in [56], a method to estimate the equivalent inertia of virtual power plants is formulated. In [57,58], grey-box equivalents of active distribution networks, which host SGs, are developed. The aggregated contribution of the installed SGs to the overall system inertia is reflected by the equivalent inertia constant, i.e., the identified inertia constant of the equivalent model. In [59,60], equivalent models for passive distribution networks, dominated by induction motors, are developed. The inertia constant of the equivalents reflects the overall contribution of the distribution network to the system inertia.

In [61,62,63], reduced-order dynamic electro-mechanical models are developed for extended transmission systems, based on the concept of the coherent generators [64]. Each area of the examined transmission system is then represented with an aggregated equivalent SG, the parameters of which are estimated by exploiting PMU measurements. The inertia constants of the equivalent SGs provide insights concerning the regional inertia levels. The concept of coherent generators is also adopted in [65,66,67,68], where system identification techniques are used to identify modal parameters of inter-area oscillations [69]. Regional inertia estimates are extracted on a second stage, using the frequency and the damping of the inter-area modes.

The theory of the system-state matrix is used to estimate inertia constants of SGs in [70,71,72,73,74]. In these approaches, the examined system is linearized and the corresponding state matrix is computed. During the normal operation, PMU measurements are used to determine, close to real time, the electromechanical modes of the examined power system. Using the modal information, the state matrix of the power system is updated and, thus, new (updated) inertia estimates are provided.

In [75], system frequency response models (SFRMs) are utilized to determine the inertia constants of synchronous and non-synchronous devices. In [76], SFRMs are used to estimate inertia constants by analyzing the modal parameters of the examined power system. Methods based on SFRMs and moving-horizon estimation are proposed in [17,77], while the dynamic regressor and mixing procedure are used in [78].

3.2. Measurement-Based Methods

Measurement-based methods can be classified as: (i) offline post-mortem approaches and (ii) online real-time techniques [1].

3.2.1. Offline Post-Mortem Approaches

Offline approaches are also referred in the literature as disturbance-based methods [2]. Indeed, these approaches estimate inertia using frequency and active power measurements, obtained during transient events. The majority of these methods ignores the system damping and determine inertia constants using (6) [1,2]. Additionally, they completely neglect the impact of power-system loads on active power variations. In fact, the impact of loads is considered in only a few publications (see, for instance, [79,80]).

This type of method may result in inaccurate inertia estimates, since transient frequency responses contain oscillatory components, caused by inter-area oscillations [1,11] and they are also prone to noise [2]. To overcome these issues, several approaches have been proposed in the literature.

In [81], a fifth-order polynomial is used to approximate the time-domain (TD) frequency response, in order to suppress the impact of oscillatory components on the calculation of the RoCoF. Fifth-order polynomials have also been tested in [22,82], while in [29,83], first-order and seventh-order polynomials are used. A more generic approach is presented in [84], where the use of variable-order polynomials is discussed for the approximation of the grid frequency response. In [85,86], the TD frequency response is approximated by a sum of damped sinusoids.

To eliminate the impact of noise, the use of low-pass filters is discussed in [87,88], while a Butterworth filter is proposed in [89]. In [40,90], a method based on four sliding windows (SWs) is developed. The SWs act as smoothing filters, aiming to eliminate the noise from frequency and active power measurements.

Moreover, it is worth noting that the performance of disturbance-based methods is highly affected by the accurate identification of the onset of the event [1,91] and the length of the analysis window [88,89]. In addition, the location of the recording devices, relative to the location of the power disturbance, affects frequency measurements, thus complicating inertia estimation [1].

3.2.2. Online Real-Time Methods

Online inertia estimation can be performed either using transfer-function-based modeling or by adopting statistical and AI methods.

In the former case, active power and frequency measurements are used to develop low-order transfer functions, which describe the active power–frequency relationship. In this context, in [39], a closed-loop identification scheme is proposed, to estimate, in real time, the inertia time constants of SGs. Nevertheless, this approach requires the injection of a well-designed probing signal, which complicates its implementation. In [13,92,93,94,95,96], non-intrusive methods are proposed. This type of method develops low-order input–output transfer-function models, by utilizing either transient responses or ambient data, i.e., data that reflect the stochastic system response, caused due to random load and RESs variations [97]. The parameters of the transfer functions are estimated using system identification techniques, such as the autoregressive moving average exogenous input (ARMAX) modeling approach [13,92], and the subspace state-space system identification method [93]. Inertia estimates are derived, in a second stage, by processing the parameters of the computed transfer functions. For this purpose, several approaches have been proposed.

For instance, in [13], the estimated transfer function is reduced to a first-order counterpart by identifying and eliminating insignificant states. The resulted first-order transfer function has the general form of (5), thus allowing the determination of the inertia constant. However, the order reduction may introduce errors in the derived inertia estimates. Therefore, in [93,94,95], inertia constants are estimated by computing the initial slope of the unit step response of the identified transfer function. In [92,96], the impulse response of the identified transfer functions is utilized to determine inertia constants. Further information on the implementation of these approaches is provided in Section 4.

Nevertheless, it is worth noting that the performance of transfer-function-based inertia-estimation approaches is affected by several factors. The most important ones are the noise level [88] and the length of the analysis window [13], i.e., the number of samples used for the estimation of the transfer function parameters. Indeed, inappropriate window size may result in unstable transfer-function models [92], thus prohibiting inertia estimation.

To overcome the inherent drawbacks of transfer-function-based methods, statistical and AI-based approaches have also been proposed in the literature. For instance, in [98], modal parameters are used as inputs to an artificial neural network (ANN). The outputs of the ANN are the regional inertia constants. The use of multi-layer perception feed-forward ANNs for inertia estimation is discussed in [99], while convolutional ANNs are proposed in [100,101]. Finally, a statistical method, based on switching Markov Gaussian models, is presented in [102]. In the near future, statistical and AI-based methods are expected to gain further ground, due to the rapid deployment of PMUs and, thus, the increased availability of system measurements.

4. Theoretical Background

This section provides an overview of the examined measurement-based inertia-estimation techniques.

4.1. Inertia Estimation via the Direct Use of the Swing Equation

In cases where transient responses are used, the inertia constant can be estimated as follows, [11,81]:

$$H_{est}=\frac{-\Delta P}{2·\frac{\mathrm{d}\Delta f}{\mathrm{d}t}{|}_{t=t_o}}.$$

(10)

Here, $\Delta P$ is the known active power imbalance; $t_0$ denotes the exact time instant of the onset of the disturbance, i.e., $t_0=0^{+}$. An indicative set of transient active power and frequency responses is presented in Figure 1.

However, this approach may lead to considerable errors in the case of noisy frequency responses [81]. Indeed, in these cases, the RoCoF is not accurately computed, thus leading to inaccurate inertia estimates.

4.2. Calculation of the RoCoF Using the Polynomial Approximation Approach

To mitigate the impact of noise and oscillatory components on the RoCoF calculation, a polynomial approximation of $\Delta f$ is proposed in many research papers [29,81,83]. An n-th-order polynomial approximation can be expressed as:

$$\Delta f_{est}\left(t\right)=A_n·t^n+A_{n-1}·t^{n-1}+\cdots +A_1·t+A_0$$

(11)

where t is the time ($t\ge 0$, assuming that $t_0=0$) and $\Delta f_{est}$ denotes the frequency deviation, as estimated (approximated) by the adopted polynomial approximation. $A_n$–$A_0$ are the polynomial coefficients, which are determined via nonlinear least square (NLS) optimization. The objective function of the optimization is

$$J=min\sum _{k=1}^K{\left(\Delta f\left[k\right]-\Delta f_{est}\left[k\right|{\mathit{\theta }}_{\mathbf{1}}]\right)}^2.$$

(12)

Here, K is the total number of samples. $\Delta f\left[k\right]$ and $\Delta f_{est}\left[k\right]$ are the measured and the estimated (approximated) frequency deviations at the k-th sample, respectively; ${\mathit{\theta }}_{\mathbf{1}}$ is the required set of parameters, i.e., ${\mathit{\theta }}_{\mathbf{1}}=[A_n,\cdots ,A_0]$

Once the polynomial approximation of $\Delta f$ is derived, the RoCoF can be determined using (13) and the the inertia constant can be estimated using (14).

$$\frac{\mathrm{d}\Delta f}{\mathrm{d}t}{|}_{t=0^{+}}\approx \Delta f_{est}^{\prime }(t=0^{+})=A_1$$

(13)

$$H_{est}=\frac{-\Delta p}{2·A_1},$$

(14)

In most publications, fixed-order polynomials are adopted. For instance, in [29], a first-order polynomial is used, while in [81,83], fifth- and seventh-order polynomials are employed. Nevertheless, a fixed-order approximation may lead to sub-optimal inertia estimates. Therefore, a more generic approach is presented in [84], where the optimal order of the adopted polynomial is determined through an iterative procedure. This procedure is summarized by means of a pseudo-code in Algorithm 1 and it is used in this paper to define the optimal approximation order.

Algorithm 1 Determination of the Optimal Polynomial Order

1: Obtain active power and frequency responses 2: Calculation of $H_{ref}$ using (10) 3: Compute $H_{est,1}$ and $H_{est,2}$ using (11)–(14) 4: Initialization. Set $n=2$. Define $n=n_{max}$, ${\epsilon }_1$, ${\epsilon }_2$ 5: While$n\le n_{max}$ 6: if$|H_{est,n}-H_{ref}|<{\epsilon }_1$$|H_{est,n}-H_{est,n-1}|<{\epsilon }_2$then 7:     Return $H_{est,n}$ and terminate the algorithm 8: else 9:     n = n + 1 and compute $H_{est,n}$ 10: end if 11: end while

Algorithm 1 is explained step-by-step below:

• Step 1: Initially, frequency and active power responses are forwarded as inputs to the algorithm.
• Step 2: $H_{ref}$ is computed using (10). As already discussed, in cases of low noise levels, $H_{ref}$ is very close to the actual inertia constant. Therefore, it is computed in this step as a rough (initial) inertia estimate and used as a benchmark value for the convergence of the algorithm.
• Step 3: $H_{est,1}$ and $H_{est,2}$ are calculated using (11)–(14). $H_{est,1}$ and $H_{est,2}$ are inertia estimates, corresponding to first- and second-order polynomial approximations, respectively. Their calculation is required for the first iteration of the algorithm.
• Step 4: The values of parameters $n_{max}$, ${\epsilon }_1$, and ${\epsilon }_2$ are defined by the user. $n_{max}$ is the maximum permissible value of the approximation order. ${\epsilon }_1$ and ${\epsilon }_2$ are two tolerance values, used for the convergence of the algorithm. ${\epsilon }_1$ is used to compare inertia estimates, computed at each iteration, with the initial estimate $H_{ref}$ is derived from (10). ${\epsilon }_2$ is used to compare inertia estimates between two consecutive iterations. In this paper, $n_{max}$ is set to 10. ${\epsilon }_1$ and ${\epsilon }_2$ are considered equal to 1 s and 0.01 s, respectively.
• Step 5: The iterative process initiates. The iterative process lasts until $n_{max}$ is reached or until convergence has been achieved.
• Step 6 to 11: If both convergence criteria are met, then the algorithm terminates and the estimated inertia value is provided to the user. Otherwise, the approximation order n is increased by one, a new inertia estimation is computed and the algorithm moves back to Step 5. In cases where $n_{max}$ is reached and convergence criteria are not met, the algorithm fails to return an estimate. Obviously, values of ${\epsilon }_1$ and ${\epsilon }_2$ have a crucial impact on both the convergence and the accuracy of the algorithm.

4.3. Inertia Estimation Using the SW Method

In this approach, four SWs are used [40,90]. The SWs act as smoothing filters, aiming to eliminate noise from system measurements. The required SWs are labeled as $P^{-}$, $P^{+}$, $R^{-}$, and $R^{+}$. These windows are depicted in Figure 1c,d. In the above-mentioned notation, P and R denote active power and RoCoF, respectively. Superscripts (−) and (+) denote SWs that contain pre- and post-disturbance data, respectively. As shown in Figure 1c,d, each window contains B data samples. Pre- and post-disturbance windows are separated by a width of W data samples. Assuming that a disturbance occurs at $t=t_0$, then $P^{-}$, $P^{+}$, $R^{-}$, and $R^{+}$ are computed as:

$$P^{-}=\frac{1}{B}\sum _{t=t_0-B}^{t_0}P\left(t\right)$$

(15)

$$P^{+}=\frac{1}{B}\sum _{t=t_0+W}^{t_0+W+B}P\left(t\right)$$

(16)

$$R^{-}=\frac{1}{B}\sum _{t=t_0-B}^{t_0}\frac{df}{dt}\left(t\right)$$

(17)

$$R^{+}=\frac{1}{B}\sum _{t=t_0+W}^{t_0+W+B}\frac{df}{dt}\left(t\right).$$

(18)

The estimated inertia constant is derived using (19), [40,90].

$$H_{est}=\frac{1}{2}\frac{P^{-}-P^{+}}{R^{+}-R^{-}}.$$

(19)

4.4. Inertia Estimation via Transfer-Function Modeling

In this approach, frequency and active power measurements are used to develop low-order transfer functions, which have the generic form of (20).

$$G\left(s\right)=\frac{\Delta f\left(s\right)}{{\Delta }_{p_e}\left(s\right)}=\frac{{\beta }_{n-1}{s}^{n-1}+{\beta }_{n-2}{s}^{n-2}+\cdots +{\beta }_0}{{\alpha }_n{s}^n+{\alpha }_{n-1}{s}^{n-1}+\cdots +{\alpha }_0}.$$

(20)

The required set of parameters ${\mathit{\theta }}_{\mathbf{2}}=[{\beta }_{n-1},{\beta }_{n-2},\dots ,{\beta }_0,{\alpha }_n,{\alpha }_{n-1},\dots ,{\alpha }_0]$ is estimated using system identification techniques. In this paper, the ARMAX approach is used for this purpose. A brief overview of ARMAX modeling is presented in Section 4.5.

$G\left(s\right)$ contains the value of the inertia constant, but not as an explicit parameter [92]. Indeed, a post-processing analysis of the $G\left(s\right)$ parameters is required to obtain the final inertia estimate. Post-processing approaches are discussed in Section 4.4.1 and Section 4.4.2.

4.4.1. Method Based on Model Order Reduction

The most simple approach to derive the inertia constant is to reduce (20) to a first-order transfer function by identifying and eliminating insignificant states [13,88,92]. The derived first-order transfer function can be expressed as:

$$G\left(s\right)=\frac{\Delta f\left(s\right)}{{\Delta }_{p_e}\left(s\right)}\cong \frac{\beta }{s+\alpha }.$$

(21)

By observing (5) and (21), it can be inferred that:

$$H_{est}=-\frac{1}{2\beta }.$$

(22)

4.4.2. Method Based on the Impulse Response

Let us consider the transfer function of (5). The unit impulse response ($h\left(t\right)$) of (5) is given by (23), [92].

$$h\left(t\right)=-\frac{1}{2H}·e^{-\frac{D}{2H}·t}$$

(23)

It is evident that, immediately after the disturbance, i.e., at $t=0$, the value of the impulse response is equal to:

$$h\left(0\right)=-\frac{1}{2H}$$

(24)

Thus, there is a clear relationship between the inertia constant of the machine and $h\left(0\right)$.

In the general case, the identified transfer functions $G\left(s\right)$ have the form of (20), thus being more complex than the transfer function of (5). Nevertheless, the inertial response is still the fastest acting dynamic phenomenon that practically determines the first instance (value) of the impulse response [92]. Therefore, the inertia constant can be estimated by the value of the impulse response of $G\left(s\right)$ at $t=0$. In particular, inertia can be estimated as:

$$H_{est}=-\frac{1}{2·g\left(0\right)}$$

(25)

Here, $g\left(t\right)$ denotes the TD impulse response of $G\left(s\right)$.

4.5. ARMAX Modeling

ARMAX model is mathematically expressed in its discrete form by (26):

$$\begin{array}{c}\hfill y\left[k\right]+a_{1}y[k-1]+\cdots +a_{n_a}y[k-n_a]=b_{1}u[k-1]+\\ \hfill \cdots +b_{n_b}u[k-n_b]+c_{1}e[k-1]+\cdots +c_{n_c}e[k-n_c].\end{array}$$

(26)

Here, $y\left[k\right]$ and $u\left[k\right]$ denote the system response and the corresponding input at the k-th time instant, respectively. In this paper, $y\left[k\right]$ is the frequency at the connection node of an SG immediately after a disturbance. It is assumed that this frequency is equal to the corresponding rotor speed of the SG. $u\left[k\right]$ is the measured electric power of the SG. $ϵ\left[k\right]$ is the unknown system input (noise/non-measurable). $n_a$ is the order of the autoregressive model; $n_b$ and $n_c$ are the orders of the exogenous input and the moving average model, respectively.

The transfer function of the discrete ARMAX model is given by (27).

$$y\left[k\right]=\frac{B\left(q\right)}{A\left(q\right)}u\left[k\right]+\frac{C\left(q\right)}{A\left(q\right)}e\left[k\right]$$

(27)

Here, $B\left(q\right)/A\left(q\right)$ is the deterministic part, which describes the output of the system to a known input signal. $C\left(q\right)/A\left(q\right)$ is the stochastic part, describing the impact of non-measurable effects on the states of the deterministic part. Polynomials $A\left(q\right)$, $B\left(q\right)$, and $C\left(q\right)$ are defined as

$$\begin{array}{cc}\hfill & A\left(q\right)=1+a_1·q_{}^{-1}+a_2·q_{}^{-2}+\cdots +a_{n_a}·q_{}^{-n_a}\hfill \\ \hfill & B\left(q\right)=b_1·q_{}^{-1}+b_2·q_{}^{-2}+\cdots +b_{n_b}·q_{}^{-n_b}\hfill \\ \hfill & C\left(q\right)=c_o+c_1·q^{-1}+c_2·q^{-2}+\cdots +c_{n_c}·q^{-n_c}.\hfill \end{array}$$

(28)

Here, $q^{-1}$ is the backward shift operator. The parameters of (28) are estimated using a prediction error formulation [13,88].

5. Performance Evaluation of Measurement-Based Inertia-Estimation Techniques

In this section, the performance of several measurement-based inertia-estimation techniques is thoroughly evaluated, by performing MC simulations on a benchmark power-system model. The system under study is described in Section 5.1. The examined inertia-estimation techniques are summarized in Section 5.2. A comparative assessment of the examined methods is conducted in Section 5.3.

5.1. System under Study

The performance of all examined methods is evaluated by performing RMS simulations on the DIgSILENT software [104], using the IEEE 9 bus test system model of [105]. A single-line diagram of the system under study is presented in Figure 2. Dynamic responses (testing data) for the evaluation of the examined inertia-estimation techniques are obtained by simulating frequency events. For this purpose, several scenarios/simulations are conducted. In each simulation, different disturbance levels and locations are considered, by changing the power consumed by Loads A, B, and C. Further, details concerning the simulations are provided in the next subsections.

In each simulation, the frequency and active power of the installed SGs (generators G1, G2, and G3 at Figure 2) are acquired at a sampling rate of 100 samples per second (SPS). These responses are forwarded as inputs to the examined inertia-estimation techniques, in order to compute the inertia constant of the machines. To quantify the accuracy of the estimates, the following prediction error, $PE$, is introduced:

$$PE(\%)=\frac{|H_{true}-H_{est}|}{H_{true}}·100\%$$

(29)

Here, $H_{true}$ denotes the actual inertia of the installed SGs. $H_{true}$ is equal to 2.6312 s, 4.1296 s, and 4.768 s for G1, G2 and G3, respectively.

5.2. Summary of the Examined Methods

In this paper, inertia constants are estimated using dynamic responses obtained during transient events, i.e., responses obtained during system disturbances. Five different measurement-based inertia-estimation approaches are considered. A summary of the examined methods is provided below:

• Method #1: Inertia estimation is performed using the principles discussed in Section 4.2. $H_{est}$ is computed using (14). A fixed-order polynomial (fifth-order polynomial) is used to approximate $\Delta f$.
• Method #2: In this approach, $H_{est}$ is computed once again using (14). Nevertheless, a variable-order polynomial is adopted to approximate $\Delta f$ and, thus, compute the RoCoF. The optimal order of the polynomial is determined using Algorithm 1.
• Method #3: Inertia estimation is performed using the principles discussed in Section 4.4.1. More specifically, second-order transfer functions are initially developed, using the simulated responses of frequency and active power. Subsequently, insignificant states of the derived transfer functions are eliminated and first-order transfer functions, which have the general form of (21), are computed. $H_{est}$ is determined using (22).
• Method #4: Simulated responses of frequency and active power are used to develop second order transfer functions. Subsequently, the impulse response of these transfer functions is computed and $H_{est}$ is calculated via (25).
• Method #5: The SW approach is used. $H_{est}$ is derived using (19).

The above-mentioned methods were chosen since they constitute the most prevalent measurement-based inertia-estimation approaches and have been used in several research papers during the last few years. An overview of these research papers is provided in 

Table 1. Overview of research papers that use the examined methods to perform inertia estimation.

Method	Reference
#1 and/or #2	[22,27,28,29,52,79,80,81,82,83,84,89]
#3 and/or #4	[13,39,75,88,92,93,94,95,96]
#5	[40,88,90,91]

.

5.3. Comparative Assessment

In this subsection, the impact of several parameters on the accuracy of the examined methods is quantified.

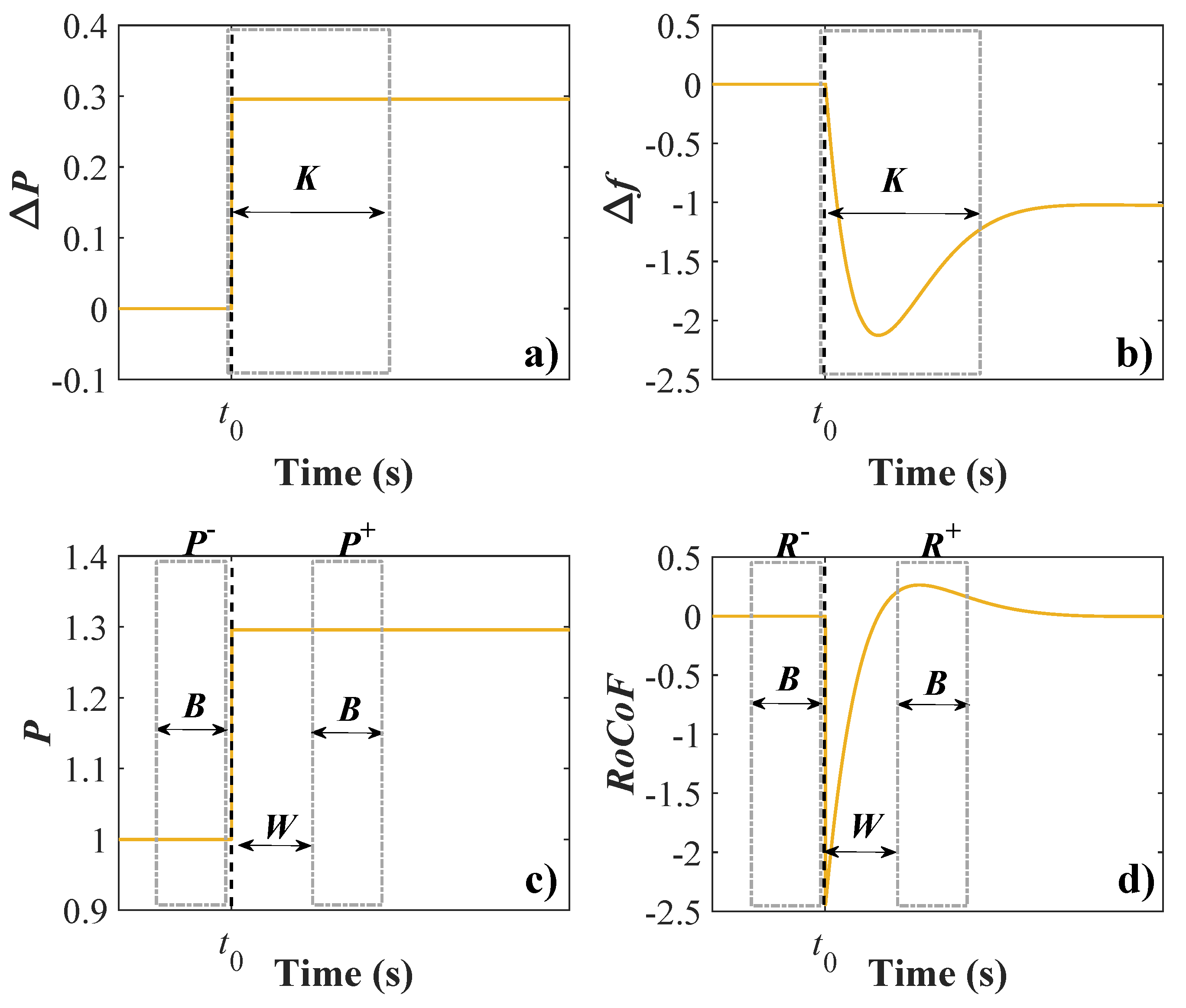
5.3.1. Impact of Window Length

To evaluate the impact of the length of the analysis window on the accuracy of the examined methods, the following procedure was applied: A frequency event was introduced at $t_0=2$ s, by decreasing the active power of Load A, by 62.5 MW. The resulting dynamic responses of the frequency and active power of G1, G2, and G3 are depicted in Figure 3. These dynamic responses were forwarded as inputs to the examined methods to estimate inertia constants of G1, G2, and G3. Subsequently, the iterative procedure of Figure 4a was used to fully quantify the impact of the length of the analysis window on the performance of Methods #1, #2, #3, and #4. Concerning Method #5, the procedure of Figure 4b was adopted.

As shown in Figure 4a, the examined methods are applied iteratively, assuming at each iteration different window lengths, i.e., windows with a different number of total samples K. Initially, K was set to the minimum possible value, i.e., to $k_{min}$. At this point, it shall be noted that $k_{min}$ differs for each examined method. Indeed, Method #1 requires a data analysis window that contains at least six samples in order to identify parameters $A_5$, $A_4$, $A_3$, $A_2$, $A_1$, and $A_0$. In Method #2, the optimal polynomial order is determined via the iterative procedure of Algorithm 1, assuming that $n_{max}$ is set to 10. Thus, at least 11 data samples are required to identify parameters of ${\mathit{\theta }}_{\mathbf{1}}$. In Method #3 and Method #4 second-order transfer functions are developed using the ARMAX approach. Thus, for these methods, a minimum of nine samples are required. Since $k_{min}$ differs for each method, the iterative process of Figure 4a is executed independently for each examined method. In each iteration, $H_{est}$ is computed for each one of the installed SGs and the corresponding $PE(\%)$ is calculated. After each iteration, K is increased by 1. The procedure terminates when $K=k_{max}=100$, i.e., when the length of the analysis window is equal to 1 s (recall that the sampling rate is set to 100 SPS). The length of the analysis window is restricted to 1 s to ensure that the primary frequency response services are not activated [1,2,82].

The impact of parameters W and B on the accuracy of Method #5 is quantified using the procedure shown in Figure 4b. Initially, W is set to 2 and B is set to 1. $H_{est}$ is computed for all installed SGs and the corresponding $PE(\%)$ is calculated. In each iteration, W and B are modified. W varies from 2 up to 20, using a step equal to 2. B varies from 1 to 40, assuming a step equal to 1.

The impact of window length on the accuracy of Methods #1–#4 is quantified in Figure 5. Concerning Method #1, Method #3, and Method #4 it is clear that as K increases, $PE$ increases as well. Therefore, a narrow window is generally required to provide accurate estimates. Nevertheless, it is obvious that for each SG, the optimal window length, i.e., the value of K that leads to the lowest $PE$, is different. Regarding Method #2, it can be perceived that its performance is not highly affected by the length of the analysis window. Indeed, for all SGs, $PE$ lower than 5% is generally observed. Nevertheless, Method #2 fails to provide inertia estimates for several cases, i.e., for several K values, since the iterative procedure of Algorithm 1 failed to converge and thus, to provide the optimal approximation order. Optimal approximation orders for the different values of K are depicted in Figure 6. As shown, the optimal order varies for most of the cases between four and nine. The sixth-order approximation is the prevalent one. Concerning Method #5, indicative results are presented in Figure 7. As shown, $PE$ increases as the length of the pre- and post-disturbance windows increase.

Based on the above results, it is clear that the length of the analysis window affects considerably the performance of the examined methods. This is especially true for Method #1, Method #3, Method #4, and Method #5. Nevertheless, results also reveal that a fine tuning of the window length, i.e., fine tuning of parameters K or W and B, can ensure in all cases accurate inertia estimates. This is better highlighted in

Table 2. Optimal value of K and resulting $PE$ for Method #1, Method #2, Method #3, and Method #4. Minimum PE are highlighted with bold font.

	G1		G2		G3
	K	$\mathit{PE}$ (%)	K	$\mathit{PE}$ (%)	K	$\mathit{PE}$ (%)
Method #1	14	0.0106	23	0.0051	76	0.0244
Method #2	13	0.0168	57	0.0396	76	0.0244
Method #3	10	0.1231	11	0.1581	13	0.0224
Method #4	100	0.0044	31	0.1143	40	0.0164

and

Table 3. Optimal values for W and A for Method #5 and resulting $PE$.

	G1			G2			G3
	W	B	$\mathit{PE}$ (%)	W	B	$\mathit{PE}$ (%)	W	B	$\mathit{PE}$ (%)
Method #5	2	1	1.26	2	1	0.60	2	3	0.11

, where the optimal values for K, W, and B are summarized alongside with the corresponding $PE$. Additionally, in Table 2, the minimum errors, for each generator, are marked with bold font.

Results indicate that all the examined methods can provide very accurate inertia estimates if parameters K, W, and B are fine-tuned. Nevertheless, the optimal values of these parameters highly depend on the individual characteristics of each method, and they also differ considerably for each SG. Therefore, it is not possible to define unique values for K, W, and B, which can be used for the analysis of all the installed SGs.

5.3.2. Impact of Noise

In this subsection, the impact of noise on the performance of the examined methods is quantified. For this purpose, the following procedure is applied: The dynamic responses of Figure 3 are distorted with additive white Gaussian noise (AWGN), assuming a signal-to-noise ratio (SNR) equal to 30 dB and 20 dB. For each distinct SNR level, a set of 100 MC simulations is performed, in order to replicate different instances of noise.

Initially, the distorted responses are used to estimate inertia constants of G1, G2, and G3 by directly using (10), i.e., by directly applying the swing equation. Results for both SNR levels are summarized in

Table 4. Inertia estimation via the direct use of the swing equation. Computed $PE$ under different noise levels.

	No Noise	SNR = 30 dB		SNR = 20 dB
		$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$
G1	0.35	11.02	4.03	15.76	12.04
G2	0.66	10.25	5.51	17.53	14.90
G3	0.33	6.88	4.47	13.07	11.72

, where the mean ($\mathsf{\mu }$) and standard deviation ($std$) of the resulting $PE$ across the examined MC simulations are presented. Deterministic results for the no-noise case are also reported in Table 4. As shown, under ideal conditions, i.e., when no noise is considered, the direct use of the swing equation can provide accurate estimates, resulting in $PE$ lower than 0.5%. Nevertheless, under noisy conditions, this approach leads to unacceptable results. Indeed, for both SNR levels, $PE$ higher than 10% are generally observed. This remark justifies the need for the development of more sophisticated inertia-estimation techniques, which can provide accurate results also under noisy conditions.

Subsequently, the performance of the examined inertia-estimation methods under noisy conditions is evaluated. For this purpose, the distorted responses of frequency and active power, resulted from the MC analysis, are forwarded as inputs to the examined methods. For each MC simulation and for each method, the optimal window length, i.e., optimal values of K or W and B, which lead to the minimum $PE$, are identified using the algorithms of Figure 4. Results for Method #1–Method #4 are summarized in

Table 5. Impact of noise on the performance of Method #1, Method #2, Method #3, and Method #4.

		SNR = 30 dB				SNR = 20 dB
		K		$\mathit{PE}$ (%)		K		$\mathit{PE}$ (%)
		$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$
	G1	55	45	0.62	3.28	50	40	1.35	5.89
Method #1	G2	10	3	0.81	3.06	27	30	2.66	7.66
	G3	11	3	4.41	2.80	31	30	5.08	6.29
	G1	29	12	7.25	0.54	31	18	5.69	2.71
Method #2	G2	17	1	4.37	0.75	19	13	4.97	8.64
	G3	19	1	0.61	0.61	21	11	2.37	8.35
	G1	23	9	4.30	4.17	37	21	4.74	5.58
Method #3	G2	27	12	4.70	5.70	38	15	5.61	6.28
	G3	33	12	2.72	2.53	50	22	2.88	3.32
	G1	56	30	2.30	3.37	53	27	2.72	4.75
Method #4	G2	51	27	1.59	2.59	54	24	2.28	4.67
	G3	52	25	0.83	1.76	59	24	1.51	3.66

. Minimum errors, per generator and noise level, are highlighted on this table using bold fonts. For Method #5, the results are reported in

Table 6. Impact of noise on the performance of Method #5.

	SNR = 30 dB						SNR = 20 dB
	W		B		$\mathit{PE}$ (%)		W		B		$\mathit{PE}$ (%)
	$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$	$\mathit{\mu }$	$\mathit{std}$
G1	2	1	4	1	5.21	5.54	6	5	6	5	7.56	20.7
G2	3	3	5	2	3.32	4.15	7	5	12	11	8.41	16.01
G3	5	4	7	4	0.99	2.17	11	7	9	7	6.31	17.54

.

The conducted analysis reveals that for each method an optimal window length, which results in acceptable $PE$ values, i.e., in $PE$ lower or close to 5%, can be identified. Nevertheless, it is worth noting that in real applications, where the inertia constants are generally unknown, the optimal window length cannot be identified using the procedures of Figure 4. In these cases, either more sophisticated techniques shall be developed to determine the optimal window length or pre-defined values, based on historical events, for parameters K, W, and B shall be used. However, as shown in Table 5 and Table 6 the $std$ of parameters K, W, and B is considerably high. Therefore, the use of pre-defined values for these parameters may lead to inaccurate results or, even worse, to total failure in inertia estimation. The latter case is especially true for Method #2, Method #3, and Method #4. Indeed, when parameter K is not fine-tuned, Method #2 may fail to provide inertia estimates due to the non-convergence of Algorithm 1. Concerning Method #3 and Method #4, unstable transfer functions may be computed, prohibiting inertia estimation.

To better demonstrate this issue, the following analysis is performed: The MC simulations are repeated once again. However, this time, the optimal value of K (the optimal window length) is not defined using the iterative procedure of Figure 4. On the contrary, K is assumed fixed across the MC simulations and equal to the mean values reported in Table 5.

Table 7. Number of cases that Method #2, Method #3, and Method #4 failed to provide inertia estimates. K is assumed constant and equal to the corresponding mean values reported in Table 5.

	Method #2			Method #3			Method #4
	G1	G2	G3	G1	G2	G3	G1	G2	G3
SNR = 30 dB	52	29	32	61	52	63	26	48	55
SNR = 20 dB	62	48	42	52	52	55	45	44	45

summarizes the number of cases across the 100 MC simulations that Method #2, Method #3, and Method #4 failed to provide inertia estimates when K is set to a pre-defined value. As shown, for almost 50% of the cases, all three methods fail to provide results. Therefore, it is evident that predetermined values of K cannot be used under noisy conditions.

Finally, based on the results of Table 5 and Table 6, it can be perceived that as the SNR level decreases, the accuracy of the examined methods is generally reduced. This is verified by the corresponding $PE$, which tends to increase as the SNR level decreases.

5.3.3. Impact of Event Detection

In this subsection, the impact of inaccurate event detection (the inaccurate identification of the onset of the event) on the accuracy of the examined methods is analyzed. Towards this objective, the following procedure is adopted: The dynamic responses of Figure 3 are forwarded as inputs to the examined methods to estimate inertia constants of G1, G2, and G3. However, it is assumed that the onset of the event is identified erroneously. To create realistic inaccuracies, it is assumed that the event detection results in errors varying from five samples prior to the occurrence of the event, to up to five samples after the occurrence of the event.

For each method and for each case, inertia estimation is performed for G1, G2, and G3 using the optimal values of K, W, and B reported in Table 2 and Table 3. Subsequently, the mean $PE$, i.e., the mean error across the estimates of G1, G2, and G3, is computed. The corresponding results are presented in Figure 8.

As shown, inaccurate event detection may result in significantly high $PE$. This remark is especially true for Method #1 and Method #5. Additionally, it is worth noting that, in several cases, Method #2, Method #3, Method #4, and Method #5 fail to provide inertia estimates, i.e., fail to estimate the inertia constant of at least one of the installed SGs. The reasons that prevent Method #2, Method #3, and Method #4 from providing inertia estimates were discussed and analyzed in Section 5.3.2. Method #5 fails to provide inertia estimates in cases of erroneous event detection, because (19) cannot be evaluated, i.e., the denominator is equal to zero.

5.3.4. Impact of Disturbance Level

To investigate the impact of disturbance level, i.e., active-power imbalance magnitude, on the accuracy of the examined methods, the following analysis was performed: Initially, ten disturbances were simulated using the model of Figure 2. All disturbances were introduced by applying step changes to the active power of Load A. The magnitude of the examined disturbances is summarized in the first row of

Table 8. Optimal K values under different disturbance levels.

		Disturbance Level (MW)
		12	25	37	50	62	75	87	100	112	125
	G1	85	85	82	7	14	12	10	67	65	65
Method #1	G2	35	26	25	23	23	18	20	22	21	22
	G3	81	82	77	75	76	76	79	80	11	88
	G1	17	33	12	22	13	11	15	16	11	97
Method #2	G2	28	58	66	61	57	32	44	58	13	43
	G3	52	11	49	81	76	75	73	100	11	99
	G1	10	10	9	9	10	10	9	9	9	9
Method #3	G2	9	12	9	9	11	9	17	9	14	10
	G3	11	11	12	11	13	9	14	12	15	10
	G1	46	32	52	36	100	50	56	64	73	83
Method #4	G2	25	30	26	29	31	29	28	82	29	28
	G3	30	40	38	39	40	40	40	40	41	41

. Subsequently, the procedures of Figure 4a,b were used to determine the optimal values for K, W, and B. The identified optimal values were summarized in Table 8 and

Table 9. Optimal W and B values under different disturbance levels.

		Disturbance Level (MW)
Method #5		12	25	37	50	62	75	87	100	112	125
	G1	1	1	4	1	1	4	1	1	3	1
$\mathit{B}$	G2	1	2	1	1	1	1	1	6	1	1
	G3	3	1	1	3	1	1	3	1	1	3
	G1	3	3	2	2	2	2	2	3	3	3
$\mathit{W}$	G2	4	3	4	2	5	3	2	2	3	4
	G3	2	2	2	2	2	2	2	2	2	2

. The associated results indicate that the disturbance level considerably affects the optimal length of the analysis window.

In case the optimal values of K, W, and B, reported in Table 8 and Table 9, are used, the mean $PE$, for Method #1, Method #2, Method #3, Method #4, and Method #5 is 0.04%, 0.27%, 0.31%, 0.03%, and 0.57%, respectively. On the contrary, the use of historical values may lead to considerable performance degradation for all methods. For instance, if the values of K, W, and B, reported in Table 2 and Table 3, are used, then the following results are derived: The mean $PE$ for Method #1 is 0.42%, i.e. ten times higher compared to the case where the optimal values were used. Concerning Method #2, in three cases, no estimates are provided due to non-convergence issues. For the rest of the examined disturbances, the mean $PE$ for Method #2 is 1.32%. The mean $PE$ for Method #3, Method #4, and Method #5 is 0.68%, 14.37%, and 1.19%, respectively.

5.3.5. Impact of Disturbance Location

In this subsection, the influence of the disturbance location on the optimal window length is evaluated. For this purpose, three distinct frequency events are simulated by changing the active power consumed by Loads A, B, and C, located at buses B5, B6, and B8, respectively. To ensure a common comparative basis, each frequency event was generated by decreasing by 62.5 MW the active power of each load. The resulting dynamic responses of frequency and active power are forwarded as inputs to the examined methods and the procedures of Figure 4 were used to determine the optimal window length, i.e., optimal values for parameters K, W, and B. The analysis was performed for all the installed SGs. The optimal values of K are summarized in Figure 9. Optimal values of W and B are reported in

Table 10. Impact of disturbance location on the optimal values of W and B.

Disturbance Location	B5		B6		B7
	$\mathit{W}$	$\mathit{B}$	$\mathit{W}$	$\mathit{B}$	$\mathit{W}$	$\mathit{B}$
G1	2	1	2	1	2	4
G2	2	1	4	3	4	1
G3	2	3	2	1	2	1

.

The conducted analysis reveals that the optimal length of the analysis window differs considerably for each SG and for each disturbance location. Thus, it is not possible for the power-system operator to determine a unique window length, based on historical events, that can be used for the inertia estimation of different devices.

5.3.6. Probabilistic Assessment

In this subsection, the performance of the examined methods is evaluated in a probabilistic manner. $M_{DL}$ = 3 disturbance locations are considered, namely disturbances introduced at Buses B5, B6, and B8. For each disturbance location, 20 discrete frequency events ($M_{FE}$ = 20) are analyzed by changing the active power of the load connected to the corresponding bus/location. Active power changes, varying from −100% up to 100% of the rated power of each load are considered, assuming steps of 10%. Hence, a total number of $M=M_{DL}·M_{FE}=60$ cases is analyzed. For each case, the resulting dynamic responses of frequency and active power of the three installed SGs are recorded and used to estimate the corresponding inertia constants.

To quantify the impact of window length on the accuracy of the examined methods, the procedures of Figure 4a,b are used. Representative results for Method #1, Method #2, Method #3, and Method #4 are depicted in Figure 10, where the $PE$ for discrete window lengths across the examined M cases is summarized by means of boxplots. Each boxplot contains results for all M cases. As already discussed and demonstrated, all methods require relatively narrow windows to perform satisfactorily. In fact, as analyzed in Section 5.3.1, as the window length increases, $PE$ increases as well. Therefore, to enhance the readability of Figure 10, K is limited to the range of [$k_{min}$,$k_{min}$ + 20].

Representative results for Method #5 are presented in Figure 11. In this case, the mean $PE$ across the M cases is presented, assuming different values for parameters W and B.

Results for Method #1 are depicted in Figure 10a. The y-axis of this figure is in logarithmic scale, to accommodate the depiction of some extremely high outliers. As shown, Method #1 results for all examined window lengths in median $PE$ values lower than 4%. However, it is clear that Method #1 results, in several cases, in unreliable estimates. These estimates are treated as outliers and they are presented in Figure 10a with red crosses.

Method #2 exhibits better performance compared to Method #1. Indeed, in all cases, Method #2 results in median $PE$ lower than 1.7%. The number of outliers (and $PE$ values of the outliers) are significantly lower compared to those of Method #1. Nevertheless, it shall be noted that for the examined range of K values, Method #2 failed to converge in several instances. The number of failed instances varies between 0 (for $K=6$ and $K=7$) and 57 (for $K=13$). These instances are not reported in Figure 10b and this is why they are mentioned separately. A total number of 610 failures of Method #2 was recorded. Note that the total number of estimates in the probabilistic assessment is 3600. Indeed, $M_{FE}$ = 60 frequency events were examined, 20 different windows sizes were considered and estimates for three different SGs are provided. Thus, it can be perceived that Method #2 failed to provide estimates in 17% of the examined instances.

Concerning Method #3, the following remarks can be drawn: The median $PE$ is lower than 1% when narrow windows are used. Nevertheless, outliers are observed for several K values. The lower the value of K, the greater the number of the outliers is. Moreover, it is clear that as the length of the analysis window increases, the median $PE$ increases as well. Finally, Method #3 failed to provide estimates in 12 instances (out of the 3600 examined in total).

Method #4, which calculates inertia constants by utilizing the impulse response of the identified transfer functions, is the most reliable and accurate method. Indeed, in all cases, Method #4 results in median $PE$ values lower than 2%. Additionally, it is worth noting that no outliers are observed and under all examined instances the maximum computed $PE$ is merely 4%. Similar to Method #3, Method #4 failed to provide estimates in 12 instances (out of the 3600 examined in total).

Regarding Method #5, it is clear based on the results of Figure 11 that narrow pre- and post-disturbance windows shall be used. Otherwise, considerable performance degradation is observed.

5.4. Discussion of the Results

The analysis conducted in Section 5.3.1, Section 5.3.2, Section 5.3.3, Section 5.3.4, Section 5.3.5 and Section 5.3.6 indicates that the performance of the examined methods is highly affected by several factors such as the SNR level, the accurate event detection, i.e., the accurate identification of the onset of the frequency event, and the length of the analysis window.

Results indicate that as the SNR decreases, the accuracy of the examined methods is generally reduced. Nevertheless, all methods can provide accurate results even under extreme noise conditions, if the length of the analysis window is fine-tuned. Accurate event detection is also crucial for the performance of the examined methods. Indeed, inaccurate event detection may lead either to extremely erroneous estimates or to total failure of the examined methods, i.e., failure to provide inertia estimates due to non-convergence issues.

The length of the analysis window is the most crucial factor for the performance of the examined methods. Indeed, results reveal that if the length of the analysis window is fine-tuned, then all examined methods can provide accurate inertia estimates. Based on the conducted analysis, it is evident that relatively narrow windows are required for accurate inertia estimation. However, the optimal length of the analysis window is affected by several factors. For instance, the SNR level, the location and magnitude of the disturbance have a crucial impact on the optimal window length. Therefore, it is practically impossible to define the optimal length of the analysis window based on historical events. Indeed, as demonstrated, the use of pre-defined window lengths may lead to extremely erroneous inertia estimates or, even worse, to total failure in inertia estimation.

To overcome the above-mentioned limitations, some modifications to the conventional implementation of the examined methods are proposed. These modifications are discussed and analyzed in the next section.

6. Proposed Modifications

To enhance the robustness and accuracy of the examined methods, Algorithm 2 is developed. The core idea of the proposed algorithm is to apply the examined inertia-estimation techniques in an iterative manner. At each iteration, a new inertia estimate is computed by utilizing different data streams, i.e., by modifying the length of the analysis window. Following this approach, a pool of inertia estimates is finally derived. Subsequently, a post-processing analysis of all inertia estimates is performed and the final inertia value is computed.

Algorithm 2 Pseudocode of the proposed iterative procedure

1: Obtain active power and frequency responses. 2: Choose method and set $k_{min}$ accordingly. Define $k_{max}$. Set $K=k_{min}$ and $m=1$. 3: while$K\le k_{max}$do 4:     Compute $H_{est}$ and $EI$. Store results at $\mathit{H}\left(m\right)$ and $\mathit{EI}\left(m\right)$, respectively.      Set $m=m+1$ and $K=K+1$ 5: end while 6: Post-processing of inertia estimates contained at $\mathit{H}$ 7: Determine $H_{final}$ as the mean value of the most accurate estimates.

The algorithmic details of the proposed approach are presented in Section 6.1. Validation results are provided in Section 6.2.

6.1. Algorithmic Details

The proposed iterative procedure is explained step-by-step below:

• Step 1 Active power and frequency responses are forwarded as inputs to Algorithm 2.
• Step 2: The user selects which method shall be used for inertia estimation. The available options are: Method #1, Method #2, Method #3, and Method #4. These methods are selected, because evaluation criteria can be used to quantify the quality of their estimates. These evaluation criteria are discussed in the next step. On the other hand, Method #5 is not considered as a candidate method, since efficient evaluation criteria cannot be easily implemented. Additionally, at this step, the value of $k_{min}$ is specified based on the selected method and on the remarks presented in Section 5.3.1. Finally, the user defines $k_{max}$, i.e., the maximum length of the analysis window. In this paper, $k_{max}$ is limited to 100. Hence, the maximum length of the analysis window is set to 1 s. As already discussed, the length of the analysis window is restricted to 1 s, to ensure that primary frequency response services are not activated, thus prohibiting the accurate estimation of inertia constants.
• Steps 3 to 5: In these steps, the selected inertia-estimation method is applied iteratively, assuming different window lengths. At each iteration, the estimated inertia constant $H_{est}$ is computed and stored at a vector variable, i.e., at $\mathit{H}$. Additionally, the evaluation criterion is computed and the corresponding value is stored on a dedicated variable, i.e., on vector $\mathit{EI}$. In this paper, the error index ($EI$) of (30) is selected as the evaluation criterion.

  $$EI=\left(1-\frac{|x-y|}{|x-mean(x\left)\right|}\right)·100\%$$

  (30)
  In the above notation, x denotes the actual (measured) data, while y denotes the corresponding estimates. For Method #1 and Method #2, x is the measured $\Delta f$, while y is the corresponding approximation computed via (11). For Method #3 and Method #4, x is the TD response of the measured $G\left(s\right)$ transfer function, i.e., the $G\left(s\right)$ as computed from the measured signals of $\Delta f$ and ${\Delta }_{p_e}$. y is the approximation of $G\left(s\right)$ by a second-order transfer function. An $EI$ equal to 100% denotes a perfect approximation.
  Finally, m and K are increased by one and the algorithm moves to the next iteration. The algorithm terminates when $K=k_{max}$.
• Step 6: In this step, a post-processing of the derived models/approximations is performed. Towards this objective, models/approximations that result in unrealistic inertia values, e.g., negative values or values higher than 15 s, are discarded. Models that lead to unstable transfer functions are also excluded from further analysis. The latter criterion is applicable only for Method #3 and Method #4.
• Step 7: In this step, the $EI$ is used to identify the most accurate approximations/models. In general, the better the quality of the approximation is, the more accurate the inertia estimate [13]. Nevertheless, the conducted analysis revealed that in some cases, models exhibiting high $EI$ values, e.g., higher than 90%, may lead to inaccurate inertia estimates, i.e., in estimates that present $PE$ values close to 10%. Therefore, to eliminate the impact of these erroneous estimates, in the proposed approach, the final inertia value $H_{final}$ is not computed by utilizing a single model/approximation; on the contrary, $H_{final}$ is computed for Method #1, Method #2, and Method #4 as the mean value of the most accurate estimates, i.e., estimates that present the highest $EI$ values. In this paper, 3% of the most accurate estimates is used for this purpose. Regarding Method #3, a different approach is applied. Indeed, to perform satisfactorily, Method #3 requires the identification and elimination of the insignificant states of the identified second-order transfer functions. Nevertheless, state elimination may result in inaccurate inertia estimates (especially when the poles of the identified second-order transfer functions are very close to each other). Therefore, the following approach is proposed: $EI$ is initially computed. Models that present $EI$ lower than 90% are discarded from the analysis. For the rest of the models, the corresponding poles are determined, i.e., the poles of the identified second-order transfer functions. In second-order transfer-function models, the pole that is closer to the imaginary axis, i.e., the pole with the lowest absolute real part, is the dominant pole that mainly affects the dynamic behavior of the examined system. Hence, it is reasonable to assume that a second-order transfer function, which has a set of well-separated poles, i.e., a pole with a very low real part and a pole with a very high real part, can be reduced to a first-order transfer function without introducing significant errors, i.e., the reduced model preserves the dynamic properties of the initial system. Therefore, in the proposed approach, for each model (identified second-order transfer function) the Euclidean distance of the poles is calculated. $H_{final}$ is computed as the mean value of the inertia estimates derived from transfer functions that present the highest Euclidean distances. To compute $H_{final}$, the 3% of the transfer functions that exhibit the highest Euclidean distances are used.

6.2. Validation Results

The performance of the proposed iterative procedure is evaluated in a probabilistic manner. For this purpose, the 60 frequency events, simulated in Section 5.3.6, are considered. For each frequency event, the resulting dynamic responses of the frequency and active power of the three installed SGs are recorded and forwarded as inputs to Algorithm 2, which is used to estimate their inertia constants. To ensure a common comparative base with the results presented in Section 5.3.6, K is limited in the range of $[k_{min},k_{min}+20]]$. For the testing, all inertia-estimation methods that are compatible with Algorithm 2 are considered. Algorithm 2 is executed separately for each SG and for each inertia-estimation method. For each method, a total number of 180 inertia estimates is computed (one estimate per frequency event and per SG).

Using these estimates, the cumulative distribution functions (CDFs) of the resulting $PE$ of all methods are computed and presented in Figure 12. In this figure, the CDFs of $PE$ of the conventional implementations of the examined methods are also presented. The latter are computed for each method by aggregating the results presented in Figure 10a–d. As shown, the proposed iterative procedure can enhance the accuracy of the examined methods. For instance, the conventional implementation of Method #1 results in 2% of the examined cases in totally unacceptable $PE$ values. In particular, these $PE$ values range from 20% up to 16,000%. Note that these values have been excluded from Figure 12 to ensure its readability. This is why the maximum value of the corresponding CDF is equal to 0.98 (and not 1). On the other hand, when Method #1 is combined with the proposed iterative approach, results in all cases in $PE$ lower than 10%. The modified version of Method #2 results in all examined cases in $PE$ being lower than 4%. On the contrary, the conventional implementation of Method #2 presents an inferior performance. Concerning Method #3, it is clear that with the proposed modifications $PE$ is lower than 5% in all examined cases. On the other hand, the conventional implementation of Method #3 provides $PE$ lower than 5% in 88.5% of the examined cases. The conventional and the modified versions of Method #4 exhibit similar performance, resulting in all cases in $PE$ lower than 4%. Nevertheless, the proposed iterative approach slightly increases the accuracy of the method. Indeed, the maximum $PE$ is reduced by almost 11% when the proposed iterative procedure is adopted.

Impact of Noise

Finally, the performance of the proposed iterative procedure was tested under noisy conditions. For this purpose, the analysis of Section 6.2 was repeated once again. However, this time, prior to implementation of Algorithm 2, the dynamic responses of frequency and active power were intentionally distorted with AWGN, assuming an SNR equal to 30 dB. For each one of the examined frequency events, a set of 100 MC simulations were performed to replicate different instances of noise. Representative results for the mean value and the standard deviation of the $PE$ are reported in

Table 11. Impact of noise on the performance of the proposed approach. Statistical results for the $PE$.

	Method #1			Method #2			Method #3			Method #4
	G1	G2	G3	G1	G2	G3	G1	G2	G3	G1	G2	G3
$\mathit{\mu }$	15.36	9.49	12.63	15.48	6.37	7.23	6.96	7.86	4.88	5.95	6.58	4.89
$\mathit{std}$	9.59	13.01	12.30	4.49	2.91	2.11	4.02	7.70	4.51	4.77	5.98	4.72

.

Results of Table 11 reveal that noise has a negative impact on the accuracy of all methods. Method #3 and Method #4, which are based on transfer-function modeling, are the most robust and accurate ones, resulting in mean values for the $PE$ close to 5%.

7. Conclusions

In this paper, a literature review of inertia-estimation techniques is performed. Special focus is given to the analysis of measurement-based inertia-estimation techniques, since they can be easily implemented for wide-area monitoring applications. Additionally, the performance of the five most prevalent inertia-estimation techniques is thoroughly assessed. Towards this objective, dynamic simulations are performed on the DIgSILENT software and several scenarios are considered and examined. Moreover, the impact of several factors on the accuracy of the examined methods is systematically quantified by means of MC analysis.

The results reveal that the accuracy of the examined methods is highly affected by the SNR level, the accurate event detection, and the length of the analysis window. The latter is the most crucial factor for the performance of the examined methods. Indeed, if the length of the analysis window is not fine-tuned, then considerable performance degradation is observed for all examined methods. Nevertheless, the optimal window length is affected by several factors such as the SNR level, the magnitude and the location of the disturbance. Thus, it is almost impossible to define the optimal length of the analysis window based on historical events.

To overcome the aforementioned issues and to enhance the robustness and accuracy of the examined methods, a new iterative procedure is proposed to determine, based only on field measurements, the optimal length of the analysis window. Results indicate that the proposed approach can enhance considerably the accuracy of all examined methods. The analysis also reveals that the proposed iterative approach can be combined well with Method #3 and Method #4, providing quite accurate inertia estimates even under noisy conditions.

The analysis performed in this paper quantifies the accuracy capabilities of the existing measurement-based inertia-estimation methods, setting also a framework for the objective assessment of new techniques that may be developed in the near future. Future work will focus on the impact of non-Gaussian measurement error on the performance of the examined methods. Post-processing and filtering techniques will also be tested, aiming to quantify their impact on inertia estimation.