1. Introduction
Buildings are the largest energy-consuming sector, with a global share of 35% of energy consumption, exceeding industry and transportation [
1]. It is estimated that 85% of the building energy consumption is attributed to heating, ventilation, and air conditioning (HVAC), lighting, and plug loads. Moreover, residential buildings account for approximately 63% [
1] of the total energy used by the building sector. In terms of electricity consumption, buildings take 50% of the world’s electricity consumption [
1]. According to the U.S. Energy Information Administration (EIA), projections show that the residential and commercial buildings will increase by 1.3% per year from 2018 to 2050 for countries in the Organization for Economic Cooperation and Development (OECD), while non-OECD countries will experience an average of 2% growth annually [
2]. Several studies have analyzed the historical and current status of energy consumed by buildings and have projected future increases in building-related energy use globally [
3] or in specific regions such as China [
4], the European Union [
5], and Gulf Cooperation Council countries [
6]. The high energy consumption by the built environment has significant detrimental effects on the environment and the climate. Several governmental agencies and global organizations are adopting initiatives and programs that target the reduction of energy consumption in the building sector. For instance, the U.S. Department of Energy has set a 2030 goal of tripling 2020 levels of commercial and residential buildings’ energy efficiency [
7]. Similarly, the UK has developed a net-zero energy strategy for buildings so that by 2050, buildings will be completely decarbonized [
8]. The goal included a plan that is driven by decisions to fund several research projects, support owners to shift the buildings’ efficiency, and subsidize clean and efficient projects [
8]. In addition, China, the largest carbon dioxide emitter, has pledged to reach neutral carbon emissions before 2060 [
9].
Such initiatives and pledges can be achieved by a combination of several approaches including enhancing renewable energy sources, setting more stringent energy efficiency regulations, and funding research to develop effective and transformative technologies in the building energy sector. However, improvements in the energy efficiency levels of existing buildings are required to attain the desired goals. Indeed, the average annual rate of replacing existing buildings is low reaching only 1% in the UK [
10]. It is argued that the environmental and economic benefits of retrofitting existing buildings outweigh those achieved by replacing them with more efficient new buildings. Hasik et al. [
11] performed a life cycle assessment (LCA) of both retrofitted and newly constructed buildings and found that retrofitting results in a reduction ranging between 53% and 75% for over six different environmental impact factors compared to new construction. Economic benefits are highest when retrofitting the least energy-efficient buildings when considering aspects such as the creation of employment and reduction of carbon emissions compared to constructing new buildings [
12].
Retrofitting existing buildings includes renovations of mechanical, structural, and electrical systems with a range of options such as refurbishment, replacement, or addition of new equipment. In the case of energy efficiency retrofits, the replacement and addition of new equipment is usually referred to as an energy conservation measure (ECM). Several ECMs can be considered for existing buildings such as changing HVAC equipment, lighting systems, and envelope features such as glazing types and wall assemblies. The deployment of ECM aims primarily at reducing the energy use and cost of the buildings. The required investments for ECMs are justified based on economic and environmental benefits. However, the implementation of ECMs can face several challenges, especially during assessment and identification, as well as installation and verification. In the first period, any missing information and documentation can hinder good assessment of the existing building energy performance and thus effective identification. Similarly, uncertainty and lack of data can affect the installation and validation process. For the validation analysis, an energy model of the building is typically needed to predict the energy use before the deployment of any ECM with minimum prediction uncertainty. Additionally, this process includes an essential step in justifying the effectiveness of the installed employed EMCs, that is, measurement and verification (M&V) analysis.
Several literature reviews have discussed data-driven models for tasks that are related to the energy performance of existing buildings. Wei et al. [
13] categorized data-driven approaches into two applications including prediction and classification. However, this literature review considers only prediction with a subset of prediction that is related to times series instead of cross-sectional data. Cross-sectional data represent observations that are not collected at unique timestamps or identified by a chronological order. Typically, data are represented in a tabular form of columns and rows. If each row represents a value assigned for a specific timestamp (e.g., the energy consumption of a building at 13:00), then the data is time series. In M&V baseline modeling, the data characteristics may require different modeling methods. On the other hand, prediction of energy consumption with cross-sectional data is performed with each realization being a single building and its response variable being a single value representing total energy consumption over a specific period. Deb et al. [
14] did a review of forecasting in building’s energy consumption using nine different techniques with a hybrid approach that represents a combination of more than one technique. Unlike M&V baseline modeling, forecasting in building’s energy consumption focuses on predicting future values using correlation from closely past values which is not possible for the created baseline when performing M&V after retrofitting. Grillone et al. [
15] conducted a literature review of deterministic and data-driven methods that can be used to estimate energy savings from retrofits. Their analysis is focused on two areas: M&V and prediction and recommendation while this literature review aims to focus on M&V and prediction extensively. Deb and Schlueter [
16] reviewed data-driven approaches in retrofitting applications including benchmarking, energy signature, and feature extraction. However, the review did not specifically discuss the baseline modeling approaches for M&V Applications.
In terms of applications, numerous reported studies have considered data-driven models to predict the energy consumption of existing buildings. Many of the reported data-driven models are based on historical data that is used for training the models and testing their prediction accuracy. However, few of such models have been applied to create a baseline for M&V analysis to determine energy savings achieved by installed ECMs. Additionally, reported data-driven models for M&V applications have been developed and tested only for specific building types and ECMs. Furthermore, models have not been evaluated for multiple buildings and ECMs. With the increasing interest in applying data-driven models for building energy retrofit analysis, there are limited guidelines on the suitability of these models for M&V applications. Therefore, this literature review examines various methods and algorithms that have been applied to develop data-driven models for M&V analysis of building energy retrofits. The contribution of this paper is to build a summary of every step in building a data-driven model for M&V analysis. The focus is specifically on only prediction with applicability to M&V analysis along with the necessary steps in processing and creating features before training the baseline model. The literature review summarizes the previous endeavors of studies and frameworks and extracts the most listed requirements and modeling approaches.
2. Overview of Measurement and Verification Analysis
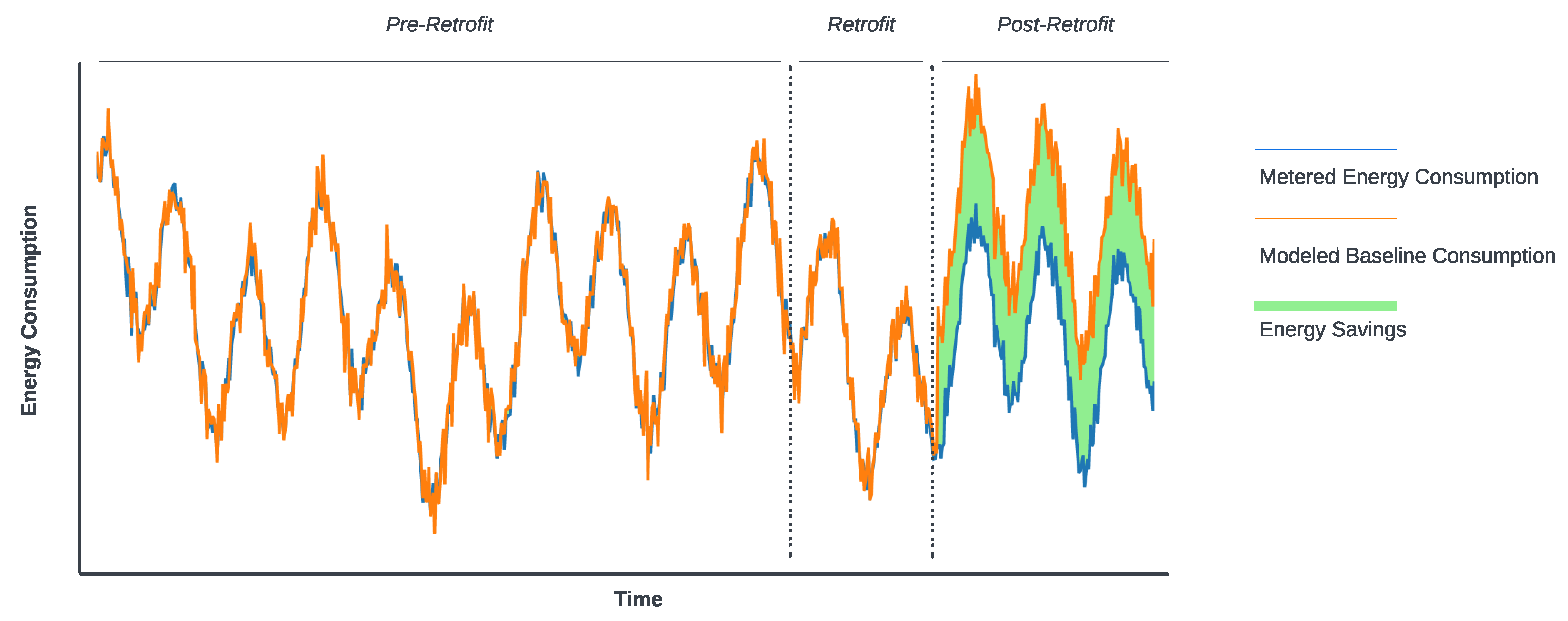
M&V analysis is a process of quantifying the energy use savings due to the deployment of ECMs when retrofitting existing buildings. A baseline energy model allows the prediction of the energy use of an existing building due to variations in environmental and behavioral factors such as different climatic conditions or changes in occupancy levels before any ECM implementation. The baseline energy model is often used as a benchmark to estimate energy savings due to installing one or several EMCs.
Figure 1 shows the difference between metered and modeled energy use of an existing building over three periods. The first period corresponds to the pre-retrofit operation of the building with the energy use data being metered using historical data collected from utility bills or a building management system (BMS). The baseline energy model is typically developed and tested during this pre-retrofit period. During the retrofit period, ECMs are installed in the building resulting in a gradual reduction in the energy consumption compared to the predictions of the baseline energy model as noted in
Figure 1. After completing the ECM installation phase, the building typically consumes less energy than during the pre-retrofit period, as demonstrated in
Figure 1 during the post-retrofit period. Indeed, the baseline energy model predicts higher energy consumption than the metered data during the post-retrofit period. The difference between the baseline and the metered energy consumption during the post-retrofit period represents energy savings incurred by the installed ECMs during the post-retrofit period. A building energy model baseline is often established for M&V analysis of retrofitting existing buildings, especially for those with energy use historical data that meet certain requirements such as date range, missing values, or reporting frequency. These requirements, however, are not well-defined and vary from one case to another depending on a wide range of factors including the nature of occupancy. The process of constructing a data-driven baseline model requires that a building has been in operation during a sufficiently long period to gather enough data to establish correlation between its energy performance and other independent factors such as weather and occupancy parameters.
2.1. Measurement and Verification Protocols
Several M&V protocols have been developed to improve consistency and reduce uncertainty in estimating the energy savings attributed to retrofitting existing buildings, such as the International Performance Measurement and Verification Protocol (IPMVP) [
17] and ASHRAE Guideline 14 [
18]. The analysis approaches outlined in these protocols differ depending on the geographical regulatory requirements, the types of ECMs, and building typologies. Additionally, specific frameworks and methodologies have been proposed to achieve the desired objectives of retrofitting projects. For instance, Ma et al. [
19] developed a systematic methodology for carrying out retrofitting projects and successfully completing the various phases and analyses including the M&V analysis.
2.1.1. International Performance Measurement and Verification Protocol (IPMVP)
The International Performance Measurement and Verification Protocol or IPMVP is one of the most common frameworks in performing M&V analysis of retrofitting existing buildings, with four evaluation options as outlined in
Table 1. The selection of the most appropriate analysis option depends on the boundary of the deployed ECMs. Options A and B are applied when the retrofit is restricted to only one specific and isolated building energy system. These two options differ depending on the analysis method and the availability of metered data. In particular, option A can be used for a M&V analysis for a lighting system retrofit using only key parameters including power ratings and operation schedules to calculate energy savings. On the other hand, option B is applied for systems whose energy performance can be monitored such as chillers and boilers. In addition, Options C and D can be applied when the retrofit affects the energy performance of the entire building. When metered building energy data can be collected before and after the retrofit periods, Option C is suitable for conducting the M&V analysis. When the historical data of metered energy consumption are not available or are unreliable before or after the retrofit, option D is considered using calibrated energy models [
17].
2.1.2. ASHRAE Guideline 14
ASHRAE has developed Guideline 14 for Measurement of Energy, Demand, and Water Savings to standardize the M&V calculations used to estimate achieved energy demand and water savings from retrofit projects. ASHRAE Guideline 14 utilizes three M&V analysis options that are similar to those specified by the IPMVP including retrofit isolation, whole facility, and whole building calibrated simulation. Instead of having two analysis options for isolated systems, ASHRAE Guideline 14 allows only one method with the flexibility of the parameters that can be used in the calculations. The whole facility option is similar to Option C of the IPMVP using the whole facility metered energy consumption along with independent variables to establish the building’s baseline energy model. The third approach is similar to the IPMVP’s option D using a calibrated baseline model to quantify savings from the retrofit. While ASHRAE Guideline 14 shares some features with IPMVP, it does not cover specific details such as energy performance contracting and metering provisions as IPMVP does [
18].
2.1.3. Advanced Measurement and Verification
Advanced M&V, usually referred to as M&V 2.0, encompasses detailed analysis approaches using high frequency metered data (i.e., sub-hourly), and end-use loads using advanced metering infrastructures (AMI) [
20]. In fact, M&V 2.0 enables metered data to be more effective for building real-time performance assessment, occupant engagement, and resource management using various analysis tools and algorithms. The improvements of both hardware and software over the last decade have resulted in better accuracy in performing various M&V tasks such as developing baseline models, detecting non-routine events, and benchmarking energy consumption. Furthermore, retrieval of metered data at higher frequencies and shorter time intervals facilitates performing data analytics and automating savings quantification for retrofit projects, which reduces the time lag between implementation and evaluation phases [
21].
2.2. Baseline Modeling
Three approaches are commonly used to establish building baseline models: deterministic (also referred to as direct or white-box), data-driven (also referred to as indirect or back-box), and hybrid (also referred to as gray-box) methods. All approaches reach the same objective in M&V (i.e., constructing a baseline) with different inputs and processes. The comparison between such means for a single case is time-consuming and rarely performed, as each approach has sub-approaches, which alone will take more time and effort. Therefore, this subsection aims to provide a concise comparison between them.
Deterministic modeling relies on physics-based tools to predict the energy consumption of buildings due to their thermal interactions with the outdoor environment. Such interactions are often represented using heat and mass balance equations that are solved using a set of algorithms that are the basis for a deterministic building energy modeling tool. There is a wide range of commercially available and open-source deterministic modeling tools that can be utilized for developing building energy models including EnergyPlus [
22], TRNSYS [
23], DOE-2 [
24], DesignBuilder [
25], Matlab/Simulink [
26], and Modelica/Dymola buildings library [
27]. Most of these deterministic modeling tools require comprehensive input data about the building features such as envelope thermal properties, mechanical equipment efficiency, and operation schedules. Ke et al. [
28] developed a deterministic (also referred to as white-box) baseline energy model using eQUEST software (based on DOE-2 simulation engine) for an existing office building with a mean bias error (MBE) of 0.37%. The building energy model includes over 50 input variables indicating the types and operation characteristics of chillers, indoor air-conditioning units, and cooling towers performance in addition to several variables describing other building systems such as the envelope elements and lighting fixtures. The study has demonstrated high levels of interpretability in understanding the specific interactions between energy end-uses of various building systems and occupancy behaviors that deterministic building energy modeling can offer. However, the interpretability as well as the high prediction accuracy of the deterministic models come with significant computing times and input data collection efforts.
Data-driven models represent relationships between energy performance indicators and environmental parameters identified using historical data. These relationships are then applied to predict the building response when all or some environmental variables would change. Thus, data-driven models are based on developing correlations between the desired input and output parameters using various statistical and machine learning approaches. In particular, the development as well as the accuracy level of data-driven models rely heavily on historical data for both input and output variables. Types and applications of data-driven modeling are discussed in detail in
Section 4. Typically, the accuracy and interpretability levels of data-drive models are lower than those achieved by white-box models, as data is usually noisy and the occupancy behavior is not consistent.
Hybrid, also referred to as gray-box, models utilize a data-driven analysis approach to tune and improve physics-based (also referred to as deterministic or white-box) models through value estimations of input parameters values using historical data. A common deterministic model using in the hybrid analysis approach is based on resistance and capacitance (RC) modeling to account for building thermal mass. Piccinini et al. [
29] developed a framework for building a hybrid modeling approach using historical monthly electricity and natural bills of a primary school building to calibrate a building energy model using the Dymola Environment. The study achieved a normalized mean bias error (NMBE) of 1.8% while using far less parameters compared to a white-box model developed using detailed simulation tools such as EnergyPlus or TRNSYS. Similarly, Giretti et al. [
30] compared the performance of reduced-order modeling using Modelica with Buildings Library against calibrated detailed models belonging to three cases: a hospital, library, and an educational building. The calibrated reduced-order models obtained a coefficient of variation of the root mean squared error (CV(RMSE)) between 5% and 8% compared to the detailed models while using only 25 parameters that are categorized into building envelope, heating/cooling system, occupancy, and weather components.
Chen et al. [
31] compared three energy modeling approaches including black-, white-, and gray-box models. The comparative analysis considered several performance metrics including development efforts, computational times, and analysis limitations. Their study found a trade-off between each metric category, with black-box models requiring the least effort and time, while white-box models had far more input parameters. Gray-box models are in the middle in terms of development effort and required input parameters as it still requires significant data correlating energy consumption and weather variables. In terms of interpretability, white-box models allow for better understanding of the impact contributed by each input on building energy performance followed by gray-box then black-box modeling approaches. This capability is due to the fact that relationships between energy consumption and input parameters are well-established for deterministic models based basic physical principles rather than inferred from historical data as required by the data-driven (black-box) models.
4. Data-Driven Approaches
This section outlines a brief description of each method used for data-driven modeling and the main reported applications for these methods. Each subsection discusses one of the main categories that are mentioned in
Section 3.2 with an explanation of the general algorithm, sub-models within the category, and a list of publications that utilized one or more of the category’s models. The tables in this section show summaries of such publications with a description of the applied case, data type, features, utilized category’s models, and data granularity or frequency. The papers listed in this section include data-driven modeling suitable not only for M&V analysis, but also for baseline building energy development. Among the reported literature, there are very limited papers that perform full M&V analysis using data-driven models, as most of the reviewed applications evaluate the prediction performance of data-driven approaches. Features, predictors, and dependent variables are terms that are used interchangeably to list input parameters that are used to train the model to perform predictions about the response, target, or independent variable that represents the model’s output. In each of the following sections’ tables, the general category of the feature will be mentioned instead of the specific features for conciseness. In
Section 5, the features will be explained further in terms of filtering and processing. Based on the conclusion reached by each study, the tables in this section will show, if the results are clearly indicating one best model, the best model within the categories mentioned in this section in bold font. Data granularity represents the interval of prediction, which can be 15-min, hourly, daily, weekly, or monthly.
4.1. Linear Regression
4.1.1. Definition
Linear regression (LR) is a term that encompasses a family of different techniques that aims to establish a linear relationship between the target
y (i.e., output) and a set of predictors
(i.e., input parameters). Equation (
1) shows the general form of a linear regression [
37].
where
: Linear regression coefficients.
: Linear regression features or predictors.
: Linear regression prediction of the output variable.
The LR modeling includes several methods, with the most basic approach being the Ordinary Least Square (OLS). Other methods can be more complex involving other equation forms and algorithms for estimating the regression coefficients.
4.1.2. Applications
The LR approach with its various forms is used extensively in building energy modeling including establishing baselines and benchmarks. Mathieu et al. [
38] used an OLS method that is called Time of Week and Temperature (TOWT) to develop a building energy baseline model. The model considers two input parameters: time of the week and temperature. The time of week segments the week into 15-min intervals, while the temperature is featured into ranges that are a function of the maximum and minimum temperature from historical data. The ranges are fitted using piecewise linear regression analysis. Existing frameworks modified the method of TOWT by using a Weighted Least Squares (WLS) regression instead of OLS and allowed for recent data to be weighted more than old data. Granderson et al. [
39] compared the prediction accuracy of 10 data-driven models including those based on linear regression methods using data from 537 buildings to gauge the accuracy of M&V modeling approaches. The study included two metrics where linear regression with appropriate feature engineering showed similar accuracy to complex models. Kim et al. [
40] modeled the energy use of an educational facility based on a set of metered data using linear regression methods along with more complex techniques over both working and non-working periods. In the study, Kim et al. [
40] found that the linear regression method predicted building energy use less accurately than the complex model during non-working days when occupancy stochastic behavior is difficult to capture. Further applications are shown in
Table 2.
Reported studies showed that LR approaches can vary in complexity and accuracy. The LR approach is often used as a benchmark for more complex models or even as a method with similar accuracy compared to more complex approaches for modeling the building energy consumption. Although LR cannot fit complex non-linear relations, the accurate selection of features, analysis before modeling, and checking LR assumptions can improve its accuracy greatly. Raw features with LR usually do not fit relationships easily while processing features with other models or simple methods allows LR to capture relationships better. This highlights the importance of the LR approach to act at least as a benchmarking model.
4.2. Decision Tree and Ensemble Methods
4.2.1. Definition
DT is a basic non-parametric supervised learning method used for classification and regression analyses. The DT method can predict the value of a target variable using simple decision rules inferred from the data features. The training process for DT follows a piecewise constant approximation approach with different prediction models for various data groups [
46]. In the context of M&V applications, decision trees act as regressors rather than classifiers using different metrics to measure their splitting homogeneity or commonly known as impurity. In regression, the case of M&V, the impurity of a leaf is measured by the residual sum of squares. The tree splits data points based on features until fitting the data or reaching specified stopping criteria. The splitting relies on different metrics to decide the goodness of the criterion set at a node, which acts as a decision point that splits the data to minimize a specified cost function (i.e., residual sum of squares for M&V applications). Typically, DTs use the splitting criterion as described in Equation (
2) [
46].
where
s: A decision dividing a node into two leaves.
: Resulted leaf.
: Feature from the dataset.
X: Realizations from the dataset.
Figure 5 shows a simple DT for regression where
X represent that data points and
to
represent features from the dataset. At each decision node, the tree divides the data based on criteria,
to
, where the resulted leaves can have additional decision nodes. The tree keeps branching until minimizing the considered cost function (i.e., Residual Sum of Squares (RSS)) as shown in Equation (
3) or reaching the set stopping criteria. The end leaves represent the predicted value for the data points that fall into the leaf based on a series of decision nodes,
to
.
However, decision trees can form the basis for more complex models using ensemble methods. Random Forest (RF) is an ensemble method that fits several regressions or classification decision trees for various sub-samples of the dataset and aggregates them by averaging to improve prediction accuracy levels and control the overfitting problem. This ensemble approach is called “bagging” with sampling features and aggregating via averaging. Moreover, other ensemble approaches can be utilized instead of simple weighted averaging methods such as RF. “Stacking” is another ensemble process of generating several base models using training data such that meta-models use predictions from base models as features for out-of-sample predictions. “Blending” is a variation of stacking using testing data set to gauge the prediction accuracy of base models while a final test is applied for the meta-model [
47]. The state-of-art ensemble methods include AdaBoost [
48], Gradient Boosting Machine (GBM) [
49], Extreme Gradient Boosting Machine (XGB) [
50], and Light Gradient Boosting Machine (LGBM) [
51]. All these methods use the principle of multiple learners, except the boosting algorithm, which introduces weighting penalization before each successive learner rather than aggregating the final prediction from multiple learners directly. However, DT and DT-based models like RF and XGB are not effective at extrapolating beyond the range of the predictor’s values [
52]. Therefore, when a building’s energy consumption data include values beyond the trained data for the predictors, other algorithms must be incorporated to overcome this issue.
4.2.2. Applications
DT is a machine learning method that is used in both classification and regression applications. Touzani et al. [
53] used XGB to determine the improvements of boosting against TOWT by using date and temperature of buildings where the accuracy metric boxplots showed an improvement over the TOWT method. Afroz et al. [
54] compared six data-driven models by predicting the energy consumption of 11 office buildings located in Ottawa, Canada. RF method is found to provide superior prediction accuracy levels than those of the DT method and even better than those achieved by some models except Nonlinear Autoregressive with Exogenous inputs (NARX). Agenis-Nevers et al. [
55] applied 10 methods to model the energy performance of 11 UAE buildings including 10 commercial complexes and one housing unit. RF approach has achieved a global score that is above the average for the 11 buildings. Liu et al. [
56] used simulated data generated using DesignBuilder model for an educational building in the Northern China region to compare the energy use predictions from three models. The study found that RF provides the highest prediction accuracy. Publications that utilized DT and ensemble methods are shown in
Table 3.
Ensemble methods can be used to develop a set of new models different from base models. With several sampling and aggregating techniques, the choice of the best category approach can pose some challenges. Indeed, the best suitable model depends on several factors and is often not possible to generalize for different building types and retrofit measures. However, reported comparative studies have indicated the appropriateness of certain ensemble methods over others. For example, in several analyses, RF approach outperforms DT in regression modeling as the former prevents overfitting by introducing randomness while the latter tends to branch out until overfitting the training data. On the other hand, approaches such as stacking rely heavily on their base learners with different applications providing completely different results. While stacking can be effective, it is still a computationally expensive approach with vague transparency and unclear interpretability.
On the other hand, XGB and RF can indicate the contribution of each variable and increase the model interpretability. Given the results of the bibliometric analysis and reported applications of this modeling category, RF and XGB are the two most commonly suitable techniques in ensemble approach with limited drawbacks.
4.3. Support Vector Machine
4.3.1. Definition
Support vector machine (SVM) is a common machine learning tool used for classification and regression analyses. A SVM model is developed by fitting a hyperplane that aims to determine the underlying relationship between predictors (i.e., input parameters) and target (i.e., output). The hyperplane is supported by two vectors as shown in
Figure 6 such that the error measured with respect to these two vectors and the hyperplane is minimized by including the maximum number of points within the boundary lines and close to the hyperplane. The two parallel lines represent the supporting vectors while the middle line is the hyperplane. Equation (
4) shows the hyperplane equation where the data is mapped to a higher dimension by a dot product between points and weights. Then, SVM aims to minimize the cost function, which is shown in Equation (
5), where
represents the distance of the supporting vectors from the hyperplane and
represents the distance from the supporting vectors to the points outside the supporting vectors. The more points that lie within the boundary, the less the cost function [
66].
where
Figure 6.
One-dimensional support vector machine for regression.
Figure 6.
One-dimensional support vector machine for regression.
: Loss or cost function.
C: Direction regularization coefficient.
: The distance from data observation to any of the supporting vectors which is minimized by the cost function.
4.3.2. Applications
Edwards et al. [
67] compared using two variations of SVM against other modeling techniques including LR and ANN. The SVM is demonstrated to have a better performance compared to complex models when applied to residential buildings and to provide similar prediction accuracy levels compared to complex models for commercial buildings. Amber et al. [
68] utilized parameters denoting working and non-working days to predict energy demand for an office building which resulted in SVM models that are trained on a subset of data denoting a specific type of day (i.e., work or non-work day) outperforming SVM models that were trained on all the data in prediction accuracy. This result highlights the importance of consistency in occupancy and how the model prediction accuracy can be degraded with more stochasticity in occupant behavior. Although SVM can be computationally expensive, several fitting algorithms can be utilized to minimize the computational time such as parallelizing the training work [
69]. Zhao and Magoulès [
70] utilized a parallel implementation approach for predicting a building’s energy consumption that reduces the training time by parallelizing kernel evaluations and gradients compared to a sequential approach and provides similar prediction accuracy.
Table 4 provides some reported studies applying SVM for building energy predictions.
The Support Vector Machine is a powerful yet computationally expensive algorithm. The mapping of observation to a higher dimension makes SVM superior in fitting complex relationships and minimizing the model prediction errors. Parallelization can mitigate the slow-fitting performance of the SVM approach, especially when dealing with large datasets and when accuracy distribution over the entire dataset is required. The proper choice of kernel when using SVM is not straightforward, as the resulted mapped data points can change the prediction accuracy of the model and the process of fitting a hyperplane with no direct relation to model accuracy. Additionally, the choice of a kernel can be determined usually through k-fold cross validation. However, the number of studies using non-linear models as found by the bibliometric analysis suggests that using kernels such as Gaussian or RBF are more common. Furthermore, linear kernels can fit linear hyperplanes for non-complex applications as well as non-linear models that are more computationally expensive.
4.4. Artificial Neural Network
Deep learning or artificial neural network (ANN) is a subfield of machine learning where algorithms mimic the human brain functioning process. The ANN involves a set of neurons forming layers that are inter-connected starting from an input layer to an output layer. The connections between neurons are determined using weight coefficients that are determined based on a training process using input–output data sets. As discussed in
Section 3, the majority of ANNs used in data-driven building energy modeling are Feed Forward Neural Network (FFNN) [
75], as detailed in the following sections.
Feed Forward Neural Network
FFNN is the most commonly used ANN-based approach in building energy modeling. Each layer’s neurons, comprised of various features’ signals, are multiplied by weights
that connect them to the other layer’s neurons. Following this, a bias term
is added to the summation of each weight and signal multiplication. The result is then inserted into an activation function, which can be either a Rectified Linear Unit (ReLU) or a linear activation function. Without activation functions, the FFNN would be just a linear regression model. Equation (
6) shows the process of multiplying weights with signals and adding bias [
75].
Figure 7 illustrates the basic FFNN architecture.
Figure 7 shows the same variables in Equation (
6) with different indices, where
i denotes the layer number,
j the neuron in certain layer, and
k the connection. For example,
represents the weight
of the connection between node
i and
j.
where
W: Weights associated with the connection between neurons.
X: Inputs form the input layer or the output of an activation layer.
b: Bias term for each neuron.
: Activation function.
Figure 7.
Feed forward neural network architecture.
Figure 7.
Feed forward neural network architecture.
FFNN can have multiple hidden layers (i.e., Multi-Layer Perceptrons, MLP) or a single hidden layer (i.e., Single Layer Perceptrons, SLP). Other forms can have different processes with the same network architecture such as Radial Basis Function Neural Network (RBFNN) [
76] or Extreme Learning Machine (ELM) [
56]. Both forms have instead of multi-hidden layers, a single hidden layer. RBFNN has radial basis functions that map data to a higher dimension instead of simply activating
h. ELM is also a single hidden layer network where initial weights bias terms are initialized using a different method than MLP or SLP and fixed during the tuning phase.
Table 5 shows some reported stuides that apply FFNN to predict building energy consumption.
ANNs are gaining more popularity in building energy modeling due to the availability of better computing machines to perform cumbersome and time-consuming approaches. Furthermore, the development in ANN architecture and algorithms that enable the capture and identification of complex relationships. Nevertheless, the superiority of such methods remains the subject of debate since only slight improvements in prediction accuracy can be achieved at the expense of significant computational efforts. FFNN-based models can take several forms with the choice between them being difficult to generalize to all building energy modeling applications. Typically, the development of FFNN-based models relies on a trial and error process using cross-validation to obtain the best model’s parameters with no clear choice in the reported literature on the best general approach that leads to an accurate model’s prediction. Some papers recommended certain methods to find the first iteration’s parameters’ values such as the number of hidden layers and neurons. Ahmad et al. [
62] chose only a single hidden layer and performed a stepwise searching method to select the optimum number of neurons. On the other hand, Amber et al. [
85] and Ye and Kim [
86] relied on a formula that is a function of both the output and input layer sizes to determine the number of neurons.
4.5. Kernel Regression
4.5.1. Definition
Another category of data-driven approaches used for building energy modeling is kernel regression. This category of regression analysis approaches is also called time-varying coefficients, where response values are predicted using different coefficients for different intervals. Kernel, in this context, is a function that assigns weights to data points based on a specific metric [
87]. An example of kernel regression is K-Nearest Neighbor (KNN) [
88] regression, where Euclidean distance is used as a metric for weighing nearby points where a subset of all data points is selected and each is given an equal weight. Equation (
7) defines the K-nearest neighbor regression. However, this method can have boundary issues as the regression becomes inaccurate at the endpoints. Additionally, the method generates a curve with several discontinuities as each point has an equal weight. Another approach is Nadaraya–Watson kernel-weighted average [
89], which minimizes the weight points based on distance. Equation (
8) shows the calculation of the model predictions.
where
The kernel equation
can be Epanechnikov quadratic, Tri-cubic, or Gaussian [
87]. In each kernel function, a hyperparameter
, named smoothing parameter, determines the local neighborhood’s widths where lower and higher values can change the variance and bias of the model.
4.5.2. Applications
Ho and Yu [
90] applied a kernel regression using KNN using measured data for an educational building with a special focus on the energy performance of a chilled water plant. The model included typical features for a building and chiller operating variables such as water flow rate, water supply, and return temperatures, as well as outdoor air dry-bulb temperature, and relative humidity. The model achieved reasonable prediction accuracy levels by selecting the optimal number of clusters based on the lowest mean square error. These results highlight the ability of kernel regression to consider several factors and weight them based on Euclidean distance. Gallagher et al. [
91] modeled energy use of a biomedical facility using over 18 features (i.e., input parameters) including dry-bulb temperature data and equipment manufacturing variables such as production machinery electricity consumption, facility operation schedule, and chilled water system electricity consumption. The study showed that KNN achieved the best accuracy metrics when using weekly data compared to SVM, ANN, LR, and DT. Wang et al. [
92] compared energy use predictions for several data-driven models, stacking, RF, GBM, SVM, XGB, and KNN. The reported results indicate that the KNN-based model has mixed performance as it achieved better accuracy levels than RF and XGB in one case, but provided the worst prediction accuracy in another case.
Table 6 shows a summary of the reported studies using kernel regression for building and retrofit baseline energy modeling.
Kernel regression approach provides a powerful tool when modeling relations that are observed frequently over the dataset. By developing neighborhoods of similar points, the kernel-based models can make predictions that are based on weighted values. The similarity provides a mean for the kernel-based model to link the mapping between inputs and outputs and easily fit non-linear relations. However, several hyperparameters are encountered when selecting a kernel-based modeling approach. From the reviewed applications, there appears to be no specific selection guidelines for these parameters other than experimentation and trial and error mechanisms. Although complex kernels can produce smooth curves to fit the building energy consumption, there is no clear procedure to develop the set of complex kernels. The common recommendation from reported analyses is that kernel-based models need to be tested over a set of different data and compared against each other to determine the best modeling approach.
6. Data Requirements
Data-driven models for M&V rely heavily on historical data to establish a relationship between input variables and building energy performance. The quality and quantity of historical data can significantly affect the accuracy of a data-driven model. In particular, the following three characteristics are often used to assess the quality and quantity of the data: time range, reporting frequency, and missing values. Data time range affects the re-occurrence of certain performance levels that can help models identify repeating patterns or ignore unusual activities. Grillone et al. [
105] simulated 54 cases of three buildings with different parameters and trained two data-driven models using data specific to a period ranging from 9 to 12 months. The result showed that a significant decrease in the prediction accuracy distribution median and an increase in the distribution variance when using TOWT approach. OpenEEmeter [
108] is an open-source framework used to calculate the energy use that could be avoided by retrofitting a building. The framework sets certain requirements on the data used for developing a building energy model including the data time range. For data with hourly and daily frequency, an OpenEEmeter compliant baseline building energy model requires at least data for 365 days.
The time frequency provides the level and type of information that can be gained from data through data-driven modeling. Using hourly or sub hourly data for energy consumption, any patterns and correlations can be learned better, but more significant noise levels could be introduced as the building energy consumption becomes less consistent. On the other hand, aggregated consumption using daily or monthly frequencies exhibit less fluctuations at the expenses of extracting more information. Gallagher et al. [
77] analyzed the effect of sub-hourly, hourly, daily, and weekly frequency on four data-driven models by using a recorded measurement of a chilled water system. They found that the frequency effect varied between models with daily frequency producing the lowest CV(RMSE), except for KNN, where the hourly-based model resulted in a lower CV(RMSE).
Missing values represent another important requirement for the quality of data needed for training. Missing values are identified by periods of disconnected metering, irregular values, or missing some features’ values during a given timestamp. Although each case of missing data is usually unique and requires a certain imputation technique, several thresholds were established to prevent training models from using invalid data sets. CalTRACK [
109] dictates missing data requirements for daily and hourly frequencies specific to data-driven models. Models based on daily data must not have more than 37 days (i.e., 10% for a full-year data) while hourly frequency data must have less than 10% missing hours of the total hours in every calendar month.
9. Summary and Conclusions
To justify retrofitting buildings, M&V analysis is often needed to quantify the achieved energy savings and ultimately justify the cost-effectiveness of implemented energy efficiency measures. Data-driven modeling provides an effective approach to perform M&V analysis when compared to traditional deterministic modeling methods especially considering the growing availability of significant historical data specific to historical energy performance due to advancements in metering and monitoring of building energy systems.
In this review of the existing literature, several data-driven building energy models that are suitable for M&V applications have been described and evaluated. In particular, five categories of data-driven modeling approaches have been identified for M&V analysis of retrofitted building energy systems. The simplest data-driven modeling option consists of LR with the TOWT approach, which is found to be widely used for developing baselines of existing buildings. The TOWT method is incorporated in two of the mentioned existing frameworks (i.e., EEMeter and RMV2.0), and all the mentioned studies with an hourly frequency use such a method to build LR models. The ensemble modeling approach has two prominently applied methods for assessing building energy performance including RF and XGB. The two modeling approaches were mentioned in almost all the reported papers using ensemble approaches and, in every one of them, either XGB and RF were the models scoring best in prediction accuracy compared to the remaining ensemble methods. Several data-driven models have been developed using the SVM approach combined with a range of hyperparameters. However, there are no clear guidelines from the reported literature on determining the best combination of hyperparameters suitable for M&V analysis of building energy savings. In addition, a wide range of FFNN-based models has been considered to predict building energy performance with different architectures and features. Among the reported FFNN’s architectures, SLP is mostly used in predicting building energy consumption. One study suggests that there was no improvement in prediction accuracy when changing SLP to MLP by one hidden layer [
79]. Lastly, kernel regression methodology has been applied for building energy prediction, with KNN being mostly used, especially for M&V applications.
Two important features used in most of the data-driven models reported for building energy prediction and M&V analysis include date and outdoor dry-bulb temperature. Another effective feature considered for several data-driven modeling consists of occupancy pattern derived from indoor sensing and/or operating schedules. In terms of selecting features, EDA and feature importance by ensemble methods were demonstrated to be the widely used methods for selecting the optimum features. The popular processing techniques were applied to date and outdoor dry-bulb temperature with hot-encoding being popular for time-related features. For temperature, CDD and HDD transformation is popular for data with low frequency, while change-point and piece-wise fitting is used mainly for linear regression-based models.
Existing popular frameworks for M&V analysis were discussed along with features, modeling approaches, and used features. The usual data requirements for building a M&V baseline were derived from studies and frameworks’ requirements. Important requirements were discussed including data range, frequency, and missing values. The smallest data range for building a baseline was one year before retrofitting regardless of the data frequency. Results from reported studies demonstrated that the highest prediction accuracy usually comes with an hourly or daily frequency since sub-hourly data introduce more noise than information while lower frequencies such as weekly or monthly lack usage patterns. Few studies discussed the effect of missing data, but an emphasis was made to have less consecutive missing data as data imputation becomes difficult.
Finally, the paper discussed several evaluation performance metrics and approaches to assess the prediction accuracy of the baseline building energy model. In particular, evaluation metrics for both general building energy prediction and M&V analysis were discussed with CV(RMSE) and NMBE being the mostly used metrics to evaluate the building energy models. These two metrics complement each other and convey better information about the model’s performance. Two other evaluation approaches were outlined with their drawbacks and benefits: split without shuffle and k-folds evaluation. With sufficient data covering more than a year of building energy consumption, split without shuffle approach provides an easy and efficient evaluation metric, while the k-folds approach tests the generality of the model better. However, the selection of the evaluation approach is still dependent on the building case.
It is clear from the presented review analysis that there is a need for a general framework and a set of guidelines to develop advanced data-driven models suitable for M&V analysis and capable to estimate accurately energy savings achieved by building retrofits. While the review has revealed some existing frameworks, all of them are based mostly on LR. Several papers indicated that modeling approaches deliver varying prediction accuracy and that there is no best modeling approach for every M&V analysis. Moreover, retrofit analyses with advanced data-driven modeling approaches are currently developed only for specific case studies and their application cannot be readily generalized to any building type and location. If established, the proposed framework will enhance the use of data-driven models for various applications of building energy analysis including M&V of energy saving from retrofit projects.