Parameters Identification of Proton Exchange Membrane Fuel Cell Model Based on the Lightning Search Algorithm
Abstract
:1. Introduction
| Optimization Algorithm | Inspiration (If Any) | Approach in the Algorithm | Features | Limitations | Algorithm Implementation in Fuel Cell Application | References |
|---|---|---|---|---|---|---|
| Genetic algorithm | Inspired from evolution | Selection, crossover, and mutation are the important steps | It outpaces the radial basis function neural network approach. It is efficient, possesses a simple structure, high accuracy, validity, and stability | Lacks high robustness | Static and dynamic modeling of SOFC | [26,27,28] |
| Differential evolution algorithm | Inspired from evolution | Initialization, mutation, crossover, and selection | Higher convergence speed, accuracy, fast parameter turning, and robustness | Not specified | Modeling performance metrics of PEMFC and parameter extraction in various fuel cells | [29,30] |
| Particle swarm optimization algorithm | Inspired by swarm intelligence | Based on particle position and velocity and updating the parameters for the best position | Many learning strategies are implemented to improve the algorithm’s effectiveness. A proper balance between global exploration and local exploitation is observed. | Low convergence speed and low searching efficiency comparatively | Parameter identification for SOFC and PEMFC | [31,32,33] |
| Artificial bee colony algorithm | Inspired by the foraging behavior of bees | Exploration and exploitation is accompanied by employed bees, onlooker bees, and scout bees. Various bees update their position following different paths. | Simple, very good at global exploration and faster convergence rate. | Sometimes converges prematurely and causes weak local exploration ability | The hybrid algorithm employed to identify the parameters for PEMFC | [34,35] |
| Grasshopper optimization algorithm | Inspired by the foraging behavior of grasshoppers | Based on attractive and repulsive interaction. The search agents move rapidly during Exploration and tend to move locally during exploitation | Simplicity with minimum parameters and maximum classification performance | Lacks high accuracy | Parameter identification for SOFC | [36,37,38] |
| Chaotic binary shark smell optimization algorithm | Inspired by prey hunting strategy of sharks | Initialization, shark movement in terms of forwarding and rotational towards the odor concentrator | High efficiency, simple structure, and high stability | Assumptions reduce the robustness of the algorithm | Parameter identification for PEMFC and SOFC | [38,39] |
| Interior search algorithm | Inspired by interior space decoration strategy by architectures | Defining bounds, identifying the fittest element, composition, and mirror group work to find the better view | High accuracy and convergence speed, the minimal tuning parameter | Sometimes converges prematurely | Parameter extraction for fuel cells | [40,41] |
| Salp swarm algorithm | Inspired by the foraging behavior of forming collaborative chains by a group of salps | The chain consists of two elements, namely, leaders and followers. | Easy to tune the parameter and faster convergence speed | Accuracy is the limitation | Parameter extraction for fuel cells | [41,42] |
| Grey wolf optimization algorithm | Inspired by the collective hunting strategy of grey wolves | Prey identification, tracking and chasing, encircling and attacking the prey | Simple structure, good global exploration, high flexibility | Moderate accuracy and the speed of convergence will slow down eventually | Parameter extraction for fuel cells | [41,43] |
| Multiverse optimization algorithm | Inspired by multiverse theory in cosmology | A black hole and white hole represent global exploration, while the wormhole represents local exploitation. The inflation rate helps in determining the ranking. | Less computation, minimum parameters to tune, and simplistic construction | Convergence speed is comparatively slow | Identifying optimal parameters for the PEMFC model | [44] |
| Competitive swarm optimizer algorithm | It is a simplified version of the Particle swarm optimization algorithm | A pairwise competition mechanism is established to simplify the algorithm structure and consistency | High accuracy, robustness, and convergence speed | Not favorable for complex multi-nodal optimization and would result in low search efficiency | Parameter identification for SOFC | [45,46] |
| Whale optimization algorithm | Inspired by the bubble-net hunting strategy of humpback whales | Encircling the prey, creating a bubble net creation, capturing the victim | High computation accuracy and convergence speed | Global exploration is not much effective comparatively | Semi-empirical PEMFC model for unknown parameter identification | [47,48] |
| Biogeography based optimization | Inspired by Island biogeography | Based on two operators, namely, migration and mutation, and accommodated with immigration and emigration rate | The solution is moderately accurate | Less convergence speed and lacks local exploitation | Model parameter estimation for fuel cells | [49,50] |
| Satin bowerbird optimizer | Inspired by the mechanism of bird mating | Other bowers prefer Bowers with higher fitness. | Simple to tune the parameters, robust and random nature of the algorithm, can effectively engage with multi-modal optimizations | Complex parameter setting | SOFC parameter extraction for steady-state and dynamic models | [51,52] |
| Backtracking search algorithm | - | It uses present and historical population data to perform iteration and to achieve diversity also with the incorporation of random mutation | Good balance between exploitation and Exploration, reliable and high accuracy | Convergence speed is comparatively slow | Parameter estimation for PEMFC | [53] |
| Teaching learning-based optimization | Inspired by a teaching-learning process in the classroom | Two involved processes, namely teaching and learning. Sometimes ranking mechanism is also introduced | Simple construction, high accuracy, robustness, and better convergence speed. Many hybrid features are proposed in context with the Teaching-learning process | It might easily get trapped at the local optimum | Parameter identification of SOFC | [54,55] |
- Implementation of lightning search algorithm (LSA) for PEM fuel cell application;
- Developing a precise model and extracting the unknown parameters resulted from the shortage of manufacturer’s data;
- Comparison of the results obtained from LSA and other algorithms to project a better picture for the researchers about where its precision stands.
2. PEMFC Model
3. Problem Formulation and the LSA
3.1. Problem Formulation
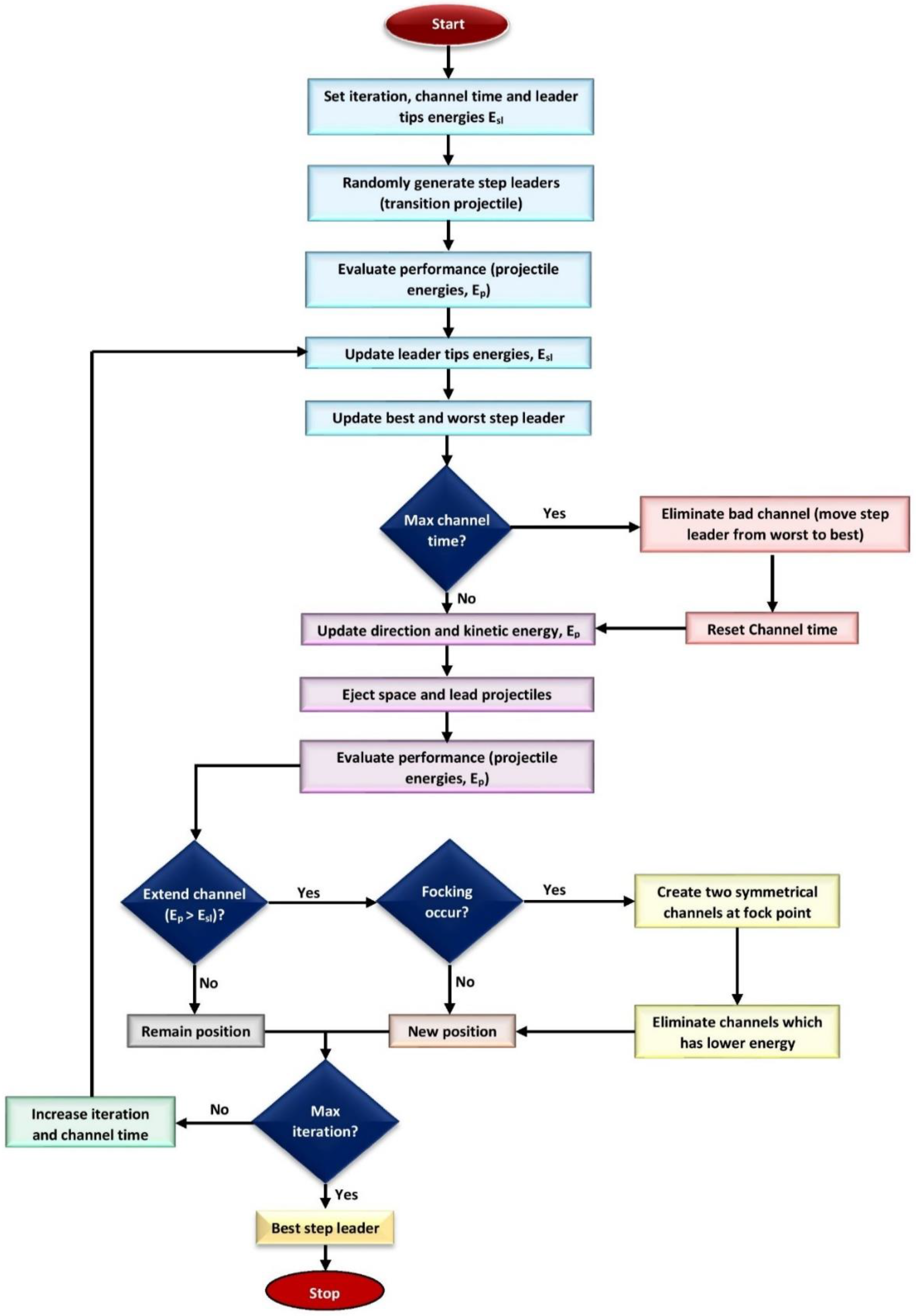
3.2. The Lightning Search Algorithm (LSA)
4. The Simulation Results
4.1. Ballard Mark V 5 kW
4.2. 500 W BCS PEMFC
4.3. Nedstack PEMFC
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Membrane area | |
| concentration of oxygen in | |
| Reversible voltage of PEMFC | |
| Operating current of PEMFC | |
| Density of actual current | |
| Maximum value of | |
| Membrane thickness | |
| Total number of PEMFC | |
| Partial pressure of | |
| Partial pressure of | |
| Pressure at which is saturated | |
| Inlet pressure of Anode | |
| Inlet pressure of Cathode | |
| membrane resistance | |
| Connection resistance | |
| Relative humidity of vapor at Anode | |
| Relative humidity of vapor at Cathode | |
| PEMFC operating temperature | |
| Activation voltage at low current values | |
| Over-potential voltage at high loading | |
| Ohmic resistive drop at linear operating conditions | |
| Overall voltage from PEMFC stack |
References
- Madurai Elavarasan, R.; Pugazhendhi, R.; Irfan, M.; Mihet-Popa, L.; Khan, I.A.; Campana, P.E. State-of-the-art sustainable approaches for deeper decarbonization in Europe—An endowment to climate neutral vision. Renew. Sustain. Energy Rev. 2022, 159, 112204. [Google Scholar] [CrossRef]
- Moriarty, P.; Honnery, D. Renewable Energy and Energy Reductions or Solar Geoengineering for Climate Change Mitigation? Energies 2022, 15, 7315. [Google Scholar] [CrossRef]
- Kochanek, E. The Role of Hydrogen in the Visegrad Group Approach to Energy Transition. Energies 2022, 15, 7235. [Google Scholar] [CrossRef]
- Taner, T. Energy and exergy analyze of PEM fuel cell: A case study of modeling and simulations. Energy 2018, 143, 284–294. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Z.; Jiang, J. Fuel Cell Technology for Distributed Generation: An Overview. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; pp. 1613–1618. [Google Scholar]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Papadopoulos, P.N.; Kandyla, M.; Kourtza, P.; Papadopoulos, T.A.; Papagiannis, G.K. Parametric analysis of the steady state and dynamic performance of proton exchange membrane fuel cell models. Renew. Energy 2014, 71, 23–31. [Google Scholar] [CrossRef]
- Arun Kumar, P.; Geetha, M.; Chandran, K.R.; Sanjeevikumar, P. PEM Fuel Cell System Identification and Control. In Advances in Smart Grid and Renewable Energy; Springer: Berlin/Heidelberg, Germany, 2018; pp. 449–457. [Google Scholar]
- Solsona, M.; Kunusch, C.; Ocampo-Martinez, C. Control-oriented model of a membrane humidifier for fuel cell applications. Energy Convers. Manag. 2017, 137, 121–129. [Google Scholar] [CrossRef] [Green Version]
- Gong, W.; Yan, X.; Hu, C.; Wang, L.; Gao, L. Fast and accurate parameter extraction for different types of fuel cells with decomposition and nature-inspired optimization method. Energy Convers. Manag. 2018, 174, 913–921. [Google Scholar] [CrossRef]
- Li, J.; Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Zhang, Z. Accurate, efficient and reliable parameter extraction of PEM fuel cells using shuffled multi-simplexes search algorithm. Energy Convers. Manag. 2020, 206, 112501. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, L.; Li, J.; Gan, Q.; Xu, X.; Ouyang, M.; Song, Z.; Kim, J. A multipoint voltage-monitoring method for fuel cell inconsistency analysis. Energy Convers. Manag. 2018, 177, 572–581. [Google Scholar] [CrossRef]
- Wang, B.; Xie, B.; Xuan, J.; Jiao, K. AI-based optimization of PEM fuel cell catalyst layers for maximum power density via data-driven surrogate modeling. Energy Convers. Manag. 2020, 205, 112460. [Google Scholar] [CrossRef]
- Xiong, G.; Shi, D.; Zhang, J.; Zhang, Y. A binary coded brain storm optimization for fault section diagnosis of power systems. Electr. Power Syst. Res. 2018, 163, 441–451. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Zhang, M.; Shu, H.; Yu, T.; Zhang, X.; Yao, W.; Sun, L. A state-of-the-art survey of solid oxide fuel cell parameter identification: Modelling, methodology, and perspectives. Energy Convers. Manag. 2020, 213, 112856. [Google Scholar] [CrossRef]
- Guo, C.; Lu, J.; Tian, Z.; Guo, W.; Darvishan, A. Optimization of critical parameters of PEM fuel cell using TLBO-DE based on Elman neural network. Energy Convers. Manag. 2019, 183, 149–158. [Google Scholar] [CrossRef]
- Yu, D.; Wang, Y.; Liu, H.; Jermsittiparsert, K.; Razmjooy, N. System identification of PEM fuel cells using an improved Elman neural network and a new hybrid optimization algorithm. Energy Rep. 2019, 5, 1365–1374. [Google Scholar] [CrossRef]
- Turgut, O.E.; Coban, M.T. Optimal proton exchange membrane fuel cell modelling based on hybrid Teaching Learning Based Optimization—Differential Evolution algorithm. Ain Shams Eng. J. 2016, 7, 347–360. [Google Scholar] [CrossRef]
- Cao, Y.; Kou, X.; Wu, Y.; Jermsittiparsert, K.; Yildizbasi, A. PEM fuel cells model parameter identification based on a new improved fluid search optimization algorithm. Energy Rep. 2020, 6, 813–823. [Google Scholar] [CrossRef]
- Cao, Y.; Li, Y.; Zhang, G.; Jermsittiparsert, K.; Razmjooy, N. Experimental modeling of PEM fuel cells using a new improved seagull optimization algorithm. Energy Rep. 2019, 5, 1616–1625. [Google Scholar] [CrossRef]
- Guo, Y.; Dai, X.; Jermsittiparsert, K.; Razmjooy, N. An optimal configuration for a battery and PEM fuel cell-based hybrid energy system using developed Krill herd optimization algorithm for locomotive application. Energy Rep. 2020, 6, 885–894. [Google Scholar] [CrossRef]
- Tian, M.-W.; Yan, S.-R.; Han, S.-Z.; Nojavan, S.; Jermsittiparsert, K.; Razmjooy, N. New optimal design for a hybrid solar chimney, solid oxide electrolysis and fuel cell based on improved deer hunting optimization algorithm. J. Clean. Prod. 2020, 249, 119414. [Google Scholar] [CrossRef]
- Bizon, N. Energy optimization of fuel cell system by using global extremum seeking algorithm. Appl. Energy 2017, 206, 458–474. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, N. Cuckoo search algorithm with explosion operator for modeling proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2019, 44, 3075–3087. [Google Scholar] [CrossRef]
- Piela, P.; Mitzel, J.; Gülzow, E.; Hunger, J.; Kabza, A.; Jörissen, L.; Valle, F.; Pilenga, A.; Malkow, T.; Tsotridis, G. Performance optimization of polymer electrolyte membrane fuel cells using the Nelder-Mead algorithm. Int. J. Hydrogen Energy 2017, 42, 20187–20200. [Google Scholar] [CrossRef]
- Nejad, H.C.; Farshad, M.; Gholamalizadeh, E.; Askarian, B.; Akbarimajd, A. A novel intelligent-based method to control the output voltage of Proton Exchange Membrane Fuel Cell. Energy Convers. Manag. 2019, 185, 455–464. [Google Scholar] [CrossRef]
- Chakraborty, U.K. Static and dynamic modeling of solid oxide fuel cell using genetic programming. Energy 2009, 34, 740–751. [Google Scholar] [CrossRef]
- Yang, J.; Li, X.; Jiang, J.H.; Jian, L.; Zhao, L.; Jiang, J.G.; Wu, X.G.; Xu, L.H. Parameter optimization for tubular solid oxide fuel cell stack based on the dynamic model and an improved genetic algorithm. Int. J. Hydrogen Energy 2011, 36, 6160–6174. [Google Scholar] [CrossRef]
- Chakraborty, U.K.; Abbott, T.E.; Das, S.K. PEM fuel cell modeling using differential evolution. Energy 2012, 40, 387–399. [Google Scholar] [CrossRef]
- Gong, W.; Yan, X.; Liu, X.; Cai, Z. Parameter extraction of different fuel cell models with transferred adaptive differential evolution. Energy 2015, 86, 139–151. [Google Scholar] [CrossRef]
- del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.-C.; Harley, R.G. Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, N.; Wang, L. Parameter identification for solid oxide fuel cells using cooperative barebone particle swarm optimization with hybrid learning. Int. J. Hydrogen Energy 2014, 39, 532–542. [Google Scholar] [CrossRef]
- Sultan, H.M.; Menesy, A.S.; Kamel, S.; Selim, A.; Jurado, F. Parameter identification of proton exchange membrane fuel cells using an improved salp swarm algorithm. Energy Convers. Manag. 2020, 224, 113341. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Zhang, X.; Li, H.; Shu, H.; Sang, Y.; Jiang, L. Dynamic leader based collective intelligence for maximum power point tracking of PV systems affected by partial shading condition. Energy Convers. Manag. 2019, 179, 286–303. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, N.; Yang, S. Hybrid artificial bee colony algorithm for parameter estimation of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2013, 38, 5796–5806. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Zakeri, A.; Hokmabadi, A. Efficient feature selection method using real-valued grasshopper optimization algorithm. Expert Syst. Appl. 2019, 119, 61–72. [Google Scholar] [CrossRef]
- Wei, Y.; Stanford, R.J. Parameter identification of solid oxide fuel cell by Chaotic Binary Shark Smell Optimization method. Energy 2019, 188, 115770. [Google Scholar] [CrossRef]
- Rao, Y.; Shao, Z.; Ahangarnejad, A.H.; Gholamalizadeh, E.; Sobhani, B. Shark Smell Optimizer applied to identify the optimal parameters of the proton exchange membrane fuel cell model. Energy Convers. Manag. 2019, 182, 1–8. [Google Scholar] [CrossRef]
- Gandomi, A.H. Interior search algorithm (ISA): A novel approach for global optimization. ISA Trans. 2014, 53, 1168–1183. [Google Scholar] [CrossRef]
- Kler, D.; Rana, K.P.S.; Kumar, V. Parameter extraction of fuel cells using hybrid interior search algorithm. Int. J. Energy Res. 2019, 43, 2854–2880. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Fathy, A.; Rezk, H. Multi-verse optimizer for identifying the optimal parameters of PEMFC model. Energy 2018, 143, 634–644. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A Competitive Swarm Optimizer for Large Scale Optimization. IEEE Trans. Cybern. 2015, 45, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Xiong, G.; Zhang, J.; Shi, D.; Yuan, X. A simplified competitive swarm optimizer for parameter identification of solid oxide fuel cells. Energy Convers. Manag. 2020, 203, 112204. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M.; Agwa, A.M. Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Convers. Manag. 2019, 201, 112197. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef] [Green Version]
- Niu, Q.; Zhang, L.; Li, K. A biogeography-based optimization algorithm with mutation strategies for model parameter estimation of solar and fuel cells. Energy Convers. Manag. 2014, 86, 1173–1185. [Google Scholar] [CrossRef]
- Samareh Moosavi, S.H.; Khatibi Bardsiri, V. Satin bowerbird optimizer: A new optimization algorithm to optimize ANFIS for software development effort estimation. Eng. Appl. Artif. Intell. 2017, 60, 1–15. [Google Scholar] [CrossRef]
- El-Hay, E.A.; El-Hameed, M.A.; El-Fergany, A.A. Steady-state and dynamic models of solid oxide fuel cells based on Satin Bowerbird Optimizer. Int. J. Hydrogen Energy 2018, 43, 14751–14761. [Google Scholar] [CrossRef]
- Askarzadeh, A.; dos Santos Coelho, L. A backtracking search algorithm combined with Burger’s chaotic map for parameter estimation of PEMFC electrochemical model. Int. J. Hydrogen Energy 2014, 39, 11165–11174. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; He, Y. Parameter identification of solid oxide fuel cells with ranking teaching-learning based algorithm. Energy Convers. Manag. 2018, 174, 126–137. [Google Scholar] [CrossRef]
- Shareef, H.; Ibrahim, A.A.; Mutlag, A.H. Lightning search algorithm. Appl. Soft Comput. 2015, 36, 315–333. [Google Scholar] [CrossRef]
- Panigrahy, D.; Samal, P. Modified lightning search algorithm for optimization. Eng. Appl. Artif. Intell. 2021, 105, 104419. [Google Scholar] [CrossRef]
- Elsisi, M.; Abdelfattah, H. New design of variable structure control based on lightning search algorithm for nuclear reactor power system considering load-following operation. Nucl. Eng. Technol. 2020, 52, 544–551. [Google Scholar] [CrossRef]
- Ali, J.A.; Hannan, M.A.; Mohamed, A.; Pin Jern, K.; Abdolrasol, M.G. Implementation of DSP-based optimal fuzzy logic speed controller for IM drive using quantum lightning search algorithm. Measurement 2020, 153, 107372. [Google Scholar] [CrossRef]
- Aljanad, A.; Mohamed, A.; Shareef, H.; Khatib, T. A novel method for optimal placement of vehicle-to-grid charging stations in distribution power system using a quantum binary lightning search algorithm. Sustain. Cities Soc. 2018, 38, 174–183. [Google Scholar] [CrossRef]
- Thangaraj, Y.; Kuppan, R. Multi-objective simultaneous placement of DG and DSTATCOM using novel lightning search algorithm. J. Appl. Res. Technol. 2017, 15, 477–491. [Google Scholar] [CrossRef]
- Moreno, S.R.; Pierezan, J.; dos Santos Coelho, L.; Mariani, V.C. Multi-objective lightning search algorithm applied to wind farm layout optimization. Energy 2021, 216, 119214. [Google Scholar] [CrossRef]
- Fawzi, M.; El-Fergany, A.A.; Hasanien, H.M. Effective methodology based on neural network optimizer for extracting model parameters of PEM fuel cells. Int. J. Energy Res. 2019, 43, 8136–8147. [Google Scholar] [CrossRef]
- Selem, S.I.; Hasanien, H.M.; El-Fergany, A.A. Parameters extraction of PEMFC’s model using manta rays foraging optimizer. Int. J. Energy Res. 2020, 44, 4629–4640. [Google Scholar] [CrossRef]









| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Low | −1.1997 | 1.00 | 3.60 | −26.00 | 13.00 | 0.10 | 0.0136 |
| High | −0.8532 | 5.00 | 9.80 | −9.54 | 23.00 | 0.80 | 0.5000 |
| Parameter | LSA | NNA [58] | GOA [58] |
|---|---|---|---|
| −1.0624 | −0.97997 | −0.8532 | |
| 3.597 | 3.6946 | 3.4173 | |
| 6.6538 | 9.0871 | 9.8000 | |
| −16.4925 | −16.2820 | −15.9555 | |
| 23.00 | 23.0000 | 22.8458 | |
| 0.103 | 0.1000 | 0.1000 | |
| 0.0188 | 0.0136 | 0.0136 | |
| 0.8140 | 0.85361 | 0.8710 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohanty, B.; Madurai Elavarasan, R.; Hasanien, H.M.; Devaraj, E.; Turky, R.A.; Pugazhendhi, R. Parameters Identification of Proton Exchange Membrane Fuel Cell Model Based on the Lightning Search Algorithm. Energies 2022, 15, 7893. https://doi.org/10.3390/en15217893
Mohanty B, Madurai Elavarasan R, Hasanien HM, Devaraj E, Turky RA, Pugazhendhi R. Parameters Identification of Proton Exchange Membrane Fuel Cell Model Based on the Lightning Search Algorithm. Energies. 2022; 15(21):7893. https://doi.org/10.3390/en15217893
Chicago/Turabian StyleMohanty, Banaja, Rajvikram Madurai Elavarasan, Hany M. Hasanien, Elangovan Devaraj, Rania A. Turky, and Rishi Pugazhendhi. 2022. "Parameters Identification of Proton Exchange Membrane Fuel Cell Model Based on the Lightning Search Algorithm" Energies 15, no. 21: 7893. https://doi.org/10.3390/en15217893
APA StyleMohanty, B., Madurai Elavarasan, R., Hasanien, H. M., Devaraj, E., Turky, R. A., & Pugazhendhi, R. (2022). Parameters Identification of Proton Exchange Membrane Fuel Cell Model Based on the Lightning Search Algorithm. Energies, 15(21), 7893. https://doi.org/10.3390/en15217893








