Dynamic Simulation of Starting and Emergency Conditions of a Hydraulic Unit Based on a Francis Turbine
Abstract
:1. Introduction
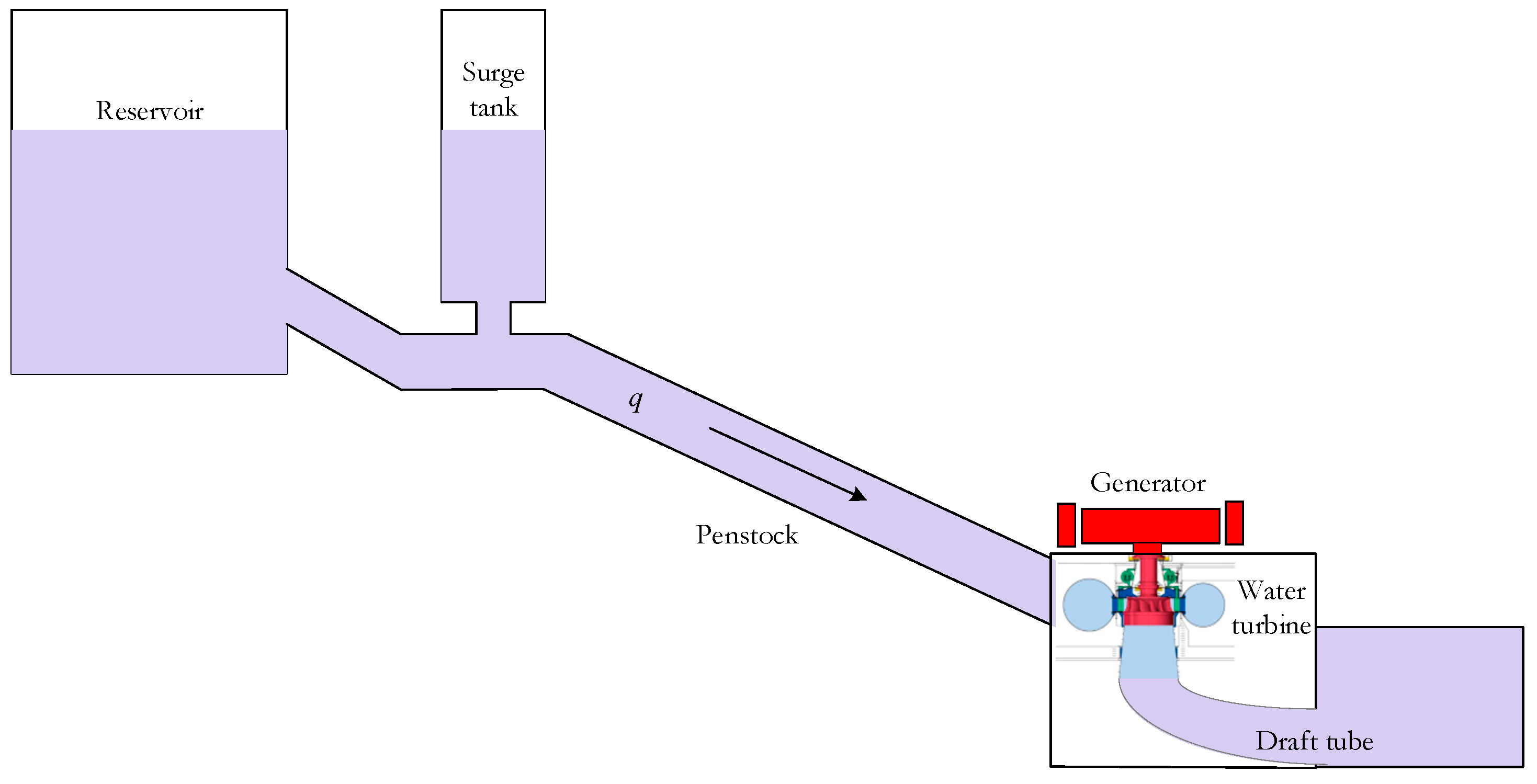
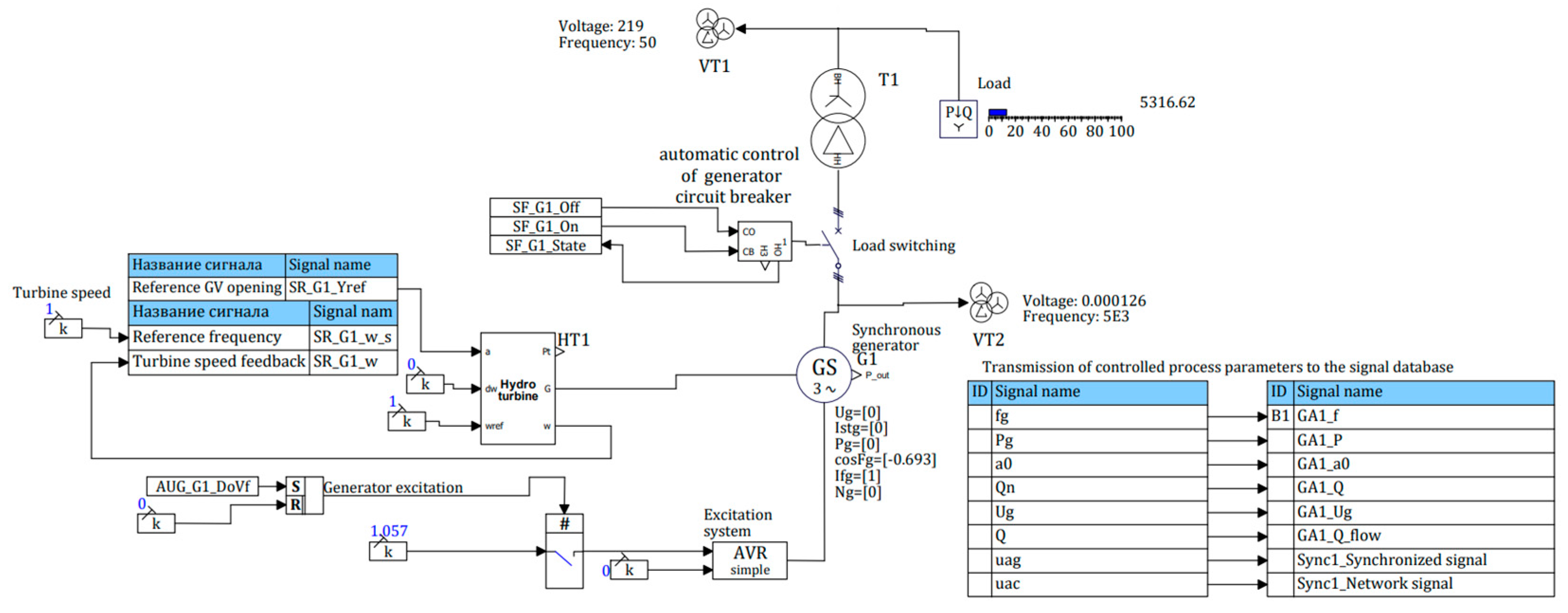
2. Construction of a Mathematical Model
3. The Mathematical Model Development
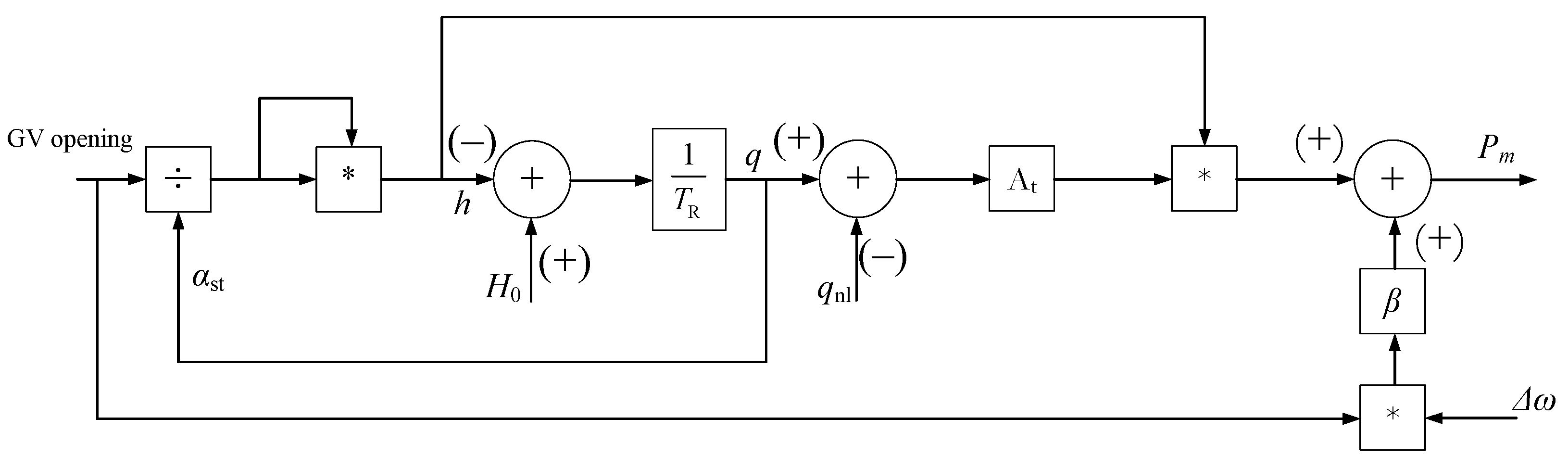
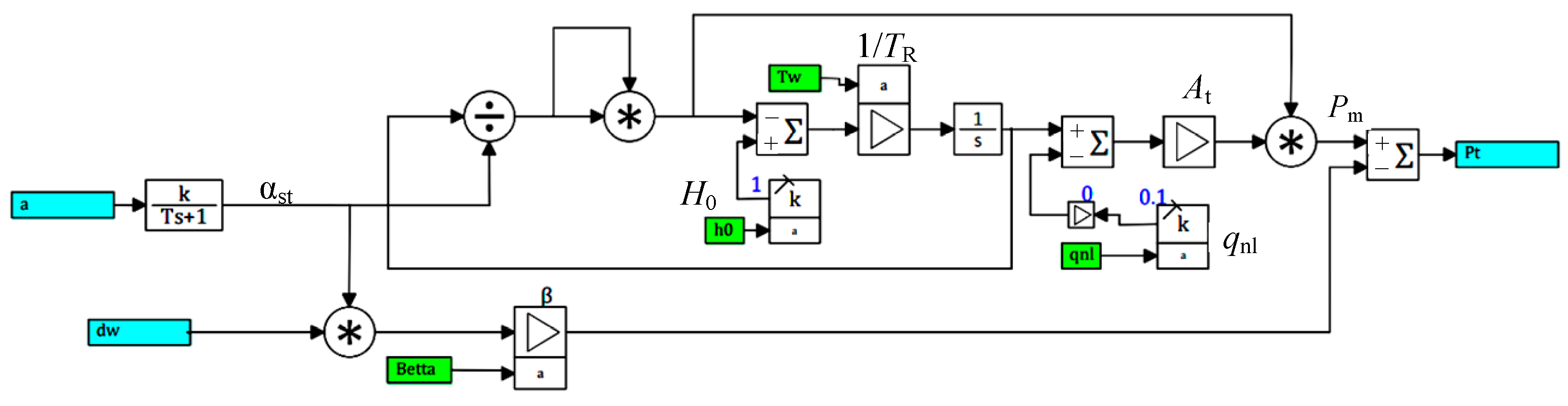
3.1. Model of a Water Turbine with Elastic Water Hammer
3.2. Generator Model
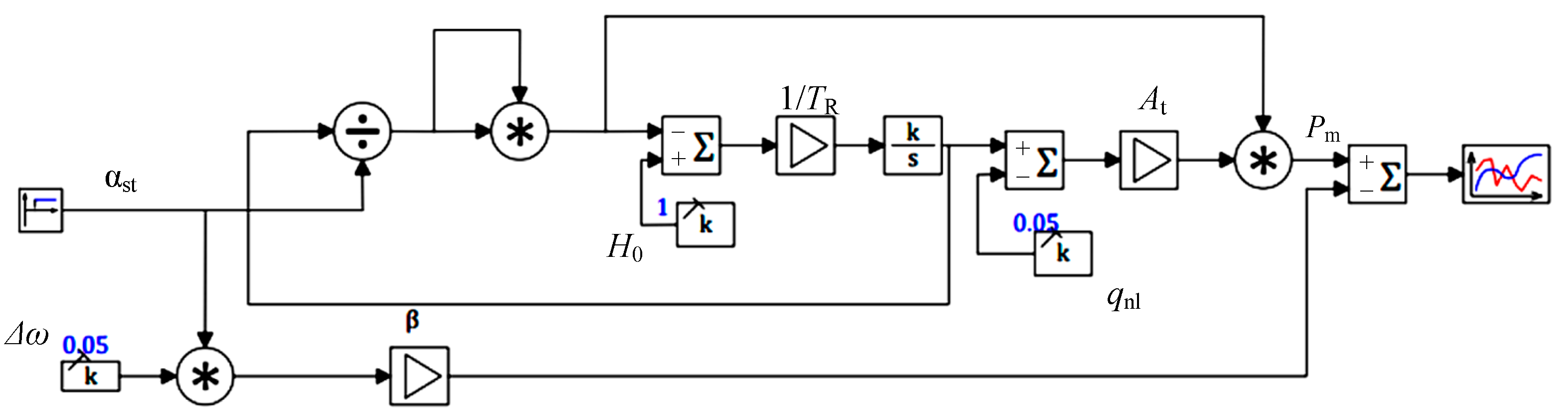
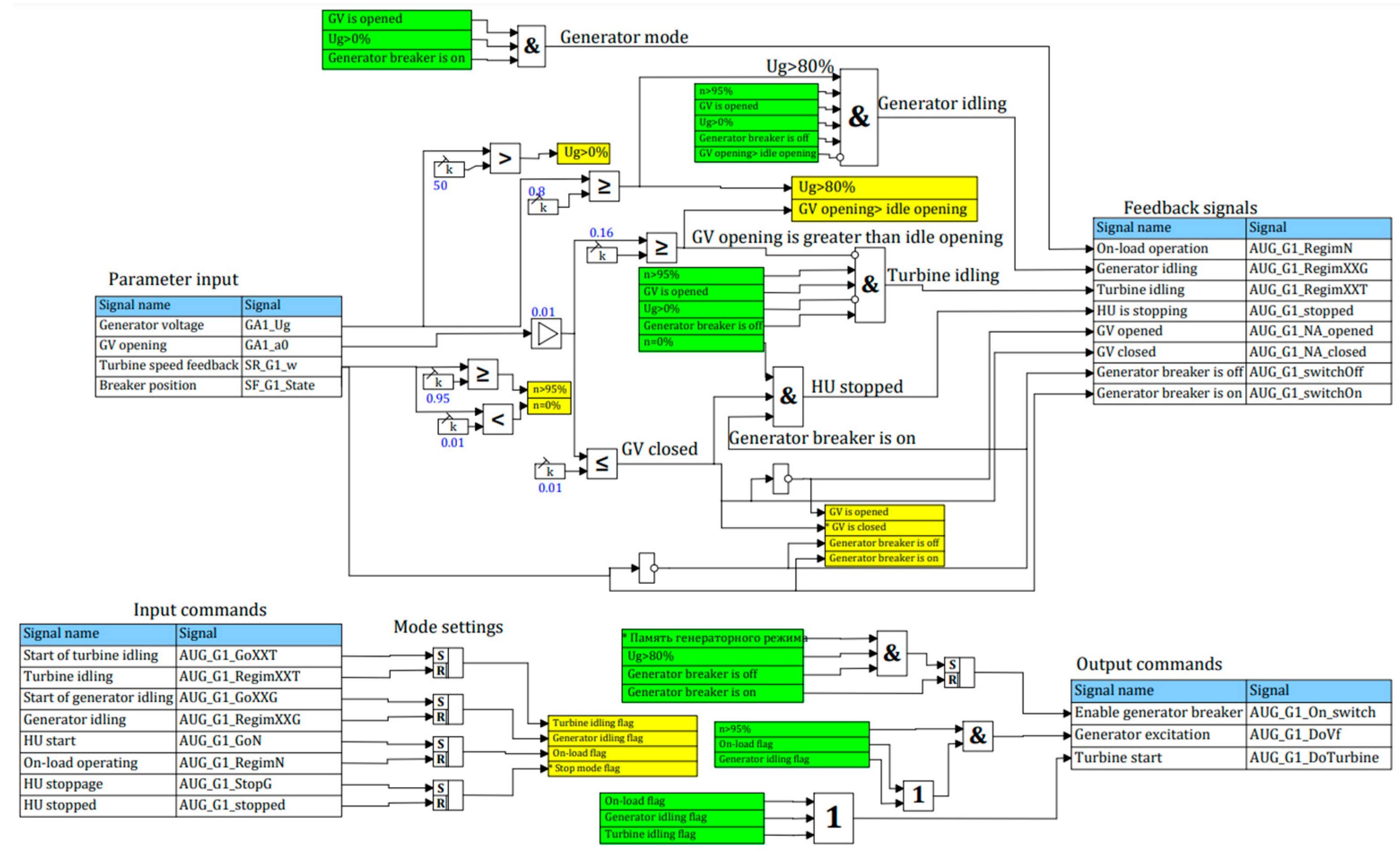
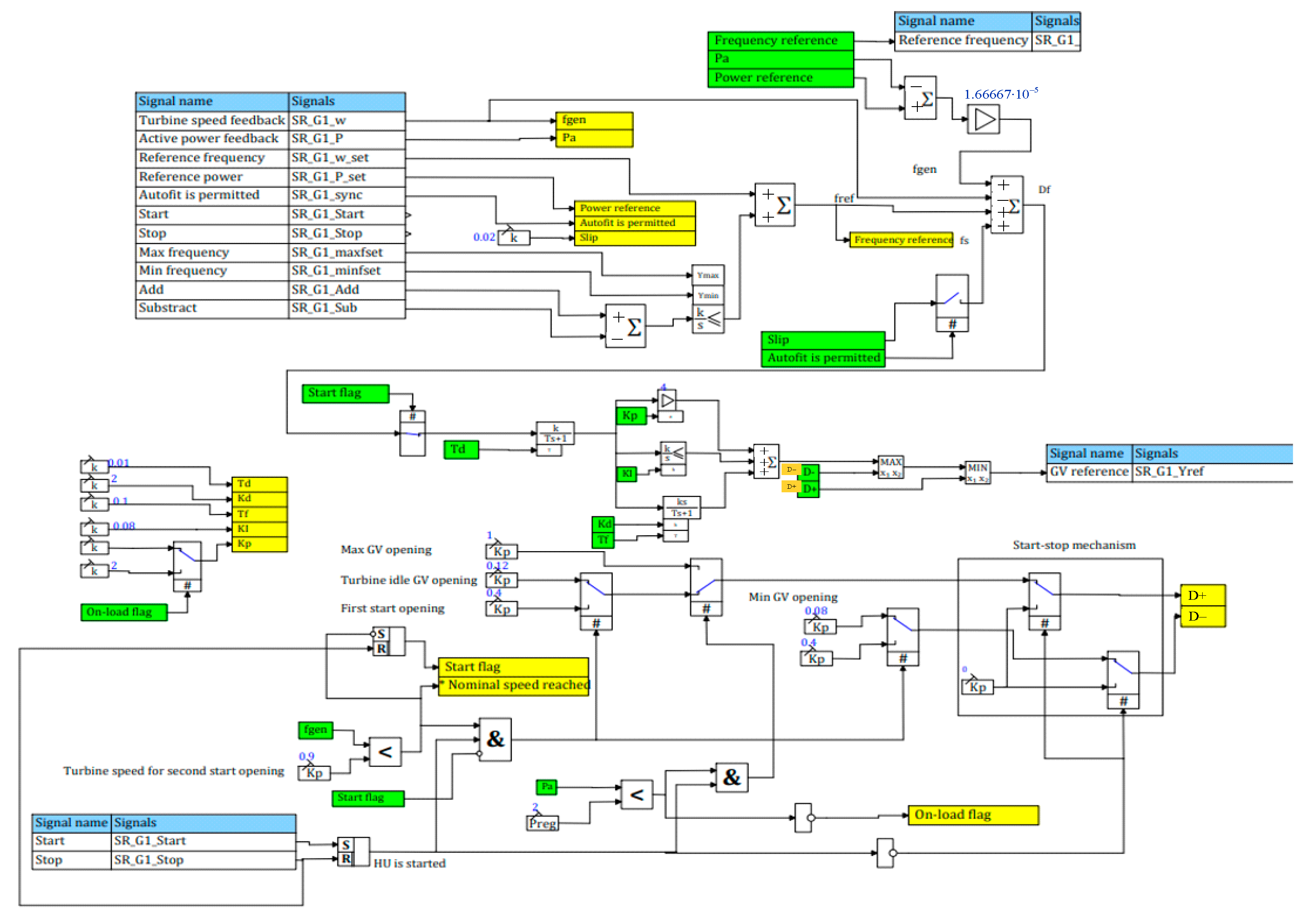
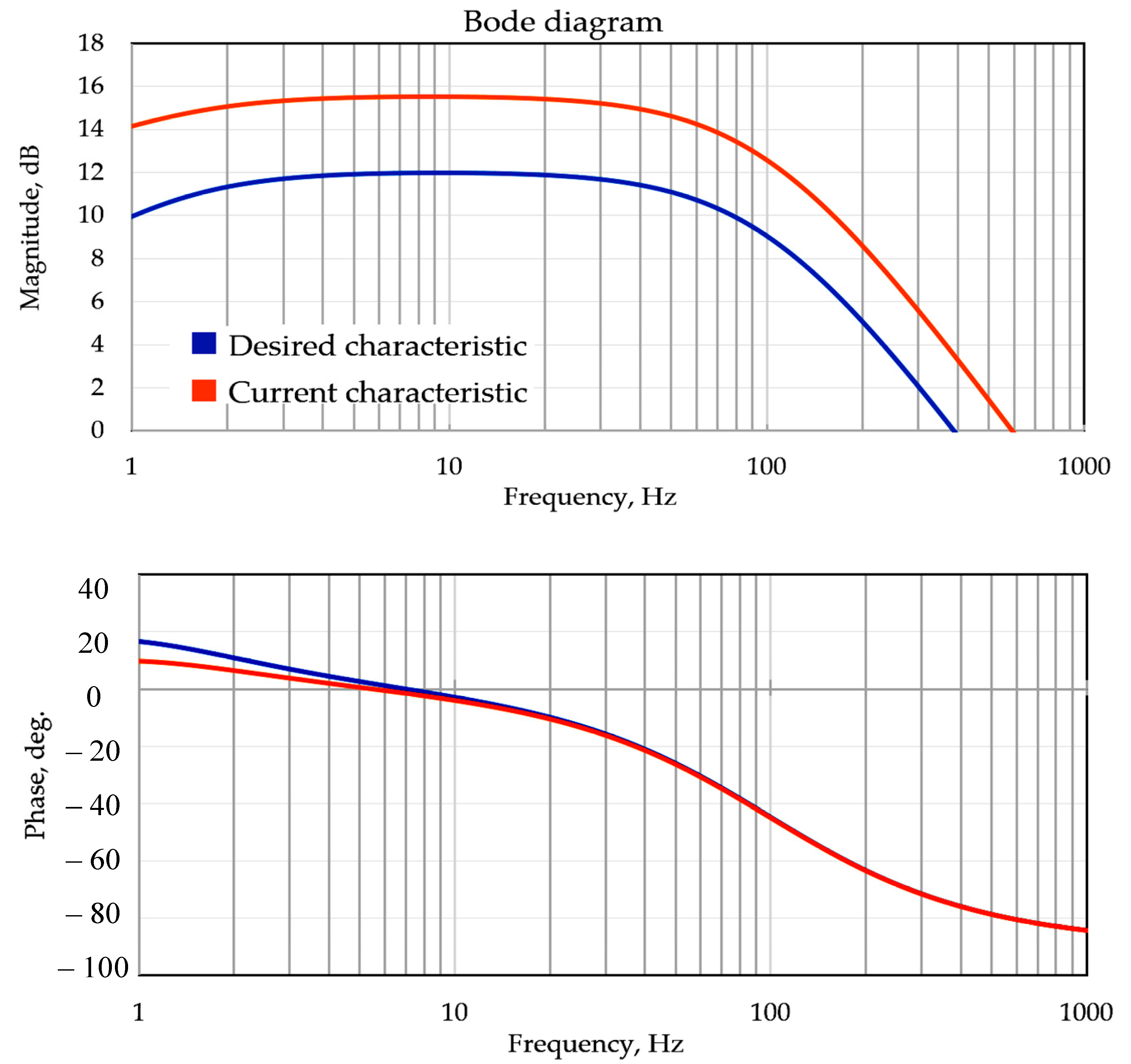
4. Francis Turbine Control Dynamics
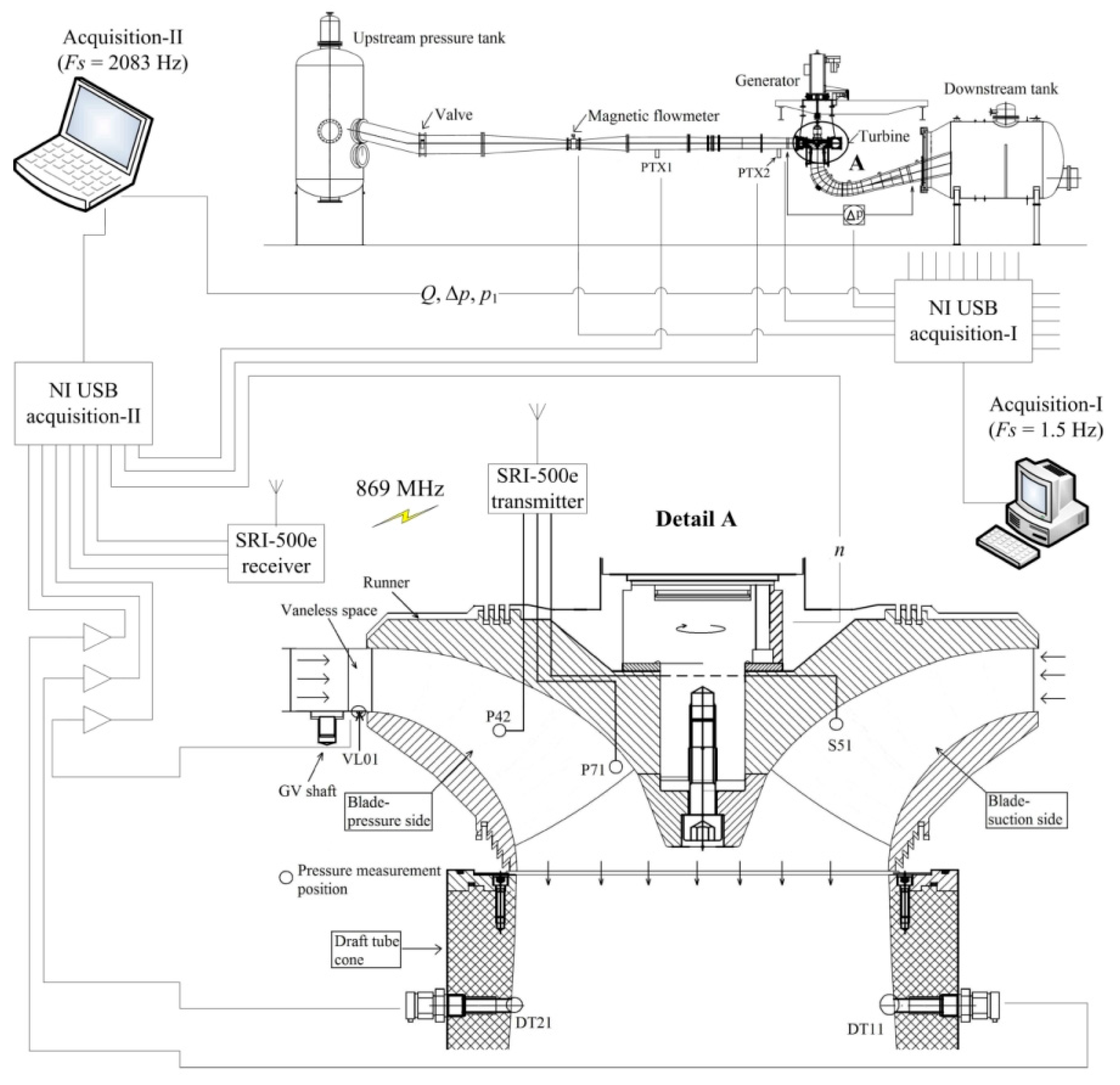
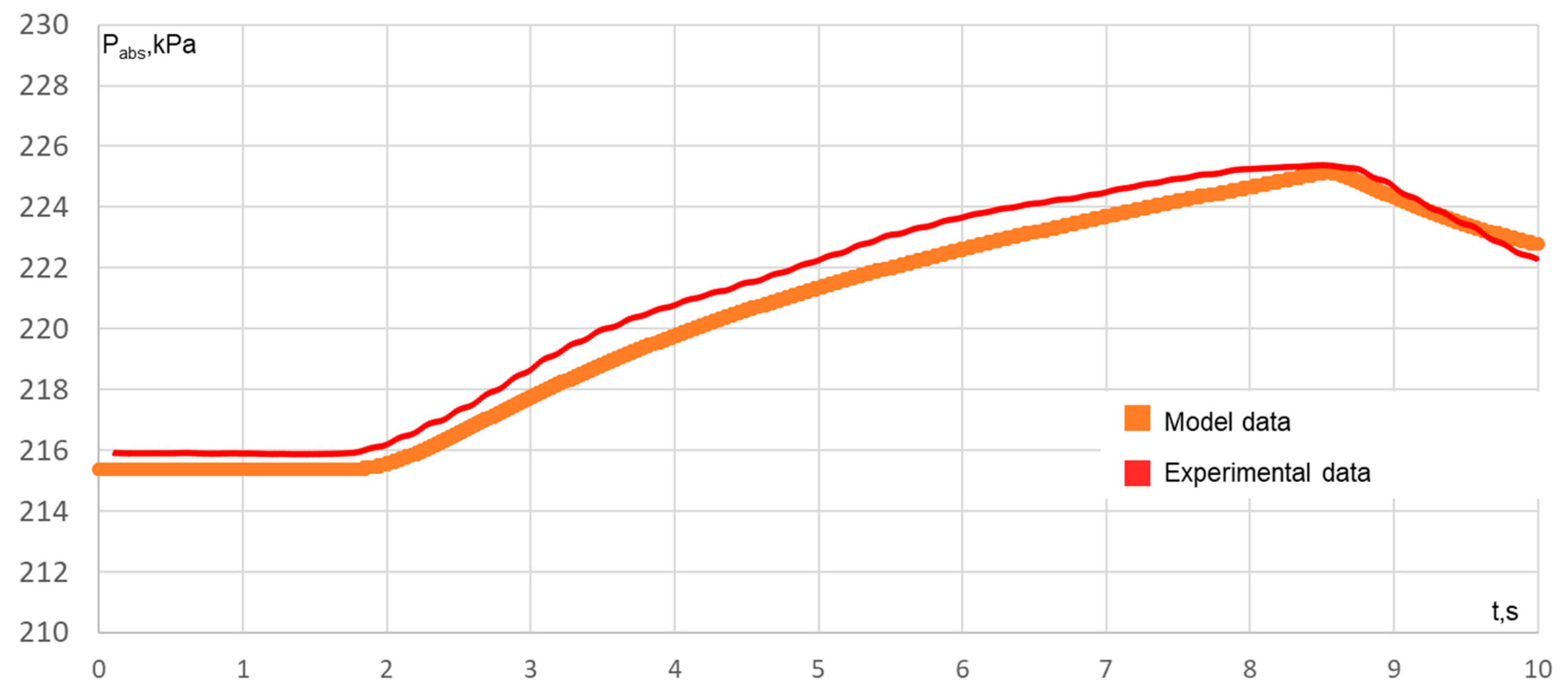
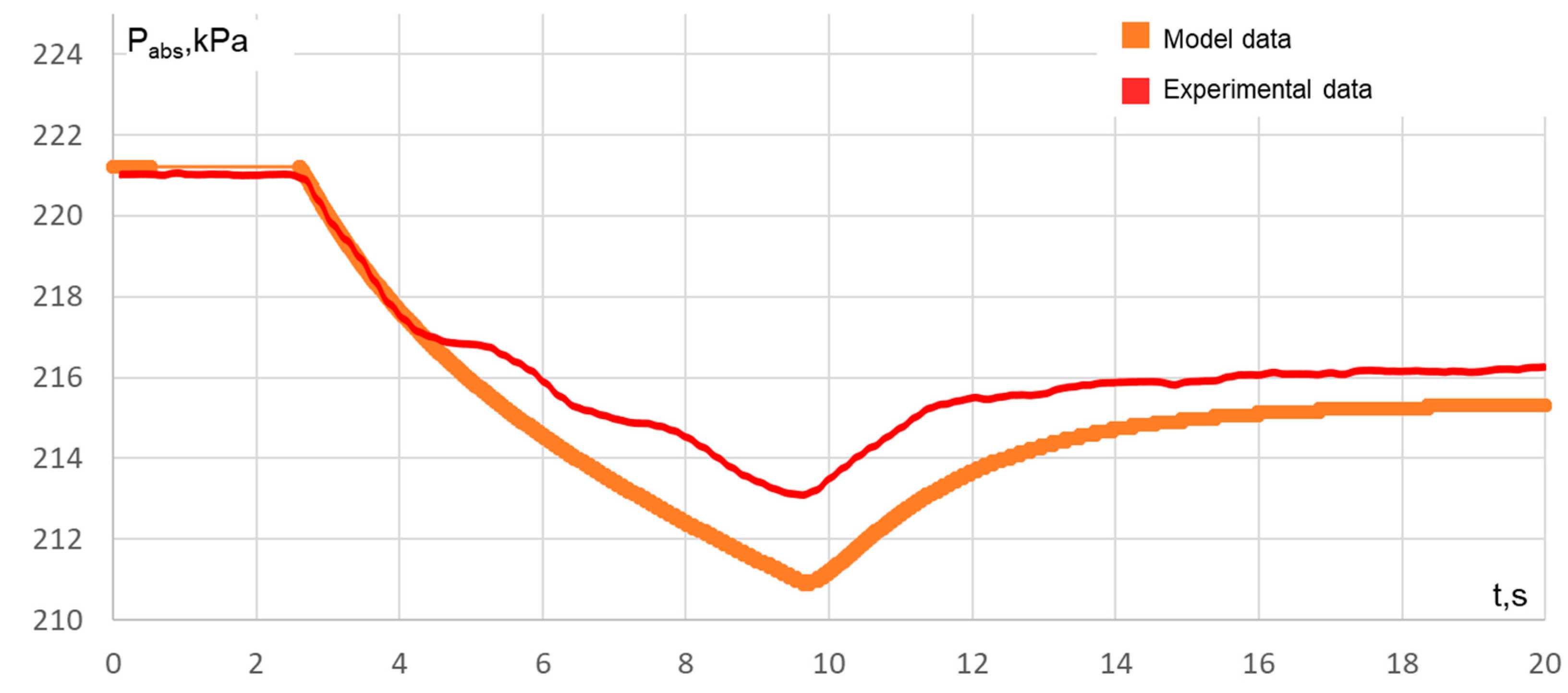
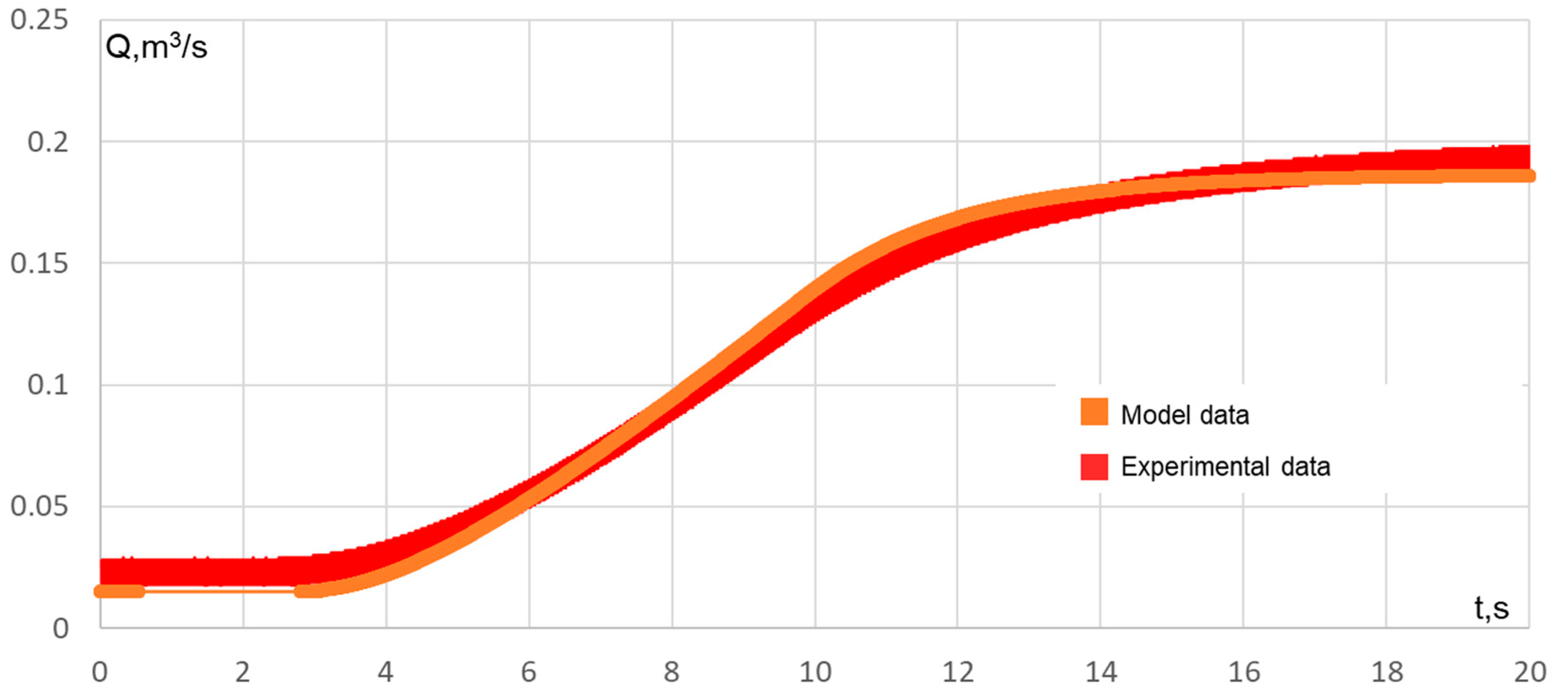
5. Comparison of Results with Experimental Data
5.1. Simulated Plant
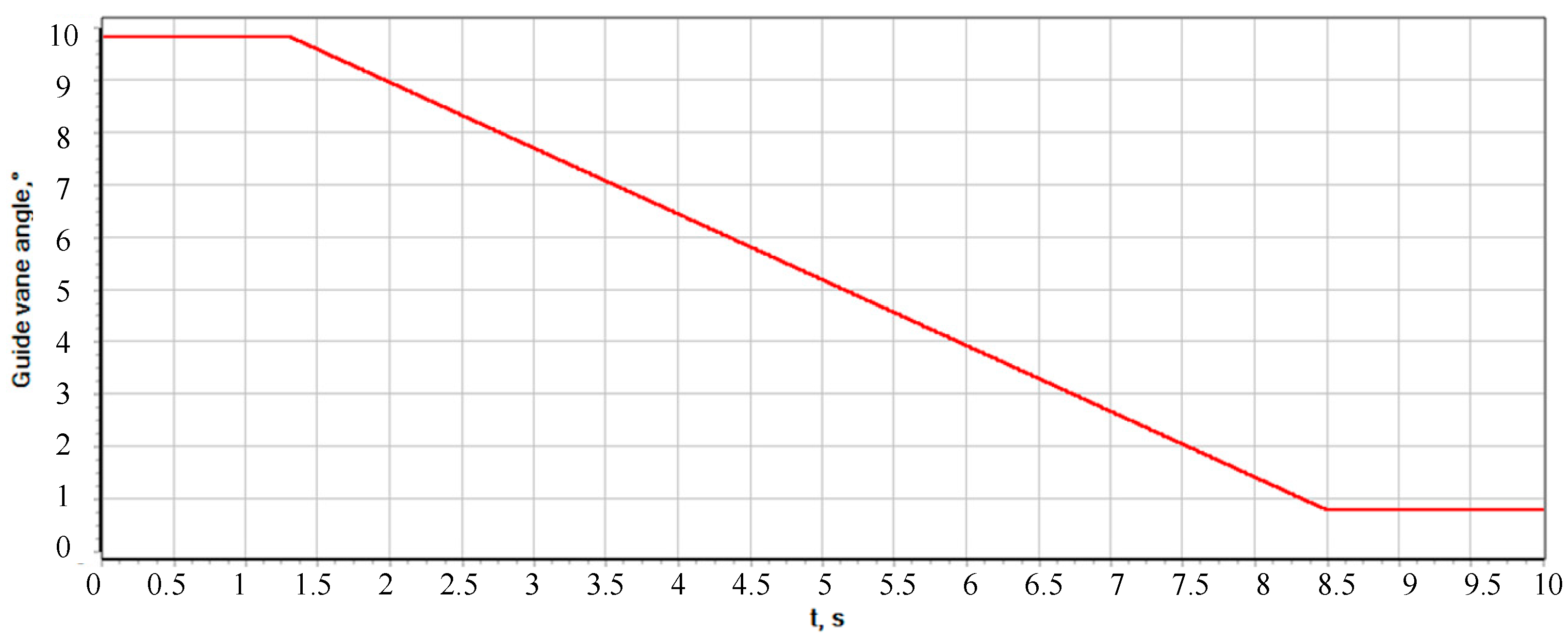
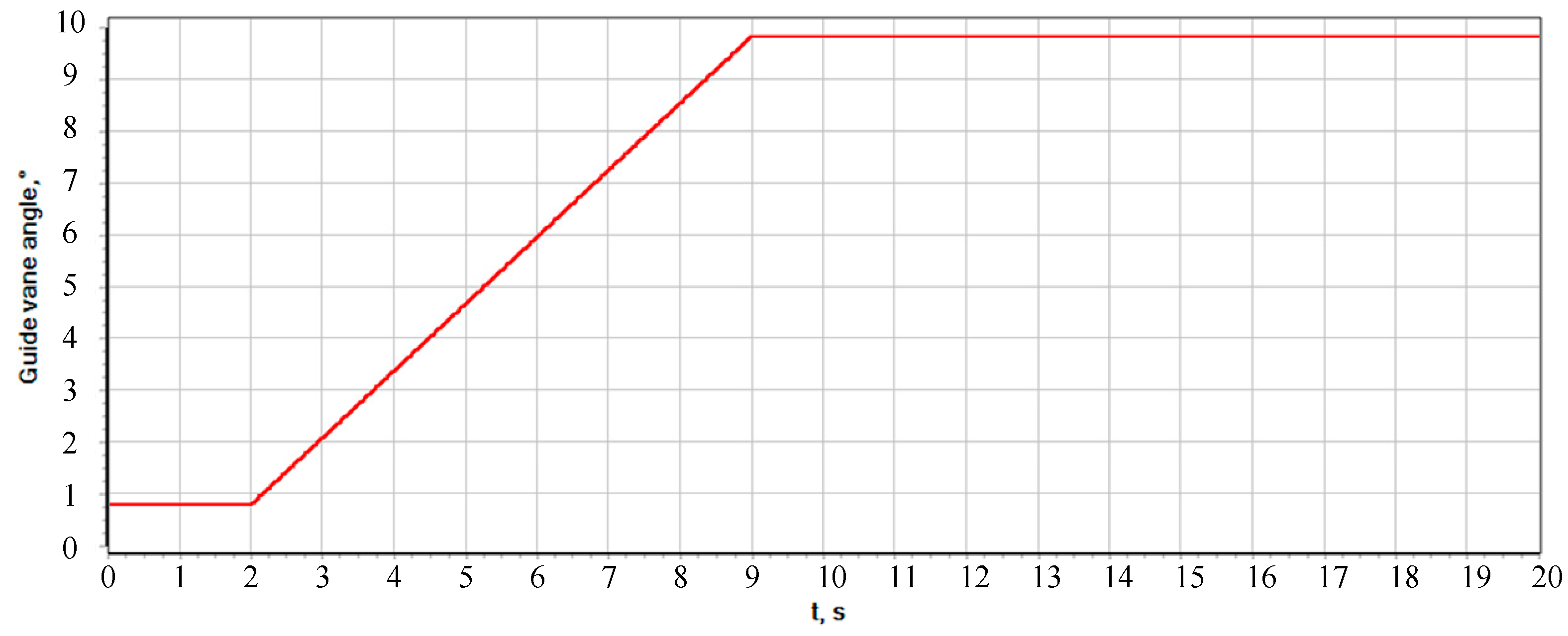
5.2. Braking Process
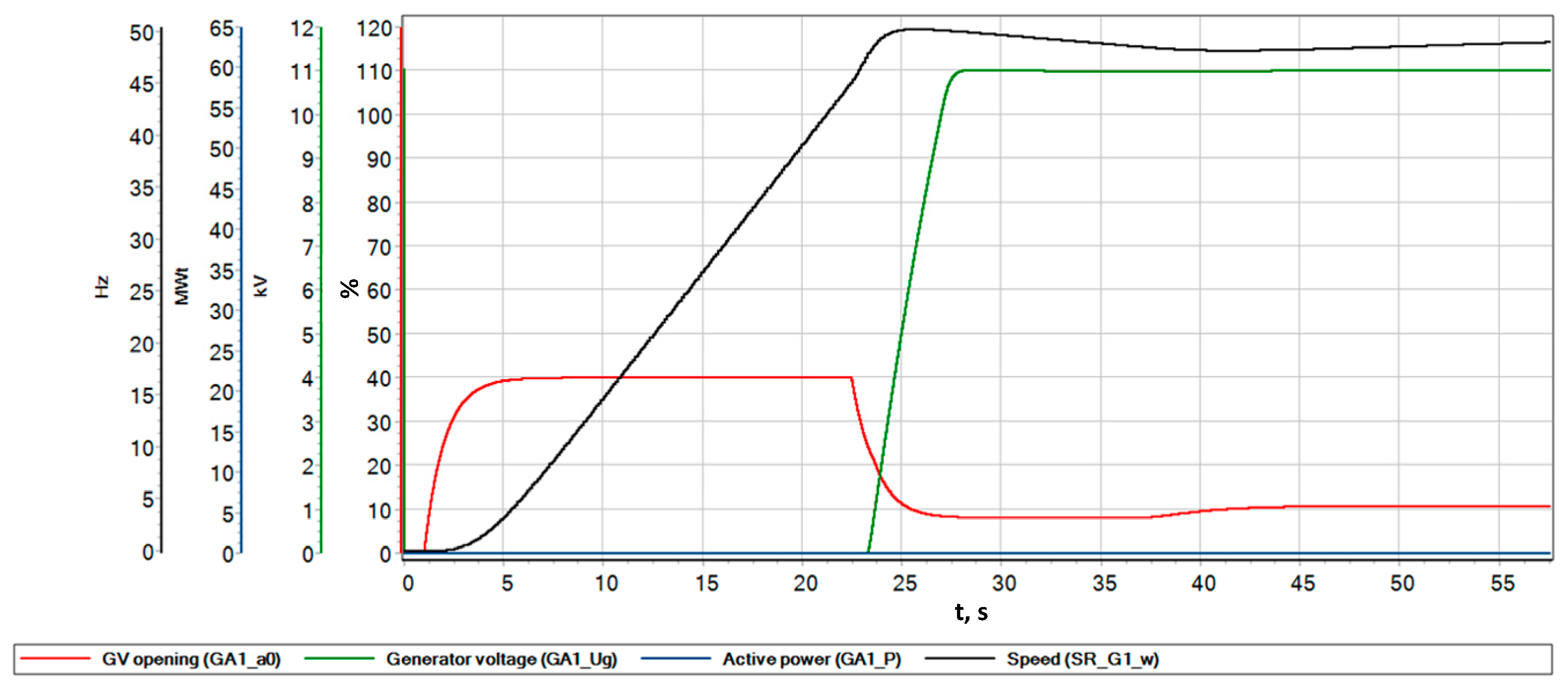
5.3. Acceleration Process
- Shutdown of the hydraulic unit
- No-load conditions of the hydraulic unit
- No-load conditions of the generator
- Generator normal operating conditions
6. Analysis of Results
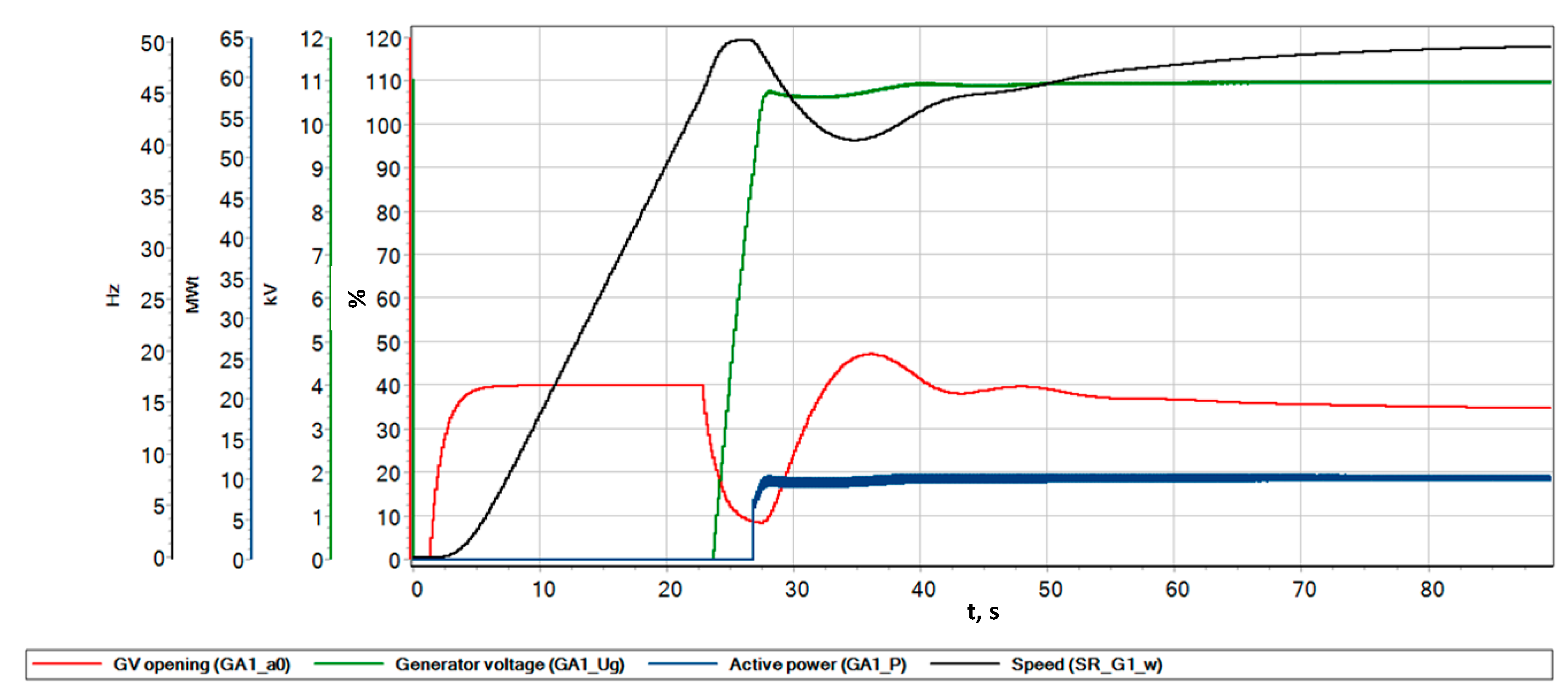
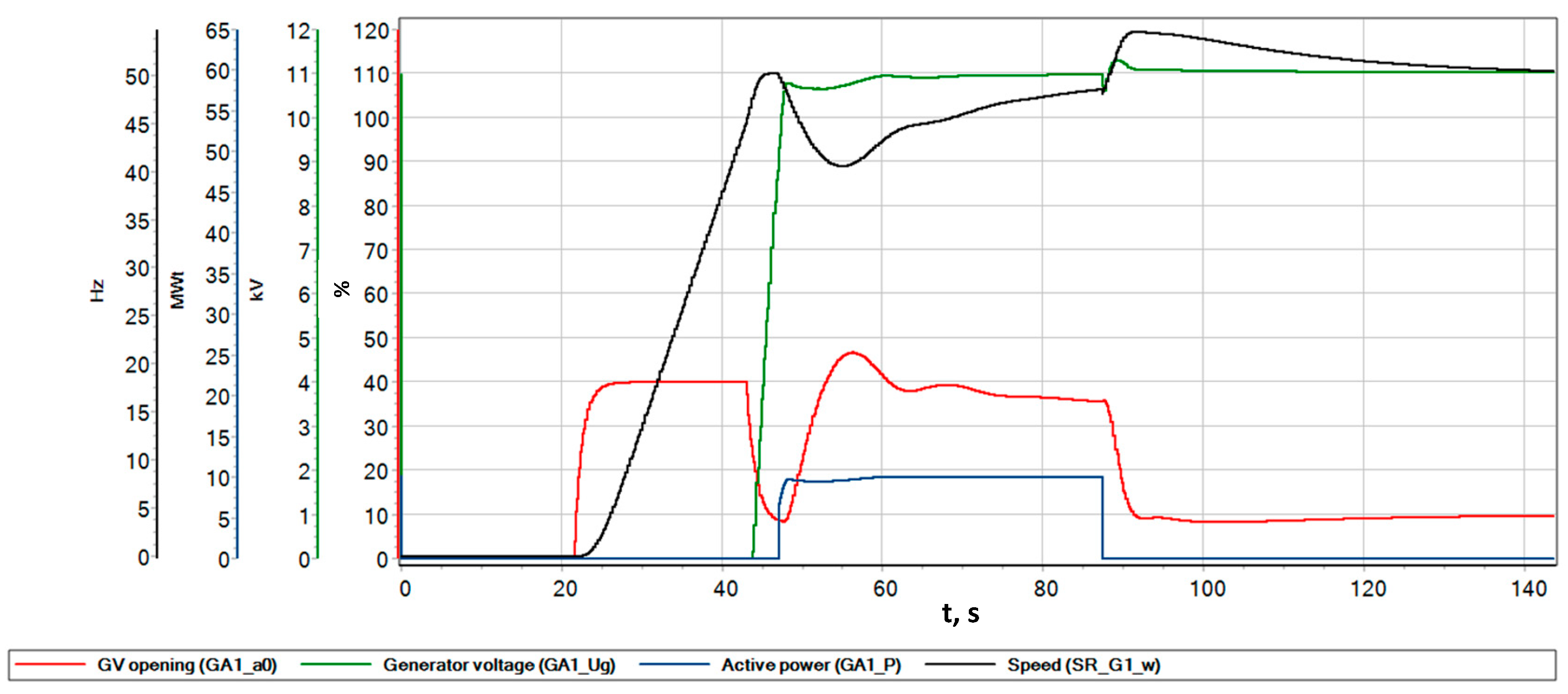
6.1. Turbine and Generator No-Load Operating Conditions
6.2. On-Load Operation and Load Increase
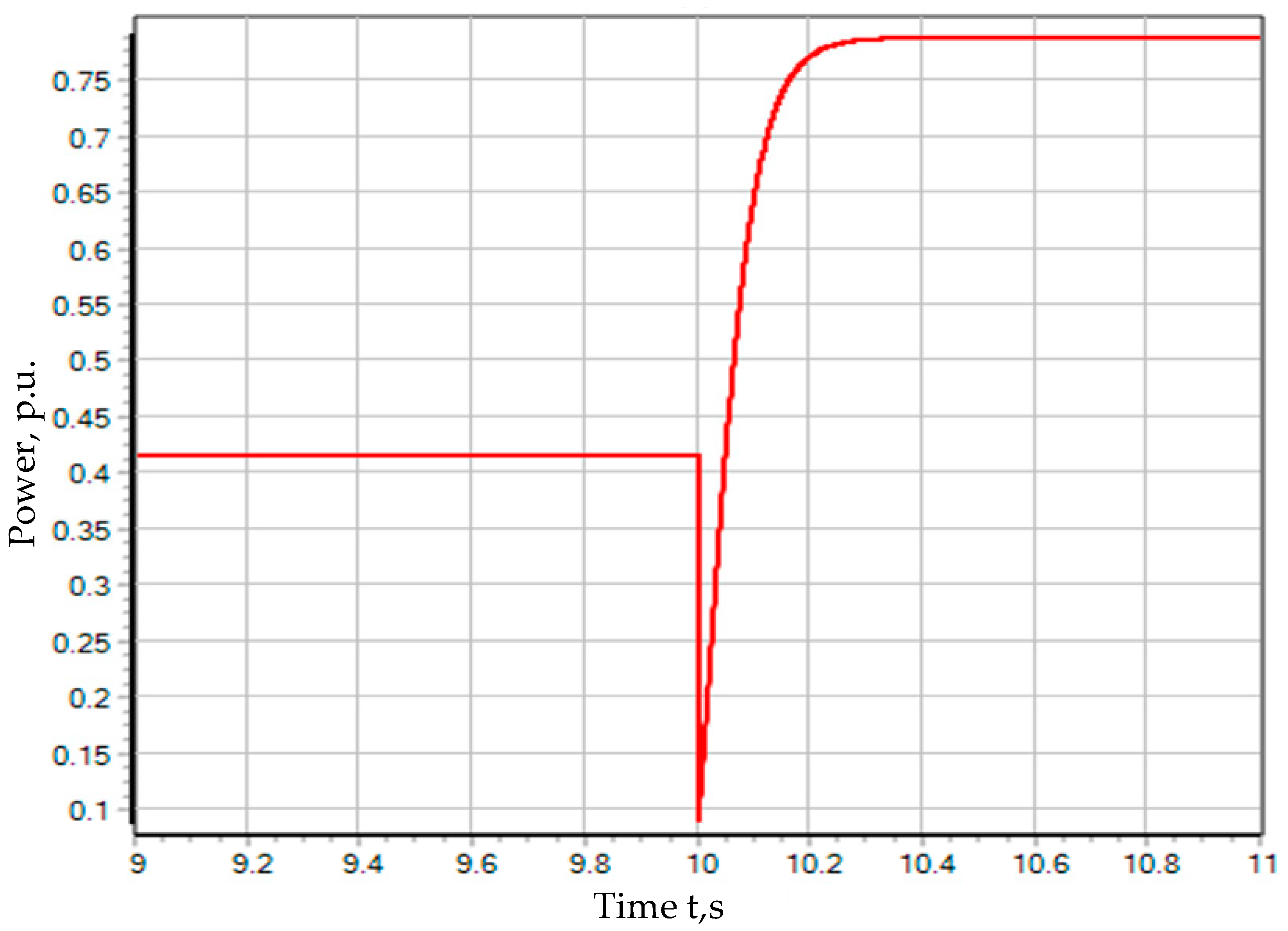
6.3. Emergency Load Shedding
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vagnonia, E.; Valentinb, D.; Avellana, F. Dynamic Behaviour of a Francis Turbine during Voltage Regulation in the Electrical Power System. Available online: https://www.semanticscholar.org/paper/Dynamic-behaviour-of-a-Francis-turbine-during-in-Vagnonia-Valentinb/b13f7e64e0c79538d11552a84bd9e7fbe3f71951 (accessed on 12 May 2022).
- Xu, Y.; Zheng, Y.; Du, Y.; Yang, W.; Peng, X.; Li, C. Adaptive Condition Predictive-Fuzzy PID Optimal Control of Start-up Process for Pumped Storage Unit at Low Head Area. Energy Convers. Manag. 2018, 177, 592–604. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, X.; Yuan, Y.; Lei, X.; Zhang, B. Parameter Estimation of Fuzzy Sliding Mode Controller for Hydraulic Turbine Regulating System Based on HICA Algorithm. Renew. Energy 2019, 133, 551–565. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, W.; Liao, Y.; Zhao, Z.; Ma, W.; Yang, J.; Yang, J. Improved Transfer Function Method for Flexible Simulation of Hydraulic-Mechanical-Electrical Transient Processes of Hydro-Power Plants. Renew. Energy 2022, 196, 390–404. [Google Scholar] [CrossRef]
- Brezovec, M.; Kuzle, I.; Krpan, M.; Holjevac, N. Improved Dynamic Model of a Bulb Turbine-Generator for Analysing Oscillations Caused by Mechanical Torque Disturbance on a Runner Blade. Int. J. Electr. Power Energy Syst. 2020, 119, 105929. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Wu, C.; Wang, X.; Lee, J.-M.; Jung, K.-H. Dynamic Modeling and Dynamical Analysis of Pump-Turbines in S-Shaped Regions during Runaway Operation. Energy Convers. Manag. 2017, 138, 375–382. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Norrlund, P.; Bladh, J.; Yang, J.; Lundin, U. Hydraulic Damping Mechanism of Low Frequency Oscillations in Power Systems: Quantitative Analysis Using a Nonlinear Model of Hydropower Plants. Appl. Energy 2018, 212, 1138–1152. [Google Scholar] [CrossRef]
- Wang, L.X.; Zheng, J.H.; Li, Z.G.; Jing, Z.X.; Wu, Q.H. Order Reduction Method for High-Order Dynamic Analysis of Heterogeneous Integrated Energy Systems. Appl. Energy 2022, 308, 118265. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, J.; Chung, C.Y.; Yang, W.; He, X.; Chen, M. Performance Enhancement of Pumped Storage Units for System Frequency Support Based on a Novel Small Signal Model. Energy 2021, 234, 121207. [Google Scholar] [CrossRef]
- Lu, X.; Li, C.; Liu, D.; Zhu, Z.; Tan, X. Influence of Water Diversion System Topologies and Operation Scenarios on the Damping Characteristics of Hydropower Units under Ultra-Low Frequency Oscillations. Energy 2022, 239, 122679. [Google Scholar] [CrossRef]
- Guo, W.; Yang, J. Dynamic Performance Analysis of Hydro-Turbine Governing System Considering Combined Effect of Downstream Surge Tank and Sloping Ceiling Tailrace Tunnel. Renew. Energy 2018, 129, 638–651. [Google Scholar] [CrossRef]
- Liu, D.; Wang, X.; Peng, Y.; Zhang, H.; Xiao, Z.; Han, X.; Malik, O.P. Stability Analysis of Hydropower Units under Full Operating Conditions Considering Turbine Nonlinearity. Renew. Energy 2020, 154, 723–742. [Google Scholar] [CrossRef]
- Xu, B.; Luo, X.; Egusquiza, M.; Ye, W.; Liu, J.; Egusquiza, E.; Chen, D.; Guo, P. Nonlinear Modal Interaction Analysis and Vibration Characteristics of a Francis Hydro-Turbine Generator Unit. Renew. Energy 2021, 168, 854–864. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, W. Multi-Frequency Dynamic Performance of Hydropower Plant under Coupling Effect of Power Grid and Turbine Regulating System with Surge Tank. Renew. Energy 2021, 171, 557–581. [Google Scholar] [CrossRef]
- Hu, J.; Yang, J.; Zeng, W.; Zhao, Z.; Yang, J. Hydraulic Interaction of Two Parallel Pump-Turbines in Constant-Speed Oscillation: Measurement, Simulation, and Sensitivity Analysis. Renew. Energy 2021, 176, 269–279. [Google Scholar] [CrossRef]
- Cao, J.; Tian, H.; Ahn, S.-H.; Duo, W.; Bi, H.; Zhao, L.; Zhao, G.; Gao, H.; Wang, M.; Ma, G.; et al. Fatigue Analysis in Rotor of a Prototype Bulb Turbine Based on Fluid-Structure Interaction. Eng. Fail. Anal. 2022, 132, 105940. [Google Scholar] [CrossRef]
- Liao, Y.; Yang, W.; Zhao, Z.; Li, X.; Ci, X.; Alizadeh Bidgoli, M.; Yang, J. Influence Mechanism of Backlash Nonlinearity on Dynamic Regulation Stability of Hydropower Units. Sustain. Energy Technol. Assess. 2022, 51, 101917. [Google Scholar] [CrossRef]
- Brito Junior, G.C.; Machado, R.D.; Chaves Neto, A. Using Simplified Models to Assist Fault Detection and Diagnosis in Large Hydrogenerators. Int. J. Rotating Mach. 2017, 2017, e9258456. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Liu, C.Q. Analysis on Oscillations between Two Generators in a Hydro Power Plant and Development of Math Model for a Compound Excitation System. In Proceedings of the Proceedings. International Conference on Power System Technology, Kunming, China, 13–17 October 2002; Volume 2, pp. 1254–1258. [Google Scholar]
- Dong, Z.; Tan, J.; Muljadi, E.; Nelms, R.M.; St-Hilaire, A.; Pevarnik, M.; Jacobson, M.D. Developing of Quaternary Pumped Storage Hydropower for Dynamic Studies. IEEE Trans. Sustain. Energy 2020, 11, 2870–2878. [Google Scholar] [CrossRef]
- Giosio, D.R.; Henderson, A.; Walker, J.; Brandner, P. Rapid Reserve Generation from a Francis Turbine for System Frequency Control. Energies 2017, 10, 496. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Zhao, Z.; Zhang, C.; Li, C.; Xu, Y. A Real-Time Accurate Model and Its Predictive Fuzzy PID Controller for Pumped Storage Unit via Error Compensation. Energies 2018, 11, 35. [Google Scholar] [CrossRef]
- Liao, S.; Zhao, H.; Li, G.; Liu, B. Short-Term Load Dispatching Method for a Diversion Hydropower Plant with Multiple Turbines in One Tunnel Using a Two-Stage Model. Energies 2019, 12, 1476. [Google Scholar] [CrossRef] [Green Version]
- Duan, C.; Minglu, Z.; Changbing, Z.; Mengjiao, Y.; Cheng, M.; Chunhe, S. Research on Hydraulic–Electric Interference and Optimisation of Multi-Turbine Hydropower System Based on the Dual Control Mode. IET Renew. Power Gener. 2019, 13, 1096–1104. [Google Scholar] [CrossRef]
- Kong, L.; Cao, J.; Li, X.; Zhou, X.; Hu, H.; Wang, T.; Gui, S.; Lai, W.; Zhu, Z.; Wang, Z.; et al. Numerical Analysis on the Hydraulic Thrust and Dynamic Response Characteristics of a Turbine Pump. Energies 2022, 15, 1580. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, L.; Liu, D.; Wang, J.; Zhao, Y.; Liu, T.; Wang, H. Dynamic Model of Kaplan Turbine Regulating System Suitable for Power System Analysis. Math. Probl. Eng. 2015, 2015, e294523. [Google Scholar] [CrossRef] [Green Version]
- Nanaware, R.A.; Sawant, S.R.; Jadhav, B.T. Modeling of Hydraulic Turbine and Governor for Dynamic Studies of HPP. In Proceedings of the IJCA Proceedings on International Conference on Recent Trends in Information Technology and Computer Science 2012 ICRTITCS 2012, Florence, Italy, 10–14 September 2012pp. 6–11. [Google Scholar]
- Guo, P.; Zhang, H.; Gou, D. Dynamic Characteristics of a Hydro-Turbine Governing System Considering Draft Tube Pressure Pulsation. IET Renew. Power Gener. 2020, 14, 1210–1218. [Google Scholar] [CrossRef]
- Choo, Y.C.; Muttaqi, K.M.; Negnevitsky, M. Modelling of Hydraulic Governor-Turbine for Control Stabilisation. ANZIAM J. 2007, 49, C681–C698. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.; Chen, Z.; Yuan, Y.; Huang, Y. Design of Fuzzy Sliding Mode Controller for Hydraulic Turbine Regulating System via Input State Feedback Linearization Method. Energy 2015, 93, 173–187. [Google Scholar] [CrossRef]
- Mover, W.G.P.; Supply, E. Hydraulic Turbine and Turbine Control Models for System Dynamic Studies. IEEE Trans. Power Syst. 1992, 7, 167–179. [Google Scholar] [CrossRef]
- De Jaeger, E.; Janssens, N.; Malfliet, B.; Van De Meulebroeke, F. Hydro Turbine Model for System Dynamic Studies. IEEE Trans. Power Syst. 1994, 9, 1709–1715. [Google Scholar] [CrossRef]
- Trivedi, C.; Gandhi, B.; Michel, C.J. Effect of Transients on Francis Turbine Runner Life: A Review. J. Hydraul. Res. 2013, 51, 121–132. [Google Scholar] [CrossRef]
- NTNU and LTU Francis-99 Workshop. Available online: https://www.ntnu.edu/nvks/f99-test-case1 (accessed on 13 June 2022).
- Dynamic Models for Turbine-Governors in Power System Studies. Available online: https://resourcecenter.ieee-pes.org/publications/technical-reports/PESTR1.html (accessed on 5 August 2022).
- Bao, H.; Yang, J.; Fu, L. Study on Nonlinear Dynamical Model and Control Strategy of Transient Process in Hydropower Station with Francis Turbine. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009. [Google Scholar] [CrossRef]
- Suslov, K.; Shushpanov, I.; Buryanina, N.; Ilyushin, P. Flexible Power Distribution Networks: New Opportunities and Applications. In Proceedings of the 9th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2020), Online, 2–4 May 2020; pp. 57–64. [Google Scholar]
- Karamov, D.N.; Ilyushin, P.V.; Suslov, K.V. Electrification of Rural Remote Areas Using Renewable Energy Sources: Literature Review. Energies 2022, 15, 5881. [Google Scholar] [CrossRef]
- Rylov, A.; Ilyushin, P.; Kulikov, A.; Suslov, K. Testing Photovoltaic Power Plants for Participation in General Primary Frequency Control under Various Topology and Operating Conditions. Energies 2021, 14, 5179. [Google Scholar] [CrossRef]
- Ilyushin, P. Emergency and Post-Emergency Control in the Formation of Micro-Grids. In E3S Web Conferences; EDP Sciences: Les Ulis, France, 2017; Volume 25, p. 02002. [Google Scholar] [CrossRef] [Green Version]
- Ilyushin, P.V.; Shepovalova, O.V.; Filippov, S.P.; Nekrasov, A.A. Calculating the Sequence of Stationary Modes in Power Distribution Networks of Russia for Wide-Scale Integration of Renewable Energy Based Installations. Energy Rep. 2021, 7, 308–327. [Google Scholar] [CrossRef]
- Lavrik, A.; Zhukovskiy, Y.; Tcvetkov, P. Optimizing the Size of Autonomous Hybrid Microgrids with Regard to Load Shifting. Energies 2021, 14, 5059. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.; Tsvetkov, P.; Buldysko, A.; Malkova, Y.; Stoianova, A.; Koshenkova, A. Scenario Modeling of Sustainable Development of Energy Supply in the Arctic. Resources 2021, 10, 124. [Google Scholar] [CrossRef]




| Parameter | Minimum Load | Optimal Load |
|---|---|---|
| Guide vane angle (°) | 0.8 | 9.84 |
| Net head (m) | 12.14 | 11.94 |
| Discharge (m3/s) | 0.022 | 0.200 |
| Torque to the generator (Nm) | 11.16 | 616.13 |
| Friction torque (Nm) | 4.66 | 4.52 |
| Efficiency (%) | 20.94 | 98.39 |
| Runner angular speed (rpm) | 332.8 | 332.59 |
| Casing inlet pressure-abs (kPa) | 221.03 | 215.57 |
| Draft tube outlet pressure-abs (kPa) | 101.85 | 111.13 |
| Water density (kg/m3) | 999.59 | 999.8 |
| Kinematic viscosity (m2/s) | 9.57 × 10−7 | 9.57 × 10−7 |
| Gravity (m/c2) | 9.82 | 9.82 |
| Parameter | Value |
|---|---|
| Proportional link P | 4-2 |
| Integral link I | 0.08 |
| Differential link D | 2 |
| Time Tf | 0.1 s. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achitaev, A.; Ilyushin, P.; Suslov, K.; Kobyletski, S. Dynamic Simulation of Starting and Emergency Conditions of a Hydraulic Unit Based on a Francis Turbine. Energies 2022, 15, 8044. https://doi.org/10.3390/en15218044
Achitaev A, Ilyushin P, Suslov K, Kobyletski S. Dynamic Simulation of Starting and Emergency Conditions of a Hydraulic Unit Based on a Francis Turbine. Energies. 2022; 15(21):8044. https://doi.org/10.3390/en15218044
Chicago/Turabian StyleAchitaev, Andrey, Pavel Ilyushin, Konstantin Suslov, and Sergey Kobyletski. 2022. "Dynamic Simulation of Starting and Emergency Conditions of a Hydraulic Unit Based on a Francis Turbine" Energies 15, no. 21: 8044. https://doi.org/10.3390/en15218044
APA StyleAchitaev, A., Ilyushin, P., Suslov, K., & Kobyletski, S. (2022). Dynamic Simulation of Starting and Emergency Conditions of a Hydraulic Unit Based on a Francis Turbine. Energies, 15(21), 8044. https://doi.org/10.3390/en15218044










