Computational Fluid Dynamics of Influence of Process Parameters and the Geometry of Catalyst Wires on the Ammonia Oxidation Process and Degradation of the Catalyst Gauze
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Catalyst Geometry and Properties
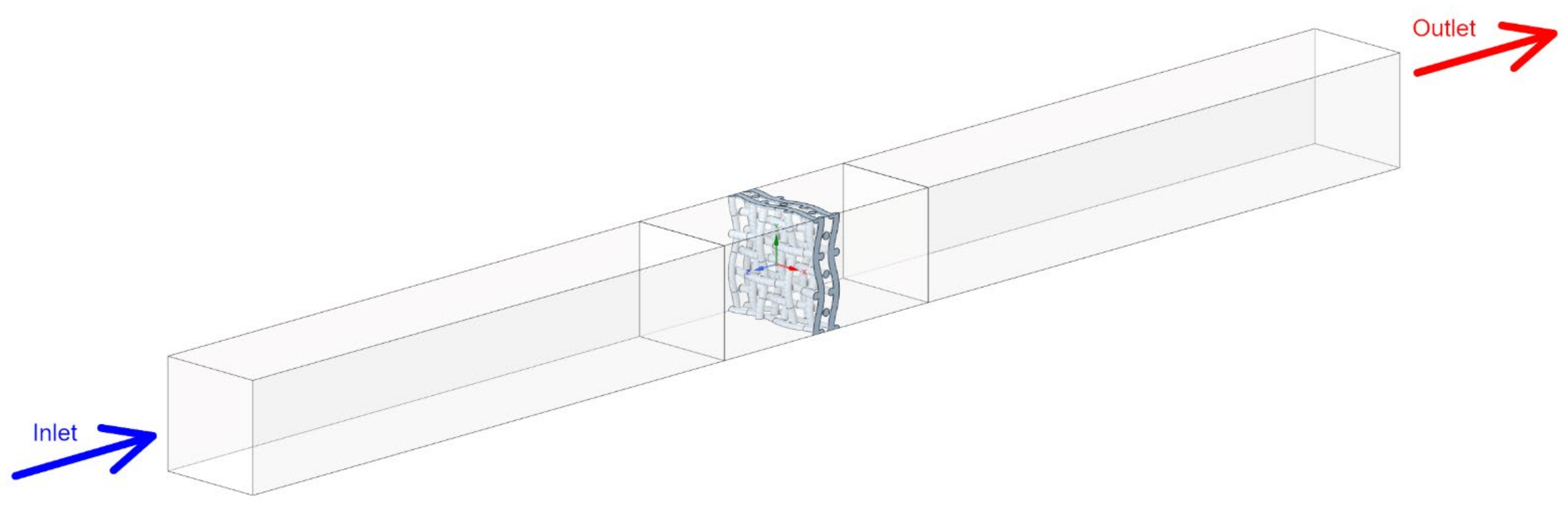
2.3. Computational Domain
2.4. Continuous Phase Modelling
2.5. Reaction Kinetics
2.6. Discrete Phase Modelling
3. Results
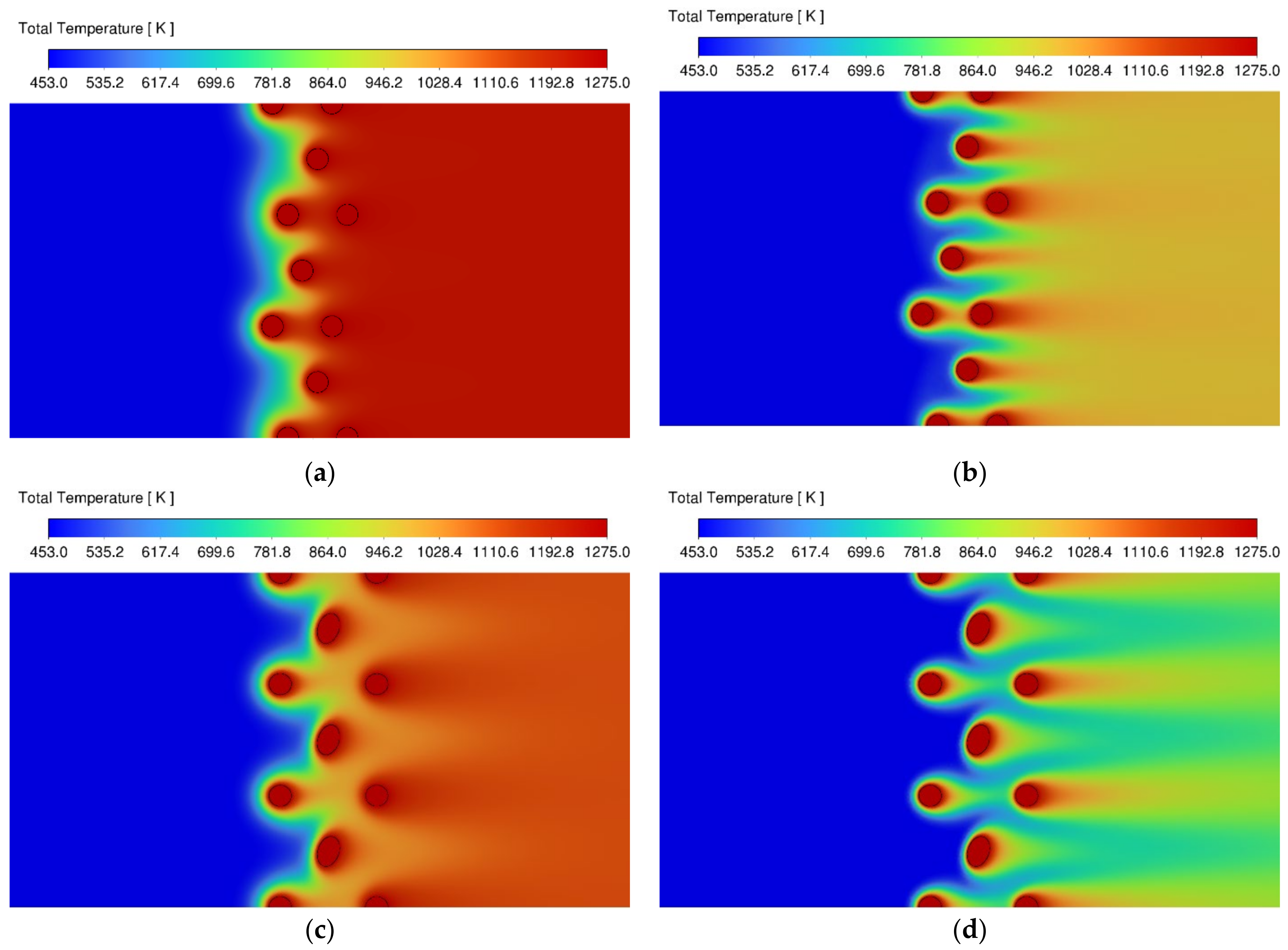
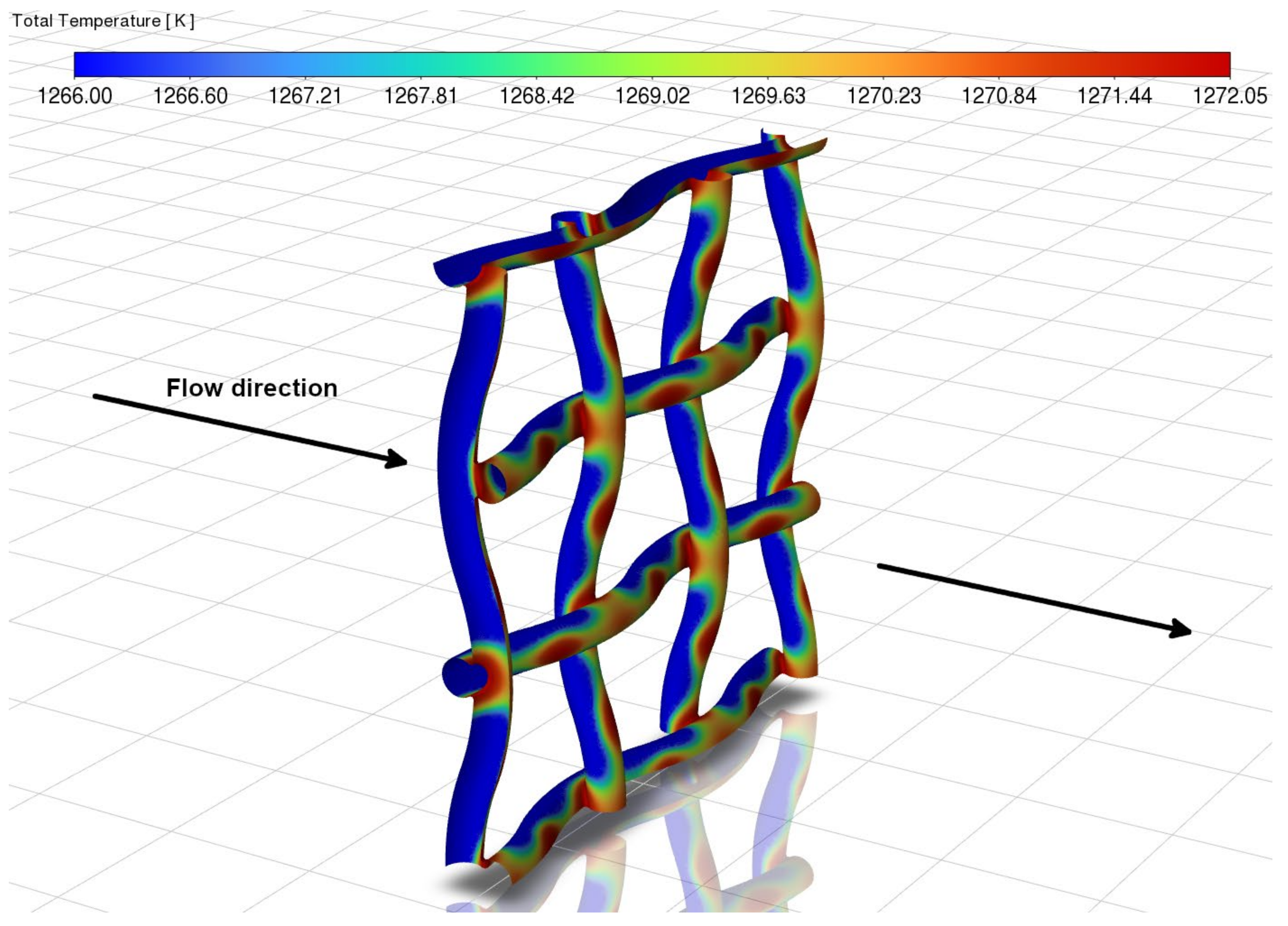
3.1. Velocity and Temperature Contours
3.2. Stagnation Areas
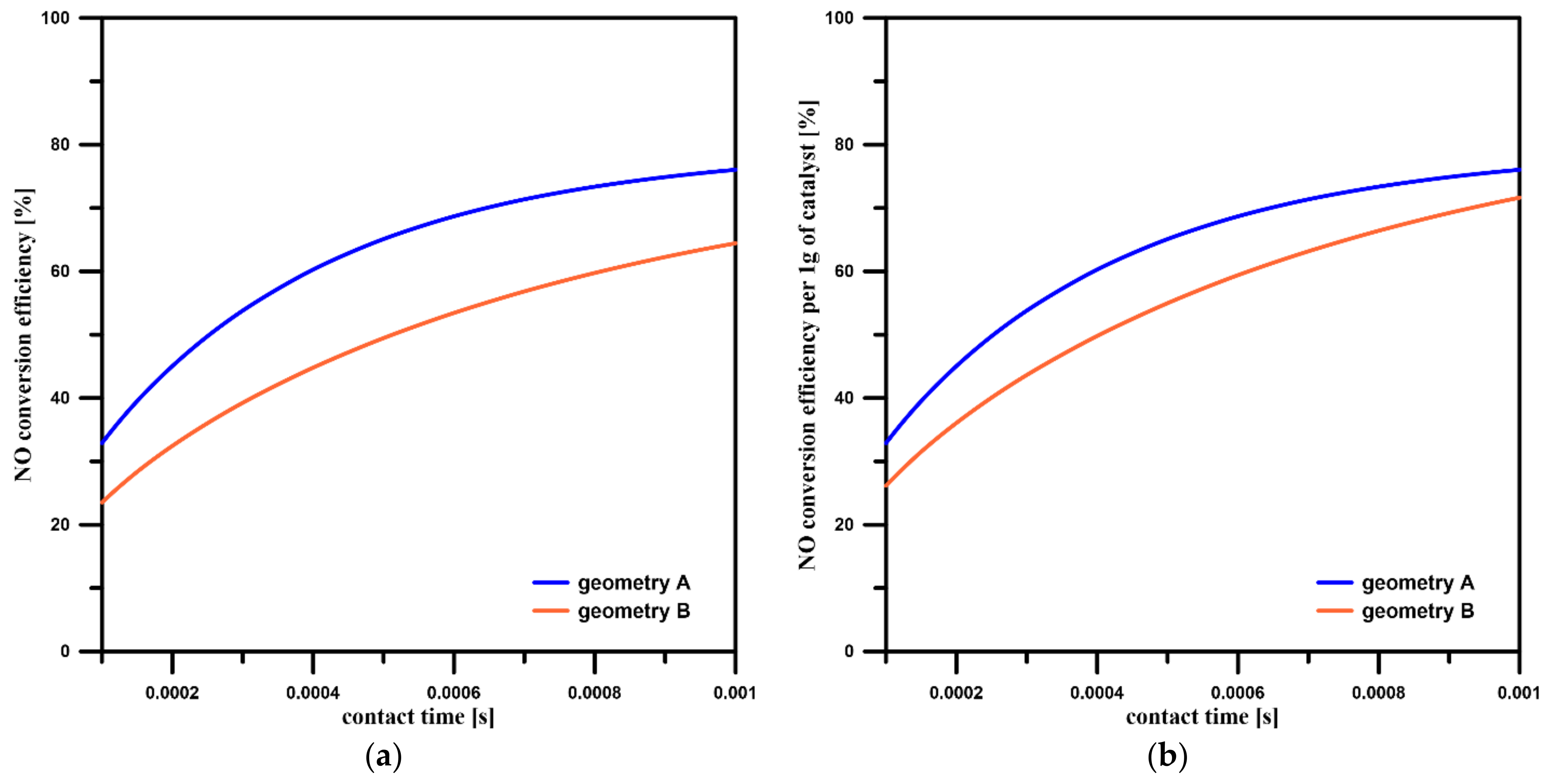
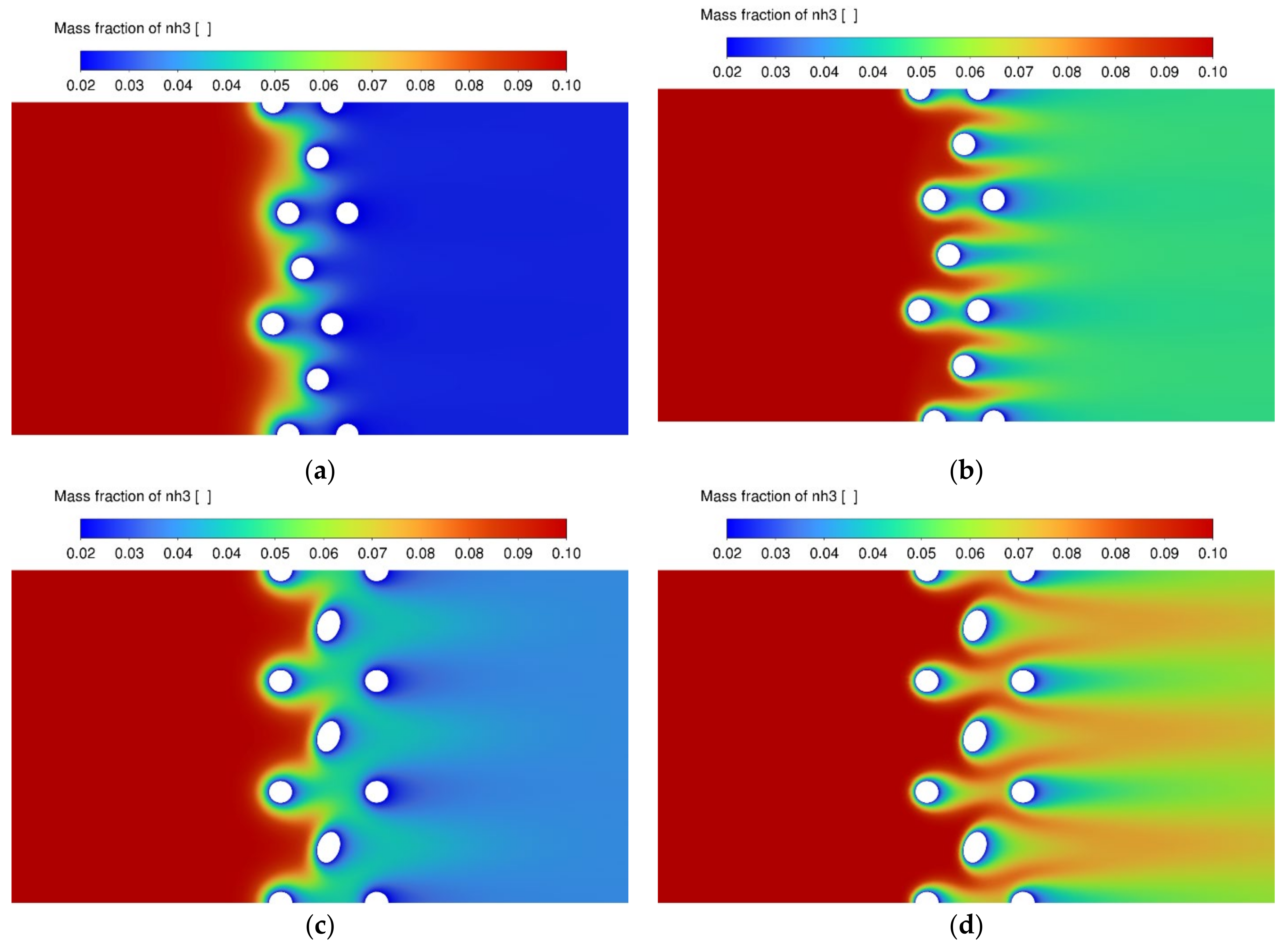
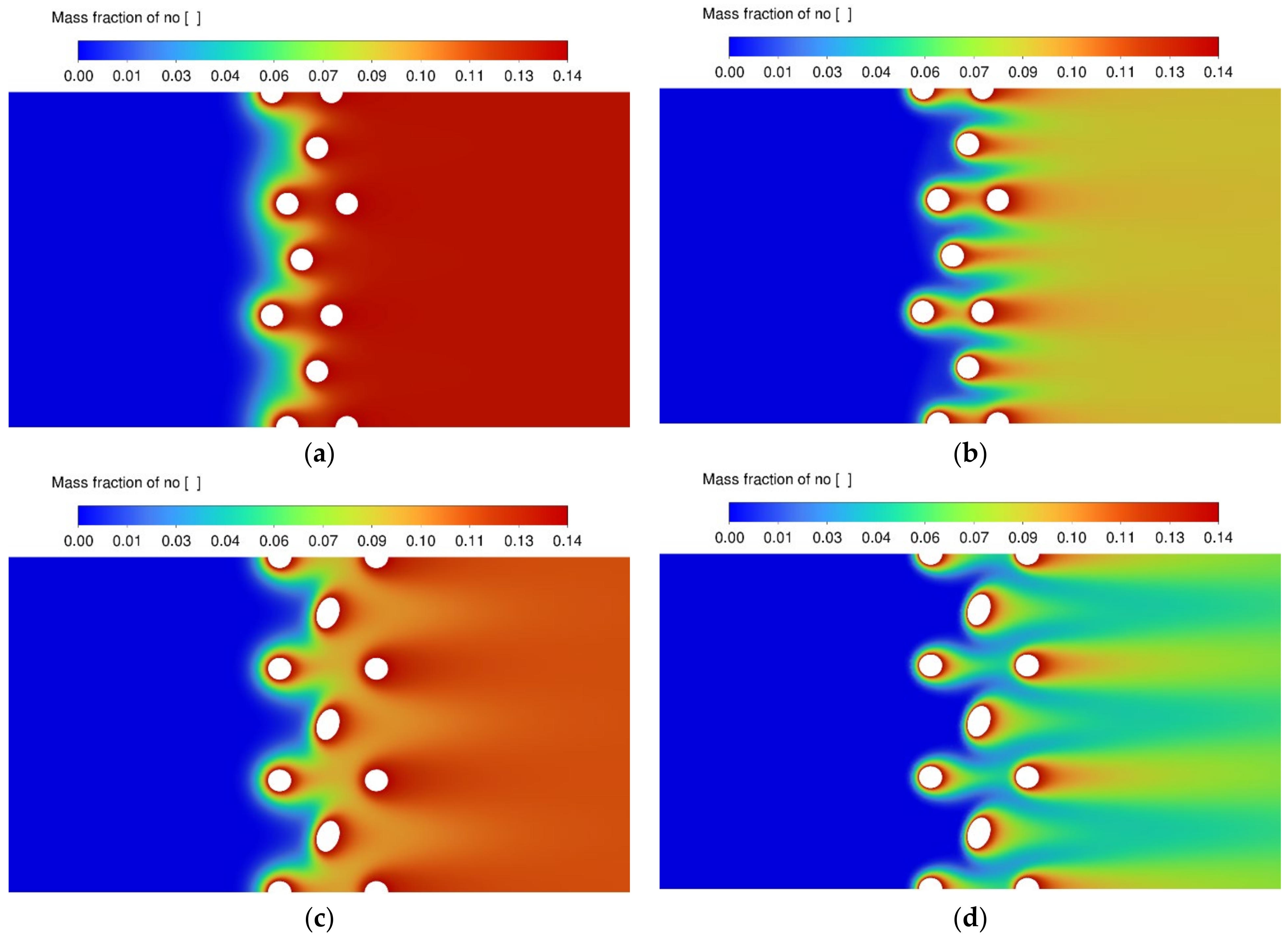
3.3. NO Conversion Efficiency and Concentration Contours
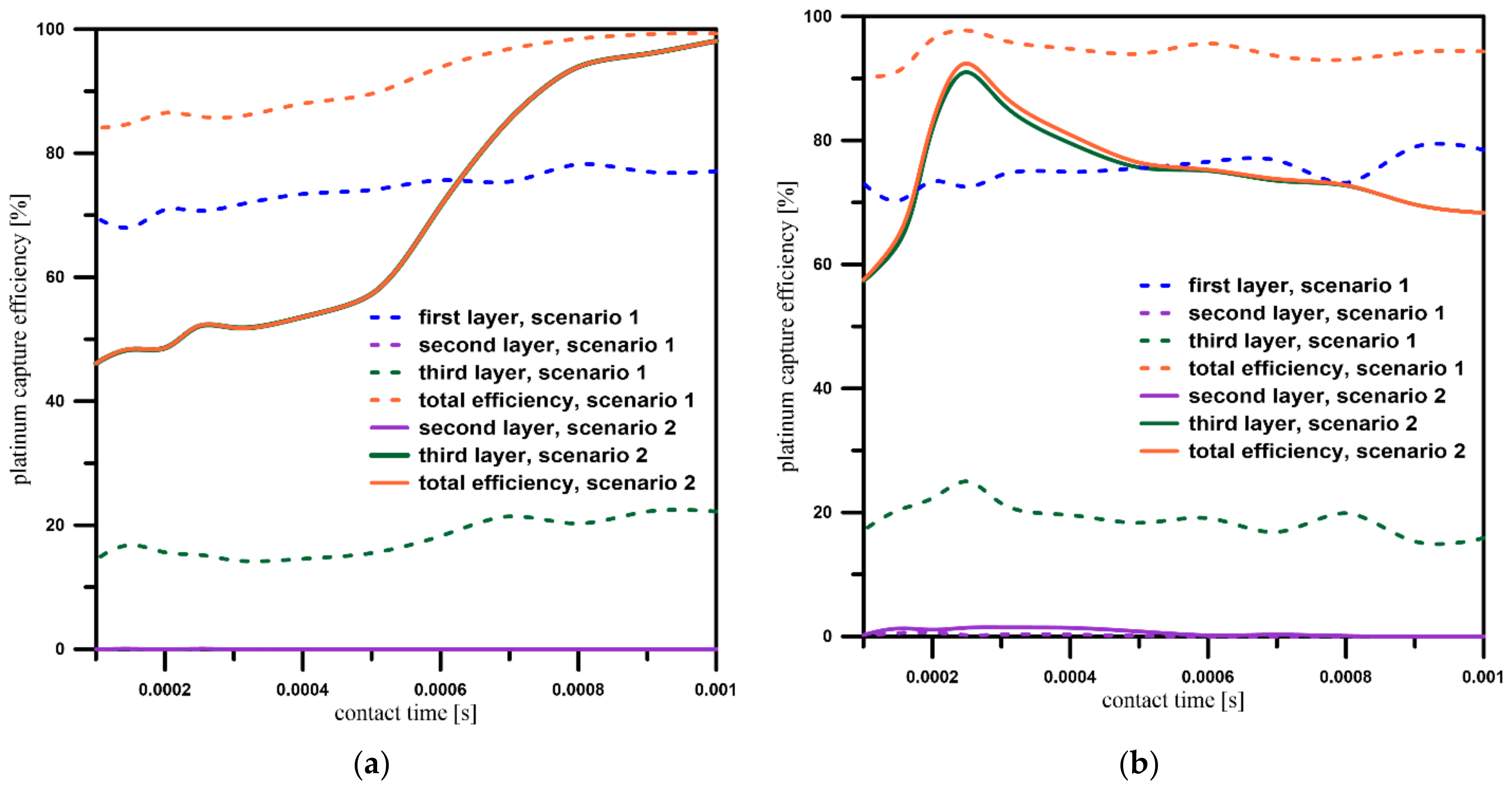
3.4. Platinum Particles’ Capture Efficiency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin symbols: | |
| Ar | pre-exponential factor, s−1 |
| C1ε, C2ε, C3ε | constants |
| ci | concentration of species i, mol m−3 |
| Di,wall | mass diffusion coefficient, m2 s−1 |
| Er | activation energy, J mol−1 |
| Gb | generation of turbulence kinetic energy due to buoyancy, kg m−1 s−2 |
| Gk | generation of turbulence kinetic energy due to the mean velocity gradients, kg m−1 s−2 |
| [Gi]wall | molar concentration of surface-adsorbed species |
| H | catalyst gauze height, m |
| I | unit tensor |
| diffusion flux of species i, kg m−2 s−1 | |
| k | reaction rate constant, s−1 |
| k | turbulent kinetic energy, m2 s−2 |
| MNH3 | molar mass of NH3, kg mol−1 |
| MNO | molar mass of NO3, kg mol−1 |
| Mw,i | molecular weight, kg mol−1 |
| net rate of mass deposition as a result of the surface reaction | |
| Ng | number of gas species |
| Ns | number of site species |
| NPt | number of tracked platinum particles |
| NPt_loss | number of lost platinum particles |
| p | pressure, Pa |
| R | universal gas constant, J mol−1 K−1 |
| Ri | net rate of production of species i by chemical reaction |
| rate of reaction in the gas phase | |
| rate of reaction on the catalyst surface | |
| rate of reaction in the bulk phase | |
| r | reaction rate, mol m−3 s−1 |
| Si | rate of creation of species i by addition from the dispersed phase plus any user-defined sources |
| [Si]wall | molar concentration of site species |
| T | temperature, K |
| t | contact time, s |
| t | time, s |
| ui | continuous phase velocity, m s−1 |
| average fluctuation of continuous phase velocity, m s−1 | |
| v | average velocity between wires, m s−1 |
| overall velocity vector, m s−1 | |
| xi, xj | computational domain dimensions, m |
| XNH3_in | mass fraction of NH3 at the inlet |
| XNO_out | mass fraction of NO at the outlet |
| Yi | local mass fraction of species i |
| Yi,wall | mass fraction at the wall of the catalyst wires |
| YM | contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate, kg m−1 s−2 |
| Zi | site coverage of species i |
| Greek symbols: | |
| α | empirical constant |
| βr | temperature exponent |
| ε | turbulent dissipation rate, m2 s−3 |
| ηr | NO conversion efficiency |
| ηPt_trap | platinum capture efficiency |
| μ | continuous phase dynamic viscosity, Pa·s |
| μt | continuous phase turbulent viscosity, Pa·s |
| ν | continuous phase kinematic viscosity, m2 s−1 |
| ρ | continuous phase density, kg m−3 |
| ρsite | site density, kg m−3 |
| ρwall | wall phase density, kg m−3 |
| σk | turbulent Prandtl number for k |
| σε | turbulent Prandtl number for ε |
| Acronyms: | |
| CFD | Computational Fluid Dynamics |
| DPM | Discrete Phase Model |
| SIMPLE | Semi-Implicit Method for Pressure Linked Equations |
References
- Hoque, A.; Mohiuddin, M.; Su, Z. Effects of Industrial Operations on Socio-Environmental and Public Health Degradation: Evidence from a Least Developing Country (LDC). Sustainability 2018, 10, 3948. [Google Scholar] [CrossRef] [Green Version]
- Klumpp, A.; Domingos, M.; Klumpp, G. Assessment of the vegetation risk by fluoride emissions from fertiliser industries at CubaGo, Brazil. Sci. Total Environ. 1996, 10, 219–228. [Google Scholar] [CrossRef]
- Roser, M.; Ritchie, H. Hunger and Undernourishment. Available online: https://ourworldindata.org/hunger-and-undernourishment (accessed on 14 September 2022).
- Warner, M. The Kinetics of Industrial Ammonia Combustion. Ph.D. Thesis, The University of Sydney, Sydney, Australia, 2013. [Google Scholar]
- Aparicio, L.M.; Dumesic, J.A. Ammonia synthesis kinetics: Surface chemistry, rate expressions, and kinetic analysis. Top. Catal. 1994, 1, 233–252. [Google Scholar] [CrossRef]
- Kraehnert, R.; Baerns, M. Kinetics of ammonia oxidation over Pt foil studied in a micro-structured quartz-reactor. Chem. Eng. J. 2008, 137, 361–375. [Google Scholar] [CrossRef] [Green Version]
- Rafti, M.; Vicente, J.L.; Albesa, A.; Scheibe, A.; Imbihl, R. Modeling ammonia oxidation over a Pt (533) surface. Surf. Sci. 2012, 606, 12–20. [Google Scholar] [CrossRef]
- Otomo, J.; Koshi, M.; Mitsumori, T.; Iwasaki, H.; Yamada, K. Chemical kinetic modeling of ammonia oxidation with improved reaction mechanism for ammonia/air and ammonia/hydrogen/air combustion. Int. J. Hydrog. Energy 2018, 43, 3004–3014. [Google Scholar] [CrossRef]
- Scheuer, A.; Votsmeier, M.; Schuler, A.; Gieshoff, J.; Drochner, A.; Vogel, H. NH3-Slip Catalysts: Experiments Versus Mechanistic Modelling. Top. Catal. 2009, 52, 1847–1851. [Google Scholar] [CrossRef]
- Hickman, D.A.; Schmidt, L.D. Modeling catalytic gauze reactors: Ammonia oxidation. Ind. Eng. Chem. Res. 1991, 30, 50–55. [Google Scholar] [CrossRef]
- Novell-Leruth, G.; Ricart, J.M.; Pérez-Ramírez, J. Pt (100)-Catalyzed Ammonia Oxidation Studied by DFT: Mechanism and Microkinetics. J. Phys. Chem. C 2008, 112, 13554–13562. [Google Scholar] [CrossRef]
- Haas, M.; Nien, T.-W.; Fadic, A.; Mmbaga, J.P.; Klingenberger, M.; Born, D.; Etzold, B.J.M.; Hayes, R.; Votsmeier, M. N2O selectivity in industrial NH3 oxidation on Pt-gauze is determined by interaction of local flow and surface chemistry: A simulation study using mechanistic kinetics. Chem. Eng. Sci. 2022, 260, 117832. [Google Scholar] [CrossRef]
- Haas, M.; Wiser, A.; Drochner, A.; Hasse, C.; Etzold, B.J.M.; Votsmeier, M. Multiscale CFD Model for the Catalyzed Ammonia Oxidation: From a Detailed Surface Kinetic Model to an Industrial Reactor. In Proceedings of the 25th International Conference on Chemical Reaction Engineering, ISCRE25, Florence, Italy, 20–23 May 2018. [Google Scholar]
- Pottbacker, J.; Jakobtorweihen, S.; Behnecke, A.S.; Abdullah, A.; Özdemir, M.; Warner, M.; Menon, M.; Bujalski, J.M.; Waller, D.; Korup, O.; et al. Resolving gradients in an ammonia oxidation reactor under industrial conditions: A combined experimental and simulation study. Chem. Eng. J. 2022, 439, 135350. [Google Scholar] [CrossRef]
- Wiser, A. Investigation of the Industrial NH3 Oxidation by CFD Simulations including Detailed Surface Kinetics. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2020. [Google Scholar]
- McCabe, A.R.; Smith, G.D.W. The Mechanism of Reconstruction of Rhodium-Platinum Catalyst Gauzes. Platin. Met. Rev. 1986, 30, 54–62. [Google Scholar]
- Pura, J.; Wieciński, P.; Kwaśniak, P.; Zwolińska, M.; Garbacz, H.; Zdunek, J.; Laskowski, Z.; Gierej, M. Investigation of the degradation mechanism of catalytic wires during oxidation of ammonia process. Appl. Surf. Sci. 2016, 388, 670–677. [Google Scholar] [CrossRef]
- Pura, J.; Kwaśniak, P.; Wiecinski, P.; Garbacz, H.; Zdunek, J.; Laskowski, Z.; Gierej, M. Investigation of the Degradation Mechanism of Platinum-Rhodium Catalytic Wires during Oxidation of Ammonia Process. Solid State Phenom. 2015, 227, 229–232. [Google Scholar] [CrossRef]
- Bobrownicki, W.; Pawlikowski, S. Otrzymywanie rozcieńczonego kwasu azotowego. In Technologia Związków Azotowych; Wydawnictwa Naukowo-Techniczne WNT: Warszawa, Poland, 1974; pp. 197–214. [Google Scholar]
- Thiemann, M.; Scheibler, E.; Wiegand, K.W. Nitric Acid, Nitrous Acid, and Nitrogen Oxides. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2000; Volume 24, pp. 177–225. ISBN 978-3-527-30673-2. [Google Scholar]
- Handforth, S.L.; Tilley, J.N. Catalysts for Oxidation of Ammonia to Oxides of Nitrogen. Ind. Eng. Chem. 1934, 26, 1287–1292. [Google Scholar] [CrossRef]
- Hatscher, S.T.; Fetzer, T.; Wagner, E.; Kneuper, H.-J. Ammonia Oxidation. In Handbook of Heterogeneous Catalysis, 8 Volume Set, 2nd ed.; Wiley: New York, NY, USA, 2008; Volume 5, pp. 2575–2592. ISBN 978-3-527-31241-2. [Google Scholar]
- Ansys® Fluent, Release 2021 R2, Help System, Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2021.
- Bortel, E.; Konieczny, H. Otrzymywanie kwasu azotowego. In Zarys Technologii Chemicznej; Wydawnictwo Naukowe PWN: Warszawa, Poland, 1992; pp. 534–550. ISBN 978-83-01-09944-2. [Google Scholar]
- Bentsen, P.C. Kinetics of Low Temperature Oxidation of Ammonia Trace Quantities. Ph.D. Thesis, Texas Tech University, Lubbock, TX, USA, 1973. [Google Scholar]
- Makowski, Ł.; Łaskowski, J.; Tyrański, M. Influence of Modification of the Geometry of the Wave-Plate Mist Eliminators on the Droplet Removal Efficiency—CFD Modelling. Processes 2021, 9, 1499. [Google Scholar] [CrossRef]



| Species Name | Concentration (Mass Fractions) |
|---|---|
| NH3 | 0.1 |
| O2 | 0.19 |
| N2 | 0.71 |
| Name | Wire Diameter [mm] | 1st and 3rd Layer Mesh Size [mm] | 2nd Layer Mesh Size [mm] | 2nd Layer Angle Relative to the 1st and 3rd Layers | 2nd Layer Shift Relative to the 1st and 3rd Layers [mm] |
|---|---|---|---|---|---|
| A | 0.06 | 0.3 × 0.3 | 0.3 × 0.3 | 90° | 0.15; two axes |
| B | 0.06 | 0.3 × 0.3 | 0.42 × 0.42 | 45° | 0.15; two axes |
| Name | Value | Source |
|---|---|---|
| contact time of gas phase with a catalyst (s) | 0.001—0.0002 | [22,24] |
| gas inlet velocity (m/s) | 0.22—3.17 | calculated, Equation (13) |
| gas inlet temperature (K) | 453 | [12] |
| operating pressure (bar) | 5 | [22] |
| Symbol | Name | Unit | Value | Source |
|---|---|---|---|---|
| E | activation energy | J mol−1 | 6.28·104 | [19] |
| A | pre-exponential factor | s−1 | 5·1011 | [4] |
| α | empirical constant | - | 0.69 | [25] |
| Geometry | Contact Time [s] | Platinum Capture Efficiency [%] |
|---|---|---|
| A | 0.001 | 98.10% |
| A | 0.00025 | 52.20% |
| B | 0.001 | 68.34% |
| B | 0.00025 | 92,42% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tyrański, M.; Pasik, I.; Bujalski, J.M.; Orciuch, W.; Makowski, Ł. Computational Fluid Dynamics of Influence of Process Parameters and the Geometry of Catalyst Wires on the Ammonia Oxidation Process and Degradation of the Catalyst Gauze. Energies 2022, 15, 8123. https://doi.org/10.3390/en15218123
Tyrański M, Pasik I, Bujalski JM, Orciuch W, Makowski Ł. Computational Fluid Dynamics of Influence of Process Parameters and the Geometry of Catalyst Wires on the Ammonia Oxidation Process and Degradation of the Catalyst Gauze. Energies. 2022; 15(21):8123. https://doi.org/10.3390/en15218123
Chicago/Turabian StyleTyrański, Mariusz, Izabela Pasik, Jakub Michał Bujalski, Wojciech Orciuch, and Łukasz Makowski. 2022. "Computational Fluid Dynamics of Influence of Process Parameters and the Geometry of Catalyst Wires on the Ammonia Oxidation Process and Degradation of the Catalyst Gauze" Energies 15, no. 21: 8123. https://doi.org/10.3390/en15218123
APA StyleTyrański, M., Pasik, I., Bujalski, J. M., Orciuch, W., & Makowski, Ł. (2022). Computational Fluid Dynamics of Influence of Process Parameters and the Geometry of Catalyst Wires on the Ammonia Oxidation Process and Degradation of the Catalyst Gauze. Energies, 15(21), 8123. https://doi.org/10.3390/en15218123








