Approximating Shading Ratio Using the Total-Sky Imaging System: An Application for Photovoltaic Systems
Abstract
:1. Introduction
2. Aim of This Work
3. Experimental Setup
4. Methods
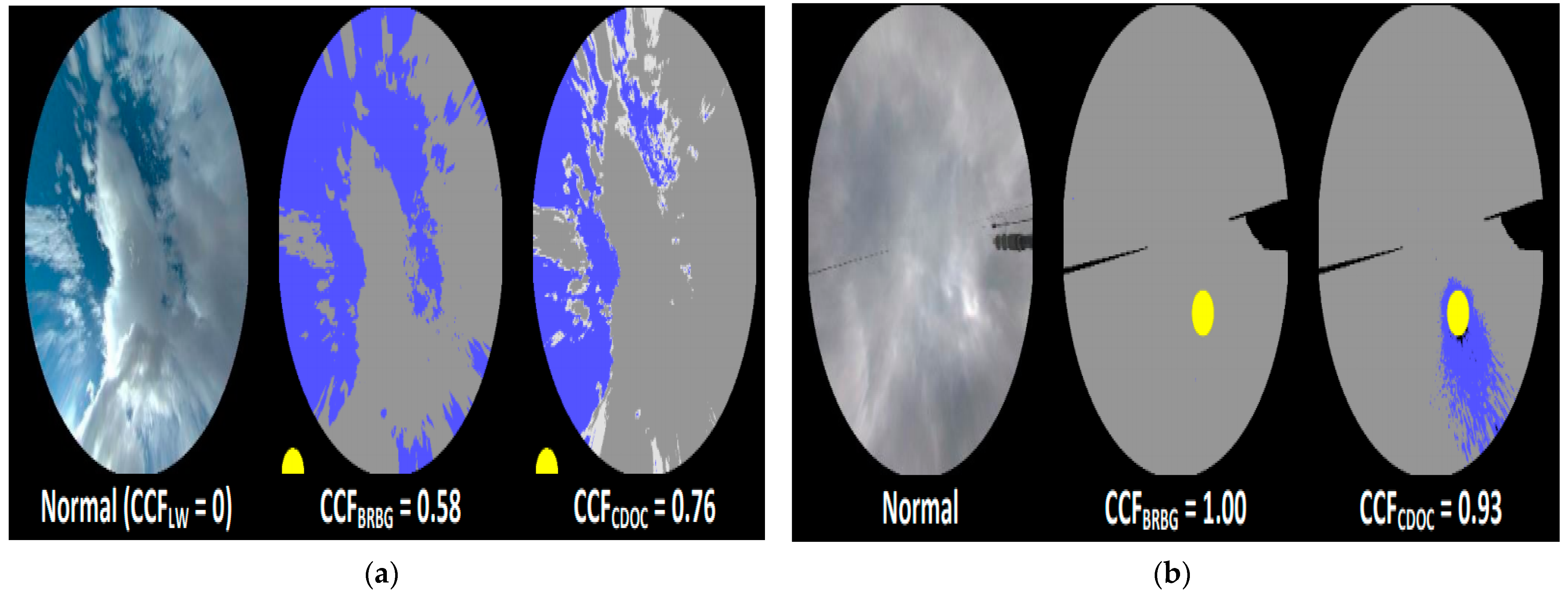
4.1. Cloud Decision Algorithm
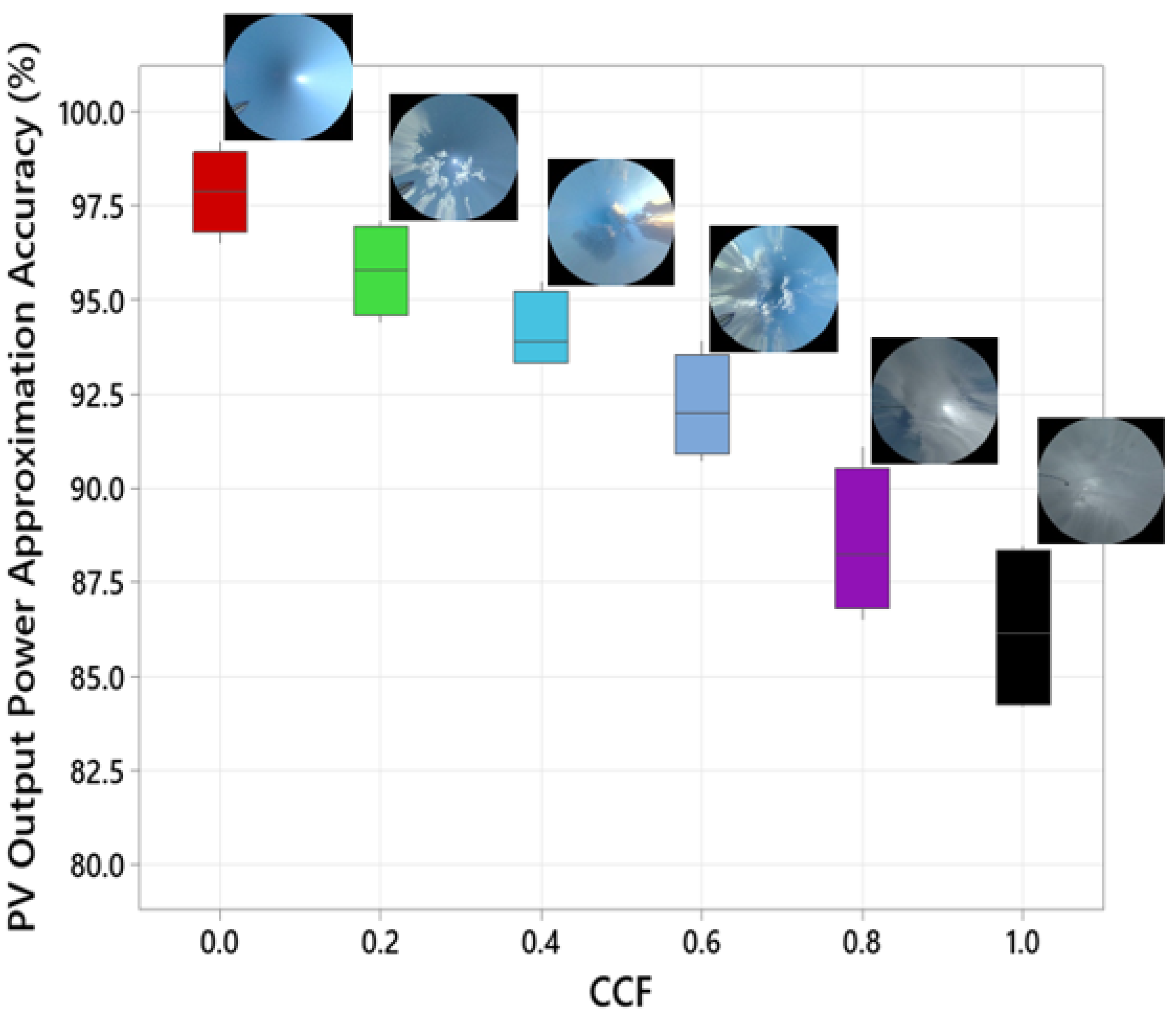
4.2. Cloud Cover Fraction Approximation
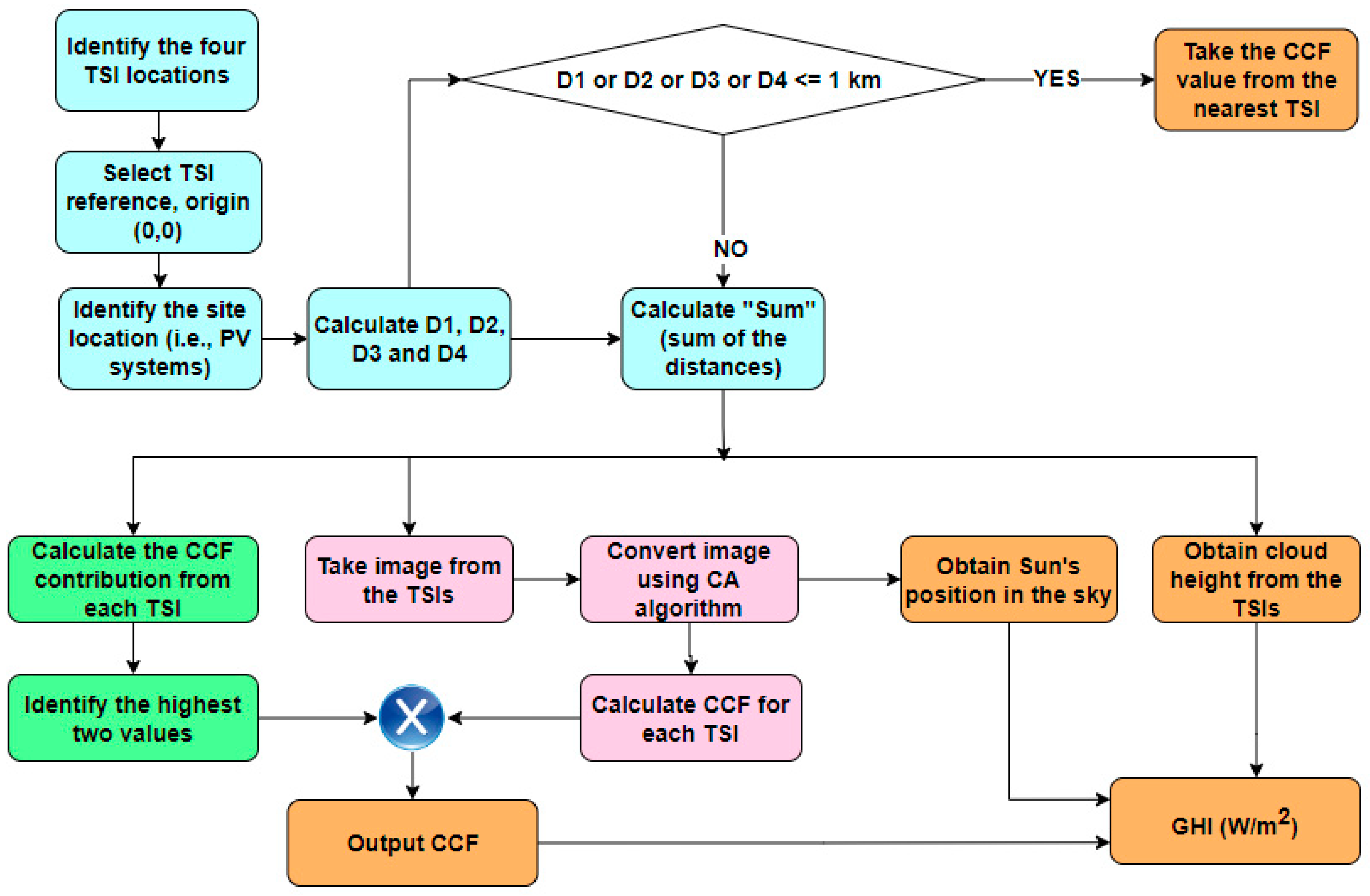
4.3. Shading Ratio Approximation Flowcode
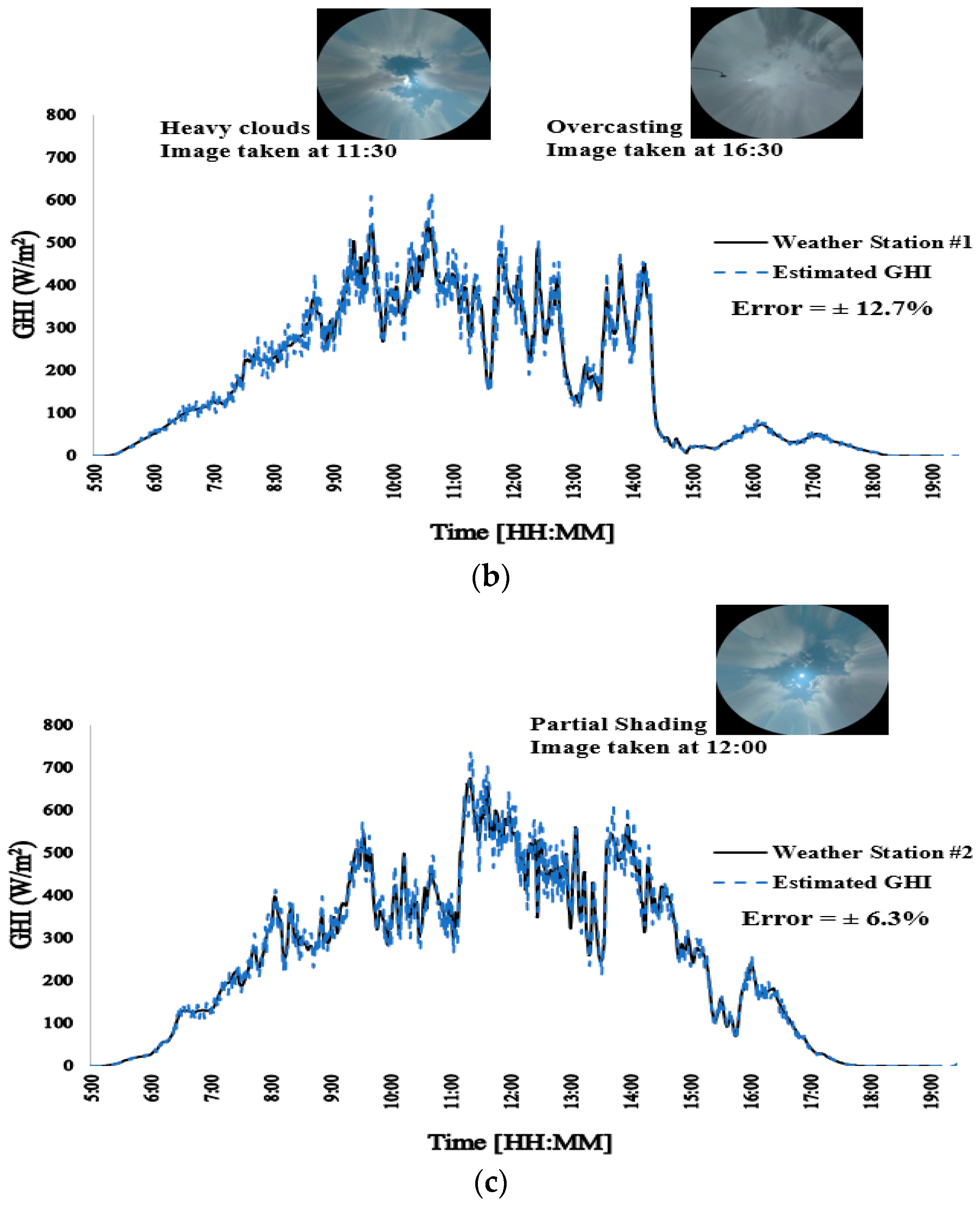
5. Results
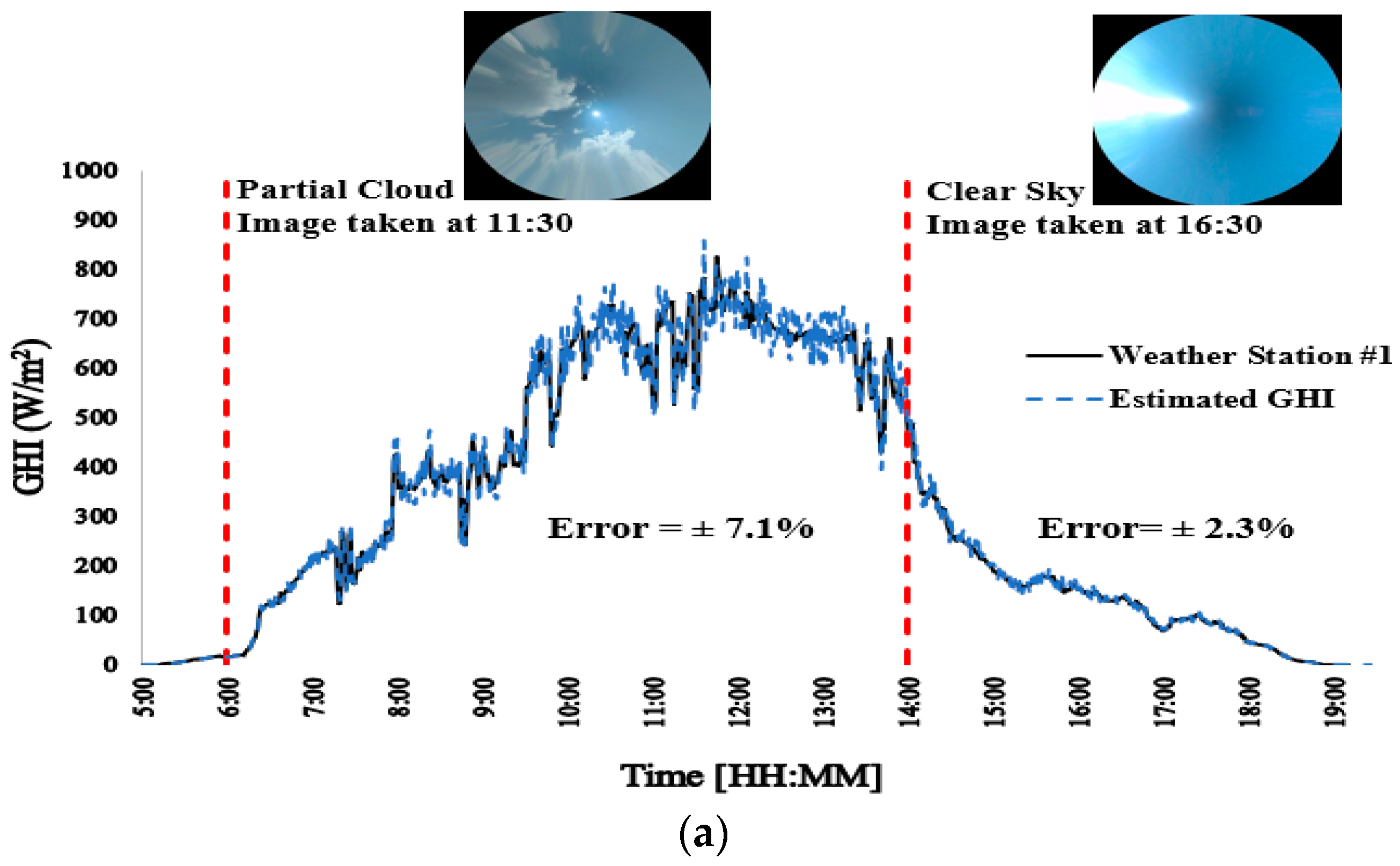
5.1. Accuracy of the Proposed Shading Ratio Approximation Technique
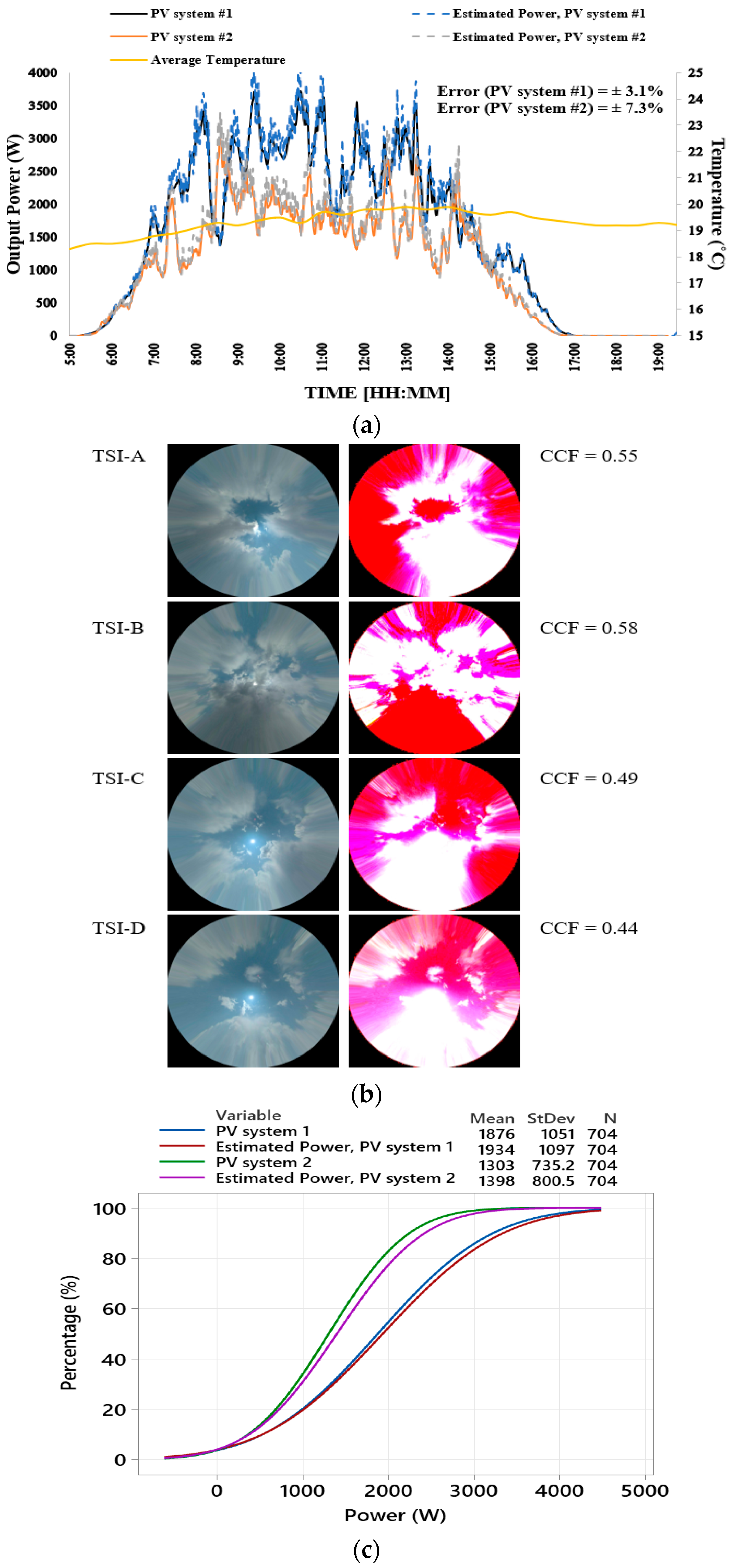
5.2. Estimating the Output Power of PV Systems
- Weather stations are no longer needed.
- It can predict the shade in relatively large areas (in our case, 25 km2).
- If a high variance is found between the estimated PV power vs the actual measured power in the PV system, a fault identification can be reported.
6. Comparative Study
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PV | photovoltaic |
| CA | color-adjusted |
| GHI | global horizontal irradiance |
| TSI | total-sky imagers |
| ANN | artificial neural network |
| I-V | current-voltage |
| MPPT | maximum power point tracking |
| LSTM | long short-term memory |
| BRBG | blue/red-plus-blue/green-ratio algorithm |
| CDOC | cloud-detection and opacity classification algorithm |
| CCF | cloud cover fraction |
| CDF | cumulative density function |
| StDev | standard deviation |
| CNN | convolutional neural network |
| LM-BP | Levenberg–Marquardt backpropagation |
References
- Su, H.Y.; Liu, T.Y.; Hong, H.H. Adaptive residual compensation ensemble models for improving solar energy generation forecasting. IEEE Trans. Sustain. Energy 2019, 11, 1103–1105. [Google Scholar] [CrossRef]
- Bochenek, B.; Ustrnul, Z. Machine learning in weather prediction and climate analyses—Applications and perspectives. Atmosphere 2022, 13, 180. [Google Scholar] [CrossRef]
- Yang, D.; Wang, W.; Hong, T. A historical weather forecast dataset from the European Centre for Medium-Range Weather Forecasts (ECMWF) for energy forecasting. Sol. Energy 2022, 232, 263–274. [Google Scholar] [CrossRef]
- Zhen, Z.; Zhang, X.; Mei, S.; Chang, X.; Chai, H.; Yin, R.; Wang, F. Ultra-short-term irradiance forecasting model based on ground-based cloud image and deep learning algorithm. IET Renew. Power Gener. 2022, 16, 2604–2616. [Google Scholar] [CrossRef]
- Lee, S.; Kim, G.; Lee, M.I.; Choi, Y.; Song, C.K.; Kim, H.K. Seasonal Dependence of Aerosol Data Assimilation and Forecasting Using Satellite and Ground-Based Observations. Remote Sens. 2022, 14, 2123. [Google Scholar] [CrossRef]
- Yang, D.; Perez, R. Can we gauge forecasts using satellite-derived solar irradiance? J. Renew. Sustain. Energy 2019, 11, 023704. [Google Scholar] [CrossRef]
- Deif, M.A.; Solyman, A.A.; Alsharif, M.H.; Jung, S.; Hwang, E. A hybrid multi-objective optimizer-based SVM model for enhancing numerical weather prediction: A study for the Seoul metropolitan area. Sustainability 2021, 14, 296. [Google Scholar] [CrossRef]
- Yang, H.; Kurtz, B.; Nguyen, D.; Urquhart, B.; Chow, C.W.; Ghonima, M.; Kleissl, J. Solar irradiance forecasting using a ground-based sky imager developed at UC San Diego. Sol. Energy 2014, 103, 502–524. [Google Scholar] [CrossRef]
- Nouri, B.; Wilbert, S.; Segura, L.; Kuhn, P.; Hanrieder, N.; Kazantzidis, A.; Schmidt, T.; Zarzalejo, L.; Blanc, F.; Pitz-Paal, R. Determination of cloud transmittance for all sky imager based solar nowcasting. Sol. Energy 2019, 181, 251–263. [Google Scholar] [CrossRef] [Green Version]
- Kong, W.; Jia, Y.; Dong, Z.Y.; Meng, K.; Chai, S. Hybrid approaches based on deep whole-sky-image learning to photovoltaic generation forecasting. Appl. Energy 2020, 280, 115875. [Google Scholar] [CrossRef]
- Zhen, Z.; Liu, J.; Zhang, Z.; Wang, F.; Chai, H.; Yu, Y.; Lu, X.; Wang, T.; Lin, Y. Deep learning based surface irradiance mapping model for solar PV power forecasting using sky image. IEEE Trans. Ind. Appl. 2020, 56, 3385–3396. [Google Scholar] [CrossRef]
- Nouri, B.; Blum, N.; Wilbert, S.; Zarzalejo, L.F. A hybrid solar irradiance nowcasting approach: Combining all sky imager systems and persistence irradiance models for increased accuracy. Sol. RRL 2022, 6, 2100442. [Google Scholar] [CrossRef]
- Eşlik, A.H.; Akarslan, E.; Hocaoğlu, F.O. Cloud Motion Estimation with ANN for Solar Radiation Forecasting. In Proceedings of the 2021 International Congress of Advanced Technology and Engineering (ICOTEN), Taiz, Yemen, 4–5 July 2021; pp. 1–5. [Google Scholar]
- Dhimish, M. 70% decrease of hot-spotted photovoltaic modules output power loss using novel MPPT algorithm. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 2027–2031. [Google Scholar]
- Guerra, M.I.; Ugulino de Araújo, F.M.; Dhimish, M.; Vieira, R.G. Assessing maximum power point tracking intelligent techniques on a pv system with a buck–boost converter. Energies 2021, 14, 7453. [Google Scholar] [CrossRef]
- Dhimish, M. Assessing MPPT techniques on hot-spotted and partially shaded photovoltaic modules: Comprehensive review based on experimental data. IEEE Trans. Electron Devices 2019, 66, 1132–1144. [Google Scholar] [CrossRef] [Green Version]
- Aslam, A.; Ahmed, N.; Qureshi, S.A.; Assadi, M.; Ahmed, N. Advances in Solar PV Systems; A Comprehensive Review of PV Performance, Influencing Factors, and Mitigation Techniques. Energies 2022, 15, 7595. [Google Scholar] [CrossRef]
- Van Noord, M.; Landelius, T.; Andersson, S. Snow-Induced PV Loss Modeling Using Production-Data Inferred PV System Models. Energies 2021, 14, 1574. [Google Scholar] [CrossRef]
- Vieira, R.G.; de Araújo, F.M.U.; Dhimish, M.; Guerra, M.I.S. A Comprehensive Review on Bypass Diode Application on Photovoltaic Modules. Energies 2020, 13, 2472. [Google Scholar] [CrossRef]
- Muteri, V.; Cellura, M.; Curto, D.; Franzitta, V.; Longo, S.; Mistretta, M.; Parisi, M.L. Review on Life Cycle Assessment of Solar Photovoltaic Panels. Energies 2020, 13, 252. [Google Scholar] [CrossRef] [Green Version]
- Olalla, C.; Hasan, M.N.; Deline, C.; Maksimović, D. Mitigation of Hot-Spots in Photovoltaic Systems Using Distributed Power Electronics. Energies 2018, 11, 726. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Rabelo, M.; Padi, S.P.; Yousuf, H.; Cho, E.-C.; Yi, J. A Review of the Degradation of Photovoltaic Modules for Life Expectancy. Energies 2021, 14, 4278. [Google Scholar] [CrossRef]
- Dhimish, M.; Mather, P. Ultrafast high-resolution solar cell cracks detection process. IEEE Trans. Ind. Inform. 2019, 16, 4769–4777. [Google Scholar] [CrossRef] [Green Version]
- Libra, M.; Daneček, M.; Lešetický, J.; Poulek, V.; Sedláček, J.; Beránek, V. Monitoring of Defects of a Photovoltaic Power Plant Using a Drone. Energies 2019, 12, 795. [Google Scholar] [CrossRef] [Green Version]
- Goudelis, G.; Lazaridis, P.I.; Dhimish, M. A Review of Models for Photovoltaic Crack and Hotspot Prediction. Energies 2022, 15, 4303. [Google Scholar] [CrossRef]
- Li, Z.; Rahman, S.M.; Vega, R.; Dong, B. A Hierarchical Approach Using Machine Learning Methods in Solar Photovoltaic Energy Production Forecasting. Energies 2016, 9, 55. [Google Scholar] [CrossRef] [Green Version]
- Khandakar, A.; Chowdhury, M.E.H.; Kazi, M.-K.; Benhmed, K.; Touati, F.; Al-Hitmi, M.; Gonzales, A.J.S.P. Machine Learning Based Photovoltaics (PV) Power Prediction Using Different Environmental Parameters of Qatar. Energies 2019, 12, 2782. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Kim, Y.; Ferrier, N.J.; Collis, S.M.; Sankaran, R.; Beckman, P.H. Prediction of Solar Irradiance and Photovoltaic Solar Energy Product Based on Cloud Coverage Estimation Using Machine Learning Methods. Atmosphere 2021, 12, 395. [Google Scholar] [CrossRef]
- Cha, J.; Kim, M.K.; Lee, S.; Kim, K.S. Investigation of Applicability of Impact Factors to Estimate Solar Irradiance: Comparative Analysis Using Machine Learning Algorithms. Appl. Sci. 2021, 11, 8533. [Google Scholar] [CrossRef]
- Esteves, J.; Cao, Y.; da Silva, N.P.; Pestana, R.; Wang, Z. Identification of clouds using an all-sky imager. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–5. [Google Scholar]
- Pu, R.; Landry, S.; Zhang, J. Evaluation of atmospheric correction methods in identifying urban tree species with WorldView-2 imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 1886–1897. [Google Scholar] [CrossRef]
- Logothetis, S.-A.; Salamalikis, V.; Nouri, B.; Remund, J.; Zarzalejo, L.F.; Xie, Y.; Wilbert, S.; Ntavelis, E.; Nou, J.; Hendrikx, N.; et al. Solar Irradiance Ramp Forecasting Based on All-Sky Imagers. Energies 2022, 15, 6191. [Google Scholar] [CrossRef]
- Zuo, H.M.; Qiu, J.; Jia, Y.H.; Wang, Q.; Li, F.F. Ten-minute prediction of solar irradiance based on cloud detection and a long short-term memory (LSTM) model. Energy Rep. 2022, 8, 5146–5157. [Google Scholar] [CrossRef]
- Du, J.; Min, Q.; Zhang, P.; Guo, J.; Yang, J.; Yin, B. Short-term solar irradiance forecasts using sky images and radiative transfer model. Energies 2018, 11, 1107. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Fang, F.; Wang, J. Probabilistic solar irradiation forecasting based on variational Bayesian inference with secure federated learning. IEEE Trans. Ind. Inform. 2020, 17, 7849–7859. [Google Scholar] [CrossRef]
- Zhang, R.; Ma, H.; Hua, W.; Saha, T.K.; Zhou, X. Data-driven photovoltaic generation forecasting based on a Bayesian network with spatial–temporal correlation analysis. IEEE Trans. Ind. Inform. 2019, 16, 1635–1644. [Google Scholar] [CrossRef]
- Andrade, J.R.; Bessa, R.J. Improving renewable energy forecasting with a grid of numerical weather predictions. IEEE Trans. Sustain. Energy 2017, 8, 1571–1580. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Gu, Y.; Xie, Y.; Yang, R.; Zhang, Y. Solar irradiance capturing in cloudy sky days–a convolutional neural network based image regression approach. IEEE Access 2020, 8, 22235–22248. [Google Scholar] [CrossRef]
- Kumar, U.; Sahoo, B.; Chatterjee, C.; Raghuwanshi, N.S. Evaluation of simplified surface energy balance index (S-SEBI) method for estimating actual evapotranspiration in Kangsabati reservoir command using landsat 8 imagery. J. Indian Soc. Remote Sens. 2020, 48, 1421–1432. [Google Scholar] [CrossRef]
- Crisosto, C.; Hofmann, M.; Mubarak, R.; Seckmeyer, G. One-Hour Prediction of the Global Solar Irradiance from All-Sky Images Using Artificial Neural Networks. Energies 2018, 11, 2906. [Google Scholar] [CrossRef] [Green Version]
- Krinitskiy, M.; Aleksandrova, M.; Verezemskaya, P.; Gulev, S.; Sinitsyn, A.; Kovaleva, N.; Gavrikov, A. On the Generalization Ability of Data-Driven Models in the Problem of Total Cloud Cover Retrieval. Remote Sens. 2021, 13, 326. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Kamil, R.; Lee, H.-J. A Deep Learning Model to Forecast Solar Irradiance Using a Sky Camera. Appl. Sci. 2021, 11, 5049. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Monterreal, R.; Fernandez-Reche, J.; Ballestrín, J.; López, G.; Polo, J.; Barbero, F.J.; Marzo, A.; Portillo, C.; Batlles, F.J. Nowcasting System Based on Sky Camera Images to Predict the Solar Flux on the Receiver of a Concentrated Solar Plant. Remote Sens. 2022, 14, 1602. [Google Scholar] [CrossRef]

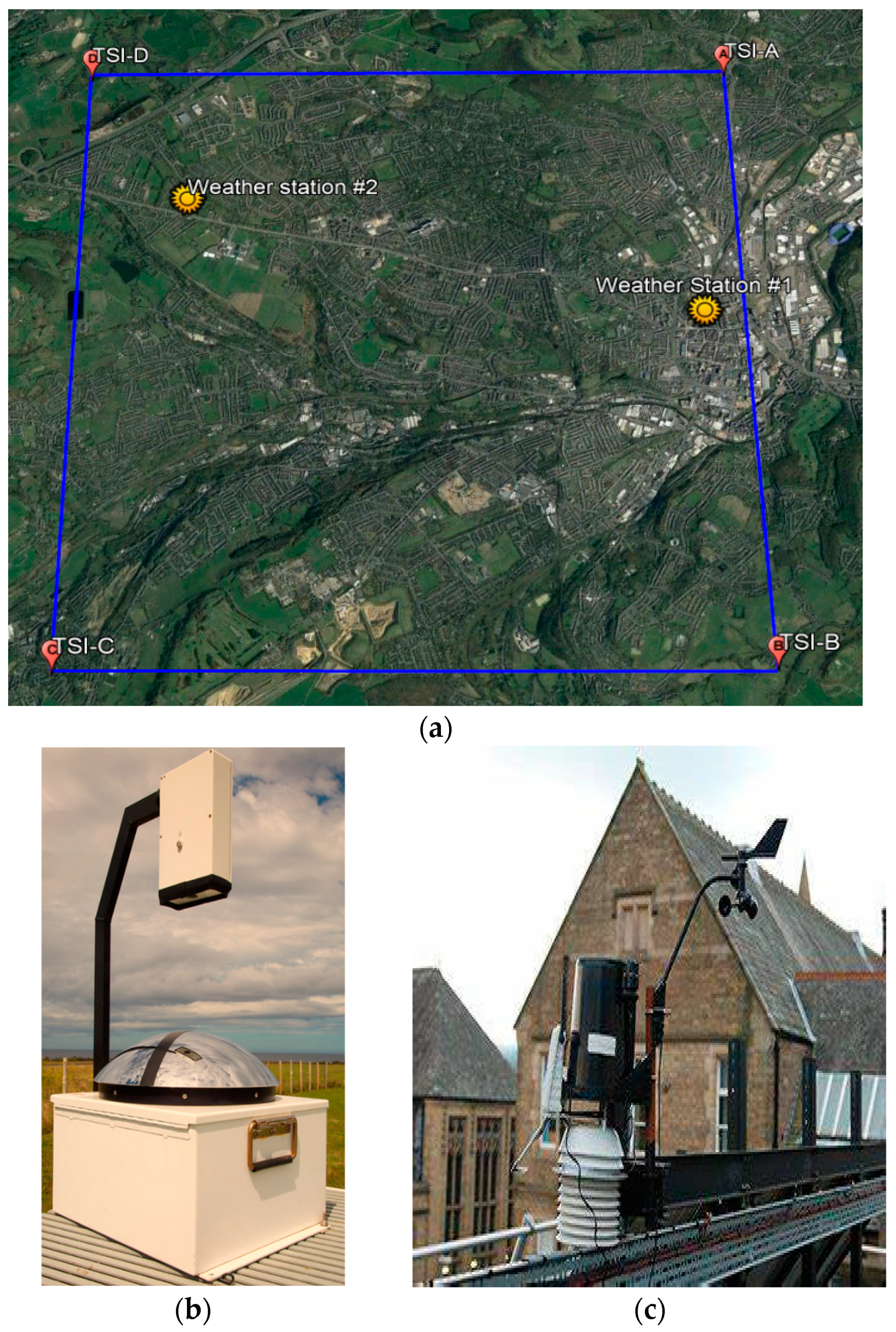


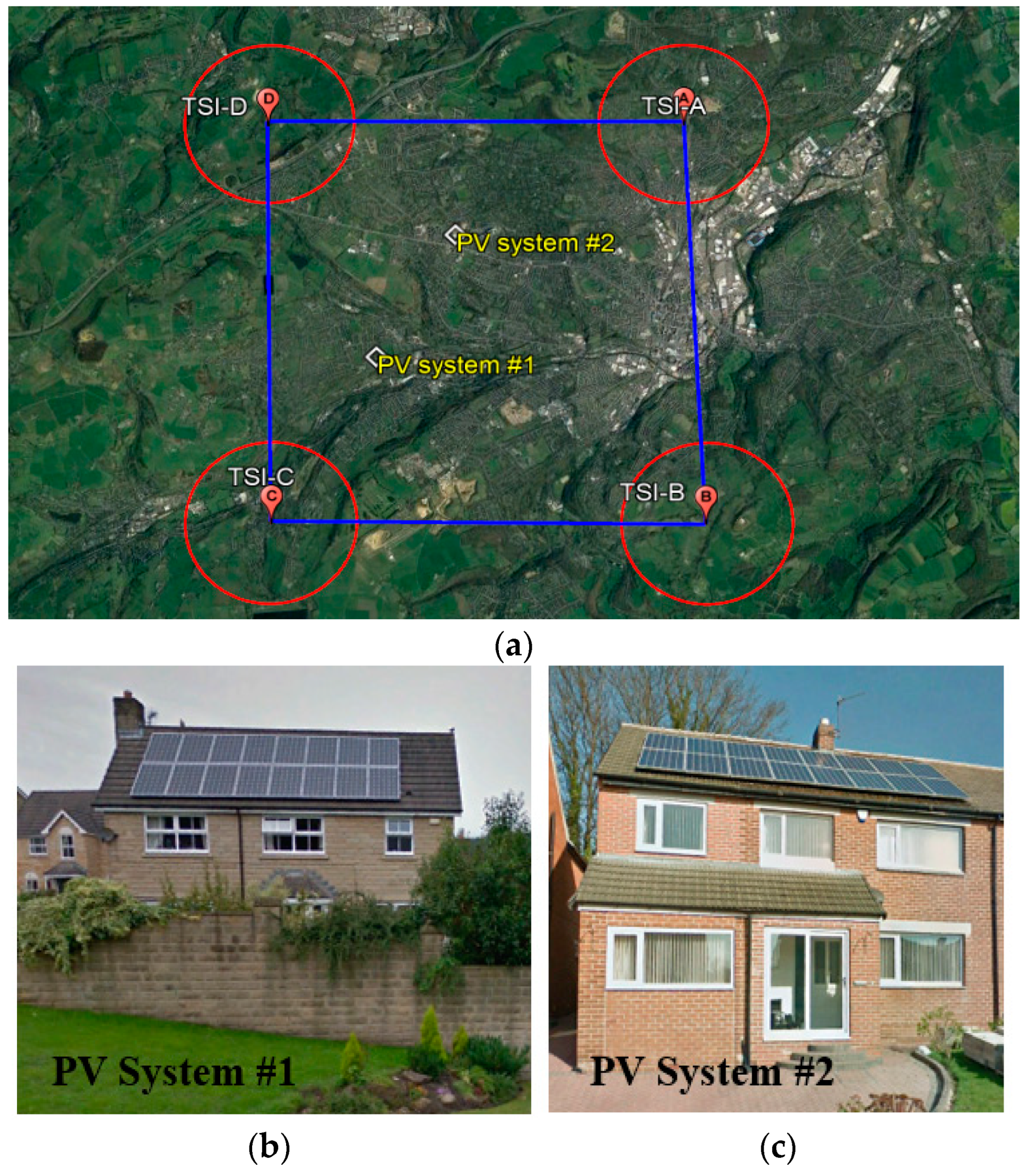
| TSI/Weather Stations | Latitude | Longitude |
|---|---|---|
| TSI-A | 53°40′1.87″ N | 1°46′51.78″ W |
| TSI-B | 53°37′20.80″ N | 1°46′39.65″ W |
| TSI-C | 53°37′22.57″ N | 1°51′14.75″ W |
| TSI-D | 53°40′3.13″ N | 1°51′18.08″ W |
| Weather Station #1 | 53°38′49.31″ N | 1°47′3.30″ W |
| Weather Station #2 | 53°39′22.65″ N | 1°50′34.38″ W |
| Weather Station | D1 (km) | D2 (km) | D3 (km) | D4 (km) | Sum (km) | CCF Contribution TSI-A | CCF Contribution TSI-B | CCF Contribution TSI-C | CCF Contribution TSI-D | Output CCF |
|---|---|---|---|---|---|---|---|---|---|---|
| #1 | 2 | 3 | 5.6 | 5.1 | 15.7 | 0.87 | 0.81 | 0.64 | 0.68 | 0.50 |
| #2 | 4.3 | 5.8 | 4.1 | 1.3 | 15.5 | 0.72 | 0.63 | 0.74 | 0.92 | 0.59 |
| Item | [40] | [41] | [42] | [43] | This Work |
|---|---|---|---|---|---|
| Month/Year of Study | October 2018 | January 2021 | May 2021 | March 2022 | Novemebr 2022 |
| Desctiption of the proposed approximation shading ratio technique | Predicting GHI using feed-forward neural network with Levenberg–Marquardt backpropagation (LM-BP) | Total cloud cover optimization using convolutional neural networks (CNN) | Estimation of 10 min ahead of solar irradiance using long short-term memory (LSTM) algorithm | Predicting the irradiance at the solar-field level using minute-by-minute images taken with a TSI | Using the images of four TSIs and converting the images using the proposed cloud approximation model |
| GHI Estimation | Included | Excluded | Included | Included | Included |
| Method disadvantages | The algorithm does not accurately predict one hour ahead for low irradiation levels under 80–100 W/m2 | No estimation of the cloud base height, and the algorithm is unautomated for cloud cover identification | There are no details on the total GHI prediction area covered. n addition, it is unclear how low irradiance levels affect the accuracy of the algorithm | The algorithm lack the ability to detect atmospheric attenuation, which resulted in high prediction errors in some instances | If the area is increased, a reduction of the shading approximation accuracy is expected |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhimish, M.; Lazaridis, P.I. Approximating Shading Ratio Using the Total-Sky Imaging System: An Application for Photovoltaic Systems. Energies 2022, 15, 8201. https://doi.org/10.3390/en15218201
Dhimish M, Lazaridis PI. Approximating Shading Ratio Using the Total-Sky Imaging System: An Application for Photovoltaic Systems. Energies. 2022; 15(21):8201. https://doi.org/10.3390/en15218201
Chicago/Turabian StyleDhimish, Mahmoud, and Pavlos I. Lazaridis. 2022. "Approximating Shading Ratio Using the Total-Sky Imaging System: An Application for Photovoltaic Systems" Energies 15, no. 21: 8201. https://doi.org/10.3390/en15218201
APA StyleDhimish, M., & Lazaridis, P. I. (2022). Approximating Shading Ratio Using the Total-Sky Imaging System: An Application for Photovoltaic Systems. Energies, 15(21), 8201. https://doi.org/10.3390/en15218201








