Stress and Displacement of Cylindrical Lithium-Ion Power Battery during Charging and Discharging
Abstract
:1. Introduction
2. Geometric Modeling
3. Mechanical–Electrochemical Model
3.1. The Fundamental Equations of the Battery
3.1.1. The Fundamental Equations of the Steel Core and Case
3.1.2. The Fundamental Equations of the Jellyroll
3.2. The Boundary Conditions
- In the first case, the three components of the battery interact with each other. Then, the displacement and radial compressive stress on the steel core can be obtained, Therefore, the boundary conditions are as follows:
- In the second case, . In this case, the steel core is under tension in radial direction and the steel core expands radially. Physically, this situation can be regarded as nonexistence.
- The third case is . There is no interaction between the steel core and the jellyroll, namely the stress at the contact region is 0. Then, the boundary conditions are as follows:
3.3. Analysis of Hoop Stress, Radial Stress, and Displacement
4. Stress Analysis and Calculation Cases
4.1. Computational Analysis of 18650 Battery
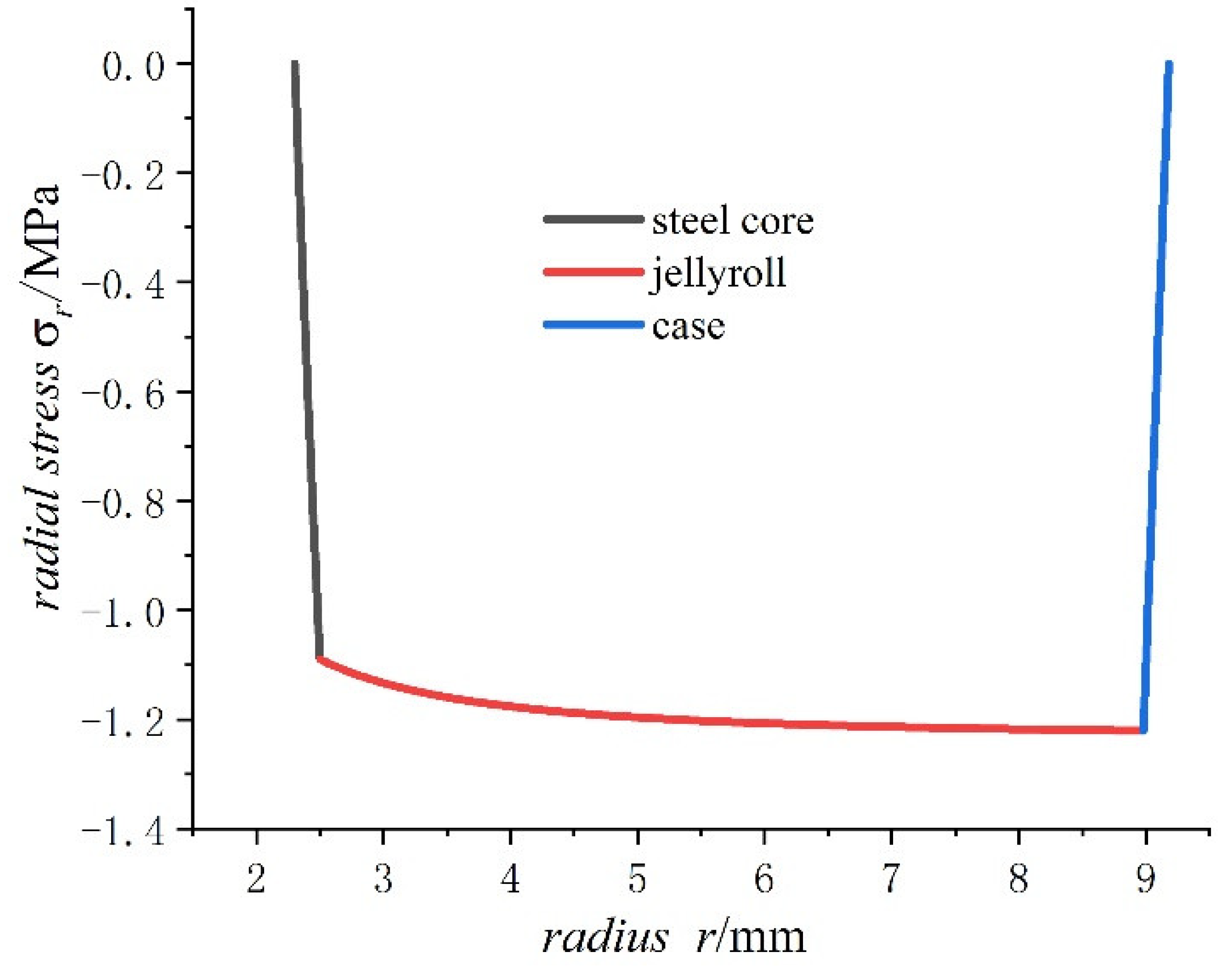
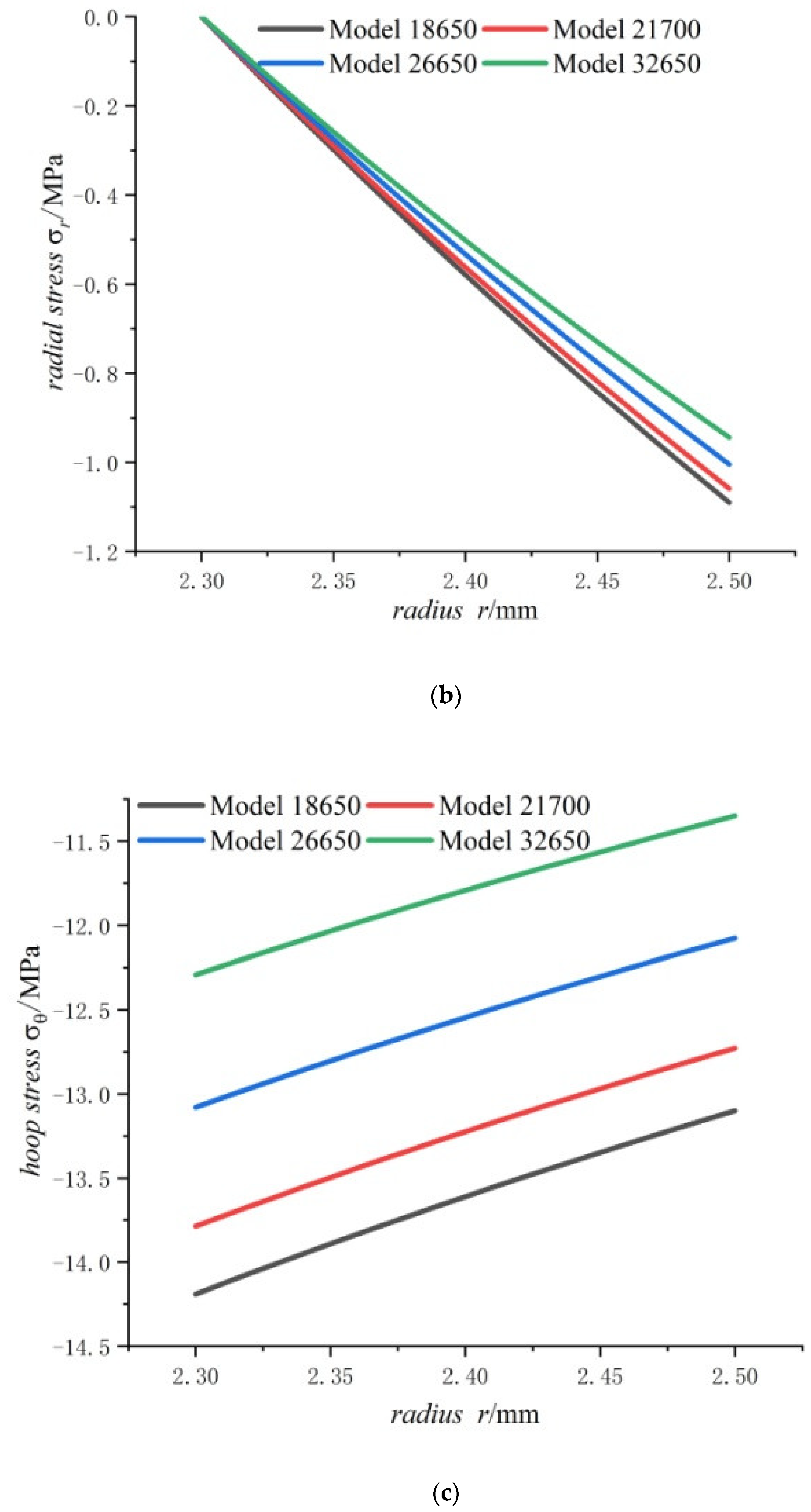
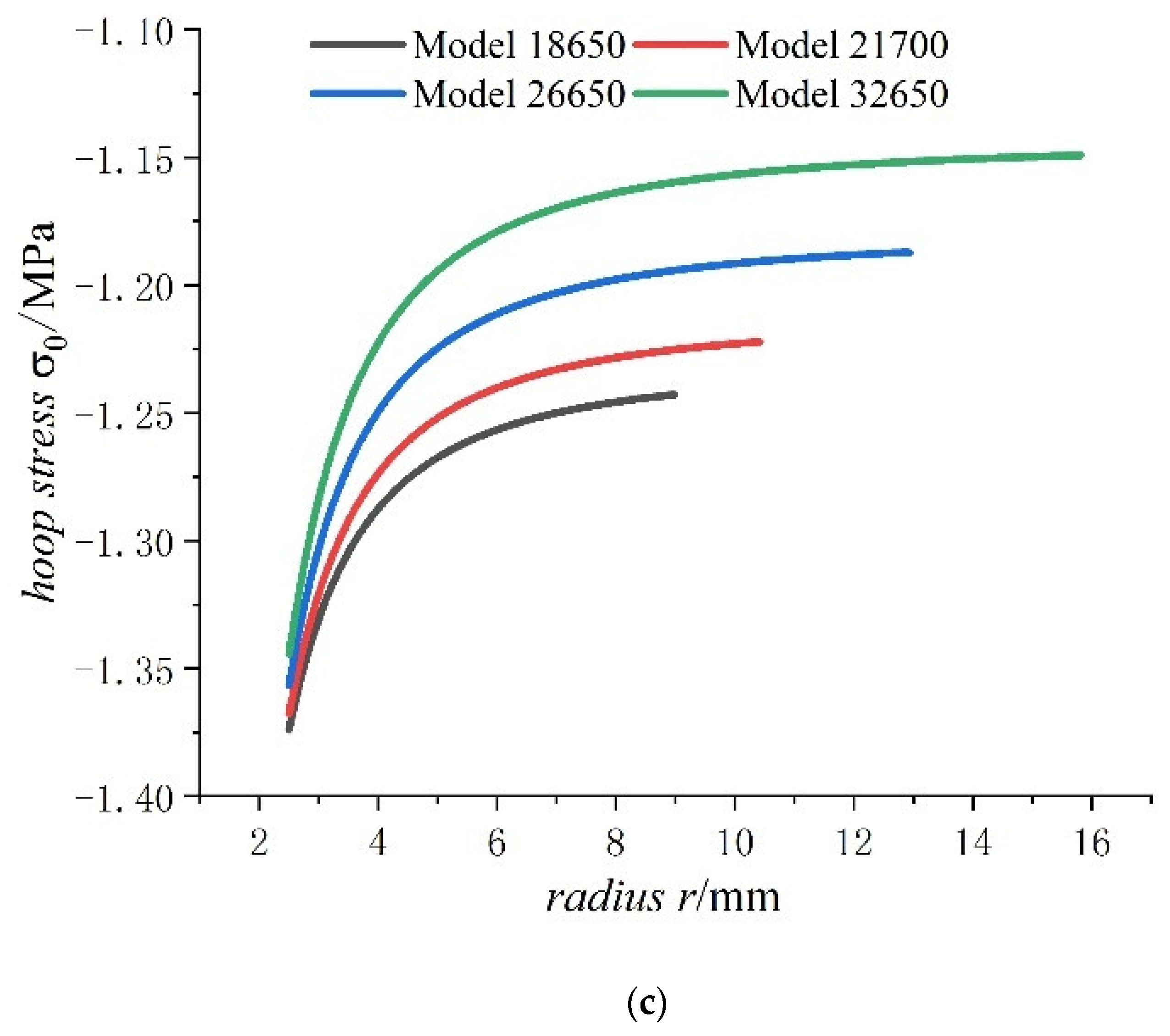
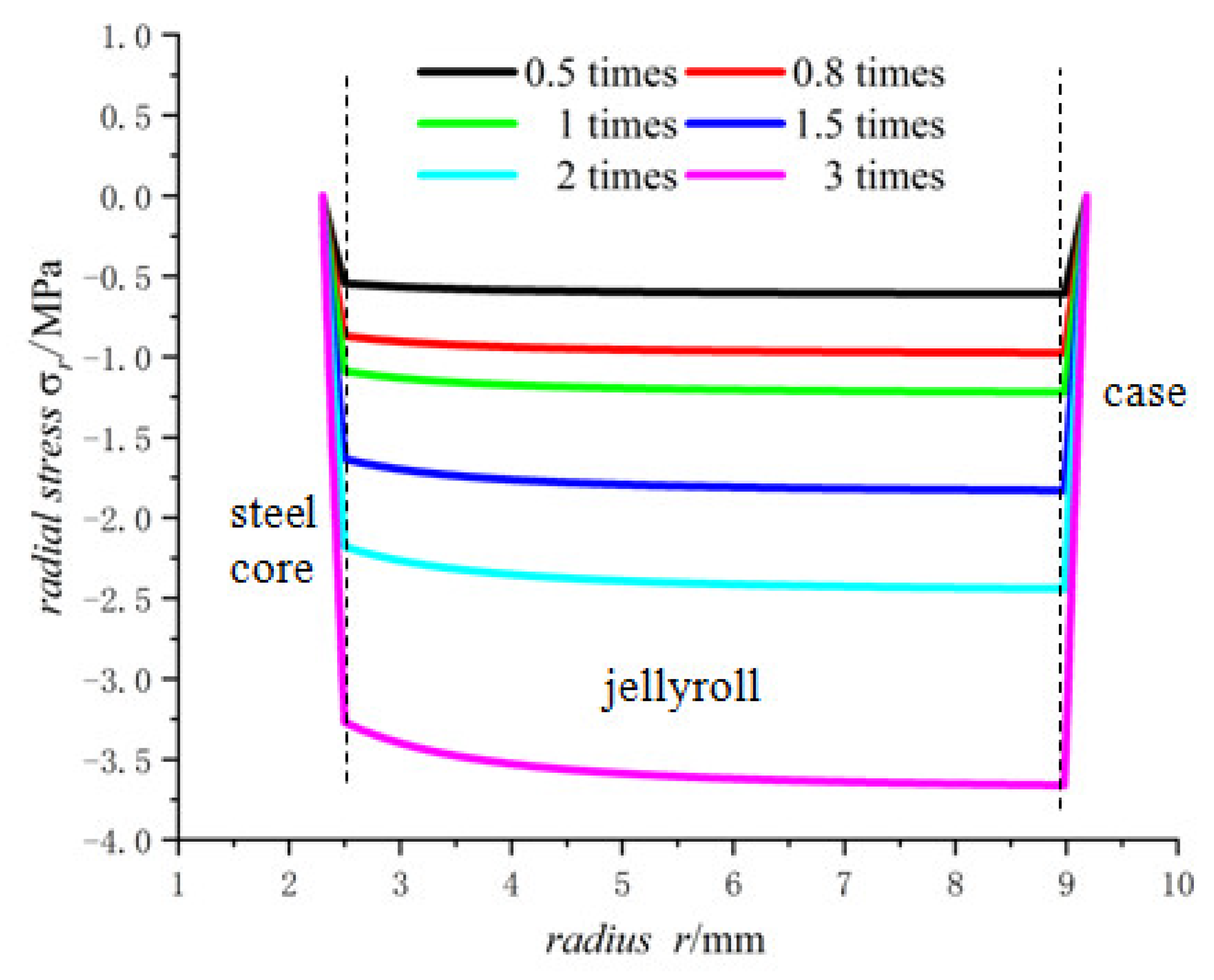
- The radial stress generated by charging is all compressive. As the radius increases from the inner radius to the outer radius, the radial compressive stress of the steel core and jellyroll increases gradually, while the radial compressive stress of the case decreases until it reaches zero.
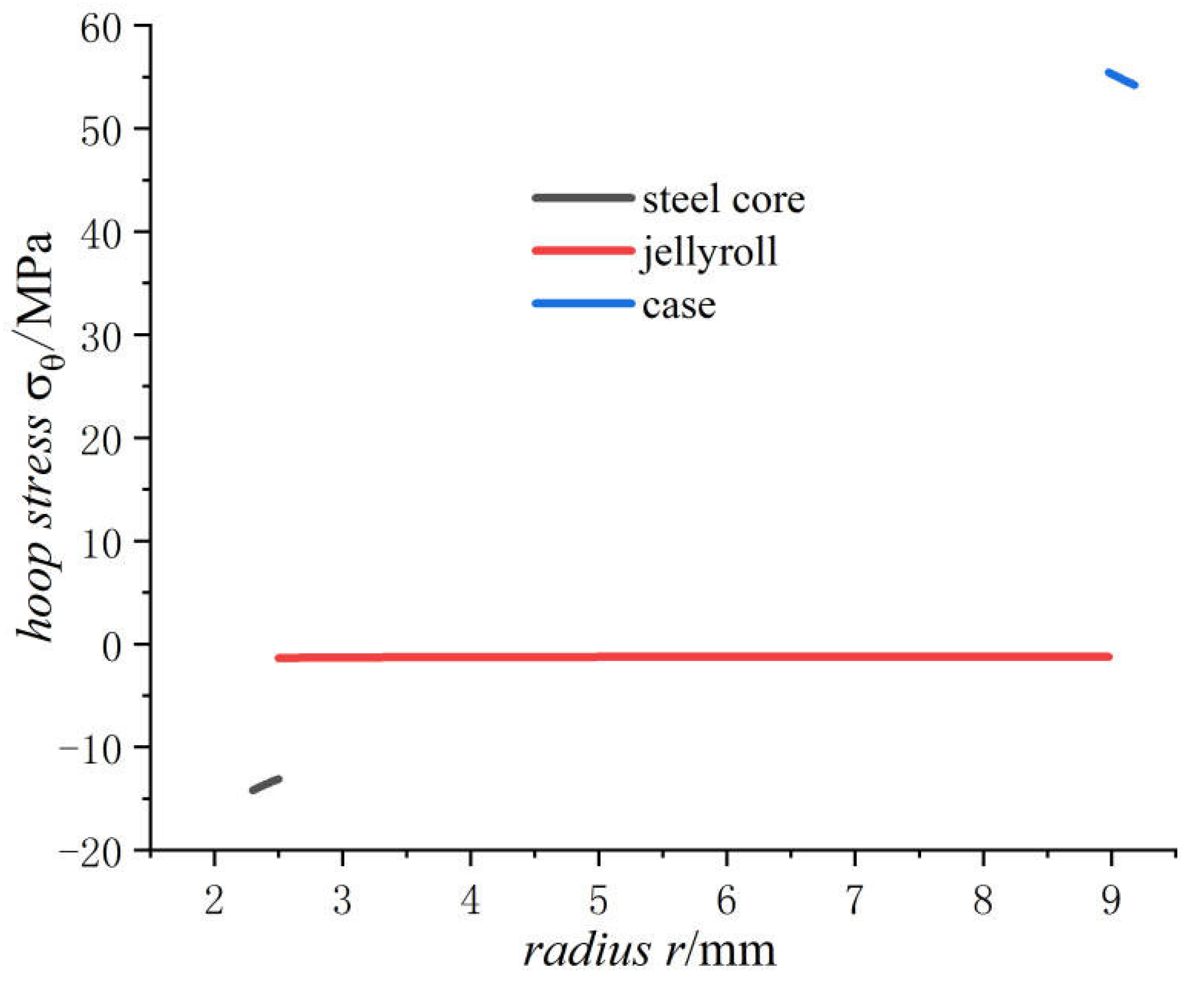
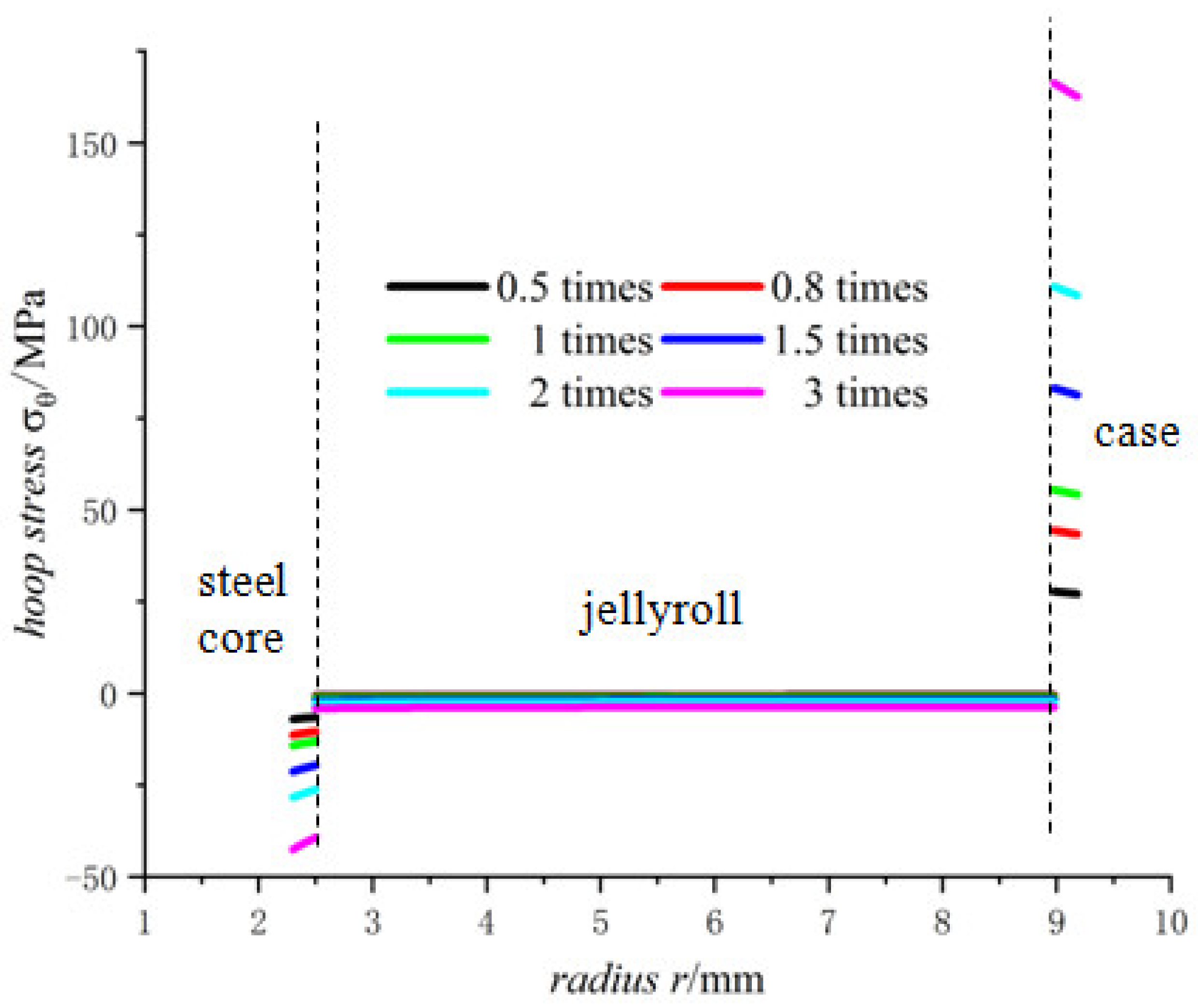
- The hoop stress of the steel core and jellyroll under charging are all compressive, and its value decreases with the increase in the radius. Meanwhile the hoop stress of the case generated by charging is tensile, which decreases with the increase in radius. It should be noted that the stress distribution of the electrode in Figure 6 is not constant, and the magnitude decreases marginally.
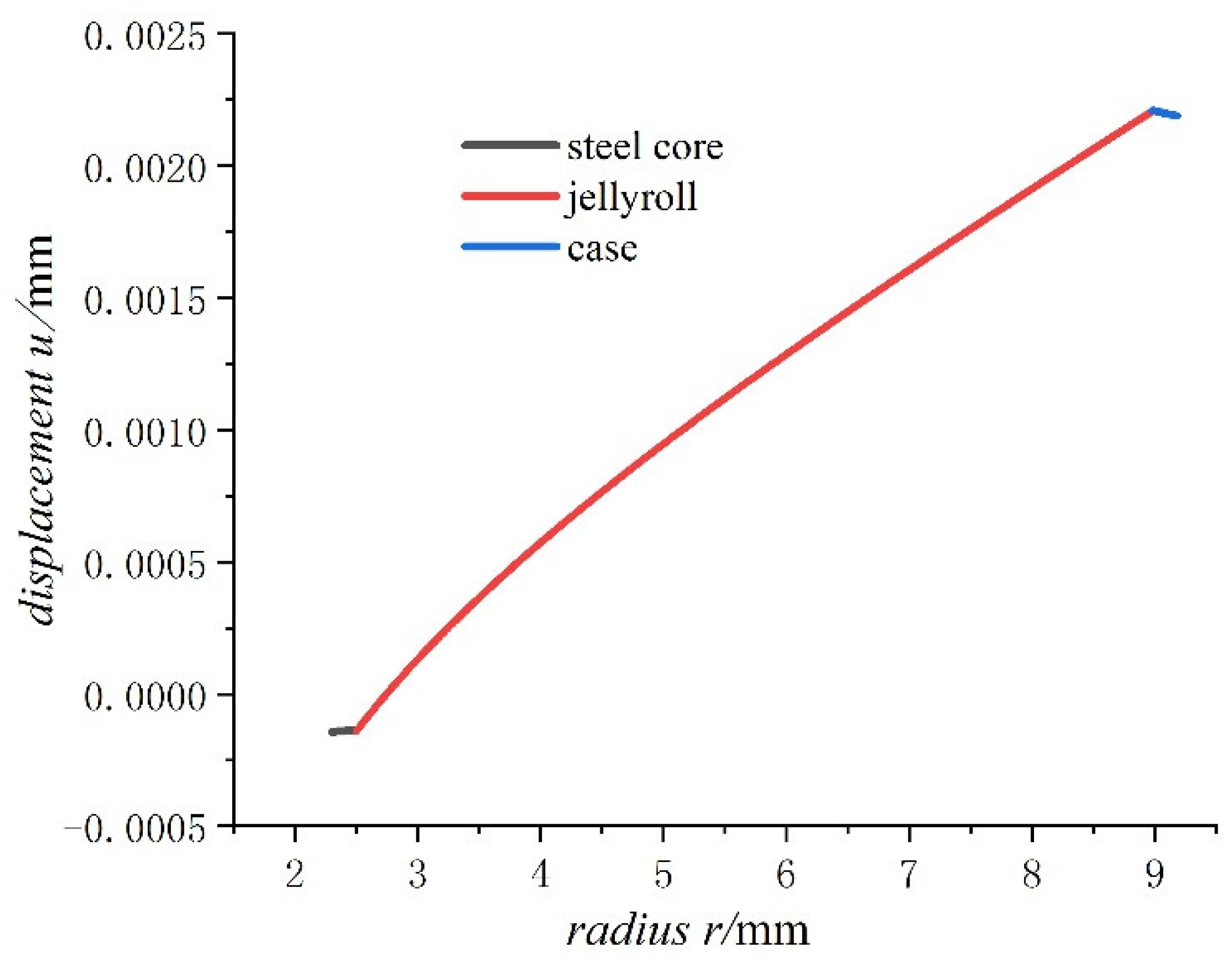
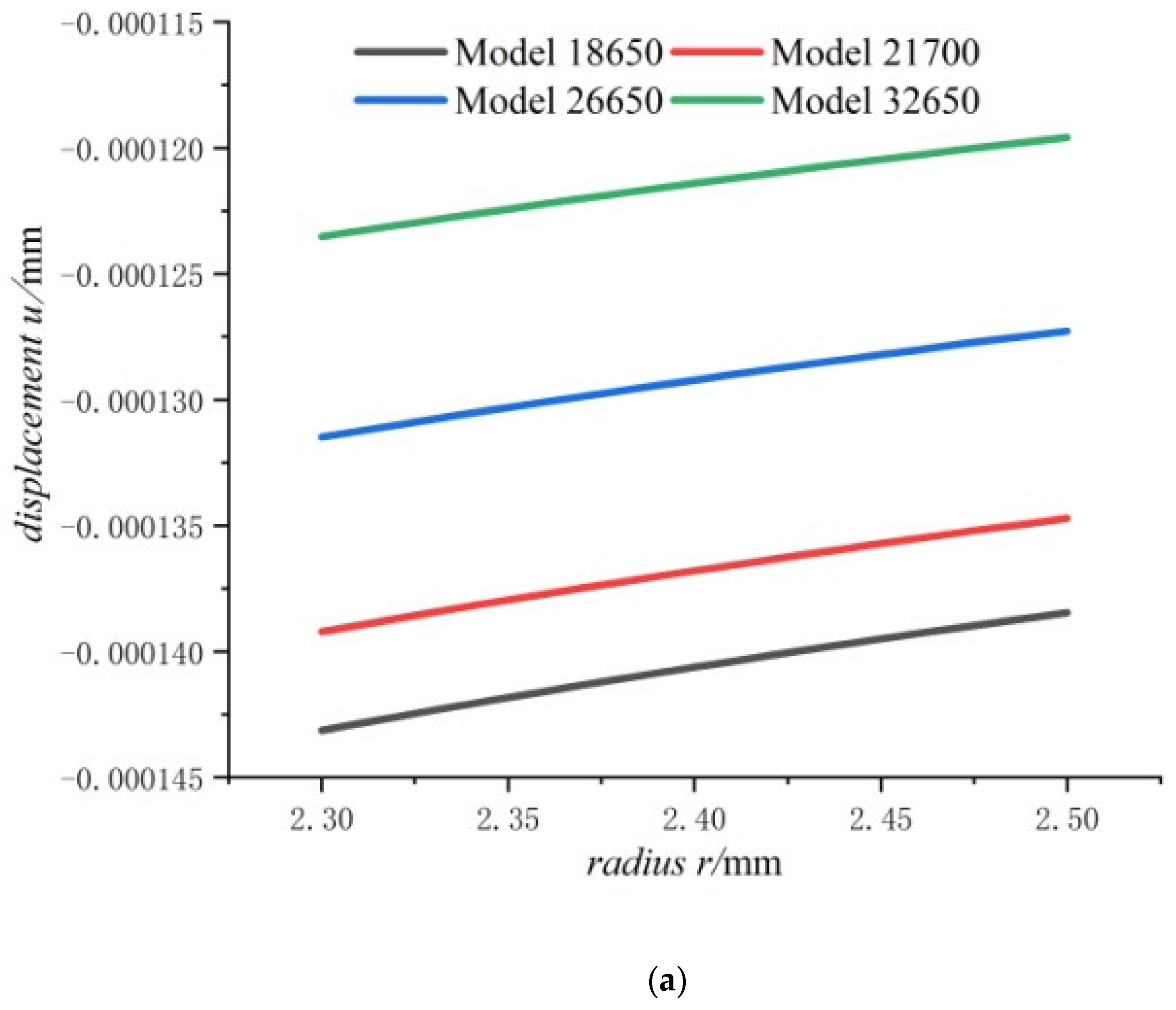
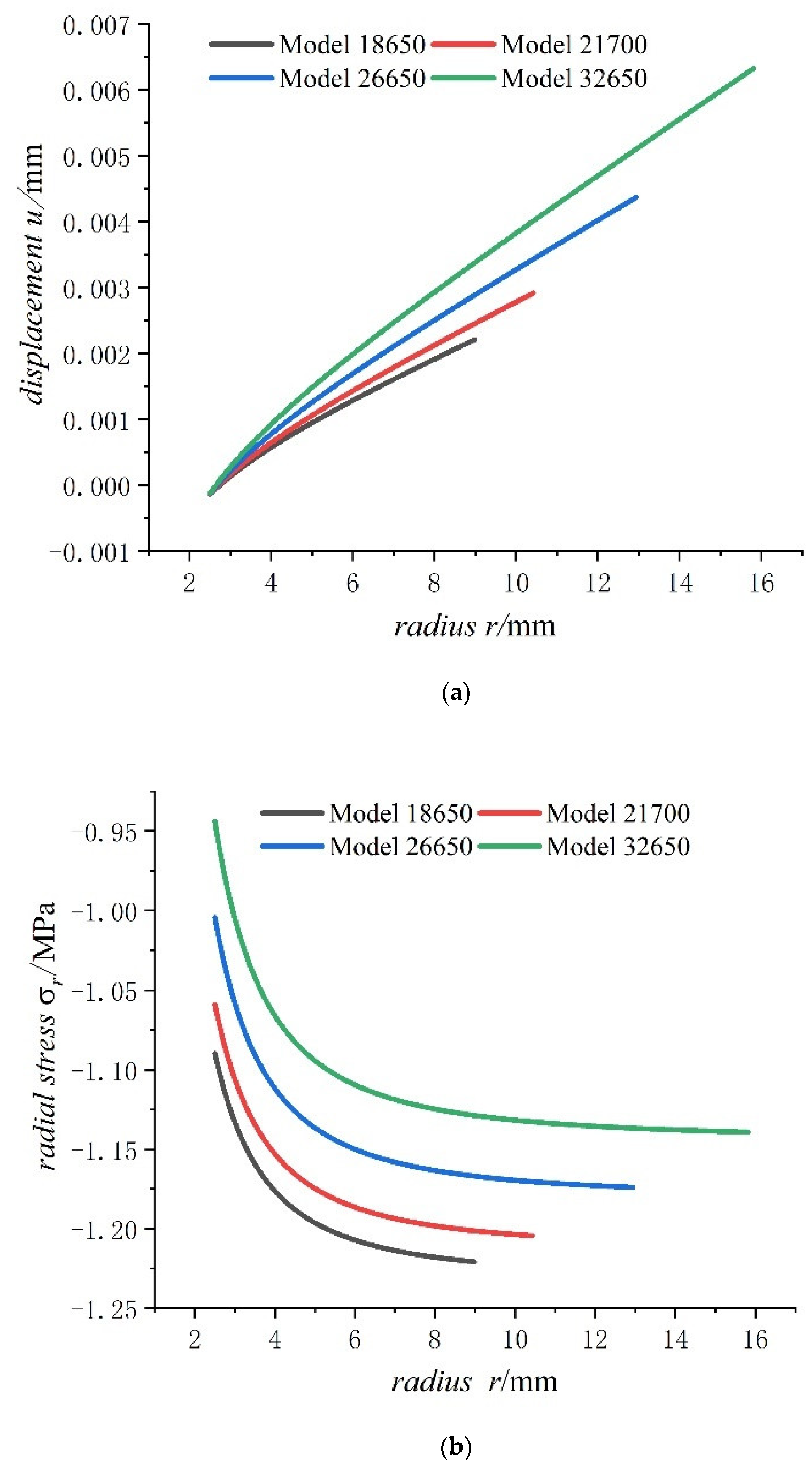
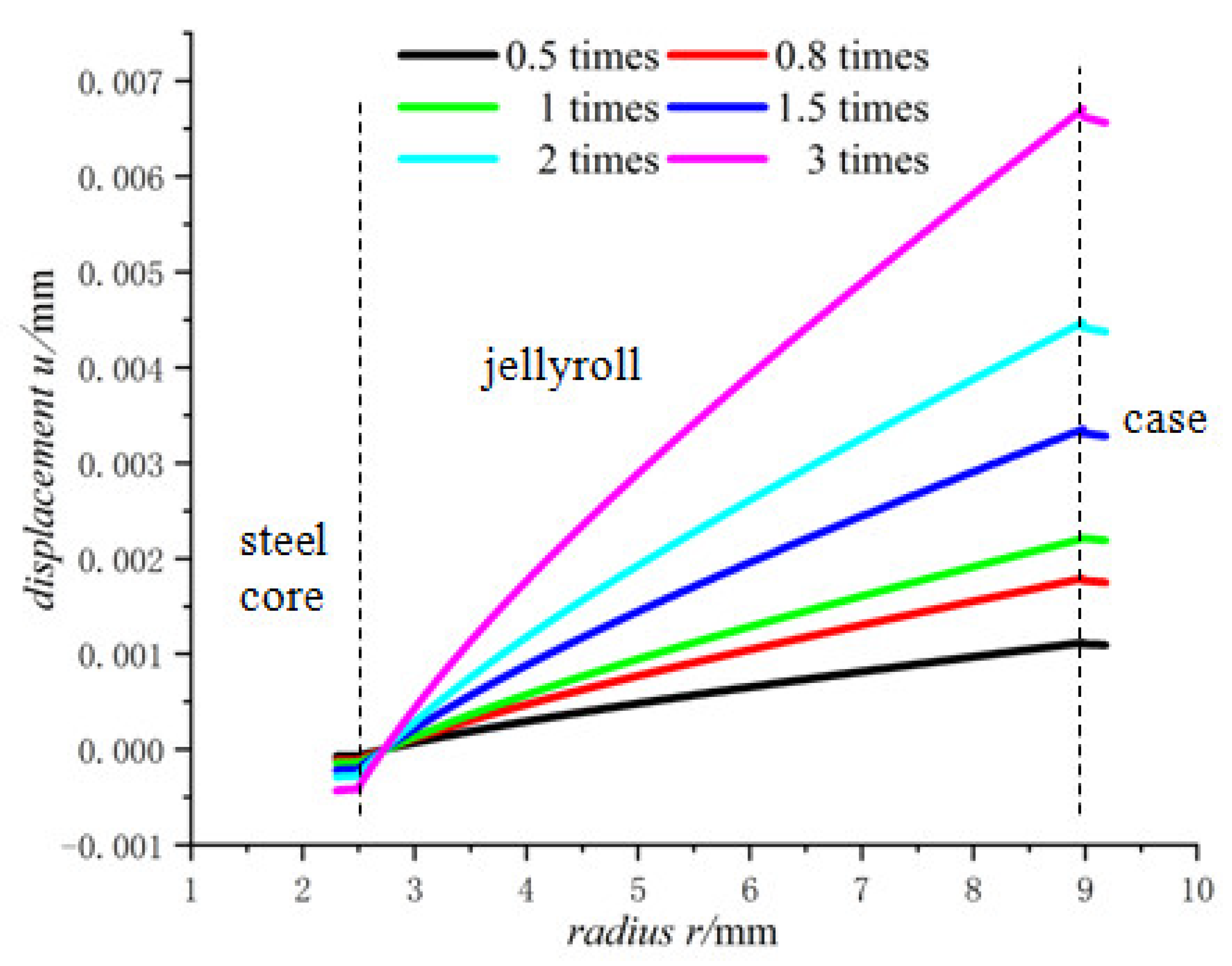
- For the fully charged battery, the displacement of the steel core shows negative values for contraction inwards. The displacement of the case shows positive values for expansion outward. The displacement of the jellyroll is zero at The value near the steel core is negative and the value near the case is positive. Therefore, we can conclude that the jellyroll deforms both inward and outward and is constrained by the steel core and the case.
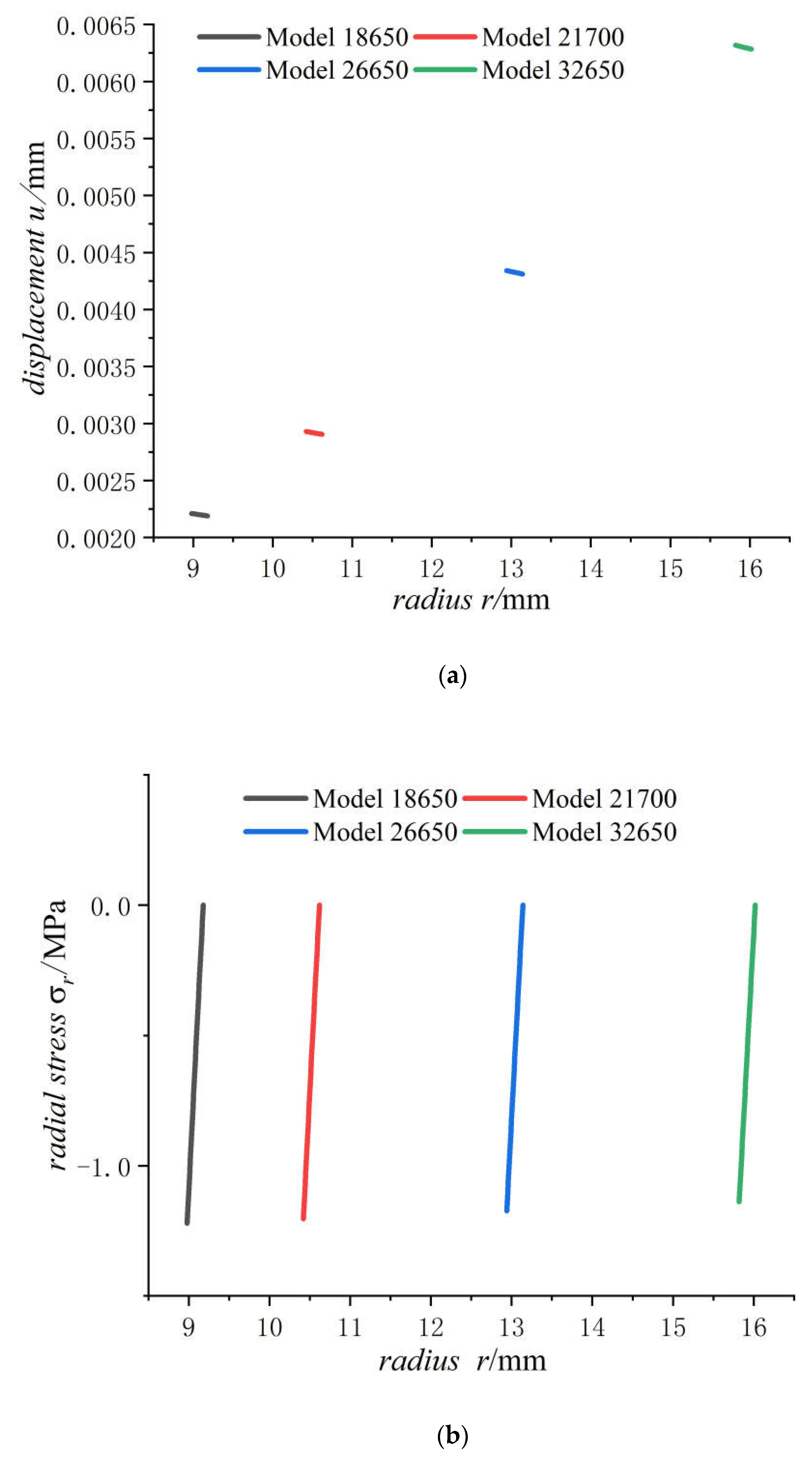
4.2. Stress Comparison of Batteries at Different Sizes after Charging
4.3. Effect of Lithium-Ion Concentration on Mechanical Properties of Battery
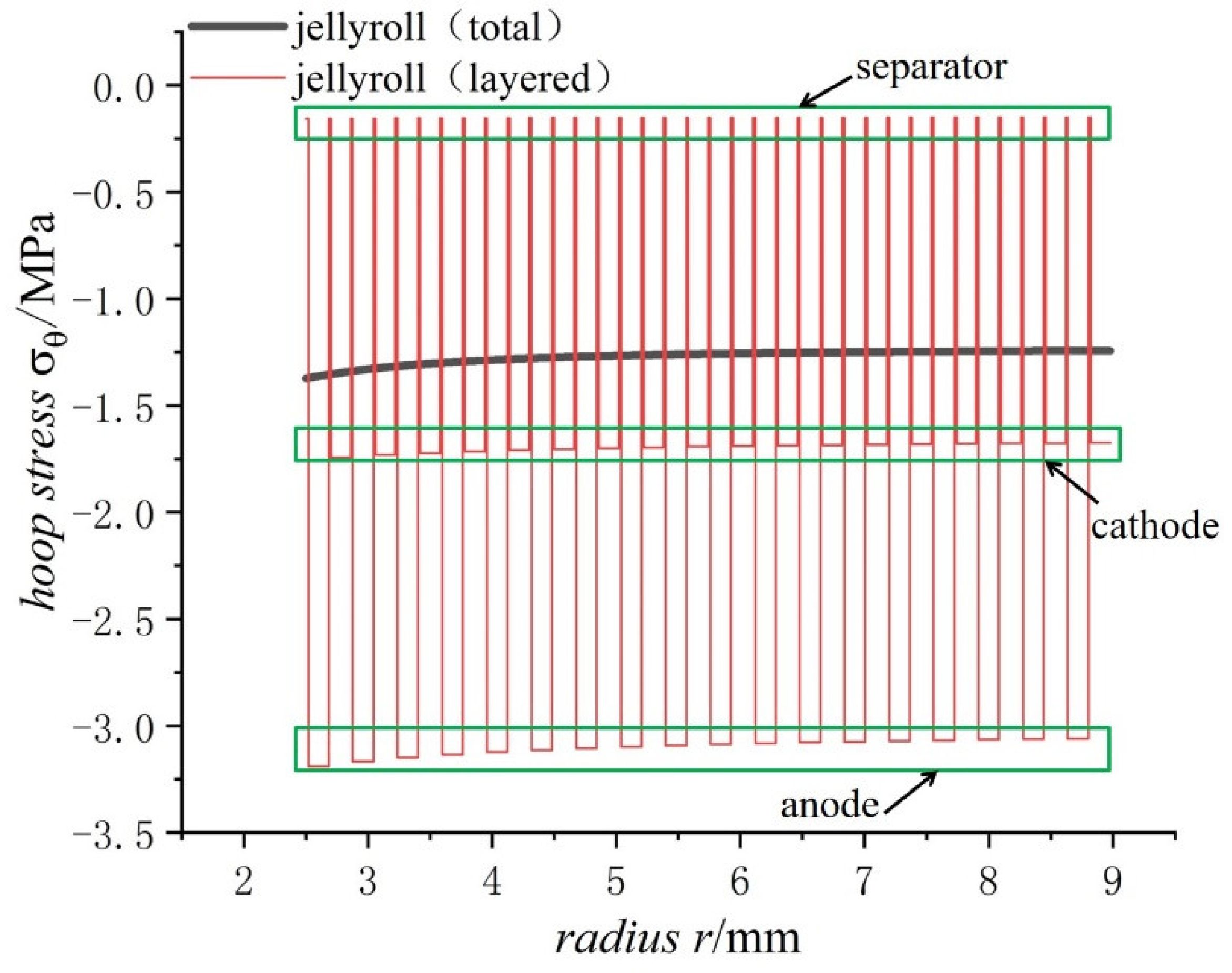
5. Layer Analyses of the Jellyroll
5.1. Calculation of the Hoop Stress of Each Jellyroll Component
5.2. Hoop Stress Distribution in the Winding
6. Conclusions
- Displacement of the jellyroll near the steel core is negative and the value near the case is positive, which means the positive part of the jellyroll expands outward and the negative part contracts inward. There is a zero displacement point in the jellyroll and the point moves inwards towards the core with the increase in the size of the battery.
- The radial stress of the case, jellyroll, and steel core is compressive stress. The radial stress of the jellyroll and the steel core increase with respect to the radius, while the radial stress of the case decreases with the increase in radius. The hoop stresses in the steel core and the jellyroll are compressive, and decrease with the increase in the radius, while the case has tensile hoop stress, which also decreases gradually with the increase in radius. The hoop stress of each layer of winding changes in a stepped pattern.
- With the increase in battery size, the displacement, the radial compressive stress, and the hoop compressive stress of the steel core decrease, and the radial and the hoop stresses in the jellyroll decrease. The displacement of the case increases with the increase in the external radius of the battery. The case is subjected to radial compression stress, and the stress value decreases with the increase in the external radius. Meanwhile, it is subjected to hoop tension stress, the stress value increases with the increase in the cell size.
- The lithium-ion concentration has obvious effects on the mechanical properties of the battery, the larger the lithium-ion concentration, the larger the displacement as well as the radial and hoop stresses.
7. Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Q.; Wang, S.; Zhang, J.; Zheng., J.; Yu, X.; Li, H. Overview of the failure analysis of lithium-ion batteries. Energy Storage Sci. Technol. 2017, 6, 1008–1025. [Google Scholar]
- Zhao, Y.; Stein, P.; Bai, Y.; Al-Siraj, M.; Yang, Y.; Xu, B.X. A review on modeling of electrochemo-mechanics in lithium-ion batteries. J. Power Sources 2019, 413, 259–283. [Google Scholar] [CrossRef]
- Willenberg, L.K.; Dechent, P.; Fuchs, G.; Sauer, D.U.; Figgemeier, E. High-Precision Monitoring of Volume Change of Commercial Lithium-Ion Batteries by Using Strain Gauges. Sustainability 2020, 12, 557. [Google Scholar] [CrossRef] [Green Version]
- Pfrang, A.; Kersys, A.; Kriston, A.; Sauer, D.U.; Rahe, C.; Kabitz, S.; Figgemeier, E. Long-term cycling induced jelly roll deformation in commercial 18650 cells. J. Power Sources 2018, 392, 168–175. [Google Scholar] [CrossRef]
- Diao, W.; Xu, B.; Pecht, M. Charging induced electrode layer fracturing of 18650 lithium-ion batteries. J. Power Sources 2021, 484, 229260. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Wang, Z.; Li, Q.; Lian, C.; He, X. Progress on Failure Mechanism of Lithium Ion Battery Caused by Diffusion Induced Stress. J. Inorg. Mater. 2020, 35, 1071–1087. [Google Scholar]
- Xia, W.; Zhang, Q.; Xu, F.; Sun, L. New Insights into Electrochemical Lithiation/Delithiation Mechanism of α-MoO3 Nanobelt by in Situ Transmission Electron Microscopy. ACS Appl. Mater. Interfaces 2016, 8, 9170–9177. [Google Scholar] [CrossRef]
- Xia, W.; Zhang, Q.; Xu, F.; Ma, H.; Chen, J.; Qasim, K.; Ge, B.; Zhu, C.; Sun, L. Visualizing the Electrochemical Lithiation/Delithiation Behaviors of Black Phosphorus by in Situ Transmission Electron Microscopy. J. Phys. Chem. C 2016, 120, 5861–5868. [Google Scholar] [CrossRef]
- Chen, B.B.; Zhou, J.Q.; Pang, X.M.; Wei, P.F.; Wu, Y.B.; Deng, K.J. Fracture damage of nanowire lithium-ion battery electrode affected by diffusion-induced stress and bending during lithiation. Rsc Adv. 2014, 4, 21072–21078. [Google Scholar] [CrossRef]
- Mei, W.; Duan, Q.; Qin, P.; Xu, J.; Wang, Q.; Sun, J. A Three-Dimensional Electrochemical-Mechanical Model at the Particle Level for Lithium-Ion Battery. J. Electrochem. Soc. 2019, 166, A3319–A3331. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Chen, H.S.; Fang, D.N. Diffusion-induced stress of electrode particles with spherically isotropic elastic properties in lithium-ion batteries. J. Solid State Electrochem. 2016, 20, 2835–2845. [Google Scholar] [CrossRef]
- Christensen, J.; Newman, J. Stress generation and fracture in lithium insertion materials. J. Solid State Electrochem. 2007, 10, 293–319. [Google Scholar] [CrossRef]
- Peng, Y.Z.; Zhang, K.; Zheng, B.L.; Li, Y. Stress analysis of a cylindrical composition-gradient electrode of lithium-ion battery in generalized plane strain condition. Acta Phys. Sin. 2016, 65, 100201. [Google Scholar] [CrossRef]
- Peng, Y.Z.; Li, Y.; Zheng, B.L.; Zhang, K.; Xu, Y.C. Influence of local velocity on diffusion-induced stress and axial reaction force in a hollow cylindrical electrode of lithium-ion batteries with cosidering expasion rate of medium. Acta Phys. Sin. 2018, 67, 070203. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, S.; Li, M.; Wu, J.; Wang, B.; Song, H. Deformation and Failure Properties of High-Ni Lithium-Ion Battery under Axial Loads. Materials 2021, 14, 7844. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Wierzbicki, T.; Li, W. A review of safety-focused mechanical modeling of commercial lithium-ion batteries. J. Power Sources 2018, 378, 153–168. [Google Scholar] [CrossRef]
- Kermani, G.; Sahraei, E. Review: Characterization and Modeling of the Mechanical Properties of Lithium-Ion Batteries. Energies 2017, 10, 1730. [Google Scholar] [CrossRef] [Green Version]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Liu, B.; Yin, S.; Xu, J. Integrated computation model of lithium-ion battery subject to nail penetration. Appl. Energy 2016, 183, 278–289. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Liu, B.H.; Wang, X.Y.; Hu, D.Y. Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies. Appl. Energy 2016, 172, 180–189. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, Q.M.; Xing, Y. Porosity variation of lithium-ion battery separators under uniaxial tension. Int. J. Mech. Sci. 2020, 174, 105496. [Google Scholar] [CrossRef]
- Song, Y.; Shao, X.; Guo, Z.; Zhang, J. Role of material properties and mechanical constraint on stress-assisted diffusion in plate electrodes of lithium ion batteries. J. Phys. D Appl. Phys. 2013, 46, 105307. [Google Scholar] [CrossRef]
- Zhao, K.; Pharr, M.; Hartle, L.; Vlassak, J.; Suo, Z. Fracture and debonding in lithium-ion batteries with electrodes of hollow core-shell nanostructures. J. Power Sources 2012, 218, 6–14. [Google Scholar] [CrossRef]
- Zhang, X.C.; Shyy, W.; Sastry, A.M. Numerical simulation of intercalation-induced stress in Li-ion battery electrode particles. J. Electrochem. Soc. 2007, 154, A910–A916. [Google Scholar] [CrossRef]
- Qi, Y.; Guo, H.; Hector, L.G.; Timmons, A. Threefold Increase in the Young’s Modulus of Graphite Negative Electrode during Lithium Intercalation. J. Electrochem. Soc. 2010, 157, A558–A566. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, X.; Suo, Z. Averting cracks caused by insertion reaction in lithium-ion batteries. J. Mater. Res. 2010, 25, 1007–1010. [Google Scholar] [CrossRef]
- Huggins, R.A.; Nix, W.D. Decrepitation model for capacity loss during cycling of alloys in rechargeable electrochemical systems. Ionics 2000, 6, 57–63. [Google Scholar] [CrossRef]
- Bhandakkar, T.K.; Gao, H. Cohesive modeling of crack nucleation under diffusion induced stresses in a thin strip: Implications on the critical size for flaw tolerant battery electrodes. Int. J. Solids Struct. 2010, 47, 1424–1434. [Google Scholar] [CrossRef] [Green Version]
- Woodford, W.H.; Carter, W.C. “Electrochemical Shock” of Intercalation Electrodes: A Fracture Mechanics Analysis. J. Electrochem. Soc. 2010, 157, A1052–A1059. [Google Scholar] [CrossRef]
- Zhao, K.; Pharr, M.; Vlassak, J.J.; Suo, Z. Fracture of electrodes in lithium-ion batteries caused by fast charging. J. Appl. Phys. 2010, 108, 073517. [Google Scholar] [CrossRef]
- Divakaran, A.M.; Minakshi, M.; Bahri, P.A.; Paul, S.; Kumari, P.; Divakaran, A.M.; Manjunatha, K.N. Rational design on materials for developing next generation Lithium-ion secondary battery. Prog. Solid State Chem. 2020, 62, 100298. [Google Scholar] [CrossRef]
- Minakshi, M.; Singh, P.; Issa, T.B.; Thurgate, S.; De Marco, R. Lithium insertion into manganese dioxide electrode in MnO2/Zn aqueous battery. J. Power Sources 2004, 138, 319–322. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, S.; Wang, Z.; Zhou, P.; Xie, P.; Zhou, J.; Chen, H.S.; Song, W.L.; Fang, D.N. In-situ investigations of the inhomogeneous strain on the steel case of 18650 silicon/graphite lithium-ion cells. Electrochim. Acta 2021, 367, 137516. [Google Scholar] [CrossRef]
- Chen, J.C. Roles of Binder and Separator Mechanical Behavior in the Lithium-Ion Battery Ageing and Safety. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2014. [Google Scholar]

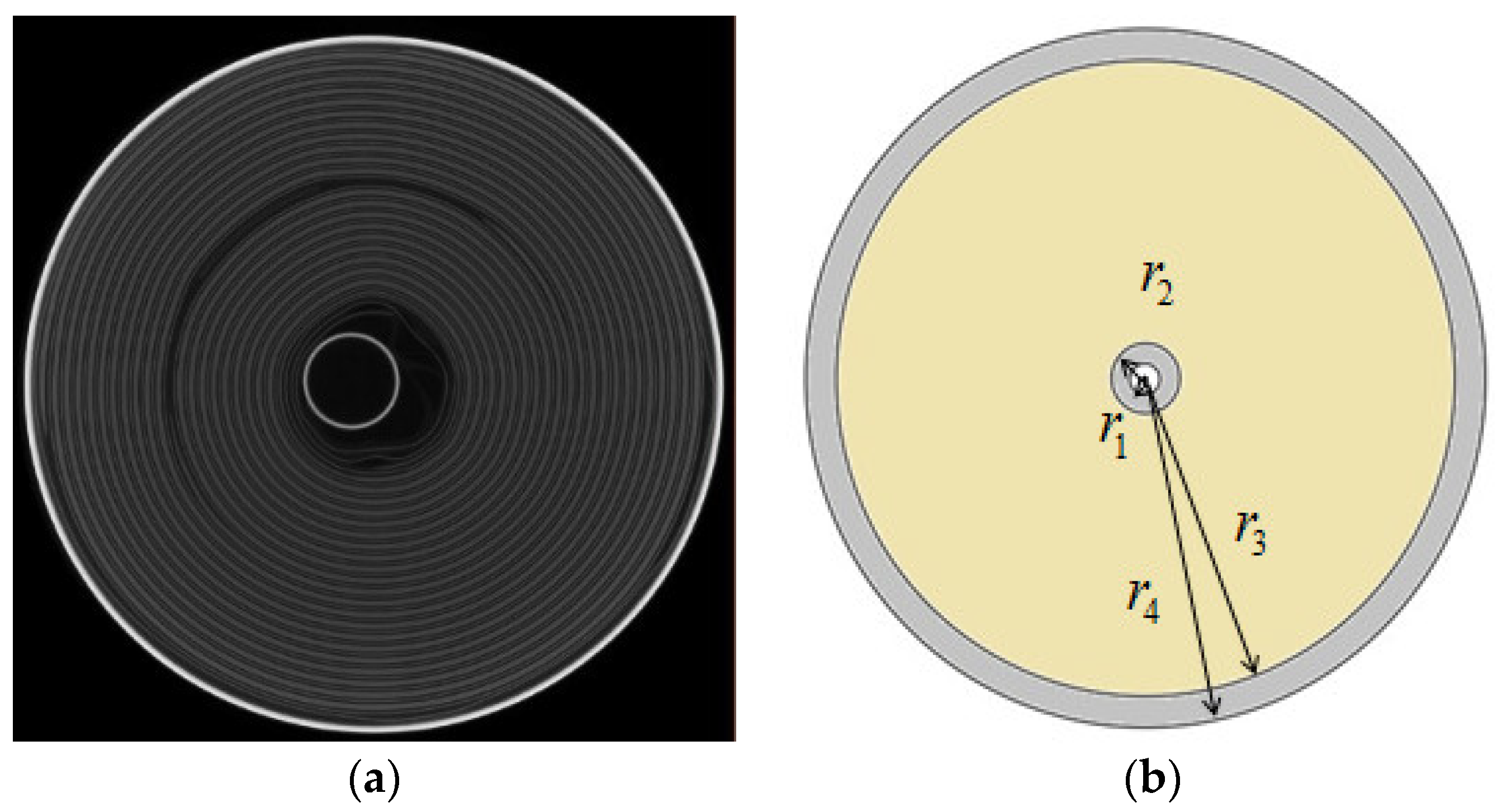


| Component of Jellyroll | Elastic Modulus E (MPa) | Poisson’s Ratio ν | |
|---|---|---|---|
| Separator (PP) | |||
| Anode | |||
| Cathode | |||
| Jellyroll | In-plane | ||
| Axial direction | |||
| Battery Model | Winding Turns (n) | Internal Radius of Steel Core (mm) | Internal Radius of Winding (mm) | External Radius of Winding (mm) | External Radius of Case (mm) |
|---|---|---|---|---|---|
| 18650 | 18 | 2.3 | 2.5 | 8.98 | 9.18 |
| 21700 | 22 | 2.3 | 2.5 | 10.42 | 10.62 |
| 26650 | 29 | 2.3 | 2.5 | 12.94 | 13.14 |
| 32650 | 37 | 2.3 | 2.5 | 15.82 | 16.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Wang, G.; Song, H.; Wang, B.; Wu, G.; Lei, J. Stress and Displacement of Cylindrical Lithium-Ion Power Battery during Charging and Discharging. Energies 2022, 15, 8244. https://doi.org/10.3390/en15218244
Chen J, Wang G, Song H, Wang B, Wu G, Lei J. Stress and Displacement of Cylindrical Lithium-Ion Power Battery during Charging and Discharging. Energies. 2022; 15(21):8244. https://doi.org/10.3390/en15218244
Chicago/Turabian StyleChen, Jingyi, Genwei Wang, Hui Song, Bin Wang, Guiying Wu, and Jianyin Lei. 2022. "Stress and Displacement of Cylindrical Lithium-Ion Power Battery during Charging and Discharging" Energies 15, no. 21: 8244. https://doi.org/10.3390/en15218244
APA StyleChen, J., Wang, G., Song, H., Wang, B., Wu, G., & Lei, J. (2022). Stress and Displacement of Cylindrical Lithium-Ion Power Battery during Charging and Discharging. Energies, 15(21), 8244. https://doi.org/10.3390/en15218244







