Techno-Economic Analysis of Renewable-Energy-Based Micro-Grids Considering Incentive Policies

Abstract

Renewable-energy-based microgrids (MGs) are being advocated around the world in response to increasing energy demand, high levels of greenhouse gas (GHG) emissions, energy losses, and the depletion of conventional energy resources. However, the high investment cost of the MGs besides the low selling price of the energy to the main grid are two main challenges to realize the MGs in developing countries such as Iran. For this reason, the government should define some incentive policies to attract investor attention to MGs. This paper aims to develop a framework for the optimal planning of a renewable energy-based MG considering the incentive policies. To investigate the effect of the incentive policies on the planning formulation, three different policies are introduced in a pilot system in Iran. The minimum penetration rates of the RESs in the MG to receive the government incentive are defined as 20% and 40% in two different scenarios. The results show that the proposed incentive policies reduce the MG’s total net present cost (NPC) and the amount of carbon dioxide (CO₂) emissions. The maximum NPC and CO₂ reduction in comparison with the base case (with incentive policies) are 22.87% and 56.13%, respectively. The simulations are conducted using the hybrid optimization model for electric renewables (HOMER) software.

1. Introduction

Producing a large amount of greenhouse gas (GHG) emissions from power plants, high system expansion costs, and high energy losses in the transmission and distribution networks are three main challenges of electrical energy systems. Supplying a large percentage of the electrical demand in developing countries from fossil fuel-based power plants produces a large amount of carbon dioxide (CO₂) emissions. Furthermore, the conversion of only one-third of fuel energy into electrical power in bulk power generation units, compounded with the high voltage transmission network’s poor efficiency, makes microgrids (MGs) in distribution networks more viable [1,2]. Realization of MGs, as one of the main components of smart grids, has become an emergent research area in the electrical industry [3]. Due to the high investment cost of the local energy resources, however, realizing the MG concept to satisfy the load is not a very practical plan in developing countries. Therefore, it seems that incentive policies should be defined by the government to encourage investors to realize the renewable energy sources (RESs)-based MG. Hence, this paper aims to formulate an optimal plan for a RESs-based MG considering the incentive policies which in turn decrease the net present cost (NPC) and CO₂ emission.

There are many studies on the optimal planning of MGs to meet the load from different viewpoints. A comprehensive review of the optimal design of MGs in grid-connected and stand-alone modes is undertaken in [4]. The authors of [5] performed a technical and economic feasibility study using a hybrid optimization model for electric renewable (HOMER) pro version 3.12.2. The optimal planning formulation of the MGs considering electric vehicles (EVs) was investigated using the multi-objective particle swarm optimization (PSO) approach in [6]. A combination of a photovoltaic (PV) system, wind power, and a battery was proposed as the best plan to satisfy the load of a community area in Egypt using HOMER software in [7]. The authors of [8] employed HOMER to calculate an optimal plan, consisting of a PV system, wind turbine, and biomass, to supply the load in China. The MG configuration consisting of a PV system, and biomass was determined to meet electrical energy needs in a rural area in India [9]. An MG based on renewable energy sources was designed for an urban area in Egypt using the HOMER [10]. Several studies have also been performed in Iran to investigate the deployment of RES-based MGs for a variety of applications, including educational buildings [11], rural areas [12,13,14], and residential buildings [15,16,17]. However, the majority of these works have concentrated on the feasibility of using stand-alone MG and NPC minimization. Furthermore, the research so far fails to consider incentive policies in the problem formulation.

Table 1. The specification of hybrid system simulation research works.

Ref.	MG Mode	Component	Optimization Tool	Objective Functions		Incentive Policy
				Total Cost Minimization	Pollution Emissions Minimization
[18]	Stand-alone	WT/PV/Battery	Genetic algorithm (GA), PSO and multi-objective PSO algorithms, and HOMER software	✓	-	-
[19]	Stand-alone	PV/WT/Battery	HOMER and GAMS	✓	-	-
[20]	Stand-alone	PV/DG/Battery	HOMER	✓	-	-
[21]	Grid-connected/Stand-alone	DG/PV/WT/Micro/Hydro	HOMER	✓	-	-
[22]	Stand-alone	Biogas generator/PV/DG/WT/Battery	HOMER	✓	-	-
[23]	Stand-alone	PV/DG	Crow search algorithm	✓	✓	-
[24]	Stand-alone	PV/WT/DG/Battery	HOMER	✓	-	-
[25]	Stand-alone	PV/WT/Hydrogen storage/Battery	Hybrid chaotic search, harmony search, simulated annealing algorithms	✓	-	-
[12]	Grid-connected/Stand-alone	PV/WT/Biogas generator/Fuel cell	HOMER	✓	✓	-
[26]	Stand-alone	PV/WT/DG/Biogas generator/Battery	Artificial bee colony (ABC), PSO algorithms, and HOMER	✓	-	-
[27]	Grid-connected	PV/WT/Biogas generator/Battery	HOMER	✓	-	-
[28]	Stand-alone	WT/PV/Battery/Biomass generator	Multi-objective GA, epsilon multi-objective genetic algorithm (ε-MOGA)	✓	-	-
[29]	Stand-alone	PV/Diesel/Battery	HOMER	✓	-	-
[30]	Grid-connected	PV/Biomass gasifiers/Battery	HOMER	✓	-	-
[31]	Grid-connected	PV/DG/Battery	HOMER	✓	-	-
[32]	Grid-connected	PV/WT/Battery	MOPSO and MOGA	✓	-	-
[33]	Grid-connected	PV/WT/Microturbine/Fuel cell/Battery	Improved differential evolutionary and PSO techniques	✓	✓	-
[34]	Grid-connected	PV/WT/Battery/Fuel cell/Electrolyzer/Hydrogen tank	HOMER	✓	-	-
[35]	Stand-alone	PV/DG/Battery	HOMER	✓	✓	-
[36]	Stand-alone	PV/WT/Battery	HOMER	✓	-	-
[37]	Stand-alone	PV/WT/Battery/DG	HOMER	✓	✓	-
This paper	Grid-connected	PV/DG/Battery	HOMER	✓	✓	✓

“✓” refers to considered; “-” refers to not considered.

summarizes the contributions of the research so far in the state of the art.

Investigating the effect of RES incentive policies on the power system studies is undertaken in several studies. In general, these policies can be divided into two categories: (1) price-based, and (2) quantity-based policies. In the early one, the power from RESs is purchased at a specific price, which can be fixed or variable for different periods. Later, the governments announce the scheduled RES capacity, and the selling energy price is decided by the supply and demand mechanism. Currently, the feed-in-tariff (FIT) policy, as a fixed-price-based policy, is implemented in most countries [38,39]. The effect of several incentive policies on the increasing penetration rate of PV systems in China was investigated in [40] using a leader–follower approach. In [41], the effect of incentive policies on the reduction of GHG emissions was investigated. The generation expansion planning (GEP) problem was addressed in [42] and [43] regarding the need for incentive policies to employ diesel generators (DGs) and RESs to supply the demand of the systems, respectively. The financial mechanism was addressed in [44] to enhance the usage of electrical energy storage in electrical power systems.

Investigation of the previous studies shows that although incentive policies should be defined to increase the penetration rate of renewable-energy-based MGs, this issue is not properly addressed in the literature. More precisely, the incentive policies in the research so far are impractical for developing countries. Furthermore, the researches fails to simultaneously consider NPC, CO₂ emissions reduction, and incentive policies. Therefore, this study investigates the planning problem of a renewable-energy-based MG for an educational complex in Iran considering incentive policies. Three new incentive policies, appropriate for developing as well as developed countries, are developed in which the NPC and the quantity of CO₂ emissions are taken into account. It should be noted that the considered incentive policies are technically feasible, scalable, and implementable in real power systems. Therefore, the following are the key contributions of this paper:

• Tackling the incentive policies of the governments in the optimal planning problem formulation of grid-connected RES-based MGs;
• Determining the optimum size of the RES-based MG’s components considering three new incentive policies;
• Investigating the social, economic, and technical impacts of grid-connected RES-based MGs in developing countries;
• Proposing a strategy for implementing incentive policies in commercial software.

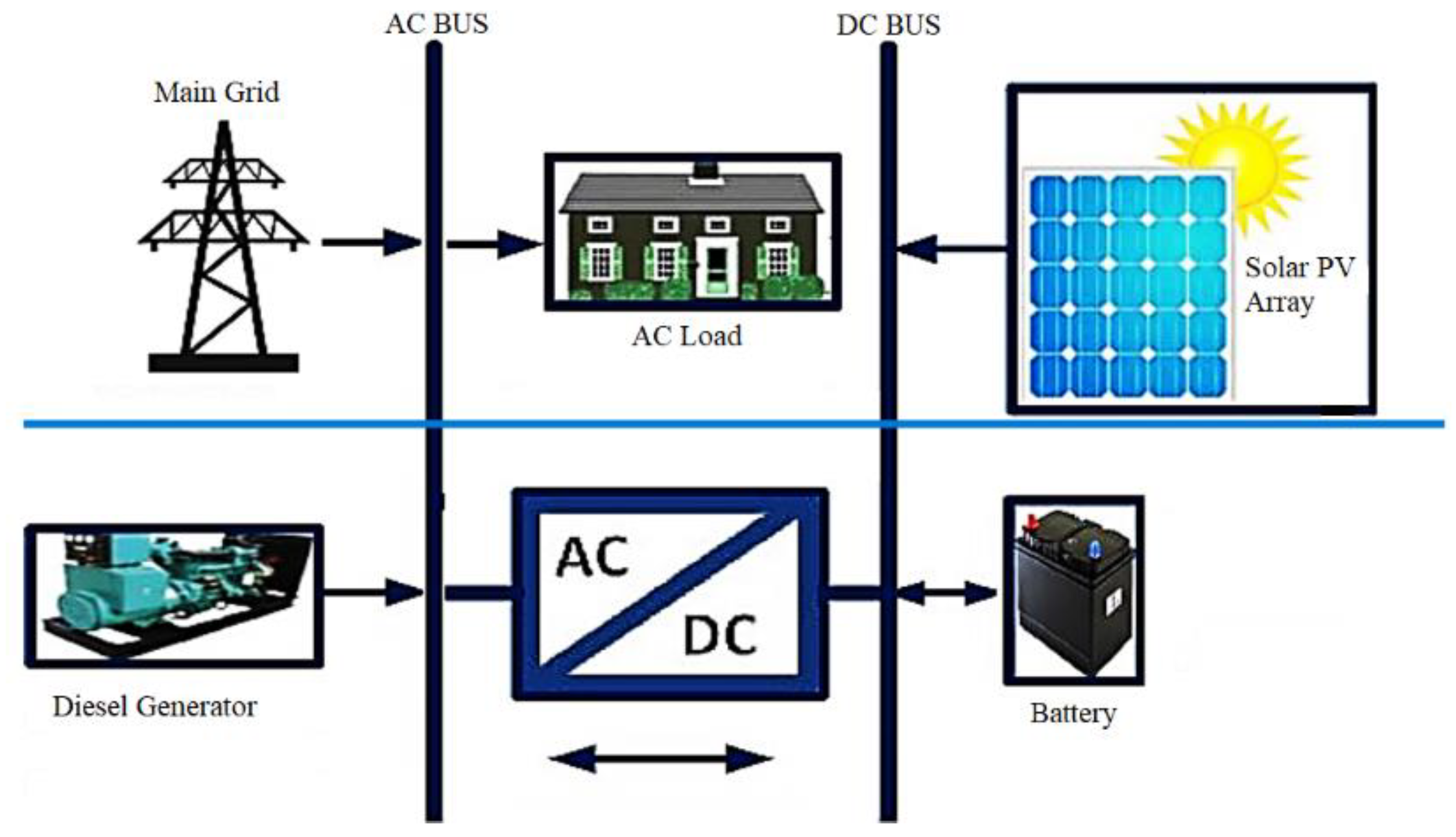
2. System Modeling

A two-pronged method is used to simulate the intended MG: (1) modeling of components, and (2) modeling of economics. The MG components help in planning the net power generation, while the economic model facilitates estimating whether the desired model is feasible or not.

2.1. System Components Modeling

2.1.1. Solar Photovoltaic Panel Modeling

Solar radiation and temperature may influence the performance of the PV system. The PV generation is calculated using [22]:

$$P_t^{\mathrm{PV}}={\overline{\mathrm{P}}}^{\mathrm{PV}}{\mathrm{D}}^{\mathrm{PV}}\left(\frac{S{R}_t^{\mathrm{PV}}}{S{R}^{\mathrm{PV\_Stan}.}}\right)\left[1+{\alpha }_p\left(T_t^{\mathrm{PV}}-T^{\mathrm{PV\_Stan}.}\right)\right]$$

(1)

where ${\overline{\mathrm{P}}}^{\mathrm{PV}}$ refers to the PV system’s power output under standard test conditions [kW]. The PV system de-rating factor is a scaling factor that is applied to the PV array power output to account for lower output in real-world operating circumstances than when the PV panel was rated. In this paper, to simulate realistic conditions, the de-rating factor of 90% is considered owing to the changing effect of dust and temperature.

2.1.2. Diesel Generator Modeling

The model of a fuel-based DG is assumed to be a straight-line curve. Thus, electrical output is computed by

$$F_t^{\mathrm{DG}}=A{\overline{\mathrm{P}}}^{\mathrm{DG}}+B{P}_t^{\mathrm{DG}}$$

(2)

2.1.3. Battery System

The excess PV energy is stored in the battery and utilized when needed. This paper uses a battery to store the extra power generated from PV panels. The supplementary battery energy and prime movers are calculated as [45,46]:

$$Q_{Bat}=Q_{Bat,0}+{\displaystyle {\int }_0^t{V}_{Bat}}{I}_{Bat}dt$$

(3)

The battery state of charge (SOC) can be calculated as [47]:

$$SOC\left(\Delta t\right)=SOC\left(0\right)-\frac{{\displaystyle {\int }_0^{\Delta t}\xi p\left(t\right)dt}}{E_{ESS,rated}}$$

(4)

where

$$\xi =\left\{\begin{array}{ll}{\xi }_c& p\left(t\right)<0\\ \frac{1}{{\xi }_d}& p\left(t\right)>0\end{array}\right.$$

and p(t) is battery power which has negative values for the charging procedure and positive values for the discharging period, E_ESS,rated, Δt, ζ_c, and ζ_d are the nominal energy capacity, charge/discharge time, and charging and discharging efficiencies of the battery, respectively.

The total amount of energy stored in the storage component at any time is the sum of the available and bound energy. The energy that is quickly available for conversion to DC power is known as available energy (Q₁); in contrast, the energy that is chemically bonded and hence not immediately available for transmission is known as bound energy (Q₂). Hence, one could write:

Q = Q₁ + Q₂

(5)

The greatest amount of power that the battery can store over a certain period is described by [22]:

$$P_{Bat,c\max ,kbm}=\frac{k{Q}_1{e}^{-k\Delta t}+Qkc\left(1-e^{-k\Delta t}\right)}{1-e^{-k\Delta t}+c\left(k\Delta t-1+e^{-k\Delta t}\right)}$$

(6)

where k and c are set to 2.12 h⁻¹ and 0.305, respectively. Similarly, the maximum amount of power that the storage may discharge over a given period (∆t) can be computed by [22]:

$$P_{Bat,d\max ,kbm}=\frac{-kc{Q}_{\max }+k{Q}_1{e}^{-k\Delta t}+Qkc\left(1-e^{-k\Delta t}\right)}{1-e^{-k\Delta t}+c\left(k\Delta t-1+e^{-k\Delta t}\right)}$$

(7)

After determining the actual charge or discharge power, the following two equations are used to determine the amount of available energy at the end of ∆t [22]:

$$Q_{1,end}=Q_1{e}^{-k\Delta t}+\frac{\left(Qkc-p\right)\left(1-e^{-k\Delta t}\right)}{k}+\frac{pc\left(k\Delta t-1+e^{-k\Delta t}\right)}{k}$$

(8)

Furthermore, one has (9) for the bound energy at the end of ∆t as

$$Q_{2,end}=Q_2{e}^{-k\Delta t}+Q\left(1-c\right)\left(1-e^{-k\Delta t}\right)+\frac{p\left(1-c\right)\left(k\Delta t-1+e^{-k\Delta t}\right)}{k}$$

(9)

2.1.4. Converter

The output power of the inverter-based source is calculated as:

$$P_t^{\mathrm{out\_inv}.}=P_t^{\mathrm{in\_inv}.}\times {\eta }^{\mathrm{Inverter}}$$

(10)

2.2. Economical Modeling

2.2.1. Net Present Cost

The NPC of a system is HOMER’s main economic output, which is the present value of all costs incurred minus the present value of all revenue earned over the system’s lifetime. Investment costs, replacement costs, operation, and maintenance (O&M) costs, pollution penalties, fuel costs, and grid power purchase costs are incorporated into the problem formulation. Salvage value and grid sales revenue are two sources of revenue.

2.2.2. Total Annualized Cost

The COE is defined as the system’s average cost per kWh. In MGs with non-thermal load, COE is calculated as [48]:

$$COE=\frac{C^{\mathrm{Annual}}}{{\mathrm{P}}^{\mathrm{Demand}}}$$

(11)

where $C^{\mathrm{Annual}}$ is expressed by:

$$C^{\mathrm{Annual}}=CRF\times NPC$$

(12)

The CRF in Equation (12) is defined as

$$CRF\left(i,N\right)=\frac{i{\left(1+i\right)}^N}{{\left(1+i\right)}^N-1}$$

(13)

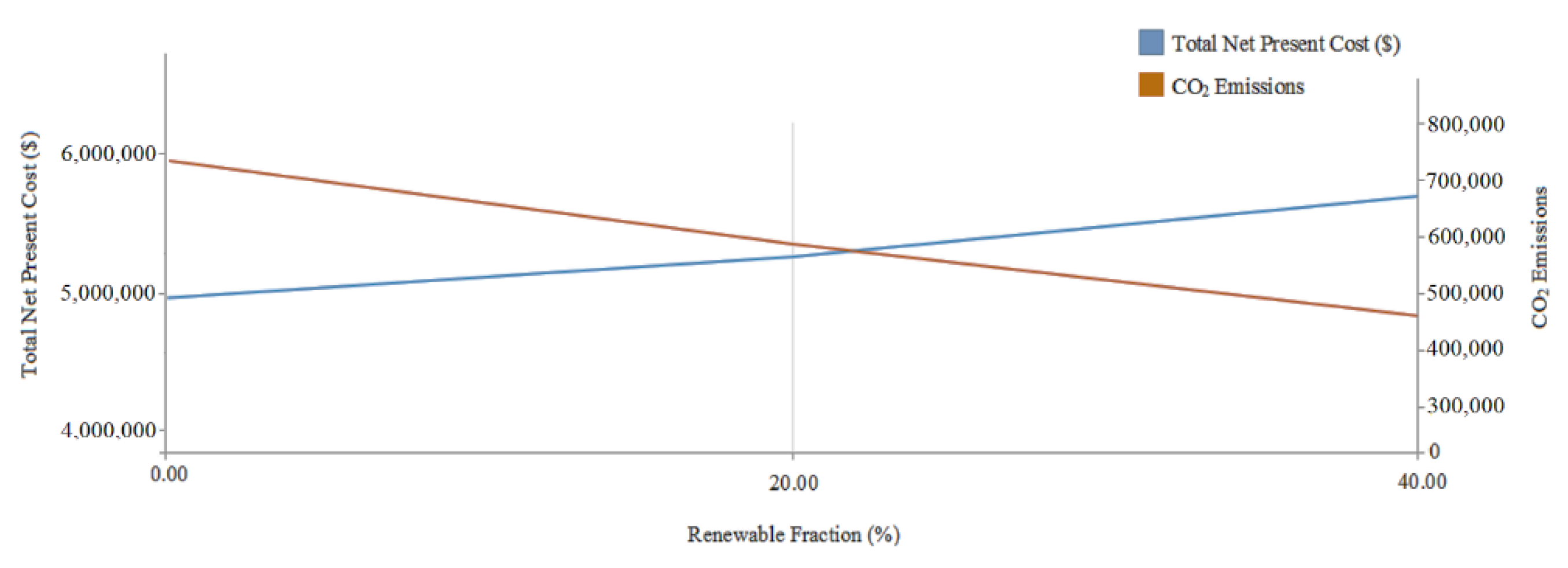
2.2.3. Renewable Fraction

The renewable fraction (RF), defined as the percentage of load supplied by RESs, is calculated as:

$$RF=\left(1-\frac{E^{\mathrm{Production}}}{E^{\mathrm{Supplied}}}\right)\times 100$$

(14)

where the energy sold to the grid is included in $E^{\mathrm{Supplied}}$.

2.3. CO₂ Emissions Calculation

The HOMER calculates the CO₂ emissions from two points of view as follows:

Generator: Before simulating the power system, the software estimates the emissions factor (kg of pollutant emitted per unit of fuel consumed) for each pollutant. The annual emissions are computed by multiplying the emissions factor by the total annual fuel consumption.

Main grid: To calculate emissions, HOMER multiplies net grid purchased power (in kWh) by the emission factor (in g/kWh) for each pollutant. The net grid purchased power is defined as

$$Netgridpurchases=E^{\mathrm{Supplied}}-E^{\mathrm{Production}}$$

(15)

3. Input Data

This section is devoted to describing the required input data for the formulation of the proposed planning problem.

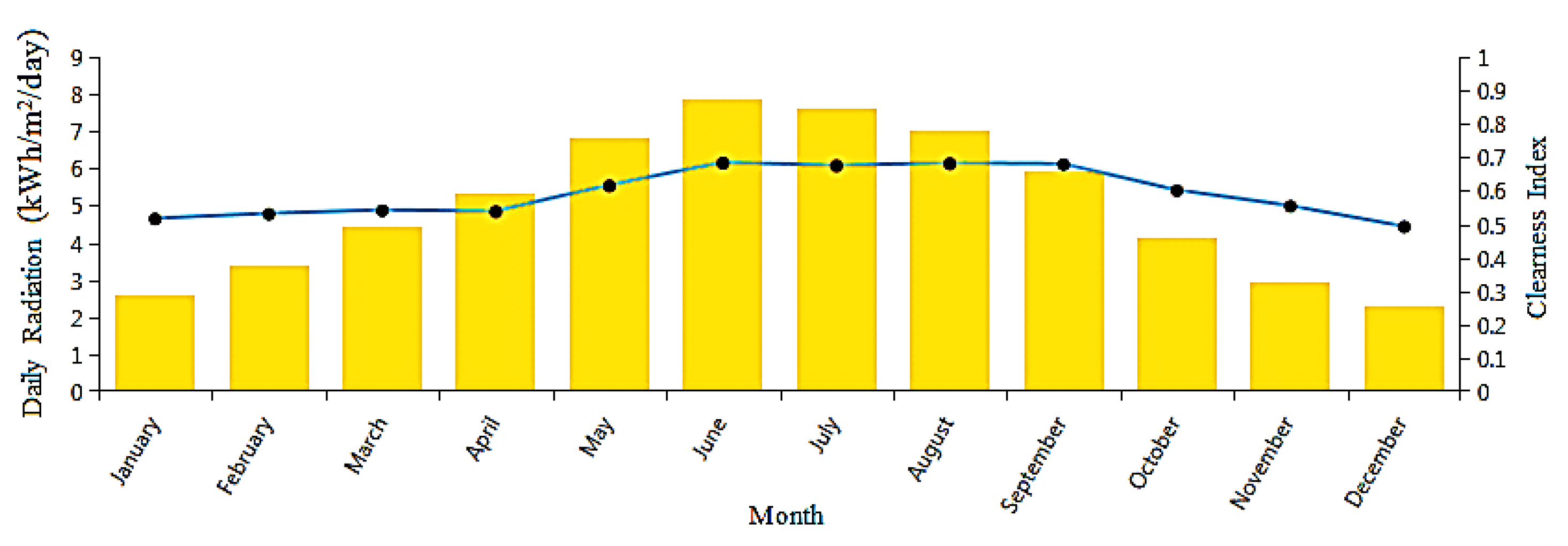
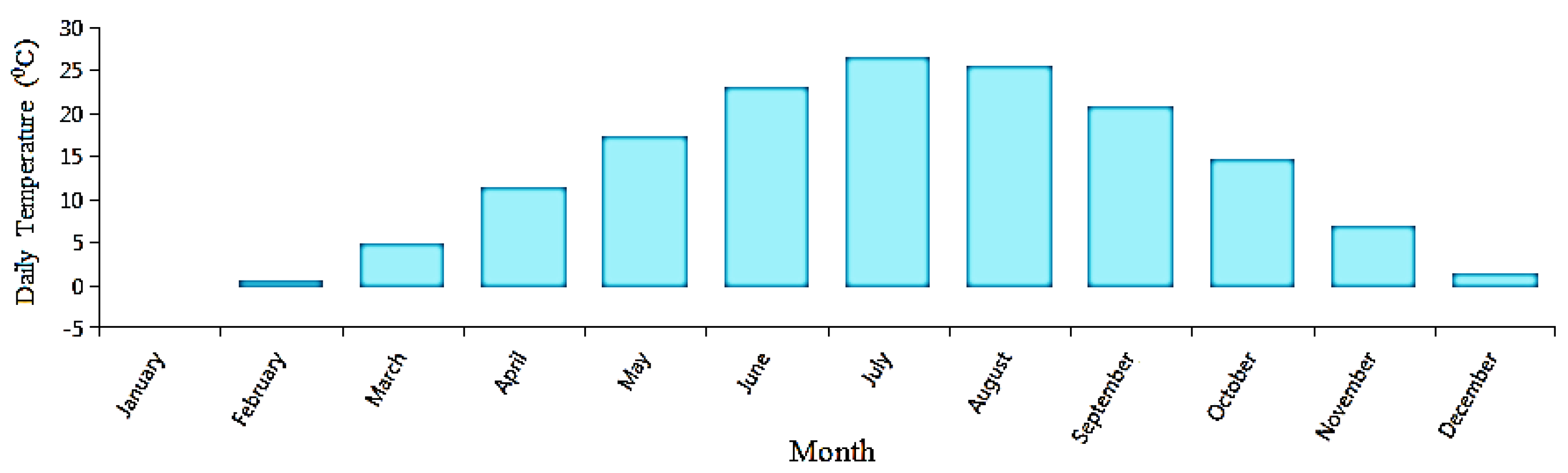
3.1. The Solar Radiation

The proposed case study is an educational complex in Sanandaj, Iran. The latitude and longitude of Sanandaj are 35.3219° N and 46.9862° E, respectively. The average amount of solar radiation and the clearness index, defined as a measure of atmosphere clearness, are shown in Figure 1. The monthly average data of temperature is also represented in Figure 2.

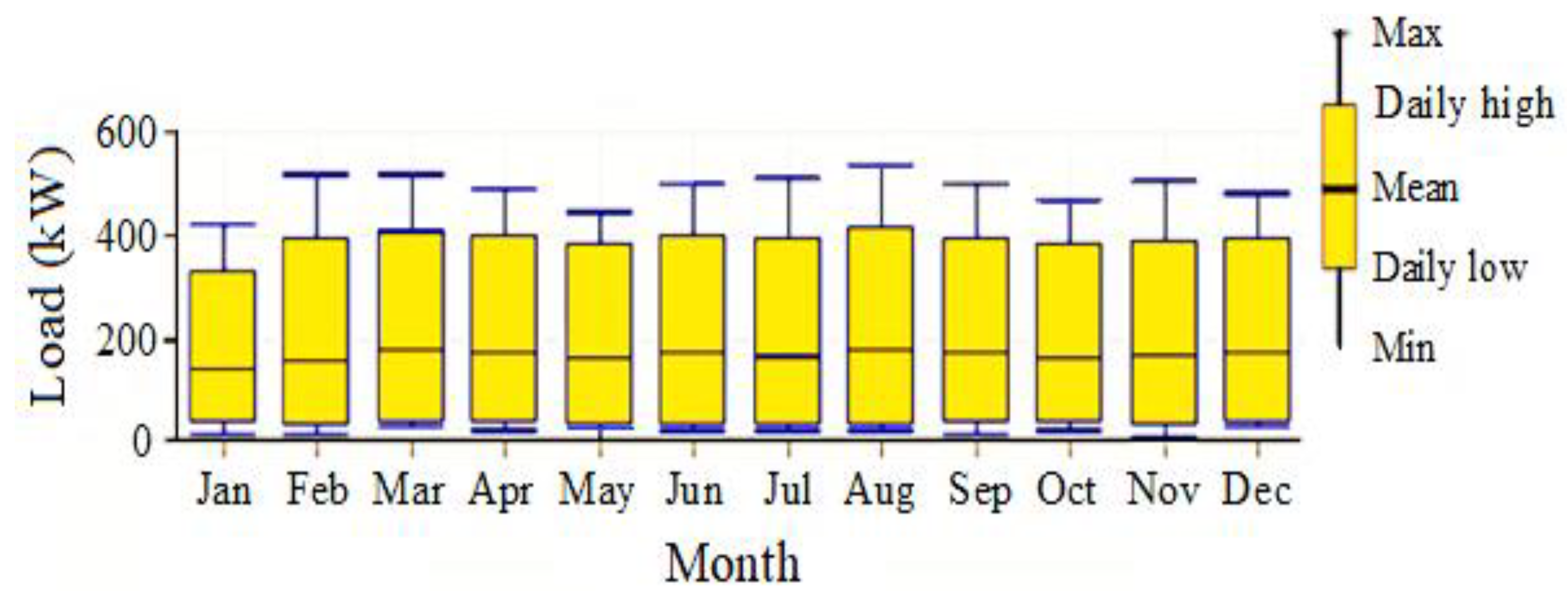
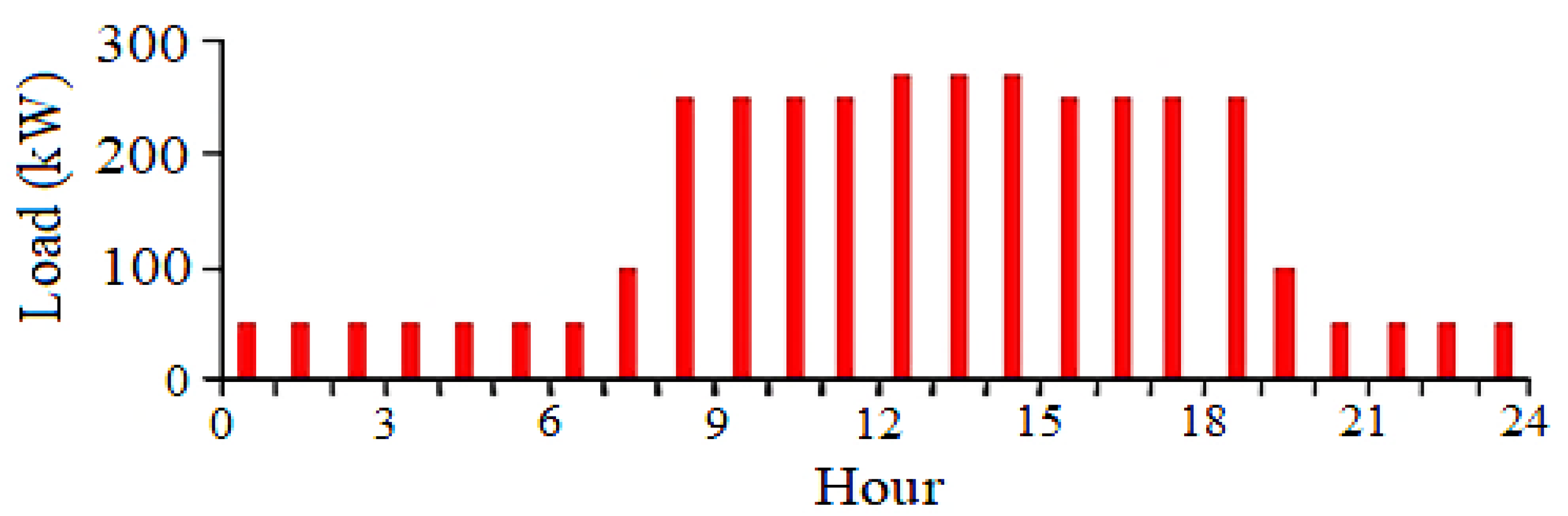
3.2. Load Consumption

The peak load of the under-study case study is 514.82 kW; the average energy consumption is 4060.6 kWh/day, and 169.17 kW; the load factor is assumed to be 0.33, with a 5% random variety factor (day-to-day and hour-to-hour). The proposed case study’s average seasonal profile and daily load profile are shown in Figure 3 and Figure 4, respectively. More details about the load classification can be found in

Table 2. Classified breakdown of educational complex loads.

Particulars	Total Energy Consumption (%)
Uninterrupted power supply	35
Air conditioning	26
Air handling unit	10
Lighting	15
Others	14

.

3.3. System Description and Requirements

The under-study MG is assumed to operate in grid-connected mode and capable of trading energy with the main grid at predetermined prices. The equipment data are presented in Table 3. In addition, details of pricing are given in Table 4. Furthermore, note that:

• To generate more electricity, 10 batteries are connected in series, forming a battery string.
• The batteries’ initial and minimum SOCs are set to 100% and 40%, respectively.

Table 3. The MG components description and specification [50].

Item	Specification	Item	Specification
PV panel		Minimum load ratio (%)	30
Model	MF100-EC4	Lifetime	15,000 h
Rated power	250 kW	Battery
Capital cost (USD)	7300/kW	Type	Surrette-6CS25P
Replacement cost (USD)	2974/kW	Capital cost (USD)	1229/single cell
O&M cost (USD)	10/year	Replacement cost (USD)	1229/single cell
Temperature coefficient	−0.5%/°C	O&M cost (USD)	10/year
De-rating factor (%)	80	Inverter
Lifetime	25 years	Type	Leonics GTP519S
Diesel generator		Rated power	900 kW
Type	Perkins	Capital cost (USD)	300/kW
Rated power	250 kVA	Replacement cost (USD)	300/kW
Capital cost (USD)	500/kW	O&M cost (USD)	10/year
Replacement cost (USD)	500/kW	Efficiency (%)	90
O&M cost (USD)	0.03/hours	Lifetime	10 years

Table 3. The MG components description and specification [50].

Item	Specification	Item	Specification
PV panel		Minimum load ratio (%)	30
Model	MF100-EC4	Lifetime	15,000 h
Rated power	250 kW	Battery
Capital cost (USD)	7300/kW	Type	Surrette-6CS25P
Replacement cost (USD)	2974/kW	Capital cost (USD)	1229/single cell
O&M cost (USD)	10/year	Replacement cost (USD)	1229/single cell
Temperature coefficient	−0.5%/°C	O&M cost (USD)	10/year
De-rating factor (%)	80	Inverter
Lifetime	25 years	Type	Leonics GTP519S
Diesel generator		Rated power	900 kW
Type	Perkins	Capital cost (USD)	300/kW
Rated power	250 kVA	Replacement cost (USD)	300/kW
Capital cost (USD)	500/kW	O&M cost (USD)	10/year
Replacement cost (USD)	500/kW	Efficiency (%)	90
O&M cost (USD)	0.03/hours	Lifetime	10 years

Table 4. Grid purchase and sell tariffs [50].

	Selling Energy Cost (USD/kWh)	Buying Energy Cost (USD/kWh)
Off-peak	0.16	0.0011
Normal	0.16	0.0047
Peak	0.16	0.0155

Table 4. Grid purchase and sell tariffs [50].

	Selling Energy Cost (USD/kWh)	Buying Energy Cost (USD/kWh)
Off-peak	0.16	0.0011
Normal	0.16	0.0047
Peak	0.16	0.0155

3.4. System Control and Constraints

The other required information to formulate the system is as follows:

• The project lifetime is considered as 10 years with an annual discount rate of 18%, and an inflation rate of 19% [51].
• The system’s fixed capital cost and fixed O&M cost are considered as USD 10,000 for the entire project, and 10 USD/year, respectively.
• A maximum annual capacity shortage restriction is established throughout the simulation process. This value is set to 0 to assess the system’s ability to deliver peak demand even in the event of a short fault or interruption.
• The penalty for CO₂ pollution is considered 50 (USD/t).
• The discharge efficiency is assumed to be unity.
• The operational reserves are defined as 10% of hourly loads and 25% of PV output.

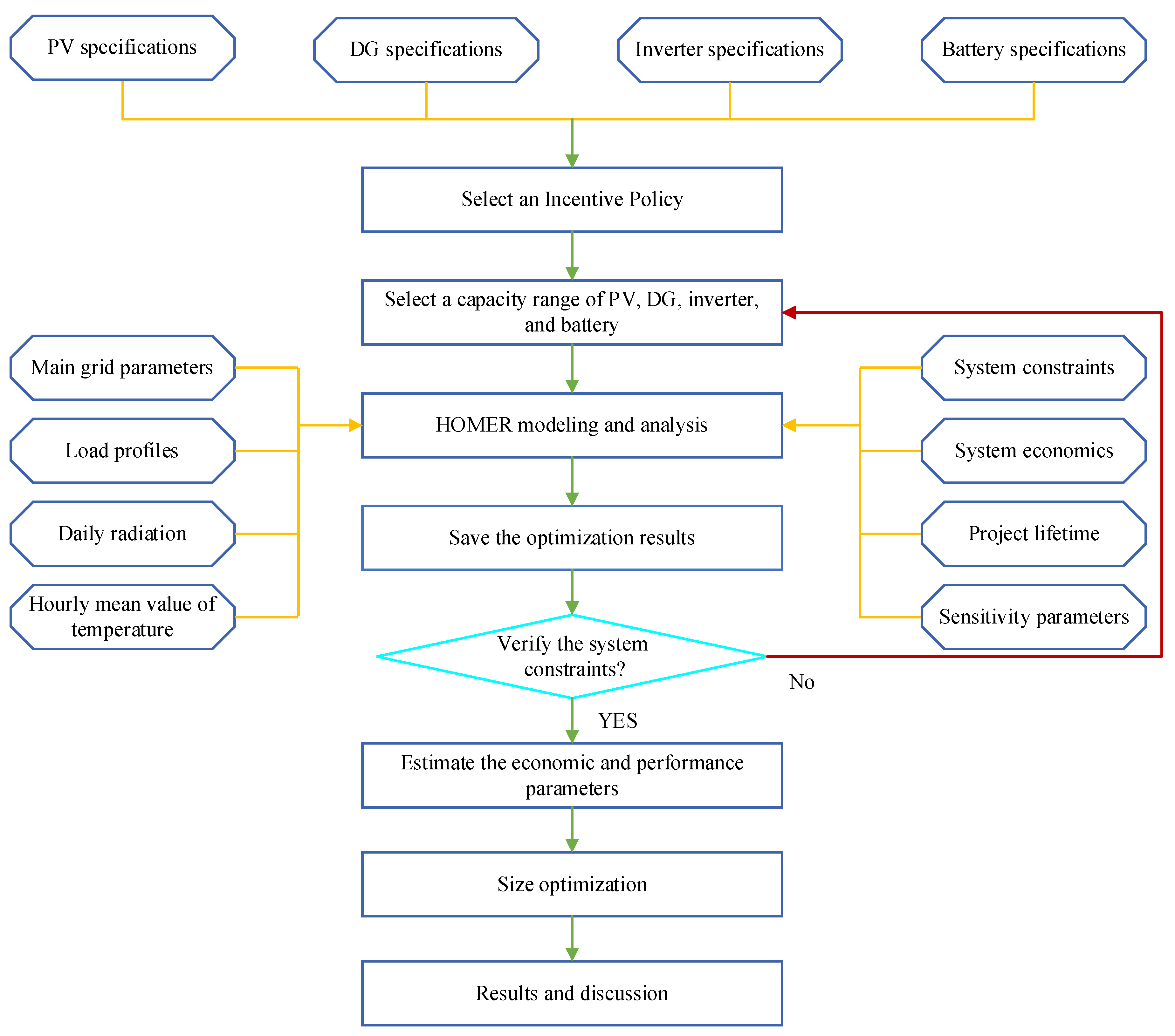
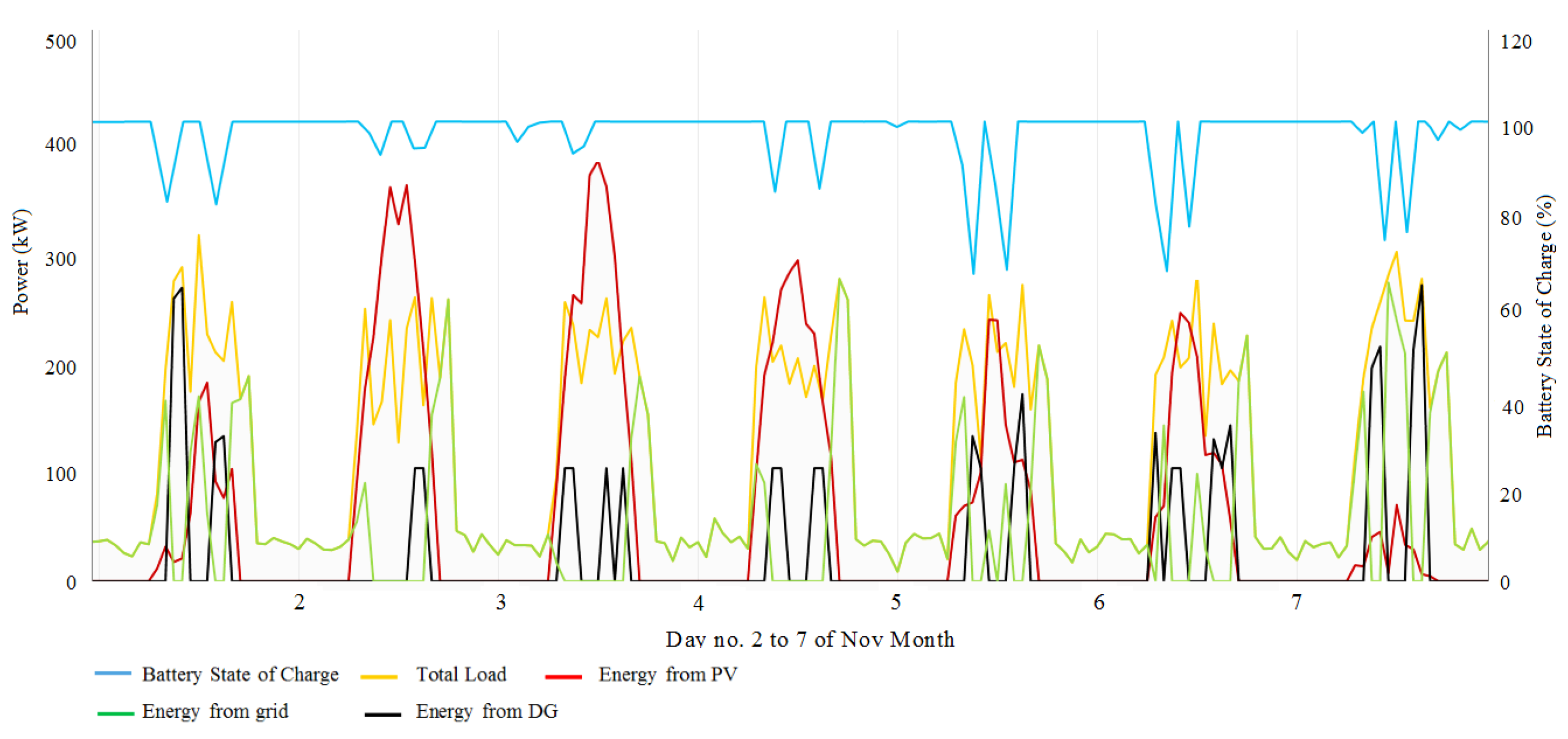
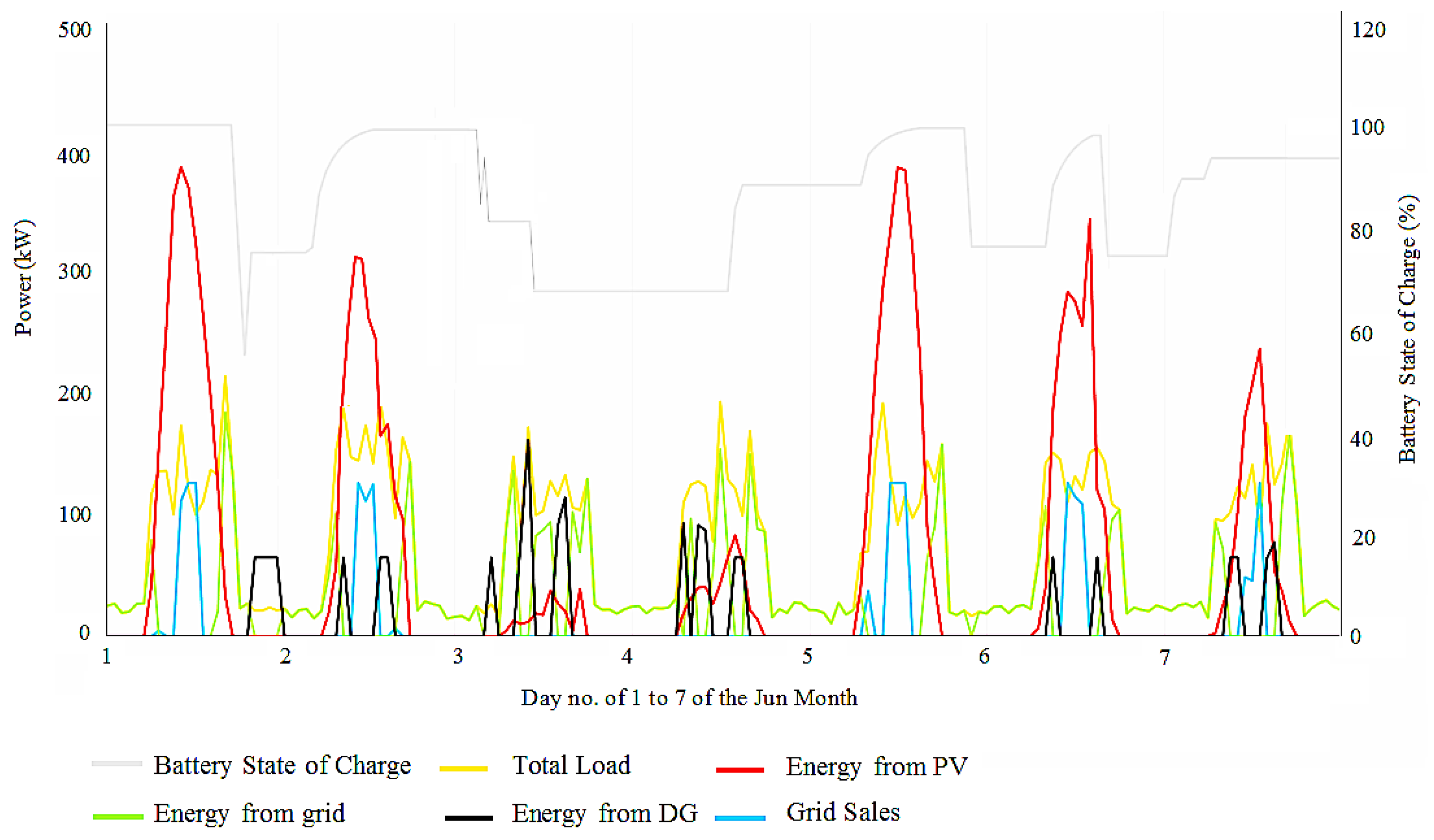
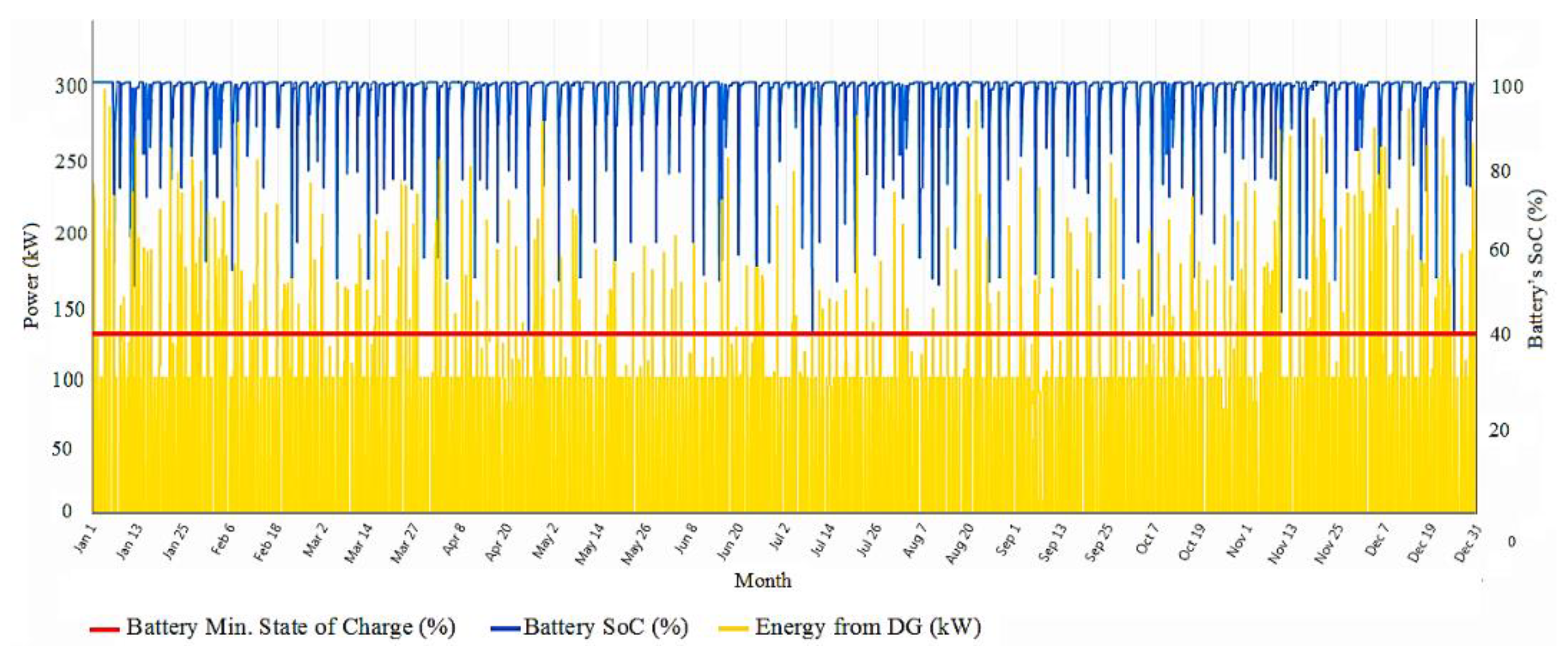
4. Simulation Results

This paper uses the HOMER simulation software to assess the performance of hybrid system structures. The under-study MG structure is shown in Figure 5. The simulation’s goal is to find the best incentive strategy and MG configuration to meet the MG’s load while reducing NPC and CO₂ emissions. To this end, the first sub-section investigates the impact of RES-based MG generation on NPC and CO₂ emissions. Then, the impact of incentive policies on the MG design from technical and economic points of view is investigated. The detailed methodology used for analysis and modeling is shown in Figure 6. The general description of the figure can be explained as follows:

• The technical features of PV panels, DGs, batteries, and converters, as well as their O&M and capital costs, are fed into HOMER software as input data.
• One of the incentive policies is chosen.
• Various sizes of the components are defined as a search space for the problem.
• An optimum solution is determined by utilizing the following data: temperature data, daily average solar radiation with the clearness index, system constraints and project economics, project lifetime, the main grid parameters, total load, and sensitivity variables.
• Optimization is completed for a different combination of devices.

Figure 5. The MG studied in this paper.

Figure 5. The MG studied in this paper.

Figure 6. Flowchart of analysis using the HOMER Pro MG analysis tool.

Figure 6. Flowchart of analysis using the HOMER Pro MG analysis tool.

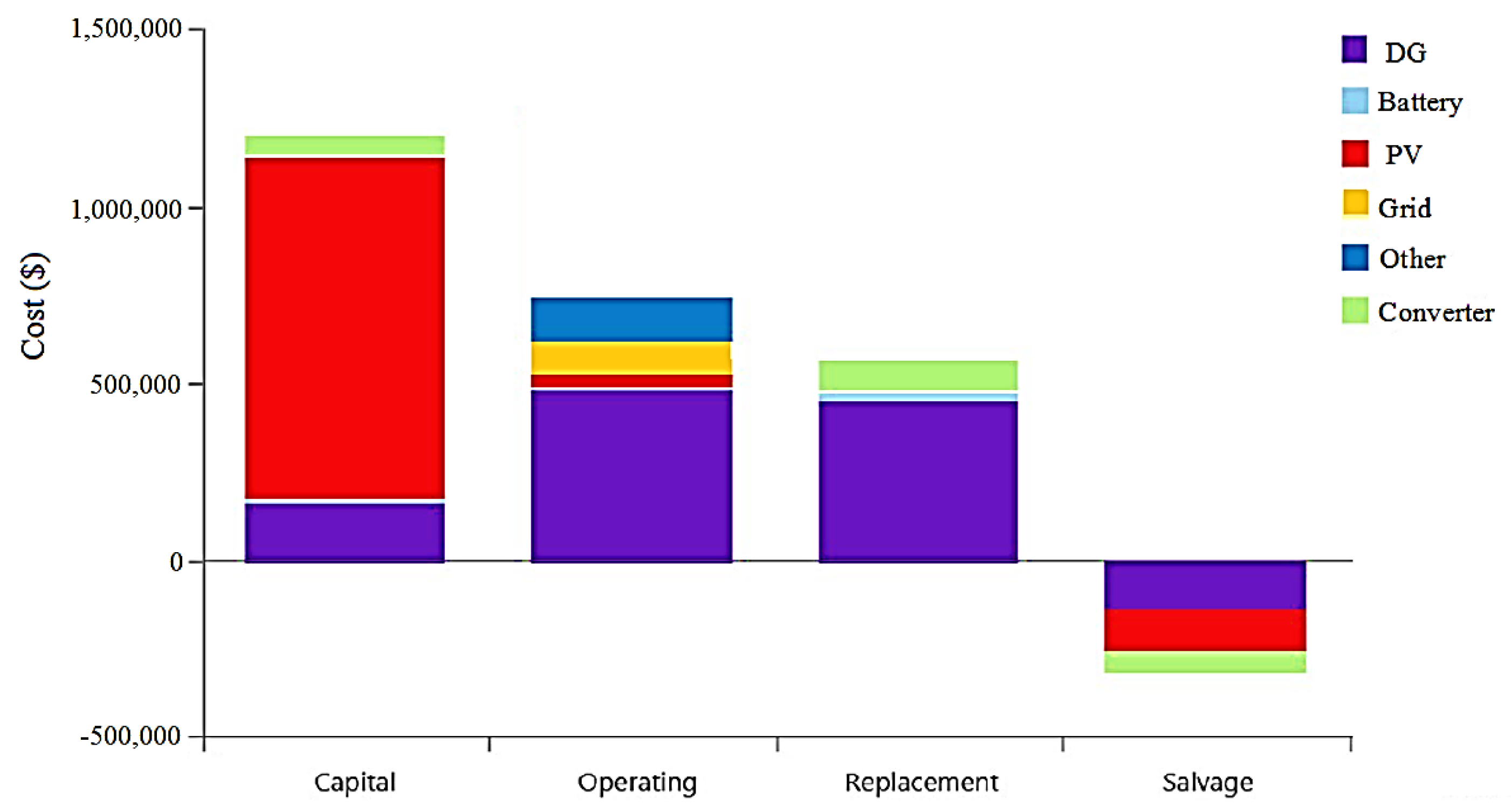
4.1. Results of the MG Design without Considering Incentive Policy

To demonstrate the effect of RES penetration on the proposed case study, three scenarios were investigated without considering incentive policies: (1) the base case (without penetration of RESs), (2) the base case with at least 20% penetration rate of RESs, and (3) the base with at least 40% penetration rate of RESs.

4.1.1. Base Case

The results of the optimal configuration of DGs and the main grid to meet the load in the basic case are shown in

Table 5. The best optimization results of the MG planning for the base case.

Scenario	Grid (kW)	DG (kW)	PV (kW)	Converter (kW)	Energy Storage (n)	Initial Capital (USD in Millions)	Operating Cost (USD/year)	COE (USD)	NPC (USD in Millions)	RF (%)
Base case	600	350	0	0	0	0.35267	187,276	0.193	4.94	0

. The electrical generation of DGs is 365,425 kWh/year, and the MG purchases 724,421 kWh/year from the main grid. This means that while DGs supply 33.6% of the total load, the main grid provides 66.4%. The excess energy is 13,381 kWh/year (1.23). The CO₂ emissions are calculated to be 734,498 kg/year, while a DG’s total fuel consumption is 106,417 L. Figure 7 shows the energy contributions from the main grid, energy from the DG, total load, and excess energy for July. From Figure 7, it can be seen that excess energy is increased when a DG provides the load by generating more electrical power than the actual demand. As a result, it may be regarded as a financial benefit in countries such as Iran, where diesel is a national product and a low-cost fuel. However, to reduce air pollution, DG usage should be kept to a minimum.

4.1.2. The Base Case with at Least 20% Penetration Rate of RESs

The results of the MG planning for the base case with an RES penetration level of 20%, as the second scenario, are shown in

Table 6. The best optimization results of the MG planning for the base case with at least 20% penetration rate of RESs.

Scenario	Grid (kW)	DG (kW)	PV (kW)	Converter (kW)	Energy Storage (n)	Initial Capital (USD in Millions)	Operating Cost (USD/year)	COE (USD)	NPC (MUSD)	RF (%)
Base case with at least 20% penetration rate of RESs	600	380	164	248	0	1.48	158,079	0.210	5.30	20.1

. In this case, the PV generation amounts to 264,449 kWh/year (23.6%), DG generation is 266,046 kWh/year (23.7%), and the main grid meets 591,369 kWh/year (52.7%) of the total load with 22,787 kWh/year excess energy (2.03%). Furthermore, 108 kWh of energy is also sold to the main grid. Moreover, the DG produces 586,959 kg/year of CO₂ emission and consumes 81,453 L of fuel. This scenario reduces CO₂ emissions compared to the base case without RES penetration because of the increased contribution of RESs and lower consumption of diesel fuel. The NPC for this system, however, is significantly higher due to the fact that the initial capital cost, replacement cost, and operating cost are all higher than the base scenario. The optimization results of the MG planning for this case are presented in Table 6. Figure 8 depicts the contribution of MG components to meet demand, main grid energy, total load, and excess energy for May.

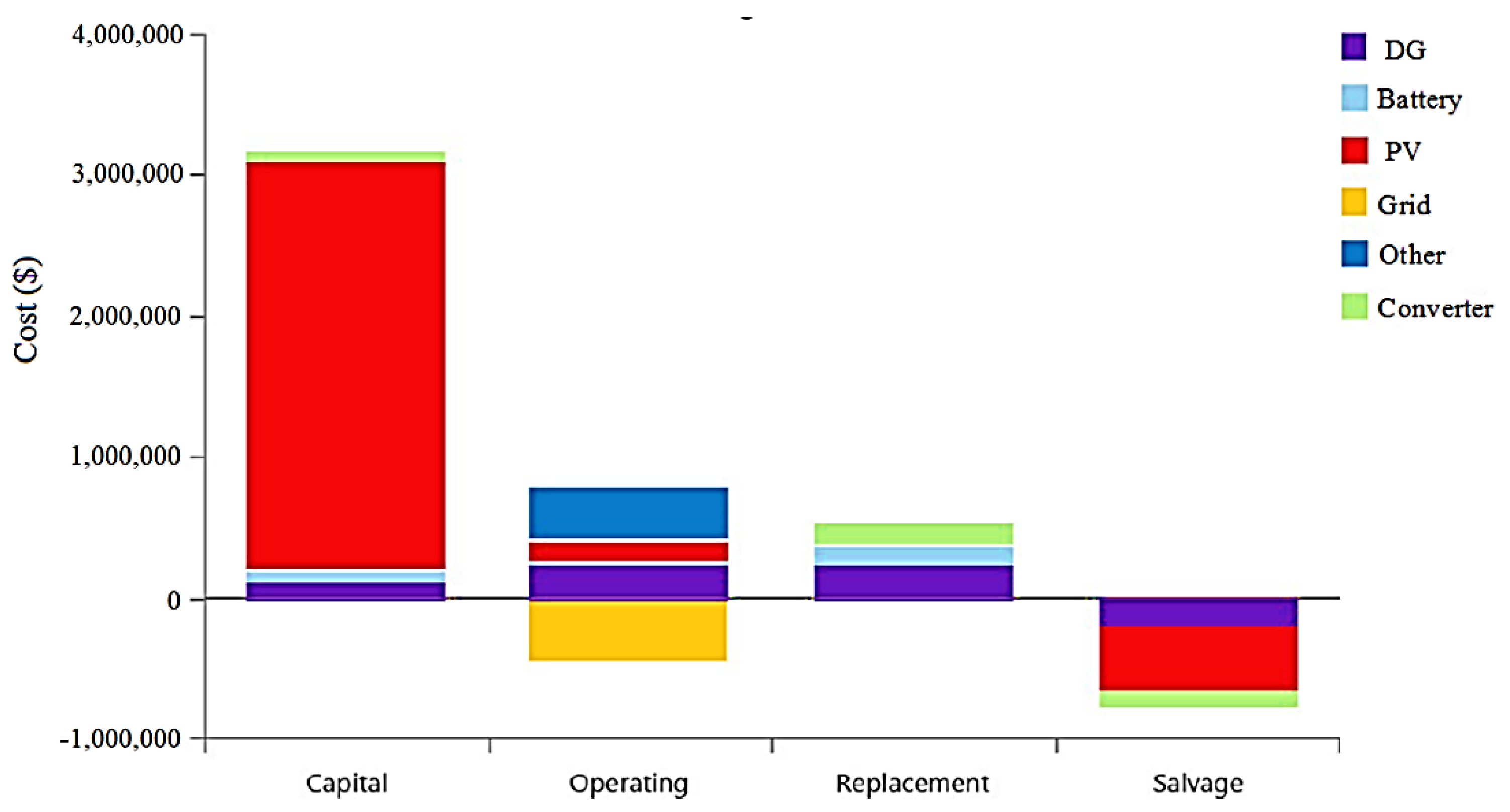
4.1.3. The Base Case with at Least 40% Penetration Rate of RESs

Finally, according to

Table 7. The best optimization results of the MG planning for the base case with at least 40% penetration rate of RESs.

Scenario	Grid (kW)	DG (kW)	PV (kW)	Converter (kW)	Energy Storage (n)	Initial Capital (USD in Millions)	Operating Cost (USD/year)	COE (USD)	NPC (MUSD)	RF (%)
Base case with at least 40% penetration rate of RESs	600	380	362	322	120	3.07	129,616	0.246	5.91	40.1

, in the base scenario with at least a 40% RES penetration rate, PV panels, a DG, and a battery are assumed to be the best components for the proposed grid-connected MG. PV panels, the DG, and the main grid provide 582,402 kWh/year (46.7%), 198,097 kWh/year (16%), and 460,789 kWh/year (37.1%), respectively. The CO₂ emissions, in this case, are 546,175 kg/year, while the excess energy is 91,232 kWh/year (7.35 percent). The DG’s total fuel consumption is 63018 L, and 26,020 kWh of MG energy is sold to the main grid. The MG component generations and status for November are shown in Figure 9. As shown in Figure 9, the battery is charged by the PV panels, but when the PV generation is insufficient to meet the load, the battery is discharged. In this case, the DG will meet the load and maintain a stable battery charge level.

According to the results of

Table 8. Overall effects of RES penetration on the NPC and CO₂ emissions.

Scenario	RF (%)	CO2 Emissions (kg/year)	COE (USD)	NPC (MUSD)
Base case	0	734,498	0.193	4.94
Base case with at least 20% penetration rate of RESs	20.1	586,959	0.210	5.30
Base case with at least 40% penetration rate of RESs	40.1	546,175	0.246	5.91

and as shown in Figure 10, increasing the penetration level of RESs reduces CO₂ emissions while increasing the NPC. The main problem of interest, however, is how to reduce NPC.

4.2. Incentive Policies’ Results

Three incentive policies are defined in this section to realize an MG.

A.

Reducing the investment cost of MG equipment;

B.

Increasing the price of selling energy by the MG to the main grid;

C.

Reducing the price of purchasing energy by the MG from the main grid.

Furthermore, it is assumed that the government’s incentive is conditional on the presence of the selected RES penetration rate.

A. Reducing the investment cost of MG equipment:

Under the first incentive program, the government pays a portion of the investment cost of the MG’s equipment to encourage the investors to realize the RES-based MG. For this aim, the following two cases would be considered.

A.1. The government pays 20% of the investment cost of the MG’s resources for an RES penetration rate of at least 20%:

In this case, the optimum MG design is a combination of PV panels, DGs, and batteries. While PV panels and DGs provide 264,449 kWh/year (23.6%), and 266,046 kWh/year (23.7%) of the load, respectively, the remaining 591,369 kWh/year (52.7%) is provided by the main grid. The excess energy is 2.03% of the load (22,787 kWh/year), while the energy sold to the main grid is 108 kWh. Furthermore, the amount of CO₂ emissions is 586,959 kg/year, and the total fuel consumption by a DG is 81,453 L. While the components’ contributions in this scenario are the same as the base case with a 20% RES penetration level, the NPC is decreased in response to the definition of an incentive scheme.

A.2. The government pays 40% of the investment cost of the MG’s resources for an RES penetration rate of at least 40%:

A combination of PV panels, DGs, and batteries is considered to be the best configuration for the proposed grid-connected MG. The contributions of PV panels, DGs, and the main grid are 1065560 kWh/year (69.2%), 107,394 kWh/year (6.97%), and 367,966 kWh/year (23.9%) of total load, respectively. The excess energy of this plan is 245,145 kWh/year (15.9%) of the load, and the DG consumes 34,240 L of fuel in total. The amount of CO₂ emissions is 322,182 kg/year is significantly lower than the other cases due to RESs’ higher penetration. The system is also financially efficient, with a 138,834 kWh energy sell-back rate to the main grid.

B. Increasing the price of selling energy by the MG to the main grid:

In the second scenario, the price of selling energy by the MG to the main grid increases as follows.

B.1. A total of 20% for the MG with at least 20% penetration rate of the RESs:

The optimal plan of this case includes the PV system, a DG, and the main grid, with the participation of 23.6% (264,449 kWh/year), 23.7% (266,046 kWh/year), and 52.7% (591,369 kWh/year), respectively. The plan’s excess energy is 2.03% of the total load (22,787 kWh/year), resulting in 108 kWh of electricity sold to the main grid. In addition, the total fuel usage of the DG is 81,453 L, and the amount of CO₂ emissions is 586,959 kg/year. The amount of increase in CO₂ emissions, in this case, is increased due to the lower RES penetration rate than in case A.1.

B.2. A total of 40% for the MG with at least 40% penetration rate of the RESs:

In this case, 47.9% (607,702 kWh/year), 16.3% (207,236), and 35.8% (453,553 kWh/year) of the load are provided by the PV system, a DG, and the main grid, respectively. The excess energy of this system is 8.91% (112,988 kWh/year) of the total load. Energy sold to the grid is 31,238 kWh, the CO₂ emissions are 459,834 kg/year, and the total fuel consumption by the DG is 66,163 L.

C. Reducing the price of purchasing energy by the MG from the main grid:

In the third scenario, the government decreases the price of selling energy to the MG through two cases as follows:

C.1. A total of 20% reduction in the price of purchasing energy from the main grid for the MG with at least 20% penetration rate of RESs:

At the 20% penetration rate of RESs, while 23.6% of the load is satisfied through the PV system (264,449 kWh/year), DG output is 23.7% (266,046 kWh/year), and 52.7% of the load is supplied through the main grid (591,369 kWh/year). In this scenario, the CO₂ emissions are 586,959 kg/year, while the total fuel use by the DG is 81453 L. Furthermore, the excess energy is 2.03% (22,787 kWh/year) of the total load, with 108 kWh sold to the main grid.

C.2. A total of 40% reduction in the price of purchasing energy from the main grid for the MG with at least 40% penetration rate of RESs:

The optimal grid-connected hybrid configuration model for this case includes the PV system, a DG, and the main grid with capacities of 627,943 kWh/year (49%), 205,748 kWh/year (16.1%), and 448,220 kWh/year (35%), respectively. The excess energy is 9.41% (120,574 kWh/year) of the load; the energy sold to the main grid is 35,806 kWh; the CO₂ emissions are 455,400 kg/year. The DG consumes 65,756 L of fuel in total.

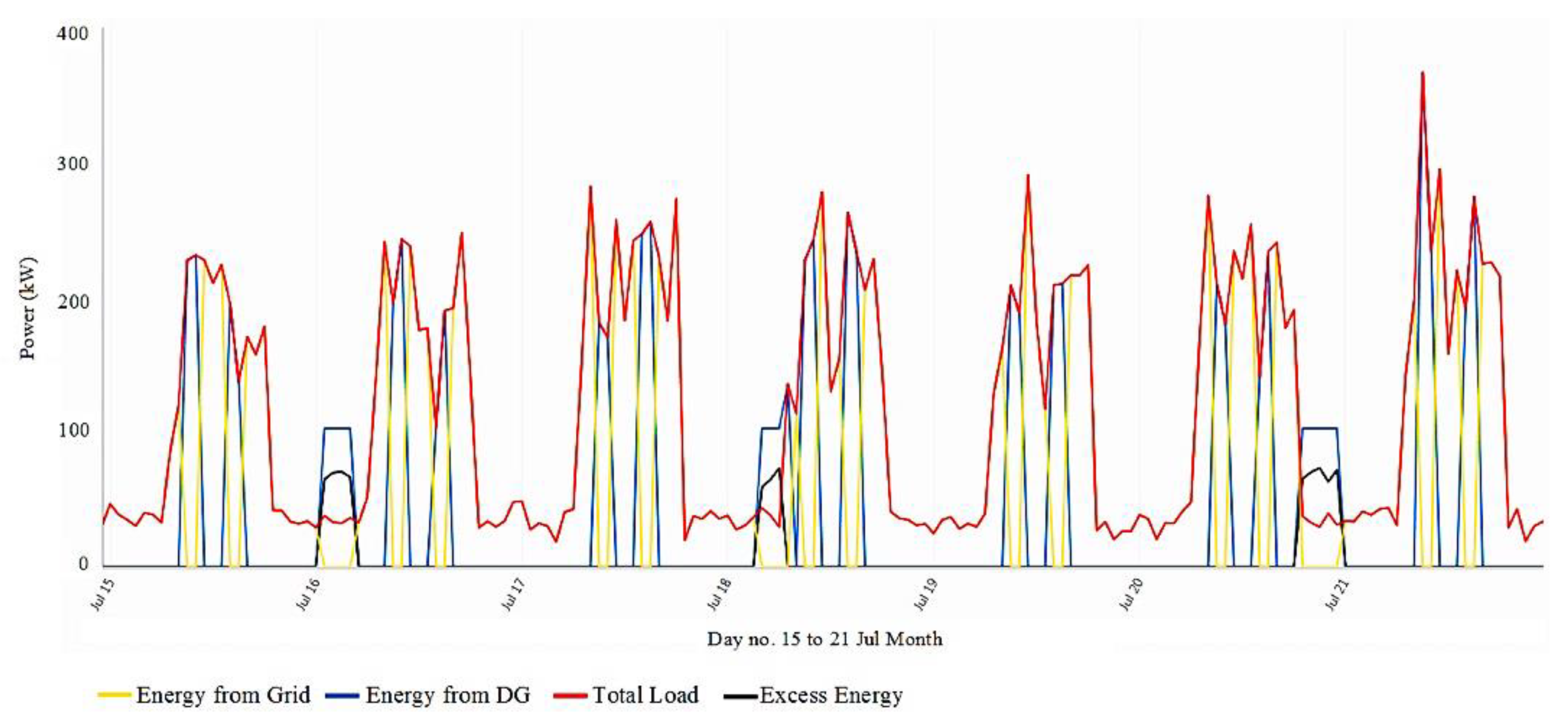
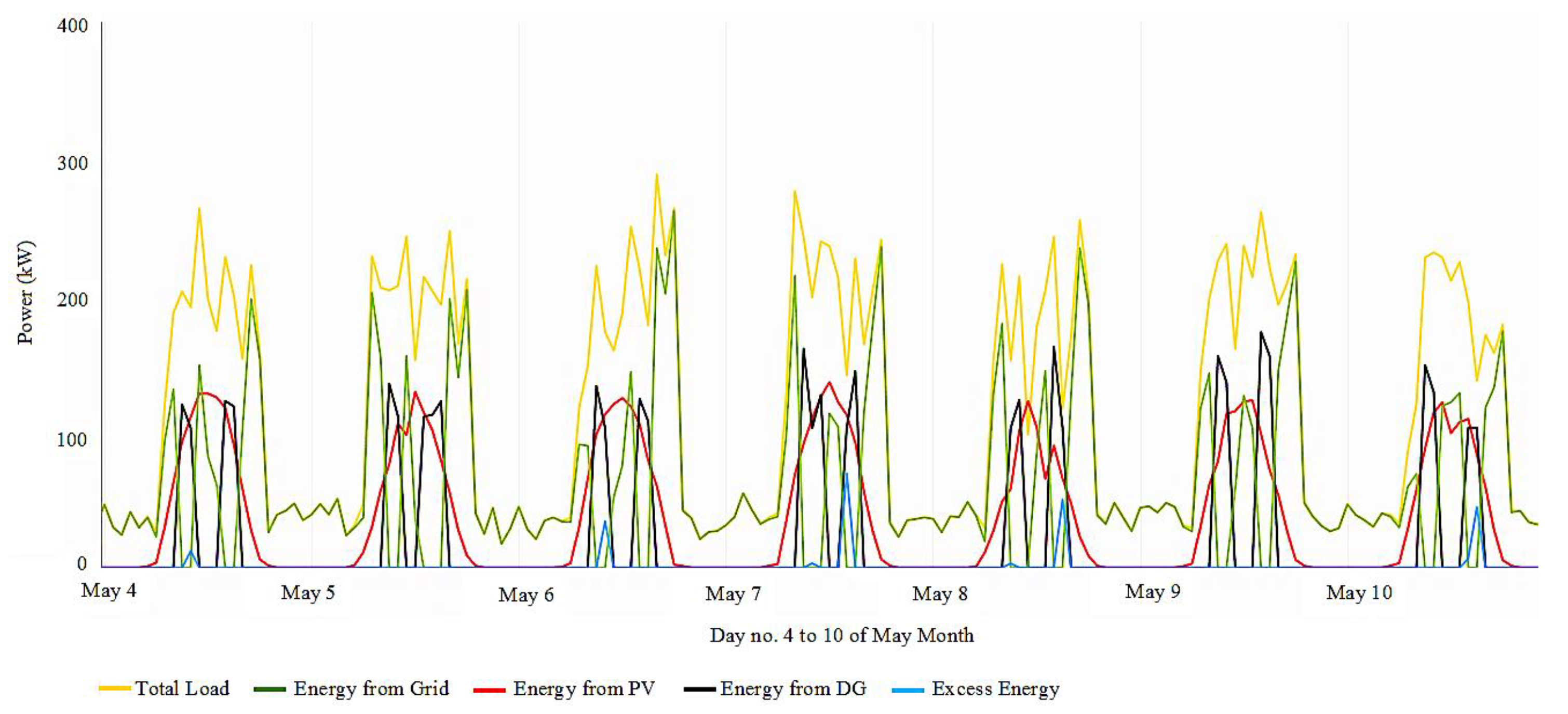
4.3. Discussion

Table 9. Optimization result of the proposed MG system with 20% injections of RESs.

Plan	Grid (kW)	DG (kW)	PV (kW)	Converter (kW)	Battery (n)	Initial Capital (USD in Millions)	Operating Cost (USD)	COE (USD/kWh)	NPC (USD in Millions)	RF (%)
A.1	600	380	164	248	20	1.2	129,544	0.172	4.03	20.1
B.1	600	380	164	248	0	1.48	128,424	0.183	4.29	20.1
C.1	600	380	164	248	40	1.5	128,390	0.183	4.31	20.1

and

Table 10. Optimization result of proposed MG system with 40% injections of RESs.

Plan	Grid (kW)	DG (kW)	PV (kW)	Converter (kW)	Battery (n)	Initial Capital (USD in Millions)	Operating Cost (USD)	CoE (USD/kWh)	NPC (USD in Milliona)	RF (%)
A.2	600	400	661	451	140	3.17	29,182	0.144	3.81	60.8
B.2	600	410	377	367	80	3.09	98,270	0.217	5.24	40.2
C.2	600	410	390	346	0	3.05	96,068	0.217	5.26	41.0

show more details of the MG’s configuration, taking into consideration incentive policies and assuming at least 20% and 40% RES penetration rates, respectively. The comparison of the scenarios in terms of CO₂ emissions is shown in

Table 11. Summary of NPC, COE, and CO2 emissions compression between cases.

	Case A		Case B		Case C
	A.1	A.2	B.1	B.2	C.1	C.2
NPC compared to the base case (%)	−18.42	−22.87	−13.15	+0.06	−12.75	+0.06
COE compared to the base case (%)	−10.88	−25.38	−0.01	+12.43	−0.01	+12.43
CO2 emissions compared to the base case (%)	−20.8	−56.13	−20.8	−37.39	−20.8	−37.99

. It shows that at a lower RES penetration rate (i.e., 20%), the scenarios reduce CO₂ emissions by the same amount. However, in terms of NPC and COE reductions, scenarios A, B, and C, respectively, have the highest NPC and COE reduction compared to the base case. Furthermore, according to Table 10, for an RES penetration level of at least 40%, scenario A gives leads to the highest reduction in NPC and COE. For scenarios B and C with an increasing RES penetration rate, not only does NPC not decrease, but it also increases due to the high initial cost of the equipment. Hence, these two incentive policies are not effective in decreasing NPC in systems with at least a 40% RES penetration. As a result, the proposed incentive policy in scenario A is suggested as the effective incentive policy from NPC and COE points of view. At this level of RES penetration, again, scenario A leads to a maximum reduction in CO₂ emissions; and between scenarios B and C, scenario C has the better performance. This is due to the fact that compared to the other cases, case A has the highest PV system penetration rate. Consequently, as shown in Table 11, reducing the investment cost of MG’s equipment may be suggested as an effective incentive policy to encourage customers to utilize MG-produced energy rather than purchasing electricity from the main grid.

To further justify the proposed formulation, individual system component costs for scenarios A.1 and A.2 are presented in Figure 11 and Figure 12, respectively. According to these figures, the PV system’s initial capital cost is the system’s dominant cost in both cases.

The simulation results of the main grid, PV system, DG, and battery, which are the fundamental elements of the hybrid system optimization process, are shown in Figure 13. The figure depicts the daily trend of the PV system and DG power generations, total load, battery SOC, energy from the main grid, and grid sales for the period of 1–7 June. Extra energy exists when the PV power provides the load, as shown in Figure 13; at these times, the DG is turned off and the excess energy is sold to the main grid. When PV generation is less than the load, the DG works to feed the load.

The fluctuation in the SOC of the battery as well as the contribution of the DG for recovering SOC for each month of the year is depicted in Figure 14. It is worth noting that the minimum value of SOC does not fall below 40%, even during the months with the least solar radiation. On three days in April, July, and December, the SOC of the battery reaches its lowest level; however, the blackout was prevented due to the availability of the DG.

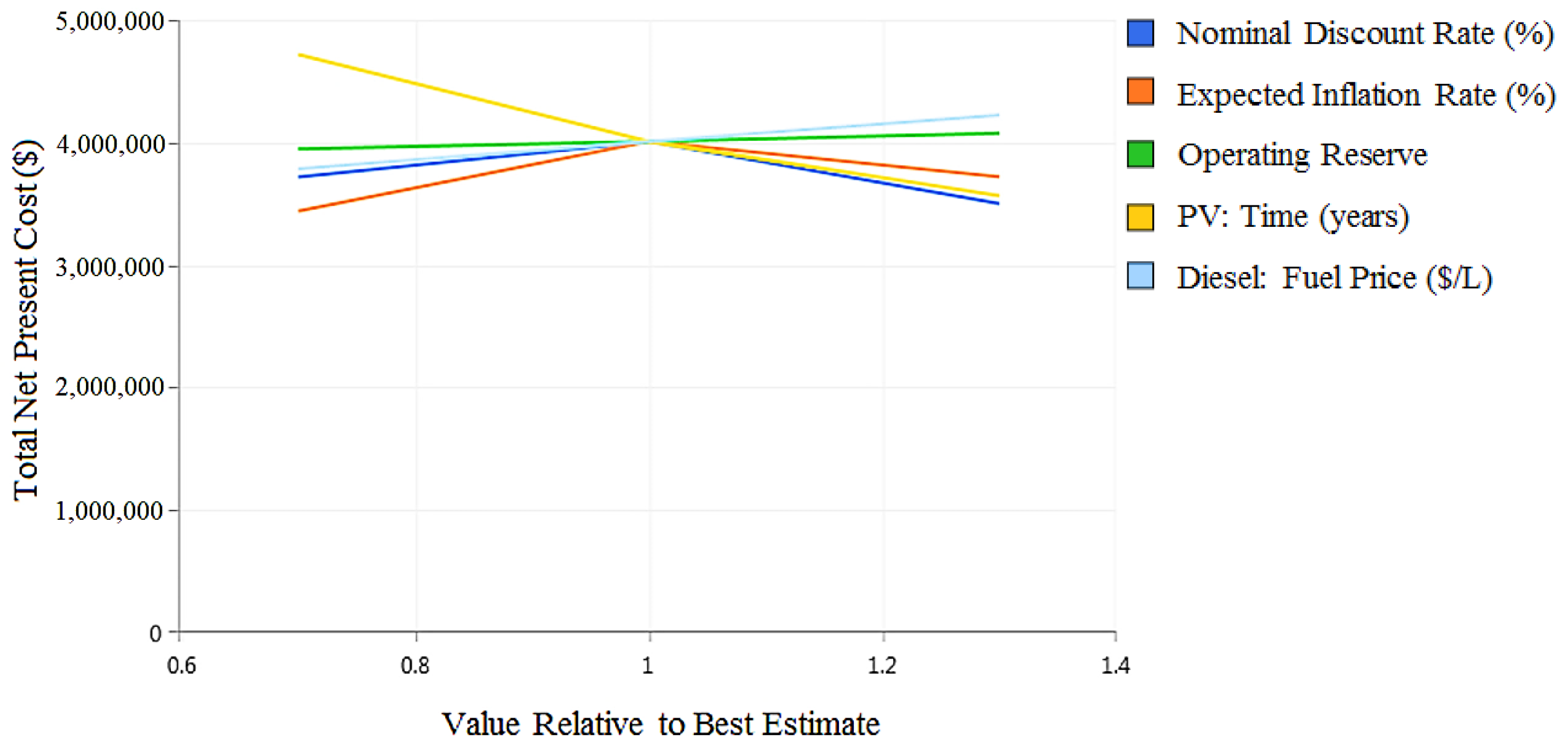
5. Uncertainty in Key Variables

One of the main challenges for MG designers is uncertainties in the key parameters of interest. This section investigates the impact of the nominal discount rate, expected inflation rate, PV lifetime, DG fuel price, and optimal reserve on the NPC. This study takes 30 percent uncertainty into account for the variables. The spider graph in Figure 15 shows the sensitivity of NPC to each type of uncertain parameter. As a result, the NPC is more sensitive to the nominal discount rate, expected inflation rate, and PV lifetime.

6. Conclusions

In this paper, the optimal combination and size of an MG’s energy resources are determined to power an educational complex in Iran, considering the incentive policies. The suggested resources in the MG are the PV system, DGs, batteries, and inverter-based sources. The simulation was conducted using the HOMER software as an accepted powerful tool for optimal planning of the MG. The base case results showed that the DGs, in addition to trading energy with the main grid, are the only choices to supply the load. The NPC and the amount of CO₂ emission of the best plan are USD 4.94 million and 734,498 kg/year. Then, three incentive policies are defined, where for each of them, two scenarios consisting of at least 20% and 40% penetration rate of RESs are proposed. The main conclusions from applying these incentive policies to the planning problem of the MG are as follows:

• The case with an incentive policy for the investment cost of the MG’s resources has the maximum impact on the NPC reduction.
• The maximum CO₂ and NPC reduction occurred in the case of reducing the investment cost of the MG’s equipment.
• The sensitivity analysis results, carried out based on a variation of some parameters, including the expected inflation rate, the PV lifetime, DG fuel price, and optimal reserve show a significant influence of the nominal discount rate, expected inflation rate, and PV lifetime on the NPC.
• The considering incentive policy for investors has resulted in increasing RES penetration and minimizing the dependence on harmful emissions and fossil fuels. Finally, it should be noted that the present work fails to consider uncertainties in load and weather data, which may affect simulation results. Furthermore, the results for the high penetration of inverter-based sources should consider technical aspects regarding stability rather than the economical perspective.