Mean Flow, Turbulent Structures, and SPOD Analysis of Thermal Mixing in a T-Junction with Variation of the Inlet Flow Profile
Abstract
:1. Introduction
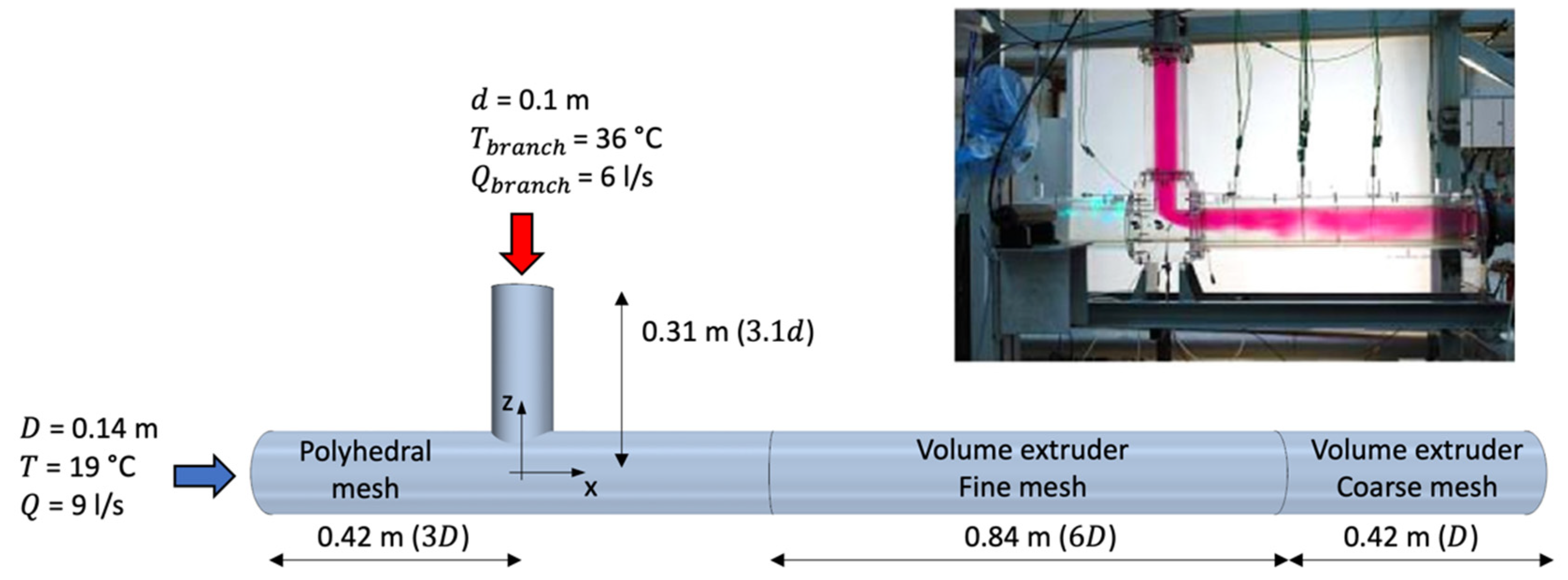
2. Description of the CFD Models
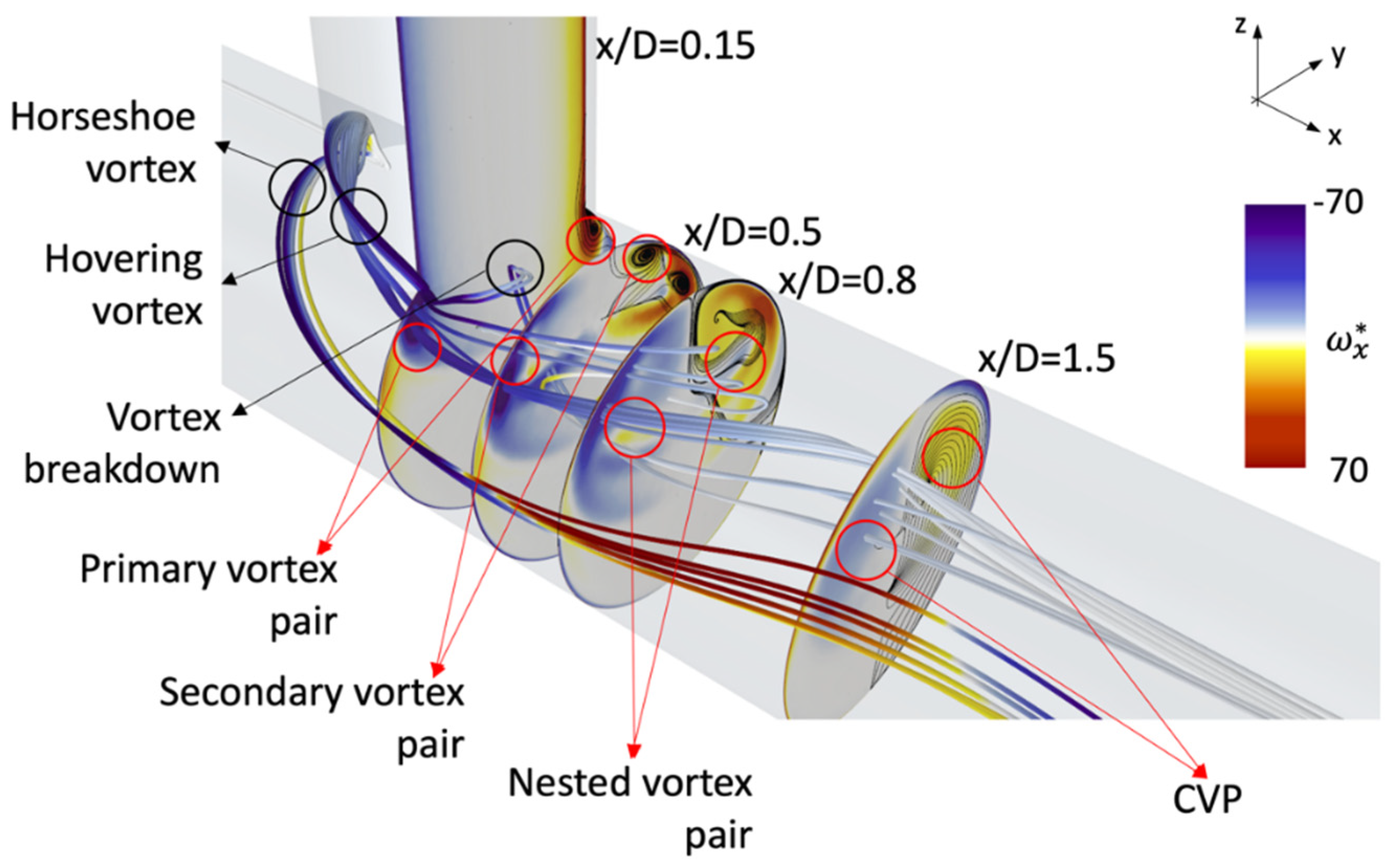
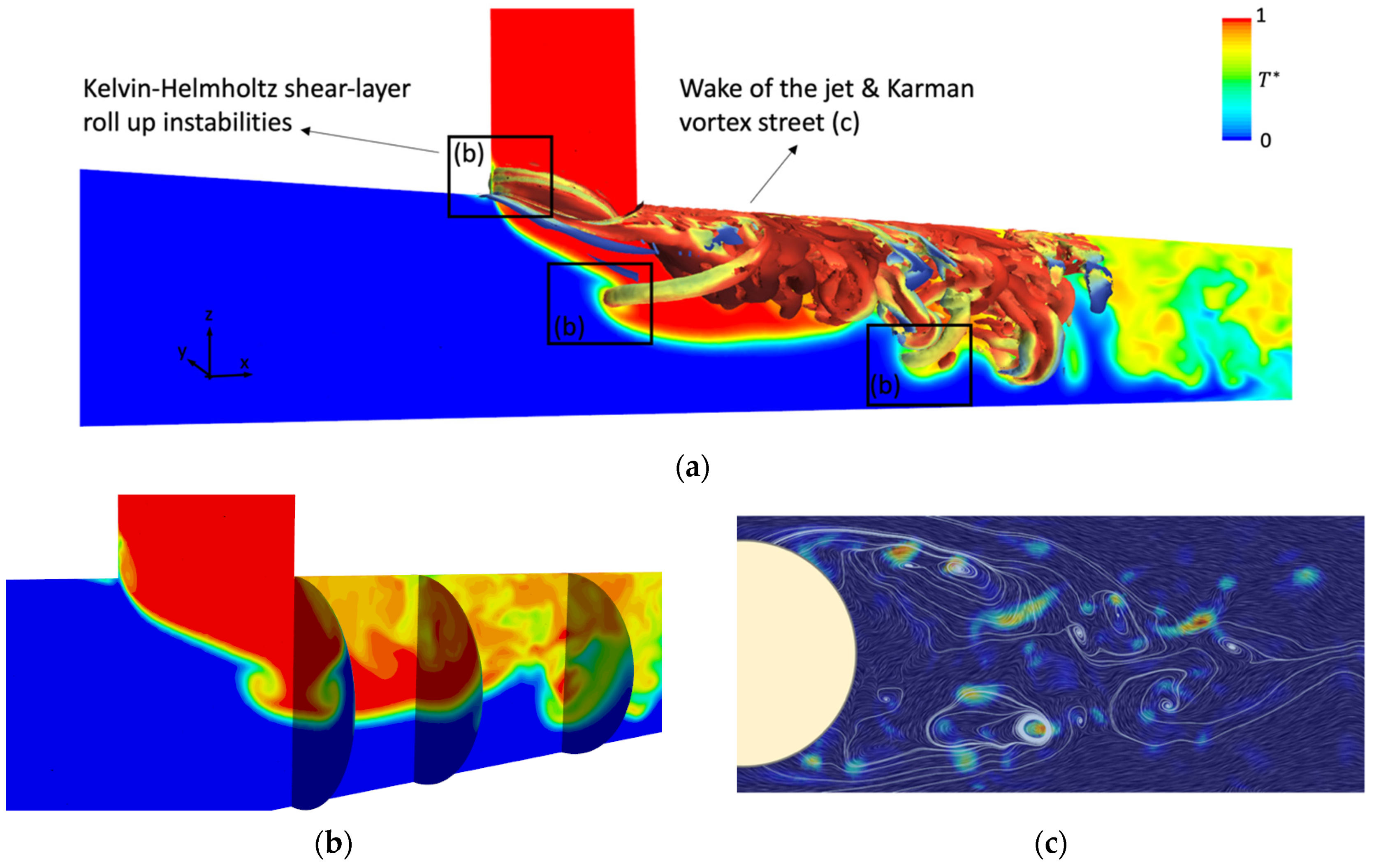
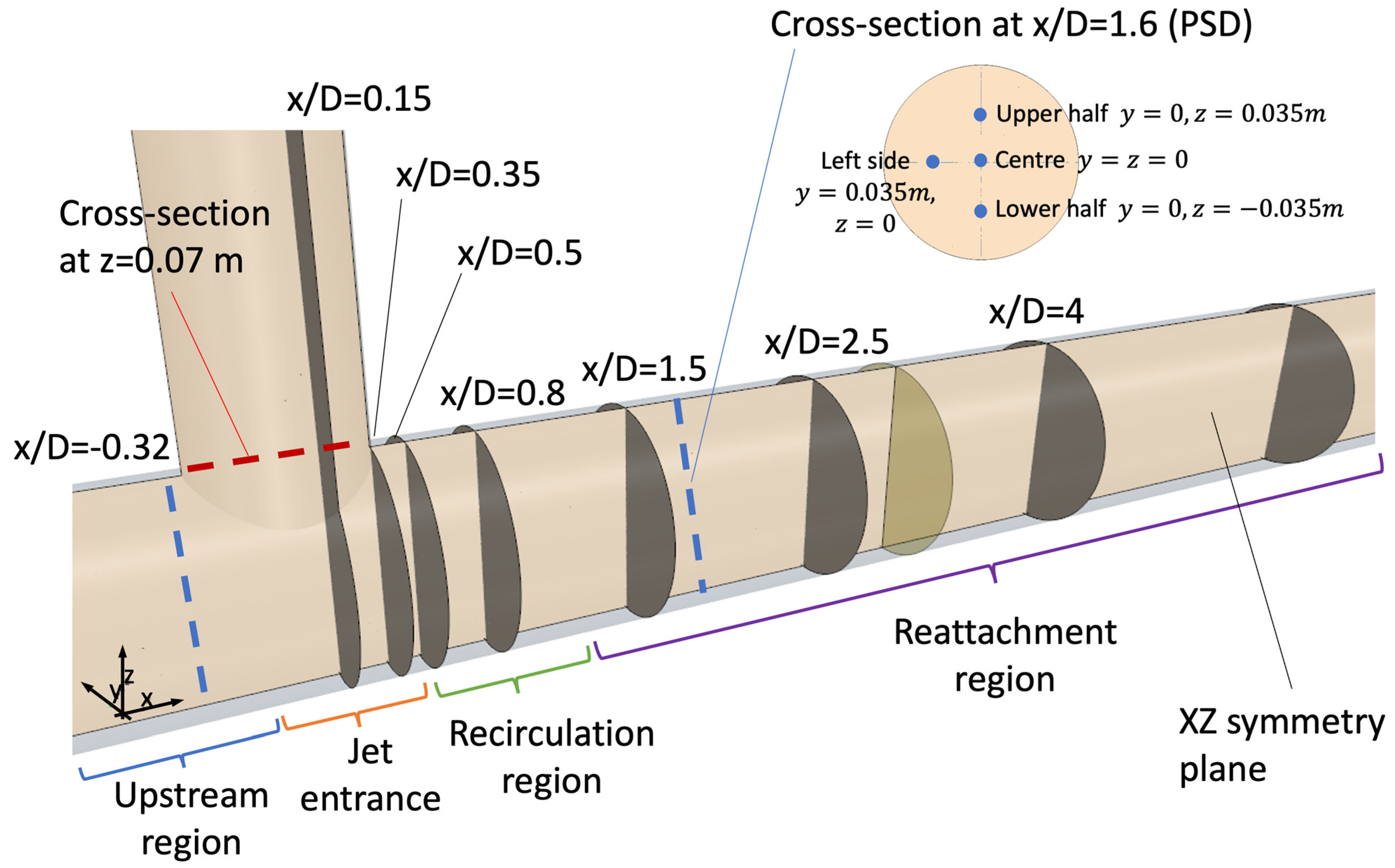
3. Overview of the Flow Structure
4. Results and Discussion
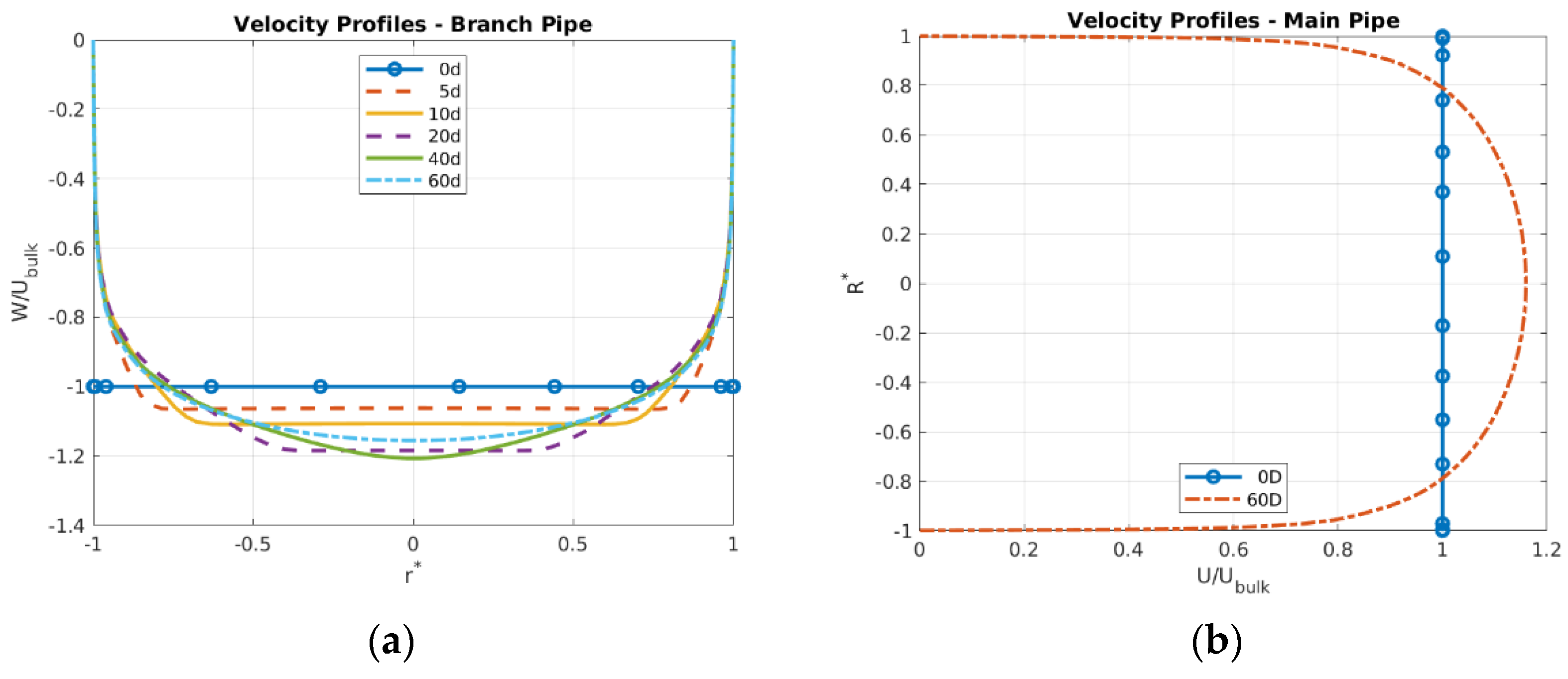
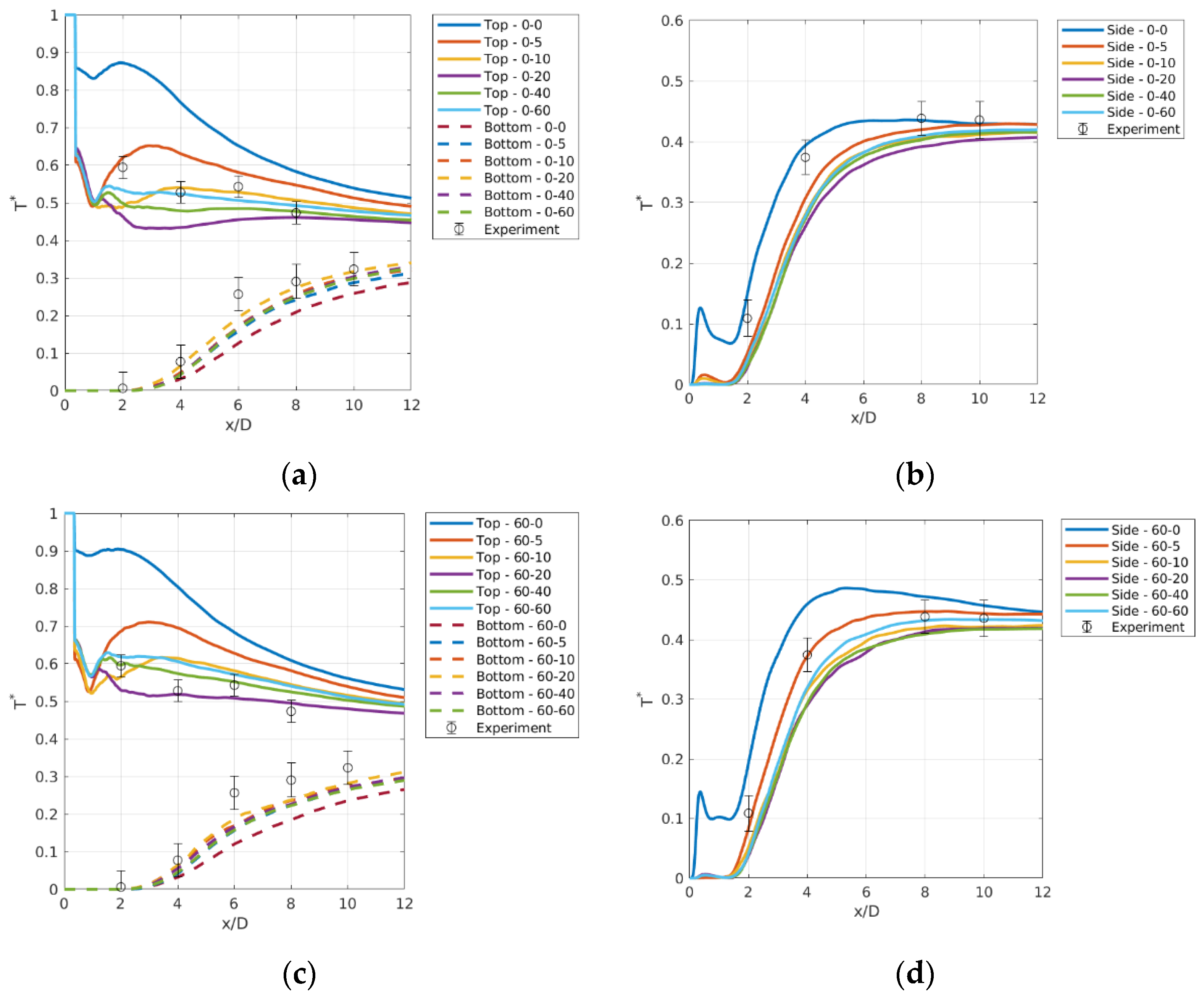
4.1. Profiles of Mean Temperature and Velocity
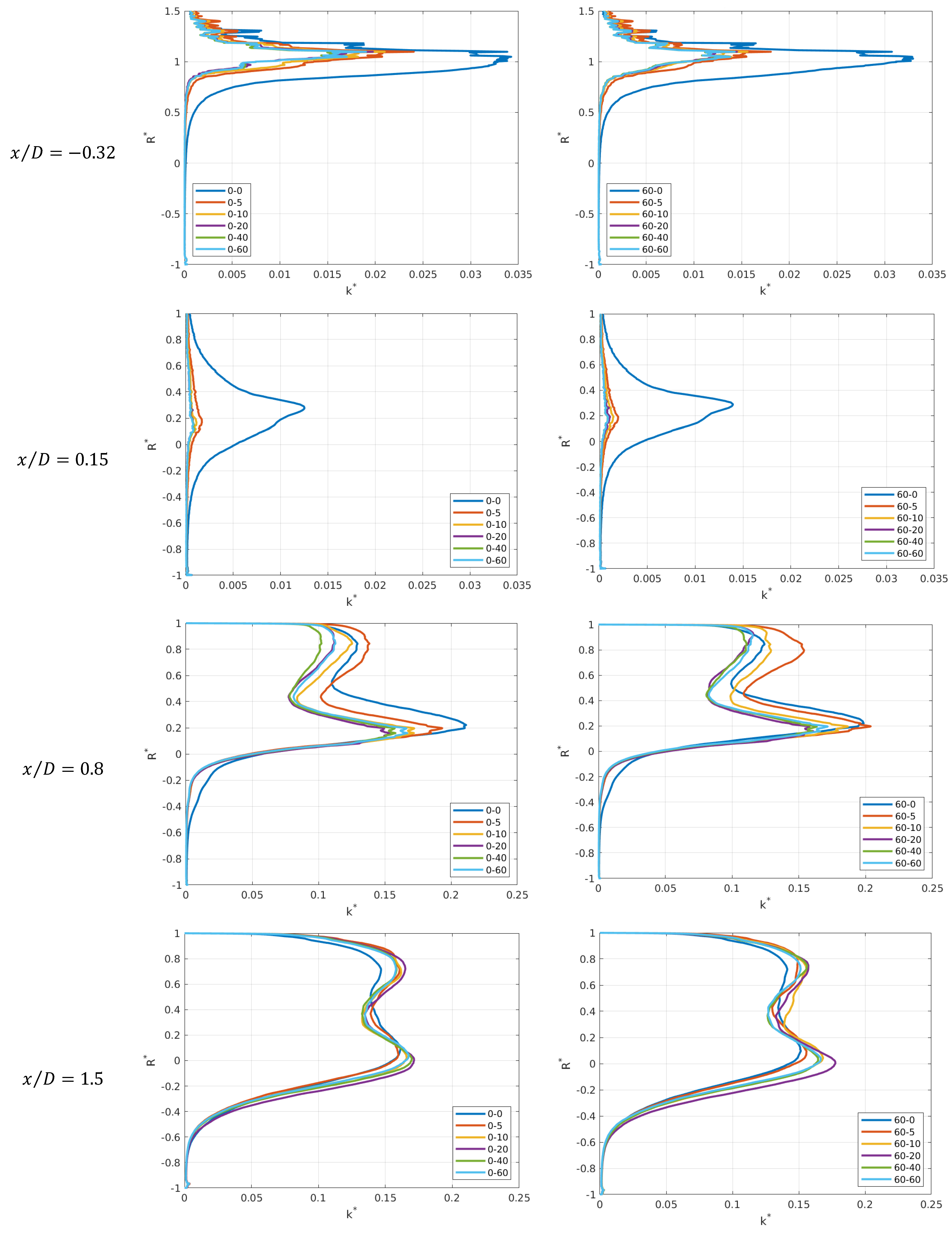
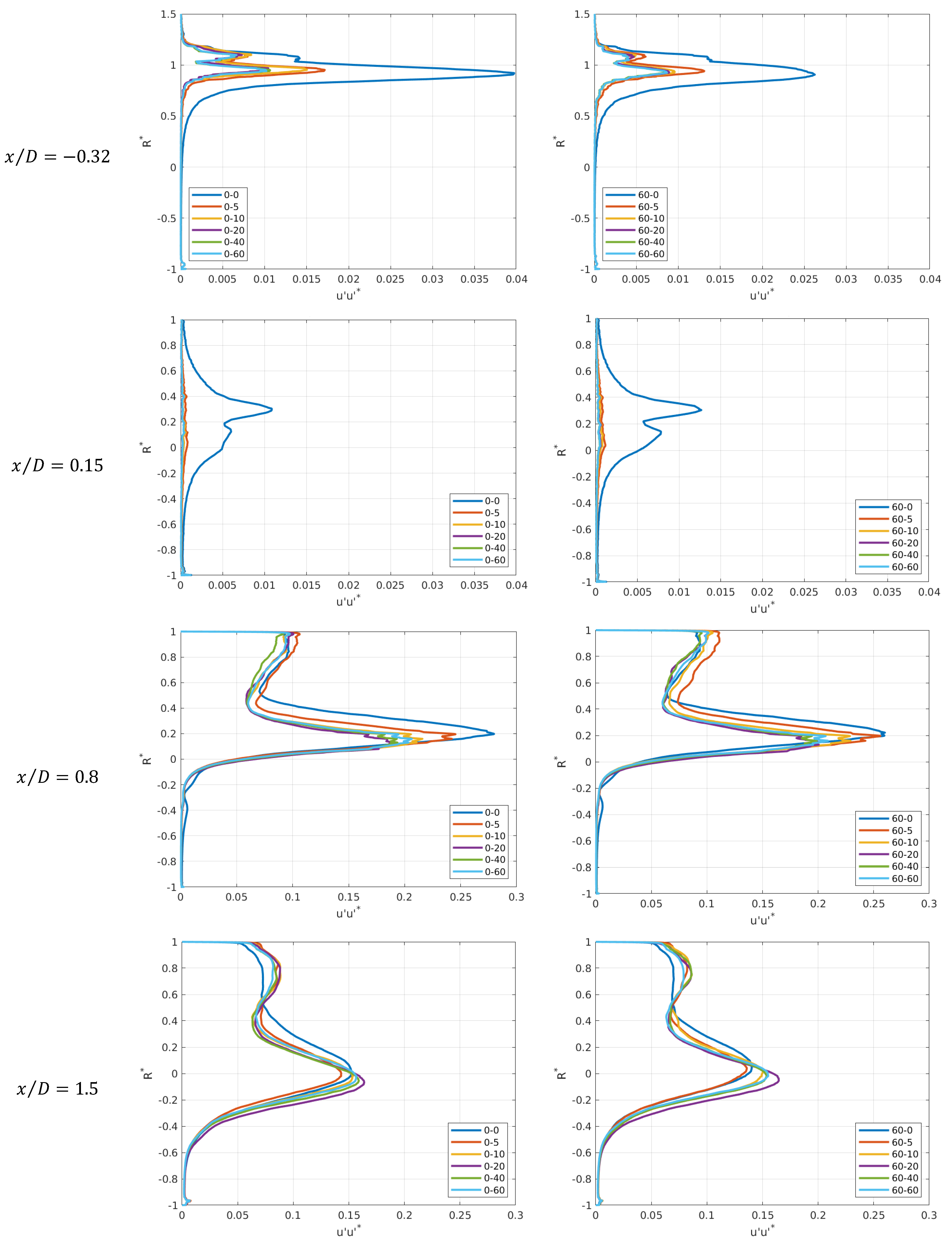
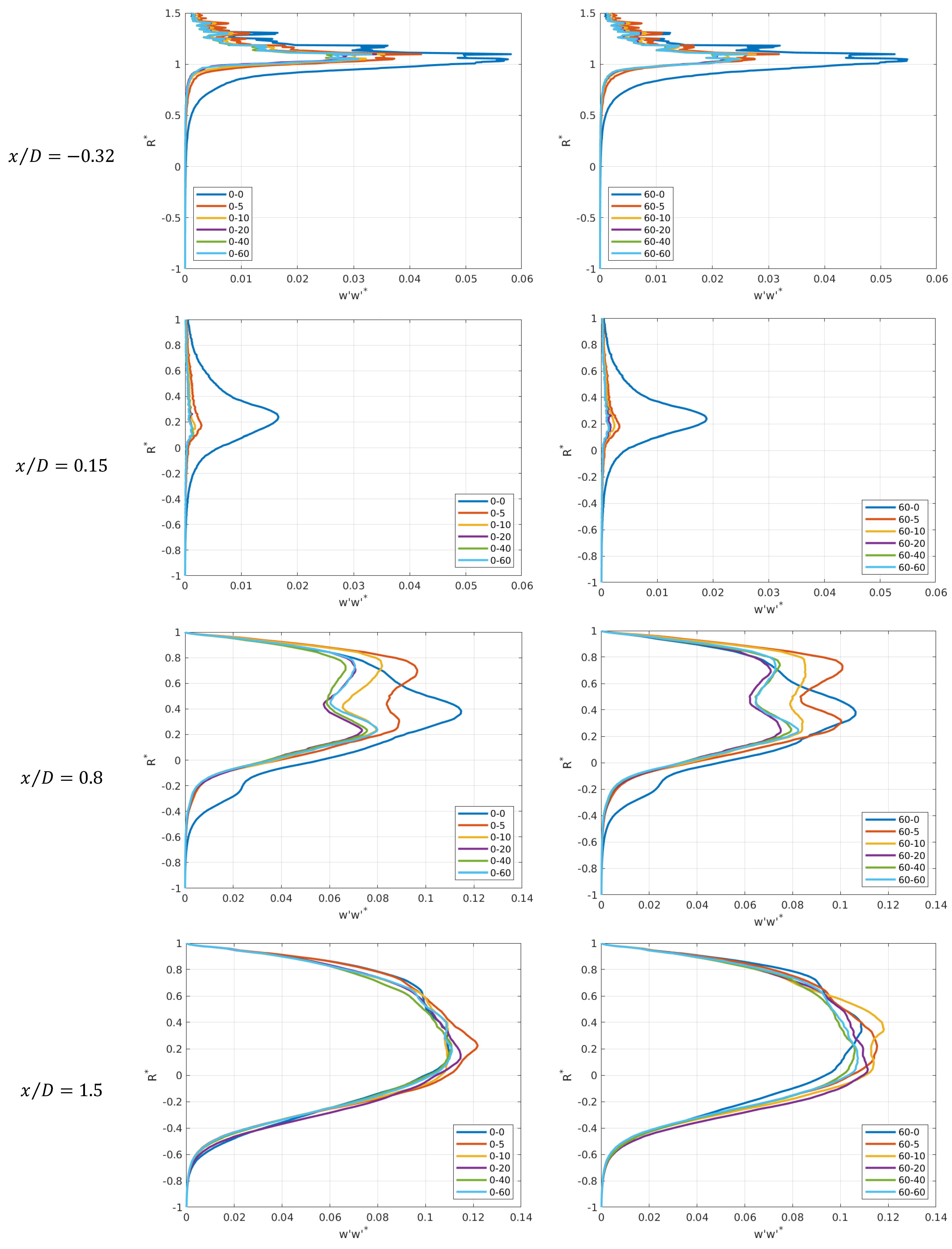
4.2. Effects of Different Inlet Flow Profiles on Turbulent Quantities
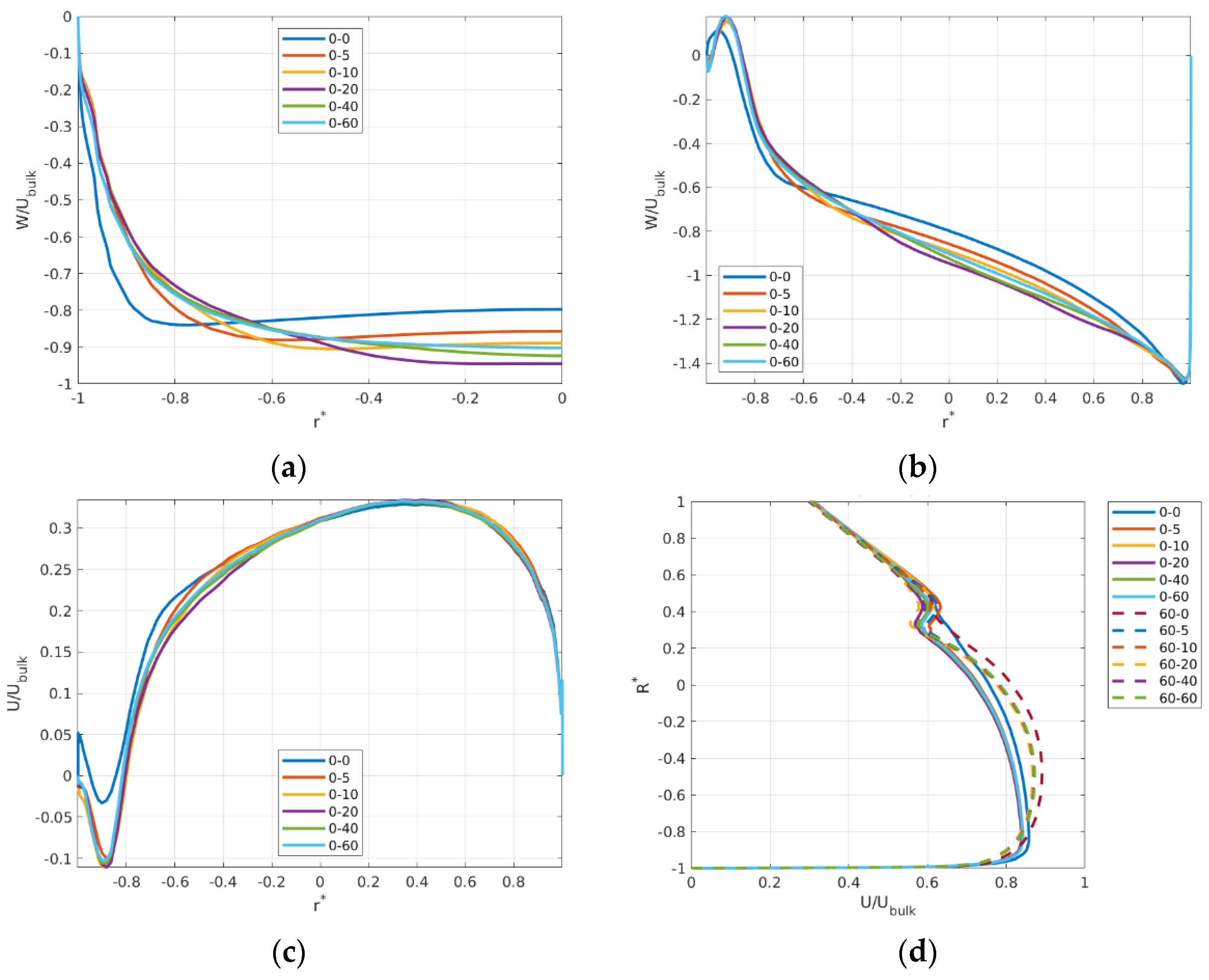
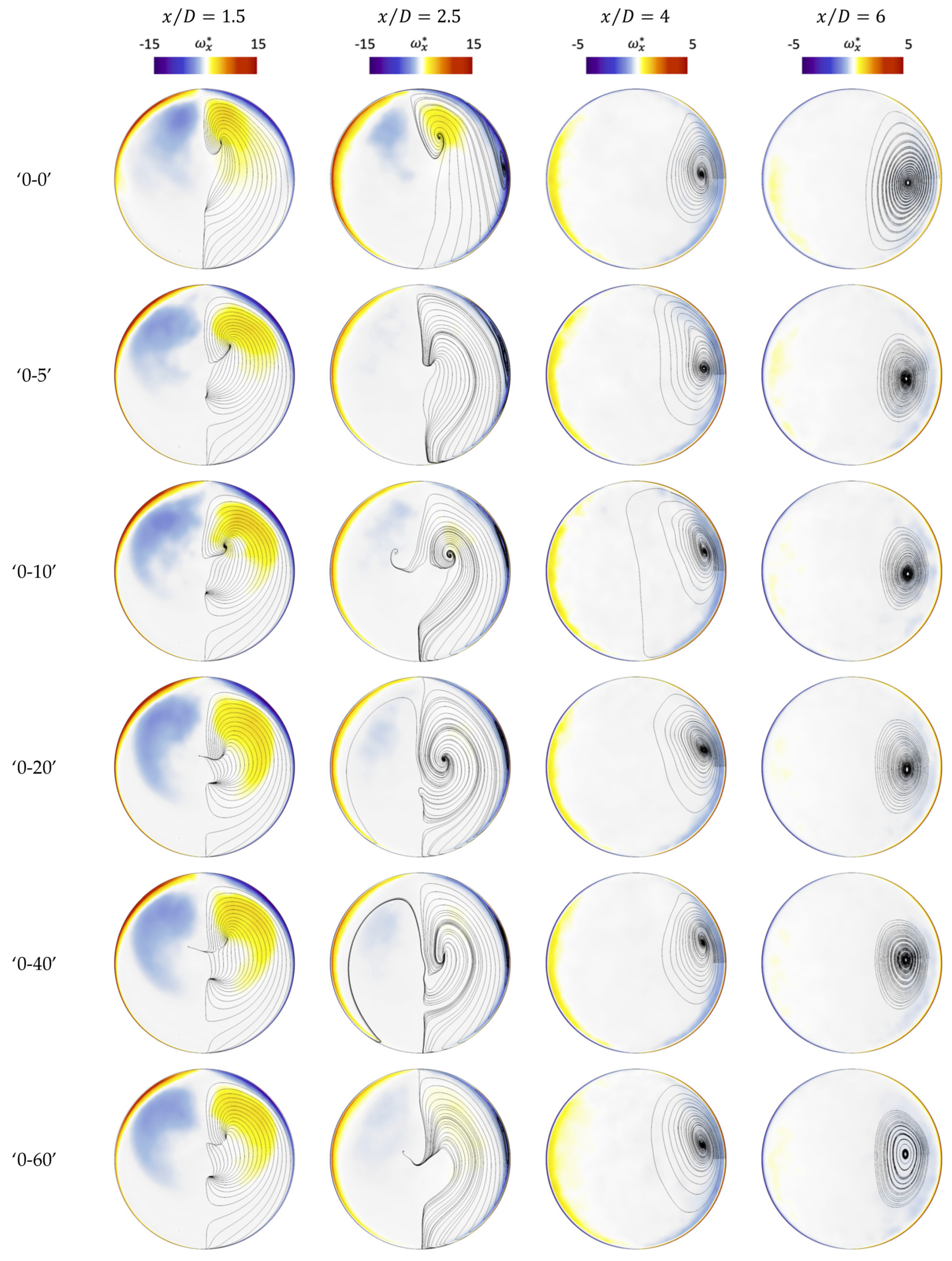
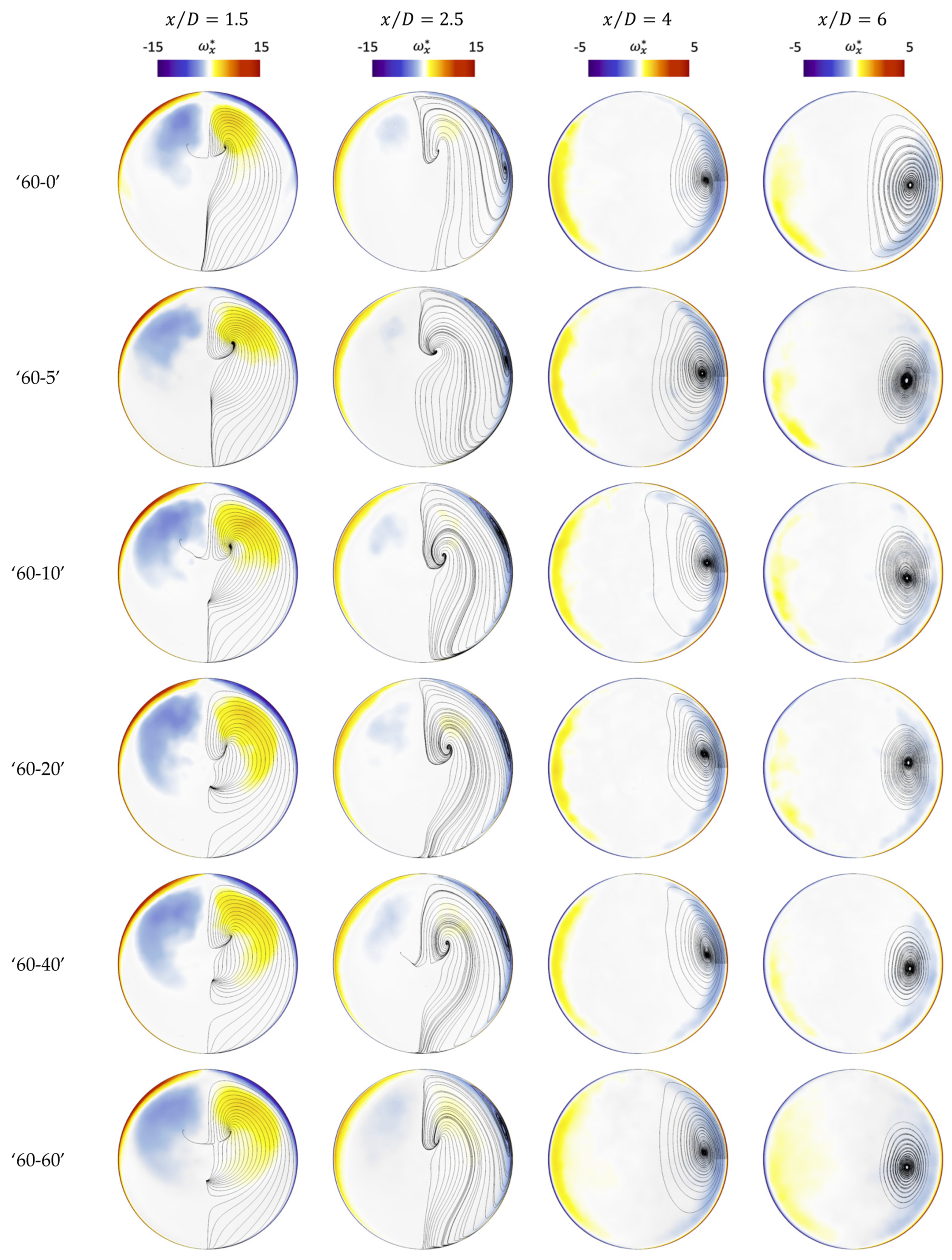
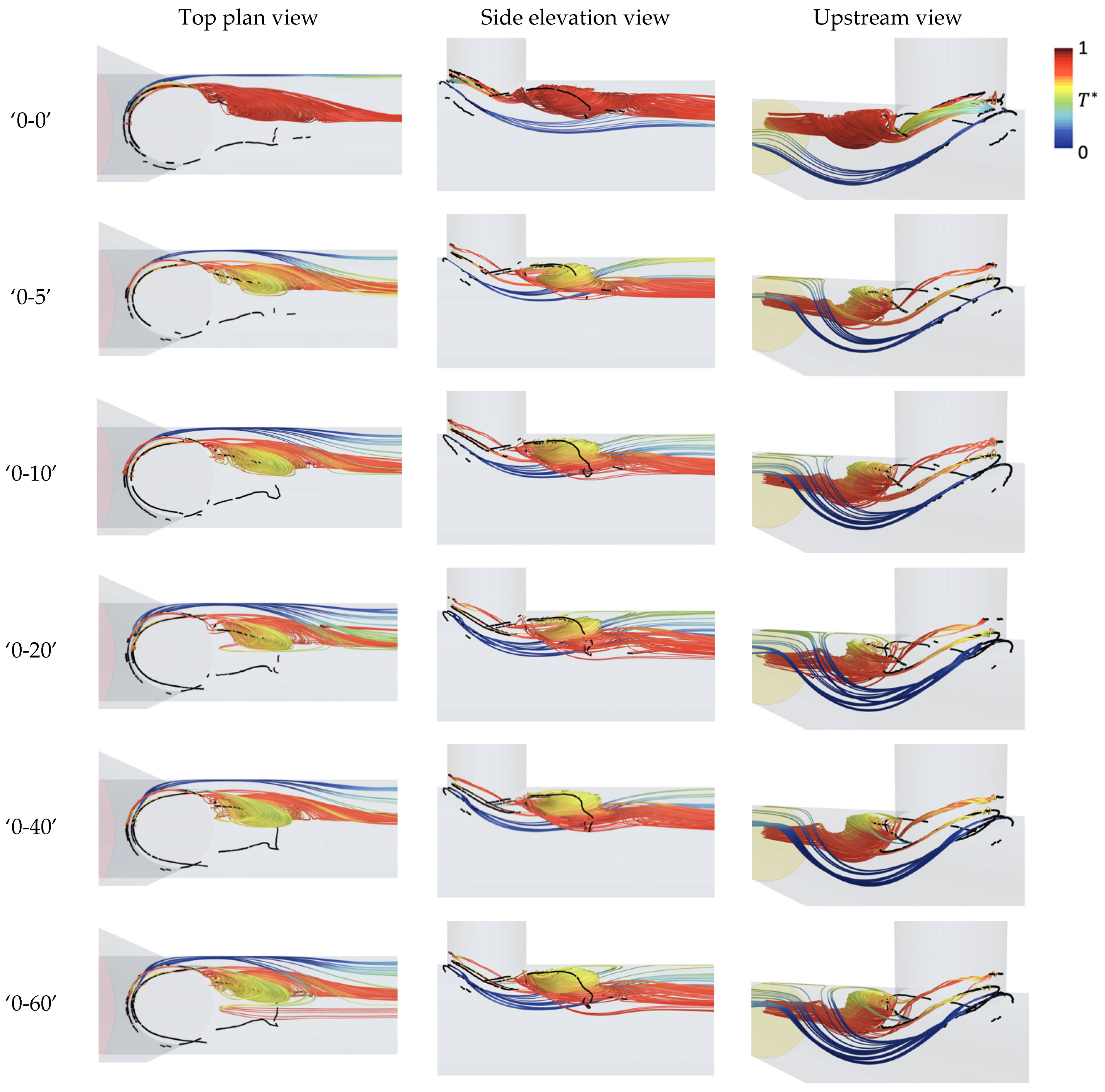
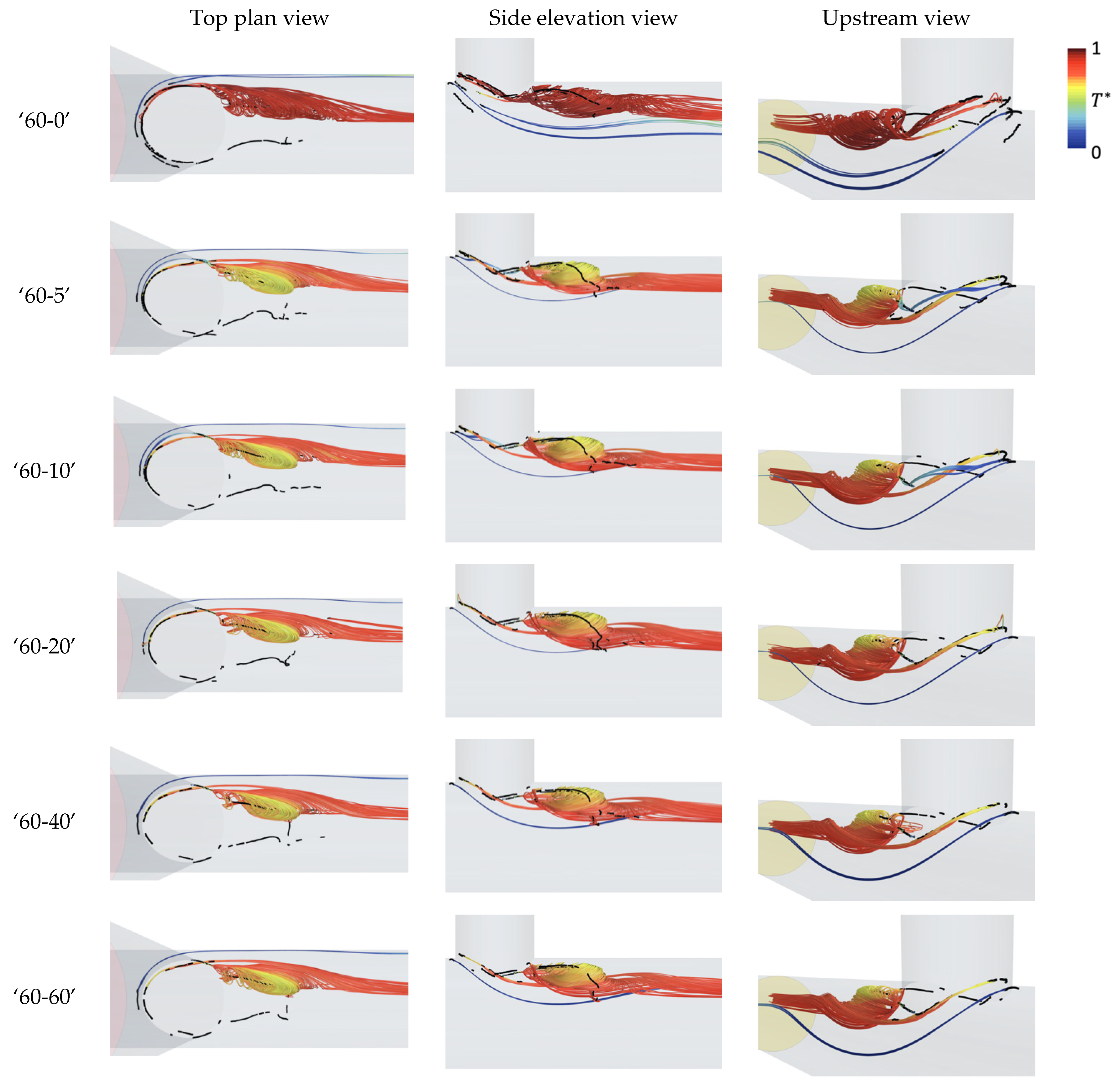
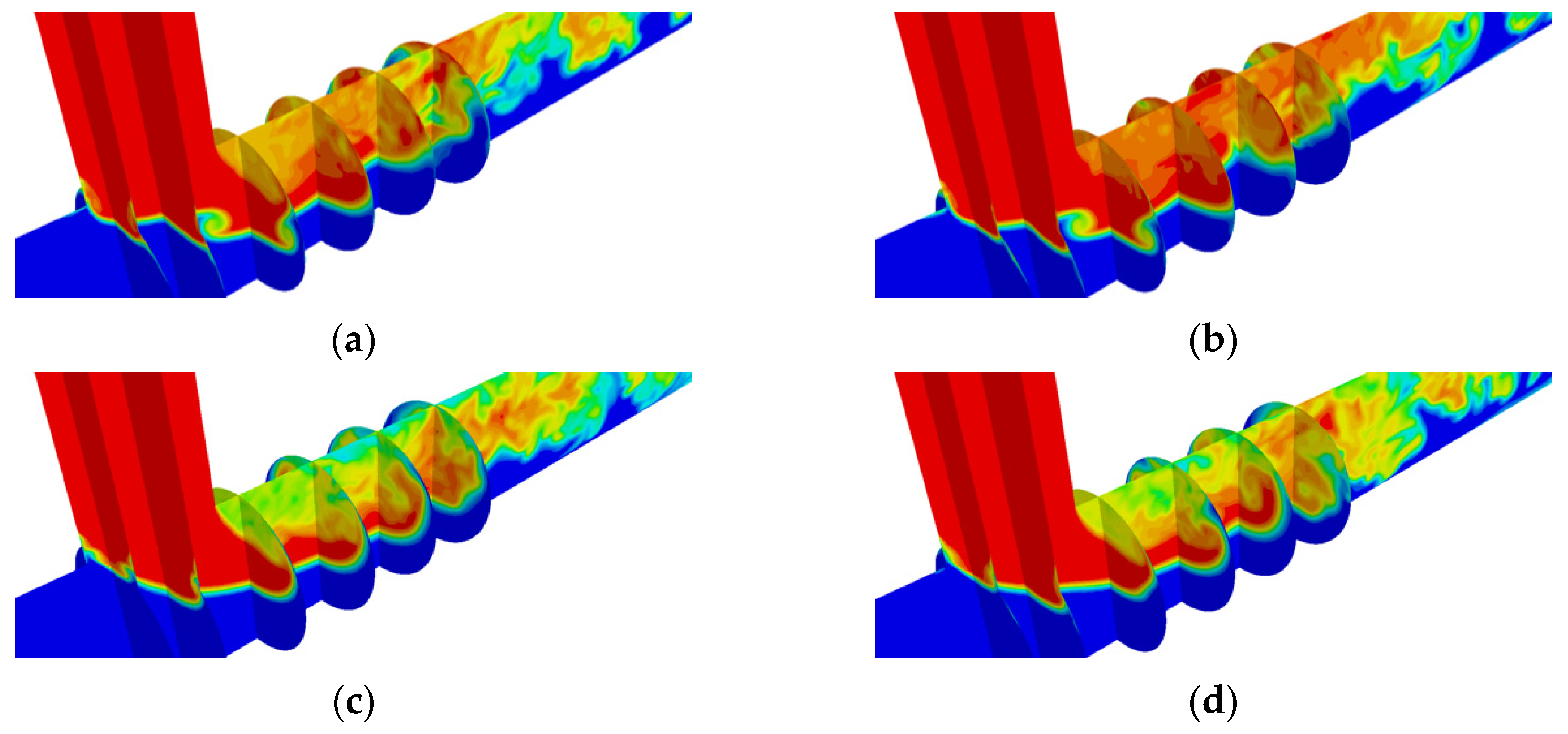
4.3. Effects of Different Inlet Flow Profiles on the Mean Flow Structure
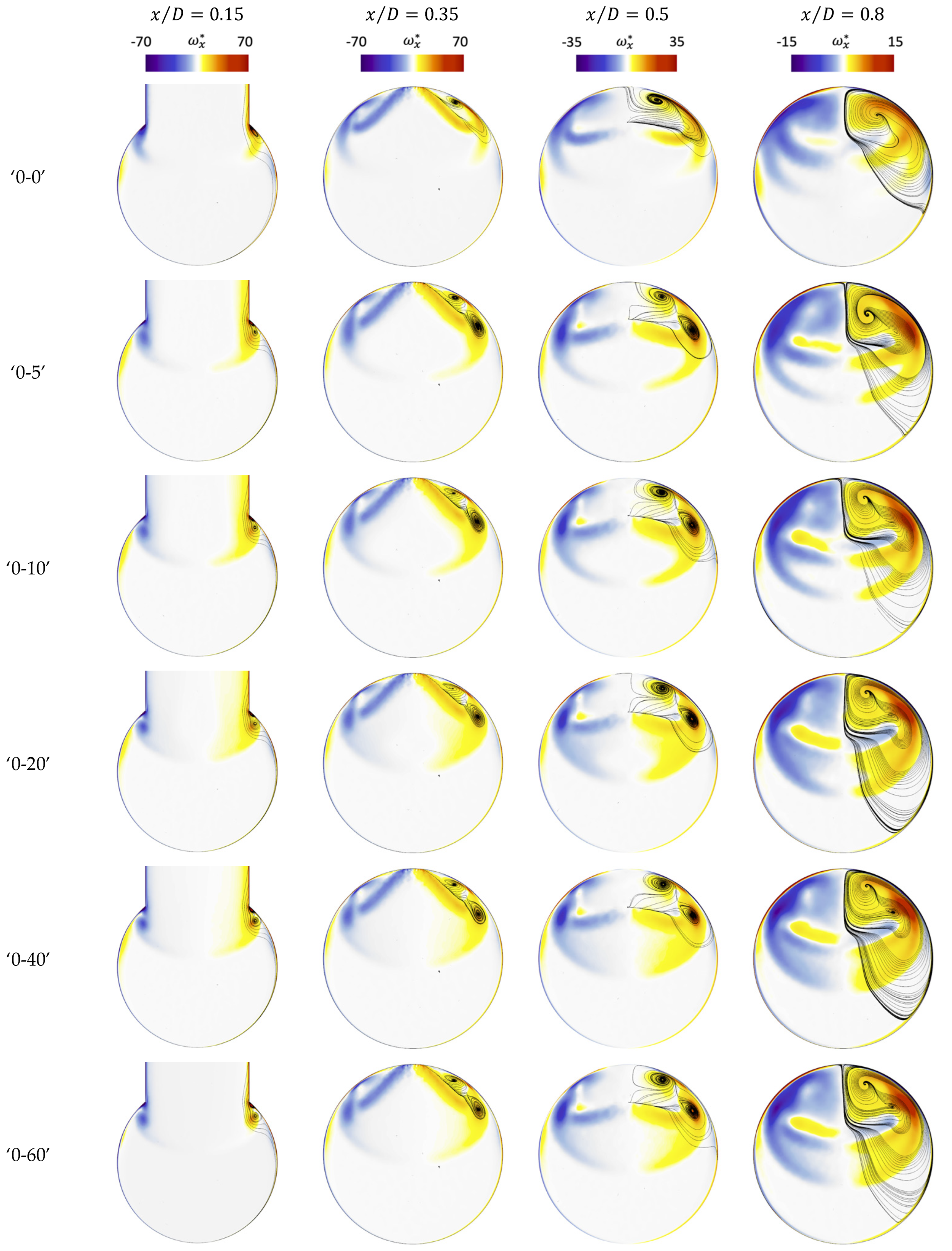
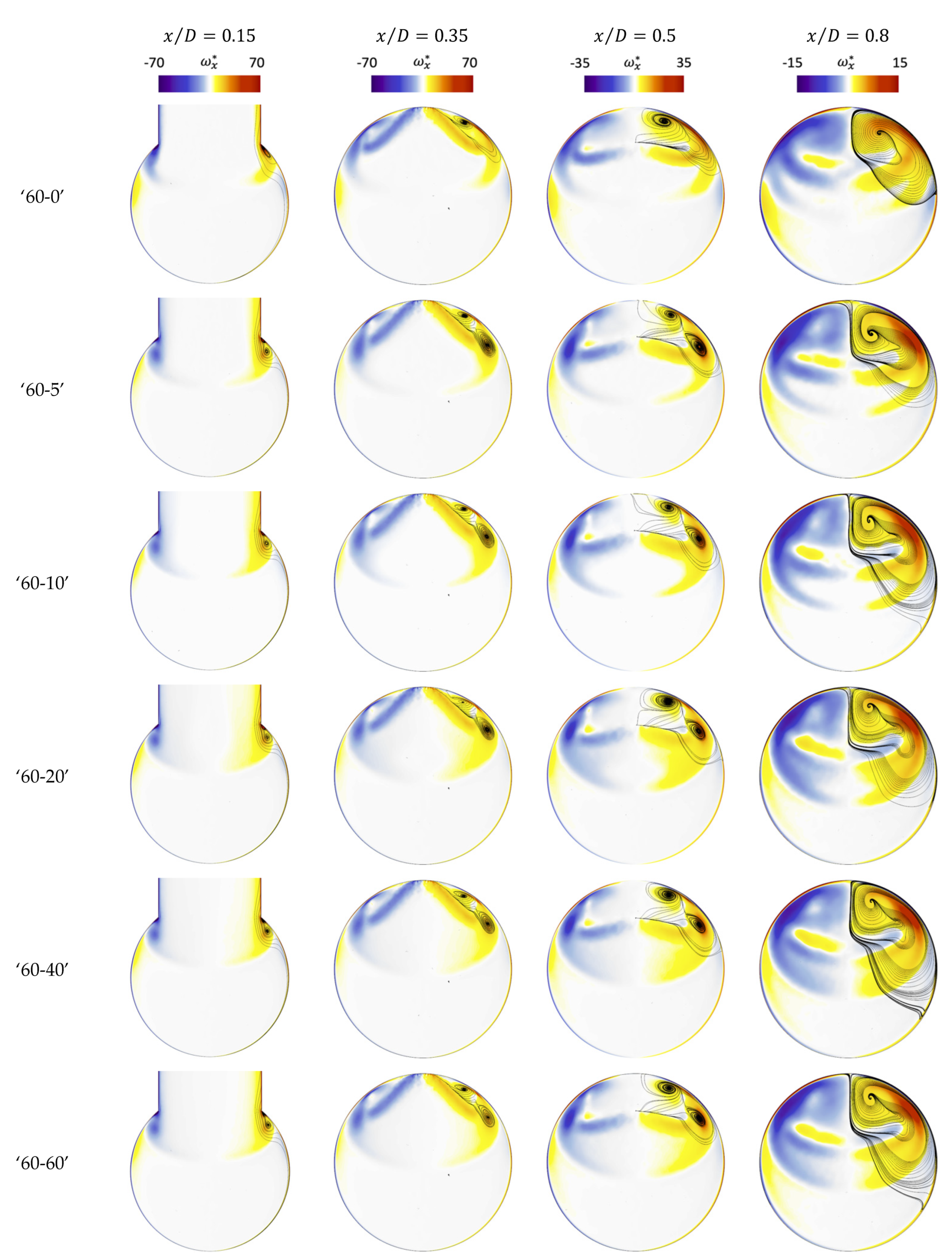
4.4. Effects of Different Inlet Flow Profiles on Transient Flow Behaviours
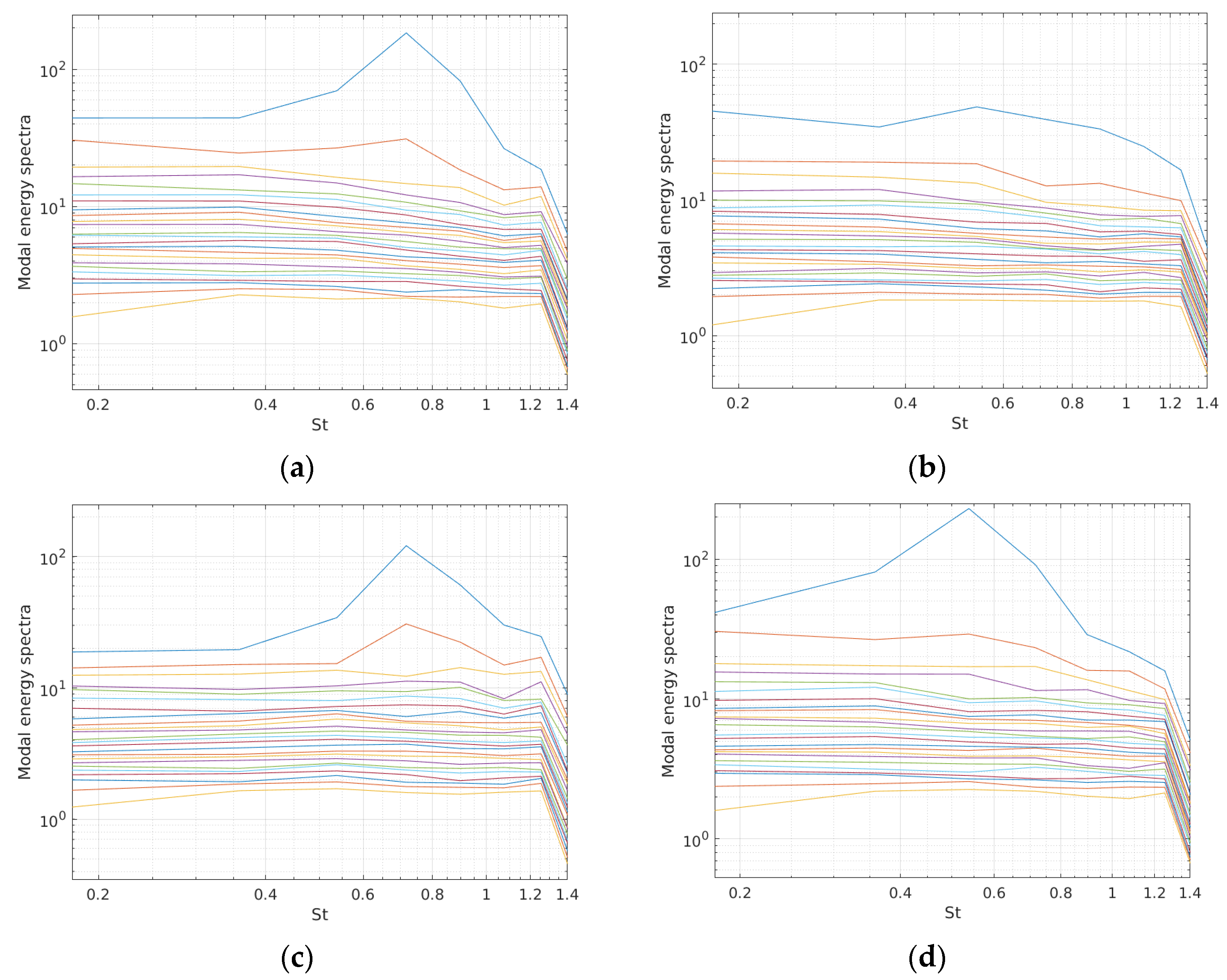
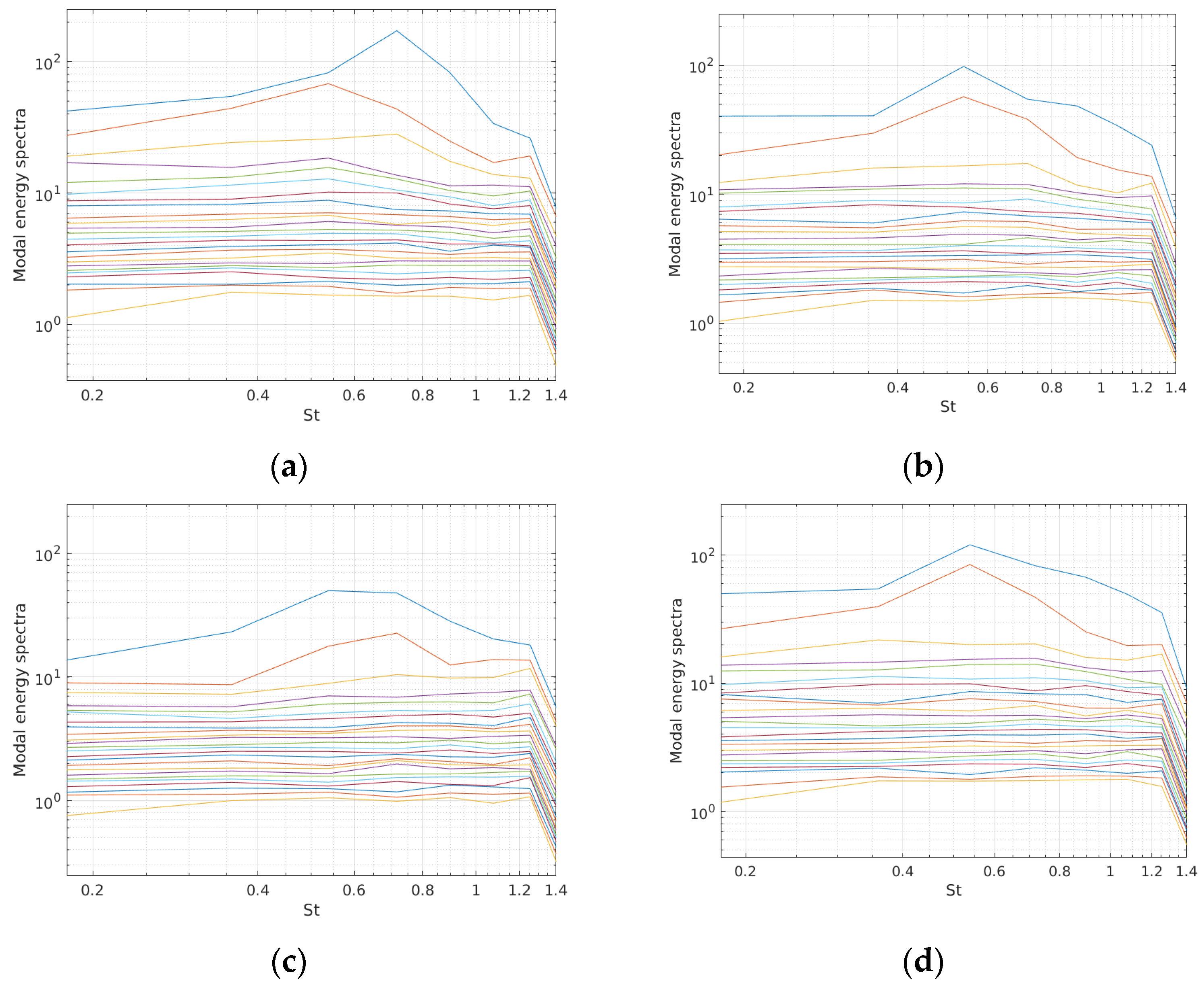
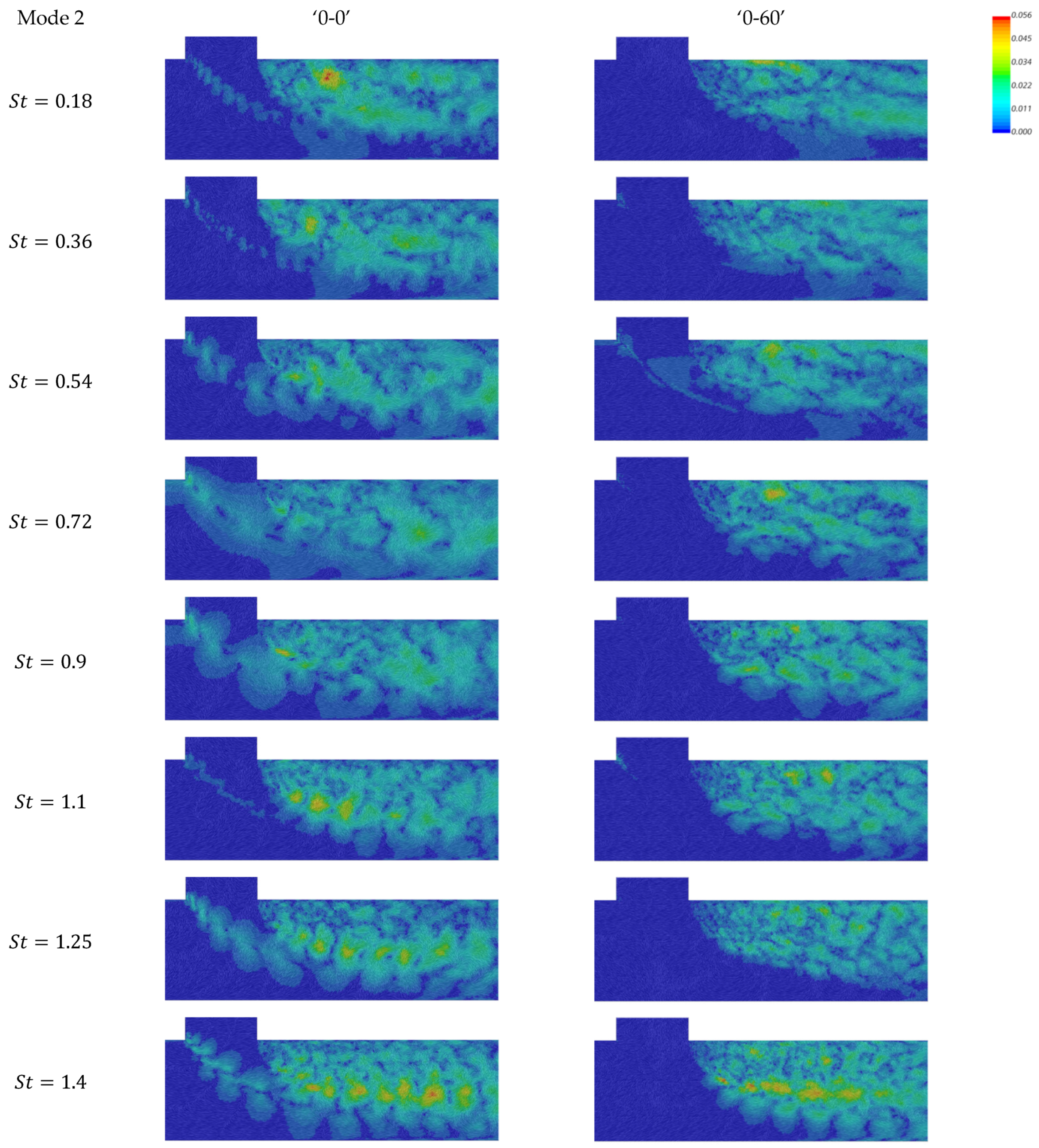
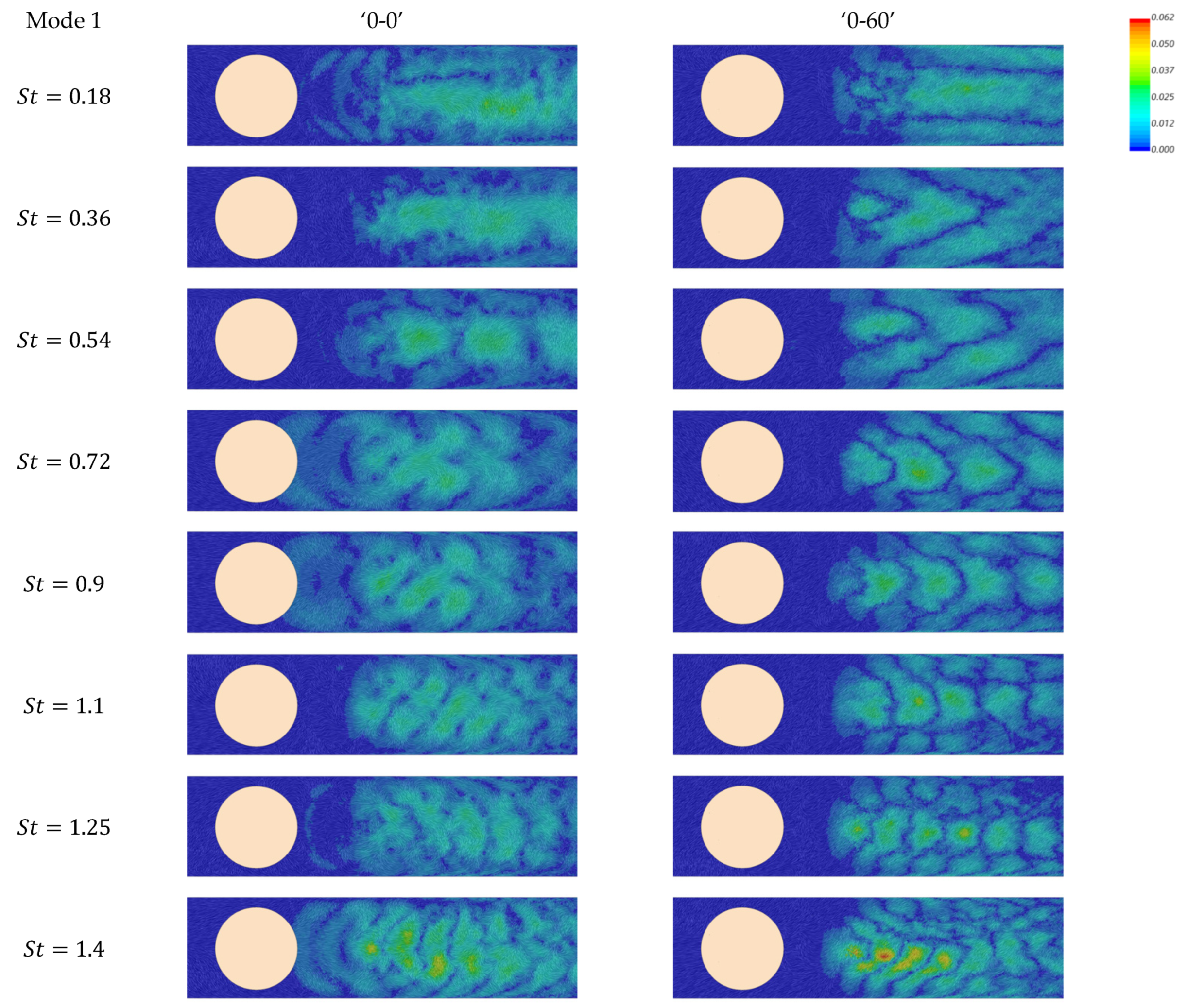
4.4.1. Spectral Proper Orthogonal Decomposition (SPOD) Analysis
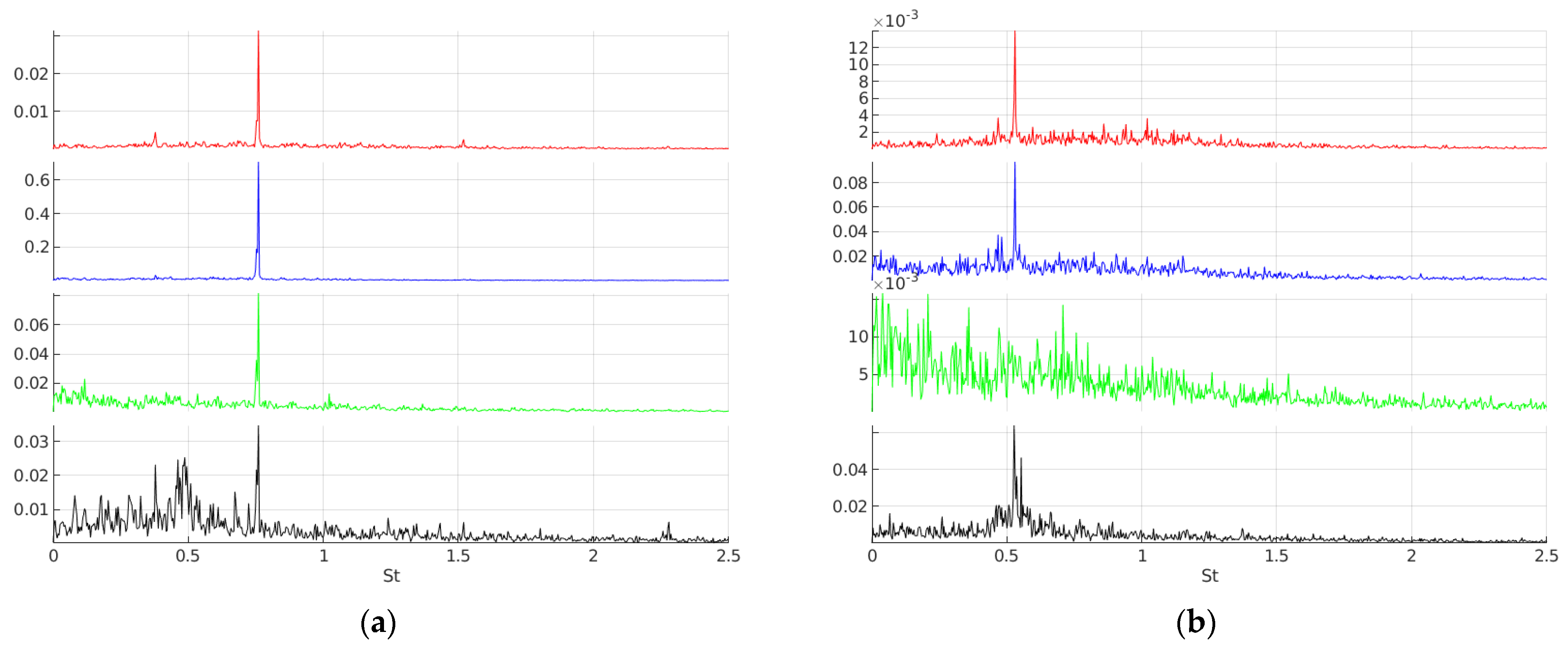
4.4.2. Power Spectral Density (PSD) Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, J.H.; Roidt, R.M.; Deardorff, A.F. Thermal stratification and reactor piping integrity. Nucl. Eng. Des. 1993, 139, 83–95. [Google Scholar] [CrossRef]
- Jawad, M.H. Stress in ASME Pressure Vessels, Boilers, and Nuclear Components; Wiley-ASME Press Series; 2017. Available online: https://www.wiley.com/en-ae/Stress+in+ASME+Pressure+Vessels,+Boilers,+and+Nuclear+Components-p-9781119259282 (accessed on 10 October 2022).
- Radu, V. Stochastic modelling of fatigue crack growth. In Applied Condition Monitoring Volume 1; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Weronski, A.; Hejwowski, T. Thermal Fatigue of Metals; Marcel Dekker: New York, NY, USA, 1991. [Google Scholar]
- Sohn, H.; Yang, J.; Lee, H.; Park, B. 20—Sensing Solutions for Assessing and Monitoring of Nuclear Power Plants (NPPs); Woodhead Publishing: Sawston, UK, 2014; pp. 605–637. [Google Scholar] [CrossRef]
- Brunings, J. LMFBR Thermal-Striping Evaluation; United States, 1982. Available online: https://www.osti.gov/servlets/purl/6887039 (accessed on 10 October 2022).
- Jones, I.S. Thermal striping fatigue damage in multiple edge-cracked geometries. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 123–134. [Google Scholar] [CrossRef]
- Gelineau, O.; Sperandio, M.; Martin, P.; Ricard, J.B.; Martin, L.; Bougault, A. Thermal Fluctuation Problems Encountered in LMFRs (IWGFR–90); International Atomic Energy Agency (IAEA): Vienna, Austria, 1994. [Google Scholar]
- Gelineau, O.; Sperandio, M.; Simoneau, J.P.; Hamy, J.M.; Roubin, P.H.L. Thermomechanical and Thermohydraulic Analyses of a T-Junction Using Experimental Data (IAEA-TECDOC–1318); International Atomic Energy Agency (IAEA): Vienna, Austria, 2002. [Google Scholar]
- Chapuliot, S.; Gourdin, C.; Payen, T.; Magnaud, J.; Monavon, A. Hydro-thermal-mechanical analysis of thermal fatigue in a mixing tee. Nucl. Eng. Des. 2005, 235, 575–596. [Google Scholar] [CrossRef]
- Shah, V.N.; MacDonald, P.E. (Eds.) Aging and Life Extension of Major Light Water Reactor Components; Elsevier Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- IAEA. Assessment and Management of Ageing of Major Nuclear Power Plant Components Important to Safety: Primary Piping in PWRs; IAEA-TECDOC 1361; IAEA: Vienna, Austria, 2003. [Google Scholar]
- Bartmann, B.; Neikes, R.; Leweke, T.; Limberg, W.; Krause, E. Vortex Formation in a T-Junction; Tanida, Y., Miyashiro, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 102–106. [Google Scholar] [CrossRef]
- Perry, A.E.; Lim, T.T. Coherent structures in coflowing jets and wakes. J. Fluid Mech. 1978, 88, 451–463. [Google Scholar] [CrossRef]
- Perry, A.E.; Tan, D.K.M. Simple three-dimensional vortex motions in coflowing jets and wakes. J. Fluid Mech. 1984, 141, 197–231. [Google Scholar] [CrossRef]
- Andreopoulos, J. On the structure of jets in a crossflow. J. Fluid Mech. 1985, 157, 163–197. [Google Scholar] [CrossRef]
- Andreopoulos, J.; Rodi, W. Experimental investigation of jets in a crossflow. J. Fluid Mech. 1984, 138, 93–127. [Google Scholar] [CrossRef]
- Kelso, R.M.; Lim, T.T.; Perry, A.E. An experimental study of round jets in cross-flow. J. Fluid Mech. 1996, 306, 111–144. [Google Scholar] [CrossRef]
- Fric, T.F.; Roshko, A. Vortical structure in the wake of a transverse jet. J. Fluid Mech. 1994, 279, 1–47. [Google Scholar] [CrossRef] [Green Version]
- Brücker, C. Study of the three-dimensional flow in a T-junction using a dual-scanning method for three-dimensional scanning-particle-image velocimetry (3-D SPIV). Exp. Therm. Fluid Sci. 1997, 14, 35–44. [Google Scholar] [CrossRef]
- Brucker, C.; Althaus, W. Study of vortex breakdown by particle tracking velocimetry (PTV). Exp. Fluids 1992, 13, 339–349. [Google Scholar] [CrossRef]
- Abramovich, G.N. The Theory of Turbulent Jets; Schindel, L., Ed.; The MIT Press: Cambridge, MA, USA, 2003. [Google Scholar] [CrossRef]
- Smith, B.L.; Mahaffy, J.H.; Angele, K.; Westin, J. Report of the OECD/NEA-Vattenfall T-Junction Benchmark Exercise; OECD: Paris, France, 2011; pp. 1–92. [Google Scholar]
- Smith, B.; Mahaffy, J.; Angele, K. A CFD benchmarking exercise based on flow mixing in a T-junction. Nucl. Eng. Des. 2013, 264, 80–88. [Google Scholar] [CrossRef]
- Braillard, O.; Howard, R.; Angele, K.; Shams, A.; Edh, N. Thermal mixing in a T-junction: Novel CFD-grade measurements of the fluctuating temperature in the solid wall. Nucl. Eng. Des. 2018, 330, 377–390. [Google Scholar] [CrossRef] [Green Version]
- Shams, A.; Edh, N.; Angele, K.; Veber, P.; Howard, R.; Braillard, O.; Chapuliot, S.; Severac, E.; Karabaki, E.; Seichter, J.; et al. Synthesis of a CFD benchmarking exercise for a T-junction with wall. Nucl. Eng. Des. 2018, 330, 199–216. [Google Scholar] [CrossRef]
- Westin, J.; Alavyoon, F.; Andersson, L.; Veber, P.; Henriksson, M.; Andersson, C. Experiments and Unsteady CFD-Calculations of Thermal Mixing in a T-Junction. In Proceedings of the OECD/NEA/IAEA Workshop on the Benchmarking of CFD Codes for Application to Nuclear Reactor Safety (CFD4NRS), Munich, Germany, 5–7 September 2006; pp. 1–15. [Google Scholar]
- Westin, J.; Veber, P.; Andersson, L.; Mannetje, C.; Andersson, U.; Eriksson, J.; Henriksson, M.E.; Alavyoon, F.; Andersson, C. High-Cycle Thermal Fatigue in Mixing Tees: Large-Eddy Simulations Compared to a New Validation Experiment. In Proceedings of the 16th International Conference on Nuclear Engineering, Orlando, FL, USA, 11–15 May 2008; pp. 515–525. [Google Scholar] [CrossRef] [Green Version]
- Odemark, Y.; Green, T.M.; Angele, K.; Westin, J.; Alavyoon, F.; Lundström, S. High-Cycle Thermal Fatigue in Mixing Tees: New Large-Eddy Simulations Validated Against New Data Obtained by PIV in the Vattenfall Experiment. In Proceedings of the 17th International Conference on Nuclear Engineering, Brussels, Belgium, 12–16 July 2009; pp. 775–785. [Google Scholar] [CrossRef]
- Evrim, C.; Laurien, E. Large-Eddy Simulation of turbulent thermal flow mixing in a vertical T-Junction configuration. Int. J. Therm. Sci. 2020, 150, 106231. [Google Scholar] [CrossRef]
- Gritskevich, M.; Garbaruk, A.; Frank, T.; Menter, F. Investigation of the thermal mixing in a T-junction flow with different SRS approaches. Nucl. Eng. Des. 2014, 279, 83–90. [Google Scholar] [CrossRef]
- Kang, D.G.; Na, H.; Lee, C.Y. Detached eddy simulation of turbulent and thermal mixing in a T-junction. Ann. Nucl. Energy 2019, 124, 245–256. [Google Scholar] [CrossRef]
- Lampunio, L.; Duan, Y.; Eaton, M.D. The effect of inlet flow conditions upon thermal mixing and conjugate heat transfer within the wall of a T-Junction. Nucl. Eng. Des. 2021, 385, 111484. [Google Scholar] [CrossRef]
- Lampunio, L.; Duan, Y.; Issa, R.; Eaton, M.D. Thermal Stripping Analysis in T-junctions with Different Entry Flow Profiles. In Proceedings of the Advances in Thermal Hydraulics 2020 (ATH2020), Palaiseau, France, 20–23 October 2020; pp. 895–906. [Google Scholar]
- Lampunio, L.; Duan, Y.; Issa, R.; Eaton, M.D. Effects of inlet velocity profiles for thermal stripping phenomena in T-junctions. J. Phys. Conf. Ser. 2021, 2116, 12026. [Google Scholar] [CrossRef]
- Schmidt, J. (Ed.) Process and Plant Safety Applying Computational Fluid Dynamics; Wiley-VCH Verlag & Co. KGaA: Weinheim, Germany, 2012. [Google Scholar]
- Lampunio, L.; Duan, Y.; Eaton, M.D. Effects of different entry flow profiles on thermal striping in mixing T-junction. In Proceedings of the UK Heat Transfer Conference (UKHTC 2022), Manchester, UK, 3–5 April 2022. [Google Scholar]
- Lampunio, L.; Duan, Y.; Eaton, M.D. Surrogate modelling and uncertainty quantification for the analysis of turbulent thermal mixing phenomena within a T-junction. In Proceedings of the 19th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-19), Brussels, Belgium, 6–11 March 2022. [Google Scholar]
- Siemens Industries Digital Software. Simcenter STAR-CCM+, version 2020.1.1; Siemens: Waltham, MA, USA, 2020.
- Gritskevich, M.S.; Garbaruk, A.V.; Schütze, J.; Menter, F.R. Development of DDES and IDDES formulations for the K-ω shear stress transport model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Igarashi, M.; Tanaka, M.; Kawashima, S.; Kamide, H. Experimental Study on Fluid Mixing for Evaluation of Thermal Striping in T-Pipe Junction. In Proceedings of the 10th International Conference on Nuclear Engineering, Arlington, VA, USA, 14–18 April 2002; pp. 383–390. [Google Scholar] [CrossRef]
- Kamide, H.; Igarashi, M.; Kawashima, S.; Kimura, N.; Hayashi, K. Study on mixing behavior in a tee piping and numerical analyses for evaluation of thermal striping. Nucl. Eng. Des. 2009, 239, 58–67. [Google Scholar] [CrossRef]
- Foss, J.F. Interaction Region Phenomena for the Jet in a Crossflow Problem; SFB Report SFB 80/E/161; University Karlsruhe: Karlsruhe, Germany, 1984. [Google Scholar]
- Sujudi, D.; Haimes, R. Identification of swirling flow in 3-D vector fields. In Proceedings of the AIAA 12th Computational Fluid Dynamics Conference, San Diego, CA, USA, 19–22 June 1995. [Google Scholar] [CrossRef] [Green Version]
- Haimes, R.; Kenwright, D. On the velocity gradient tensor and fluid feature extraction. In Proceedings of the AIAA 14th Computational Fluid Dynamics Conference, Norfolk, VA, USA, 1–5 November 1999. [Google Scholar] [CrossRef]
- Siemens Industries Digital Software. Simcenter STAR-CCM+ User Guide, version 2020.1.1; Siemens: Waltham, MA, USA, 2020.
- Hirota, M.; Mohri, E.; Asano, H.; Goto, H. Experimental study on turbulent mixing process in cross-flow type T-junction. Int. J. Heat Fluid Flow 2010, 31, 776–784. [Google Scholar] [CrossRef]
- Sieber, M.; Paschereit, C.O.; Oberleithner, K. Spectral proper orthogonal decomposition. J. Fluid Mech. 2016, 792, 798–828. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, O.; Colonius, T. Guide to Spectral Proper Orthogonal Decomposition. AIAA J. 2020, 58, 1023–1033. [Google Scholar] [CrossRef]
- Towne, A.; Schmidt, O.T.; Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 2018, 847, 821–867. [Google Scholar] [CrossRef] [Green Version]
- Nekkanti, A.; Schmidt, O.T. Frequency–time analysis, low-rank reconstruction and denoising of turbulent flows using SPOD. J. Fluid Mech. 2021, 926, A26. [Google Scholar] [CrossRef]
- Wakamatsu, M.; Nei, H.; Hashiguchi, K. Attenuation of Temperature Fluctuations in Thermal Striping. J. Nucl. Sci. Technol. 1995, 32, 752–762. [Google Scholar] [CrossRef]





| Case | Main Inlet BC | Branch Inlet BC | Case | Main Inlet BC | Branch Inlet BC |
|---|---|---|---|---|---|
| ‘0-0’ | 0D | 0d | ‘60-0’ | 60D | 0d |
| ‘0-5’ | 0D | 5d | ‘60-5’ | 60D | 5d |
| ‘0-10’ | 0D | 10d | ‘60-10’ | 60D | 10d |
| ‘0-20’ | 0D | 20d | ‘60-20’ | 60D | 20d |
| ‘0-40’ | 0D | 40d | ‘60-40’ | 60D | 40d |
| ‘0-60’ | 0D | 60d | ‘60-60’ | 60D | 60d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lampunio, L.; Duan, Y.; Eaton, M.D.; Bluck, M.J. Mean Flow, Turbulent Structures, and SPOD Analysis of Thermal Mixing in a T-Junction with Variation of the Inlet Flow Profile. Energies 2022, 15, 8415. https://doi.org/10.3390/en15228415
Lampunio L, Duan Y, Eaton MD, Bluck MJ. Mean Flow, Turbulent Structures, and SPOD Analysis of Thermal Mixing in a T-Junction with Variation of the Inlet Flow Profile. Energies. 2022; 15(22):8415. https://doi.org/10.3390/en15228415
Chicago/Turabian StyleLampunio, Lisa, Yu Duan, Matthew D. Eaton, and Michael J. Bluck. 2022. "Mean Flow, Turbulent Structures, and SPOD Analysis of Thermal Mixing in a T-Junction with Variation of the Inlet Flow Profile" Energies 15, no. 22: 8415. https://doi.org/10.3390/en15228415
APA StyleLampunio, L., Duan, Y., Eaton, M. D., & Bluck, M. J. (2022). Mean Flow, Turbulent Structures, and SPOD Analysis of Thermal Mixing in a T-Junction with Variation of the Inlet Flow Profile. Energies, 15(22), 8415. https://doi.org/10.3390/en15228415






