A Virtual Inertia Method for Stability Control of DC Distribution Systems with Parallel Converters
Abstract
:1. Introduction
- (1)
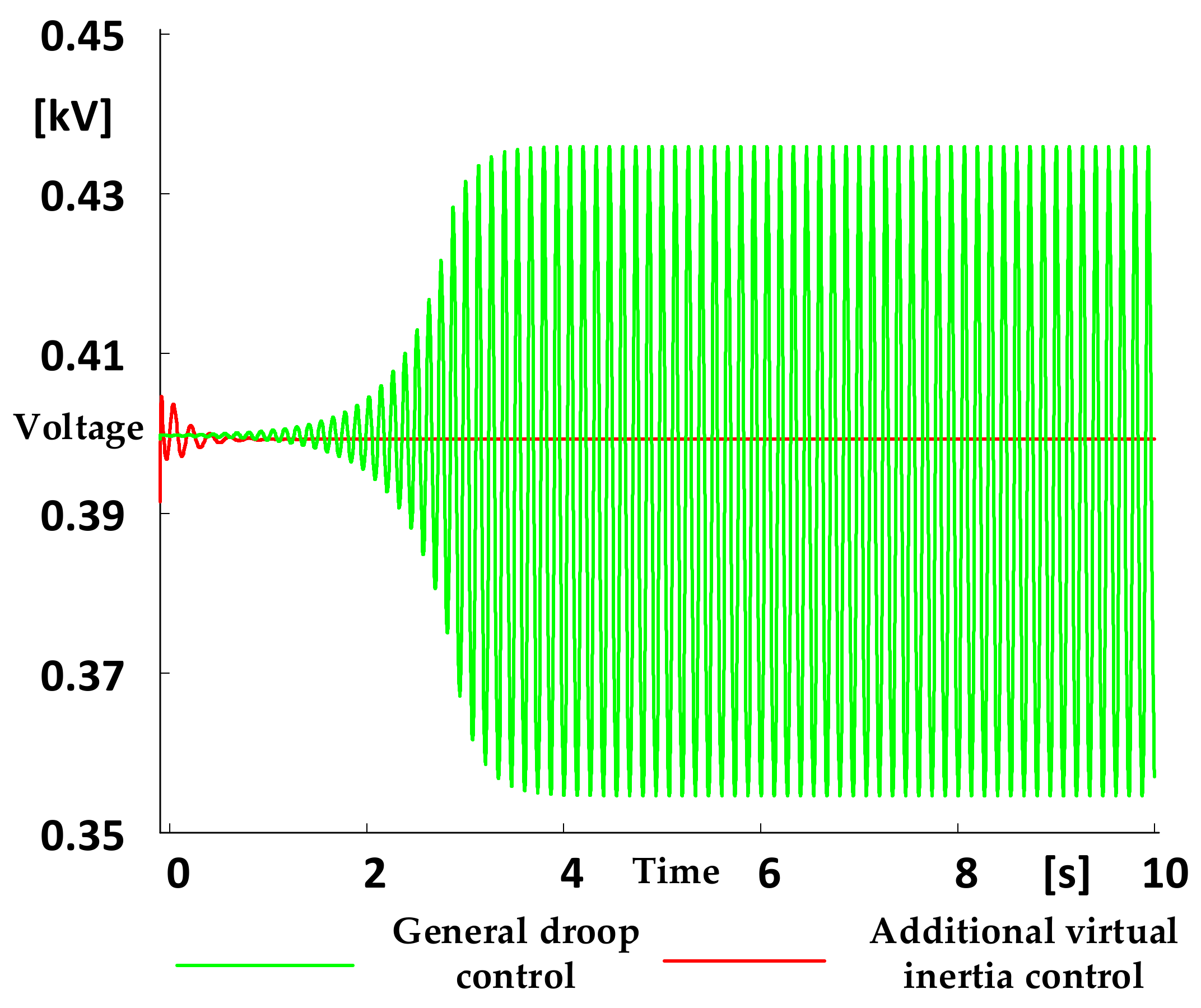
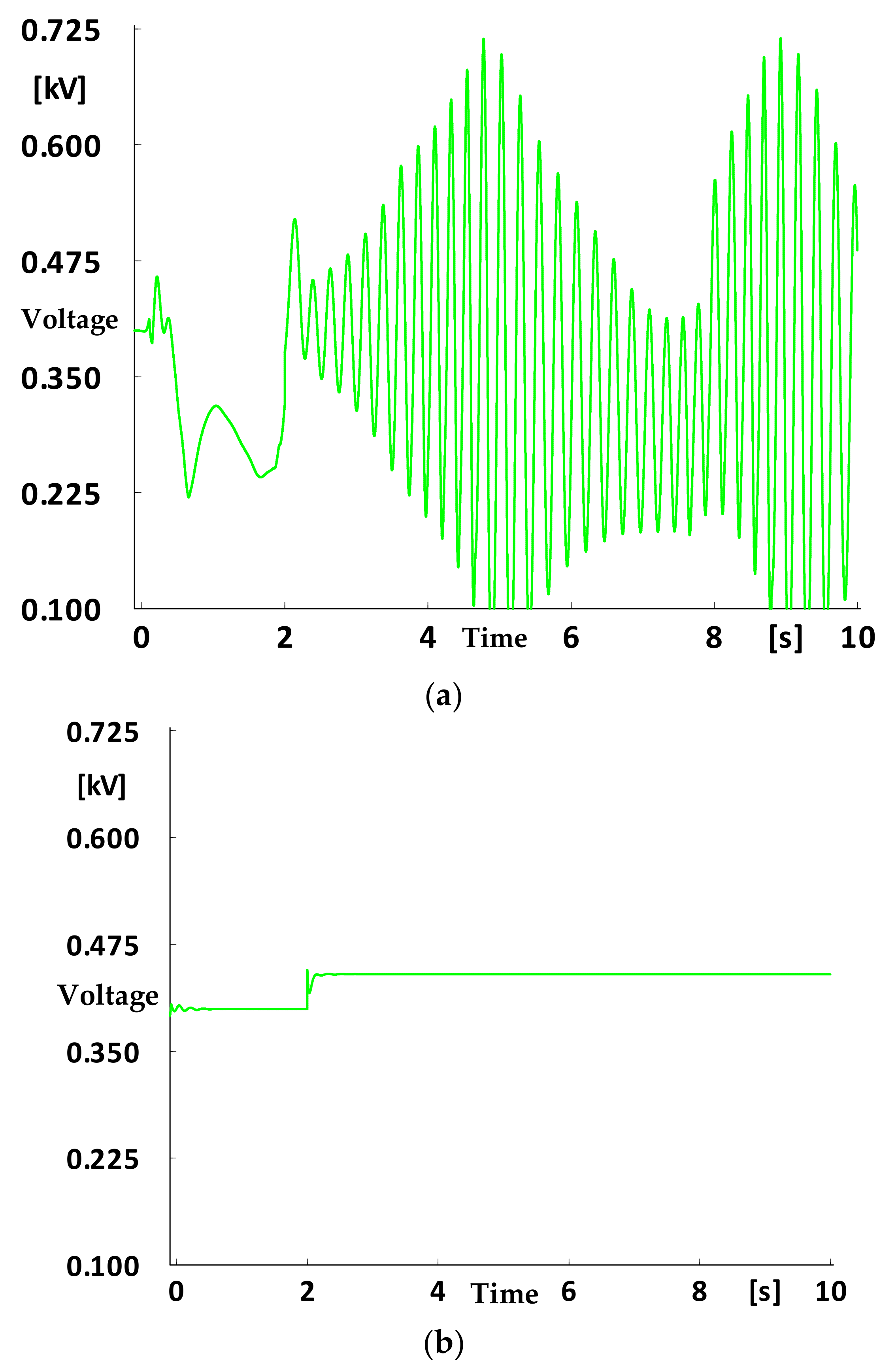
- A virtual inertia control based on a first-order filter for parallel converters with P-Udc droop control was proposed. The additional inertia control reduced the voltage change rate and improved the system’s inertia by adjusting the virtual capacitance value on the DC side of the converter, which achieved a more smooth and accurate voltage control and prevented continuous voltage oscillation.
- (2)
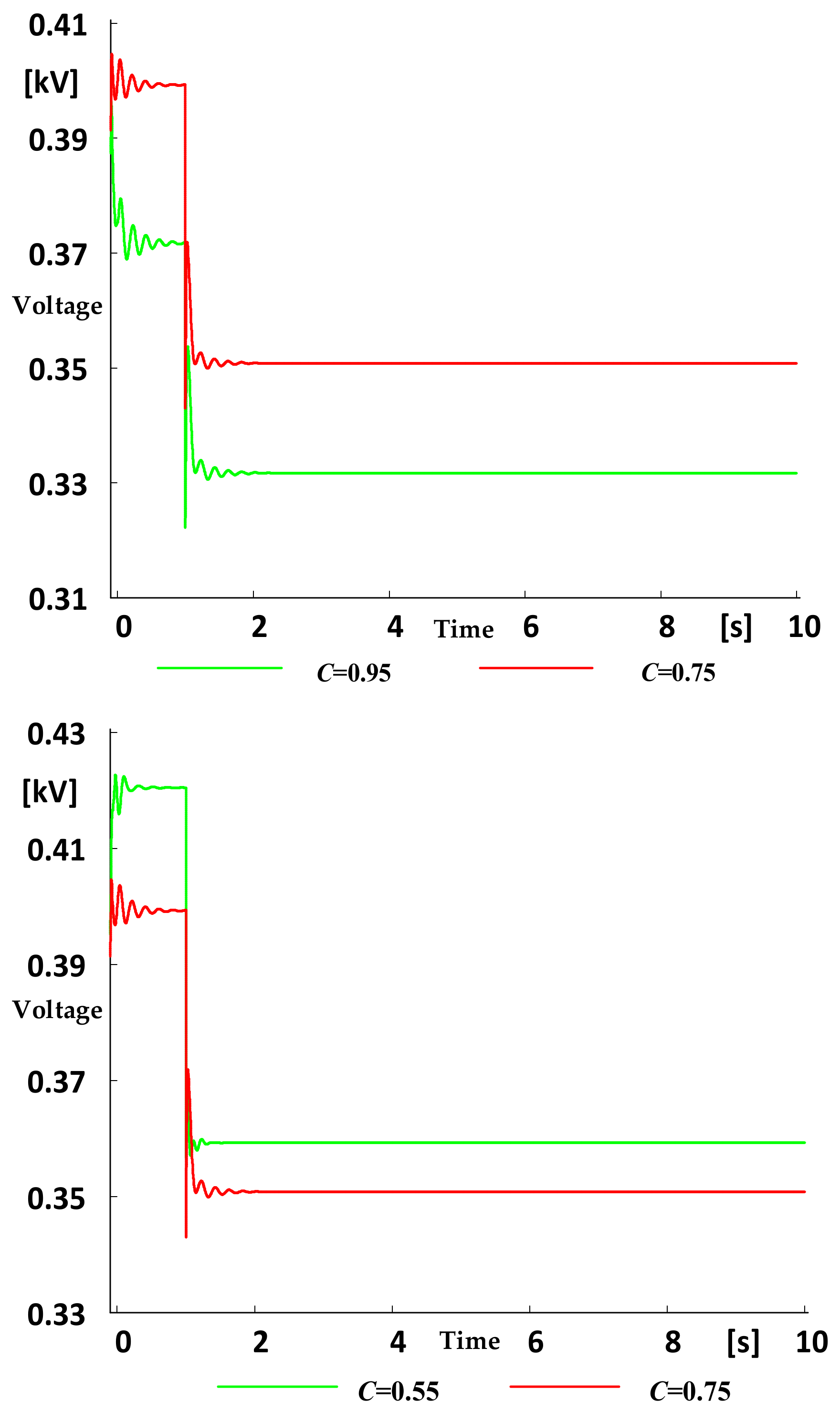
- The relationship between inertia control parameters and voltage sag fluctuation was obtained. When the damping coefficient Dr or virtual capacitance Cvir increased, the DC bus voltage drop was larger, and it took a longer time to recover to the new steady-state value. It is worth noting that when the damping coefficient Dr was changed, the variation range of voltage drop was significantly reduced, indicating that the voltage damping coefficient could improve the bus voltage’s ability to respond to load changes and ensure the voltage quality.
- (3)
- A simulation model and a hardware-in-the-loop system were built to verify the effectiveness of the proposed control strategy. By comparing the voltage curves before and after the application of virtual inertia control, it demonstrated that the proposed strategy could effectively suppress the distributed generations and loads fluctuation, which provided an effective stable control scheme for the parallel operation of converters.
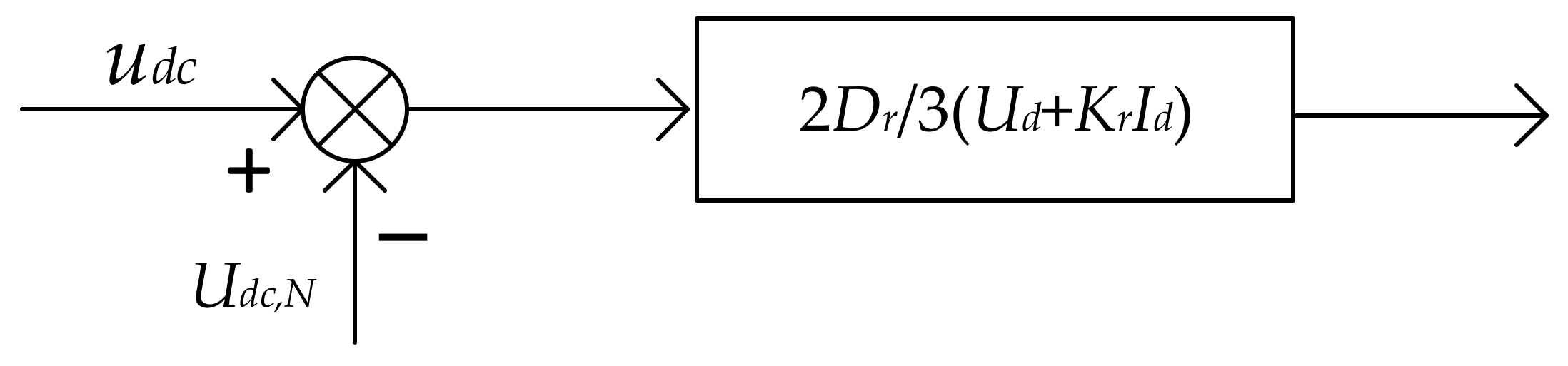
2. DC Distribution System Converter Control Model
3. Virtual Inertia Control
3.1. Time Constant of Inertia
3.2. Virtual Inertia Control Based on First-Order Filters
4. Simulation Analysis and Discussion
4.1. Simulation Analysis
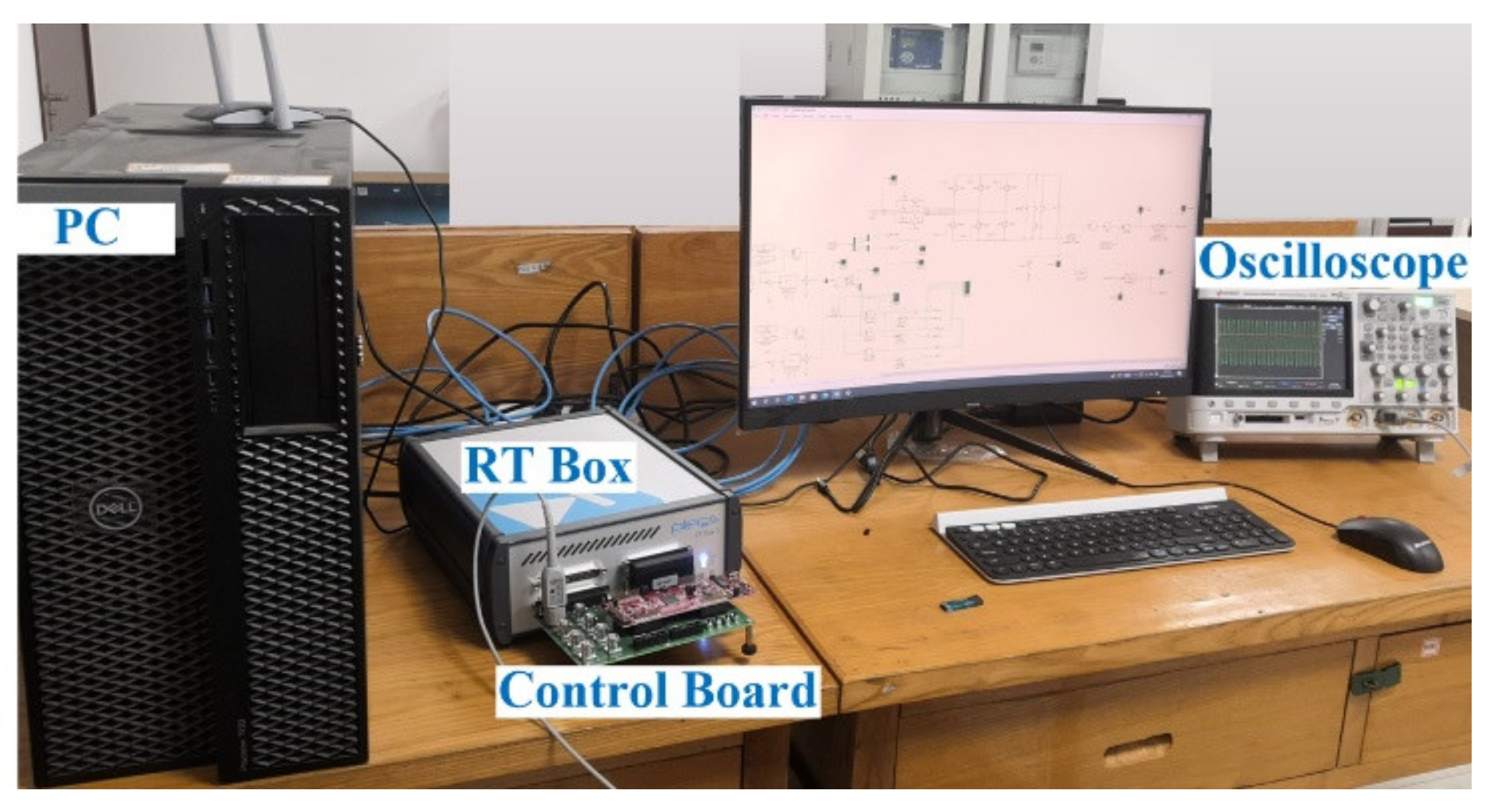
4.2. Experimental Verification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| DC | direct current |
| AC | alternating current |
| HFO | High-frequency oscillations |
| PLL | phase-locked loop |
| VSG | virtual synchronous generator |
| ROCOF | rate of change of frequency |
| MPC | adaptive virtual inertia system |
| MG | islanded microgrid |
| OSVI | optimized second-order virtual inertia |
| RESs | renewable energy sources |
| VSC-HVDC | line-commutated converter based on a voltage source converter |
| MMC | modular multilevel converter |
| Greek symbols | |
| ω | angular velocity |
| English symbols | |
| P | active power |
| Q | reactive power |
| U | voltage |
| I | current |
| R | resistor |
| L | inductor |
| C | capacitor |
| H | inertia time constant |
| W | energy |
| S | capacity |
| Y | voltage difference |
| d | d-axis |
| q | q-axis |
| T | time period |
| n | number of capacitors |
| N | rated value |
| Dr | voltage damping factor |
| Mr | voltage damping |
| ref | reference value |
| vir | virtualization |
References
- Zou, W.; Dong, H.; Chen, X.; Liu, K. Small Signal Modeling and Decoupling Control of VSC-MTDC. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 2786–2792. [Google Scholar] [CrossRef]
- Li, X.; Peng, K.; Zhang, X.; Gong, Q.; Liu, Y.; Jiang, S. Robust stability control for high frequency oscillations in flexible DC distribution systems. Int. J. Electr. Power Energy Syst. 2022, 137, 107833. [Google Scholar] [CrossRef]
- Yao, G.; Peng, K.; Li, X.; Jiang, S.; Liu, Y. A reduced-order model for high-frequency oscillation mechanism analysis of droop control based flexible DC distribution system. Int. J. Electr. Power Energy Syst. 2021, 130, 106927. [Google Scholar] [CrossRef]
- Ji, Y.; Yuan, Z.; Zhao, J.; Zhao, Y.; Li, G.; Li, Y. Control scheme for multi-terminal VSC-basedmedium-voltage DC distribution networks. Inst. Eng. Technol. 2019, 16, 2935–2940. [Google Scholar]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y. Robust Virtual Inertia Control of a Low Inertia Microgrid Considering Frequency Measurement Effects. IEEE Access 2019, 7, 57550–57560. [Google Scholar] [CrossRef]
- Sun, D.; Liu, H.; Gao, S.; Wu, L.; Song, P.; Wang, X. Comparison of Different Virtual Inertia Control Methods for Inverter-based Generators. J. Mod. Power Syst. Clean Energy 2020, 8, 768–777. [Google Scholar] [CrossRef]
- Wang, X.; Yang, T. Study on dynamic characteristic optimization of virtual inertia control for the grid-connected converters in DC micro grid. J. Phys. Conf. Ser. 2021, 1885, 042066. [Google Scholar] [CrossRef]
- Liao, H.; Zeng, G.; Huang, B.; Ma, C.; Chen, G.; Zhao, J. Optimal Control Virtual Inertia of Optical Storage Microgrid Based on Improved Sailfish Algorithm. Wuhan Univ. J. Nat. Sci. 2022, 27, 218–230. [Google Scholar] [CrossRef]
- Shi, K.; Ye, H.; Song, W.; Zhou, G. Virtual Inertia Control Strategy in Microgrid Based on Virtual Synchronous Generator Technology. IEEE Access 2018, 6, 27949–27957. [Google Scholar] [CrossRef]
- Fawzy, A.; Bakeer, A.; Magdy, G.; Atawi, I.E.; Roshdy, M. Adaptive Virtual Inertia-Damping System Based on Model Predictive Control for Low-Inertia Microgrids. IEEE Access 2021, 9, 109718–109731. [Google Scholar] [CrossRef]
- Xu, H.; Yu, C.; Mao, F.; Liu, C.; Wang, Q.; Zhang, X. A Power Oscillation Damping Algorithm of Distributed Generators Based on Optimized Second-order Virtual Inertia. In Proceedings of the IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2369–2374. [Google Scholar] [CrossRef]
- Kerdphol, T.; Watanabe, M.; Hongesombut, K.; Mitani, Y. Self-Adaptive Virtual Inertia Control-Based Fuzzy Logic to Improve Frequency Stability of Microgrid With High Renewable Penetration. IEEE Access 2019, 7, 76071–76083. [Google Scholar] [CrossRef]
- Ren, M.; Li, T.; Shi, K.; Xu, P.; Sun, Y. Coordinated Control Strategy of Virtual Synchronous Generator Based on Adaptive Moment of Inertia and Virtual Impedance. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 99–110. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, Z.; Ren, B.; Bu, S.; Wang, P. Damping Torque Analysis of VSC-HVDC Supplementary Damping Controller for Small-Signal Stability. IEEE Access 2020, 8, 202696–202706. [Google Scholar] [CrossRef]
- Gu, M.; Meegahapola, L.; Wong, K.L. Damping Performance Analysis and Control of Hybrid AC/Multi-Terminal DC Power Grids. IEEE Access 2019, 7, 118712–118726. [Google Scholar] [CrossRef]
- Tirtashi, M.R.S.; Samuelsson, O.; Svensson, J. Impedance Matching for VSC–HVDC and Energy Storage Damping Controllers. IEEE Trans. Power Deliv. 2017, 33, 1016–1017. [Google Scholar] [CrossRef]
- Tinajero, M.Z.; Ornelas-Tellez, F.; Garcia-Barriga, N. Optimal Control of an Inverter-based Virtual Synchronous Generator with Inertial Response. IEEE Lat. Am. Trans. 2022, 20, 780–786. [Google Scholar] [CrossRef]
- Iqbal, M.T.; Maswood, A.I.; Tariq, M.; Iqbal, A.; Verma, V.; Urooj, S. A Detailed Full-Order Discrete-Time Modeling and Stability Prediction of the Single-Phase Dual Active Bridge DC-DC Converter. IEEE Access 2022, 10, 31868–31884. [Google Scholar] [CrossRef]
- Iqbal, M.T.; Maswood, A.I. A switchable bilinear discrete-time modeling for the stability analysis of the digitally controlled three-phase dual active bridge dc-dc converter. In Proceedings of the IECON 2020: The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3291–3296. [Google Scholar] [CrossRef]
- Carbone, L.; Cosso, S.; Kumar, K.; Marchesoni, M.; Passalacqua, M.; Vaccaro, L. Stability Analysis of Open-Loop V/Hz Controlled Asynchronous Machines and Two Novel Mitigation Strategies for Oscillations Suppression. Energies 2022, 15, 1404. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Xue, Y.; Qiu, R.; Liu, Z. Stability Analysis Method of Parallel Inverter. Math. Probl. Eng. 2017, 2017, 6062798. [Google Scholar] [CrossRef]
- Iqbal, M.T.; Maswood, A.I.; Tafti, H.D.; Tariq, M.; Bingchen, Z. Explicit discrete modelling of bidirectional dual active bridge dc–dc converter using multi-time scale mixed system model. IET Power Electron. 2020, 13, 4252–4260. [Google Scholar] [CrossRef]
- Iqbal, M.T.; Maswood, A.I. A frequency domain based large and small signal modeling of three phase dual active bridge. In Proceedings of the IECON 2020: The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3421–3426. [Google Scholar] [CrossRef]
- Sanders, S.; Noworolski, J.; Liu, X.; Verghese, G. Generalized averaging method for power conversion circuits. IEEE Trans. Power Electron. 1991, 6, 251–259. [Google Scholar] [CrossRef] [Green Version]
- Lammert, G.; Yamashita, K.; Ospina, L.D.P.; Renner, H.; Villanueva, S.M.; Pourbeik, P.; Ciausiu, F.E.; Braun, M. Modelling and Dynamic performance of inverter based generation in power system transmission and Distribution studie. Water Energy Int. 2017, 2017, 1899–1902. [Google Scholar] [CrossRef] [Green Version]
- Meng, Y.; Yu, J.; Shang, S.; Liu, B.; Gao, X. Modeling and Control of Modular Multilevel AC/AC Converter in Y Configuration for Fractional Frequency Transmission System. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 741–750. [Google Scholar] [CrossRef]
- Gruson, F.; Tlemcani, A.; Li, Y.; Delarue, P.; Le Moigne, P.; Guillaud, X. Model and control of the DC–DC modular multilevel converter with DC fault tolerance. EPE J. 2020, 30, 153–164. [Google Scholar] [CrossRef]












| Subsystem | Parameter Name | Parameter Value |
|---|---|---|
| VSC_1/2 | Droop factor Kp | 5 |
| Inner-loop scale factor Kip,d | 0.22 | |
| Inner-loop integration factor Kii,d | 11 | |
| Outer-loop scale factor Kpp,d | 0.04 | |
| Outer-loop integration factor Kpi,d | 40 | |
| VSC_1side | Input Voltage Ug/V | 200 |
| AC Line Rg1/Lg1 | 0.018 Ω/0.5 mH | |
| Filter Rf1/Lf1/Cf1 | 50 mΩ/2 mH/45 µF | |
| VSC_2side | Input Voltage Ug/V | 200 |
| AC Line Rg2/Lg2 | 0.018 Ω/0.5 mH | |
| Filter Rf2/Lf2/Cf2 | 50 mΩ/5 mH/45 µF | |
| DC side | Bus Voltage Udc/V | 400 |
| DC Load/KW | 20 | |
| DC Line Rs/Ls | 0.007 Ω/0.22 mH |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Jiang, Y.; Peng, K.; Liu, L. A Virtual Inertia Method for Stability Control of DC Distribution Systems with Parallel Converters. Energies 2022, 15, 8581. https://doi.org/10.3390/en15228581
Gao Q, Jiang Y, Peng K, Liu L. A Virtual Inertia Method for Stability Control of DC Distribution Systems with Parallel Converters. Energies. 2022; 15(22):8581. https://doi.org/10.3390/en15228581
Chicago/Turabian StyleGao, Qun, Yan Jiang, Ke Peng, and Lei Liu. 2022. "A Virtual Inertia Method for Stability Control of DC Distribution Systems with Parallel Converters" Energies 15, no. 22: 8581. https://doi.org/10.3390/en15228581




