Hydrodynamic Response and Tension Leg Failure Performance Analysis of Floating Offshore Wind Turbine with Inclined Tension Legs
Abstract
1. Introduction
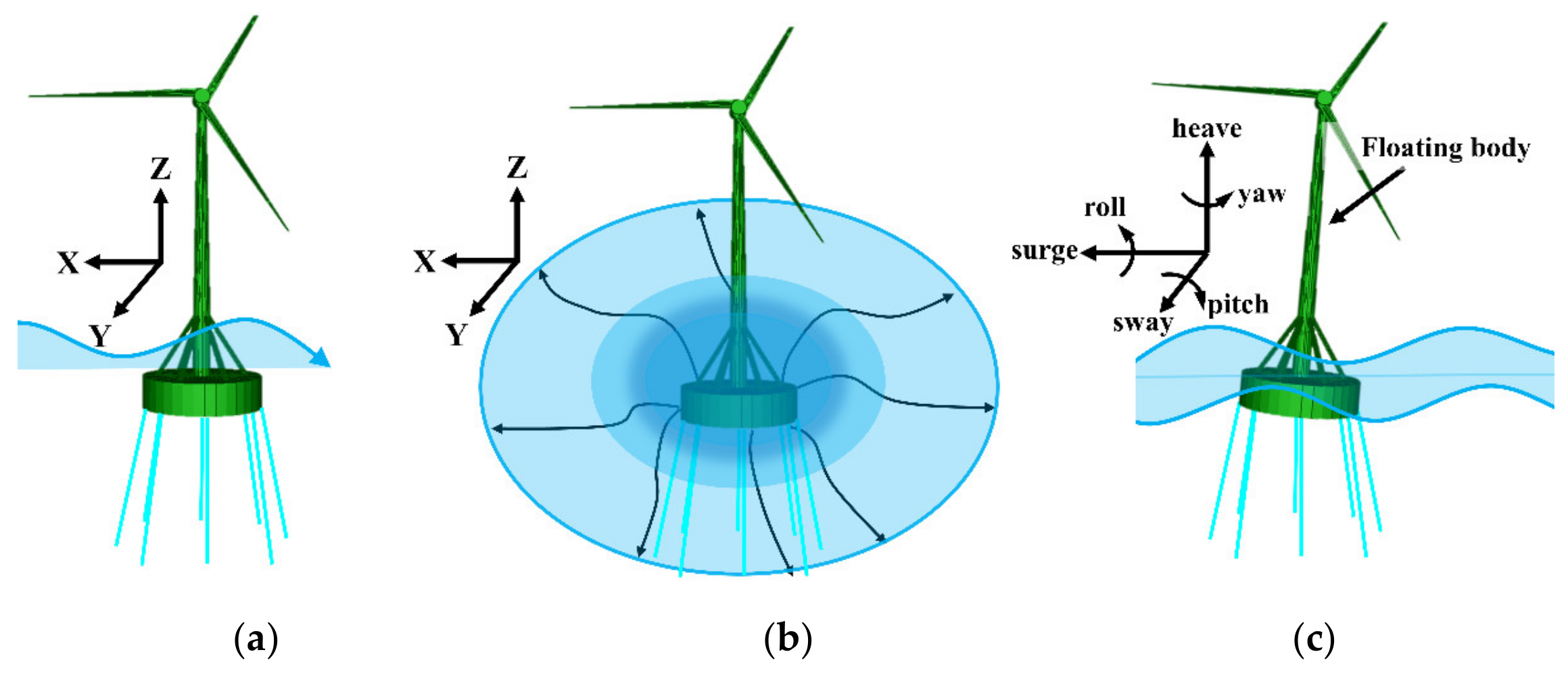
2. Hydrodynamic Theory of Floating Body
2.1. Assumptions
- (1)
- The fluid is uniform, incompressible, and inviscid.
- (2)
- The water flow is irrotational.
- (3)
- The free surface wave is a linear, small-amplitude wave.
- (4)
- The floating body moves in a small-amplitude and simple harmonic motion.
2.2. Load Calculation
3. Hydrodynamic Modeling of FOWT with Inclined Tension Legs
3.1. Hydrodynamic Model
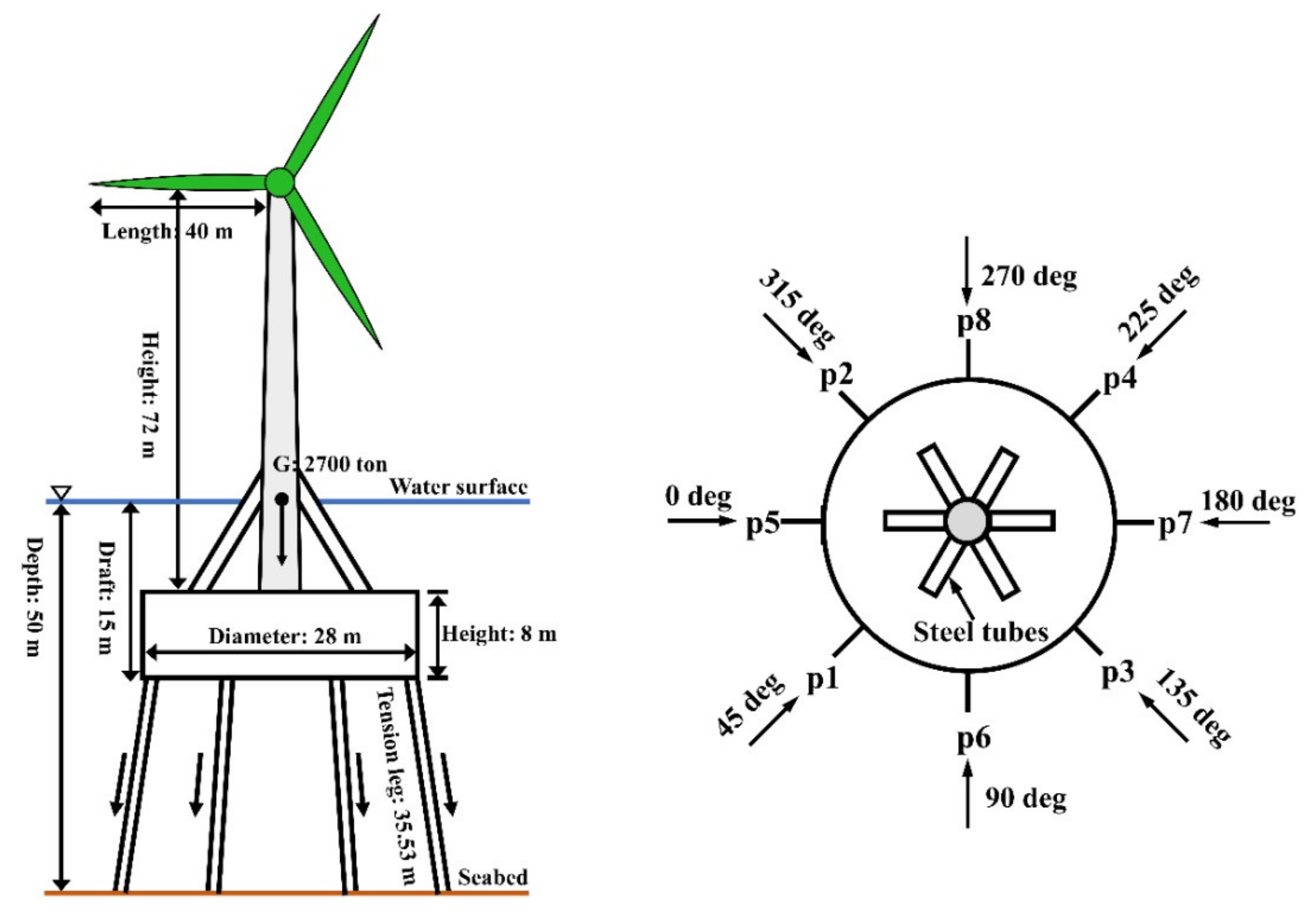
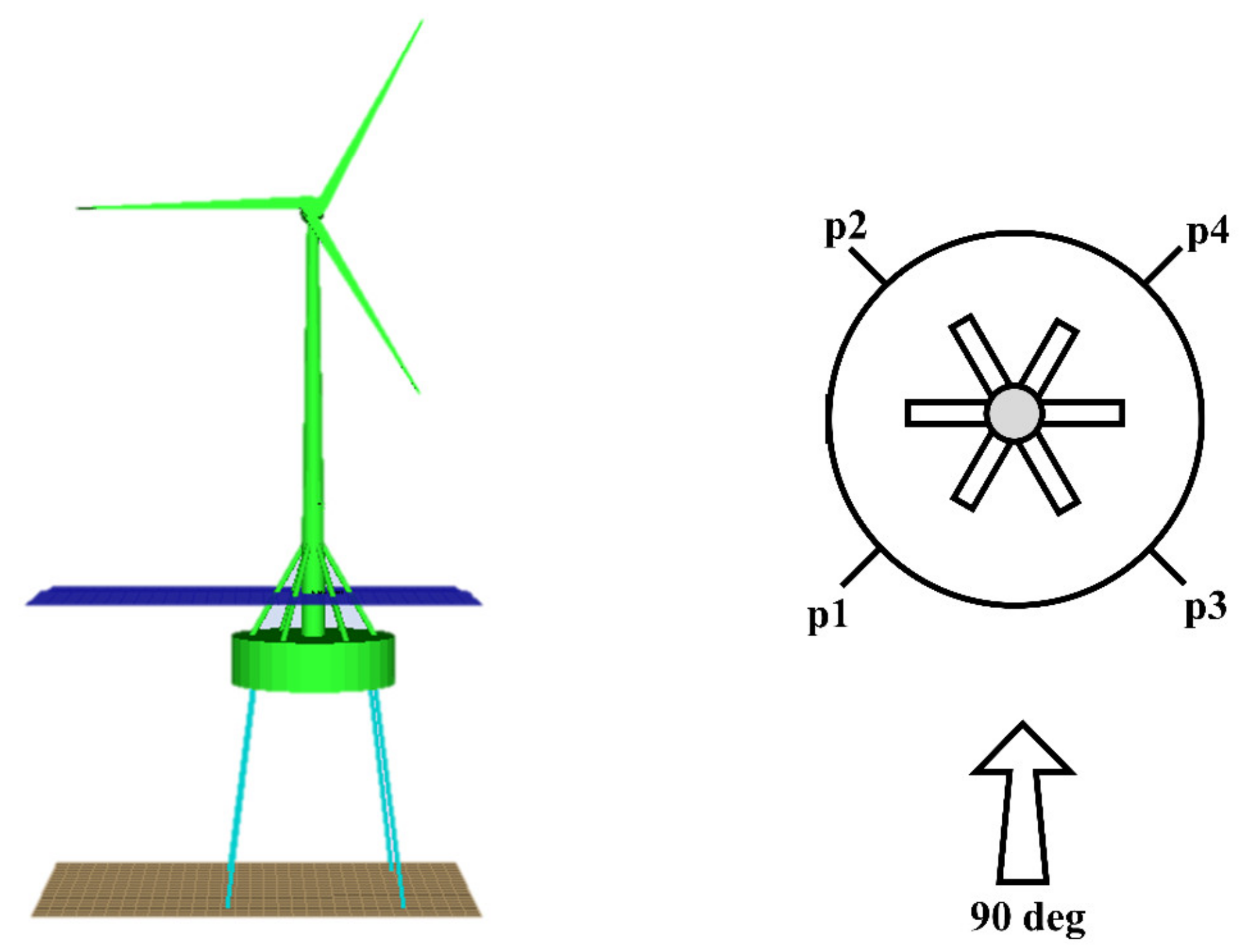
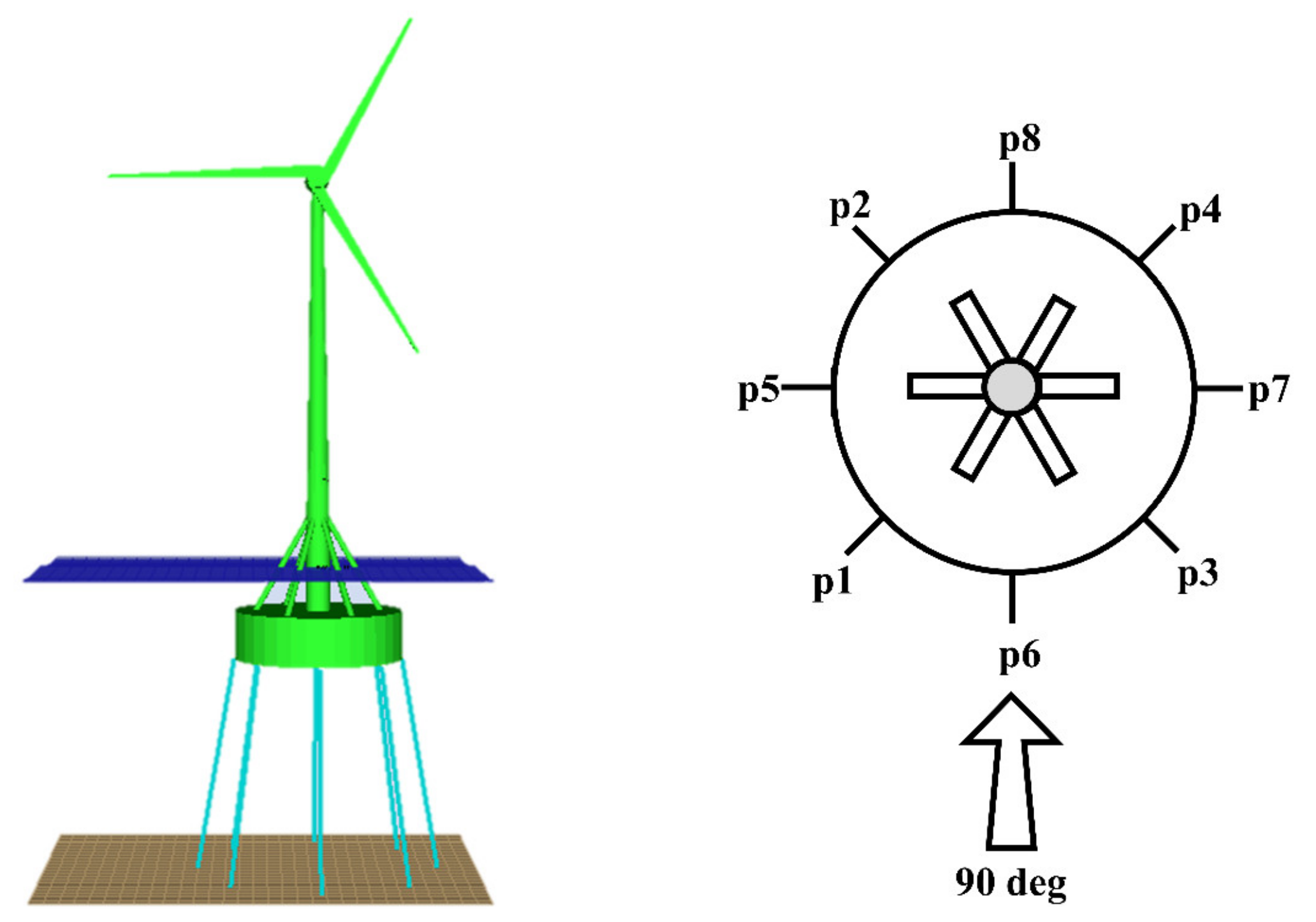
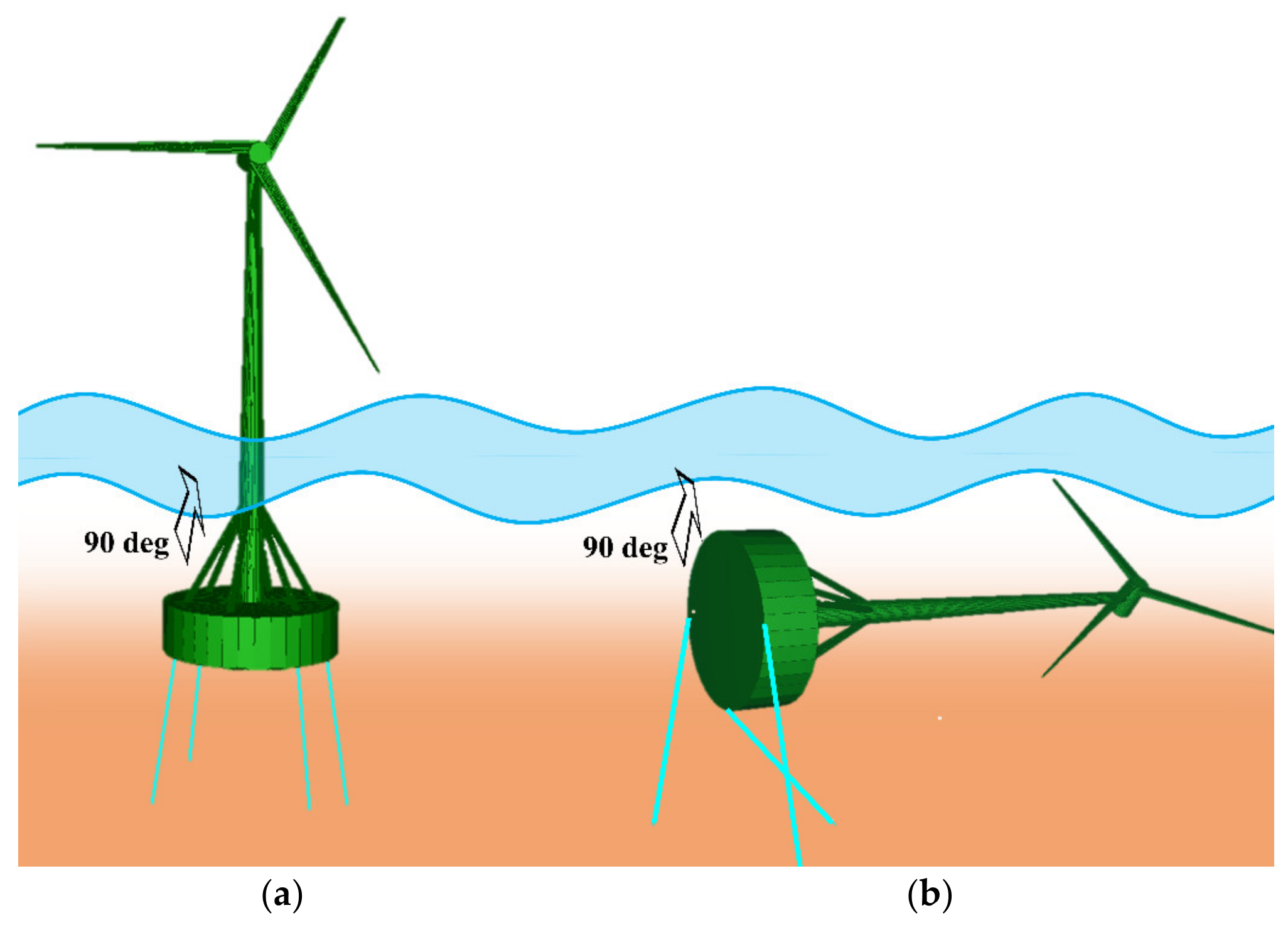
3.2. Numerical Model of FOWT with Inclined Tension Legs
3.3. RAOs and Motion Responses of FOWT with Inclined Tension Legs
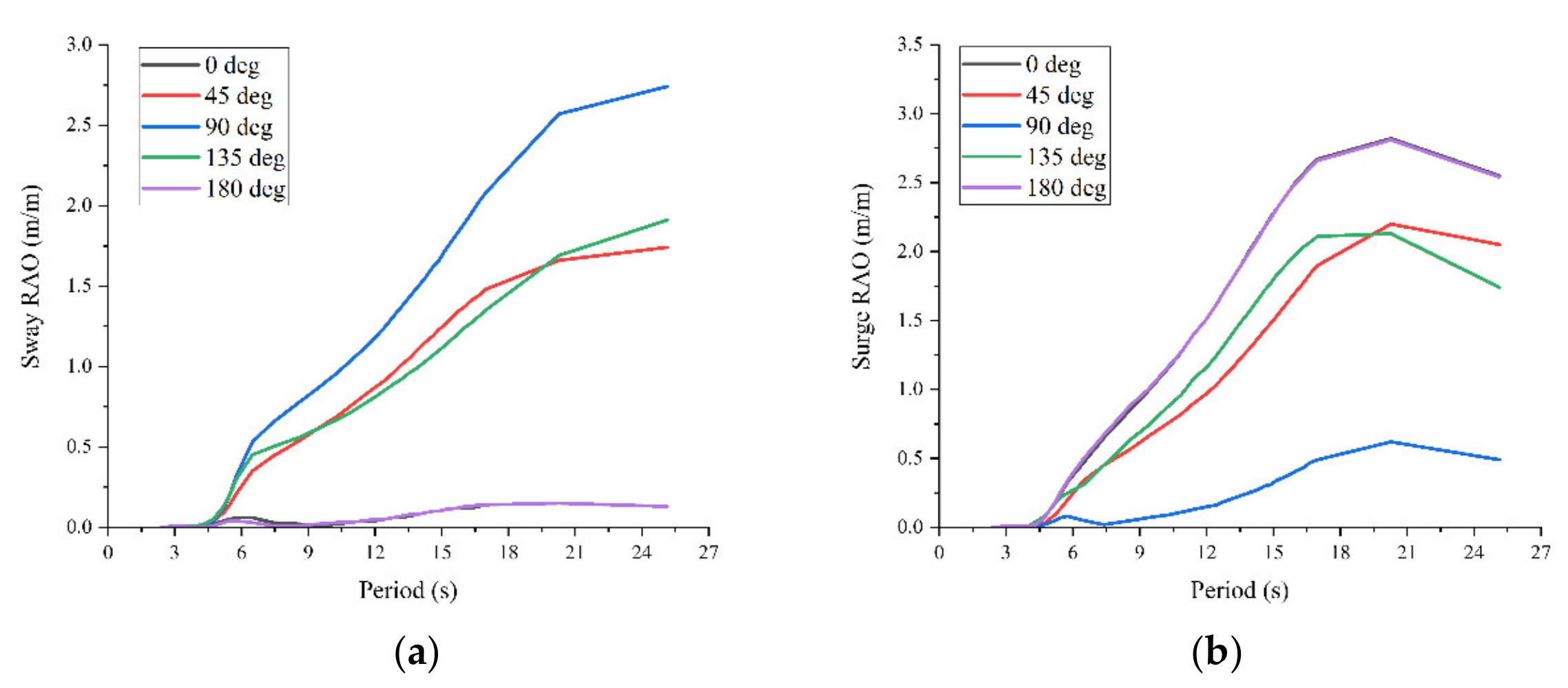
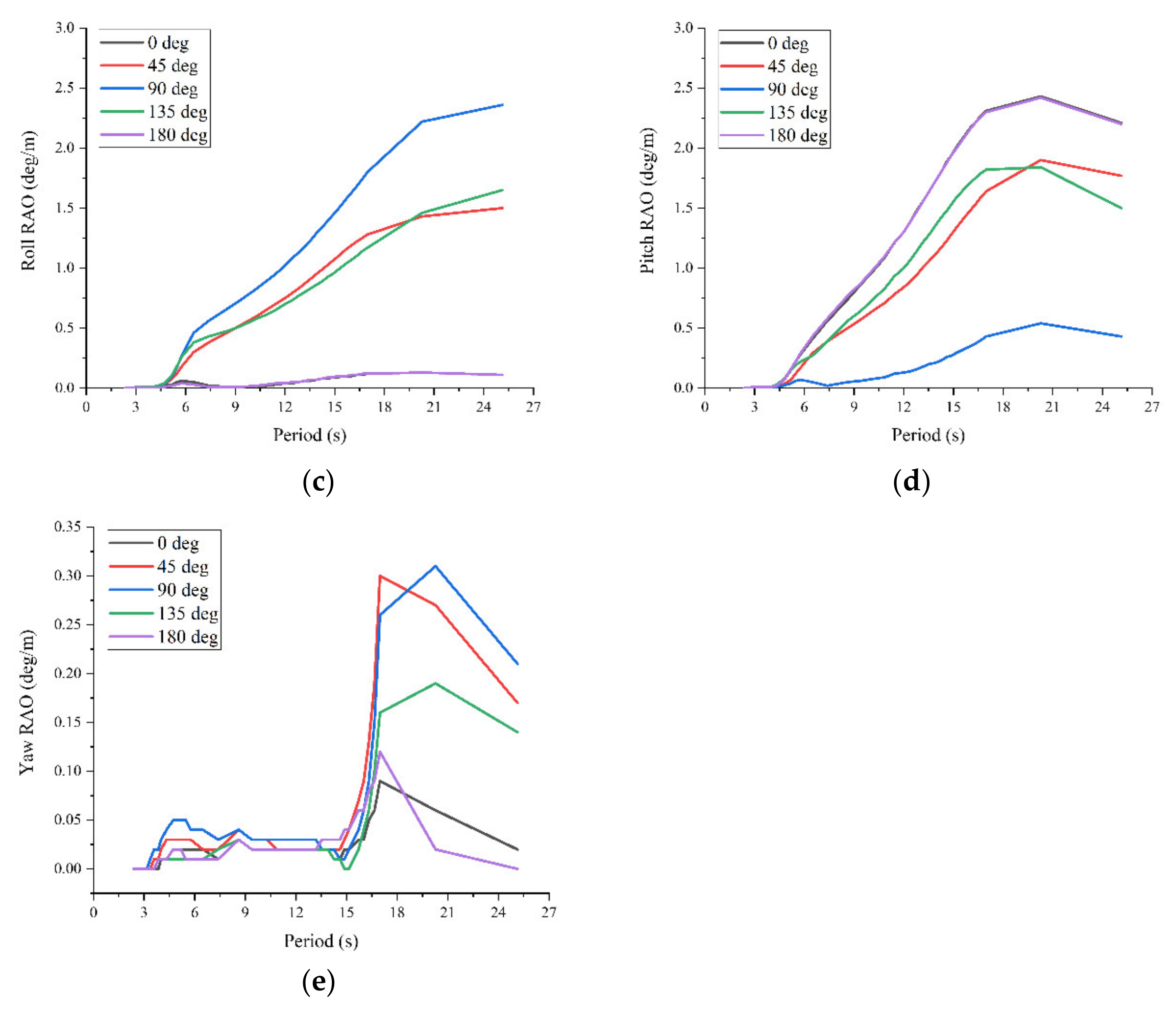
3.3.1. RAOs
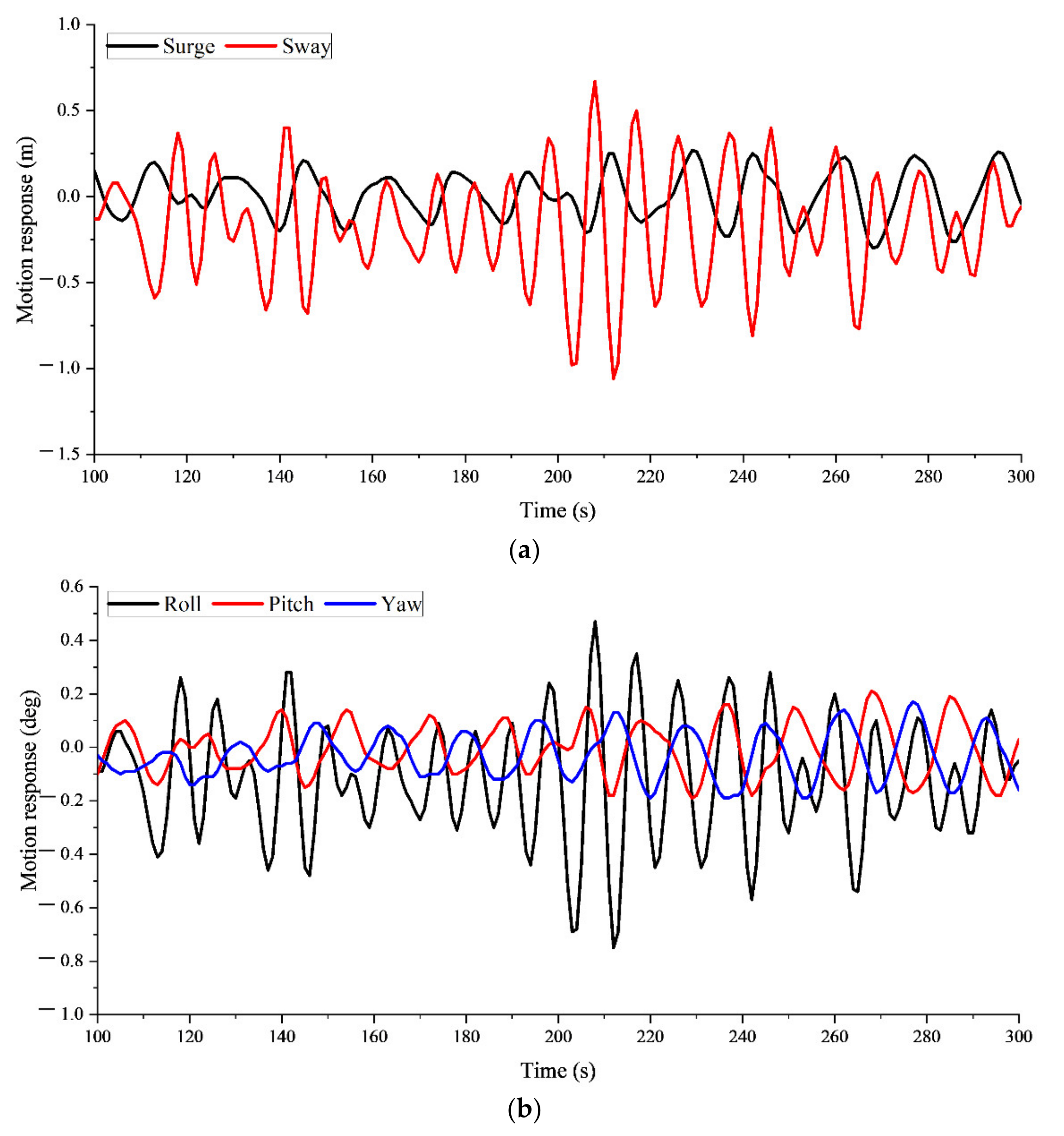
3.3.2. Motion Responses
3.4. Parametric Study of FOWT with Inclined Tension Legs
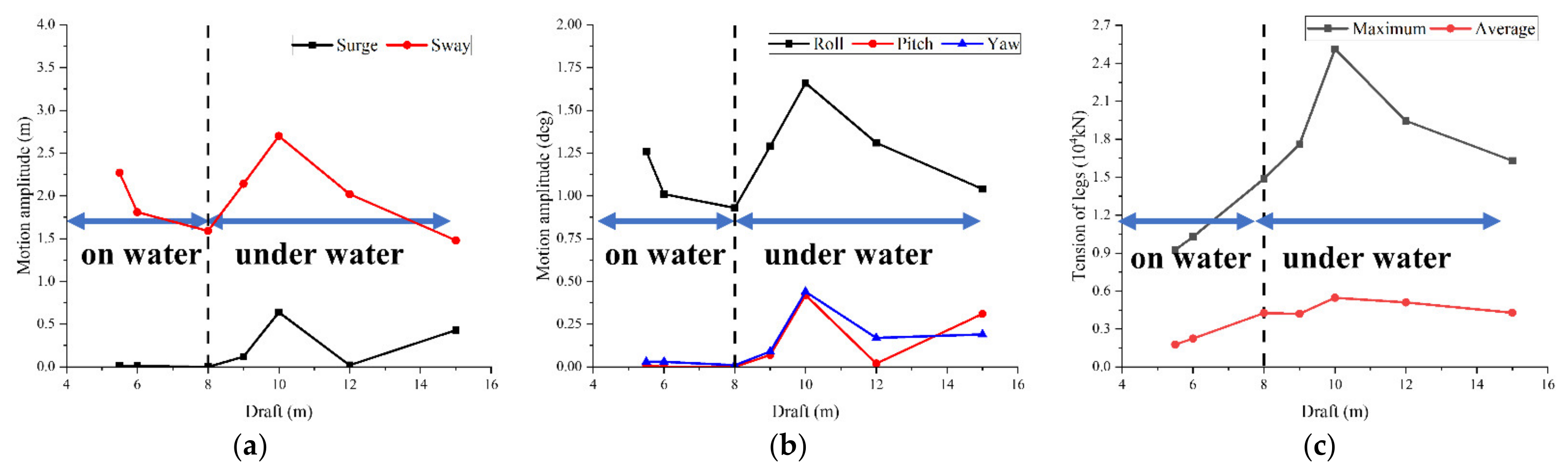
3.4.1. Effect of Draft
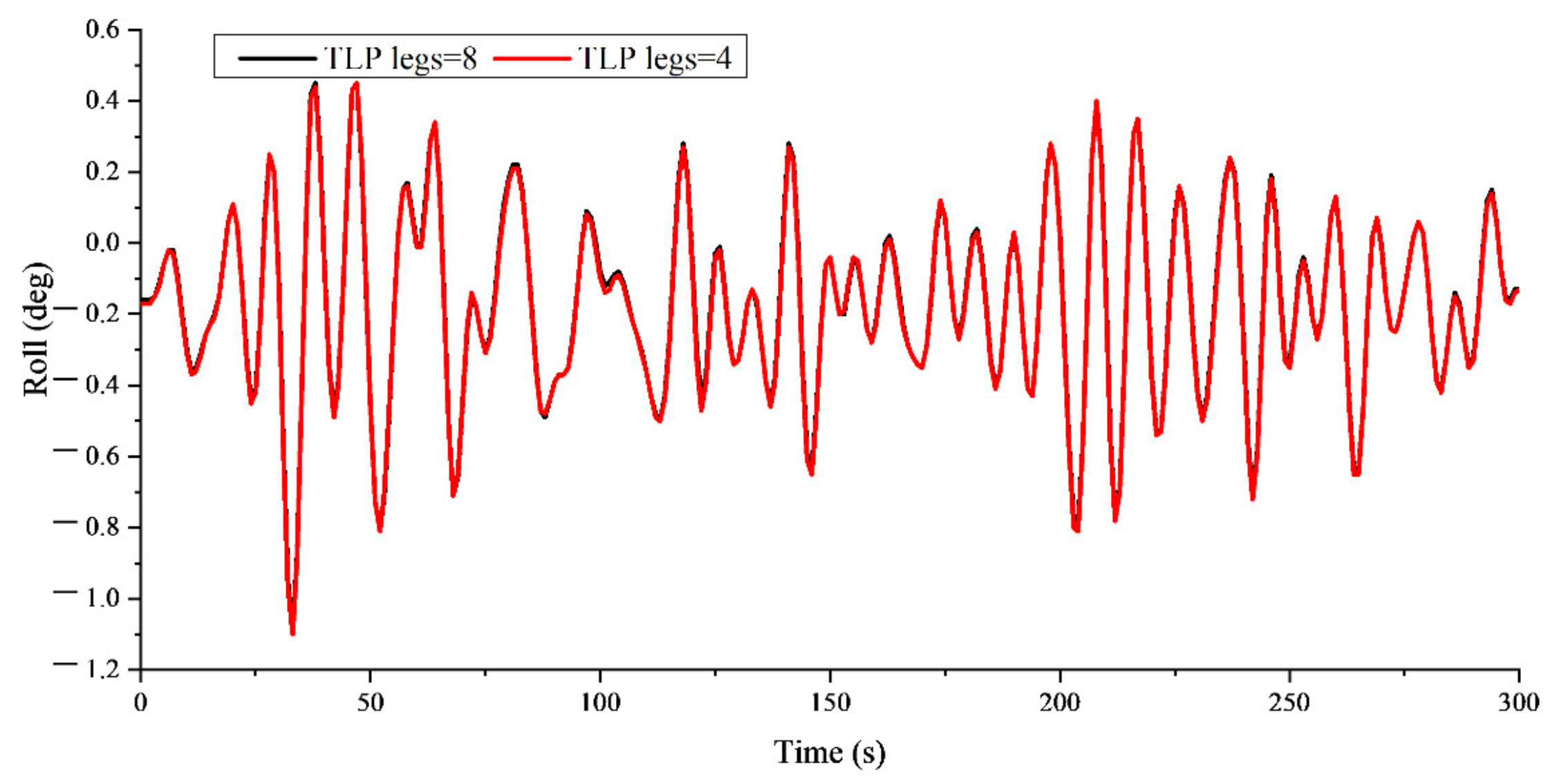
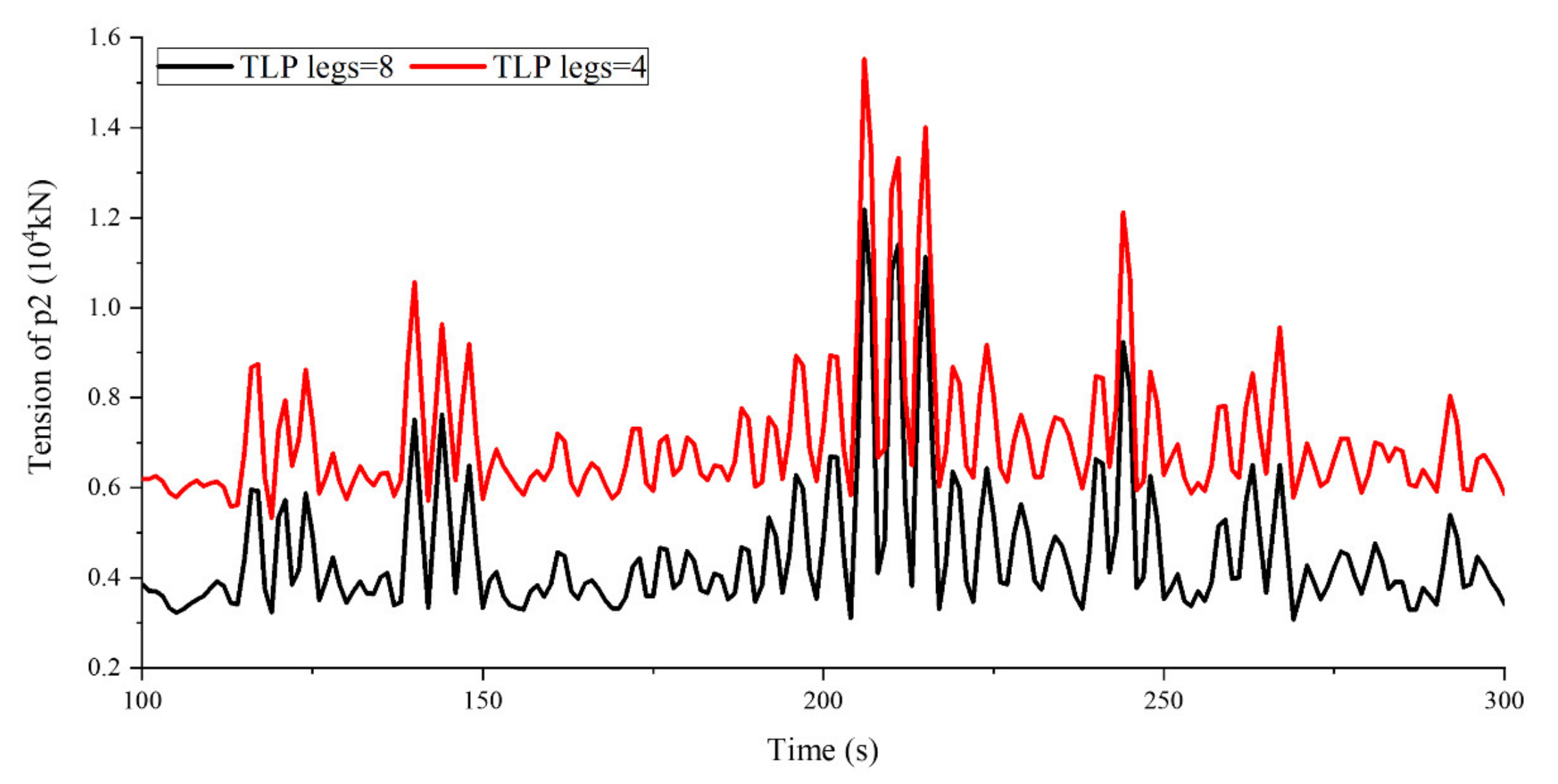
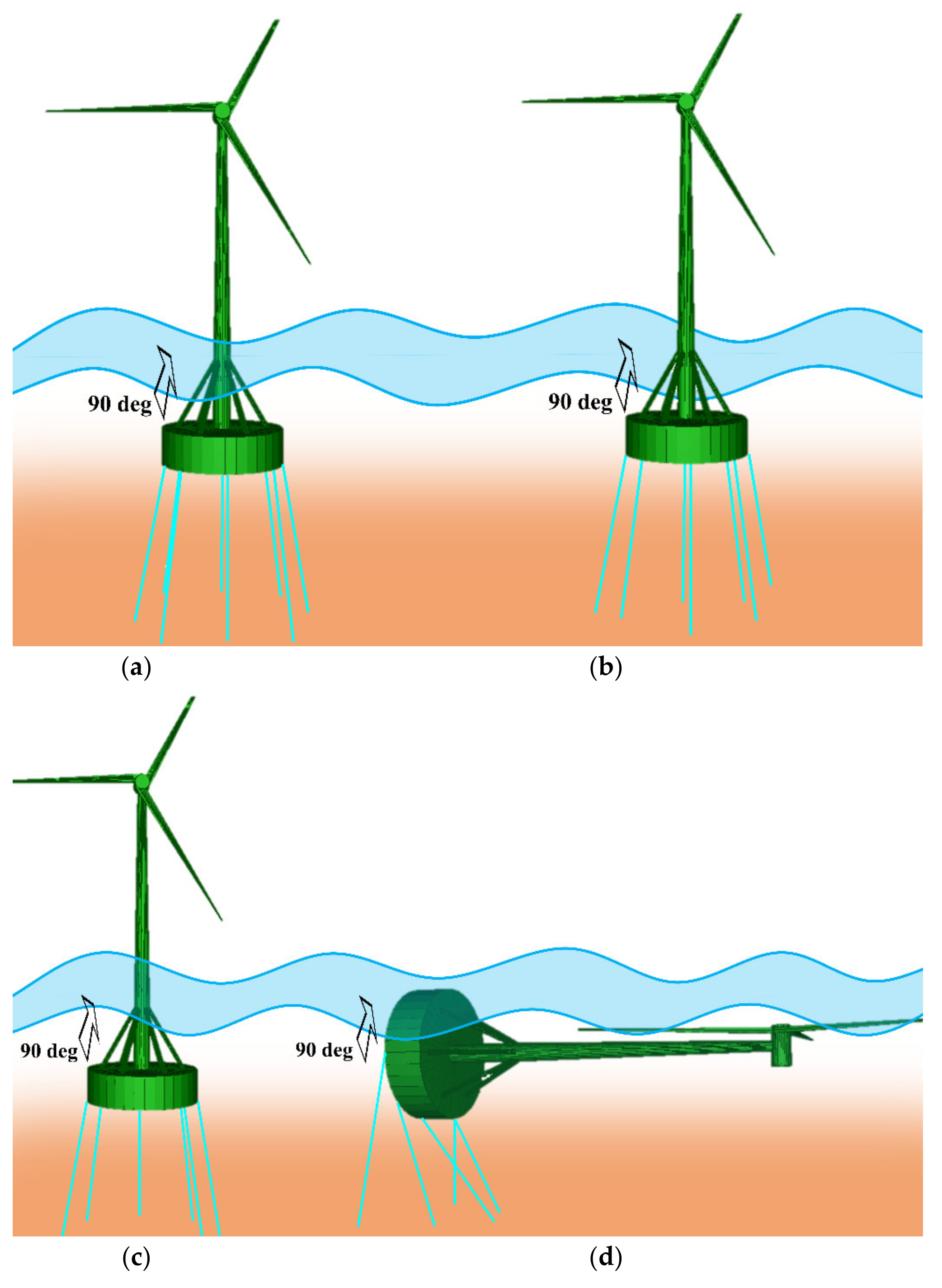
3.4.2. Effect of Tension Leg Arrangement
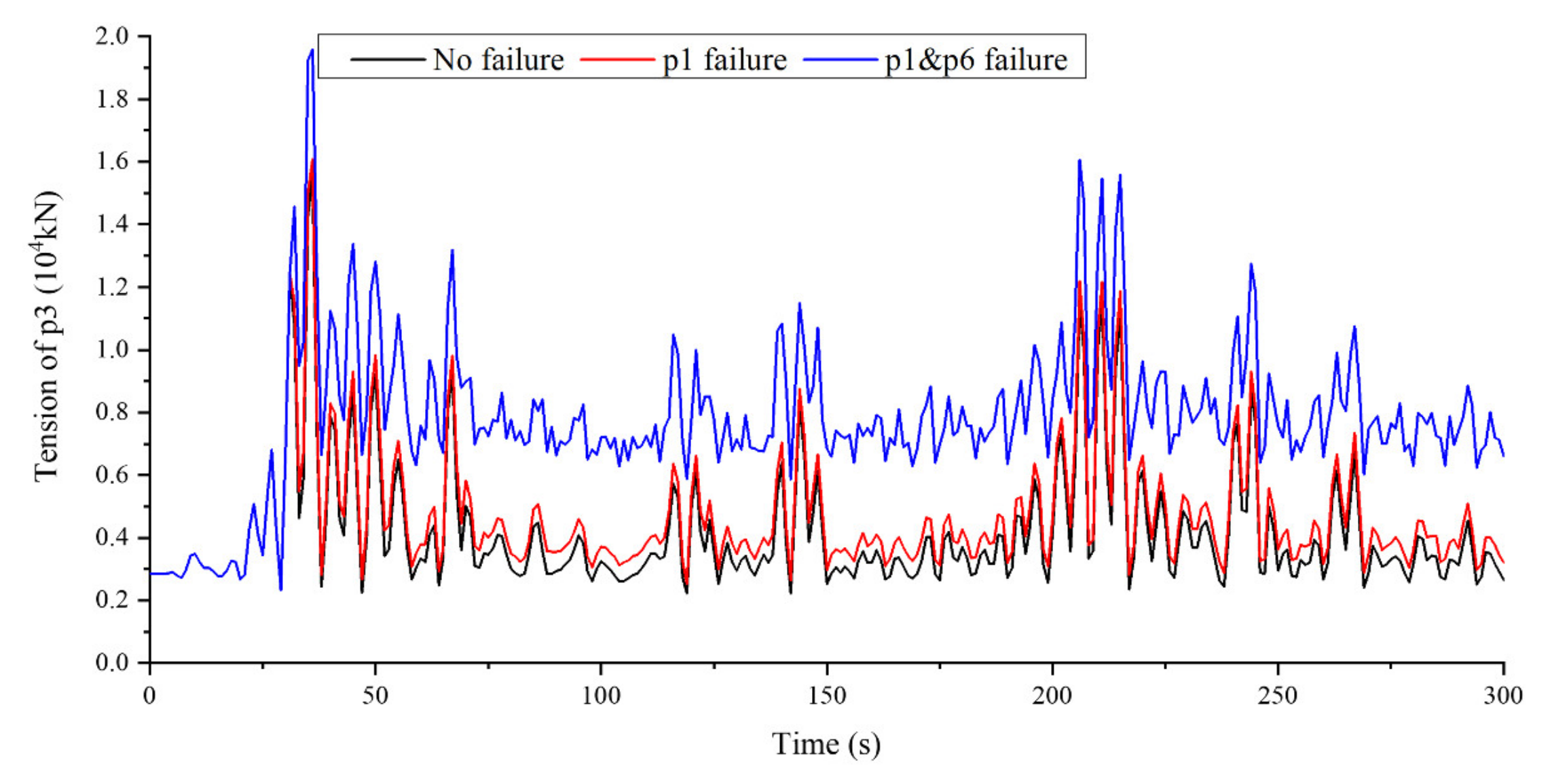
4. Failure Performance of Tension Legs
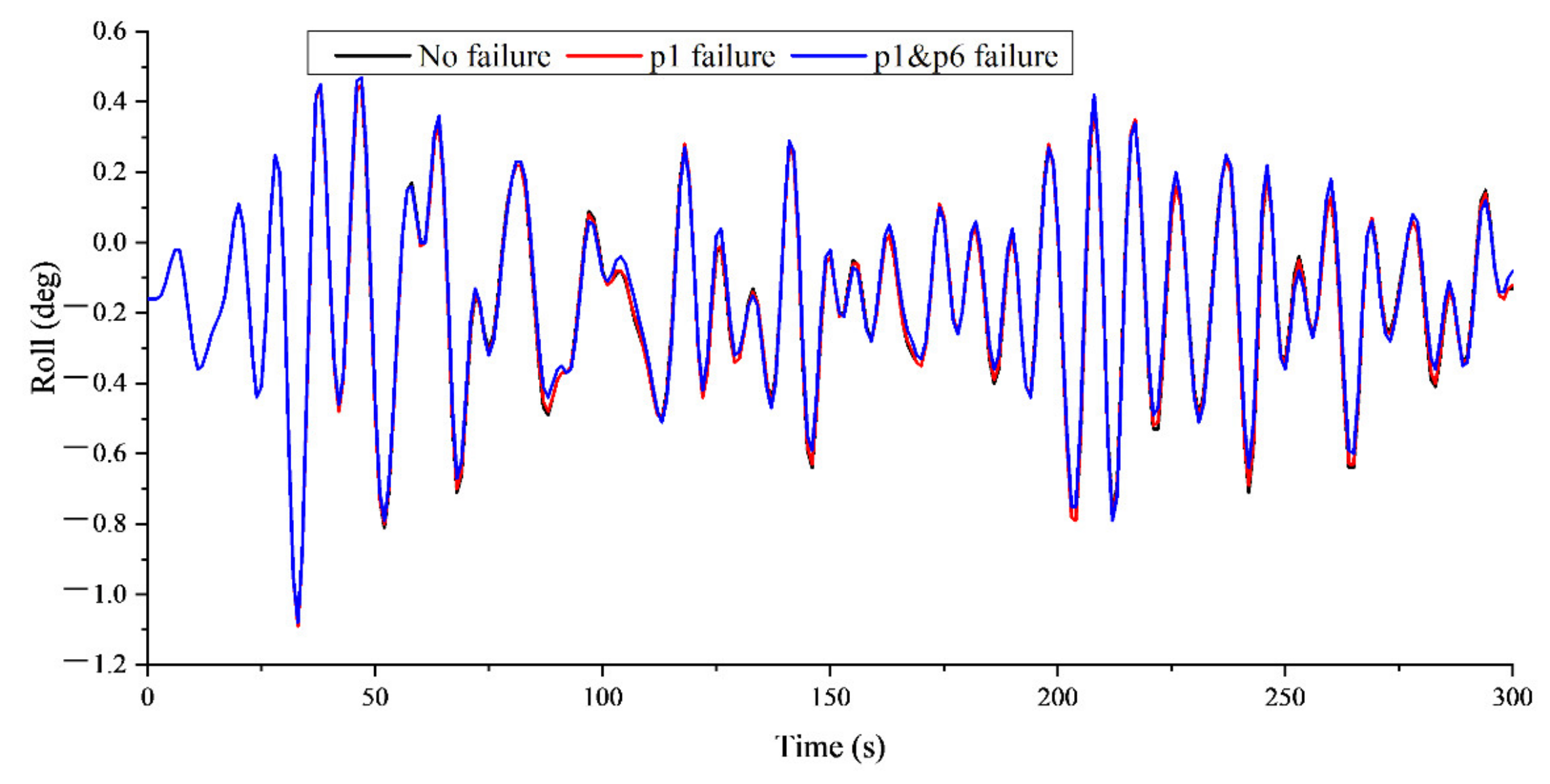
4.1. Failure Conditions of Tension Legs
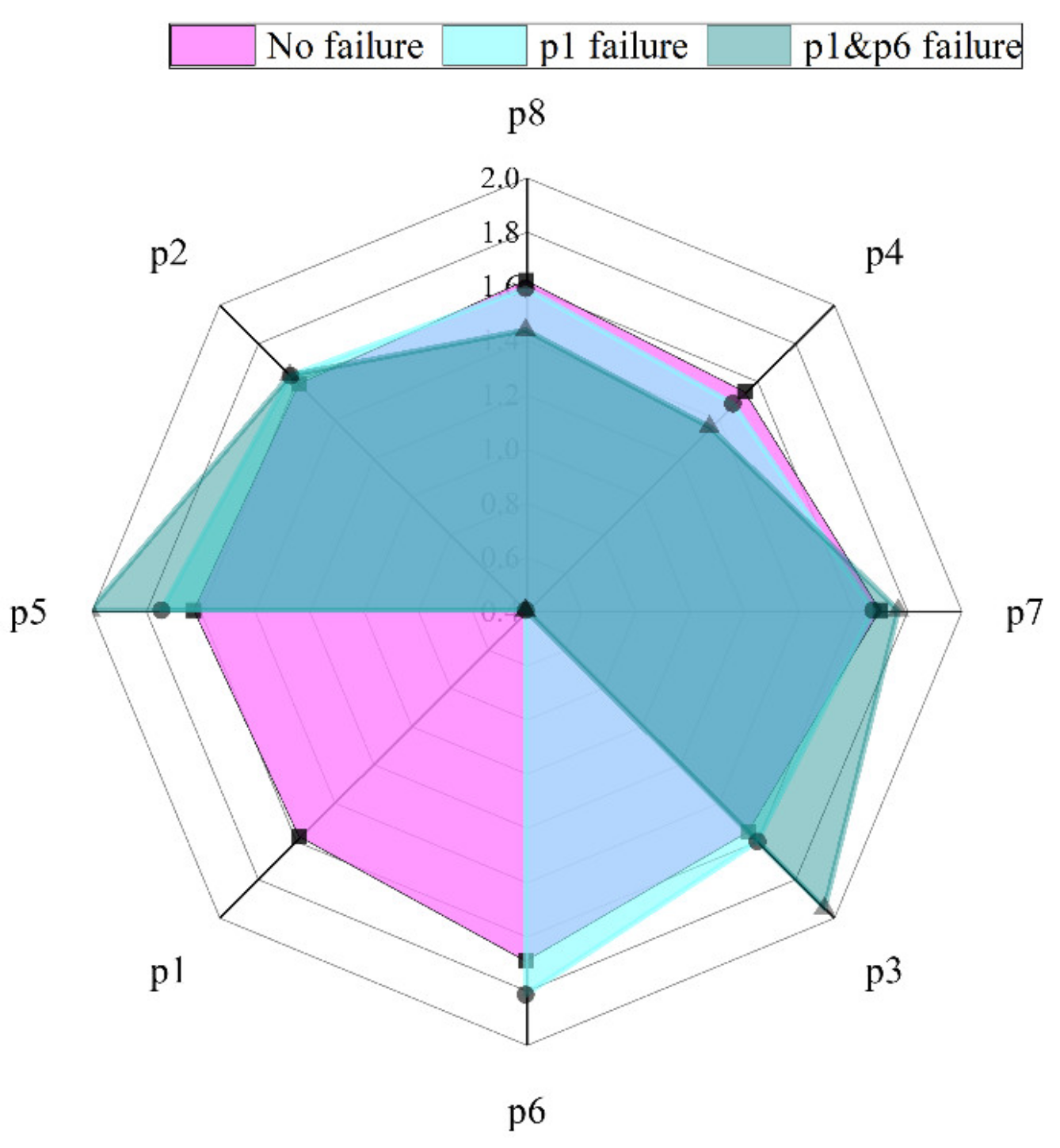
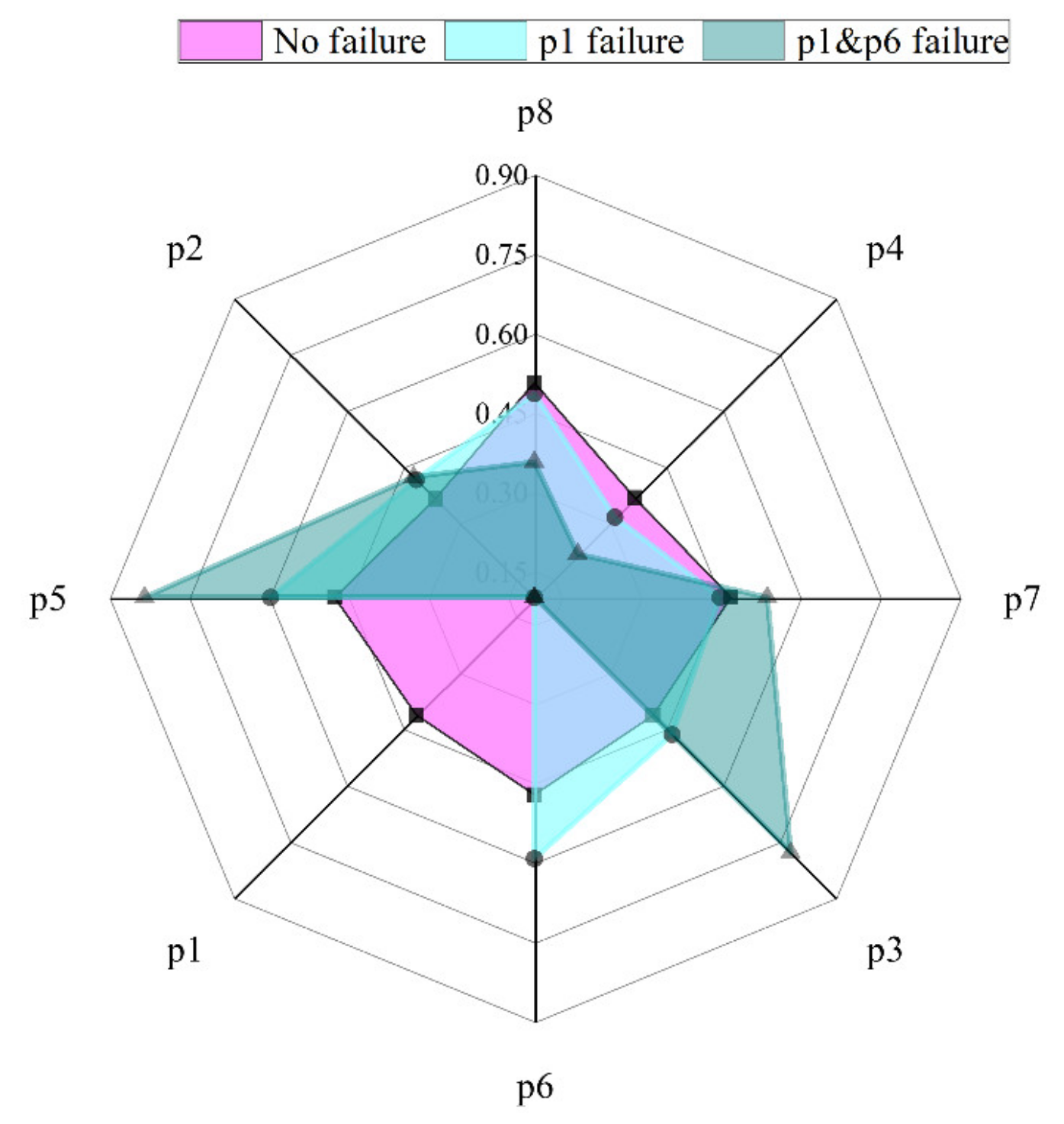
4.2. Envelope Diagram of Tensions of New Tension Leg Arrangement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leung, D.Y.C.; Yang, Y. Wind energy development and its environmental impact: A review. Renew. Sust. Energ. 2012, 16, 1031–1039. [Google Scholar] [CrossRef]
- Kumar, Y.; Ringenberg, J.; Depuru, S.S.; Devabhaktuni, V.K.; Lee, J.W.; Nikolaidis, E.; Andersen, B.; Afjeh, A. Wind energy: Trends and enabling technologies. Renew. Sust. Energ. 2016, 53, 209–224. [Google Scholar] [CrossRef]
- Ren, Y.; Venugopal, V.; Shi, W. Dynamic analysis of a multi-column TLP floating offshore wind turbine with tendon failure scenarios. Ocean. Eng. 2022, 245, 110247. [Google Scholar] [CrossRef]
- Walia, D.; Schünemann, P.; Hartmann, H.; Adam, F.; Groβmann, J. Numerical and physical modeling of a tension-leg platform for offshore wind turbines. Energies 2021, 14, 3554. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, S.; Wang, Y.; Ren, N.; Zhai, G. Experimental and numerical study on the multi-body coupling dynamic response of a Novel Serbuoys-TLP wind turbine. Ocean. Eng. 2019, 192, 106570. [Google Scholar] [CrossRef]
- Ma, Z.; Ren, N.; Wang, Y.; Wang, S.; Shi, W.; Zhai, G. A Comprehensive study on the serbuoys offshore wind tension leg platform coupling dynamic response under typical operational conditions. Energies 2019, 12, 2067. [Google Scholar] [CrossRef]
- Song, J.; Lim, H.C. Study of Floating Wind Turbine with Modified Tension Leg Platform Placed in Regular Waves. Energies 2019, 12, 703. [Google Scholar] [CrossRef]
- Zhao, Y.; She, X.; He, Y.; Yang, J.; Peng, T.; Kou, Y. Experimental study on new multi-column tension-leg-type floating wind turbine. China. Ocean. Eng. 2018, 32, 123–131. [Google Scholar] [CrossRef]
- Ha, K.; Truong, H.V.A.; Dang, T.D.; Ahn, K.K. Recent control technologies for floating offshore wind energy system: A review. Int. J. Pr. Eng. Man-Gt. 2021, 8, 281–301. [Google Scholar] [CrossRef]
- Cruz, A.M.; Krausmann, E. Damage to offshore oil and gas facilities following hurricanes Katrina and Rita: An overview. J. Loss Prev. Proc. 2008, 21, 620–626. [Google Scholar] [CrossRef]
- Yang, C.K.; Kim, M.H. Transient effects of tendon disconnection of a TLP by hull-tendon-riser coupled dynamic analysis. Ocean. Eng. 2010, 37, 667–677. [Google Scholar] [CrossRef]
- Jameel, M.; Oyejobi, D.O.; Siddiqui, N.A.; Sulong, N.H.R. Nonlinear dynamic response of tension leg platform under environmental loads. KSCE J. Civ. Eng. 2017, 21, 1022–1030. [Google Scholar] [CrossRef]
- Oyejobi, D.O.; Jameel, M.; Sulong, N.H.R. Nonlinear response of tension leg platform subjected to wave, current and wind forces. Int. J. Civ. Eng. 2016, 14, 521–533. [Google Scholar] [CrossRef]
- Oyejobi, D.O.; Jameel, M.; Sulong, N.H.R. Stochastic response of intact and a removed tendon tension leg platform to random wave and current forces. Arab. J. Sci. Eng. 2017, 42, 1065–1076. [Google Scholar] [CrossRef]
- Tabeshpour, M.R.; Ahmadi, A.; Malayjerdi, E. Investigation of TLP behavior under tendon damage. Ocean. Eng. 2018, 156, 580–595. [Google Scholar] [CrossRef]
- Yu, J.; Hao, S.; Yu, Y.; Chen, B.; Cheng, S.; Wu, J. Mooring analysis for a whole TLP with TTRs under tendon one-time failure and progressive failure. Ocean. Eng. 2019, 182, 360–385. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, Y.; He, Y.; Shao, Y.; Mao, W.; Han, Z.; Huang, C.; Gu, X.; Jiang, Z. Transient response of a TLP-type floating offshore wind turbine under tendon failure conditions. Ocean. Eng. 2021, 220, 108486. [Google Scholar] [CrossRef]
- Cheng, S.; Yu, Y.; Yu, J.; Wu, J.; Li, Z.; Huang, Z. Mechanistic research on the complex motion response of a TLP under tendon breakage. Ocean. Eng. 2021, 240, 109984. [Google Scholar] [CrossRef]
- Qi, Y.; Tian, X.; Guo, X.; Lu, H.; Liu, L. The hydrodynamic performance of a tension leg platform with one-tendon failure. Ships. Offshore. Struc. 2018, 14, 523–533. [Google Scholar] [CrossRef]
- Chung, W.C.; Pestana, G.R.; Kim, M. Structural health monitoring for TLP-FOWT (floating offshore wind turbine) tendon using sensors. Appl. Ocean. Res. 2021, 113, 102740. [Google Scholar] [CrossRef]
- Choi, Y.-M.; Nam, B.W.; Hong, S.Y.; Jung, D.W.; Kim, H.J. Coupled motion analysis of a tension leg platform with a tender semi-submersible system. Ocean. Eng. 2018, 156, 224–239. [Google Scholar] [CrossRef]
- Jeon, S.H.; Cho, Y.U.; Seo, M.W.; Cho, J.R.; Jeong, W.B. Dynamic response of floating substructure of spar-type offshore wind turbine with catenary mooring cables. Ocean. Eng. 2013, 72, 356–364. [Google Scholar] [CrossRef]
- Koo, B.J.; Goupee, A.J.; Kimball, R.W.; Lambrakos, K.F. Model tests for a floating wind turbine on three different floaters. J. Offshore. Mech. 2014, 136, 020907. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Y. Platform stabilization of floating offshore wind turbines by artificial muscle based active mooring line force control. IEEE ASME T. Mech. 2020, 25, 2765–2776. [Google Scholar] [CrossRef]
- Bae, Y.H.; Kim, M.H.; Kim, H.C. Performance changes of a floating offshore wind turbine with broken mooring line. Renew. Energ. 2017, 101, 364–375. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Q.; Liu, L.; Tang, Y. Transient response of a SPAR-type floating offshore wind turbine with fractured mooring lines. Renew. Energ. 2018, 122, 576–588. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Ding, H. Study on the coupled dynamic responses of a submerged floating wind turbine under different mooring conditions. Energies 2019, 12, 418. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Li, C.; Wang, J. Investigation on mooring breakage effects of a 5 MW barge-type floating offshore wind turbine using F2A. Ocean. Eng. 2021, 233, 108887. [Google Scholar] [CrossRef]
- Ahmed, M.O.; Yenduri, A.; Kurian, V.J. Evaluation of the dynamic responses of truss spar platforms for various mooring configurations with damaged lines. Ocean. Eng. 2016, 123, 411–421. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Michailides, C.; Mei, X.; Wang, J.; Li, C. Coupled analysis of a 10 MW multi-body floating offshore wind turbine subjected to tendon failures. Renew. Energ. 2021, 176, 89–105. [Google Scholar] [CrossRef]
- Sakaris, C.S.; Bashir, M.; Yang, Y.; Michailides, C.; Wang, J.; Sakellariou, J.S. Diagnosis of damaged tendons on a 10 MW multibody floating offshore wind turbine platform via a response-only functional model based method. Eng. Struct. 2021, 242, 112384. [Google Scholar] [CrossRef]
- Sakaris, C.S.; Yang, Y.; Bashir, M.; Michailides, C.; Wang, J.; Sakellariou, J.S.; Li, C. Structural health monitoring of tendons in a multibody floating offshore wind turbine under varying environmental and operating conditions. Renew. Energ. 2021, 179, 1897–1914. [Google Scholar] [CrossRef]
- Wang, T.; Jin, H.; Wu, X. Coupled dynamic analysis of a tension leg platform floating offshore wind turbine. J. Offshore Mech. Arct. 2020, 142, 011901. [Google Scholar] [CrossRef]
- Wei, N.; Zhang, Z.; Xu, X.; Yao, W. Stability analysis of a TLP with inclined tension legs under different marine survival conditions. J. Mar. Sci. Eng. 2022, 10, 1058. [Google Scholar] [CrossRef]
- Milano, D.; Peyrard, C.; Capaldo, M.; Ingram, D.; Xiao, Q.; Johanning, L. Impact of high order wave loads on a 10 MW tension-leg platform floating wind turbine at different tendon inclination angles. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering: Volume 10 Ocean Renewable Energy, Glasgow, Scotland, UK, 9–14 June 2019; ASME: New York, NY, USA, 2019; p. V010T09A076. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deut. Hydrogr. Z. 1973, 8, 1–95. [Google Scholar]
- Manual, M. Moses Pdf. 2009. Available online: http://www.ultramarine.com/hdesk/document/ref_man.htm (accessed on 1 August 2020).


| Wind | Current | Wave | ||||
|---|---|---|---|---|---|---|
| Speed | Heading | Speed | Heading | Significant Wave Height | Heading | Spectrum Peak Period |
| 15 m/s | 90 degrees | 1 m/s | 90 degrees | 1.5 m | 90 degrees | 6.67 s |
| Parameter (Unit) | Value |
|---|---|
| Model weight (ton) | 2700 |
| Seawater depth (m) | 50 |
| Draft (m) | 15 |
| Roll Gyradius (m) | 35.9 |
| Pitch Gyradius (m) | 35.9 |
| Yaw Gyradius (m) | 20.1 |
| Column diameter (m) | 28 |
| Column height (m) | 8 |
| Tension leg outer diameter (m) | 0.6 |
| Tension leg length (m) | 35.53 |
| Tower diameter (m) | 4 m (bottom) to 2 m (top) |
| Tower length (m) | 72 |
| Hollow steel tube diameter (m) | 1 |
| Hollow steel tube length (m) | 20 |
| Blade length (m) | 40 |
| Material Property (Unit) | Value |
|---|---|
| Yield stress of steel used for FOWT (MPa) | 248.04 |
| Coefficient of thermal expansion of steel (℃) | 3.6111 × 10−6 |
| Poisson’s ratio of steel | 0.3 |
| Steel density (g/cm3) | 7.8492 |
| Modulus of elasticity of steel (MPa) | 1.9981 × 105 |
| Tension leg weight in water (kg/m) | 7884 |
| Tension leg axial stiffness (kN) | 3.6 × 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Z.; Wu, H.; Chen, H.; Li, W.; Li, X.; Lian, J.; He, S.; Zhang, X.; Zhao, Q. Hydrodynamic Response and Tension Leg Failure Performance Analysis of Floating Offshore Wind Turbine with Inclined Tension Legs. Energies 2022, 15, 8584. https://doi.org/10.3390/en15228584
Jia Z, Wu H, Chen H, Li W, Li X, Lian J, He S, Zhang X, Zhao Q. Hydrodynamic Response and Tension Leg Failure Performance Analysis of Floating Offshore Wind Turbine with Inclined Tension Legs. Energies. 2022; 15(22):8584. https://doi.org/10.3390/en15228584
Chicago/Turabian StyleJia, Zhaolin, Han Wu, Hao Chen, Wei Li, Xinyi Li, Jijian Lian, Shuaiqi He, Xiaoxu Zhang, and Qixiang Zhao. 2022. "Hydrodynamic Response and Tension Leg Failure Performance Analysis of Floating Offshore Wind Turbine with Inclined Tension Legs" Energies 15, no. 22: 8584. https://doi.org/10.3390/en15228584
APA StyleJia, Z., Wu, H., Chen, H., Li, W., Li, X., Lian, J., He, S., Zhang, X., & Zhao, Q. (2022). Hydrodynamic Response and Tension Leg Failure Performance Analysis of Floating Offshore Wind Turbine with Inclined Tension Legs. Energies, 15(22), 8584. https://doi.org/10.3390/en15228584







