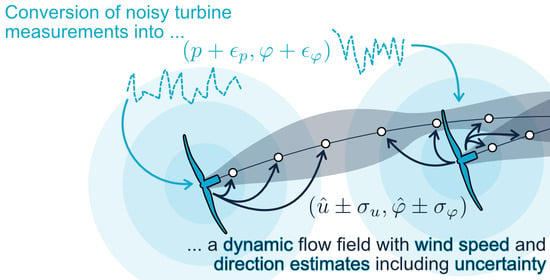
Ensemble-Based Flow Field Estimation Using the Dynamic Wind Farm Model FLORIDyn
Abstract
1. Introduction
2. Materials and Methods
2.1. Properties of the FLORIDyn Approach
2.2. Ensemble Kalman Filter Formulation
2.2.1. EnKF Correction of the Wind Speed
2.2.2. EnKF Correction of the Wind Direction
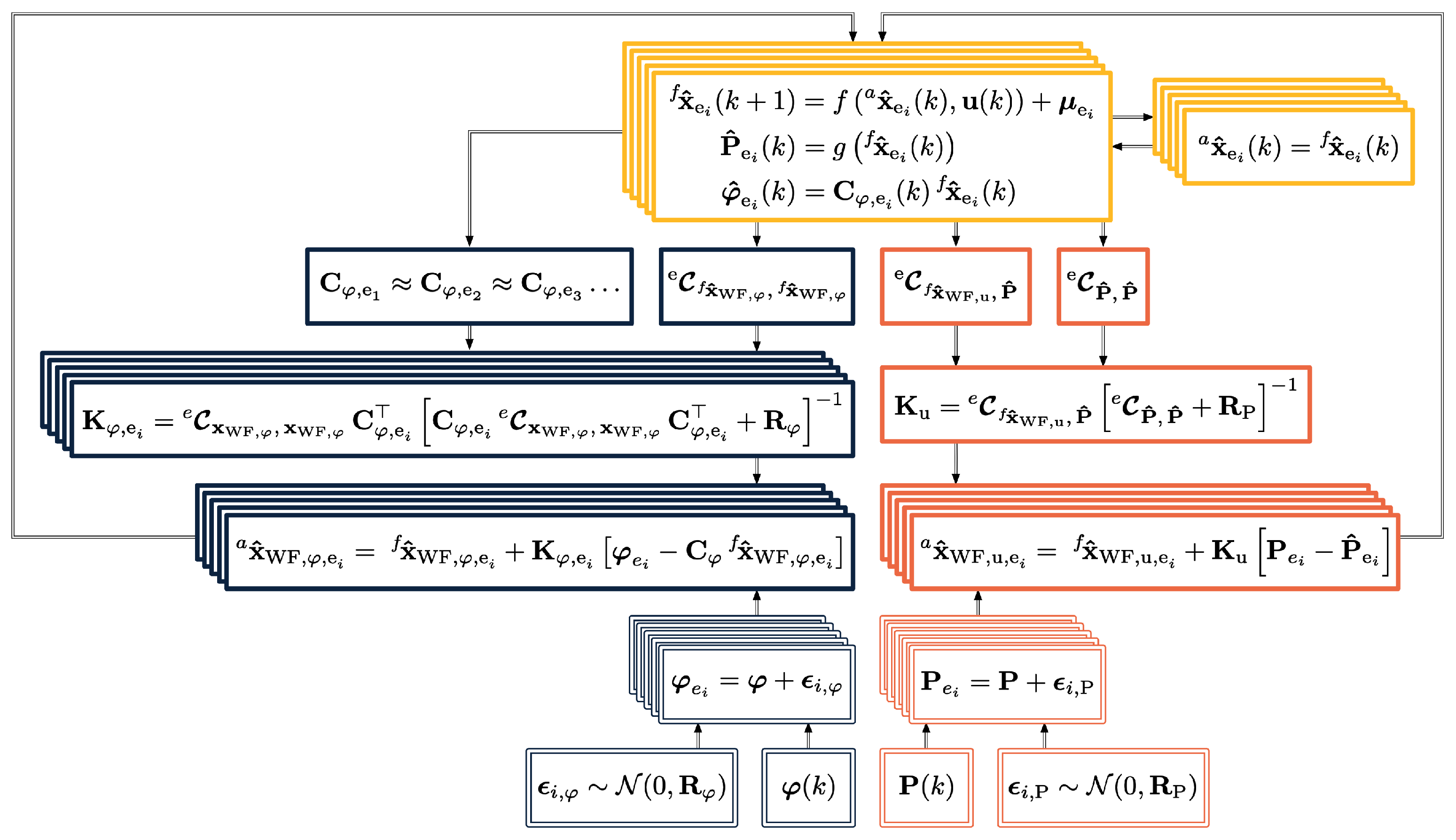
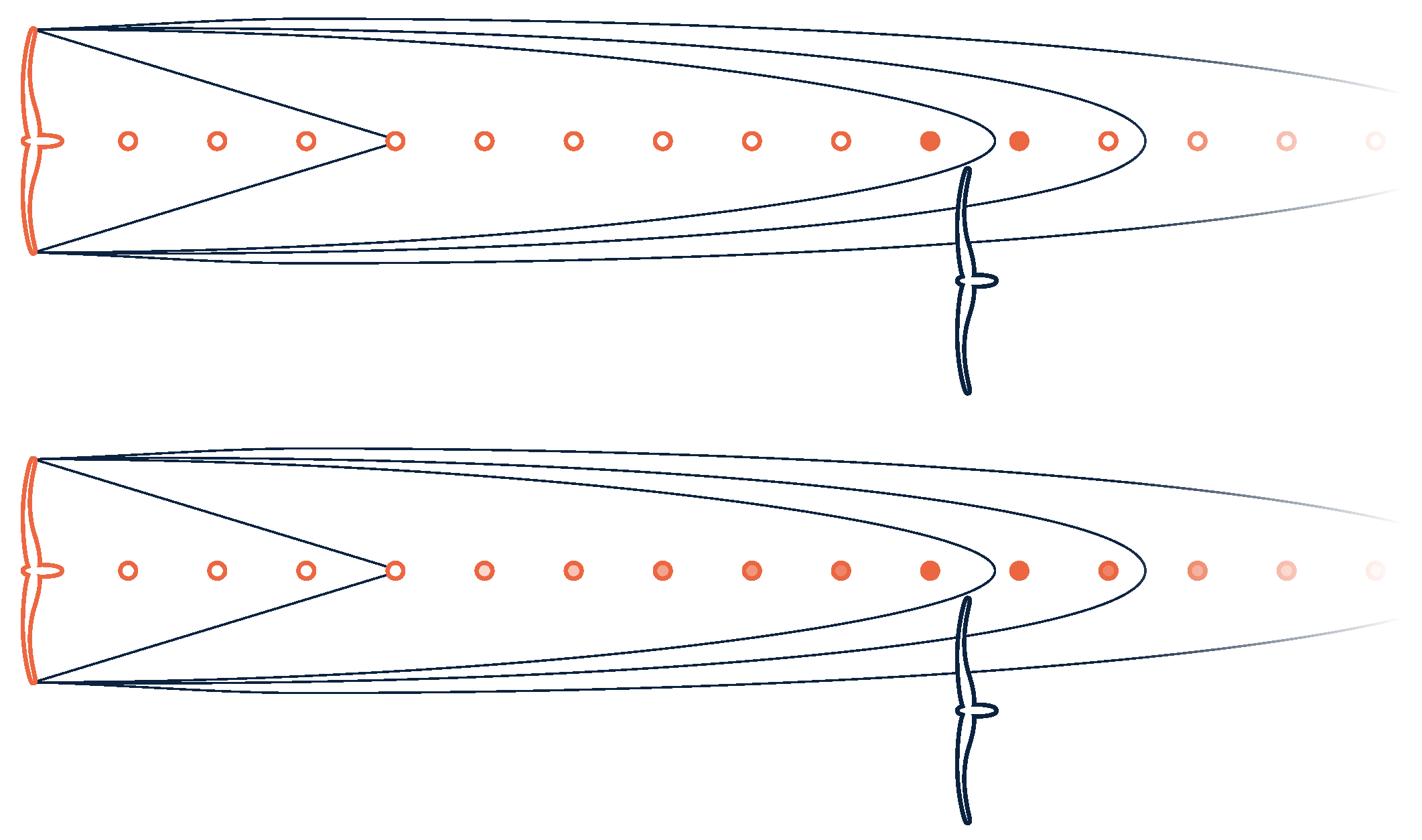
2.2.3. Localization
3. Results and Discussion
3.1. Ensemble Kalman Filter and Localization Parameters
3.2. FLORIDyn as Validation Platform
3.3. SOWFA as Validation Platform
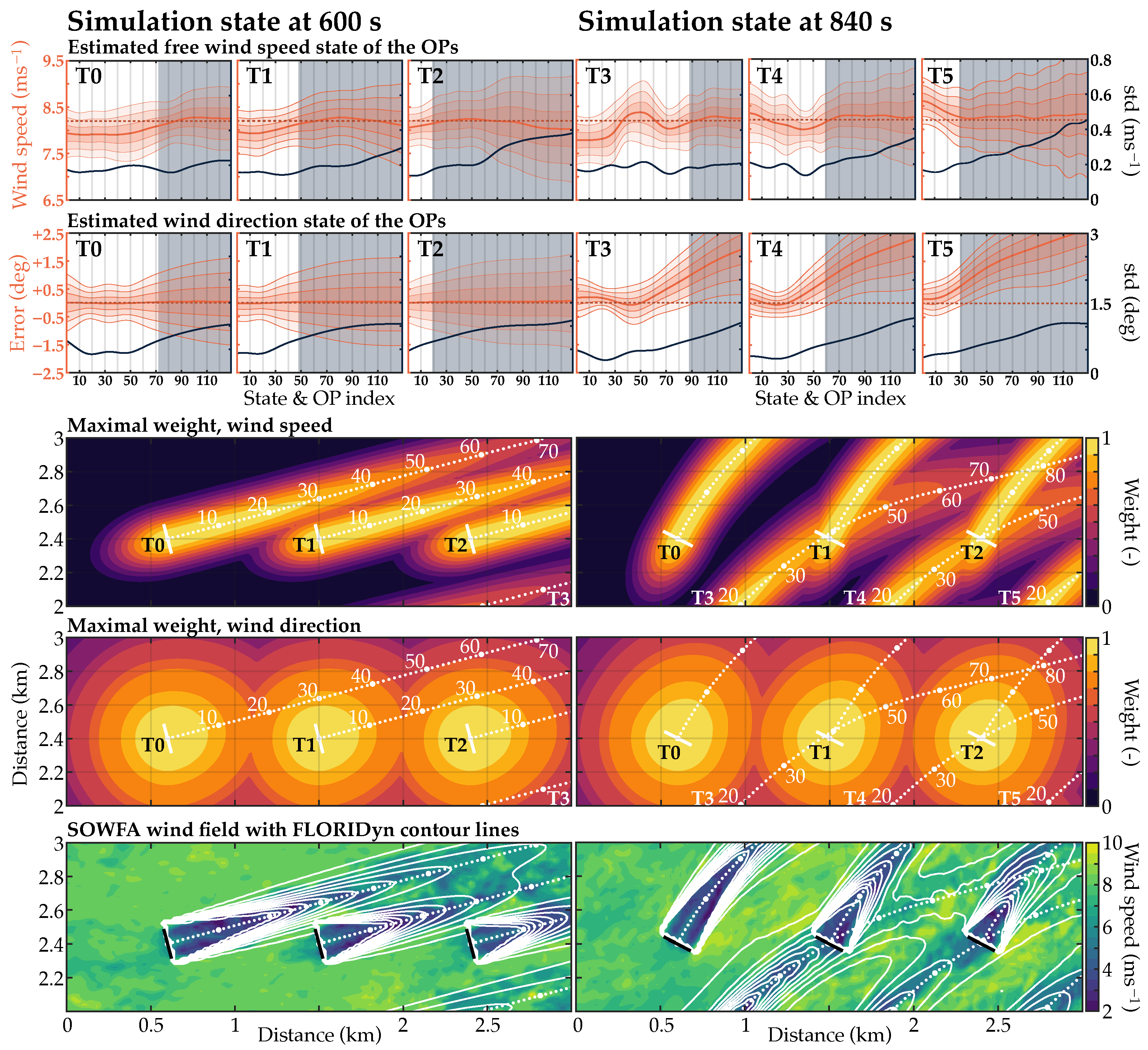
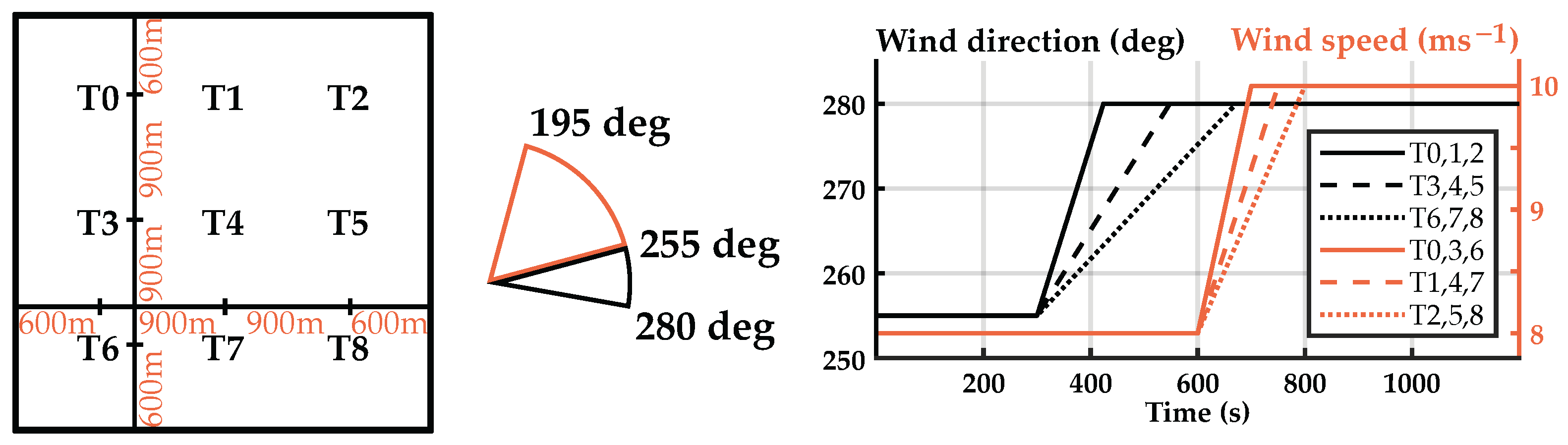
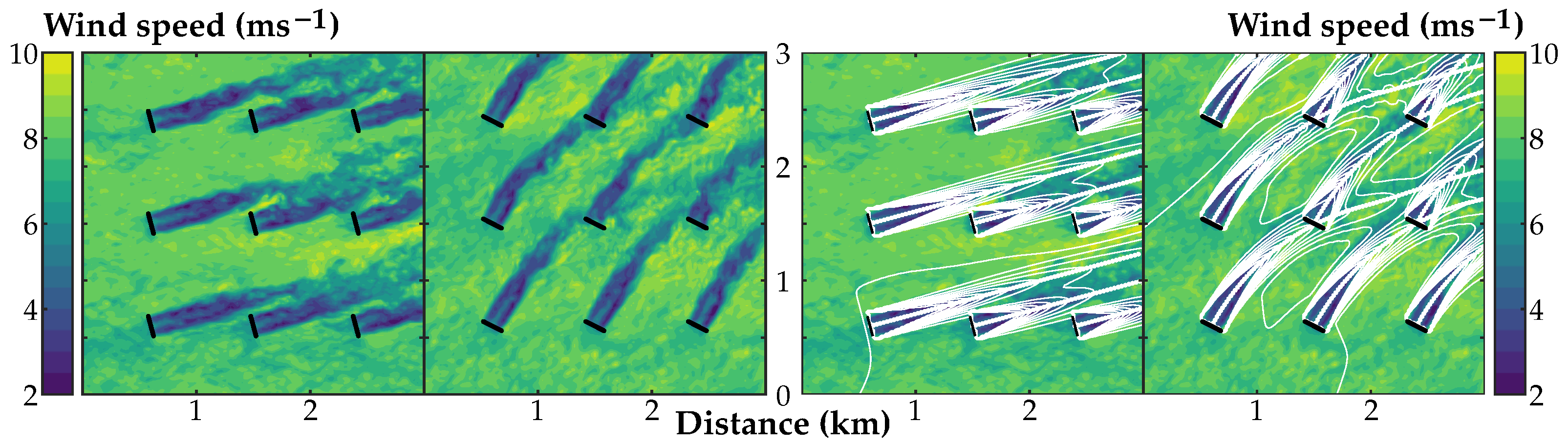
3.3.1. Simulation Case
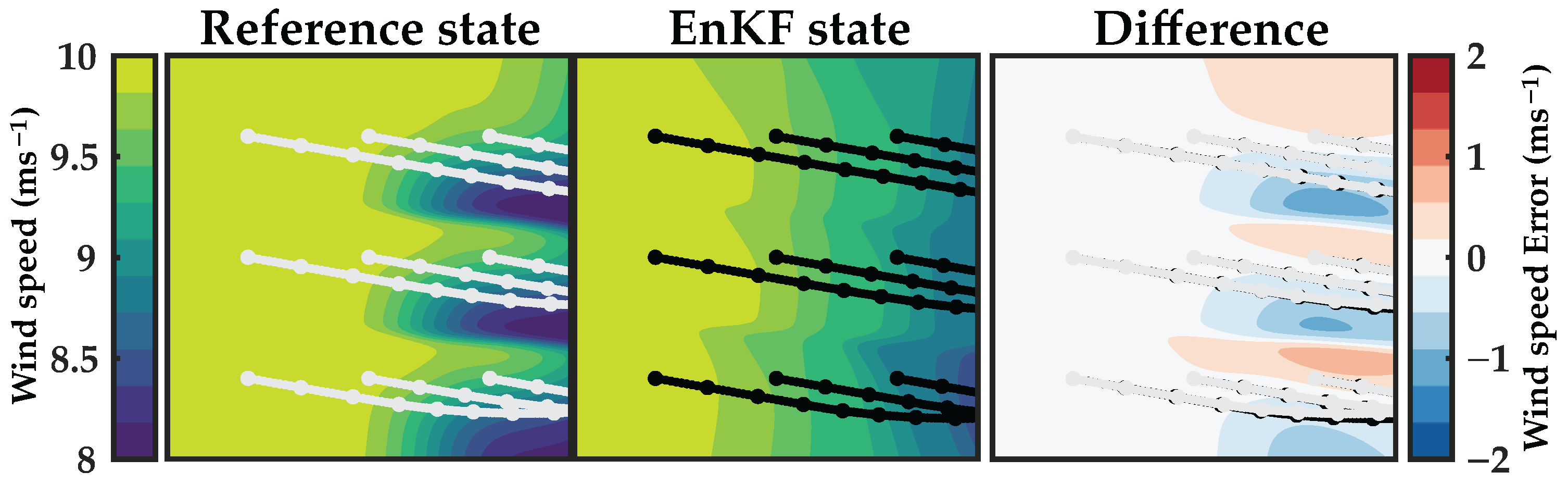
3.3.2. Wake Location and Estimated Wind Speed
3.3.3. Wind Direction States
3.3.4. Weighting and Corrections
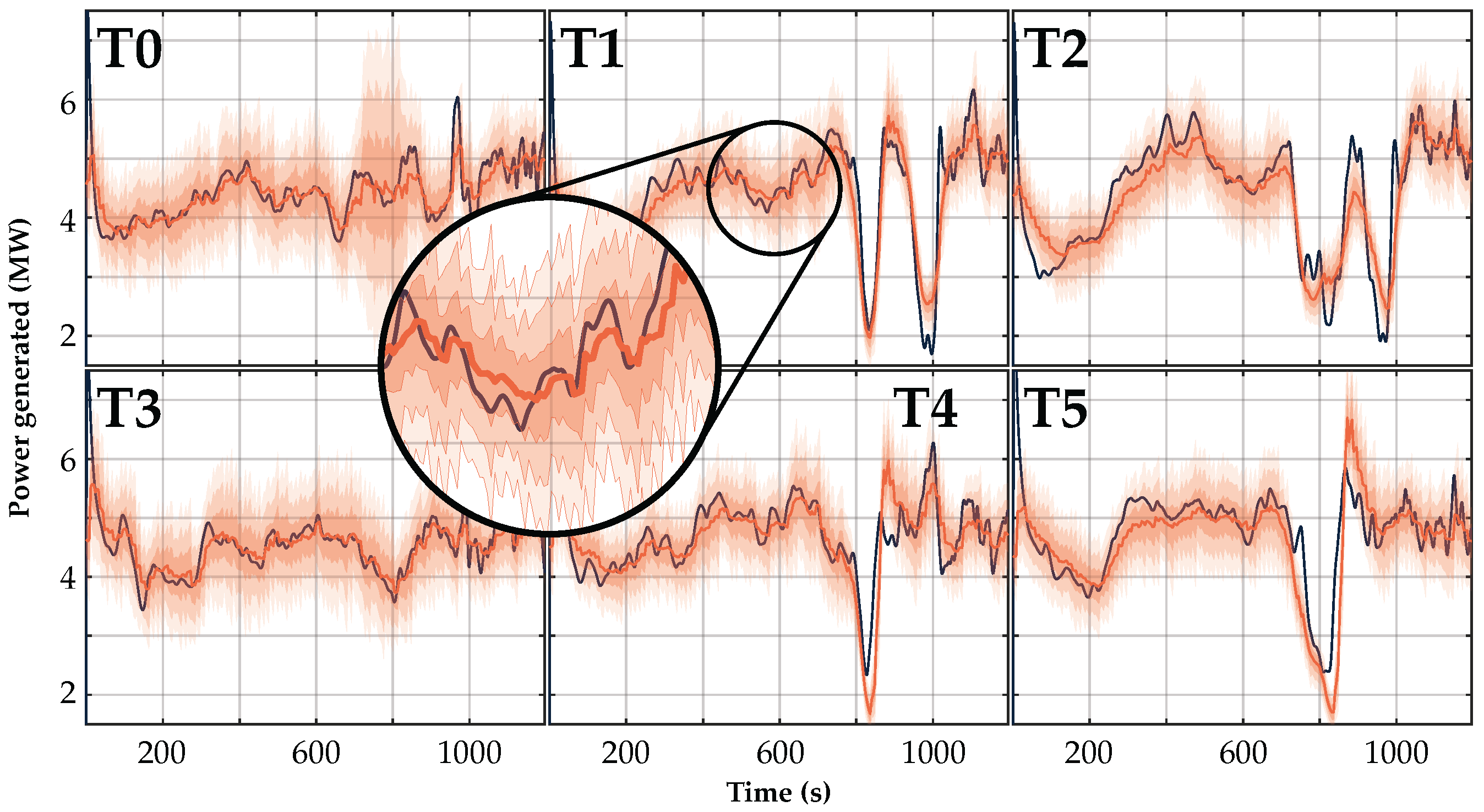
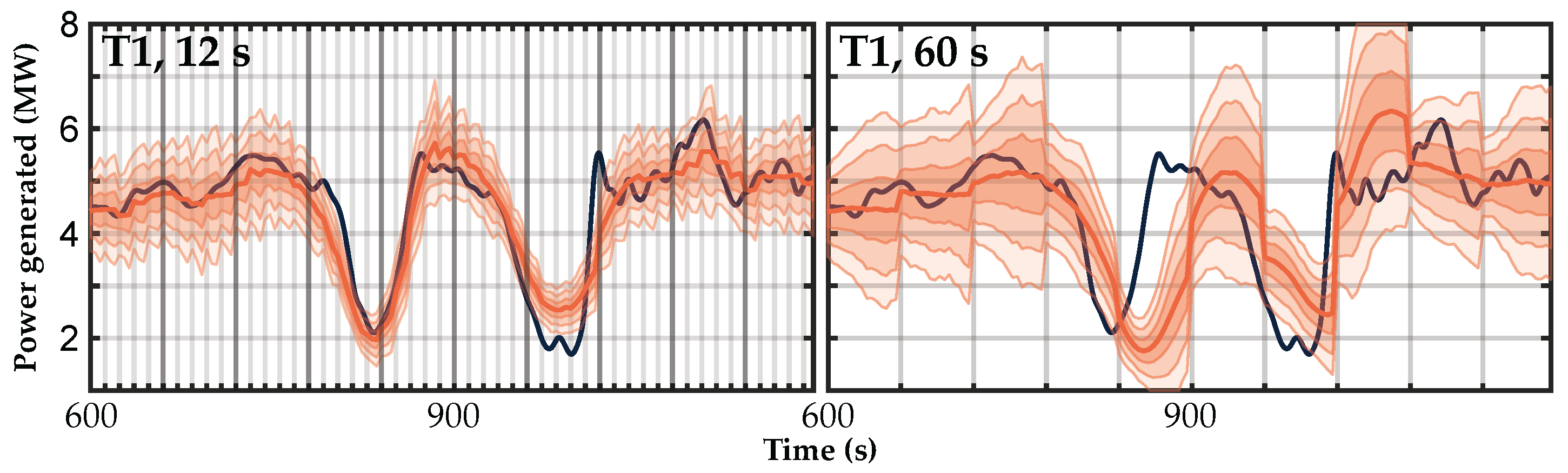
3.3.5. Power Generated
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EnKF | Ensemble Kalman Filter |
| FLORIDyn | FLOw Redirection and Induction Dynamics model |
| WFC | Wind Farm Control |
| OP | Observation Point |
| SOWFA | Simulator fOr Wind Farm Applications |
Appendix A. State Space Description
Appendix A.1. Simple Propagation
Appendix A.2. Weighted Propagation
References
- Fleming, P.; Annoni, J.; Shah, J.J.; Wang, L.; Ananthan, S.; Zhang, Z.; Hutchings, K.; Wang, P.; Chen, W.; Chen, L. Field Test of Wake Steering at an Offshore Wind Farm. Wind. Energy Sci. Discuss. 2017, 2, 229–239. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Nagamune, R. A Quantitative Review of Wind Farm Control with the Objective of Wind Farm Power Maximization. J. Wind. Eng. Ind. Aerodyn. 2019, 192, 45–73. [Google Scholar] [CrossRef]
- van den Broek, M.J.; De Tavernier, D.; Sanderse, B.; van Wingerden, J.W. Adjoint Optimisation for Wind Farm Flow Control with a Free-Vortex Wake Model. Renew. Energy 2022, in press. [Google Scholar] [CrossRef]
- Howland, M.F.; Ghate, A.S.; Lele, S.K.; Dabiri, J.O. Optimal Closed-Loop Wake Steering – Part 1: Conventionally Neutral Atmospheric Boundary Layer Conditions. Wind. Energy Sci. 2020, 5, 1315–1338. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; van Wingerden, J.W. A Control-Oriented Dynamic Model for Wakes in Wind Plants. J. Phys. Conf. Ser. 2014, 524, 012186. [Google Scholar] [CrossRef]
- Becker, M.; Ritter, B.; Doekemeijer, B.; van der Hoek, D.; Konigorski, U.; Allaerts, D.; van Wingerden, J.W. The Revised FLORIDyn Model: Implementation of Heterogeneous Flow and the Gaussian Wake. Wind. Energy Sci. 2022, 7, 2163–2179. [Google Scholar] [CrossRef]
- Becker, M.; Allaerts, D.; van Wingerden, J.W. FLORIDyn—A Dynamic and Flexible Framework for Real-Time Wind Farm Control. J. Phys. Conf. Ser. 2022, 2265, 032103. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Nagamune, R. A Low-Fidelity Dynamic Wind Farm Model for Simulating Time-Varying Wind Conditions and Floating Platform Motion. Ocean. Eng. 2021, 234, 109313. [Google Scholar] [CrossRef]
- Foloppe, B.; Munters, W.; Buckingham, S.; Vandevelde, L.; van Beeck, J. Development of a Dynamic Wake Model Accounting for Wake Advection Delays and Mesoscale Wind Transients. J. Phys. Conf. Ser. 2022, 2265, 022055. [Google Scholar] [CrossRef]
- Lejeune, M.; Moens, M.; Chatelain, P. A Meandering-Capturing Wake Model Coupled to Rotor-Based Flow-Sensing for Operational Wind Farm Flow Prediction. Front. Energy Res. 2022, 10, 884068. [Google Scholar] [CrossRef]
- Braunbehrens, R.; Schreiber, J.; Bottasso, C.L. Application of an Open-Loop Dynamic Wake Model with High-Frequency SCADA Data. J. Phys. Conf. Ser. 2022, 2265, 022031. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; Fleming, P.A.; van Wingerden, J.W. Wind Turbine Wake Estimation and Control Using FLORIDyn, a Control-Oriented Dynamic Wind Plant Model. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 1702–1708. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical Formulation and Practical Implementation. Ocean. Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Tossavainen, O.P.; Percelay, J.; Tinka, A.; Wu, Q.; Bayen, A.M. Ensemble Kalman Filter Based State Estimation in 2D Shallow Water Equations Using Lagrangian Sensing and State Augmentation. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancún, Mexico, 9–11 December 2008; pp. 1783–1790. [Google Scholar] [CrossRef]
- Du, J.; Zhu, J.; Fang, F.; Pain, C.C.; Navon, I.M. Ensemble Data Assimilation Applied to an Adaptive Mesh Ocean Model: Ensemble Data Assimilation Applied to an Adaptive Mesh Ocean Model. Int. J. Numer. Methods Fluids 2016, 82, 997–1009. [Google Scholar] [CrossRef]
- Doekemeijer, B.M.; Boersma, S.; Pao, L.Y.; van Wingerden, J.W. Ensemble Kalman Filtering for Wind Field Estimation in Wind Farms. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 19–24. [Google Scholar] [CrossRef]
- Kumar Jain, P.; Mandli, K.; Hoteit, I.; Knio, O.; Dawson, C. Dynamically Adaptive Data-Driven Simulation of Extreme Hydrological Flows. Ocean. Model. 2018, 122, 85–103. [Google Scholar] [CrossRef]
- Shapiro, C.R.; Starke, G.M.; Meneveau, C.; Gayme, D.F. A Wake Modeling Paradigm for Wind Farm Design and Control. Energies 2019, 12, 2956. [Google Scholar] [CrossRef]
- Sampson, C.; Carrassi, A.; Aydoğdu, A.; Jones, C.K. Ensemble Kalman Filter for Nonconservative Moving Mesh Solvers with a Joint Physics and Mesh Location Update. Q. J. R. Meteorol. Soc. 2021, 147, 1539–1561. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New Extension of the Kalman Filter to Nonlinear Systems. Signal Process. Sens. Fusion Target Recognit. 1997, 3086, 182–193. [Google Scholar] [CrossRef]
- Talagrand, O.; Courtier, P. Variational Assimilation of Meteorological Observations with the Adjoint Vorticity Equation. I: Theory: VARIATIONAL ASSIMILATION. I: THEORY. Q. J. R. Meteorol. Soc. 1987, 113, 1311–1328. [Google Scholar] [CrossRef]
- Wan, E.; Van Der Merwe, R. The Unscented Kalman Filter for Nonlinear Estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373), Lake Louise, AB, Canada, 1–4 October 2000; pp. 153–158. [Google Scholar] [CrossRef]
- Bauweraerts, P.; Meyers, J. Reconstruction of Turbulent Flow Fields from Lidar Measurements Using Large-Eddy Simulation. J. Fluid Mech. 2021, 906, A17. [Google Scholar] [CrossRef]
- Skachko, S.; Errera, Q.; Ménard, R.; Christophe, Y.; Chabrillat, S. Comparison of the Ensemble Kalman Filter and 4D-Var Assimilation Methods Using a Stratospheric Tracer Transport Model. Geosci. Model Dev. 2014, 7, 1451–1465. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. Experimental and Theoretical Study of Wind Turbine Wakes in Yawed Conditions. J. Fluid Mech. 2016, 806, 506–541. [Google Scholar] [CrossRef]
- Betz, A. Introduction to the Theory of Flow Machines; Elsevier Science: Amsterdam, The Netherlands, 1966. [Google Scholar]
- Evensen, G. Sequential Data Assimilation with a Nonlinear Quasi-Geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics. J. Geophys. Res. Ocean 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Burgers, G.; van Leeuwen, P.J.; Evensen, G. Analysis Scheme in the Ensemble Kalman Filter. Mon. Weather. Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Petrie, R. Localization in the Ensemble Kalman Filter. Master’s. Thesis, University of Reading, Reading, UK, August 2008. [Google Scholar]
- Gaspari, G.; Cohn, S.E. Construction of Correlation Functions in Two and Three Dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Lorenc, A.C. The Potential of the Ensemble Kalman Filter for NWP—A Comparison with 4D-Var. Q. J. R. Meteorol. Soc. 2003, 129, 3183–3203. [Google Scholar] [CrossRef]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine. Available online: https://orbit.dtu.dk/en/publications/the-dtu-10-mw-reference-wind-turbine (accessed on 27 October 2022).
- National Renewable Energy Laboratory. Simulator for Offshore Wind Farm Applications. GitHub Repositories 2022. Available online: https://zenodo.org/record/3632051#.Y3tg_n1BxPY (accessed on 28 October 2022).
- Becker, M. SOWFA Simulation Setup Belonging to the Paper: The Revised FLORIDyn Model: Implementation of Heterogeneous Flow and the Gaussian Wake. 4TU.ResearchData 2022. Available online: https://data.4tu.nl/articles/dataset/SOWFA_simulation_setup_belonging_to_the_paper_The_revised_FLORIDyn_model_Implementation_of_heterogeneous_flow_and_the_Gaussian_wake/20026406 (accessed on 27 October 2022).
- Becker, M. Dataset Belonging to the Paper: Ensemble Based Flow Field Estimation Using the Dynamic Wind Farm Model FLORIDyn. 4TU.ResearchData 2022. Available online: https://data.4tu.nl/articles/dataset/Dataset_belonging_to_the_paper_Ensemble_based_flow_field_estimation_using_the_dynamic_wind_farm_model_FLORIDyn/21215924 (accessed on 3 November 2022).
- Liu, Y.; Pamososuryo, A.K.; Ferrari, R.M.G.; van Wingerden, J.W. The Immersion and Invariance Wind Speed Estimator Revisited and New Results. IEEE Control. Syst. Lett. 2022, 6, 361–366. [Google Scholar] [CrossRef]






| Ensemble Kalman Filter | Localization | ||||
|---|---|---|---|---|---|
| (-) | Cf (s) | (m) | (m) | ||
| 50 | |||||
| Noise Per 4 s | |||||
| (MW) | (deg) | (ms) | (deg) | ||
| Weighted Average | |||||
| (m) | (m) | (s) | (m) | (m) | (s) |
| 256 | 126 | 256 | 512 | 512 | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, M.; Allaerts, D.; van Wingerden, J.-W. Ensemble-Based Flow Field Estimation Using the Dynamic Wind Farm Model FLORIDyn. Energies 2022, 15, 8589. https://doi.org/10.3390/en15228589
Becker M, Allaerts D, van Wingerden J-W. Ensemble-Based Flow Field Estimation Using the Dynamic Wind Farm Model FLORIDyn. Energies. 2022; 15(22):8589. https://doi.org/10.3390/en15228589
Chicago/Turabian StyleBecker, Marcus, Dries Allaerts, and Jan-Willem van Wingerden. 2022. "Ensemble-Based Flow Field Estimation Using the Dynamic Wind Farm Model FLORIDyn" Energies 15, no. 22: 8589. https://doi.org/10.3390/en15228589
APA StyleBecker, M., Allaerts, D., & van Wingerden, J.-W. (2022). Ensemble-Based Flow Field Estimation Using the Dynamic Wind Farm Model FLORIDyn. Energies, 15(22), 8589. https://doi.org/10.3390/en15228589