Full-Scale Digesters: Model Predictive Control with Online Kinetic Parameter Identification Strategy
Abstract
:1. Introduction
2. Optimal Parameter Identification Algorithm
2.1. Proposed Mass-Balance Mathematical Model for Anaerobic Reactors
2.2. Experimental Data Results
3. Optimal Parameter Identification and Online Measurements
3.1. Parameter Identification Using Pattern Search by Step-Ahead
3.2. Asymptotic Estimator When Reaction Rates Are Unknown
Observer Design
3.3. Kinetic Parameter Reaction Estimator
Observer Design
4. Nonlinear Model Predictive Controller (Mpc)
4.1. Controller Design
- The reactor has to be balanced to react against perturbations, always working within the physical and operational boundaries.
- Methane production needs to be maximized all the time.
- The environmental regulations and the capacity of the reactor to reduce the concentration of substrates at the inlet, S and S, conditioned the programming. Therefore, the rule S(t) + S(t) ≤ Kt, where Kt denotes the maximum effluent concentration of the both substrates considered, has to be followed.
- The reactor has to be protected against failures due to unexpected high variations on VFA, and in consequence, inhibitions on the metabolism of microorganisms. Thus, an alternative is to use alkalinity as a base to neutralize the level of acids.
4.2. Structure of the Controller
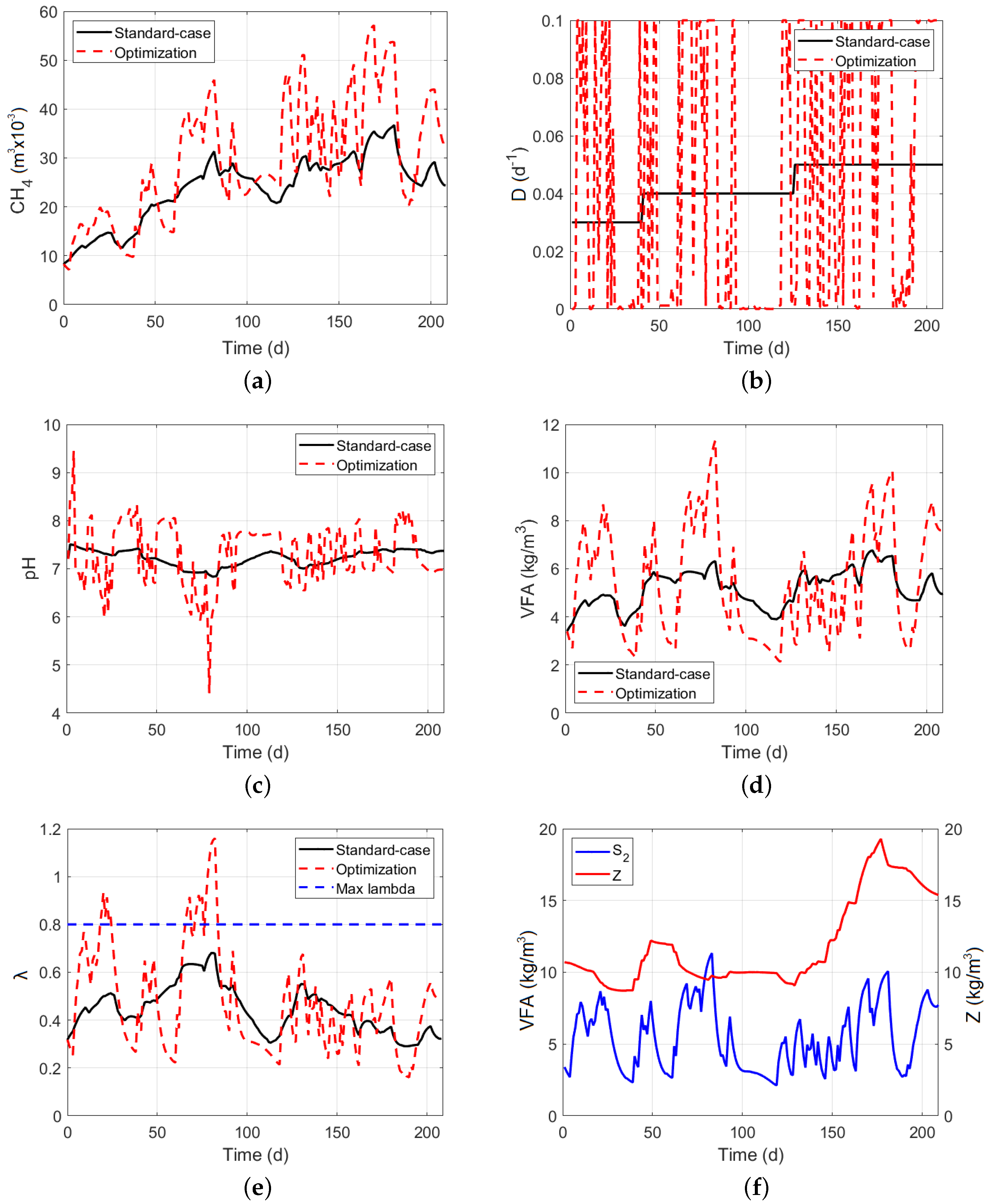
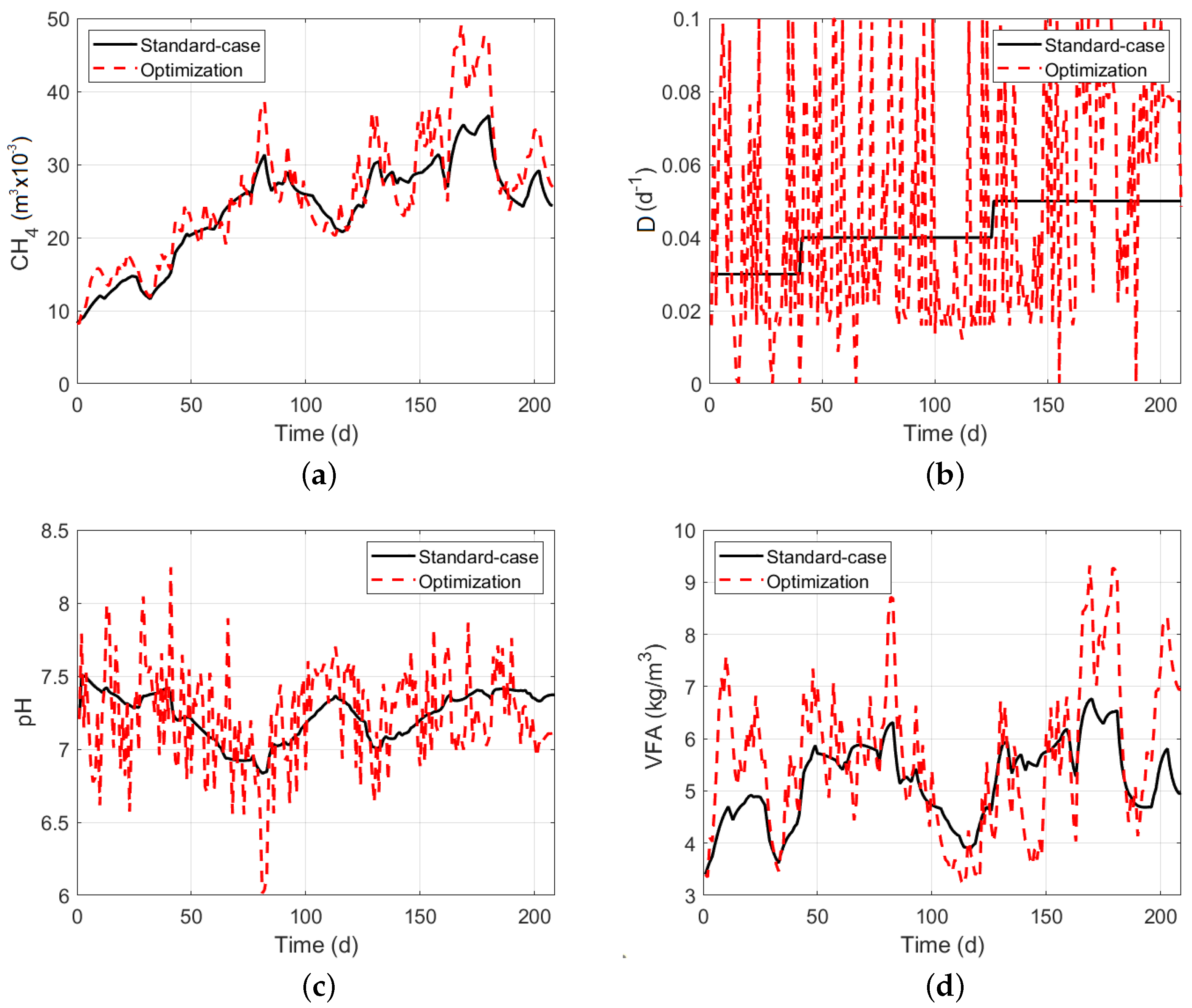
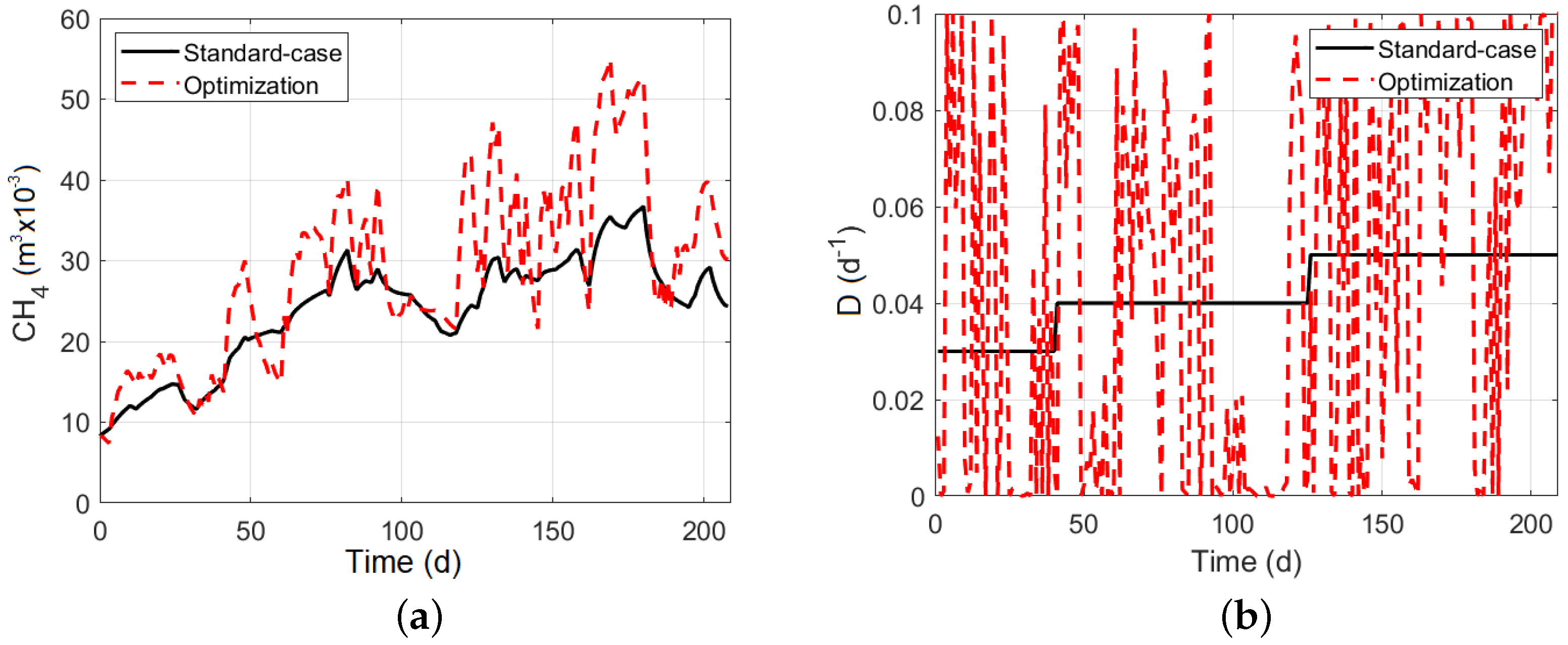
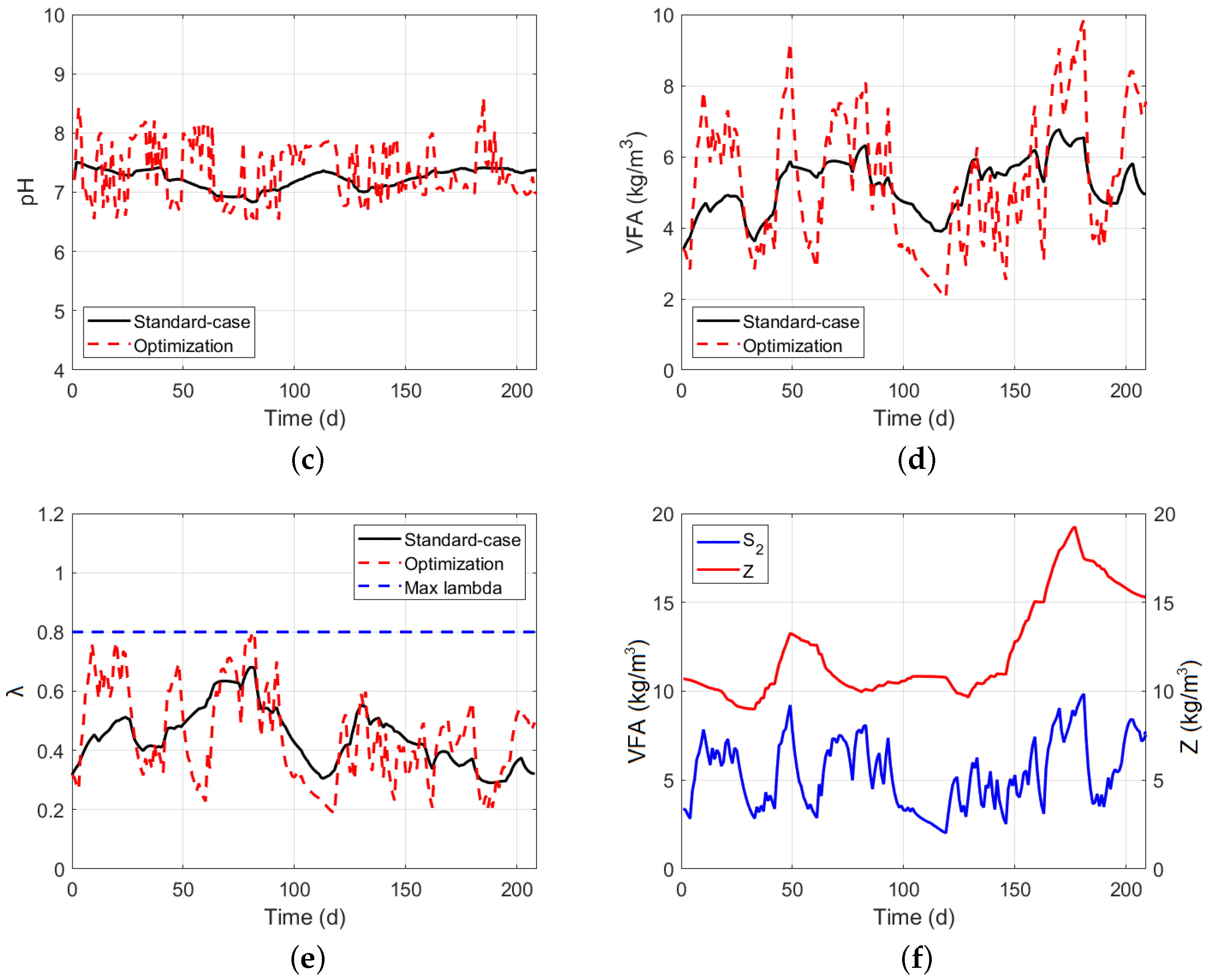
5. Simulation Results and Analysis
5.1. Asymptotic Observer
5.2. Kinetic Parameter Reaction Estimator
5.3. Pid Controller Performance on Anerobic Digesters
5.4. Mpc Controller without Restrictions
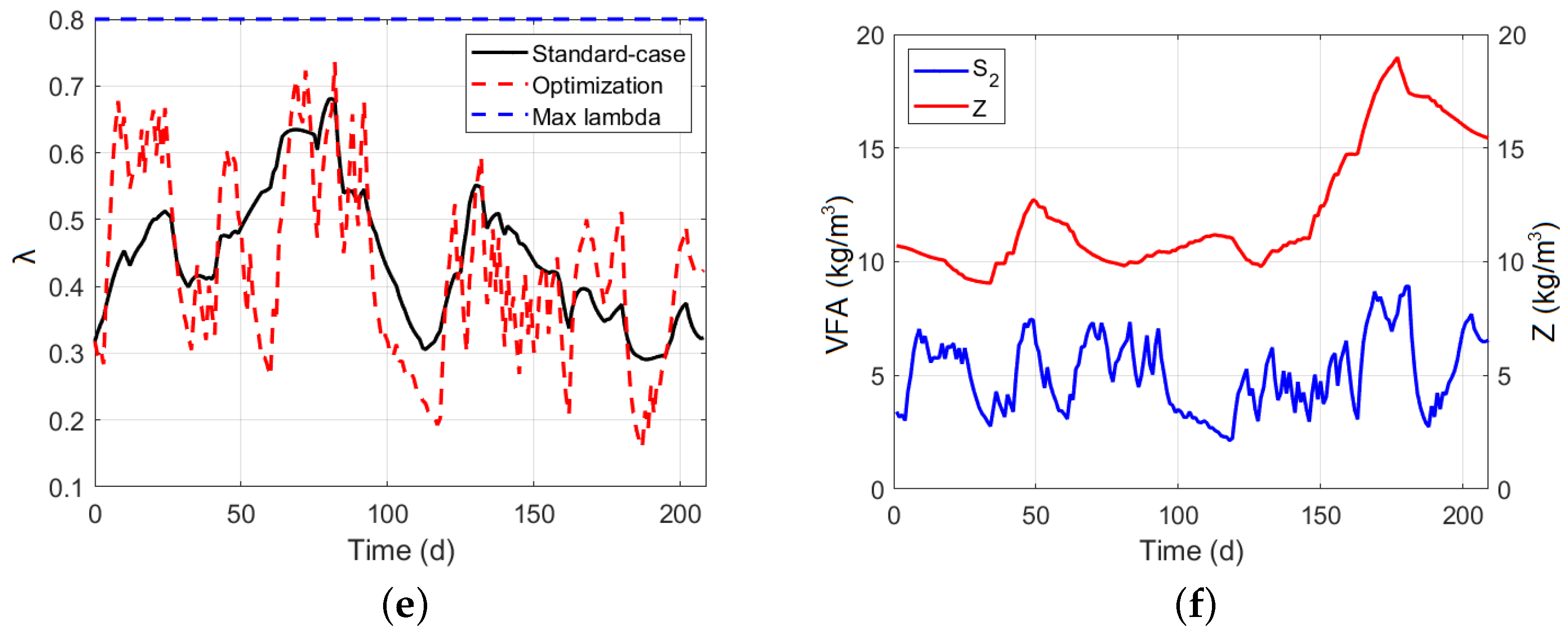
5.5. Model Predictive Controller with Restrictions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Total inorganic carbon concentration (kg/m) | |
| D | Dilution rate (d) |
| Yield substrate degradation | |
| Yield for VFA production | |
| Yield for VFA consumption | |
| Yield for CO production | |
| Yield for CO production | |
| Yield for CH production (m) | |
| Half-saturation constant (kg/m) | |
| Half-saturation constant (kg/m) | |
| Yield for ammonium production (kg/m) | |
| Yield for ammonium production (kg/m) | |
| Carbon dioxide flow rate (m/d) | |
| Methane flow rate (m/d) | |
| r, r | Reaction rates (d) |
| , | Organic substrate concentration (kg acid acetic/m) |
| , | Volatile fatty acids concentration (kg/m) |
| Concentration of acidogenic bacteria (kg/m) | |
| Concentration of methanogenic bacteria (kg/m) | |
| Total alkalinity (kg/m) | |
| Fraction of bacteria in the liquid phase | |
| Specific growth rate of acidogenic bacteria (d) | |
| Specific growth rate of methanogenic bacteria (d) | |
| Maximum acidogenic bacteria growth rate (d) | |
| Maximum methanogenic bacteria growth rate (d) | |
| Vector of measured state variables | |
| Vector of non-measurable state variables | |
| Vector of parameters | |
| , | Control action (d) |
| Vector of state variables | |
| K | Matrix with the kinetics of the biochemical |
| Microbiological reactions involved on system | |
| Q | Gaseous rate of mass outflow from reactor |
| F | Mass feed rate due to external substrates |
| Unknown functions of all states | |
| H | Known functions of all the states |
| Gain matrix of the updating law | |
| Square gain convergence matrix | |
| Buffer capacity | |
| Prediction horizon (d) | |
| Control horizon (d) |
References
- Singh, R.; Sahay, A.; Karry, K.M.; Muzzio, F.; Ierapetritou, M.; Ramachandran, R. Implementation of an advanced hybrid MPC–PID control system using PAT tools into a direct compaction continuous pharmaceutical tablet manufacturing pilot plant. Int. J. Pharm. 2014, 473, 38–54. [Google Scholar] [CrossRef] [PubMed]
- le Roux, J.; Olivier, L.; Naidoo, M.; Padhi, R.; Craig, I. Throughput and product quality control for a grinding mill circuit using non-linear MPC. J. Process Control 2016, 42, 35–50. [Google Scholar] [CrossRef] [Green Version]
- Corbett, B.; Macdonald, B.; Mhaskar, P. Model Predictive Quality Control of Polymethyl Methacrylate. IEEE Trans. Control Syst. Technol. 2015, 23, 687–692. [Google Scholar] [CrossRef]
- Lora Grando, R.; de Souza Antune, A.M.; da Fonseca, F.V.; Sánchez, A.; Barrena, R.; Font, X. Technology overview of biogas production in anaerobic digestion plants: A European evaluation of research and development. Renew. Sustain. Energy Rev. 2017, 80, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Marquez-Ruiz, A.; Mendez-Blanco, C.; Porru, M.; Özkan, L. State and Parameter Estimation Based On Extent Transformations. Comput. Aided Chem. Eng. 2018, 44, 583–588. [Google Scholar]
- Gaida, D.; Wolf, C.; Bongards, M. Feed control of anaerobic digestion processes for renewable energy production: A review. Renew. Sustain. Energy Rev. 2017, 68, 869–875. [Google Scholar] [CrossRef]
- Association, E.B. EBA Statistical Report; European Biogas Association: Brussels, Belgium, 2017. [Google Scholar]
- Méndez-Acosta, H.; Palacios-Ruiz, B.; Alcaraz-González, V.; González-Álvarez, V.; García-Sandoval, J. A robust control scheme to improve the stability of anaerobic digestion processes. J. Process. Control 2010, 20, 375–383. [Google Scholar] [CrossRef]
- Anukam, A.; Mohammadi, A.; Naqvi, M.; Granström, K. A Review of the Chemistry of Anaerobic Digestion: Methods of Accelerating and Optimizing Process Efficiency. Processes 2019, 7, 504. [Google Scholar] [CrossRef] [Green Version]
- Bernard, O.; Hadj-Sadok, Z.; Dochain, D.; Genovesi, A.; Steyer, J. Dynamicals Model Development and Parameter Identification for an Anaerobic Wastewater Treatment Process. Biotechnol. Bioeng. 2001, 75, 424–438. [Google Scholar] [CrossRef]
- Kil, H.; Li, D.; Xi, Y.; Li, J. Model Predictive Control with On-line Model Identification for Anaerobic Digestion Processes. Biochem. Eng. J. 2017, 128, 63–75. [Google Scholar] [CrossRef]
- López Buriticá, K.; Trujillo, S.; Acosta-Medina, C.; Granada, D.H. Dynamical Analysis of a Continuous Stirred-Tank Reactor with the Formation of Biofilms for Wastewater Treatment. Math. Probl. Eng. 2015, 2015, 512404. [Google Scholar] [CrossRef]
- Cortés, L.G.; Barbancho, J.; Larios, D.F.; Marín-Batista, J.; Mohedano, A.F.; Portilla, C.; de la Rubia, M.A. Full-Scale Digesters: An Online Model Parameter Identification Strategy. Energies 2022, 15, 7685. [Google Scholar] [CrossRef]
- Bastin, G.; Dochain, D. On-line Estimation and Adaptive Control of Bioreactors. Process Meas. Control. 1990, 10, 707–723. [Google Scholar] [CrossRef]
- Das, S.; Pan, I.; Halder, K.; Das, S.; Gupta, A. LQR based improved discrete PID controller design via optimum selection of weighting matrices using fractional order integral performance index. Appl. Math. Model. 2013, 37, 4253–4268. [Google Scholar] [CrossRef]
- Mauky, E.; Weinrich, S.; Jacobi, H.; Naegele, H.J.; Liebetrau, J.; Nelles, M. Model Predictive Control for Demand-Driven Biogas Production in Full Scale. Chem. Eng. Technol. 2016, 39, 652–664. [Google Scholar] [CrossRef]
- González, A.; Adam, E.; Marchetti, J. Conditions for offset elimination in state space receding horizon controllers: A tutorial analysis. Chem. Eng. Process. Process Intensif. 2008, 47, 2184–2194. [Google Scholar] [CrossRef]
- Hanema, J.; Lazar, M.; Tóth, R. Tube-based LPV Constant Output Reference Tracking MPC with Error Bound. IFAC-Pap. 2017, 50, 8612–8617. [Google Scholar]
- Wang, Y.; Witarsa, F. Application of Contois, Tessier, and first-order kinetics for modeling and simulation of a composting decomposition process. Bioresour. Technol. 2016, 220, 384–393. [Google Scholar] [CrossRef]
- Andrews, J.F. A Mathematical Model for the Continuous Culture of Microorganisms Utilizing Inhibitory Substrates. Biotechnol. Bioeng. 1968, 10, 707–723. [Google Scholar] [CrossRef]
- Rossi, E.; Pecorini, I.; Ferrara, G.; Iannelli, R. Dry Anaerobic Digestion of the Organic Fraction of Municipal Solid Waste: Biogas Production Optimization by Reducing Ammonia Inhibition. Energies 2022, 15, 5515. [Google Scholar] [CrossRef]
- Haldane, J. Enzynmes; MIT Press: Cambridge, MA, USA, 1965; p. 184. [Google Scholar]
- Marquez-Ruiz, A.; Mendez-Blanco, C.; Ozcan, L. Constrained Control and Estimation of Homogeneous Reaction Systems Using Extent-Based Linear Parameter Varying Models. Ind. Eng. Chem. Res. 2020, 59, 2242–2251. [Google Scholar] [CrossRef]
- García-Diéguez, C.; Bernard, O.; Roca, E. Reducing the Anaerobic Digestion Model No. 1 for its application to an industrial wastewater treatment plant treating winery effluent wastewater. Bioresour. Technol. 2013, 132, 244–253. [Google Scholar] [CrossRef] [PubMed]
- Chaib Draa, K.; Zemouche, A.; Alma, M.; Voos, H.; Darouach, M. A discrete-time nonlinear state observer for the anaerobic digestion process. Int. J. Robust Nonlinear Control 2019, 29, 1279–1301. [Google Scholar] [CrossRef]
- Song, Y.J.; Oh, K.S.; Lee, B.; Pak, D.W.; Cha, J.H.; Park, J.G. Characteristics of Biogas Production from Organic Wastes Mixed at Optimal Ratios in an Anaerobic Co-Digestion Reactor. Energies 2021, 14, 6812. [Google Scholar] [CrossRef]
- Batstone, D.; Keller, J.; Newell, B.; Newland, M. Model Development and Full Scale Validation for Anaerobic Treatment of Protein and Tat Based Wastewater. Water Sci. Technol. 1997, 36, 423–431. [Google Scholar] [CrossRef]
- Isaza-Hurtado, J.; Botero-Castro, H.; Alvarez, H. Robust Estimation for LPV Systems in the Presence of Non-uniform Measurements. Automatica 2020, 115, 108901. [Google Scholar] [CrossRef]
- Meegoda, J.N.; Li, B.; Patel, K.; Wang, L.B. A Review of the Processes, Parameters, and Optimization of Anaerobic Digestion. Int. J. Environ. Res. Public Health 2018, 15, 2224. [Google Scholar] [CrossRef] [Green Version]
- Bora, B.J.; Dai Tran, T.; Prasad Shadangi, K.; Sharma, P.; Said, Z.; Kalita, P.; Buradi, A.; Nhanh Nguyen, V.; Niyas, H.; Tuan Pham, M.; et al. Improving combustion and emission characteristics of a biogas/biodiesel-powered dual-fuel diesel engine through trade-off analysis of operation parameters using response surface methodology. Sustain. Energy Technol. Assess. 2022, 53, 102455. [Google Scholar] [CrossRef]
- Condrachi, L.; Vilanova, R.; Meneses, M.; Barbu, M. Anaerobic Digestion Process Control Using a Data-Driven Internal Model Control Method. Energies 2021, 14, 6746. [Google Scholar] [CrossRef]
- de la Rubia, M.; Perez, M.; Romero, L.; Sales, D. Effect of Solids Retention Time (SRT) on Pilot Scale Anaerobic Thermophilic Sludge Digestion. Process Biochem. 2006, 41, 79–86. [Google Scholar] [CrossRef]
- Valencia, F.; López, J.D.; Núñez, A.; Portilla, C.; Cortes, L.G.; Espinosa, J.; Schutter, B.D. Congestion Management in Motorways and Urban Networks through a Bargaining-Game-Based Coordination Mechanism; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–40. [Google Scholar]
- Batstone, D.; Keller, J.; Angelidaki, I.; Kalyuzhnyi, S.; Pavlostathis, S.; Rozzi, A.; Sanders, W.; Siegrist, H.; Vavilin, V. Anaerobic Digestion Model No 1 (ADM1). Water Sci. Technol. 2002, 45, 65–73. [Google Scholar] [CrossRef] [PubMed]


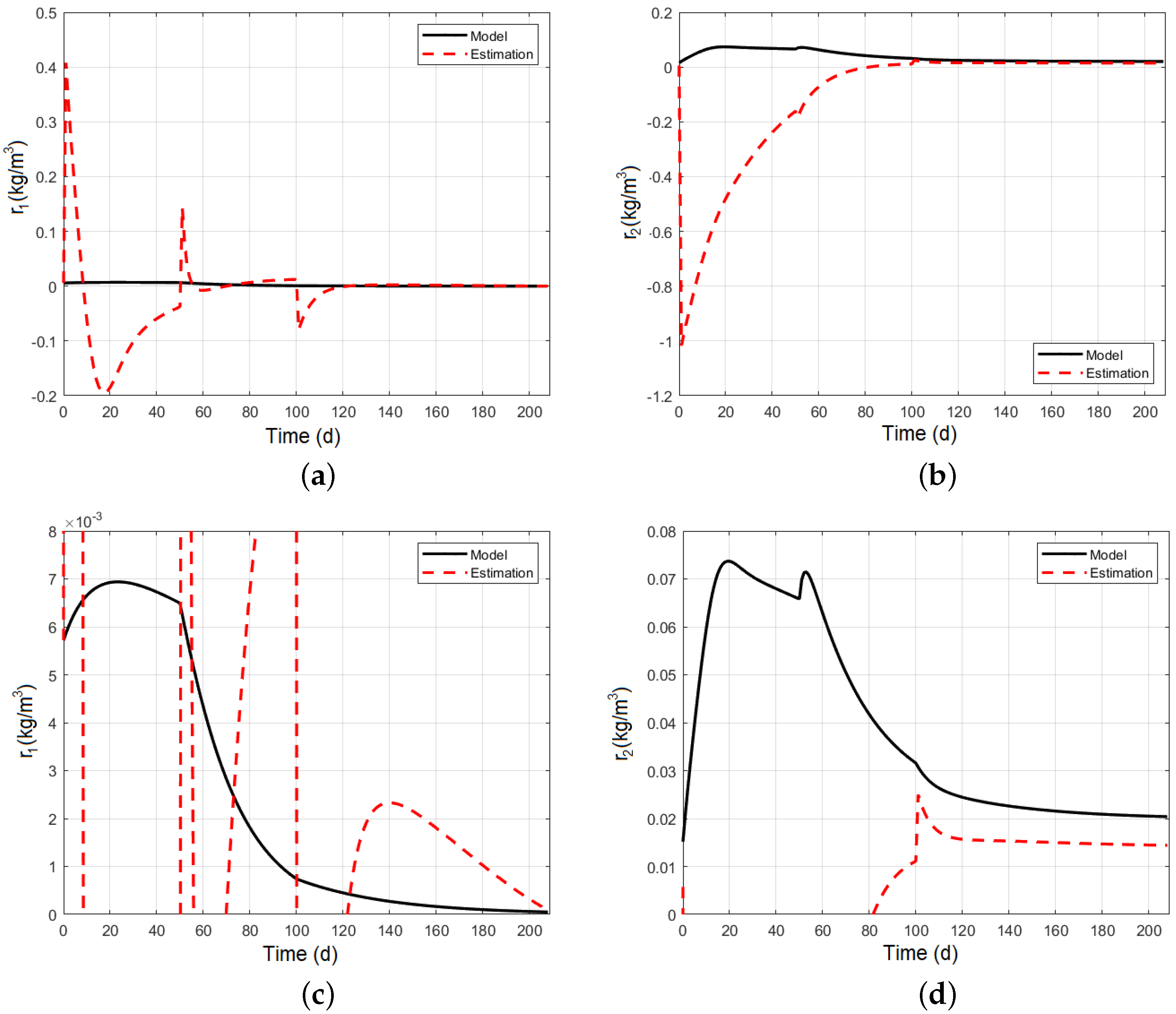
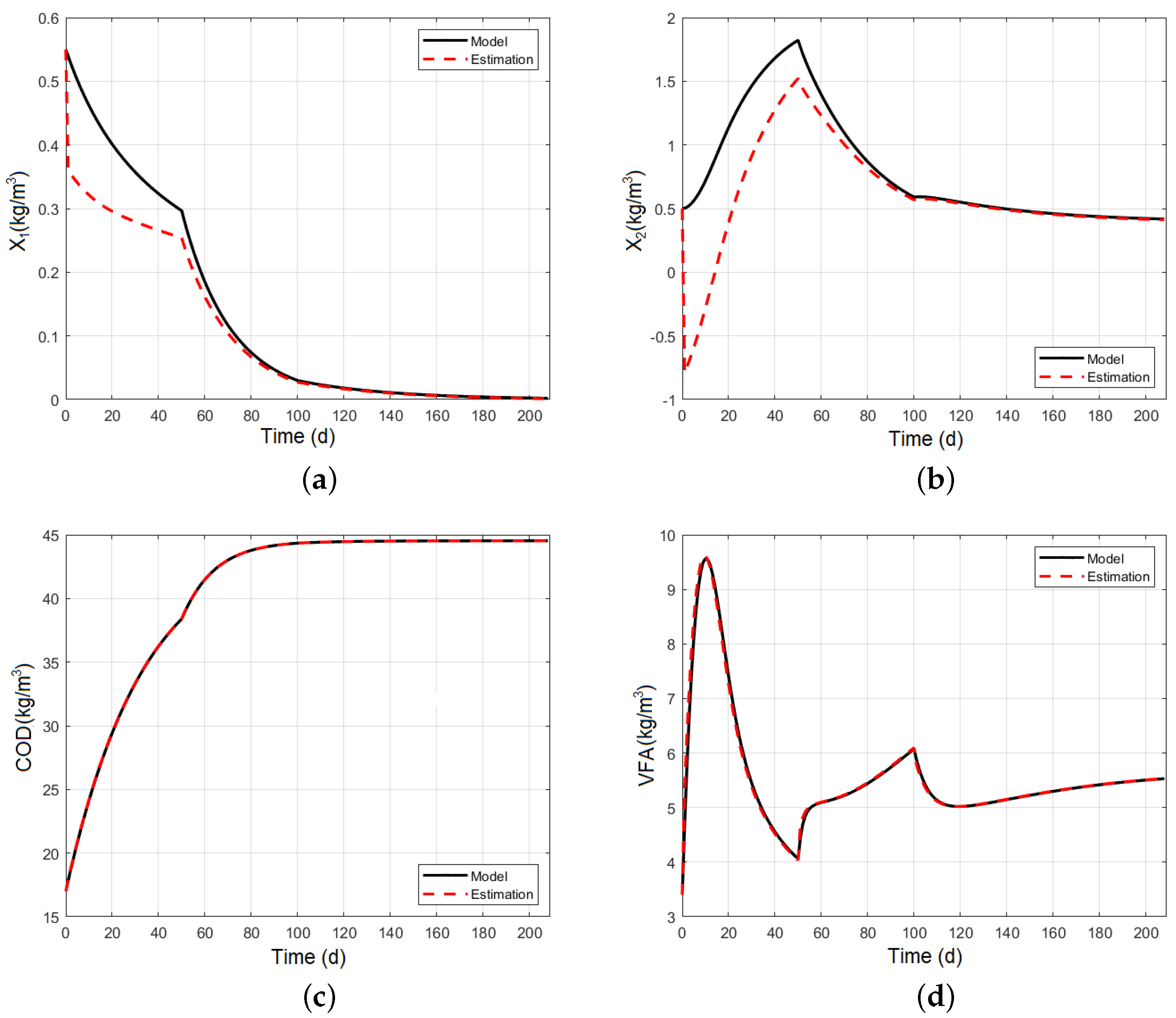
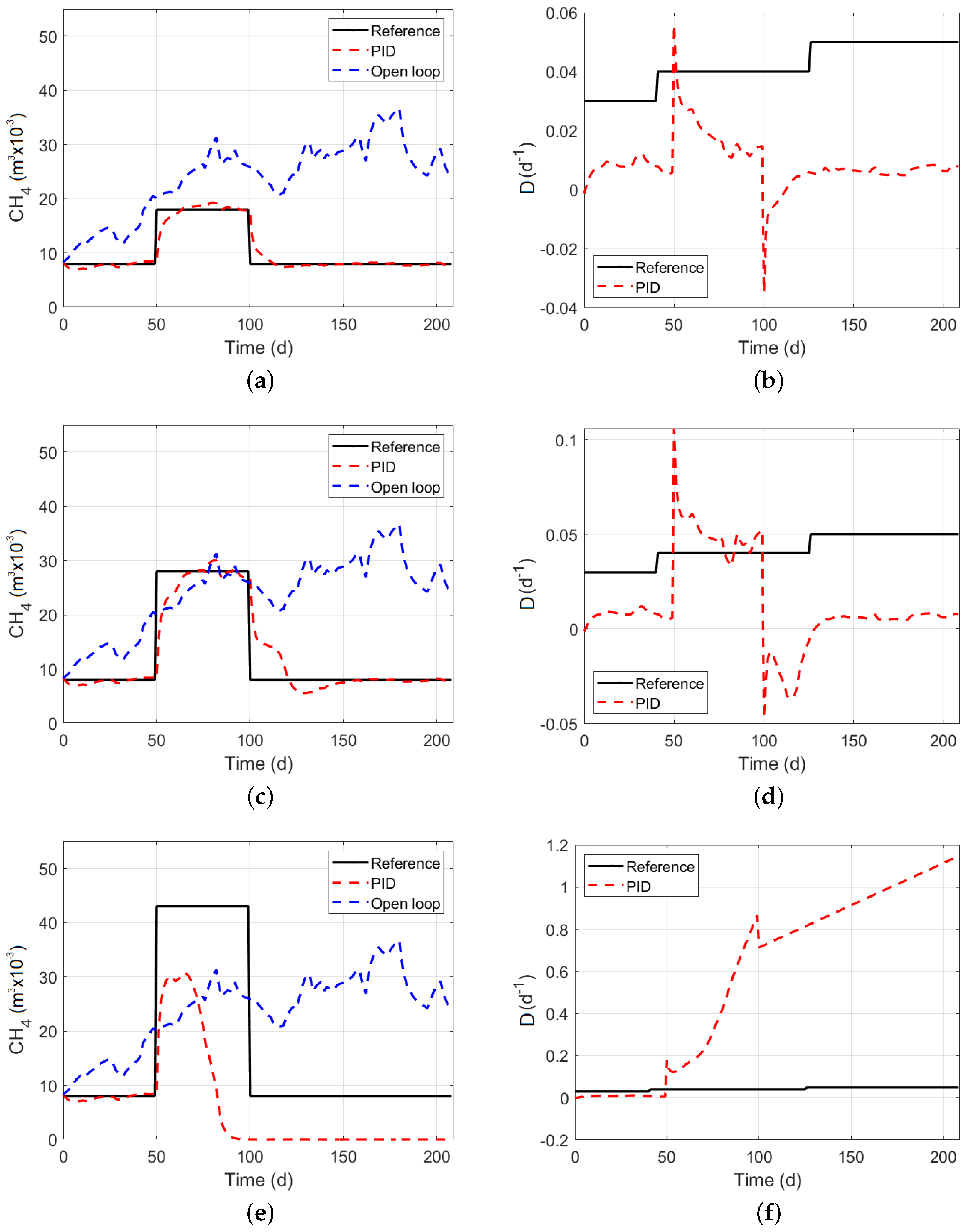
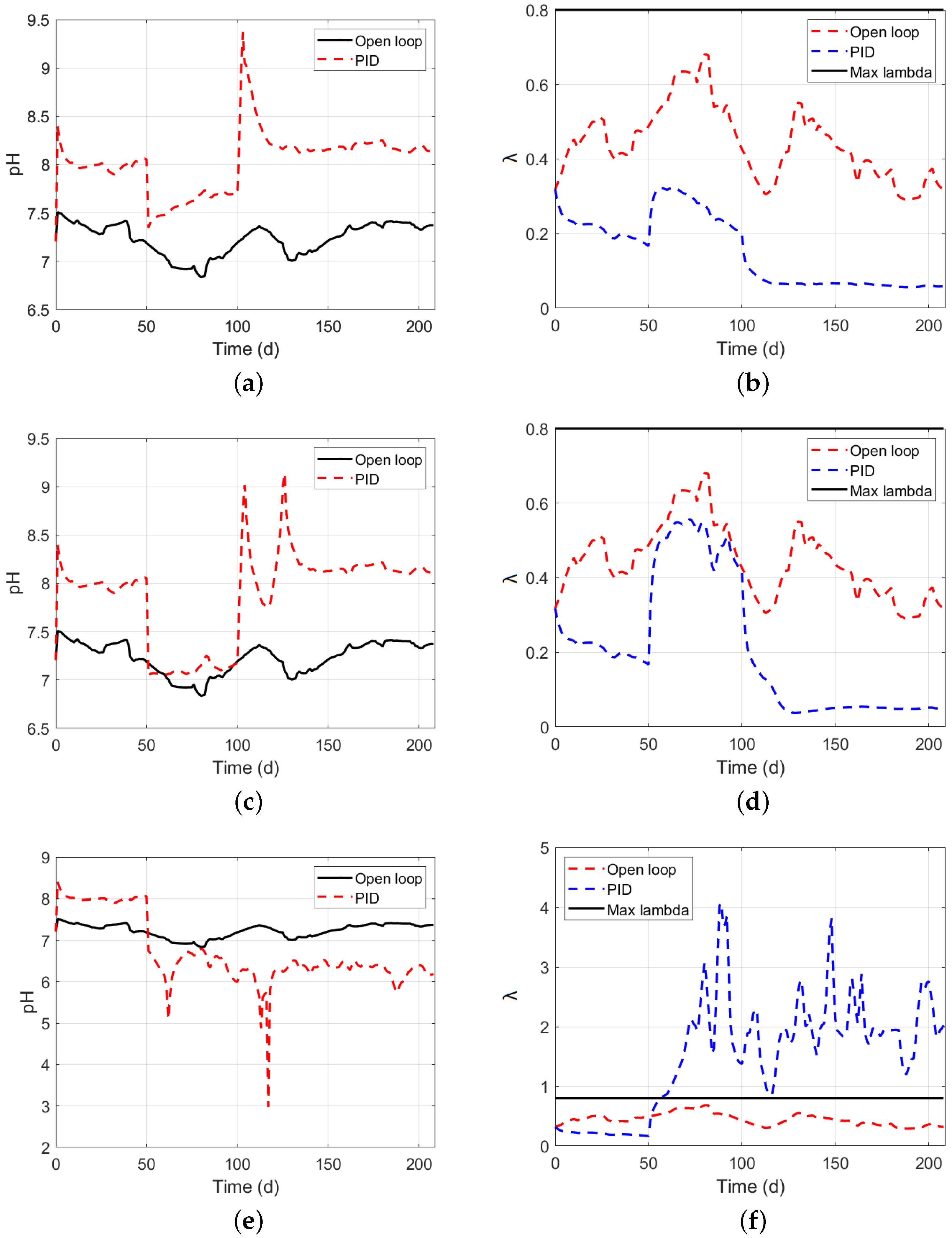


| Schemes | Without Restrictions | With Restrictions | ||
|---|---|---|---|---|
| No Multistart | Multistart | No Multistart | Multistart | |
| Increase on efficiency | 17.4 % | 24.4% | 18.8% | 20.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortés, L.G.; Barbancho, J.; Larios, D.F.; Marin-Batista, J.D.; Mohedano, A.F.; Portilla, C.; de la Rubia, M.A. Full-Scale Digesters: Model Predictive Control with Online Kinetic Parameter Identification Strategy. Energies 2022, 15, 8594. https://doi.org/10.3390/en15228594
Cortés LG, Barbancho J, Larios DF, Marin-Batista JD, Mohedano AF, Portilla C, de la Rubia MA. Full-Scale Digesters: Model Predictive Control with Online Kinetic Parameter Identification Strategy. Energies. 2022; 15(22):8594. https://doi.org/10.3390/en15228594
Chicago/Turabian StyleCortés, Luis G., J. Barbancho, D. F. Larios, J. D. Marin-Batista, A. F. Mohedano, C. Portilla, and M. A. de la Rubia. 2022. "Full-Scale Digesters: Model Predictive Control with Online Kinetic Parameter Identification Strategy" Energies 15, no. 22: 8594. https://doi.org/10.3390/en15228594
APA StyleCortés, L. G., Barbancho, J., Larios, D. F., Marin-Batista, J. D., Mohedano, A. F., Portilla, C., & de la Rubia, M. A. (2022). Full-Scale Digesters: Model Predictive Control with Online Kinetic Parameter Identification Strategy. Energies, 15(22), 8594. https://doi.org/10.3390/en15228594









