Numerical Analysis for Coal Gasification Performance in a Lab-Scale Gasifier: Effects of the Wall Temperature and Oxygen/Coal Ratio
Abstract
1. Introduction
2. Computational Model
2.1. Design and Mesh of the Gasifier
2.2. Governing Equation
2.3. Main Reaction of Gasification
2.4. Simulation Method
3. Results and Discussion
3.1. Various Grid Sensitivity for Validation of the Model
3.2. Selection of the Reaction Mechanism for Further Simulations
3.3. Influence of the O/C Ratio and Wall Temperature on the Syngas Production
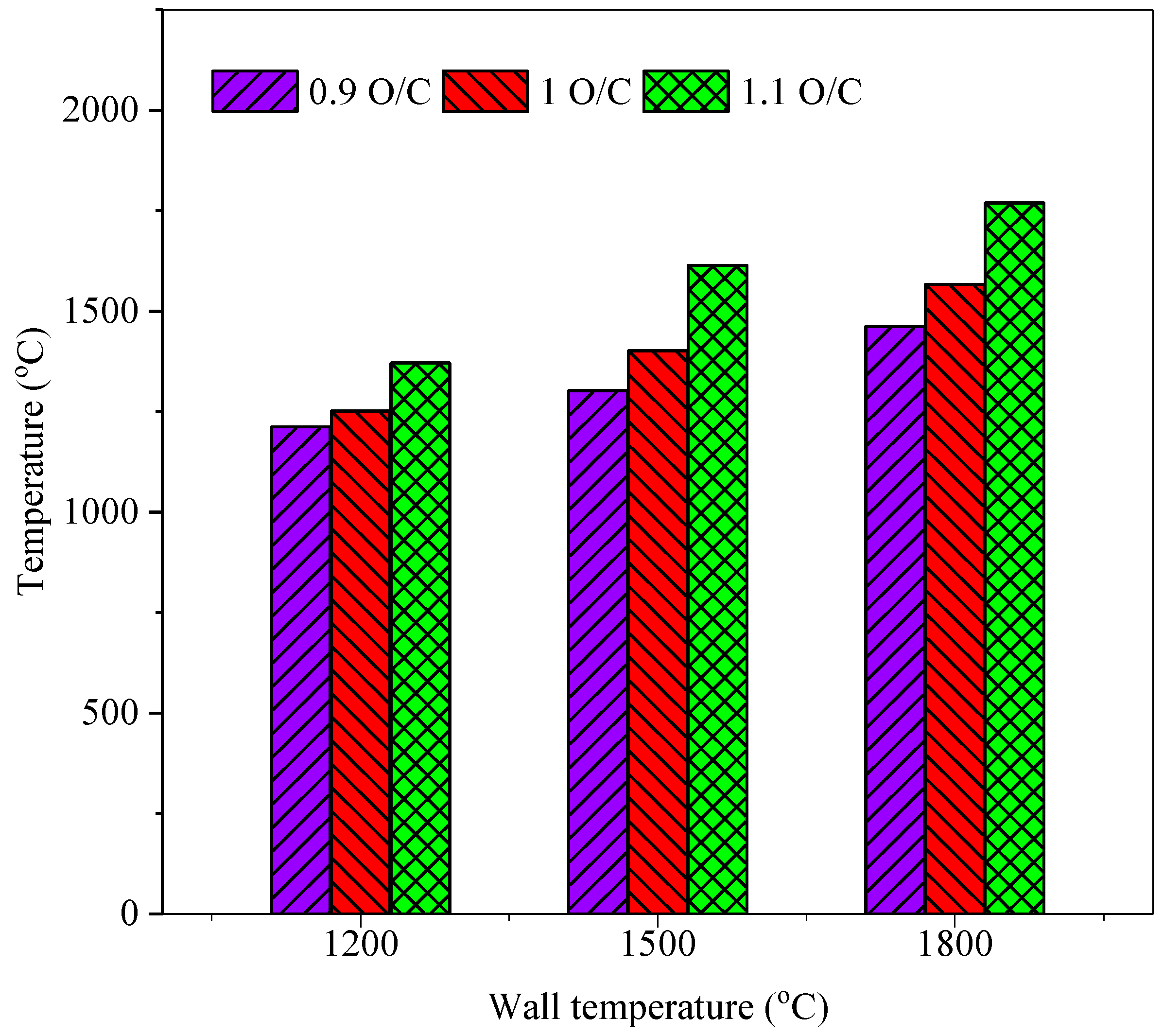
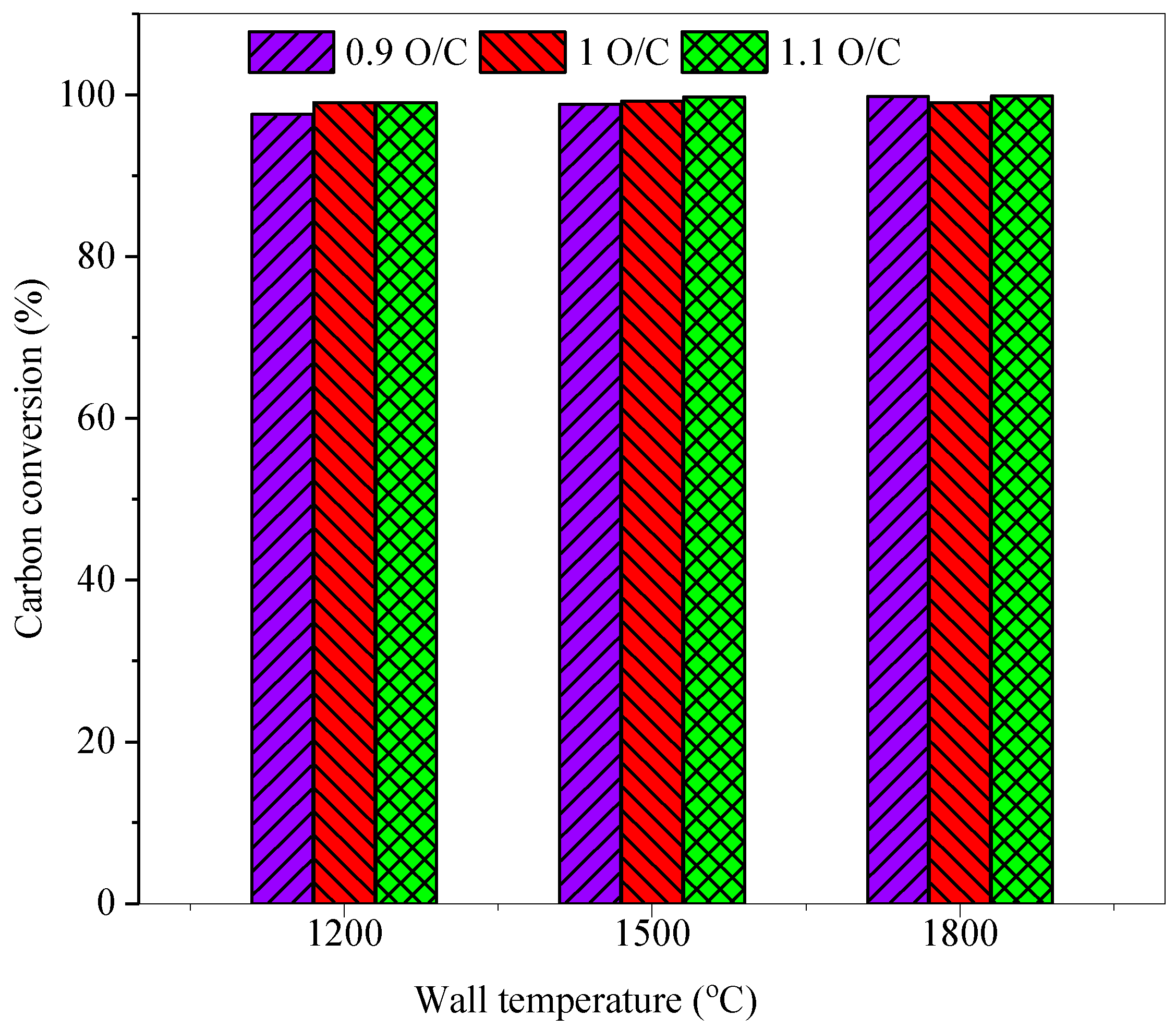
3.4. Effect on the Coal Gas Exit Temperature and Carbon Conversion
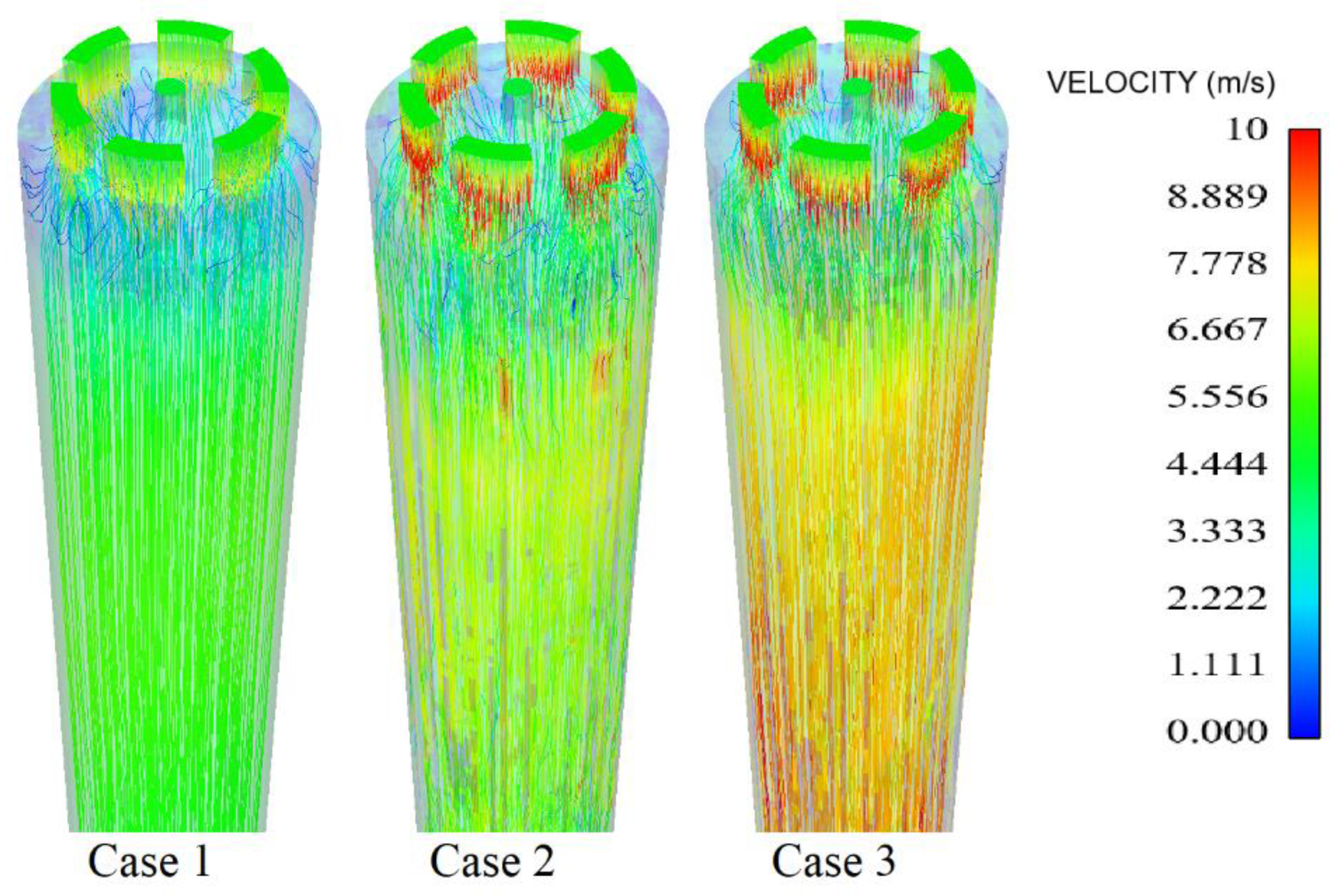
3.5. Turbulent Intensity and Velocity Profile for Selected Cases
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| u, up | Velocity, velocity of particles (m/s) |
| ρ, ρp | Density, density of particles (kg/m3) |
| Sm, Sj, Sh, Sr | Source terms for mass, momentum, energy, and species |
| cp | Specific heat at constant pressure (J/kg K) |
| Symmetric stress tensor | |
| T | Temperature (K) |
| Turbulent thermal conductivity (W/m K) | |
| Cj | Mole fraction of species j |
| Di | Diffusivity (m2/s) |
| FD | Drag force (kg m/s) |
| µ | Dynamic viscosity (N S/m2) |
| ƙ | Kinetic energy of turbulence (m2/s2) |
| ε | Dissipation rate of turbulence (m2/s3) |
| µt | Turbulence viscosity |
| Cµ | Viscosity constant |
| Gƙ | Mean velocity gradients |
| Dt | Diffusion coefficient for turbulence (m2/s) |
| Prt | Prandtl number for turbulence |
| Sct | Schmidt number for turbulence |
| qr | Heat flux for radiation heat (J/m2 s) |
| G | Incident radiation |
| C | Coefficient of function for linear anisotropic phase |
| α | Absorption coefficient |
| σs | Scattering coefficient (m−1) |
| σ | Stefan–Boltzmann constant |
| ƐW | Emissivity |
| Wj,r | Net production rate of species i via chemical reactions (K mol/m3 S) |
| Mj | Molecular weight of species j |
| ʋ″j,r | Stoichiometric coefficient for product j in reaction r |
| ʋ′i,r | Stoichiometric coefficient for reactant i in reaction r |
| [C] | Molar concentration of species (K mol/m3) |
| η″ | Rate exponent for product species |
| η′ | Rate exponent for product reactant species |
| ƙf | Forward reaction rate constant |
| A | Pre-exponential factor (consistent units) |
| B | Temperature constant (dimensionless) |
| Ea | Activation energy for reaction (J/K mol) |
References
- Yamauchi, Y.; Akiyama, K. Innovative Zero-emission Coal Gasification Power Generation Project. Enrgy Proced 2013, 37, 6579–6586. [Google Scholar] [CrossRef][Green Version]
- Wang, Q.; Li, R. Journey to burning half of global coal: Trajectory and drivers of China׳s coal use. Renew. Sustain. Energy Rev. 2016, 58, 341–346. [Google Scholar] [CrossRef]
- Taniguchi, M.; Yamamoto, K.; Kobayashi, H.; Kiyama, K. A reduced NOx reaction model for pulverized coal combustion under fuel-rich conditions. Fuel 2002, 81, 363–371. [Google Scholar] [CrossRef]
- Taniguchi, M.; Kamikawa, Y.; Okazaki, T.; Yamamoto, K.; Orita, H. A role of hydrocarbon reaction for NOx formation and reduction in fuel-rich pulverized coal combustion. Combust. Flame 2010, 157, 1456–1466. [Google Scholar] [CrossRef]
- Molina, A.; Murphy, J.J.; Winter, F.; Haynes, B.S.; Blevins, L.G.; Shaddix, C.R. Pathways for conversion of char nitrogen to nitric oxide during pulverized coal combustion. Combust. Flame 2009, 156, 574–587. [Google Scholar] [CrossRef]
- Ampah, J.D.; Jin, C.; Agyekum, E.B.; Afrane, S.; Geng, Z.; Adun, H.; Yusuf, A.A.; Liu, H.; Bamisile, O. Performance analysis and socio-enviro-economic feasibility study of a new hybrid energy system-based decarbonization approach for coal mine sites. Sci. Total Environ. 2023, 854, 158820. [Google Scholar] [CrossRef]
- Xu, S.; Ren, Y.; Wang, B.; Xu, Y.; Chen, L.; Wang, X.; Xiao, T. Development of a novel 2-stage entrained flow coal dry powder gasifier. Appl. Energy 2014, 113, 318–323. [Google Scholar] [CrossRef]
- Qin, S.; Chang, S.; Yao, Q. Modeling, thermodynamic and techno-economic analysis of coal-to-liquids process with different entrained flow coal gasifiers. Appl. Energy 2018, 229, 413–432. [Google Scholar] [CrossRef]
- Fletcher, D.F.; Haynes, B.S.; Christo, F.C.; Joseph, S.D. A CFD based combustion model of an entrained flow biomass gasifier. Appl. Math. Model. 2000, 24, 165–182. [Google Scholar] [CrossRef]
- Gharebaghi, M.; Irons, R.M.; Pourkashanian, M.; Williams, A. An investigation into a carbon burnout kinetic model for oxy–coal combustion. Fuel Process. Technol. 2011, 92, 2455–2464. [Google Scholar] [CrossRef]
- Jeong, H.J.; Seo, D.K.; Hwang, J. CFD modeling for coal size effect on coal gasification in a two-stage commercial entrained-bed gasifier with an improved char gasification model. Appl. Energy 2014, 123, 29–36. [Google Scholar] [CrossRef]
- Slezak, A.; Kuhlman, J.M.; Shadle, L.J.; Spenik, J.; Shi, S. CFD simulation of entrained-flow coal gasification: Coal particle density/sizefraction effects. Powder Technol. 2010, 203, 98–108. [Google Scholar] [CrossRef]
- Silaen, A.; Wang, T. Effect of turbulence and devolatilization models on coal gasification simulation in an entrained-flow gasifier. Int. J. Heat Mass Transf. 2010, 53, 2074–2091. [Google Scholar] [CrossRef]
- Gerun, L.; Paraschiv, M.; Vîjeu, R.; Bellettre, J.; Tazerout, M.; Gøbel, B.; Henriksen, U. Numerical investigation of the partial oxidation in a two-stage downdraft gasifier. Fuel 2008, 87, 1383–1393. [Google Scholar] [CrossRef]
- Du, S.H.; Yuan, S.Z.; Zhou, Q. Numerical investigation of co-gasification of coal and PET in a fluidized bed reactor. Renew. Energ 2021, 172, 424–439. [Google Scholar] [CrossRef]
- Kim, M.; Sohn, G.; Ye, I.; Ryu, C.; Kim, B.; Lee, J. Numerical analysis on the performance of a 300 MW IGCC coal gasifier under various operating conditions. Fuel 2019, 257, 116063. [Google Scholar] [CrossRef]
- Diba, M.F.; Karim, M.R.; Naser, J. CFD modelling of coal gasification in a fluidized bed with the effects of calcination under different operating conditions. Energy 2022, 239, 122284. [Google Scholar] [CrossRef]
- Fang, N.; Lu, Y.; Li, Z.Q.; Lu, Y.; Chen, Z.C. Improving mixing and gasification characteristics in an industrial-scale entrained flow gasifier with a novel burner. J. Clean Prod. 2022, 362, 132157. [Google Scholar] [CrossRef]
- Wang, B.; Qiu, J.Y.; Guo, Q.H.; Gong, Y.; Xu, J.L.; Yu, G.S. Numerical Simulations of Solidification Characteristics of Molten Slag Droplets in Radiant Syngas Coolers for Entrained-Flow Coal Gasification. Acs Omega 2021, 6, 20388–20397. [Google Scholar] [CrossRef]
- Vicente, W.; Ochoa, S.; Aguillón, J.; Barrios, E. An Eulerian model for the simulation of an entrained flow coal gasifier. Appl. Eng. 2003, 23, 1993–2008. [Google Scholar] [CrossRef]
- Álvarez, L.; Gharebaghi, M.; Jones, J.M.; Pourkashanian, M.; Williams, A.; Riaza, J.; Pevida, C.; Pis, J.J.; Rubiera, F. Numerical investigation of NO emissions from an entrained flow reactor under oxy-coal conditions. Fuel Process. Technol. 2012, 93, 53–64. [Google Scholar] [CrossRef]
- Choi, Y.C.; Li, X.Y.; Park, T.J.; Kim, J.H.; Lee, J.G. Numerical study on the coal gasification characteristics in an entrained flow coal gasifier. Fuel 2001, 80, 2193–2201. [Google Scholar] [CrossRef]
- Watanabe, H.; Otaka, M. Numerical simulation of coal gasification in entrained flow coal gasifier. Fuel 2006, 85, 1935–1943. [Google Scholar] [CrossRef]
- Ajilkumar, A.; Sundararajan, T.; Shet, U.S.P. Numerical modeling of a steam-assisted tubular coal gasifier. Int. J. Therm. Sci. 2009, 48, 308–321. [Google Scholar] [CrossRef]
- Huynh, C.V.; Kong, S.-C. Performance characteristics of a pilot-scale biomass gasifier using oxygen-enriched air and steam. Fuel 2013, 103, 987–996. [Google Scholar] [CrossRef]
- Hongtao, L.; Feng, C.; Xia, P.; Kai, Y.; Shuqin, L. Method of oxygen-enriched two-stage underground coal gasification. Min. Sci. Technol. 2011, 21, 191–196. [Google Scholar] [CrossRef]
- Silva, V.B.; Rouboa, A. Using a two-stage equilibrium model to simulate oxygen air enriched gasification of pine biomass residues. Fuel Process. Technol. 2013, 109, 111–117. [Google Scholar] [CrossRef]
- Kong, X.; Zhong, W.; Du, W.; Qian, F. Compartment modeling of coal gasification in an entrained flow gasifier: A study on the influence of operating conditions. Energy Convers. Manag. 2014, 82, 202–211. [Google Scholar] [CrossRef]
- Seo, H.-K.; Park, S.; Lee, J.; Kim, M.; Chung, S.-W.; Chung, J.-H.; Kim, K. Effects of operating factors in the coal gasification reaction. Korean J. Chem. Eng. 2011, 28, 1851. [Google Scholar] [CrossRef]
- Du, S.-W.; Chen, W.-H.; Lucas, J. Performances of pulverized coal injection in blowpipe and tuyere at various operational conditions. Energy Convers. Manag. 2007, 48, 2069–2076. [Google Scholar] [CrossRef]
- Singer, S.; Chen, L.; Ghoniem, A.F. The influence of gasification reactions on char consumption under oxy-combustion conditions: Effects of particle trajectory and conversion. Proc. Combust. Inst. 2013, 34, 3471–3478. [Google Scholar] [CrossRef]
- Chen, C.-J.; Hung, C.-I.; Chen, W.-H. Numerical investigation on performance of coal gasification under various injection patterns in an entrained flow gasifier. Appl. Energy 2012, 100, 218–228. [Google Scholar] [CrossRef]
- Unar, I.N.; Wang, L.J.; Pathan, A.G.; Mahar, R.B.; Li, R.D.; Uqaili, M.A. Numerical simulations for the coal/oxidant distribution effects between two-stages for multi opposite burners (MOB) gasifier. Energ Convers Manag. 2014, 86, 670–682. [Google Scholar] [CrossRef]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Gonzalo-Tirado, C.; Jiménez, S.; Ballester, J. Gasification of a pulverized sub-bituminous coal in CO2 at atmospheric pressure in an entrained flow reactor. Combust. Flame 2012, 159, 385–395. [Google Scholar] [CrossRef]
- Chen, W.-H.; Du, S.-W.; Yang, T.-H. Volatile release and particle formation characteristics of injected pulverized coal in blast furnaces. Energy Convers. Manag. 2007, 48, 2025–2033. [Google Scholar] [CrossRef]
- Wen, C.Y.; Chaung, T.Z. Entrainment coal gasification modeling. Ind. Eng. Chem. Process Des. Dev. 1979, 18, 684–695. [Google Scholar] [CrossRef]
- Wang, L.; Jia, Y.; Kumar, S.; Li, R.; Mahar, R.B.; Ali, M.; Unar, I.N.; Sultan, U.; Memon, K. Numerical analysis on the influential factors of coal gasification performance in two-stage entrained flow gasifier. Appl. Therm. Eng. 2017, 112, 1601–1611. [Google Scholar] [CrossRef]
- Chui, E.H.; Majeski, A.J.; Lu, D.Y.; Hughes, R.; Gao, H.; McCalden, D.J.; Anthony, E.J. Simulation of entrained flow coal gasification. Energy Procedia 2009, 1, 503–509. [Google Scholar] [CrossRef]
- Ubhayakar, S.K.; Stickler, D.B.; Von Rosenberg, C.W.; Gannon, R.E. Rapid devolatilization of pulverized coal in hot combustion gases. Symp. (Int.) Combust. 1977, 16, 427–436. [Google Scholar] [CrossRef]

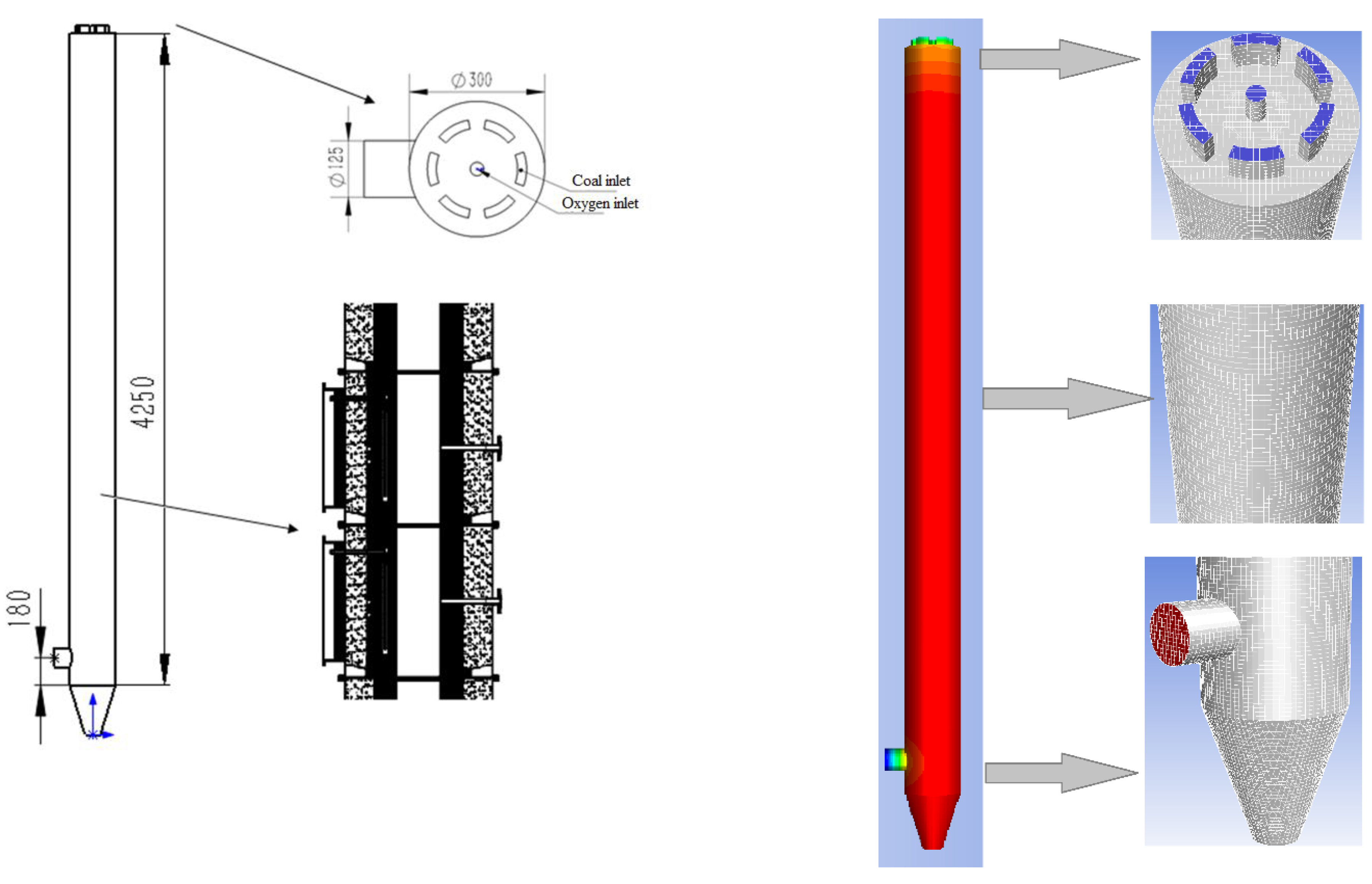






| Proximate Analysis (% ad) | Qnet,ad (J/g) | Ultimate Analysis (% ad) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| M | A | V | FC | C | H | N | S | O | |
| 13.84 | 10.30 | 28.77 | 47.09 | 24,237 | 62.03 | 3.27 | 0.70 | 0.37 | 9.49 |
| Devolatization | |||||
|---|---|---|---|---|---|
| Yh | 1 | ||||
| Yl | 0.3 | ||||
| kh (s−1) | 1.3 × 107 | ||||
| kl (s−1) | 2 × 105 | ||||
| Eh (kJ mol−1) | 167.4 | ||||
| El (kJ mol−1) | 104.6 | ||||
| Gasification or Combustion Reactions | A | B | Ea (J Kmol−1) | ||
| Solid–Gas Phase (Heterogeneous Reactions) | |||||
| C(s) + CO2 → 2CO | 242 | 0 | 2.75 × 108 | ||
| C(s) + 0.5O2 → CO | 0.052 | 0 | 6.1 × 107 | ||
| C(s) + O2 → CO2 | 0.002 | 0 | 7.9 × 107 | ||
| C(s) + H2O → CO + H2 | 426 | 0 | 3.16 × 108 | ||
| Gas Phase (Homogeneous Reaction) | |||||
| H2 + 0.5O2 → H2O | 6.8 × 1015 | 0 | 1.68 × 108 | ||
| CO + H2O ↔ CO2 + H2 | (1) | f | 2.75 × 1010 | 0 | 8.38 × 107 |
| b | 2.65 × 10−2 | 0 | 3.96 × 103 | ||
| CO + 0.5O2 → CO2 | 2.239 × 1012 | 0 | 1.7 × 108 | ||
| C1.37H4.58O0.44 (volatile) + 2.29O2 → 1.37CO2 + 2.29H2O | (2) | 2.119 × 1011 | 0 | 2.119 × 1011 | |
| C1.37H4.58O0.44 (volatile) + 1.61O2 → 1.37CO + 2.29H2O | (3) | 2.119 × 1011 | 0 | 2.027 × 108 | |
| Reaction | Simulation Cases | ||||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | ||
| H2 + 0.5O2 → H2O | (1) | γ | γ | γ | γ | γ | γ |
| CO + H2O ↔ CO2 + H2 | (2) | γ | γ | γ | γ | γ | γ |
| C(s) + O2 → CO2 | (3) | γ | γ | γ | |||
| C(s) + 0.5O2 → CO | (4) | γ | γ | γ | γ | ||
| C(s) + O2 → CO2 | (5) | γ | |||||
| C(s) + H2O → CO + H2 | (6) | γ | γ | γ | γ | γ | γ |
| C(s) + CO2 → 2CO | (7) | γ | γ | γ | γ | γ | γ |
| Vol + 1.61O2 → 1.37CO + 2.29H2O | (8) | γ | γ | ||||
| Vol + 2.29O2 → 1.37CO2 + 2.29H2O | (9) | γ | γ | γ | γ | ||
| Case | O/Coal Ratio | Wall Temperature (K) |
|---|---|---|
| 1 | 0.9 | 1200 |
| 2 | 0.9 | 1500 |
| 3 | 0.9 | 1800 |
| 4 | 1 | 1200 |
| 5 | 1 | 1500 |
| 6 | 1 | 1800 |
| 7 | 1.1 | 1200 |
| 8 | 1.1 | 1500 |
| 9 | 1.1 | 1800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Wang, Z.; He, Y.; Zhu, Y.; Cen, K. Numerical Analysis for Coal Gasification Performance in a Lab-Scale Gasifier: Effects of the Wall Temperature and Oxygen/Coal Ratio. Energies 2022, 15, 8645. https://doi.org/10.3390/en15228645
Kumar S, Wang Z, He Y, Zhu Y, Cen K. Numerical Analysis for Coal Gasification Performance in a Lab-Scale Gasifier: Effects of the Wall Temperature and Oxygen/Coal Ratio. Energies. 2022; 15(22):8645. https://doi.org/10.3390/en15228645
Chicago/Turabian StyleKumar, Sunel, Zhihua Wang, Yong He, Yanqun Zhu, and Kefa Cen. 2022. "Numerical Analysis for Coal Gasification Performance in a Lab-Scale Gasifier: Effects of the Wall Temperature and Oxygen/Coal Ratio" Energies 15, no. 22: 8645. https://doi.org/10.3390/en15228645
APA StyleKumar, S., Wang, Z., He, Y., Zhu, Y., & Cen, K. (2022). Numerical Analysis for Coal Gasification Performance in a Lab-Scale Gasifier: Effects of the Wall Temperature and Oxygen/Coal Ratio. Energies, 15(22), 8645. https://doi.org/10.3390/en15228645










