Distributed Permanent Magnet Direct-Drive Belt Conveyor System and Its Control Strategy
Abstract
:1. Introduction
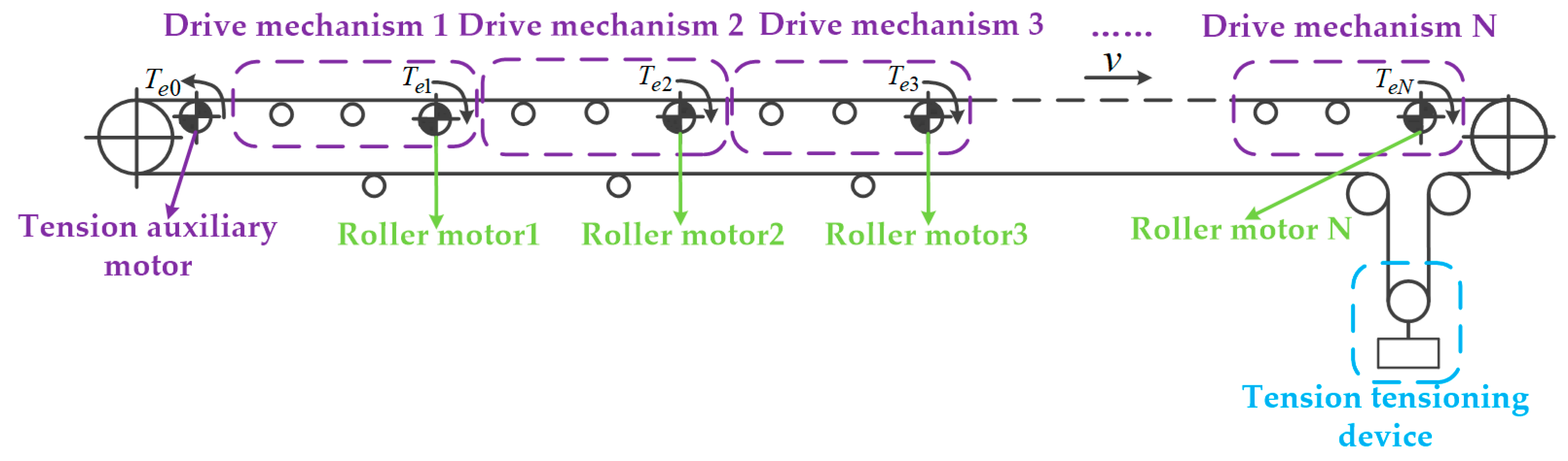
2. System Composition
3. Dynamic Model of Conveying System
3.1. Dynamic Model of Conveyor Belt
3.2. Dynamic Model of Roller Motor
3.3. Output Power of Roller Motor
4. Vector Control Strategy Modeling
4.1. Direct Torque Control Strategy Based on Double Sliding Mode Control
4.2. Multi-Motor Ring Coupling Control Strategy
5. Mechanical-Electrical Coupling Dynamics Modeling
6. Simulation Verification
6.1. Simulation Comparison under Light Load Operation
6.2. Simulation Comparison under Variable Load Operation
7. Experimental Verification
8. Conclusions
- When the driving mechanism of the distributed permanent magnet direct-drive belt conveyor is in steady-state operation, the tension between each other will not accumulate with the transportation distance. The distributed permanent magnet direct-drive belt conveyor composed of N groups of driving units can reduce the tension increment of the bearing section of the traditional belt conveyor by N times.
- The distributed permanent magnet direct-drive control system based on multi-motor ring coupling control strategy and double sliding mode direct torque control strategy can perform the low speed and light load starting of the belt conveyor. Compared with the traditional belt conveyor, the distributed permanent magnet direct-drive belt conveyor has a shorter start-up time, the tension and speed fluctuation curves of the conveyor belt are closer, and the fluctuation amplitude is smaller, which has good dynamic characteristics and works efficiency.
- When the local load fluctuates, the speed and tension of the whole traditional belt conveyor system will fluctuate, while the distance between the roller motors of the distributed permanent magnet direct-drive belt conveyor is smaller and the reaction is more rapid, which significantly reduces the influence range of local load disturbance and improves the robustness of the conveyor system.
- The simulation experiments of the traditional belt conveyor and the distributed permanent magnet direct-drive conveyor under the same working conditions verify that the proposed new transportation technology can well suppress the accumulation of the tension increment and tension fluctuations, and the experiments proved that the distributed permanent magnet direct-drive belt conveyor has better dynamic regulation performance than the single motor-driven belt conveyor, which provides new methods and ideas for current modes of engineering transportation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.H.; Yu, B.; Kang, H.P. Key technologies and equipment for a fully mechanized top-coal caving operation with a large mining height at ultra-thick coal seams. Int. J. Coal Sci. Technol. 2015, 2, 97–161. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.L.; Wang, B.K.; Zhang, X.F.; Li, F.Q. Forty years’ development and future prospect on mechanized short-wallmining technology with continuous miner in China. J. China Coal Soc. 2021, 46, 86–99. [Google Scholar]
- Deng, Y.X.; Yang, M.; Liu, Y.J.; Wang, Z.; Chen, C.L.P. Adaptive fuzzy tracking control for uncertain nonlinear systems with multiple actuators and sensors faults. IEEE Trans. Fuzzy Syst. 2022. [Google Scholar] [CrossRef]
- Zeng, F.; Yan, C.; Wu, Q. Dynamic behaviour of a conveyor belt considering non-uniform bulk material distribution for speed control. Appled Sci. 2020, 10, 4436. [Google Scholar] [CrossRef]
- He, D.J.; Pang, Y.S.; Lodewijks, G. Healthy speed control of belt conveyors on conveying bulk materials. Powder Technol. 2018, 327, 408–419. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Bao, J.S.; Ge, S.R.; Yin, Y.; Wang, S.B.; Zhang, L. Simulation and experimental study on electromechanical coupling model of permanent magnet direct drive system for scraper conveyor. J. China Coal Soc. 2020, 45, 2127–2139. [Google Scholar]
- Jia, L.; Deng, X.L.; Wen, G.X.; Li, L.; Wang, Z.; Chen, C.L.P. Game-Based Backstepping Design for Strict-Feedback Nonlinear Multi-Agent Systems Based on Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Zhang, L.; Bao, J.S.; Ge, S.R.; Yang, X.L.; Yin, Y.; Bao, Z.Y. Permanent magnet driving technology and its application status in the field of mining equipment. Coal Sci. Technol. 2022, 50, 275–285. [Google Scholar]
- Semenov, D.; Bing, T.; Li, S. Advanced fault-tolerant current control of five-phase PMSM for mining applications. In Proceedings of the IEEE Applications Society Meeting, Atlanta, GA, USA, 10–14 June 2016; pp. 1–7. [Google Scholar]
- Semykina, I.; Tarnetskaya, A.; Tyulenev, M. Magnet synchronous machine of mine belt conveyor gearless drum-motor. In E3S Web Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 41, pp. 1–6. [Google Scholar]
- Wang, D.L.; Wang, R.F.; Lai, C.L. Design of dual-motor driving control system of belt conveyor. Ind. Mine Autom. 2018, 44, 74–78. [Google Scholar]
- Yang, C.Y.; Liu, J.H.; Li, H.; Zhou, L.N. Energy modeling and parameter identification of dual-notor-driven belt conveyors without speed sensors. Energies 2018, 11, 3313. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.L.; Ge, S.R.; Zu, H.B.; Bao, J.S.; Chang, G.Q.; Zhang, L.; Li, H.Y. Permanent magnet intelligent drive system and control straegy of belt conveyor. J. China Coal Soc. 2020, 45, 2116–2126. [Google Scholar]
- He, B.Y.; Sun, Y.H.; Nie, R.; Li, G.P. Dynamic behavior analysis on the ring chain transmission system of an armoured face coveyor. J. Mech. Eng. 2012, 48, 50–56. [Google Scholar] [CrossRef]
- Yao, Y.P.; Zhang, B.S. Influence of the elastic modulus of a conveyor belt on the power allocation of multi-drive conveyors. PLoS ONE 2020, 15, e0235768. [Google Scholar] [CrossRef] [PubMed]
- He, D.J.; Pang, Y.; Gabriel, L. Green operations of belt conveyors by means of speed control. Appl. Energy 2017, 188, 330–341. [Google Scholar] [CrossRef]
- Witold, K.; Natalia, S.; Martyna, K.; Robert, K. Specific Energy Consumption of a Belt Conveyor System in a Continuous Surface Mine. Energies 2020, 13, 5214. [Google Scholar]
- Zhang, S.R.; Xia, X.H. Modeling and energy efficiency optimization of belt conveyors. Appl. Energy 2010, 88, 3061–3071. [Google Scholar] [CrossRef]
- Michael, J.C.; Craig, A.W.; Peter, W.R.; Bin, C. Reducing the energy intensity of overland conveying using a novel rail-running conveyor system. Int. J. Min. Reclam. Environ. 2020, 35, 183–198. [Google Scholar]
- Ye, Y.H.; Peng, F.; Huang, Y.K. Overview of multi-motor synchronous motion control technology. Trans. China Electrotech. Soc. 2021, 36, 2922–2935. [Google Scholar]
- Vedrana, J.S.; Toni, V.; Tin, B.; Marinko, B. A survey of fuzzy algorithms used in multi-motor systems control. Electronics 2022, 9, 1788. [Google Scholar]



















| Parameter | Value of Drive Motor | Value of Roller Motor |
|---|---|---|
| Rated power (kW) | 144.5 | 12.6 |
| Rated speed (r/min) | 60 | 60 |
| Rated torque (N·m) | 23,000 | 2000 |
| Rotor inertia (kg·m2) | 56 | 10 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Length of conveyor (m) | 2 | Rated power of motor (kW) | 22 |
| Rated speed of conveyor (m/s) | 2.5 | Rated speed of motor (r/min) | 56 |
| Belt width (m) | 1 | Rated frequency of motor (Hz) | 14 |
| Diameter of motor (m) | 0.5 | Rated torque of brake (N·m) | 2000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Gong, H.; Du, G.; Zhang, Y.; He, H. Distributed Permanent Magnet Direct-Drive Belt Conveyor System and Its Control Strategy. Energies 2022, 15, 8699. https://doi.org/10.3390/en15228699
Zhou Q, Gong H, Du G, Zhang Y, He H. Distributed Permanent Magnet Direct-Drive Belt Conveyor System and Its Control Strategy. Energies. 2022; 15(22):8699. https://doi.org/10.3390/en15228699
Chicago/Turabian StyleZhou, Qixun, Hao Gong, Guanghui Du, Yingxing Zhang, and Hucheng He. 2022. "Distributed Permanent Magnet Direct-Drive Belt Conveyor System and Its Control Strategy" Energies 15, no. 22: 8699. https://doi.org/10.3390/en15228699
APA StyleZhou, Q., Gong, H., Du, G., Zhang, Y., & He, H. (2022). Distributed Permanent Magnet Direct-Drive Belt Conveyor System and Its Control Strategy. Energies, 15(22), 8699. https://doi.org/10.3390/en15228699









