Modelling of Flow-Induced Vibration of Bluff Bodies: A Comprehensive Survey and Future Prospects
Abstract
1. Introduction
2. Fundamental Concepts and Background of FIV
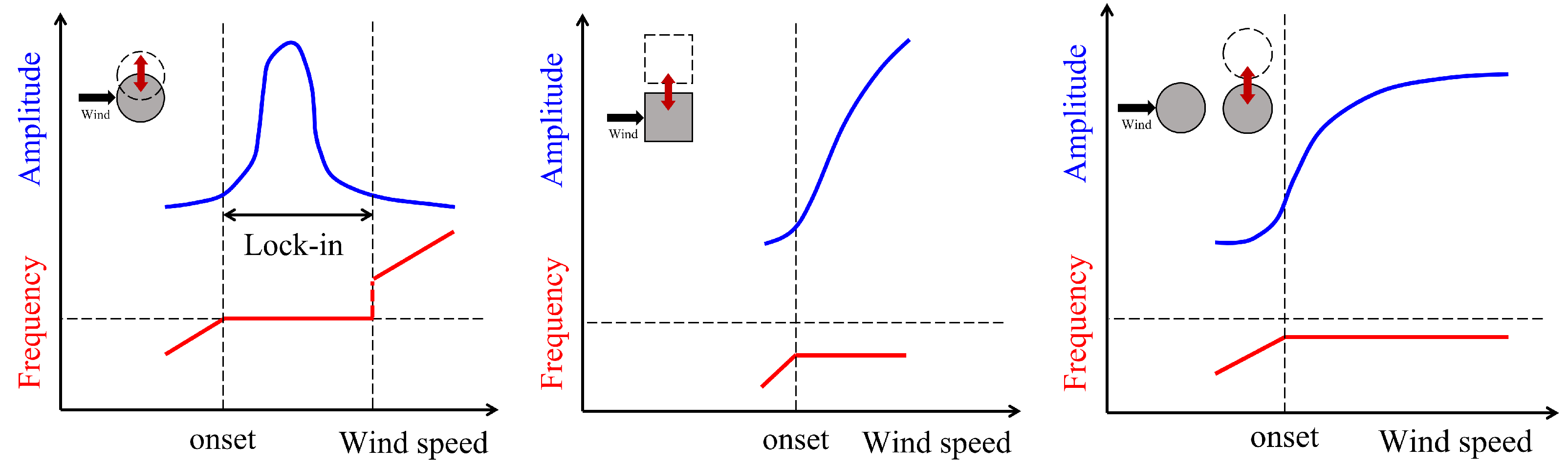
2.1. Vortex-Induced Vibration
2.2. Buffeting
2.3. Galloping
2.4. Flutter
3. Mathematical Modelling of FIV
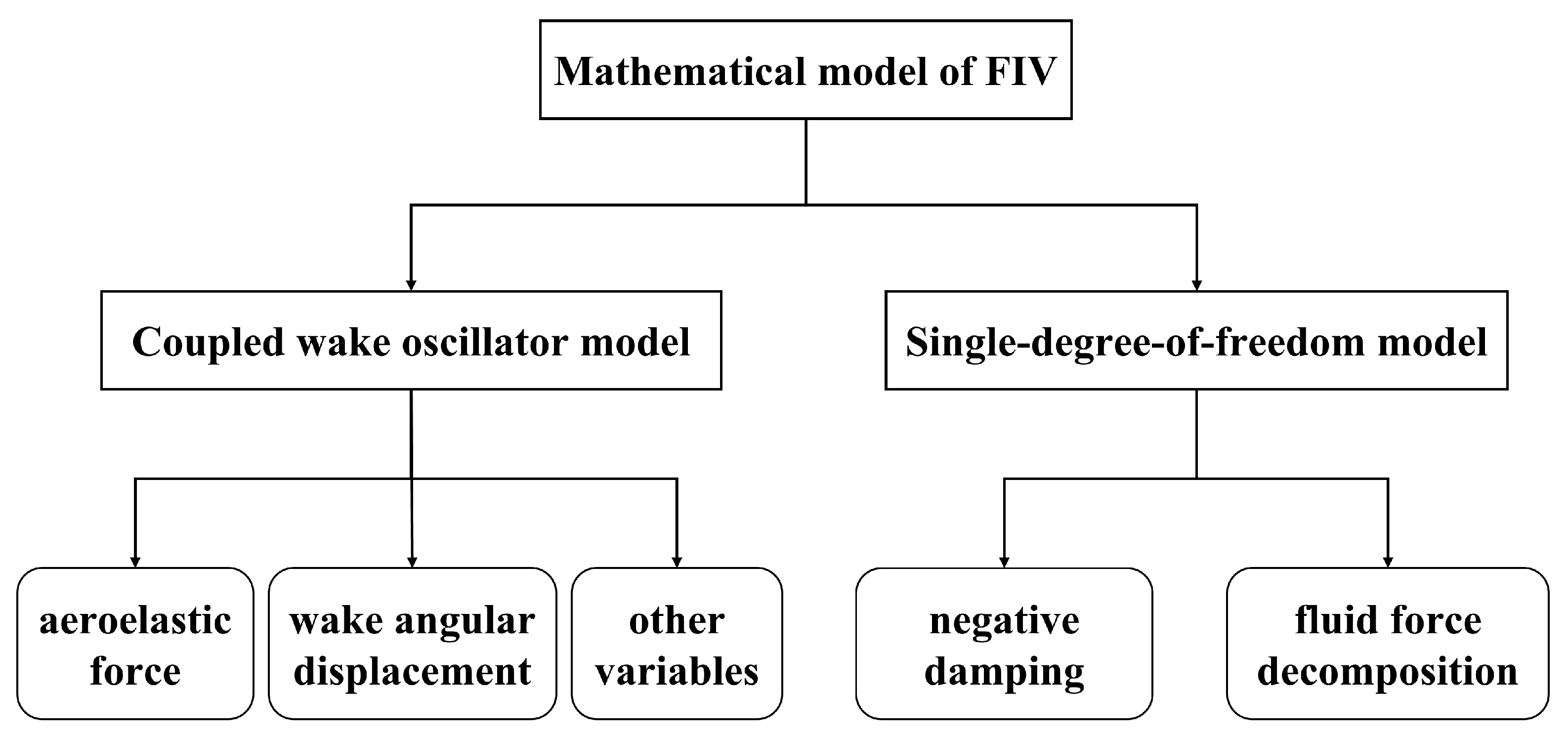
3.1. Classification
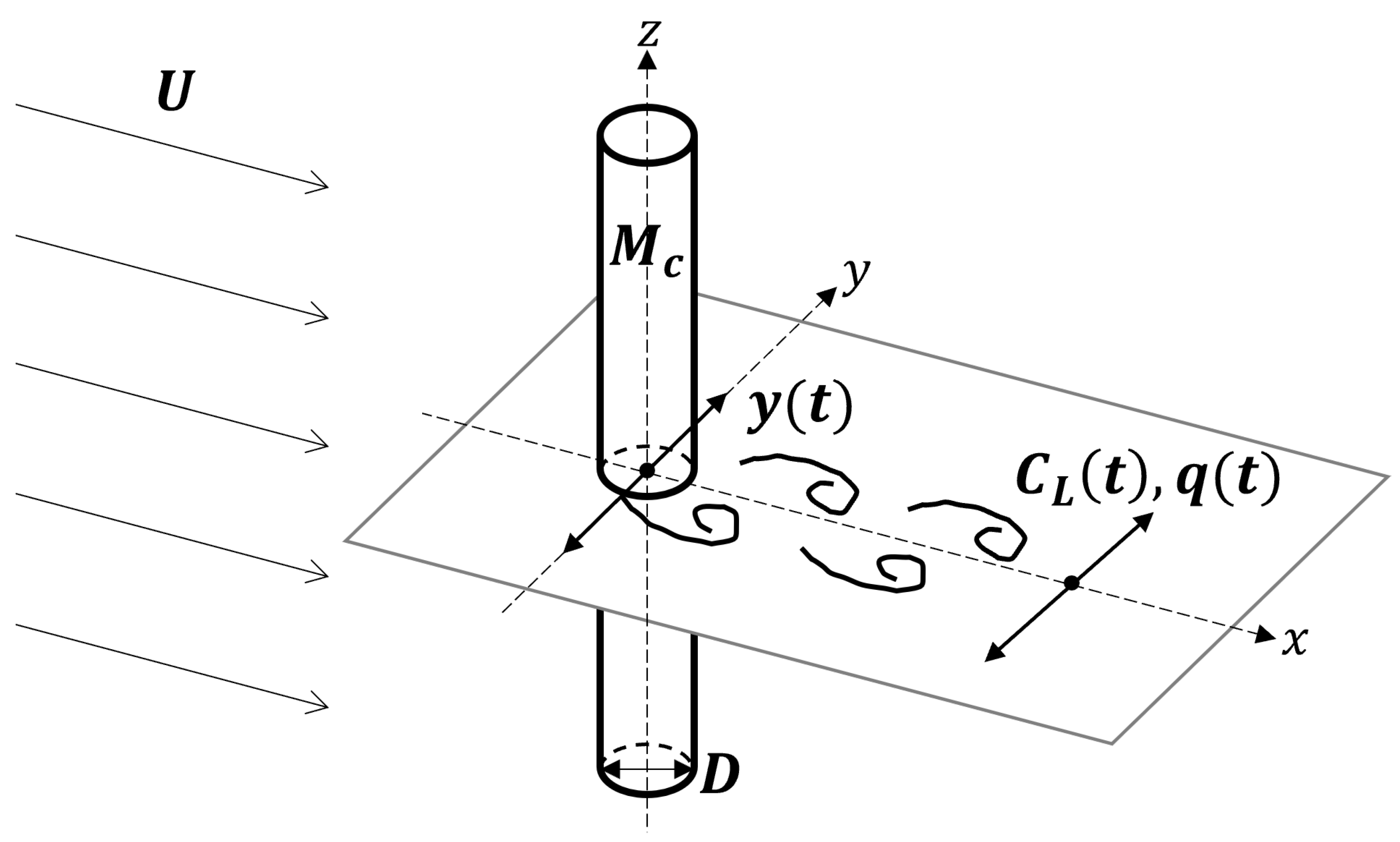
3.2. Vortex-Induced Vibration
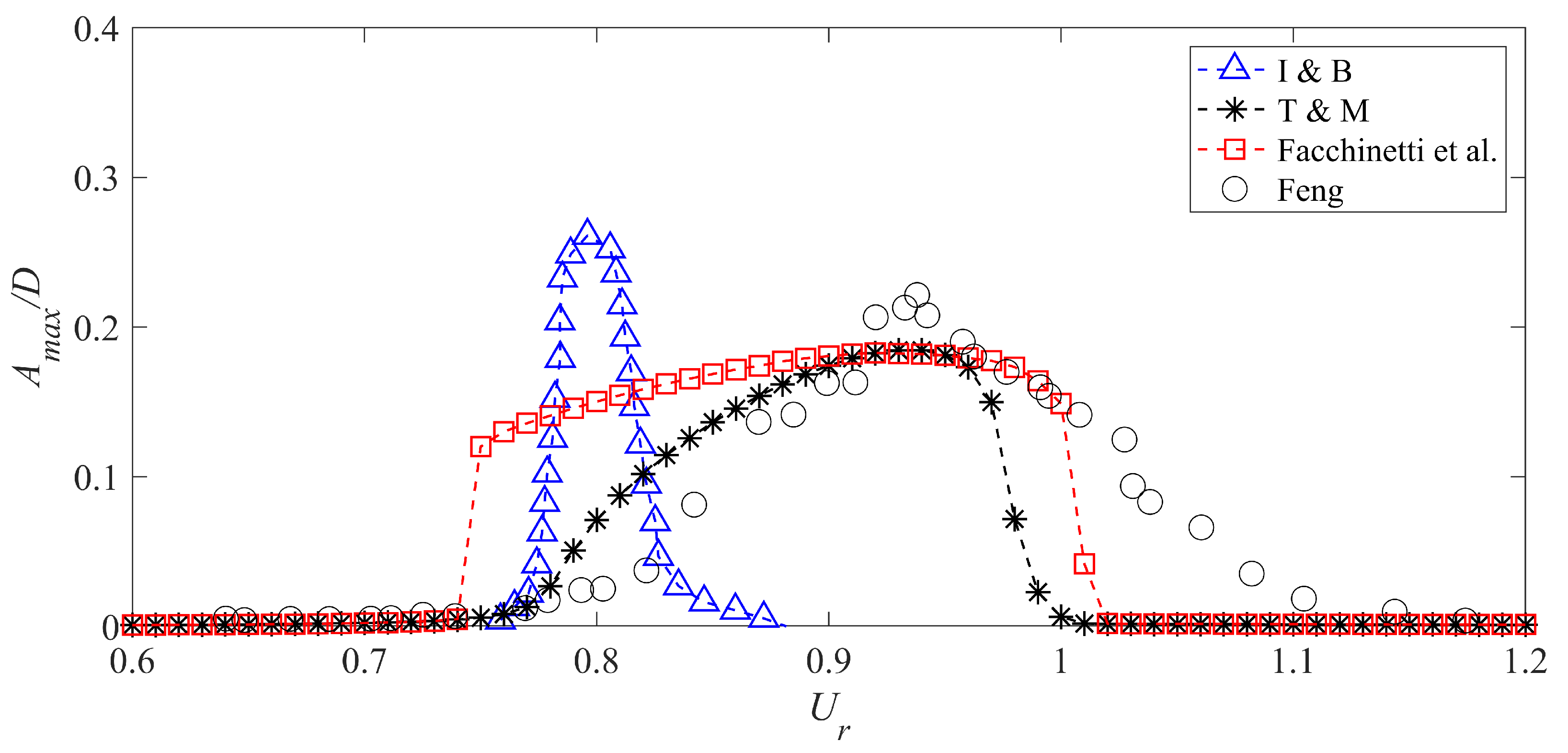
3.2.1. Coupled Wake-Oscillator Model
- (1)
- Aerodynamic force coefficient.
- (2)
- Wake angular displacement.
- (3)
- Other wake variables.
3.2.2. Single-Degree-of-Freedom Model
3.3. Galloping
3.4. Combined VIV and Galloping
4. Numerical Modelling
4.1. Numerical Techniques for FSI Simulation
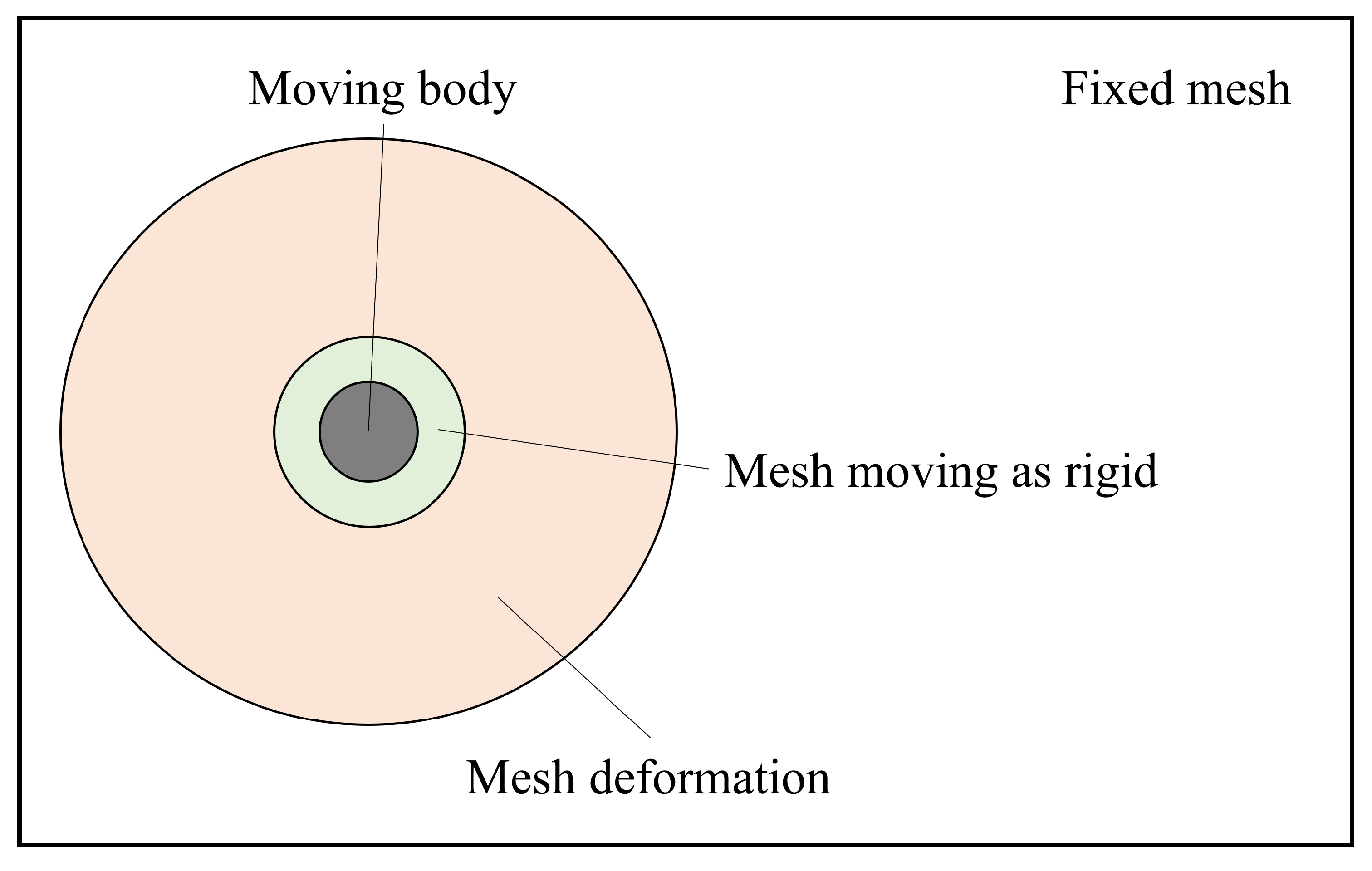
- (1)
- Moving mesh.
- (2)
- Fixed mesh.
4.2. Two-Dimensional or Three-Dimensional Numerical Simulations of FIV
4.3. Direct Numerical Simulation (DNS) of FIV
4.3.1. Two-Dimensional DNS in the Laminar Regime
- (1)
- Single cylinder.
- (2)
- Passive turbulence control cylinder.
- (3)
- Array of cylinders.
4.3.2. Three-Dimensional DNS in the Turbulent Regime
4.4. Large-Eddy Simulation (LES) of FIV
4.5. Reynolds-Averaged Navier–Stokes (RANS) Modelling of FIV
4.6. Detached-Eddy Simulation (DES) of FIV
5. Machine Learning and FIV
5.1. Data-Driven Reduced-Order Models (ROM) of FIV
5.1.1. Projection-Based ROM
5.1.2. System Identification-Based ROM
5.1.3. Non-Linear ROM
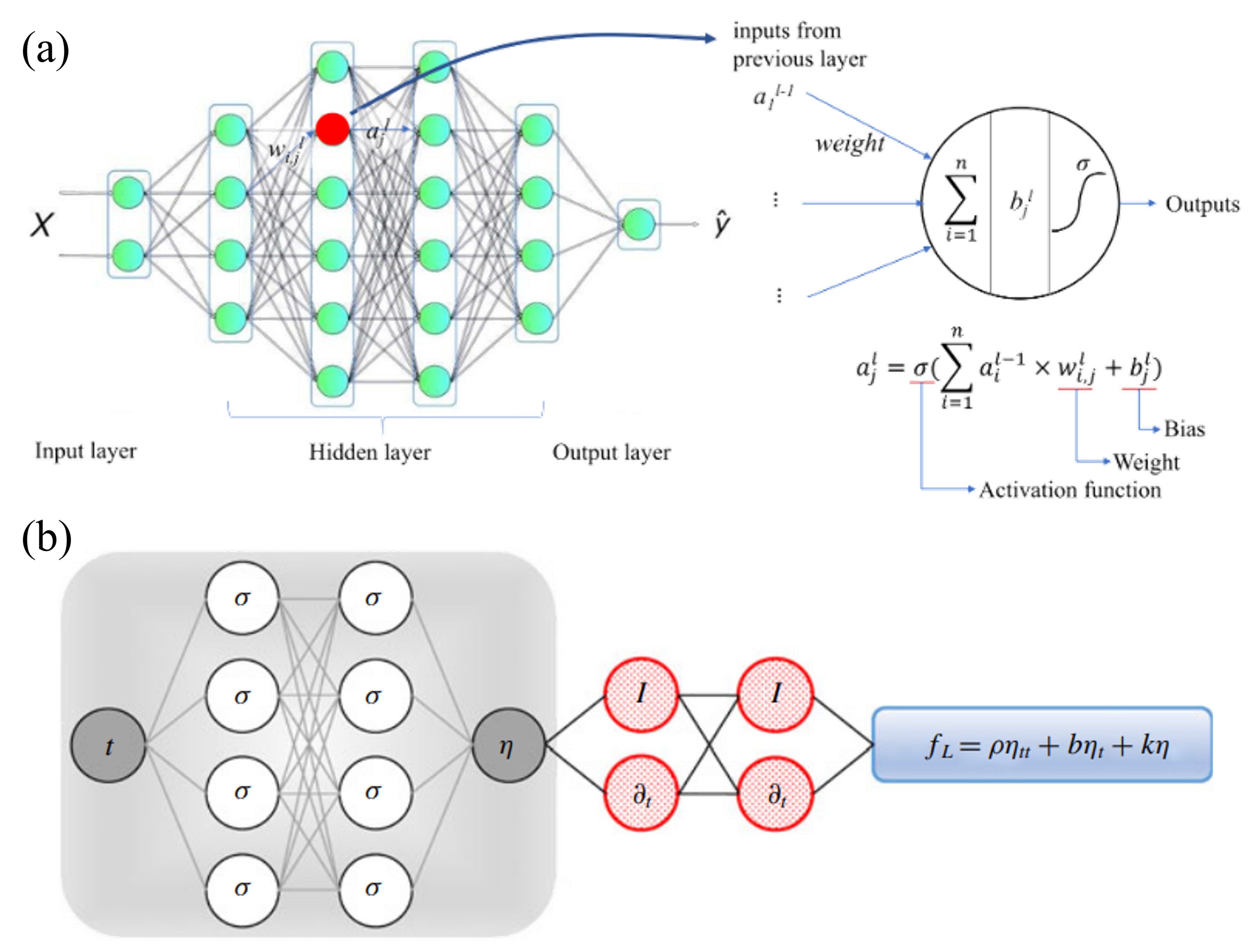
5.2. Data-Driven Deep Neural Network Applied to FIV
5.2.1. DNN-Accelerated Fluid Modelling
5.2.2. Physics-Informed Neural Network of FIV
5.2.3. DNN-Based FIV Force Model
6. Energy Harvesting Based on FIV
6.1. Mathematical and Numerical Modelling of FIVEH
6.2. Machine Learning for Modelling FIVEH
7. Outlook
7.1. Future Issues
- (1)
- Mathematical modelling.
- Mathematical modelling plays an indispensable role in our understanding of the underlying physics of the FIV phenomenon. However, formulating an accurate mathematical model for a highly non-linear dynamical system, such as FIV phenomena is highly challenging. The mathematical models proposed to date based on experimental data and/or engineering experience are not purely analytical models derived from first principles using a comprehensive theory and, as a result, these models have a limited range of applicability. Is it possible to develop a more complete theory of various aspects of FIV phenomena that will allow the formulation of more general analytical models?
- Most theoretical models for FIV, whether a coupled wake-oscillator model or single-degree-of-freedom model, are semi-empirical in nature—implying that the model has unknown parameters whose values need to be determined (fitted) to available experimental data. As a result, these models tend to have a very limited range of applicability (viz., a model that has been developed for VIV for a particular bluff body shape cannot be used for VIV for another body shape or for galloping for the same body shape without changing either the structure of the model and/or re-fitting the free parameters that define the model). More specifically, the need for reformulating the structure of terms and/or inclusion of new terms in the model along with a re-fitting of the free coefficients using available experimental data need to be conducted for new scenarios.
- Most of the current mathematical models for FIV phenomena have been developed for VIV, which can also include galloping behavior in the formulation through use of the quasi-steady assumption—this usually involves inclusion of an odd-order polynomial approximation of the aerodynamic force responsible for galloping in the mathematical model. Although some other methods (e.g., neural network mappings) have been proposed to improve the curve fitting accuracy of the forcing term responsible for galloping, it is stressed that the quasi-steady assumption has inherent limitations and is applicable only under certain conditions.
- (2)
- Numerical modelling.
- Owing to its moderate computational cost, RANS modelling will remain the workhorse of CFD applications to engineering and industrial FIV problems of practical relevance into the foreseeable future. The essential element for the successful use of RANS modelling is formulation of turbulence closure models. Is it possible to simulate FIV for these engineering and industrial applications using lower-fidelity numerical models such as unsteady RANS?
- Even so, for FIV problems that require greater accuracy or detailed information on the spatial and temporal fluctuations of the flow field, hybrid methods may be the numerical tool of choice (at least in the near future) given that these methods are not as computationally prohibitive as either LES or DNS. Hybrid methods represent the amalgamation of closure modelling with eddy-resolving simulation. The key question here is what blending and/or interpolation functions should be used in hybrid methods to give the best prediction of FIV phenomena?
- (3)
- Machine learning technique.
- In machine learning, the availability of large public datasets has spurred rapid progress in computer vision, speech recognition, and other applications. Many sophisticated machine learning techniques (including those for numerical simulation of turbulent flows) require large datasets consisting of high-quality information. Perhaps the biggest challenge for machine learning techniques within FIV simulation is the lack of availability of data. Every investigator that applies a state-of-the-art machine learning method to FIV simulation must generate their own dataset. Currently, it is impossible to benchmark various machine learning techniques, such as PINN or augmented RANS modelling as applied to FIV, because there exists no suitable public dataset for this purpose.
- Aside from the lack of available data, there are major physics-based challenges for applying machine learning technique to FIV simulation. Changes in the Reynolds number, in the freestream turbulence, in vibration parameters, and in the body shape all greatly affect the FIV response. Even without incorporating machine learning techniques, traditional physics-based numerical methods, such as RANS and LES, often struggle to reproduce the complicated interactions within FIV. When applying a machine learning technique for FIV, the design of the training dataset will be of utmost importance. Generalizability issues within machine learning greatly affect the model’s ability to perform outside of the parameters given in the training dataset. For example, a model trained at Re = 2000 may produce erroneous results at Re = 30,000, because transitional turbulence regions in the former case become fully turbulent in the latter case [269]. These small changes in turbulence can have large effects on the vibration response. Therefore, the training dataset should be designed to incorporate a wide variety of FIV parameters, so that the model can perform well for a variety of test cases. The issue of generalizability within machine learning augmented turbulence modelling is currently under investigation. Machine learning techniques may be better suited to provide accelerated and higher-accuracy simulation results within a known range of parameters, rather than attempting to uncover new physics (for example, at a higher-Reynolds number than any of the cases included in the training dataset).
- While several PINN techniques have been developed and applied to the unsteady FIV problem, RANS-based machine learning techniques for unsteady cases are still in development. The overwhelming majority of machine learning augmented RANS investigations use a steady state flow for training and testing. Some techniques within augmented RANS (e.g., iterative methods) are more suited for unsteady flows, but have not been rigorously tested. Therefore, another key issue is the ability of augmented turbulence models to be used for transient cases. Machine learning augmented LES closures are more immediately applicable for unsteady flow simulation due to the nature of LES. However, the suitability of these closure for the FIV problem is yet to be demonstrated.
7.2. Future Work and Perspectives
- With respect to the mathematical modelling of FIV phenomena, the development of a general theory for one or more aspects of FIV phenomena from first principles and the comprehensive analysis following from the application of such a general theory is a worthwhile (albeit extremely difficult) avenue of investigation.
- To allow mathematical models for FIV phenomena to have greater flexibility/generality (and lacking a general theory for FIV at present), research into the application of improved optimization methods for determination of model parameters along with an uncertainty quantification of the prediction provided by such models would be extremely beneficial.
- Work on the development of an improved mathematical representation for the inclusion of galloping in mathematical models for FIV could potentially improve significantly the prediction accuracy of the current generation of models for a bluff body experiencing either pure galloping or a combined FIV that includes galloping.
- More work needs to be done to improve the predictive accuracy of low-fidelity numerical methodologies, such as unsteady RANS modelling for routine application to FIV problems of industrial relevance. Schemes to provide improved closure models for addressing the FIV problem need to be developed. From this perspective, the application of data-driven approaches using ML (e.g., neural nets, gradient boosting machines [270]) or inverse modelling (e.g., Bayesian optimization [271], likelihood-free inference [272]) can be used to design application specific closure models for FIV phenomena.
- More effort needs to be focused on the proper application of hybrid methods to the prediction of FIV phenomena. To this purpose, more research should be conducted on the appropriate selection of the mode of computation (whether RANS modelling or eddy-resolving simulation) that is specifically tailored to address the peculiarities of FIV phenomena (e.g., development of a specific hybrid blending or interpolation function that more intelligently selects whether RANS or eddy-resolving simulation should be used in various regions of the FIV flows).
- Methods of machine learning can be applied potentially to provided improved closure models for numerical simulation of FIV phenomena. However, for this to occur, a considerable effort should be made to obtain high-quality FIV datasets from high-fidelity numerical simulation (DNS and/or LES). The authors strongly encourage the future publication of public-domain FIV datasets that can be used for bench marking machine learning techniques.
- Work should be undertaken to better understand the synergy in mathematical, numerical, and machine learning techniques for the modelling of FIV phenomena (and, more specifically, on how to exploit this synergy to advance future modelling efforts in this field of endeavor). For example, high-fidelity numerical simulation methodologies (DNS and/or LES) provide the data for machine learning algorithms that can potentially lead to improved closure models for low-fidelity RANS models. The predictions obtained from these models provide the information required to obtain deeper insights and a better understanding of FIV phenomenology—this better understanding can potentially lead to the development of improved and more principled and general mathematical models of FIV phenomena.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ALE | Arbitrary Lagrangian–Eulerian |
| AOA | Angle of Attack |
| ARX | Autoregressive with Exogenous Input |
| BPNN | Back Propagation Neural Network |
| BPOD | Balanced POD |
| CAE | Computer-Aided Engineering |
| CFD | Computational Fluids Dynamics |
| CNN | Convolutional Neural Network |
| CRAN | Convolutional Recurrent Autoencoder Network |
| DDES | Delayed Detached-Eddy Simulation |
| DES | Detached-Eddy Simulation |
| DEIM | Discrete Empirical Interpolation Method |
| DMD | Dynamic Mode Decomposition |
| DNN | Deep Neural Network |
| DNS | Direct Numerical Simulation |
| DSD/SST | Deforming-Spatial-Domain/Stabilized Space-Time |
| DTR | Decision-Tree Regression |
| DVM | Discrete Vortex Method |
| EB | embedded boundary |
| ERA | Eigensystem Realization Algorithm |
| EVM | Entropy–Viscosity Method |
| FD | Fictitious Domain |
| FDM | Finite Differencing Method |
| FEM | Finite Element Method |
| FIV | Flow-Induced Vibration |
| FIVEH | Flow-Induced Vibration Energy Harvesting |
| FOM | Full-Order Model |
| FSI | Flow-Structure Interaction |
| FVM | Finite Volume Method |
| GBRT | Gradient Boosting Regression Trees |
| IBM | Immersed Boundary Method |
| LBM | Lattice-Boltzmann Method |
| LES | Large-Eddy Simulation |
| LSA | Linear Stability Analysis |
| LSTM | Long Short-Term Memory |
| ML | Machine Learning |
| MTS | Multiple Time Scales |
| NS | Navier–Stokes |
| NS-PINN | Navier–Stokes equations-based PINN |
| ODE | Ordinary Differential Equation |
| PDE | Partial Differential Equation |
| PG-FEM | Petrov–Galerkin Finite Element Method |
| PINN | Physics-Informed Neural Networks |
| PNS-PINN | Parameterized Navier–Stokes equations-based PINN |
| POD | Proper Orthogonal Decomposition |
| PTC | Passive Turbulence Control |
| QS | Quasi-Steady |
| RANS | Reynolds-averaged Navier–Stokes |
| RBFNN | Radial Basis Function Neural Network |
| RF | Random Forest |
| RNN | Recurrent Neural Network |
| ROM | Reduced-Order Model |
| SA | Spalart–Allmaras |
| SDOF | Single Degree-Of-Freedom |
| SEM | Spectral Elements Method |
| SGS | Sub-grid Scale |
| SM | Smagorinsky |
| SPOD | Spectral POD |
| SST | Shear Stress Transport |
| SST-FEM | Stabilized Space–Time FEM |
| SVD | Singular Value Decomposition |
| TBNN | Tensor Basis Neural Network |
| VIV | Vortex-Induced Vibration |
| WALE | Wall-Adapting Local-Eddy |
| mPOD | Multiscale POD |
| 1DOF | One-Degree-Of-Freedom |
| 2DOF | Two-Degree-Of-Freedom |
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
References
- Nakamura, T.; Kaneko, S.; Inada, F.; Kato, M.; Ishihara, K.; Nishihara, T.; Mureithi, N.W.; Langthjem, M.A. Flow-Induced Vibrations: Classifications and Lessons from Practical Experiences; Butterworth-Heinemann: Portsmouth, NH, USA, 2013. [Google Scholar]
- Parkinson, G. Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aerosp. Sci. 1989, 26, 169–224. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]
- Usman, A.; Rafiq, M.; Saeed, M.; Nauman, A.; Almqvist, A.; Liwicki, M. Machine learning computational fluid dynamics. In Proceedings of the IEEE 2021 Swedish Artificial Intelligence Society Workshop (SAIS), Stockholm, Sweden, 14–15 June 2021; pp. 1–4. [Google Scholar]
- Ma, X.; Zhou, S. A review of flow-induced vibration energy harvesters. Energy Convers. Manag. 2022, 254, 115223. [Google Scholar] [CrossRef]
- Wang, J.; Geng, L.; Ding, L.; Zhu, H.; Yurchenko, D. The state-of-the-art review on energy harvesting from flow-induced vibrations. Appl. Energy 2020, 267, 114902. [Google Scholar] [CrossRef]
- Lv, Y.; Sun, L.; Bernitsas, M.M.; Sun, H. A comprehensive review of nonlinear oscillators in hydrokinetic energy harnessing using flow-induced vibrations. Renew. Sustain. Energy Rev. 2021, 150, 111388. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibration; Van Nostrand Reinhold Company: New York, NY, USA, 1977. [Google Scholar]
- Rostami, A.B.; Armandei, M. Renewable energy harvesting by vortex-induced motions: Review and benchmarking of technologies. Renew. Sustain. Energy Rev. 2017, 70, 193–214. [Google Scholar] [CrossRef]
- Tamura, Y. Mathematical models for understanding phenomena: Vortex-induced vibrations. Jpn. Archit. Rev. 2020, 3, 398–422. [Google Scholar] [CrossRef]
- Su, Y.; Di, J.; Li, S.; Jian, B.; Liu, J. Buffeting response prediction of long-span bridges based on different wind tunnel test techniques. Appl. Sci. 2022, 12, 3171. [Google Scholar] [CrossRef]
- Luongo, A.; Piccardo, G. Linear instability mechanisms for coupled translational galloping. J. Sound Vib. 2005, 288, 1027–1047. [Google Scholar] [CrossRef]
- Gabbai, R.D.; Benaroya, H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 2005, 282, 575–616. [Google Scholar] [CrossRef]
- Païdoussis, M.P.; Price, S.J.; De Langre, E. Fluid-Structure Interactions: Cross-Flow-Induced Instabilities; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Rayleigh, J.W.S.B. The Theory of Sound; Macmillan: New York, NY, USA, 1896; Volume 2. [Google Scholar]
- van der Pol, B.; van der Mark, J. LXXII. The heartbeat considered as a relaxation oscillation, and an electrical model of the heart. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1928, 6, 763–775. [Google Scholar] [CrossRef]
- Goswami, U. Toward an interactive analogy model of reading development: Decoding vowel graphemes in beginning reading. J. Exp. Child Psychol. 1993, 56, 443–475. [Google Scholar] [CrossRef]
- Bishop, R.E.D.; Hassan, A. The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1964, 277, 51–75. [Google Scholar]
- Hartlen, R.T.; Currie, I.G. Lift-oscillator model of vortex-induced vibration. J. Eng. Mech. Div. 1970, 96, 577–591. [Google Scholar] [CrossRef]
- Skop, R.; Griffin, O. A model for the vortex-excited resonant response of bluff cylinders. J. Sound Vib. 1973, 27, 225–233. [Google Scholar] [CrossRef]
- Griffin, O.; Skop, R.; Koopmann, G. The vortex-excited resonant vibrations of circular cylinders. J. Sound Vib. 1973, 31, 235–IN3. [Google Scholar] [CrossRef]
- Landl, R. A mathematical model for vortex-excited vibrations of bluff bodies. J. Sound Vib. 1975, 42, 219–234. [Google Scholar] [CrossRef]
- Skop, R.; Griffin, O. On a theory for the vortex-excited oscillations of flexible cylindrical structures. J. Sound Vib. 1975, 41, 263–274. [Google Scholar] [CrossRef]
- Skop, R.; Balasubramanian, S. A new twist on an old model for vortex-excited vibrations. J. Fluids Struct. 1997, 11, 395–412. [Google Scholar] [CrossRef]
- Skop, R.; Luo, G. An inverse-direct method for predicting the vortex-induced vibrations of cylinders in uniform and nonuniform flows. J. Fluids Struct. 2001, 15, 867–884. [Google Scholar] [CrossRef]
- Facchinetti, M.L.; De Langre, E.; Biolley, F. Coupling of structure and wake oscillators in vortex-induced vibrations. J. Fluids Struct. 2004, 19, 123–140. [Google Scholar] [CrossRef]
- Ogink, R.; Metrikine, A. A wake oscillator with frequency dependent coupling for the modeling of vortex-induced vibration. J. Sound Vib. 2010, 329, 5452–5473. [Google Scholar] [CrossRef]
- Furnes, G.K.; Sørensen, K. Flow induced vibrations modeled by coupled non-linear oscillators. In Proceedings of the Seventeenth International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007; OnePetro: Richardson, TX, USA, 2007. [Google Scholar]
- Ge, F.; Long, X.; Wang, L.; Hong, Y. Flow-induced vibrations of long circular cylinders modeled by coupled nonlinear oscillators. Sci. China Ser. Phys. Mech. Astron. 2009, 52, 1086–1093. [Google Scholar] [CrossRef]
- Srinil, N.; Zanganeh, H. Modelling of coupled cross-flow/in-line vortex-induced vibrations using double Duffing and van der Pol oscillators. Ocean Eng. 2012, 53, 83–97. [Google Scholar] [CrossRef]
- Bai, X.; Qin, W. Using vortex strength wake oscillator in modelling of vortex induced vibrations in two degrees of freedom. Eur. J. Mech. B Fluids 2014, 48, 165–173. [Google Scholar] [CrossRef]
- Postnikov, A.; Pavlovskaia, E.; Wiercigroch, M. 2DOF CFD calibrated wake oscillator model to investigate vortex-induced vibrations. Int. J. Mech. Sci. 2017, 127, 176–190. [Google Scholar] [CrossRef]
- Birkhoff, G. Formation of vortex streets. J. Appl. Phys. 1953, 24, 98–103. [Google Scholar] [CrossRef]
- Kutta, W. Auftriebskräfte in strömenden Flüssigkeiten. Illus. Aeronaut. Mitteilung. 1902, 6, 133–135. [Google Scholar]
- Joukowsky, N. Über die konturen der Tragflächen der Drachenflieger. Z. Flugtech. Mot. 1910, 1, 281–285. [Google Scholar]
- Funakawa, M. Excitation mechanism of elastically supported circular cylinder in the flow. Bull. Jpn. Soc. Mech. Eng. 1970, 36, 303–312. [Google Scholar]
- Tamura, Y. Vortex induced vibration of circular cylinder (Part I Wake oscillator model). Trans. Archit. Inst. Jpn. 1978, 266, 87–95. [Google Scholar] [CrossRef]
- Tamura, Y.; Matsui, G. Wind Engineering, Proceedings of the 5th International Conference on Wind Engineering, Fort Collins, CO, USA, 8–13 July 1979; Cermak, J.E., Ed.; Pergamon Press Ltd.: Amsterdam, The Netherlands, 1979; Volume 266, pp. 1085–1094. [Google Scholar]
- Tamura, Y.; Amano, A. Mathematical model for vortex-induced oscillations of continuous systems with circular cross section. J. Wind. Eng. Ind. Aerodyn. 1983, 14, 431–442. [Google Scholar] [CrossRef]
- Iwan, W.; Blevins, R. A model for vortex induced oscillation of structures. J. Appl. Mech. 1974, 41, 581–586. [Google Scholar] [CrossRef]
- Krenk, S.; Nielsen, S.R. Energy balanced double oscillator model for vortex-induced vibrations. J. Eng. Mech. 1999, 125, 263–271. [Google Scholar] [CrossRef]
- Scanlan, R.H. State-of-the-Art Methods For Calculating Flutter, Vortex-Induced, and Buffeting Response of Bridge Structures; Technical Report No. FHWA/RD-80-050; Federal Highway Administration: Washington, DC, USA, 1981. [Google Scholar]
- Simiu, E.; Scanlan, R. Wind Effects on Structures, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1986. [Google Scholar]
- Ehsan, F.; Scanlan, R.H.; Bosch, H.R. Modeling spanwise correlation effects in the vortex-induced response of flexible bridges. J. Wind. Eng. Ind. Aerodyn. 1990, 36, 1105–1114. [Google Scholar] [CrossRef]
- Billah, K.Y.R. A Study of Vortex-Induced Vibration. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1989. [Google Scholar]
- Goswami, I.; Scanlan, R.H.; Jones, N.P. Vortex-induced vibration of circular cylinders. II: New model. J. Eng. Mech. 1993, 119, 2288–2302. [Google Scholar] [CrossRef]
- Sarpkaya, T. Fluid forces on oscillating cylinders. J. Waterw. Port, Coast. Ocean. Div. 1978, 104, 275–290. [Google Scholar] [CrossRef]
- Staubli, T. Calculation of the vibration of an elastically mounted cylinder using experimental data from forced oscillation. J. Fluids Eng. 1983, 105, 225–229. [Google Scholar] [CrossRef]
- Stäubli, M.; Bircher, J.; Galeazzi, R.; Remund, H.; Studer, H. Serum concentrations of amiodarone during long term therapy. Relation to dose, efficacy and toxicity. Eur. J. Clin. Pharmacol. 1983, 24, 485–494. [Google Scholar] [CrossRef]
- Griffin, O.; Koopmann, G. The vortex-excited lift and reaction forces on resonantly vibrating cylinders. J. Sound Vib. 1977, 54, 435–448. [Google Scholar] [CrossRef]
- Feng, C. The Measurement of Vortex Induced Effect in Flow Past Stationary and Oscillating Circular and D-Section Cylinders. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 1968. [Google Scholar]
- Parkinson, G.; Sullivan, P. Galloping response of towers. J. Wind. Eng. Ind. Aerodyn. 1979, 4, 253–260. [Google Scholar] [CrossRef]
- den Hartog, J. Transmission line vibration due to sleet. Trans. Am. Inst. Electr. Eng. 1932, 51, 1074–1076. [Google Scholar] [CrossRef]
- Meseguer Ruiz, J.; Sanz Andres, A.P.; Alonso Rodrigo, G. Determination of maximum mechanical energy efficiency in energy galloping systems. J. Eng. Mech. 2015, 141, 1–8. [Google Scholar] [CrossRef]
- Alonso, G.; Meseguer, J.; Pérez-Grande, I. Galloping stability of triangular cross-sectional bodies: A systematic approach. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 928–940. [Google Scholar] [CrossRef]
- Simiu, E.; Yeo, D. Wind Effects on Structures: Modern Structural Design for Wind; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Parkinson, G.; Brooks, N. On the aeroelastic instability of bluff cylinders. J. Appl. Mech. 1961, 28, 252–258. [Google Scholar] [CrossRef]
- Parkinson, G.; Smith, J. The square prism as an aeroelastic non-linear oscillator. Q. J. Mech. Appl. Math. 1964, 17, 225–239. [Google Scholar] [CrossRef]
- Luo, S.; Chew, Y.; Ng, Y. Hysteresis phenomenon in the galloping oscillation of a square cylinder. J. Fluids Struct. 2003, 18, 103–118. [Google Scholar] [CrossRef]
- Ng, Y.; Luo, S.; Chew, Y. On using high-order polynomial curve fits in the quasi-steady theory for square-cylinder galloping. J. Fluids Struct. 2005, 20, 141–146. [Google Scholar] [CrossRef]
- Barrero-Gil, A.; Sanz-Andres, A.; Roura, M. Transverse galloping at low Reynolds numbers. J. Fluids Struct. 2009, 25, 1236–1242. [Google Scholar] [CrossRef]
- Joly, A.; Etienne, S.; Pelletier, D. Galloping of square cylinders in cross-flow at low Reynolds numbers. J. Fluids Struct. 2012, 28, 232–243. [Google Scholar] [CrossRef]
- Piccardo, G.; Pagnini, L.C.; Tubino, F. Some research perspectives in galloping phenomena: Critical conditions and post-critical behavior. Contin. Mech. Thermodyn. 2015, 27, 261–285. [Google Scholar] [CrossRef]
- Bearman, P.; Gartshore, I.; Maull, D.; Parkinson, G. Experiments on flow-induced vibration of a square-section cylinder. J. Fluids Struct. 1987, 1, 19–34. [Google Scholar] [CrossRef]
- Norberg, C. Flow around rectangular cylinders: Pressure forces and wake frequencies. J. Wind. Eng. Ind. Aerodyn. 1993, 49, 187–196. [Google Scholar] [CrossRef]
- Desai, Y.; Shah, A.; Popplewell, N. Galloping analysis for two-degree-of-freedom oscillator. J. Eng. Mech. 1990, 116, 2583–2602. [Google Scholar] [CrossRef]
- Jones, K.F. Coupled vertical and horizontal galloping. J. Eng. Mech. 1992, 118, 92–107. [Google Scholar] [CrossRef]
- He, M.; Macdonald, J.H. An analytical solution for the galloping stability of a 3 degree-of-freedom system based on quasi-steady theory. J. Fluids Struct. 2016, 60, 23–36. [Google Scholar] [CrossRef]
- He, M.; Macdonald, J. 3DOF galloping analysis based on quasi-steady theory with reference to the aerodynamic stiffness coupling. In Proceedings of the 7th European and African Conference on Wind Engineering, Liege, Belgium, 4–7 July 2017. [Google Scholar]
- Parkinson, G.; Wawzonek, M. Some considerations of combined effects of galloping and vortex resonance. J. Wind. Eng. Ind. Aerodyn. 1981, 8, 135–143. [Google Scholar] [CrossRef]
- Parkinson, G.; Bouclin, D. Hydroelastic oscillations of square cylinders. In Proceedings of the International Research Seminar on Safety of Structures under Dynamic Loading, Trondheim, Norway, 25–30 June 1977. [Google Scholar]
- Corless, R.M.; Parkinson, G. A model of the combined effects of vortex-induced oscillation and galloping. J. Fluids Struct. 1988, 2, 203–220. [Google Scholar] [CrossRef]
- Han, P.; Hémon, P.; Pan, G.; de Langre, E. Nonlinear modeling of combined galloping and vortex-induced vibration of square sections under flow. Nonlinear Dyn. 2021, 103, 3113–3125. [Google Scholar] [CrossRef]
- Tamura, Y.; Shimada, K. A mathematical model for the transverse oscillations of square cylinders. In Proceedings of the International Conference on Flow Induced Vibrations, Bowness-Windermere, UK, 12–14 May 1987; pp. 12–14. [Google Scholar]
- Mannini, C.; Massai, T.; Marra, A.M.; Bartoli, G. Modelling the interaction of VIV and galloping for rectangular cylinders. In Proceedings of the 14th International Conference on Wind Engineering, Porto Alegre, Brazil, 21–26 June 2015; pp. 1–20. [Google Scholar]
- Mannini, C.; Massai, T.; Marra, A.M. Modeling the interference of vortex-induced vibration and galloping for a slender rectangular prism. J. Sound Vib. 2018, 419, 493–509. [Google Scholar] [CrossRef]
- Mannini, C. Incorporation of turbulence in a nonlinear wake-oscillator model for the prediction of unsteady galloping response. J. Wind. Eng. Ind. Aerodyn. 2020, 200, 104141. [Google Scholar] [CrossRef]
- Chen, C.; Mannini, C.; Bartoli, G.; Thiele, K. Wake oscillator modeling the combined instability of vortex induced vibration and galloping for a 2: 1 rectangular cylinder. J. Fluids Struct. 2022, 110, 103530. [Google Scholar] [CrossRef]
- Funakawa, M. The vibration of a cylinder caused by wake force in a flow. Bull. JSME 1969, 12, 1003–1010. [Google Scholar] [CrossRef][Green Version]
- ANSYS Homepage. Available online: http:www.ansys.com (accessed on 30 August 2022).
- Siemens PLM STAR-CCM+ Homepage. Available online: https://mdx.plm.automation.siemens.com/star-ccm-plus (accessed on 30 August 2022).
- OpenFOAM Project Homepage. Available online: http://www.openfoam.org (accessed on 30 August 2022).
- Selvam, R.P. Computational Fluid Dynamics for Wind Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Zhao, M.; Cheng, L. Vortex-induced vibration of a circular cylinder of finite length. Phys. Fluids 2014, 26, 2548. [Google Scholar] [CrossRef]
- Hou, G.; Wang, J.; Layton, A. Numerical methods for fluid-structure interaction—A review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Singh, S.; Mittal, S. Vortex-induced oscillations at low Reynolds numbers: Hysteresis and vortex-shedding modes. J. Fluids Struct. 2005, 20, 1085–1104. [Google Scholar] [CrossRef]
- Mittal, S. Free vibrations of a cylinder: 3-D computations at Re = 1000. J. Fluids Struct. 2013, 41, 109–118. [Google Scholar]
- Alauzet, F. A changing-topology moving mesh technique for large displacements. Eng. Comput. 2014, 30, 175–200. [Google Scholar] [CrossRef]
- Mittal, S.; Kumar, V. Finite element study of vortex-induced cross-flow and in-line oscillations of a circular cylinder at low Reynolds numbers. Int. J. Numer. Methods Fluids 1999, 31, 1087–1120. [Google Scholar] [CrossRef]
- Longatte, E.; Bendjeddou, Z.; Souli, M. Application of arbitrary Lagrange Euler formulations to flow-induced vibration problems. J. Press. Vessel Technol. 2003, 125, 411–417. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L. Numerical simulation of two-degree-of-freedom vortex-induced vibration of a circular cylinder close to a plane boundary. J. Fluids Struct. 2011, 27, 1097–1110. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L. Numerical simulation of vortex-induced vibration of four circular cylinders in a square configuration. J. Fluids Struct. 2012, 31, 125–140. [Google Scholar] [CrossRef]
- Zhao, M. Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by-side arrangements at a low Reynolds number of 150. Phys. Fluids 2013, 25, 123601. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Zhou, T. Numerical simulation of vortex-induced vibration of a square cylinder at a low Reynolds number. Phys. Fluids 2013, 25, 023603. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; An, H.; Lu, L. Three-dimensional numerical simulation of vortex-induced vibration of an elastically mounted rigid circular cylinder in steady current. J. Fluids Struct. 2014, 50, 292–311. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; An, H.; Tong, F. Flow and flow-induced vibration of a square array of cylinders in steady currents. Fluid Dyn. Res. 2015, 47, 045505. [Google Scholar] [CrossRef]
- Griffith, B.E.; Patankar, N.A. Immersed methods for fluid-structure interaction. Annu. Rev. Fluid Mech. 2020, 52, 421. [Google Scholar] [CrossRef]
- Chen, W.; Ji, C.; Xu, W.; Liu, S.; Campbell, J. Response and wake patterns of two side-by-side elastically supported circular cylinders in uniform laminar cross-flow. J. Fluids Struct. 2015, 55, 218–236. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow Patterns Around Heart Valves: A Digital Computer Method for Solving the Equations of Motion; Yeshiva University: Manhattan, NY, USA, 1972. [Google Scholar]
- Ji, C.; Xiao, Z.; Wang, Y.; Wang, H. Numerical investigation on vortex-induced vibration of an elastically mounted circular cylinder at low Reynolds number using the fictitious domain method. Int. J. Comput. Fluid Dyn. 2011, 25, 207–221. [Google Scholar] [CrossRef]
- Löhner, R.; Baum, J.D.; Mestreau, E.; Sharov, D.; Charman, C.; Pelessone, D. Adaptive embedded unstructured grid methods. Int. J. Numer. Methods Eng. 2004, 60, 641–660. [Google Scholar] [CrossRef]
- Gonzalez Cornejo, F.A.; Cruchaga, M.A.; Celentano, D.J. Modelling low Reynolds number vortex-induced vibration problems with a fixed mesh fluid-solid interaction formulation. Phys. Fluids 2017, 29, 113601. [Google Scholar] [CrossRef]
- Wall, W.A.; Gerstenberger, A.; Gamnitzer, P.; Förster, C.; Ramm, E. Large deformation fluid-structure interaction–Advances in ALE methods and new fixed grid approaches. In Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 195–232. [Google Scholar]
- Al-Jamal, H.; Dalton, C. Vortex induced vibrations using large-eddy simulation at a moderate Reynolds number. J. Fluids Struct. 2004, 19, 73–92. [Google Scholar] [CrossRef]
- Carmo, B.S.; Sherwin, S.J.; Bearman, P.W.; Willden, R. Flow-induced vibration of a circular cylinder subjected to wake interference at low Reynolds number. J. Fluids Struct. 2011, 27, 503–522. [Google Scholar] [CrossRef]
- Williamson, C.H.; Roshko, A. Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Barkley, D.; Henderson, R.D. Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 1996, 322, 215–241. [Google Scholar] [CrossRef]
- Jiang, H.; Cheng, L.; An, H. Three-dimensional wake transition of a square cylinder. J. Fluid Mech. 2018, 842, 102–127. [Google Scholar] [CrossRef]
- Ryan, K.; Thompson, M.C.; Hourigan, K. Three-dimensional transition in the wake of bluff elongated cylinders. J. Fluid Mech. 2005, 538, 1–29. [Google Scholar] [CrossRef]
- Leontini, J.S.; Jacono, D.L.; Thompson, M.C. Stability analysis of the elliptic cylinder wake. J. Fluid Mech. 2015, 763, 302–321. [Google Scholar] [CrossRef]
- Leontini, J.S.; Thompson, M.C.; Hourigan, K. Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 2007, 577, 79–104. [Google Scholar] [CrossRef]
- Prasanth, T.; Behara, S.; Singh, S.; Kumar, R.; Mittal, S. Effect of blockage on vortex-induced vibrations at low Reynolds numbers. J. Fluids Struct. 2006, 22, 865–876. [Google Scholar] [CrossRef]
- Prasanth, T.; Premchandran, V.; Mittal, S. Hysteresis in vortex-induced vibrations: Critical blockage and effect of m. J. Fluid Mech. 2011, 671, 207–225. [Google Scholar] [CrossRef]
- Prasanth, T.; Mittal, S. Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 2008, 594, 463–491. [Google Scholar] [CrossRef]
- Mittal, S. A new regime of multiple states in free vibration of a cylinder at low Re. J. Fluids Struct. 2017, 68, 310–321. [Google Scholar]
- Leontini, J.S.; Thompson, M.C.; Hourigan, K. The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 2006, 22, 857–864. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Zhang, W. Nonlinear characteristics of vortex-induced vibration at low Reynolds number. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2753–2771. [Google Scholar] [CrossRef]
- Étienne, S.; Pelletier, D. The low Reynolds number limit of vortex-induced vibrations. J. Fluids Struct. 2012, 31, 18–29. [Google Scholar] [CrossRef]
- Bourguet, R.; Jacono, D.L. Flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 2014, 740, 342–380. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Lu, L. Vortex induced vibrations of a rotating circular cylinder at low Reynolds number. Phys. Fluids 2014, 26, 073602. [Google Scholar] [CrossRef]
- Garg, H.; Soti, A.K.; Bhardwaj, R. Vortex-induced vibration of a cooled circular cylinder. Phys. Fluids 2019, 31, 083608. [Google Scholar] [CrossRef]
- Shen, L.; Chen, J. Irregular vortex-induced vibrations of a two-dimensional circular cylinder at a low Reynolds number. Eur. J. Mech. B Fluids 2022, 94, 128–147. [Google Scholar] [CrossRef]
- Dorogi, D.; Baranyi, L. Identification of upper branch for vortex-induced vibration of a circular cylinder at Re = 300. J. Fluids Struct. 2020, 98, 103135. [Google Scholar] [CrossRef]
- Yogeswaran, V.; Sen, S.; Mittal, S. Free vibrations of an elliptic cylinder at low Reynolds numbers. J. Fluids Struct. 2014, 51, 55–67. [Google Scholar]
- Chen, G.; Liang, X.F.; Li, X.B.; Zhou, D.; Lien, F.S. Numerical investigation of vortex induced vibration effects on the heat transfer for various aspect ratios ellipse cylinder. Int. J. Therm. Sci. 2021, 170, 107138. [Google Scholar] [CrossRef]
- Leontini, J.S.; Griffith, M.; Jacono, D.L.; Sheridan, J. The flow-induced vibration of an elliptical cross-section at varying angles of attack. J. Fluids Struct. 2018, 78, 356–373. [Google Scholar] [CrossRef]
- Sen, S.; Mittal, S. Free vibration of a square cylinder at low Reynolds numbers. J. Fluids Struct. 2011, 27, 875–884. [Google Scholar] [CrossRef]
- He, T.; Zhou, D.; Bao, Y. Combined interface boundary condition method for fluid–rigid body interaction. Comput. Methods Appl. Mech. Eng. 2012, 223, 81–102. [Google Scholar] [CrossRef]
- Sen, S.; Mittal, S. Effect of mass ratio on free vibrations of a square cylinder at low Reynolds numbers. J. Fluids Struct. 2015, 54, 661–678. [Google Scholar] [CrossRef]
- Sourav, K.; Sen, S. Transition of VIV-only motion of a square cylinder to combined VIV and galloping at low Reynolds numbers. Ocean Eng. 2019, 187, 106208. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Hajj, M.R.; Nayfeh, A.H. Power harvesting from transverse galloping of square cylinder. Nonlinear Dyn. 2012, 70, 1355–1363. [Google Scholar] [CrossRef]
- Su, Z.; Liu, Y.; Zhang, H.; Zhang, D. Numerical simulation of vortex-induced vibration of a square cylinder. J. Mech. Sci. Technol. 2007, 21, 1415–1424. [Google Scholar] [CrossRef]
- Sun, W.; Zhou, D.; Tu, J.; Han, Z. Vortex-induced vibrations of a square cylinder under linear shear flow. Fluid Dyn. Res. 2017, 49, 025502. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, D.; Yang, W.; Yu, G. Numerical investigation on flow-induced vibration of a triangular cylinder at a low Reynolds number. Fluid Dyn. Res. 2014, 47, 015501. [Google Scholar] [CrossRef]
- Liu, M.; Jin, R.; Tang, G.; Li, C. Numerical investigation of vortex-induced vibration for two tandem circular cylinders with different diameters. Proc. Inst. Mech. Eng. Part M J. Eng. Mar.Environ. 2020, 234, 676–685. [Google Scholar] [CrossRef]
- Ming-Ming, L.; Hao-Cheng, W.; Fei-Fei, S.; Xin, J.; Tang, G.Q.; Fan, Y. Numerical investigation on vortex-induced vibration of an elastically mounted circular cylinder with multiple control rods at low Reynolds number. Appl. Ocean. Res. 2022, 118, 102987. [Google Scholar]
- Sahu, T.R.; Furquan, M.; Jaiswal, Y.; Mittal, S. Flow-induced vibration of a circular cylinder with rigid splitter plate. J. Fluids Struct. 2019, 89, 244–256. [Google Scholar] [CrossRef]
- Zhu, H.; Li, G.; Wang, J. Flow-induced vibration of a circular cylinder with splitter plates placed upstream and downstream individually and simultaneously. Appl. Ocean. Res. 2020, 97, 102084. [Google Scholar] [CrossRef]
- Wang, H.; Zhai, Q.; Zhang, J. Numerical study of flow-induced vibration of a flexible plate behind a circular cylinder. Ocean Eng. 2018, 163, 419–430. [Google Scholar] [CrossRef]
- Borazjani, I.; Sotiropoulos, F. Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity–wake interference region. J. Fluid Mech. 2009, 621, 321–364. [Google Scholar] [CrossRef]
- Griffith, M.D.; Jacono, D.L.; Sheridan, J.; Leontini, J.S. Flow-induced vibration of two cylinders in tandem and staggered arrangements. J. Fluid Mech. 2017, 833, 98–130. [Google Scholar] [CrossRef]
- Han, Z.; Zhou, D.; He, T.; Tu, J.; Li, C.; Kwok, K.C.; Fang, C. Flow-induced vibrations of four circular cylinders with square arrangement at low Reynolds numbers. Ocean Eng. 2015, 96, 21–33. [Google Scholar] [CrossRef]
- Newman, D.J.; Karniadakis, G.E. A direct numerical simulation study of flow past a freely vibrating cable. J. Fluid Mech. 1997, 344, 95–136. [Google Scholar] [CrossRef]
- Evangelinos, C.; Lucor, D.; Karniadakis, G.E. DNS-derived force distribution on flexible cylinders subject to vortex-induced vibration. J. Fluids Struct. 2000, 14, 429–440. [Google Scholar] [CrossRef]
- Lucor, D.; Foo, J.; Karniadakis, G. Correlation length and force phasing of a rigid cylinder subject to VIV. In Proceedings of the IUTAM Symposium on Integrated Modeling of Fully Coupled Fluid Structure Interactions Using Analysis, Computations and Experiments, New Brunswick, NJ, USA, 2–6 June 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 187–199. [Google Scholar]
- Lucor, D.; Karniadakis, G.E. Effects of oblique inflow in vortex-induced vibrations. Flow Turbul. Combust. 2003, 71, 375–389. [Google Scholar] [CrossRef]
- Lucor, D.; Foo, J.; Karniadakis, G. Vortex mode selection of a rigid cylinder subject to VIV at low mass-damping. J. Fluids Struct. 2005, 20, 483–503. [Google Scholar] [CrossRef]
- Gsell, S.; Bourguet, R.; Braza, M. Two-degree-of-freedom vortex-induced vibrations of a circular cylinder at Re = 3900. J. Fluids Struct. 2016, 67, 156–172. [Google Scholar] [CrossRef]
- Chen, W.; Ji, C.; Xu, D.; Zhang, Z. Three-dimensional direct numerical simulations of vortex-induced vibrations of a circular cylinder in proximity to a stationary wall. Phys. Rev. Fluids 2022, 7, 044607. [Google Scholar] [CrossRef]
- Zhang, J.; Dalton, C. Interactions of vortex-induced vibrations of a circular cylinder and a steady approach flow at a Reynolds number of 13,000. Comput. Fluids 1996, 25, 283–294. [Google Scholar] [CrossRef]
- Dalheim, J. Numerical prediction of VIV on deepwater risers subjected to shear currents and waves. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–7 November 1999. [Google Scholar]
- Herfjord, K.; Drange, S.O.; Kvamsdal, T. Assessment of vortex-induced vibrations on deepwater risers by considering fluid-structure interaction. J. Offshore Mech. Arct. Eng. 1999, 121, 207–212. [Google Scholar] [CrossRef]
- Tutar, M.; Holdo, A.E. Large eddy simulation of a smooth circular cylinder oscillating normal to a uniform flow. J. Fluids Eng. 2000, 122, 694–702. [Google Scholar] [CrossRef]
- Pastrana, D.; Cajas, J.; Lehmkuhl, O.; Rodríguez, I.; Houzeaux, G. Large-eddy simulations of the vortex-induced vibration of a low mass ratio two-degree-of-freedom circular cylinder at subcritical Reynolds numbers. Comput. Fluids 2018, 173, 118–132. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, D.; Triantafyllou, M.S.; Karniadakis, G.E. A large-eddy simulation study on the similarity between free vibrations of a flexible cylinder and forced vibrations of a rigid cylinder. J. Fluids Struct. 2021, 101, 103223. [Google Scholar] [CrossRef]
- Janocha, M.J.; Ong, M.C.; Yin, G. Large eddy simulations and modal decomposition analysis of flow past a cylinder subject to flow-induced vibration. Phys. Fluids 2022, 34, 045119. [Google Scholar] [CrossRef]
- Daniels, S.J.; Castro, I.P.; Xie, Z.T. Numerical analysis of freestream turbulence effects on the vortex-induced vibrations of a rectangular cylinder. J. Wind. Eng. Ind. Aerodyn. 2016, 153, 13–25. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C. Dynamics of a hydroelastic cylinder with very low mass and damping. J. Fluids Struct. 1996, 10, 455–472. [Google Scholar] [CrossRef]
- Guilmineau, E.; Queutey, P. Numerical simulation of vortex-induced vibration of a circular cylinder with low mass-damping in a turbulent flow. J. Fluids Struct. 2004, 19, 449–466. [Google Scholar] [CrossRef]
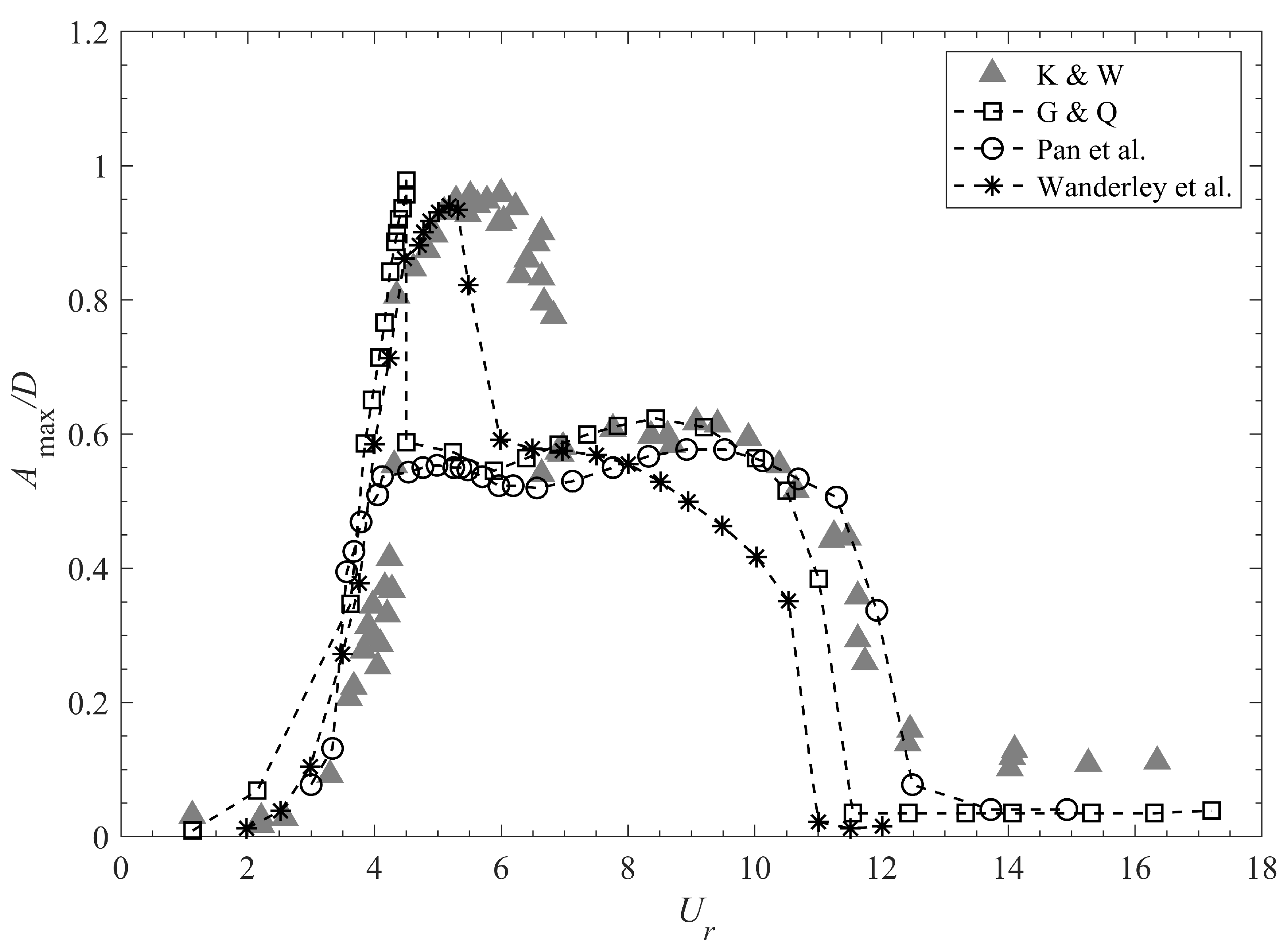
- Pan, Z.; Cui, W.; Miao, Q. Numerical simulation of vortex-induced vibration of a circular cylinder at low mass-damping using RANS code. J. Fluids Struct. 2007, 23, 23–37. [Google Scholar] [CrossRef]
- Wanderley, J.B.; Souza, G.H.; Sphaier, S.H.; Levi, C. Vortex-induced vibration of an elastically mounted circular cylinder using an upwind TVD two-dimensional numerical scheme. Ocean Eng. 2008, 35, 1533–1544. [Google Scholar] [CrossRef]
- Wanderley, J.B.; Soares, L.F.N. Vortex-induced vibration on a two-dimensional circular cylinder with low Reynolds number and low mass-damping parameter. Ocean Eng. 2015, 97, 156–164. [Google Scholar] [CrossRef]
- Gu, J.; Fernandes, A.C.; Han, X.; Kuang, X.; Chen, W. Numerical investigation of Reynolds number effects on vortex-induced vibrations at low and moderate Re regimes. Ocean Eng. 2022, 245, 110535. [Google Scholar] [CrossRef]
- Kang, Z.; Zhang, C.; Chang, R.; Ma, G. A numerical investigation of the effects of Reynolds number on vortex-induced vibration of the cylinders with different mass ratios and frequency ratios. Int. J. Nav. Archit. Ocean. Eng. 2019, 11, 835–850. [Google Scholar] [CrossRef]
- Khan, N.B.; Ibrahim, Z.; Nguyen, L.T.T.; Javed, M.F.; Jameel, M. Numerical investigation of the vortex-induced vibration of an elastically mounted circular cylinder at high Reynolds number (Re = 104) and low mass ratio using the RANS code. PLoS ONE 2017, 12, e0185832. [Google Scholar] [CrossRef] [PubMed]
- Anwar, M.U.; Lashin, M.; Khan, N.B.; Munir, A.; Jameel, M.; Muhammad, R.; Guedri, K.; Galal, A.M. Effect of variation in the mass ratio on vortex-induced vibration of a circular cylinder in crossflow directio n at Reynold Number = 104: A numerical study using RANS model. J. Mar. Sci. Eng. 2022, 10, 1126. [Google Scholar] [CrossRef]
- Martins, F.; Avila, J. Effects of the Reynolds number and structural damping on vortex-induced vibrations of elastically-mounted rigid cylinder. Int. J. Mech. Sci. 2019, 156, 235–249. [Google Scholar] [CrossRef]
- Cui, Z.; Zhao, M.; Teng, B.; Cheng, L. Two-dimensional numerical study of vortex-induced vibration and galloping of square and rectangular cylinders in steady flow. Ocean Eng. 2015, 106, 189–206. [Google Scholar] [CrossRef]
- Han, P.; Huang, Q.; Pan, G.; Wang, W.; Zhang, T.; Qin, D. Energy harvesting from flow-induced vibration of a low-mass square cylinder with different incidence angles. AIP Adv. 2021, 11, 025126. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, L.; Wu, C.; Mao, X.; Jiang, D. Flow induced motion and energy harvesting of bluff bodies with different cross sections. Energy Convers. Manag. 2015, 91, 416–426. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Tian, W.; Li, B. Numerical investigation on VIV energy harvesting of bluff bodies with different cross sections in tandem arrangement. Energy 2017, 133, 723–736. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Li, B.; Gu, M. Hydrokinetic energy harnessing by spring-mounted oscillators in FIM with different cross sections: From triangle to circle. Energy 2019, 189, 116249. [Google Scholar] [CrossRef]
- Wang, W.; Song, B.; Mao, Z.; Tian, W.; Zhang, T.; Han, P. Numerical investigation on vortex-induced vibration of bluff bodies with different rear edges. Ocean Eng. 2020, 197, 106871. [Google Scholar] [CrossRef]
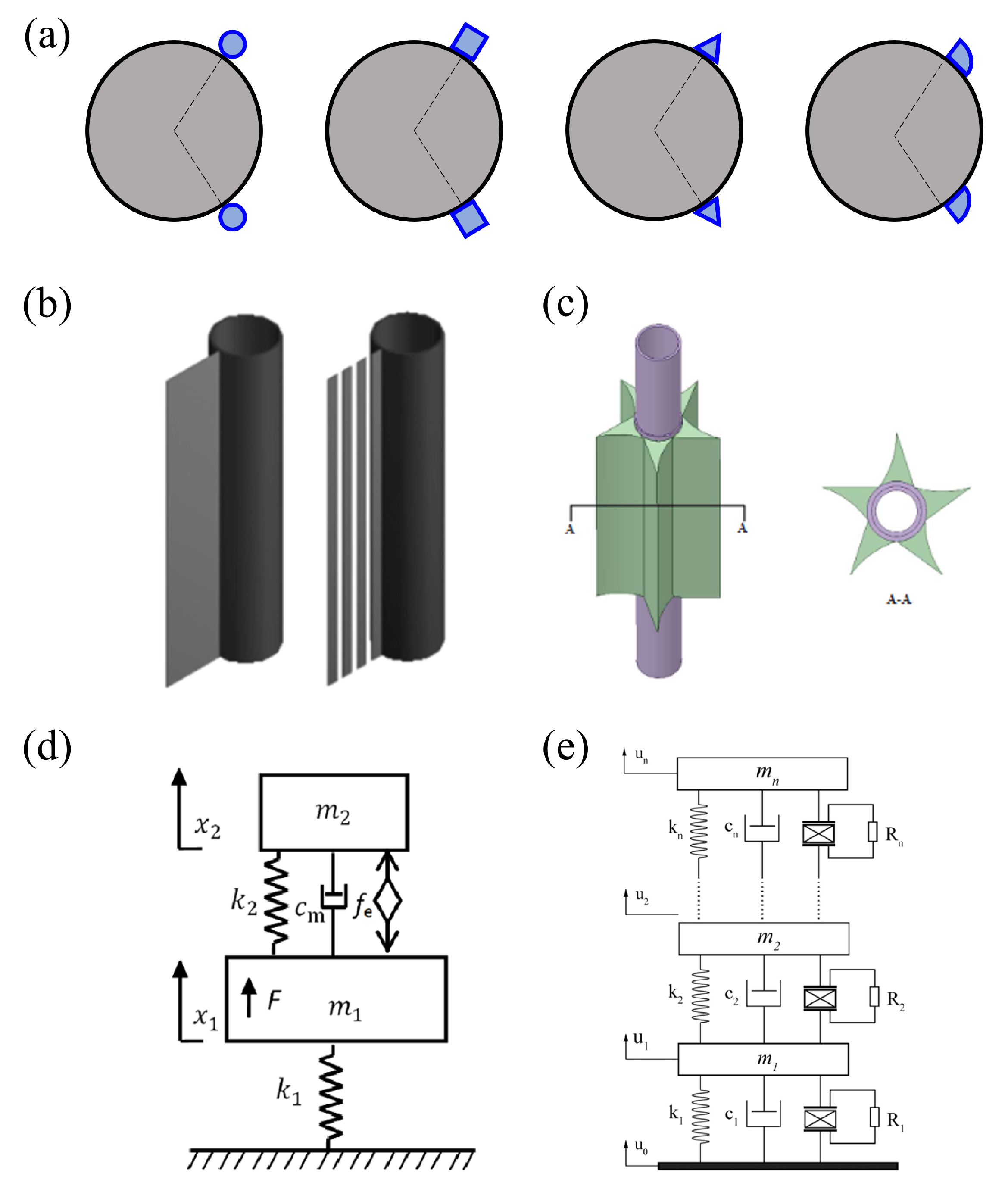
- Zhu, H.; Yao, J. Numerical evaluation of passive control of VIV by small control rods. Appl. Ocean. Res. 2015, 51, 93–116. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, L.; Bernitsas, M.M.; Chang, C.C. Numerical simulation and experimental validation for energy harvesting of single-cylinder VIVACE converter with passive turbulence control. Renew. Energy 2016, 85, 1246–1259. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, W.; Su, Z.; Zhang, G.; Li, P.; Yurchenko, D. Enhancing vortex-induced vibrations of a cylinder with rod attachments for hydrokinetic power generation. Mech. Syst. Signal Process. 2020, 145, 106912. [Google Scholar] [CrossRef]
- Rahmanian, M.; Cheng, L.; Zhao, M.; Zhou, T. Vortex induced vibration and vortex shedding characteristics of two side-by-side circular cylinders of different diameters in close proximity in steady flow. J. Fluids Struct. 2014, 48, 260–279. [Google Scholar] [CrossRef]
- Zhao, M.; Murphy, J.M.; Kwok, K. Numerical simulation of vortex-induced vibration of two rigidly connected cylinders in side-by-side and tandem arrangements using RANS model. J. Fluids Eng. 2016, 138, 1257. [Google Scholar] [CrossRef]
- Cui, Z.; Zhao, M.; Teng, B. Vortex-induced vibration of two elastically coupled cylinders in side-by-side arrangement. J. Fluids Struct. 2014, 44, 270–291. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Nguyen, H.H. Detached eddy simulations of flow induced vibrations of circular cylinders at high Reynolds numbers. J. Fluids Struct. 2016, 63, 103–119. [Google Scholar] [CrossRef]
- Joshi, V.; Jaiman, R.K. A variationally bounded scheme for delayed detached eddy simulation: Application to vortex-induced vibration of offshore riser. Comput. Fluids 2017, 157, 84–111. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, W.; Wan, D. Numerical investigations of the flow-induced vibration of a three-dimensional circular cylinder with various symmetric strips attached. Phys. Fluids 2022, 34, 065102. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, W.; Wan, D. Numerical investigations of three-dimensional flows around a cylinder attaching with symmetric strips. Phys. Fluids 2021, 33, 075101. [Google Scholar] [CrossRef]
- Hollenbach, R.; Kielb, R.; Hall, K. Extending a van der Pol-based reduced-order model for fluid-structure interaction applied to non-synchronous vibrations in turbomachinery. J. Turbomach. 2021, 144, 031006. [Google Scholar] [CrossRef]
- Sanders, A.J. Non-synchronous vibration (NSV) due to a flow-induced aerodynamic instability in a composite fan stator. Turbo Expo Power Land Sea Air 2004, 6, 507–516. [Google Scholar] [CrossRef]
- Zhang, M.; Fu, S.; Ren, H.; Ma, L.; Xu, Y. A hybrid FEM-DNN-based vortex-induced vibration prediction method for flexible pipes under oscillatory flow in the time domain. Ocean Eng. 2022, 246, 110488. [Google Scholar] [CrossRef]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2019, 861, 119–137. [Google Scholar] [CrossRef]
- Dowell, E.; Curtiss, H.; Scanlan, R.; Sisto, F. A Modern Course in Aeroelasticity; Springer: Berlin/Heidelberg, Germany, 2021; Volume 264. [Google Scholar]
- Lumley, J. Coherent Structures in Turbulence. In Transition and Turbulence; Meyer, R.E., Ed.; Academic Press: London, UK, 1981; pp. 215–242. [Google Scholar] [CrossRef]
- Star, S.; Stabile, G.; Rozza, G.; Degroote, J. A POD-Galerkin reduced order model of a turbulent convective buoyant flow of sodium over a backward-facing step. Appl. Math. Model. 2021, 89, 486–503. [Google Scholar] [CrossRef]
- Lorenzi, S.; Cammi, A.; Luzzi, L.; Rozza, G. POD-Galerkin method for finite volume approximation of Navier–Stokes and RANS equations. Comput. Methods Appl. Mech. Eng. 2016, 311, 151–179. [Google Scholar] [CrossRef]
- Sieber, M.; Paschereit, C.O.; Oberleithner, K. Spectral proper orthogonal decomposition. J. Fluid Mech. 2016, 792, 798–828. [Google Scholar] [CrossRef]
- Rowley, C.W. Model reduction for fluids, using balanced proper orthogonal decomposition. Int. J. Bifurc. Chaos 2005, 15, 997–1013. [Google Scholar] [CrossRef]
- Schubert, Y.; Sieber, M.; Oberleithner, K.; Martinuzzi, R. Towards robust data-driven reduced-order modelling for turbulent flows: Application to vortex-induced vibrations. Theor. Comput. Fluid Dyn. 2022, 36, 1–27. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W.; Liu, Y.; Li, X. The lowest Reynolds number of vortex-induced vibrations. Phys. Fluids 2017, 29, 041701. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ye, Z.; Jiang, Y. Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers. J. Fluid Mech. 2015, 783, 72–102. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Gao, C. Proximity-interference wake-induced vibration at subcritical Re: Mechanism analysis using a linear dynamic model. Phys. Fluids 2018, 30, 033606. [Google Scholar] [CrossRef]
- Li, X.; Lyu, Z.; Kou, J.; Zhang, W. Mode competition in galloping of a square cylinder at low Reynolds number. J. Fluid Mech. 2019, 867, 516–555. [Google Scholar] [CrossRef]
- Luo, F.; Gao, C.; Zhang, W. The key to suppress vortex-induced vibration: Stability of the structural mode. J. Fluids Struct. 2022, 113, 103692. [Google Scholar] [CrossRef]
- Navrose; Mittal, S. Lock-in in vortex-induced vibration. J. Fluid Mech. 2016, 794, 565–594. [Google Scholar] [CrossRef]
- Juang, J.N.; Pappa, R.S. An Eigensystem Realization Algorithm (ERA) for Modal Parameter Identification, NASA. In Proceedings of the JPL Workshop on Identification and Control of Flexible Space Structures, Pasadena, CA, USA, 4–6 July 1984. [Google Scholar]
- Yao, W.; Jaiman, R.K. Model reduction and mechanism for the vortex-induced vibrations of bluff bodies. J. Fluid Mech. 2017, 827, 357–393. [Google Scholar] [CrossRef]
- Yao, W.; Jaiman, R. Feedback control of unstable flow and vortex-induced vibration using the eigensystem realization algorithm. J. Fluid Mech. 2017, 827, 394–414. [Google Scholar] [CrossRef]
- Reddy, S.B.; Magee, A.R.; Jaiman, R.K. A data-driven approach for the stability analysis of vortex-induced vibration. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51210, p. V002T08A004. [Google Scholar]
- Bukka, S.; Magee, A.; Jaiman, R. Stability analysis of passive suppression for vortex-induced vibration. J. Fluid Mech. 2020, 886, A12. [Google Scholar] [CrossRef]
- Chizfahm, A.; Jaiman, R. Data-driven stability analysis and near-wake jet control for the vortex-induced vibration of a sphere. Phys. Fluids 2021, 33, 044104. [Google Scholar] [CrossRef]
- Cheng, Z.; Lien, F.S.; Yee, E.; Zhang, J.H. Mode transformation and interaction in vortex-induced vibration of laminar flow past a circular cylinder. Phys. Fluids 2022, 34, 033607. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. A hybrid reduced-order framework for complex aeroelastic simulations. Aerosp. Sci. Technol. 2019, 84, 880–894. [Google Scholar] [CrossRef]
- Rowley, C.W.; Dawson, S.T. Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef]
- Miyanawala, T.P.; Jaiman, R.K. Decomposition of wake dynamics in fluid—Structure interaction via low-dimensional models. J. Fluid Mech. 2019, 867, 723–764. [Google Scholar] [CrossRef]
- Murata, T.; Fukami, K.; Fukagata, K. Nonlinear mode decomposition with convolutional neural networks for fluid dynamics. J. Fluid Mech. 2020, 882, A13. [Google Scholar] [CrossRef]
- Miyanawala, T.; Jaiman, R.K. A hybrid data-driven deep learning technique for fluid-structure interaction. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, Scotland, 9–14 June 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 58776, p. V002T08A004. [Google Scholar]
- Reddy, S.B.; Magee, A.R.; Jaiman, R.K.; Liu, J.; Xu, W.; Choudhary, A.; Hussain, A. Reduced order model for unsteady fluid flows via recurrent neural networks. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, Scotland, 9–14 June 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 58776, p. V002T08A007. [Google Scholar]
- Bukka, S.R.; Gupta, R.; Magee, A.R.; Jaiman, R.K. Assessment of unsteady flow predictions using hybrid deep learning based reduced-order models. Phys. Fluids 2021, 33, 013601. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. Layered reduced-order models for nonlinear aerodynamics and aeroelasticity. J. Fluids Struct. 2017, 68, 174–193. [Google Scholar] [CrossRef]
- Chizfahm, A.; Jaiman, R. Deep Learning for Stability Analysis of a Freely Vibrating Sphere at Moderate Reynolds Number. arXiv 2021, arXiv:abs/2112.09858. [Google Scholar]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine learning accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef]
- Maulik, R.; San, O.; Rasheed, A.; Vedula, P. Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 2019, 858, 122–144. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Wu, J.L.; Xiao, H.; Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys. Rev. Fluids 2018, 7, 1–28. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, W.; Wang, Y. Explore missing flow dynamics by physics-informed deep learning: The parameterized governing systems. Phys. Fluids 2021, 33, 095116. [Google Scholar] [CrossRef]
- Bai, X.D.; Zhang, W. Machine learning for vortex induced vibration in turbulent flow. Comput. Fluids 2022, 235, 105266. [Google Scholar] [CrossRef]
- Cheng, C.; Meng, H.; Li, Y.Z.; Zhang, G.T. Deep learning based on PINN for solving 2 DOF vortex induced vibration of cylinder. Ocean Eng. 2021, 240, 109932. [Google Scholar] [CrossRef]
- Nikoo, H.M.; Bi, K.; Hao, H. Three-dimensional vortex-induced vibration of a circular cylinder at subcritical Reynolds numbers with low-Re correction. Mar. Struct. 2019, 66, 288–306. [Google Scholar] [CrossRef]
- Mosaferi, A.A.; Esmaeili, M.; Rabiee, A.H. Effect of aligned magnetic field on the 2DOF VIV suppression and convective heat transfer characteristics of a circular cylinder. Int. Commun. Heat Mass Transf. 2022, 130, 105807. [Google Scholar] [CrossRef]
- Ma, C.; Wang, J.; Li, Q.; Qin, H.; Liao, H. Vortex-induced vibration performance and suppression mechanism for a long suspension bridge with wide twin-box girder. J. Struct. Eng. 2018, 144, 04018202. [Google Scholar] [CrossRef]
- Sui, J.; Wang, J.; Liang, S.; Tian, Q. VIV suppression for a large mass-damping cylinder attached with helical strakes. J. Fluids Struct. 2016, 62, 125–146. [Google Scholar] [CrossRef]
- Wang, J.; Yurchenko, D.; Hu, G.; Zhao, L.; Tang, L.; Yang, Y. Perspectives in flow-induced vibration energy harvesting. Appl. Phys. Lett. 2021, 119, 100502. [Google Scholar] [CrossRef]
- Andrianne, T.; Aryoputro, R.P.; Laurent, P.; Colson, G.; Amandolese, X.; Hémon, P. Energy harvesting from different aeroelastic instabilities of a square cylinder. J. Wind. Eng. Ind. Aerodyn. 2018, 172, 164–169. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, M. Effects of side ratio on energy harvesting from transverse galloping of a rectangular cylinder. Energy 2021, 226, 120420. [Google Scholar] [CrossRef]
- Javed, U.; Abdelkefi, A.; Akhtar, I. An improved stability characterization for aeroelastic energy harvesting applications. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Sirohi, J.; Mahadik, R. Harvesting wind energy using a galloping piezoelectric beam. J. Vib. Acoust. 2012, 134, 011009. [Google Scholar] [CrossRef]
- Quadrante, L.A.R.; Nishi, Y. Amplification/suppression of flow-induced motions of an elastically mounted circular cylinder by attaching tripping wires. J. Fluids Struct. 2014, 48, 93–102. [Google Scholar] [CrossRef]
- Song, J.; Hu, G.; Tse, K.; Li, S.; Kwok, K. Performance of a circular cylinder piezoelectric wind energy harvester fitted with a splitter plate. Appl. Phys. Lett. 2017, 111, 223903. [Google Scholar] [CrossRef]
- Hu, G.; Tse, K.T.; Wei, M.; Naseer, R.; Abdelkefi, A.; Kwok, K.C. Experimental investigation on the efficiency of circular cylinder-based wind energy harvester with different rod-shaped attachments. Appl. Energy 2018, 226, 682–689. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, Y.; Zhou, T. CFD analysis of energy harvesting from flow induced vibration of a circular cylinder with an attached free-to-rotate pentagram impeller. Appl. Energy 2018, 212, 304–321. [Google Scholar] [CrossRef]
- Ramlan, R.; Brennan, M.; Mace, B.; Kovacic, I. Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dyn. 2010, 59, 545–558. [Google Scholar] [CrossRef]
- Zhang, B.; Li, B.; Fu, S.; Mao, Z.; Ding, W. Vortex-induced vibration (VIV) hydrokinetic energy harvesting based on nonlinear damping. Renew. Energy 2022, 195, 1050–1063. [Google Scholar] [CrossRef]
- Tang, X.; Zuo, L. Enhanced vibration energy harvesting using dual-mass systems. J. Sound Vib. 2011, 330, 5199–5209. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, X.; John, S. A multi-degree of freedom piezoelectric vibration energy harvester with piezoelectric elements inserted between two nearby oscillators. Mech. Syst. Signal Process. 2016, 68, 138–154. [Google Scholar] [CrossRef]
- Wu, Y.; Qiu, J.; Zhou, S.; Ji, H.; Chen, Y.; Li, S. A piezoelectric spring pendulum oscillator used for multi-directional and ultra-low frequency vibration energy harvesting. Appl. Energy 2018, 231, 600–614. [Google Scholar] [CrossRef]
- Yang, B.; Lee, C.; Kee, W.L.; Lim, S.P. Hybrid energy harvester based on piezoelectric and electromagnetic mechanisms. J. Micro Nanolithogr. Mems Moems 2010, 9, 023002. [Google Scholar] [CrossRef]
- Assi, G.R.; Bearman, P.W. Transverse galloping of circular cylinders fitted with solid and slotted splitter plates. J. Fluids Struct. 2015, 54, 263–280. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Issues in mathematical modeling of piezoelectric energy harvesters. Smart Mater. Struct. 2008, 17, 065016. [Google Scholar] [CrossRef]
- Dai, H.; Abdelkefi, A.; Wang, L. Theoretical modeling and nonlinear analysis of piezoelectric energy harvesting from vortex-induced vibrations. J. Intell. Mater. Syst. Struct. 2014, 25, 1861–1874. [Google Scholar] [CrossRef]
- Hou, C.; Shan, X.; Zhang, L.; Song, R.; Yang, Z. Design and modeling of a magnetic-coupling monostable piezoelectric energy harvester under vortex-induced vibration. IEEE Access 2020, 8, 108913–108927. [Google Scholar] [CrossRef]
- Wang, J.; Tang, L.; Zhao, L.; Hu, G.; Song, R.; Xu, K. Equivalent circuit representation of a vortex-induced vibration-based energy harvester using a semi-empirical lumped parameter approach. Int. J. Energy Res. 2020, 44, 4516–4528. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, L.; Tang, L. Comparative study of tip cross-sections for efficient galloping energy harvesting. Appl. Phys. Lett. 2013, 102, 064105. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, G.; Wang, J. Study on fluid-induced vibration power harvesting of square columns under different attack angles. Geofluids 2017, 2017, 1–18. [Google Scholar] [CrossRef]
- Sirohi, J.; Mahadik, R. Piezoelectric wind energy harvester for low-power sensors. J. Intell. Mater. Syst. Struct. 2011, 22, 2215–2228. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Yan, Z.; Hajj, M.R. Modeling and nonlinear analysis of piezoelectric energy harvesting from transverse galloping. Smart Mater. Struct. 2013, 22, 025016. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, B.; Chen, X.; Wang, X.; Liu, J. Modeling and experimental study of a piezoelectric energy harvester from vortex shedding-induced vibration. Energy Convers. Manag. 2018, 162, 145–158. [Google Scholar] [CrossRef]
- Song, R.; Shan, X.; Lv, F.; Li, J.; Xie, T. A novel piezoelectric energy harvester using the macro fiber composite cantilever with a bicylinder in water. Appl. Sci. 2015, 5, 1942–1954. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Cao, Z. Modeling of piezoelectric energy harvesting from freely oscillating cylinders in water flow. Math. Probl. Eng. 2014, 2014, 985360. [Google Scholar] [CrossRef]
- Dai, H.; Abdelkefi, A.; Wang, L. Piezoelectric energy harvesting from concurrent vortex-induced vibrations and base excitations. Nonlinear Dyn. 2014, 77, 967–981. [Google Scholar] [CrossRef]
- Franzini, G.R.; Bunzel, L.O. A numerical investigation on piezoelectric energy harvesting from vortex-induced vibrations with one and two degrees of freedom. J. Fluids Struct. 2018, 77, 196–212. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Gu, S.; Yang, K.; Li, H.; Lai, Y.; Yurchenko, D. Enhancement of low-speed piezoelectric wind energy harvesting by bluff body shapes: Spindle-like and butterfly-like cross-sections. Aerosp. Sci. Technol. 2020, 103, 105898. [Google Scholar] [CrossRef]
- Wang, J.; Gu, S.; Zhang, C.; Hu, G.; Chen, G.; Yang, K.; Li, H.; Lai, Y.; Litak, G.; Yurchenko, D. Hybrid wind energy scavenging by coupling vortex-induced vibrations and galloping. Energy Convers. Manag. 2020, 213, 112835. [Google Scholar] [CrossRef]
- Sun, W.; Zhao, D.; Tan, T.; Yan, Z.; Guo, P.; Luo, X. Low velocity water flow energy harvesting using vortex induced vibration and galloping. Appl. Energy 2019, 251, 113392. [Google Scholar] [CrossRef]
- Ramirez, J.M. A coupled formulation of fluid-structure interaction and piezoelectricity for modeling a multi-body energy harvester from vortex-induced vibrations. Energy Convers. Manag. 2021, 249, 114852. [Google Scholar] [CrossRef]
- Barbounis, T.G.; Theocharis, J.B.; Alexiadis, M.C.; Dokopoulos, P.S. Long-term wind speed and power forecasting using local recurrent neural network models. IEEE Trans. Energy Convers. 2006, 21, 273–284. [Google Scholar] [CrossRef]
- Kusiak, A.; Zheng, H.; Song, Z. Short-term prediction of wind farm power: A data mining approach. IEEE Trans. Energy Convers. 2009, 24, 125–136. [Google Scholar] [CrossRef]
- Hu, G.; Kwok, K.C. Predicting wind pressures around circular cylinders using machine learning techniques. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104099. [Google Scholar] [CrossRef]
- Clifton, A.; Kilcher, L.; Lundquist, J.; Fleming, P. Using machine learning to predict wind turbine power output. Environ. Res. Lett. 2013, 8, 024009. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, G.; Yurchenko, D.; Lin, P.; Gu, S.; Song, D.; Peng, H.; Wang, J. Machine learning based prediction of piezoelectric energy harvesting from wake galloping. Mech. Syst. Signal Process. 2021, 160, 107876. [Google Scholar] [CrossRef]
- Hu, G.; Wang, J.; Lan, C.; Tang, L.; Liang, J. Deep-learning assisted finite element model of a galloping piezoelectric energy harvester. In Proceedings of the Active and Passive Smart Structures and Integrated Systems XV. SPIE, Online, 22–26 March 2021; Volume 11588, pp. 58–66. [Google Scholar]
- Zdravkovich, M.M. Conceptual overview of laminar and turbulent flows past smooth and rough circular cylinders. J. Wind. Eng. Ind. Aerodyn. 1990, 33, 53–62. [Google Scholar] [CrossRef]
- Mohri, M.; Rostamizadeh, A.; Talwalker, A. Foundations of Machine Learning; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Shan, S.; Wang, G. Survy of modeling and optimization strategies to solve high-dimensional design problems with computationally-expensive black-box functions. Struct. Multidiscip. Optim. 2010, 52, 219–241. [Google Scholar] [CrossRef]
- Gutmann, M.U.; Corander, J. Bayesian optimization for likelihood-free inference of simulator-based statistical models. J. Mach. Learn. Res. 2016, 17, 1–47. [Google Scholar]



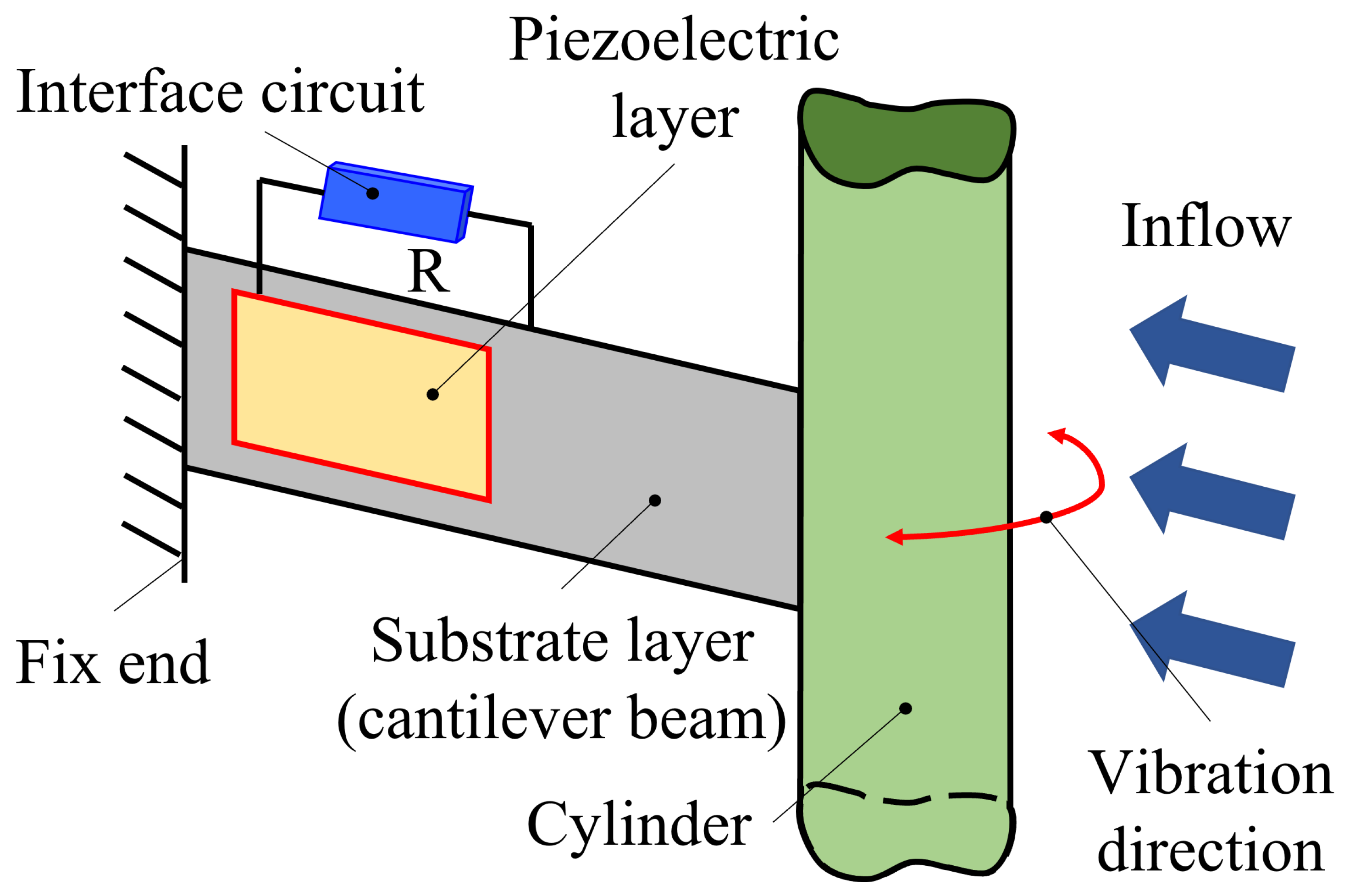
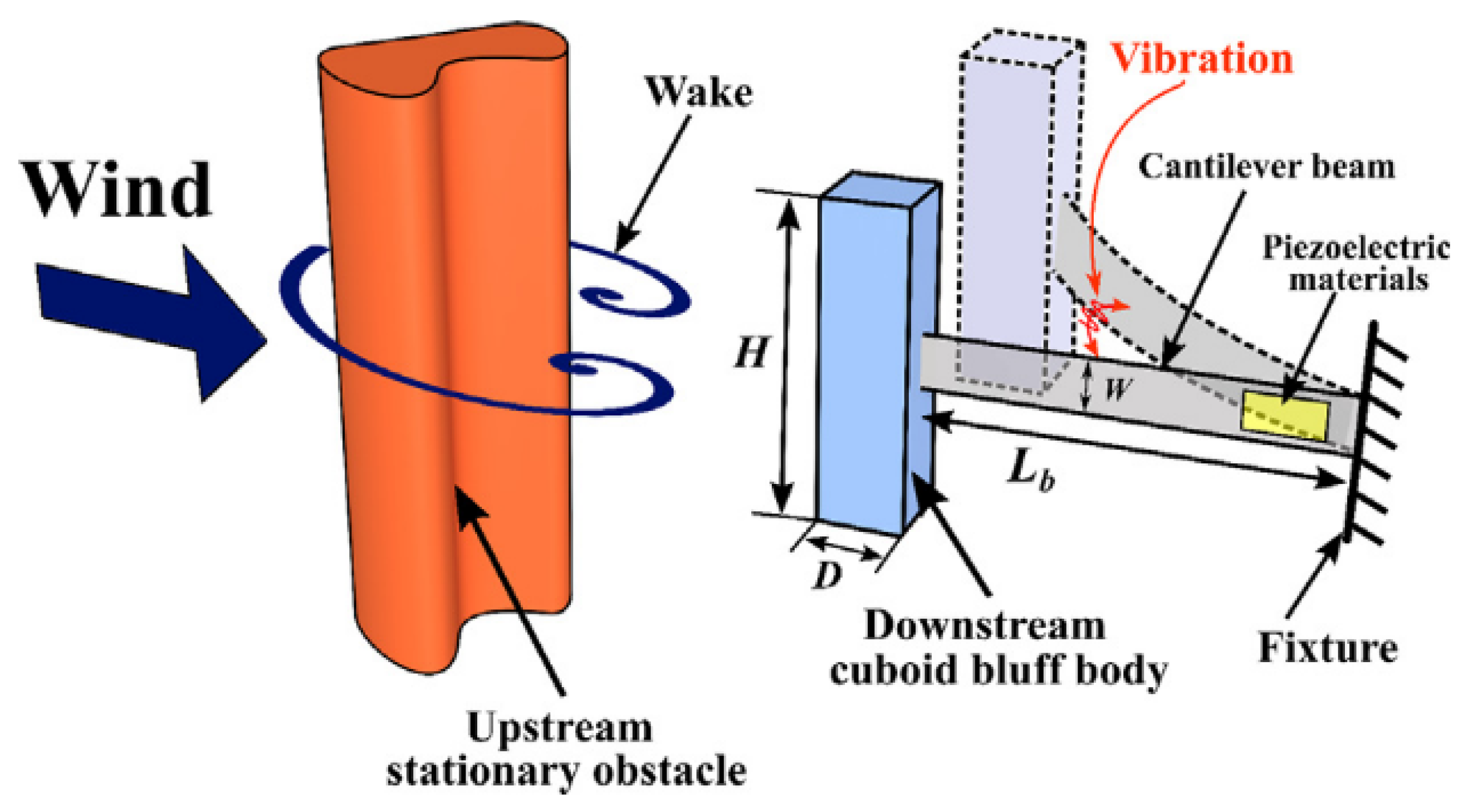

| Author/Year | Motion | Shape | CFD | FSI Scheme | |||
|---|---|---|---|---|---|---|---|
| Mittal and Kumar [90] 1/1999 | 2DOF-VIV | circular | 4.72 | 0.0003 | 325 | SST-FEM | DSD/SST |
| Singh and Mittal [87]/2005 | 2DOF-VIV | circular | 10 | 0 | 50–500 | SST-FEM | DSD/SST |
| Prasanth et al. [113]/2006 | 2DOF-VIV | circular | 10 | 0 | 60–125 | SST-FEM | DSD/SST |
| Prasanth and Mittal [115]/2008 | 2DOF-VIV | circular | 10 | 0 | 60–200 | SST-FEM | DSD/SST |
| Prasanth et al. [114]/2011 | 2DOF-VIV | circular | 1–100 | 0–0.1 | 60–150 | SST-FEM | DSD/SST |
| Mittal [116]/2017 | 1DOF-VIV | circular | 70 | 0 | 100 | SST-FEM | DSD/SST |
| Leontini et al. [117]/2006 | 1DOF-VIV | circular | 10 | 0.01 | 200 | SEM | fixed mesh |
| Ji et al. [101]/2011 | 2DOF-VIV | circular | 1.27 | 0.003–3.3 | 60–300 | FDM | FD |
| Li et al. [118]/2011 | 1DOF-VIV | circular | 1 | 0.003 | 200 | ST-FEM | moving mesh |
| Étienne et al. [119]/2012 | 2DOF-VIV | circular | 0 | 0 | 15–45 | FEM | ALE |
| Bourguet and Jacono [120]/2014 | 1DOF-VIV | circular | 10 | 0 | 100 | SEM | fixed mesh |
| Zhao et al. [121]/2014 | 2DOF-VIV | circular | 2 | 0 | 150 | PG-FEM | ALE |
| Garg et al. [122]/2019 | 1DOF-VIV | circular | 2 | 0 | 150 | FDM | IBM |
| Dorogi and Baranyi [124]/2020 | 1DOF-VIV | circular | 10 | 0–0.05 | 300 | FDM | fixed mesh |
| Shen and Chen [123]/2022 | 1DOF-VIV | circular | 2–50 | 0.041 | 150 | FVM | IBM |
| Yogeswaran et al. [125]/2014 | 2DOF-VIV | elliptic | 10 | 0 | 60–140 | SST-FEM | DSD/SST |
| Leontini et al. [127]/2018 | 1DOF-FIV | elliptic | 1 | 0 | 200 | SEM | fixed mesh |
| Chen et al. [126]/2021 | 1DOF-VIV | elliptic | 10 | 0 | 150 | FVM | moving mesh |
| Su et al. [133]/2007 | 1DOF-FIV | square | 3 | 0 | 100 | FEM | ALE |
| Sen and Mittal [128]/2011 | 2DOF-FIV | square | 10 | 0 | 60–250 | SST-FEM | DSD/SST |
| Joly et al. [63]/2012 | DOF-FIV | square | 1–20 | 0–0.01 | 150 | FEM | moving mesh |
| He et al. [129]/2012 | 2DOF-FIV | square | 10, 20, 40 | 0 | 60–250 | FEM | ALE |
| Sen and Mittal [130]/2015 | 2DOF-FIV | square | 1, 5, 10, 20 | 0 | 60–250 | SST-FEM | DSD/SST |
| Zhao et al. [95]/2013 | 2DOF-VIV | square | 3 | 0 | 100 | PG-FEM | ALE |
| Sun et al. [134]/2017 | 2DOF-FIV | square | 2 | 0 | 80,160 | FEM | ALE |
| Sourav and Sen [131]/2019 | 2DOF-FIV | square | 3–4 | 0 | 60–250 | SST-FEM | DSD/SST |
| Zhao [97]/2015 | 2DOF-VIV | rectangular | 10 | 0 | 200 | PG-FEM | ALE |
| Wang et al. [135]/2014 | 2DOF-FIV | triangular | 2 | 0 | 100 | FEM | ALE |
| Zhao et al. [95]/2013 | 2DOF-FIV | circular-rod | 2 | 0 | 250 | PG-FEM | ALE |
| Liu et al. [136]/2020 | 2DOF-FIV | circular-rod | 2 | 0.007 | 150 | FEM | ALE |
| Liu et al. [137]/2022 | 1DOF-FIV | circular-rod | 2 | 0 | 200 | FEM | ALE |
| Sahu et al. [138]/2019 2 | 1DOF-FIV | circular-plate | 2–1000 | 0 | 92–150 | SST-FEM | moving mesh |
| Zhu et al. [139]/2020 3 | 2DOF-FIV | circular-plate | 6.9 | 0.01 | 120 | FVM | moving mesh |
| Wang et al. [140]/2018 4 | 2DOF-FIV | circular-plate | 10 | 0 | 100, 200 | FEM | ALE |
| Borazjani and Sotiropoulos [141]/2009 | 2DOF-VIV | 2-circular | 2 | 0 | 200 | IBM | IBM |
| Carmo et al. [106]/2010 | 1DOF-FIV | 2-circular | 2 | 0.007 | 150 | SEM | ALE |
| Griffith et al. [142]/2017 | 1DOF-FIV | 2-circular | 2.546 | 0 | 200 | FDM | IBM |
| Zhao [94]/2013 | 1DOF-FIV | 2-circular | 2 | 0 | 150 | PG-FEM | ALE |
| Han et al. [143]/2015 | 2DOF-VIV | 4-circular | 6 | 0 | 80–160 | CBS-FEM 5 | ALE |
| Zhao [97]/2015 | 1DOF-FIV | 36-circular | 2.5 | 0 | 100 | PG-FEM | ALE |
| Author/Year | Motion | Shape | CFD | FSI Scheme | |||
|---|---|---|---|---|---|---|---|
| Newman and Karniadakis [144]/1997 | 1DOF-VIV | circular | 2 | 0 | 200 | SEM | fixed mesh |
| Evangelinos et al. [145]/2000 | 1DOF-VIV | circular | 2 | 0 | 1000 | SEM | fixed mesh |
| Lucor et al. [148]/2005 | 1DOF-VIV | circular | 2 | 0 | 1000–3000 | SEM | fixed mesh |
| Carmo et al. [106]/2010 | 2DOF-VIV | 2-circular | 2 | 0.007 | 300 | SST-FEM | ALE |
| Mittal [88]/2013 | 2DOF-VIV | circular | 10 | 0 | 1000 | SST-FEM | ALE |
| Zhao et al. [96]/2014 | 1DOF-VIV | circular | 2 | 0 | 1000 | PG-FEM | ALE |
| Gsell et al. [149]/2016 | 2DOF-VIV | circular | 2 | 0 | 3900 | FVM | fixed mesh |
| Chen et al. [150]/2022 | 2DOF-VIV | circular | 2 | 0 | 500 | FDM | IBM |
| Author/Year | Motion | Shape | Re | Scale | SGS | CFD | FSI Scheme | ||
|---|---|---|---|---|---|---|---|---|---|
| Zhang and Dalton [151] 1/1996 | 1DOF-VIV | circular | 10 | 0.02 | 13,000 | 2D | SM | FDM | fixed mesh |
| Al-Jamal and Dalton [105] 2/2004 | 1DOF-VIV | circular | 7.85 | 0.02 | 8000 | 2D | SM | FDM | fixed mesh |
| Tutar and Holdo [154] 3/2000 | 1DOF-forced | circular | / | / | 24,000 | 3D | SM | FEM | fixed mesh |
| Pastrana et al. [155] 4/2018 | 2DOF-VIV | circular | 2.6 | 0 | 3900–11,000 | 2D | WALE | FVM | ALE |
| Wang et al. [156] 5/2021 | 1DOF-VIV | circular | 4 | 0.087 | 550–900 | 3D | / | EVM | fixed mesh |
| Janocha et al. [157] 6/2022 | 1DOF-VIV | circular | / | / | 3900 | 3D | WALE | FVM | ALE |
| Daniels et al. [158]/2016 | 1DOF-VIV | rectangular | 57 | 0.0021 | 40,000 | 3D | MTS | FVM | ALE |
| Author/Year | Motion | Shape | Re1 | Turbulence | CFD | ||
|---|---|---|---|---|---|---|---|
| Guilmineau and Queutey [160]/2004 | 1DOF-VIV | circular | 2.4 | 0.0054 | 900–15,000 | SST k- | FVM |
| Pan et al. [161]/2007 | 1DOF-VIV | circular | 2.4 | 0.0054 | 2500–13,000 | SST k- | FVM |
| Wanderlay et al. [162]/2008 | 1DOF-VIV | circular | 1.88 | 0.00542 | 2000–12,000 | k- | FDM |
| Zhao and Cheng [92]/2011 | 2DOF-VIV | circular | 2.6 | 0.005 | 1000–15,000 | SST k- | PG-FEM |
| Wanderlay and Soures [163]/2015 | 1DOF-VIV | circular | 1.88 | 0.00542 | 100–24,000 | k- | FDM |
| Gu et al. [164]/2022 | 1DOF-VIV | circular | 1.28, 2.4 | 0.01, 0.006 | 200–27,000 | SST k- | FEM |
| Kang et al. [165]/2019 | 2DOF-VIV | circular | 2.6, 13 | 0.005 | 1450–91,800 | SST k- | FVM |
| Anwar et al. [167]/2022 | 1DOF-VIV | circular | 2.4, 11 | / | 10,000 | SST k- | FEM |
| Martins and Avila [168] 2/2019 | 2DOF-VIV | circular | 2.4 | 0.005–0.01 | 750–130,000 | SST k- | FEM |
| Cui et al. [169]/2016 | 1DOF-FIV | rectangular | 2.4 | 0.0054 | 385–19,250 | SST k- | PG-FVM |
| Han et al. [170]/2021 | 1DOF-FIV | square | 1.45 | 0.01–0.7 | 24,000–160,000 | SST k- | FEM |
| Ding et al. [171] 3/2015 | 1DOF-FIV | various | varied | 0.017 | 10,000–130,000 | SA | FVM |
| Zhang et al. [172]/2017 | 1DOF-FIV | various | 0.93 | 0.1076 | 2800–12,000D | SST k- | FEM |
| Zhang et al. [173]/2019 | 1DOF-FIV | various | 2.4 | 0.0054 | 16,100–242,000 | SST k- | FEM |
| Wang et al. [174]/2020 | 1DOF-FIV | various | 2.6 | 0.002 | 8000–56,000 | SST k- | FEM |
| Zhu and Yao [175] 4/2015 | 2DOF-FIV | cir-rods | 2.4 | 0.0054 | 1631–6,387.1 | SST k- | FEM |
| Ding et al. [176]/2016 | 1DOF-FIV | cir-strips | 1.896 | 0.04 | 30,000–110,000D | SA | FVM |
| Wang et al. [177] 5/2020 | 1DOF-FIV | cir-rods | 1.68 | 0.016 | 30,000–10,0000 | SST k- | FVM |
| Zhao and Cheng [93]/2012 | 2DOF-VIV | 4-circular | 2 | 0.001 | 1000–20,000 | SST k- | PG-FVM |
| Rahmanian et al. [178]/2014 | 1DOF-VIV | 2-circular | 5 | 0.0008 | 5000D | SST k- | PG-FVM |
| Cui et al. [180]/2014 | 1DOF-VIV | 2-circular | 2 | 0 | 5000 | SST k- | PG-FVM |
| Zhao et al. [179]/2016 | 1DOF-VIV | 2-circular | 2.5 | 0 | 5000 | SST k- | PG-FVM |
| Author/Year | Motion | Shape | Re | Dimension | SGS | ||
|---|---|---|---|---|---|---|---|
| Nguyen and Nguyen [181]/2016 | 2DOF-VIV | circular | 2.6, 11 | 0.001, 0.005 | 3000–30,000 | 2D | SST k- |
| Joshi and Jaiman [182]/2017 | 2DOF-VIV | circular | 2.23 | / | 4,000 | 3D | SST-DDES |
| Ma et al. [184]/2021 | 1DOF-FIV | cir-strips | 2.4 | 0.0054 | 3900 | 3D | SST-DDES |
| Ma et al. [183]/2022 | 1DOF-FIV | cir-strips | 2.4 | 0.0054 | 3000-19,000 | 3D | SST-DDES |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Cheng, Z.; McConkey, R.; Lien, F.-S.; Yee, E. Modelling of Flow-Induced Vibration of Bluff Bodies: A Comprehensive Survey and Future Prospects. Energies 2022, 15, 8719. https://doi.org/10.3390/en15228719
Wu Y, Cheng Z, McConkey R, Lien F-S, Yee E. Modelling of Flow-Induced Vibration of Bluff Bodies: A Comprehensive Survey and Future Prospects. Energies. 2022; 15(22):8719. https://doi.org/10.3390/en15228719
Chicago/Turabian StyleWu, Ying, Zhi Cheng, Ryley McConkey, Fue-Sang Lien, and Eugene Yee. 2022. "Modelling of Flow-Induced Vibration of Bluff Bodies: A Comprehensive Survey and Future Prospects" Energies 15, no. 22: 8719. https://doi.org/10.3390/en15228719
APA StyleWu, Y., Cheng, Z., McConkey, R., Lien, F.-S., & Yee, E. (2022). Modelling of Flow-Induced Vibration of Bluff Bodies: A Comprehensive Survey and Future Prospects. Energies, 15(22), 8719. https://doi.org/10.3390/en15228719











