Optimization of the Selected Parameters of Single-Family House Components with the Estimation of Their Contribution to Energy Saving
Abstract
:1. Introduction
- -
- Shaping the external form of the building, adapted to the climate and the possibility of obtaining available solar energy, including the ratio of the window area to the wall area, the building’s shape factor, or the layout of the rooms;
- -
- Location of the building, its orientation, and urban conditions (determining the location of the building in relation to the cardinal directions and shading from the surrounding buildings, elements of small architecture, and greenery);
- -
- Construction of partitions, including material solutions (insulation parameters, accumulation capacity, and variable parameters of solar energy transmittance of transparent partitions).
- -
- Architectural and spatial, regarding the dimensions of rooms and windows (the height of rooms in the building h, and the window area changes coefficient k),
- -
- Structural, concerning the solutions of the building components (the density of the material of the inner layer of the external walls ρ1, the density of the material of internal walls ρ2, and the thickness of the internal walls d),
- -
- Physical properties of windows (the heat transfer coefficient of the glazing Ug and the total solar transmittance of the glazing g).
2. Materials and Methods
2.1. Characteristics of the Tested Building
2.2. A Method for Calculating the Annual Heating/Cooling Energy Demand
2.3. Mathematical Modeling of the Annual Energy Demand for Heating and Cooling the Selected Building
- -
- Architectural and spatial parameters: factors X1 and X2,
- -
- Structural parameters: factors X3, X4, and X5,
- -
- Physical properties of windows: factors X6 and X7.
3. Development of Mathematical Models of the Studied Dependencies
3.1. Results of Energy Simulations and Development of Mathematical Models
42.41X1X3 + 32.81X1X4 − 39.29X1X5 + 32.50X1X6 − 31.54X1X7 − 8.07X2X3 + 12.41X2X4 − 18.03X2X5 + 99.18X2X6
− 64.73X2X7 + 9.99X3X4 − 21.59X3X5 + 28.55X3X6 − 26.76X3X7 + 20.29X4X5 − 29.35X4X6 + 29.30X4X7 +
15.43X5X6 − 12.28X5X7 + 3.89X6X7 + 36.51X12 + 350.82X22 − 57.62X32 − 25.50X42 − 65.88X52 + 5.71X62 + 17.92X72;
39.48X1X4 + 28.62X1X5 − 31.43X1X6 − 13.30X1X7 + 5.45X2X3 − 12.75X2X4 + 32.00X2X5 − 76.64X2X6 +
297.48X2X7 − 19.13X3X4 + 25.01X3X5 − 27.56X3X6 + 20.49X3X7 − 29.98X4X5 + 27.88X4X6 − 32.45X4X7 −
18.73X5X6 + 8.37X5X7 − 45.25X6X7 − 50.04X12 + 58.16X22 + 39.31X32 + 28.88X42 + 76.86X52 − 5.85X62 + 101.29X72.
2.22X1X3 − 6.67X1X4 − 10.67X1X5 + 1.08X1X6 − 44.84X1X7 − 2.62X2X3 − 0.34X2X4 + 13.96X2X5 + 22.54X2X6 +
232.75X2X7 − 9.14X3X4 + 3.41X3X5 + 0.98X3X6 − 6.27X3X7 − 9.69X4X5 − 1.47X4X6 − 3.14X4X7 − 3.30X5X6 −
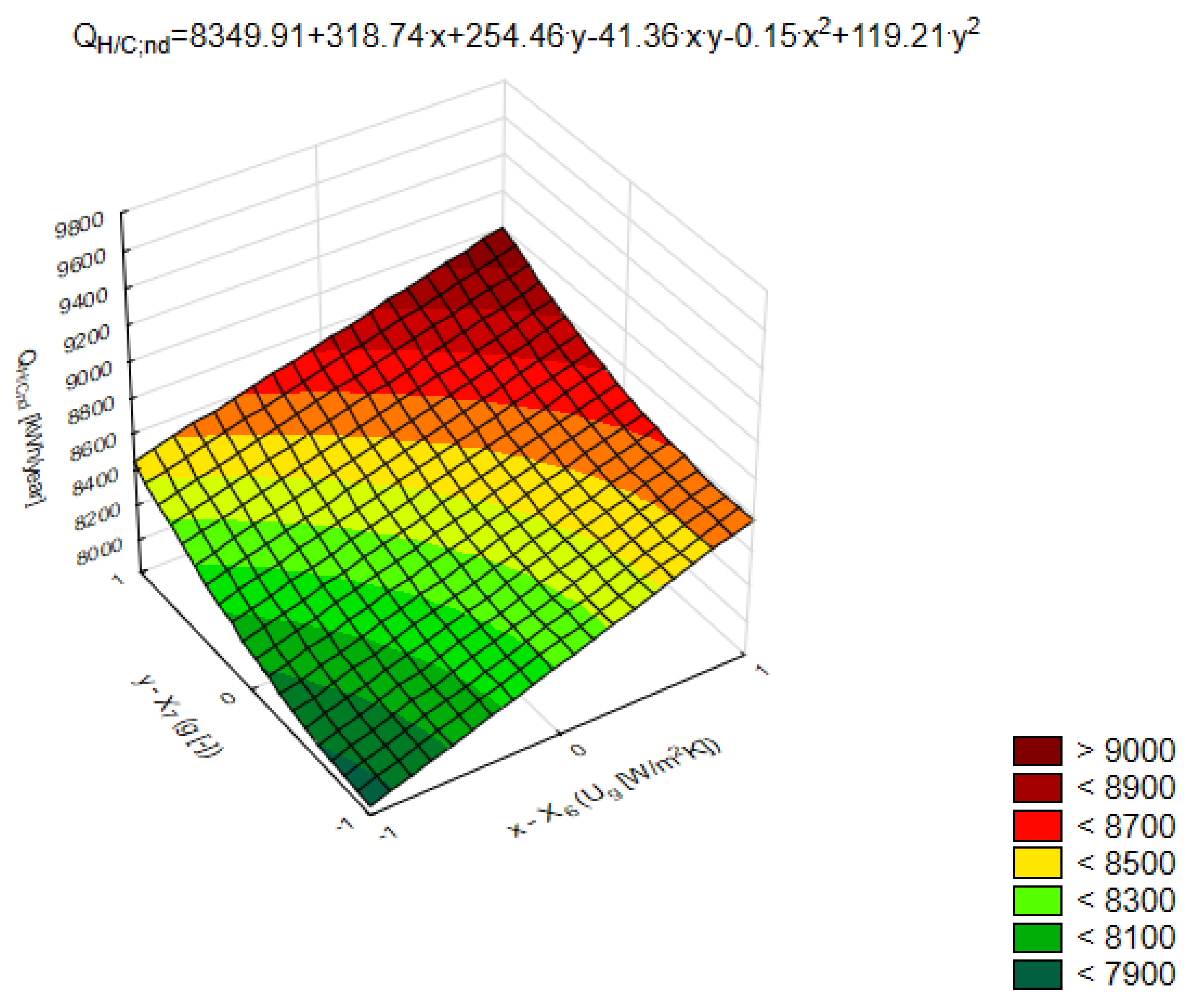
3.91X5X7 − 41.36X6X7 − 13.53X12 + 408.98X22 − 18.31X32 + 3.38X42 + 10.98X52 − 0.15X62 + 119.21X72.
3.2. Analysis of the Studied Dependencies and the Interpretation of Results
4. Optimization of the Studied Dependencies According to the Energy Criterion
5. Conclusions
- It was established that, for the model of energy demand for heating, when changing from the lower to the upper level of factors k (X2), ρ2 (X4), d (X5), and g (X7), the value of heat demand for heating QH,nd decreases by −4.8%, −0.7%, −1.2%, and −10.1%, respectively. With a similar change in the value of the factors h (X1), ρ1 (X3), and Ug (X6), the amount QH,nd increases by +13.8%, +0.4%, and +11.6%. On the other hand, the energy demand for cooling QC,nd when increasing the value of factors h (X1), ρ1 (X3), ρ2 (X4), d (X5), and Ug (X6) decreases by about −20.8%, −7.7%, −1.1%, −5.1%, and −18.1%, respectively, but increases with the increase in the value of the factors k (X2) and g (X7) by +285.1% and + 306.8%, respectively.
- After the numerical optimization procedure was performed, it was found that, for the model of annual usable energy demand for heating and cooling the selected building, the optimal parameter values ensuring the minimum of the tested QH/C;nd(min) (Y3min) = 7281.78 kWh/year are h (X1) = 2.70 m, k ((X2) = 0.95, ρ1 (X3) = 1600 kg/m3, ρ2 (X4) = 2100 kg/m3, d (X5) = 0.24 m, Ug (X6) = 0.40 W/(m2K), and g (X7) = 0.5. The parameter values were also obtained, ensuring the maximum of the tested QH/C;nd(min) (Y3min). Using the range of extreme energy demand values ΔQH/C;nd, which was about 44% of QH/C;nd(min), a great potential was found in the appropriate selection of the examined building parameters in terms of energy saving.
- According to the total amount of energy that can be reduced ΔQH/C;nd as a result of the analyzed improvements, the contribution of individual parameters and selected groups of parameters to energy saving was estimated. It was found that the most important role in saving energy is played by architectural and spatial factors related to the height of rooms and the dimensions of windows. The contribution of the two factors from this group in the analyzed building amounted to 1287.66 kWh/year, i.e., 40.0%. Factors from the group of physical parameters related to window solutions showed a slightly smaller contribution. The share of these two factors amounted to 827.81 kWh/year, i.e., 25.7%. Proper selection of the values of these four parameters in the conducted study allowed for a reduction of over 65.7% in the total amount of energy that could be saved.
- An incomparably lower contribution to energy saving was shown by factors from the group of construction parameters related to building component solutions. The share of these three factors in the analyzed building amounted to only 135.06 kWh/year or 4.2% of the total amount of energy that could be saved.
- This means that the use of reserves inherent in the parameters of the architectural and spatial group, relating to the height of rooms and window dimensions, and the group of physical parameters, relating to window solutions, is an effective way of saving energy in buildings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- United Nations Environment Programme. 2021 Global Status Report for Buildings and Construction. Towards a Zero-Emission, Efficient and Resilient Buildings and Construction Sector; Nairobi, Kenya, 2021. Available online: https://www.unep.org/resources/report/2021-global-status-report-buildings-and-construction (accessed on 12 April 2022).
- Tracking Buildings 2021—Tracking Report IEA–November 2021. Available online: https://www.iea.org/reports/global-energy-review-2020 (accessed on 12 April 2022).
- European Commission. A Clean Planet for All. A European Strategic Long-Term Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy. 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52018DC0773&from=EN (accessed on 29 December 2021).
- Global Climate Action. United Nations Climate Change. Marrakech Partnership. Climate Action Pathway. Energy. Vision and Summary. 2021. Available online: https://unfccc.int/climate-action/marrakech-partnership/reporting-tracking/pathways/energy-climate-action-pathway#eq-1 (accessed on 12 April 2022).
- Directive 2010/31/EU of The European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings. Available online: https://eur-lex.europa.eu/legal-content/PL/ALL/?uri=CELEX%3A32010L0031 (accessed on 12 April 2022).
- Pessenlehner, W.; Mahdavi, A. Building morphology, transparence, and energy performance. In Proceedings of the 8th International IBPSA Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 1025–1032. [Google Scholar]
- McKeen, P.; Fung, A.S. The effect of building aspect ratio on energy efficiency: A case study for multi-unit residentialbBuildings in Canada. Buildings 2014, 4, 336–354. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, E.; Amaral, A.R.; Gaspar, A.R.; Gomes, A. How reliable are geometry-based building indices as thermal performance indicators? Energy Convers. Manag. 2015, 101, 561–578. [Google Scholar] [CrossRef]
- Parasonis, J.; Keizikas, A.; Endriukaitytė, A.; Kalibatienė, D. Architectural solutions to increase the energy efficiency of buildings. J. Civ. Eng. Manag. 2012, 18, 71–80. [Google Scholar] [CrossRef]
- Koźniewski, E.; Sadowska, B.; Banaszak, K. Geometric aspects of assessing the anticipated energy demand of a designed single-family house. Energies 2022, 15, 3308. [Google Scholar] [CrossRef]
- Jezierski, W.; Sadowska, B.; Pawłowski, K. Impact of changes in the required thermaliInsulation of building envelope on energy demand, heating costs, emissions, and temperature in buildings. Energies 2021, 14, 56. [Google Scholar] [CrossRef]
- Pan, D.; Chan, M.; Xia, L.; Xu, X.; Deng, S. Performance evaluation of a novel bed-based task/ambient conditioning (TAC) system. Energy Build. 2012, 44, 54–62. [Google Scholar] [CrossRef]
- Zinzi, M.; Agnoli, S.; Battistini, G.; Bernabini, G. Deep energy retrofit of the T. M. Plauto School in Italy—A five years experience. Energy Build. 2016, 126, 239–251. [Google Scholar] [CrossRef]
- Goia, F. Search for the optimal window-to-wall ratio in office buildings in different European climates and the implications on total energy saving potential. Sol. Energy 2016, 132, 467–492. [Google Scholar] [CrossRef]
- Obrecht, T.; Vesn, M.P.; Leskovar, Ž. Influence of the orientation on the optimal glazing size for passive houses in different European climates (for non-cardinal directions). Sol. Energy 2019, 189, 15–25. [Google Scholar] [CrossRef]
- Szymański, P. Czy pojemność cieplna materiałów murowych jest naprawdę ważna? Mater. Bud. 2012, 3, 72–74. [Google Scholar]
- Jedrzejuk, H.; Marks, W. Optimization of shape and functional structure of buildings as well as heat source utilisation. Partial. Probl. Solution. Build. Environ. 2002, 37, 1037–1043. [Google Scholar] [CrossRef]
- Pacheco, R.; Ordonez, J.; Martinez, G. Energy efficient design of building: A review. Renew. Sustain. Energy Rev. 2012, 16, 3559–3573. [Google Scholar] [CrossRef]
- Adamczyk, J.; Dylewski, R. Changes in heat transfer coefficients in Poland and their impact on energy demand—An environmental and economic assessment. Renew. Sustain. Energy Rev. 2017, 78, 530–538. [Google Scholar] [CrossRef]
- Cao, Y.; Kamaruzzaman, S.N.; Aziz, N.M. Building Information Modeling (BIM) Capabilities in the Operation and Maintenance Phase of Green Buildings: A Systematic Review. Buildings 2022, 12, 830. [Google Scholar] [CrossRef]
- Asl, M.R.; Zarrinmehr, S.; Bergin, M.; Yan, W. BPOpt: A framework for BIM-based performance optimization. Energy Build. 2015, 108, 401–412. [Google Scholar] [CrossRef] [Green Version]
- Bruen, M. Uptake and Dissemination of Multi-Criteria Decision Support Methods in Civil Engineering—Lessons from the Literature. Appl. Sci. 2021, 11, 2940. [Google Scholar] [CrossRef]
- Cebrat, K.; Nowak, Ł. Revealing the relationships between the energy parameters of single-family buildings with the use of Self-Organizing Maps. Energy Build. 2018, 178, 61–70. [Google Scholar] [CrossRef]
- Main Office of Building Control. Construction Market in Poland in 2021. Warsaw, Poland. 2018. Available online: https://www.gunb.gov.pl/aktualnosc/ruch-budowlany-w-2021-roku (accessed on 20 May 2022).
- Statistics Poland. Occupied Buildings. National Census of Population and Housing 2021 in Poland. In Report on Preliminary Results; Central Statistical Office: Warsaw, Poland, 2022; p. 53. [Google Scholar]
- Software Informer Home Page. DesignBuilder Software-Private Limited Company No. 04514127; DESIGNBUILDER SOFTWARE LIMITED; Stroud House: Stroud, UK; Available online: https://designbuilder.co.uk/download/previous-versions (accessed on 1 April 2021).
- Garg, V.; Mathur, J.; Bhatia, A. Building Energy Simulation: A Workbook Using Designbuilder, 2nd ed.; Taylor & Francis Group: Abingdon, UK, 2020. [Google Scholar] [CrossRef]
- Al-Rukaibawi, L.S.; Szalay, Z.; Károlyi, G. Numerical simulation of the effect of bamboo composite building envelope on summer overheating problem. Case Stud. Therm. Eng. 2021, 28, 101516. [Google Scholar] [CrossRef]
- Fathalian, A.; Kargarsharifabad, H. Actual validation of energy simulation and investigation of energy management strategies (Case Study: An office building in Semnan, Iran). Case Stud. Therm. Eng. 2018, 12, 510–516. [Google Scholar] [CrossRef]
- Ismail, A.M.; Abo Elela, M.M.; Ahmed, E.B. Calibration of Design Builder program. J. Am. Sci. 2015, 11, 96–102. [Google Scholar]
- Baharvand, M.; Ahmad, M.H.B.; Safikhani, T.; Majid, R.B.A. Design Builder verification and validation for indoor natural Ventilation. J. Basic Appl. Sci. Res. 2013, 3, 182–189. [Google Scholar]
- Raji, B.; Tenpierik, M.; Bokel, R.; van den Dobbelsteen, A. Natural summer ventilation strategies for energy-saving in high-rise buildings: A case study in The Netherlands. Int. J. Vent. 2019, 19, 25–48. [Google Scholar] [CrossRef]
- Roshan, G.; Arab, M.; Klimenko, V. Modeling the impact of climate change on energy consumption and carbon dioxide emissions of buildings in Iran. J. Environ. Health Sci. Eng. 2019, 17, 889–906. [Google Scholar] [CrossRef] [PubMed]
- Al-Sakkaf, A.; Mohammed Abdelkader, E.; Mahmoud, S.; Bagchi, A. Studying Energy Performance and Thermal Comfort Conditions in Heritage Buildings: A Case Study of Murabba Palace. Sustainability 2021, 13, 12250. [Google Scholar] [CrossRef]
- U.S. Department of Energy. EnergyPlus™ Version 9.3.0 Documentation. Engineering Reference. Build: baff08990c. 2020. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s& source=web&cd=&ved=2ahUKEwi_5aqBpbftAhUllosKHQCPDR0QFjAAegQIBRAC&url=https%3A%2F%2Fenergyplus.net%2Fsites%2Fall%2Fmodules%2Fcustom%2Fnrel_custom%2Fpdfs%2Fpdfs_v9.3.0%2FEngineeringReference.pdf&usg=AOvVaw1drV7NwKPCki4unAIb0UZ6 (accessed on 1 April 2022).
- Engineering Reference–EnergyPlus–Simple Window Model. Bigladder Software. Available online: https://bigladdersoftware.com/epx/docs/8-9/engineering-reference/window-calculation-module.html (accessed on 12 April 2022).
- Arasteh, D.; Kohler, C.; Griffith, B. Modeling Windows in Energy Plus with Simple Performance Indices; Report LBNL-2804E; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2009. [Google Scholar]
- Gutenbaum, J. Mathematical Modeling of Systems; EXIT: Warsaw, Poland, 2003. [Google Scholar]
- Korzyński, M. Methodology of the Experiment. Planning, Implementation, and Statistical Analysis of the Results of Technological Experiments; WNT: Warsaw, Poland, 2006. [Google Scholar]
- EnergyPlus—Weather Data by Location. Available online: https://energyplus.net/weather-location/europe_wmo_region_6/POL//POL_Bialystok.122950_IMGW (accessed on 1 April 2022).
- Polish Ministry of Transport, Construction and Maritime Economy. Regulation of the Minister of Transport, Construction and Maritime Economy of 5 July 2013 on the Technical Conditions that Buildings and Their Location Should Satisfy; Polish Ministry of Transport; Construction and Maritime Economy: Warsaw, Poland, 2015.
- Software Informer Home Page. Available online: https://therm.software.informer.com/ (accessed on 1 April 2021).
- Durakovic, B. Design of Experiments Application, Concepts, Examples: State of the Art. Period. Eng. Nat. Sci. 2017, 5, 421–439. [Google Scholar] [CrossRef]















| No | X1 h, (m) | X2 k, (-) | X3 ρ1, (kg/m3) | X4 ρ2, (kg/m3) | X5 d, (m) | X6 Ug, (W/(m2∙K)) | X7 g, (-) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | 1 | −1 | 1 | 1 | 1 |
| 3.3 | 0.8 | 1600 | 1500 | 0.24 | 0.8 | 0.7 | |
| 2 | 1 | 1 | −1 | −1 | 1 | 1 | 1 |
| 3.3 | 1.2 | 800 | 1500 | 0.24 | 0.8 | 0.7 | |
| 3 | 1 | 1 | 1 | 1 | 1 | −1 | 1 |
| 3.3 | 1.2 | 1600 | 2100 | 0.24 | 0.4 | 0.7 | |
| 4 | −1 | 1 | 1 | −1 | 1 | −1 | 1 |
| 2.7 | 1.2 | 1600 | 1500 | 0.24 | 0.4 | 0.7 | |
| 5 | −1 | −1 | 1 | 1 | −1 | −1 | 1 |
| 2.7 | 0.8 | 1600 | 2100 | 0.12 | 0.4 | 0.7 | |
| 6 | 1 | 1 | 1 | −1 | 1 | 1 | −1 |
| 3.3 | 1.2 | 1600 | 1500 | 0.24 | 0.8 | 0.5 | |
| 7 | 1 | −1 | 1 | 1 | −1 | 1 | −1 |
| 3.3 | 0.8 | 1600 | 2100 | 0.12 | 0.8 | 0.5 | |
| 8 | −1 | −1 | −1 | 1 | −1 | 1 | −1 |
| 2.7 | 0.8 | 800 | 2100 | 0.12 | 0.8 | 0.7 | |
| 9 | 1 | −1 | 1 | 1 | 1 | −1 | −1 |
| 3.3 | 0.8 | 1600 | 2100 | 0.24 | 0.4 | 0.5 | |
| 10 | 1 | −1 | 1 | −1 | −1 | −1 | 0 |
| 3.3 | 0.8 | 1600 | 1500 | 0.12 | 0.4 | 0.6 | |
| 11 | 0 | 1 | 1 | −1 | −1 | 1 | 1 |
| 3.0 | 1.2 | 1600 | 1500 | 0.12 | 0.8 | 0.7 | |
| 12 | 0 | −1 | −1 | −1 | 1 | −1 | 1 |
| 3.0 | 0.8 | 800 | 1500 | 0.24 | 0.4 | 0.7 | |
| 13 | 0 | 1 | −1 | 1 | −1 | −1 | 1 |
| 3.0 | 1.2 | 800 | 2100 | 0.12 | 0.4 | 0.7 | |
| 14 | −1 | −1 | 0 | −1 | −1 | −1 | −1 |
| 2.7 | 0.8 | 1200 | 1500 | 0.12 | 0.4 | 0.5 | |
| 15 | 1 | 0 | −1 | 1 | −1 | 1 | 1 |
| 3.3 | 1.0 | 800 | 2100 | 0.12 | 0.8 | 0.7 | |
| 16 | −1 | 0 | −1 | 1 | 1 | −1 | 1 |
| 2.7 | 1.0 | 800 | 2100 | 0.24 | 0.4 | 0.7 | |
| 17 | −1 | 0 | 1 | 1 | 1 | 1 | −1 |
| 2.7 | 1.0 | 1600 | 2100 | 0.24 | 0.8 | 0.5 | |
| 18 | 1 | 0 | −1 | −1 | 1 | −1 | −1 |
| 3.3 | 1.0 | 800 | 1500 | 0.24 | 0.4 | 0.5 | |
| 19 | 1 | 1 | 1 | 1 | −1 | −1 | −1 |
| 3.3 | 1.2 | 1600 | 2100 | 0.12 | 0.4 | 0.5 | |
| 20 | −1 | 1 | 0 | 1 | −1 | 1 | 1 |
| 2.7 | 1.2 | 1200 | 2100 | 0.12 | 0.8 | 0.7 | |
| 21 | 1 | 1 | 0 | −1 | −1 | −1 | 1 |
| 3.3 | 1.2 | 1200 | 1500 | 0.12 | 0.4 | 0.7 | |
| 22 | −1 | −1 | −1 | 0 | −1 | −1 | 1 |
| 2.7 | 0.8 | 800 | 1800 | 0.12 | 0.4 | 0.7 | |
| 23 | 1 | −1 | −1 | 0 | 1 | 1 | −1 |
| 3.3 | 0.8 | 800 | 1800 | 0.24 | 0.8 | 0.5 | |
| 24 | 1 | −1 | −1 | 0 | −1 | 1 | −1 |
| 3.3 | 0.8 | 800 | 1800 | 0.12 | 0.8 | 0.5 | |
| 25 | −1 | 1 | −1 | 0 | 1 | −1 | −1 |
| 2.7 | 1.2 | 800 | 1800 | 0.24 | 0.4 | 0.5 | |
| 26 | −1 | −1 | 1 | 1 | 1 | 1 | 1 |
| 2.7 | 0.8 | 1600 | 2100 | 0.24 | 0.8 | 0.7 | |
| 27 | 1 | −1 | −1 | −1 | −1 | 1 | 1 |
| 3.3 | 0.8 | 800 | 1500 | 0.12 | 0.8 | 0.7 | |
| 28 | −1 | 1 | −1 | −1 | 0 | 1 | −1 |
| 2.7 | 1.2 | 800 | 1500 | 0.18 | 0.8 | 0.5 | |
| 29 | −1 | −1 | −1 | 1 | 0 | −1 | −1 |
| 2.7 | 0.8 | 800 | 2100 | 0.18 | 0.4 | 0.5 | |
| 30 | 1 | 1 | −1 | 1 | 1 | 0 | −1 |
| 3.3 | 1.2 | 800 | 2100 | 0.24 | 0.6 | 0.5 | |
| 31 | −1 | −1 | −1 | −1 | 1 | 0 | −1 |
| 2.7 | 0.8 | 800 | 1500 | 0.24 | 0.6 | 0.5 | |
| 32 | −1 | −1 | 1 | −1 | −1 | 0 | −1 |
| 2.7 | 0.8 | 1600 | 1500 | 0.12 | 0.6 | 0.5 | |
| 33 | −1 | −1 | 1 | −1 | −1 | 1 | 0 |
| 2.7 | 0.8 | 1600 | 1500 | 0.12 | 0.8 | 0.6 | |
| 34 | 1 | −1 | −1 | 1 | −1 | −1 | 0 |
| 3.3 | 0.8 | 800 | 2100 | 0.12 | 0.4 | 0.6 | |
| 35 | −1 | 1 | −1 | −1 | −1 | −1 | 0 |
| 2.7 | 1.2 | 800 | 1500 | 0.12 | 0.4 | 0.6 | |
| 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3.0 | 1.0 | 1200 | 1800 | 0.18 | 0.6 | 0.6 | |
| 37 | 1 | −1 | −1 | −1 | −1 | 0 | −1 |
| 3.3 | 0.8 | 800 | 1500 | 0.12 | 0.6 | 0.5 | |
| 38 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 3.3 | 1.2 | 1600 | 2100 | 0.18 | 0.8 | 0.7 | |
| 39 | 0 | −1 | −1 | 1 | 1 | 1 | 1 |
| 3.0 | 0.8 | 800 | 2100 | 0.24 | 0.8 | 0.7 | |
| 40 | −1 | 0 | −1 | −1 | 1 | 1 | 1 |
| 2.7 | 1.0 | 800 | 1500 | 0.24 | 0.8 | 0.7 |
| Building Envelope | Material | d (m) | λ (W/m·K) | U (W/(m2∙K)) | Umax (W/(m2∙K)) |
|---|---|---|---|---|---|
| External walls | Polystyrene EPS | 0.20 | 0.04 | 0.168 | 0.20 |
| Aerated concrete | 0.24 | 0.24 | |||
| Roof/ceiling under unheated roof space | Clay tile—roofing | 0.01 | 1.00 | 0.146 | 0.15 |
| Mineral wool | 0.24 | 0.038 | |||
| Plasterboard | 0.025 | 0.25 | |||
| Floor on the ground | Floor screed | 0.05 | 0.41 | 0.24 | 0.30 |
| EPS (expanded polystyrene) | 0.15 | 0.04 | |||
| Cast concrete | 0.10 | 1.13 |
| No | QH;nd Y1i | QC;nd Y2i | QH/C;nd Y3i |
|---|---|---|---|
| (kWh/Year) | |||
| 1 | 8221.73 | 779.51 | 9001.24 |
| 2 | 7892.73 | 2456.78 | 10,349.51 |
| 3 | 6796.66 | 2800.13 | 9596.79 |
| 4 | 5954.37 | 3162.09 | 9116.46 |
| 5 | 6750.79 | 1130.82 | 7881.61 |
| 6 | 8859.63 | 658.99 | 9518.62 |
| 7 | 9107.77 | 147.51 | 9255.28 |
| 8 | 7456.52 | 979.47 | 8435.99 |
| 9 | 8225.61 | 170.52 | 8396.13 |
| 10 | 8034.49 | 484.67 | 8519.16 |
| 11 | 7578.43 | 2548.74 | 10,127.17 |
| 12 | 7109.09 | 1081.44 | 8190.53 |
| 13 | 6547.81 | 3026.91 | 9574.72 |
| 14 | 7446.82 | 286.06 | 7732.88 |
| 15 | 7887.27 | 1529.58 | 9416.85 |
| 16 | 5995.75 | 2072.75 | 8068.50 |
| 17 | 7609.67 | 413.28 | 8022.95 |
| 18 | 7715.65 | 501.65 | 8217.30 |
| 19 | 7930.15 | 878.52 | 8808.67 |
| 20 | 7119.33 | 2696.97 | 9816.30 |
| 21 | 6983.45 | 2884.62 | 9868.07 |
| 22 | 6776.08 | 1188.50 | 7964.58 |
| 23 | 8970.36 | 158.25 | 9128.61 |
| 24 | 9129.45 | 182.10 | 9311.55 |
| 25 | 6894.84 | 1105.87 | 8000.71 |
| 26 | 7302.33 | 916.25 | 8218.58 |
| 27 | 8392.11 | 842.58 | 9234.69 |
| 28 | 7989.28 | 808.19 | 8797.47 |
| 29 | 7362.30 | 272.30 | 7634.60 |
| 30 | 8338.33 | 765.09 | 9103.42 |
| 31 | 7685.59 | 247.68 | 7933.27 |
| 32 | 7800.76 | 234.71 | 8035.47 |
| 33 | 7792.40 | 491.04 | 8283.44 |
| 34 | 8046.21 | 504.70 | 8550.91 |
| 35 | 6568.57 | 1972.88 | 8541.45 |
| 36 | 7362.52 | 989.92 | 8352.44 |
| 37 | 8778.52 | 211.69 | 8990.21 |
| 38 | 7928.26 | 2364.00 | 10,292.26 |
| 39 | 7780.59 | 858.20 | 8638.79 |
| 40 | 6844.99 | 1788.80 | 8633.79 |
| No | Energy Need (kWh/year) | h (X1) (m) | k (X2) (-) | ρ1 (X3) (kg/m3) | ρ2 (X4) (kg/m3) | d (X5) (m) | Ug (X6) (W/(m2∙K)) | g (X7) (-) |
|---|---|---|---|---|---|---|---|---|
| 1 | QH/C;nd max = 10,500.56 | 3.30 (+1) | 1.2 (+1) | 900 (−0.75) | 1500 (−1) | 0.12 (−1) | 0.80 (+1) | 0.70 (+1) |
| 8709.44 | 9173.01 | 8415.27 | 8384.84 | 8432.90 | 8668.50 | 8723.58 | ||
| 2 | QH/C;nd min = 7281.78 | 2.70 (−1) | 0.95 (−0.25) | 1600 (+1) | 2100 (+1) | 0.24 (+1) | 0.40 (−1) | 0.50 (−1) |
| 8322.85 | 8271.94 | 8369.41 | 8356.67 | 8371.87 | 8349.61 | 8214.66 | ||
| 3 | ΔQH/C;nd = 3218.78 | 386.59 | 901.07 | 45.86 | 28.17 | 61.03 | 318.89 | 508.92 |
| (12.0%) | (28.0%) | (1.4%) | (0.9%) | (1.9%) | (9.9%) | (15.8%) | ||
| 4 | ΔXi | −0.60 | −0.25 | +700 | +600 | +0.12 | −0.40 | −0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jezierski, W.; Sadowska, B. Optimization of the Selected Parameters of Single-Family House Components with the Estimation of Their Contribution to Energy Saving. Energies 2022, 15, 8810. https://doi.org/10.3390/en15238810
Jezierski W, Sadowska B. Optimization of the Selected Parameters of Single-Family House Components with the Estimation of Their Contribution to Energy Saving. Energies. 2022; 15(23):8810. https://doi.org/10.3390/en15238810
Chicago/Turabian StyleJezierski, Walery, and Beata Sadowska. 2022. "Optimization of the Selected Parameters of Single-Family House Components with the Estimation of Their Contribution to Energy Saving" Energies 15, no. 23: 8810. https://doi.org/10.3390/en15238810








