Improved Moth Flame Optimization Approach for Parameter Estimation of Induction Motor
Abstract
:1. Introduction
- An improved version of MFO is proposed for the parameter estimation of a three-phase induction motor based on experimental data.
- The Lévy flight distribution is introduced in the standard version of MFO to increase the exploitation capability.
- The proposed approach is evaluated against other recently developed metaheuristics approaches such as TSA, SCA, MFO, FPA, and PSO.
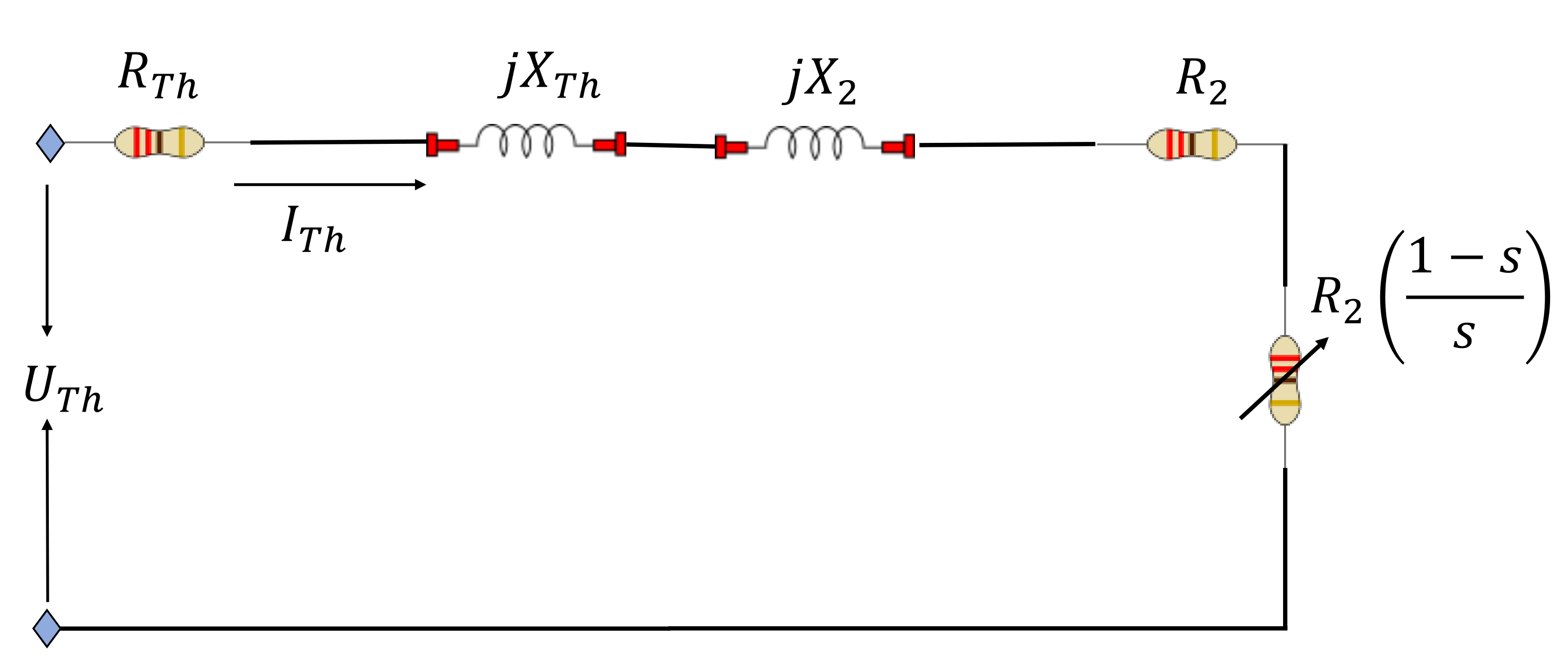
2. Materials and Methods
3. Objective Function
4. Improved Moth Flame Optimization
4.1. Moth Flame Optimization
4.2. Lévy Flight Distribution
4.3. Improved Moth Flame Optimization (IMFO)
| Algorithm 1. Pseudo-code for improved moth flame optimization (IMFO) algorithm. |
| Initialization of location of moths in the search space While(iteration <= Maximum iteration) Update the number of flames by utilizing Equation (9) OM = Fitness Function (Equation (8)) ifiteration = 1 F = sort(M); OF = sort (OM); else F = sort (Kt−1, Kt); OF = sort (Kt−1, Kt); end for i = 1: n for j = 1: d Calculate D using Equation (12) with respect to the corresponding moth Update K(i,j) using Equations (10), (11) and (13) with respect to the corresponding moth end end |
5. Results and Discussion
5.1. Parameter Estimation of Induction Motor
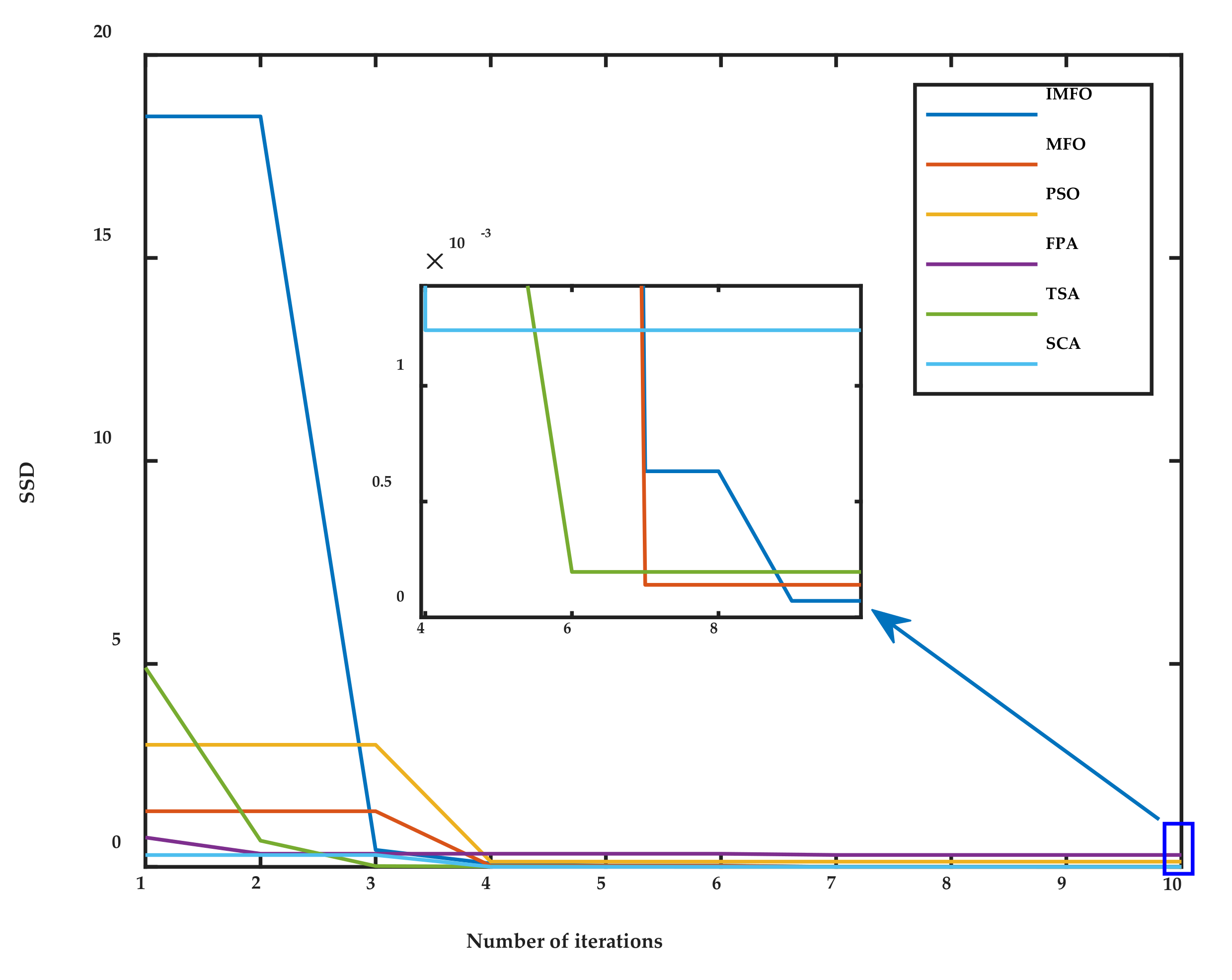
5.2. Convergence Analysis
5.3. Statistical Analysis
5.4. Computational Time
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Çaliş, H.; Cakir, A.; Dandil, E. Artificial immunity-based induction motor bearing fault diagnosis. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 1–25. [Google Scholar] [CrossRef]
- Noor, H.A.M.; Zulkifli, N.; Kassim, R.; Rahman, F.A.; Baharum, Z. Machinery Effectiveness Assessment Study in Warehouse Operation. In Advanced Transdisciplinary Engineering and Technology; Springer: Berlin/Heidelberg, Germany, 2022; pp. 61–70. [Google Scholar]
- Prakash, V.; Baskar, S.; Sivakumar, S.; Krishna, K.S. A novel efficiency improvement measure in three-phase induction motors, its conservation potential and economic analysis. Energy Sustain. Dev. 2008, 12, 78–87. [Google Scholar] [CrossRef]
- Hussain, A.P.; Patowary, M. A Relative Study on Various Control Strategies used in Induction Motor Applications. In Proceedings of the 2022 6th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 25–27 May 2022. [Google Scholar]
- Ren, Y.; Wang, R.; Rind, S.J.; Zeng, P.; Jiang, L. Speed sensorless nonlinear adaptive control of induction motor using combined speed and perturbation observer. Control Eng. Pract. 2022, 123, 105166. [Google Scholar] [CrossRef]
- Rajput, S.; Bender, E.; Averbukh, M. Simplified algorithm for assessment equivalent circuit parameters of induction motors. IET Electr. Power Appl. 2020, 14, 426–432. [Google Scholar] [CrossRef]
- Zhan, X.; Zeng, G.; Liu, J.; Wang, Q.; Ou, S. A review on parameters identification methods for asynchronous motor. Int. J. Adv. Comput. Sci. Appl. 2015, 6, 104–109. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.Q.; Liang, D.; Liu, K. Online parameter estimation for permanent magnet synchronous machines: An overview. IEEE Access 2021, 9, 59059–59084. [Google Scholar] [CrossRef]
- Lu, B.; Habetler, T.G.; Harley, R.G. A survey of efficiency-estimation methods for in-service induction motors. IEEE Trans. Ind. Appl. 2006, 42, 924–933. [Google Scholar]
- Hsu, J.S.; Kueck, J.D.; Olszewski, M.; Casada, D.A.; Otaduy, P.J.; Tolbert, L.M. Comparison of induction motor field efficiency evaluation methods. In Proceedings of the IAS’96. Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996. [Google Scholar]
- Brezočnik, L.; Fister, I.; Podgorelec, V. Swarm Intelligence Algorithms for Feature Selection: A Review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Wang, X.; Yan, B.; Li, L.; Wu, Q. A Dynamic Decoupling Control Method for PMSM of Brake-by-Wire System Based on Parameters Estimation. IEEE/ASME Trans. Mechatron. 2021, 27, 3762–3772. [Google Scholar] [CrossRef]
- Guimaraes, J.M.C.; Bernardes, J.V.; Hermeto, A.E.; da Costa Bortoni, E. Parameter determination of asynchronous machines from manufacturer data sheet. IEEE Trans. Energy Convers. 2014, 29, 689–697. [Google Scholar] [CrossRef]
- Chayakulkheeree, K.; Hengsritawat, V.; Nantivatana, P. Particle swarm optimization based equivalent circuit estimation for on-service three-phase induction motor efficiency assessment. Eng. J. 2017, 21, 101–110. [Google Scholar] [CrossRef]
- Sakthivel, V.; Bhuvaneswari, R.; Subramanian, S. An improved particle swarm optimization for induction motor parameter determination. Int. J. Comput. Appl. 2010, 1, 62–67. [Google Scholar] [CrossRef]
- Sakthivel, V.; Bhuvaneswari, R.; Subramanian, S. Artificial immune system for parameter estimation of induction motor. Expert Syst. Appl. 2010, 37, 6109–6115. [Google Scholar] [CrossRef]
- Bishop, R.R.; Richards, G.G. Identifying induction machine parameters using a genetic optimization algorithm. In IEEE Proceedings on Southeastcon; IEEE: New Orleans, LA, USA, 1990; pp. 476–479. [Google Scholar]
- Sakthivel, V.; Bhuvaneswari, R.; Subramanian, S. An accurate and economical approach for induction motor field efficiency estimation using bacterial foraging algorithm. Measurement 2011, 44, 674–684. [Google Scholar] [CrossRef]
- Perez, I.; Gomez-Gonzalez, M.; Jurado, F. Estimation of induction motor parameters using shuffled frog-leaping algorithm. Electr. Eng. 2013, 95, 267–275. [Google Scholar] [CrossRef]
- Elkholy, M.M.; El-Hay, E.A.; El-Fergany, A.A. Synergy of electrostatic discharge optimizer and experimental verification for parameters estimation of three phase induction motors. Eng. Sci. Technol. Int. J. 2022, 31, 101067. [Google Scholar] [CrossRef]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D.; Pekarek, S.D. Analysis of Electric Machinery and Drive Systems; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 75. [Google Scholar]
- Leonhard, W. Control of Electrical Drives; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Tabrez, M.; Sadhu, P.K.; Iqbal, A.; Husain, M.A.; Bakhsh, F.I.; Singh, S.P. Equivalent circuit modelling of a three-phase to seven-phase transformer using PSO and GA. J. Intell. Fuzzy Syst. 2022, 42, 689–698. [Google Scholar] [CrossRef]
- Chapman, S.J. Electric Machinery Fundamentals, 5th ed.; Mcgraw-Hill, Inc.: Columbus, OH, USA, 2012. [Google Scholar]
- Belkheiri, M.; Belkheiri, A.; Boufadene, M.; Ait Abbas, H.; Rabhi, A. Induction machine parameter identification using LMS algorithm associated with a nonlinear adaptive observer. In Proceedings of the International Conference on Electronic Engineering and Renewable Energy, Saidia, Morocco, 15–17 April 2018; pp. 597–606. [Google Scholar]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Ho, Y.-C.; Pepyne, D.L. Simple explanation of the no-free-lunch theorem and its implications. J. Optim. Theory Appl. 2002, 115, 549–570. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Yang, X.-S. Flower pollination algorithm for global optimization. In Proceedings of the International Conference on Unconventional Computing and Natural Computation, Orléans, France, 3–7 September 2012. [Google Scholar]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/products/matlab.html (accessed on 31 August 2022).





| Algorithm | Parameter | Value |
|---|---|---|
| IMFO | Constant parameter (b) | 1 |
| Number of moths | 30 | |
| Number of iterations | 10 | |
| MFO | Constant parameter (b) | 1 |
| Population size | 30 | |
| Number of iterations | 10 | |
| PSO | C1 | 1.5 |
| C2 | 1.5 | |
| Number of particles | 30 | |
| Wmin | 0.4 | |
| Wmax | 0.9 | |
| FPA | Coefficient value (a) | 2 |
| Switch probability (p) | 0.8 | |
| Population size | 30 | |
| Number of iterations | 10 | |
| TSA | Constant parameter (Pmin) | 1 |
| Constant parameter (Pmax) | 4 | |
| Population size | 30 | |
| Number of iterations | 10 | |
| SCA | Controlling parameter (r1) | [0, 2] |
| Population size | 30 | |
| Number of iterations | 10 |
| Parameter | Lower Bound | Upper Bound |
|---|---|---|
| 0 | 30 | |
| 0 | 20 | |
| 0 | 35 | |
| 0 | 35 | |
| 0 | 340 | |
| 0 | 20 |
| Algorithms | SSD | ||||||
|---|---|---|---|---|---|---|---|
| IMFO | 27.381 | 15.638 | 15.259 | 15.259 | 230.692 | 15.262 | 7.106 × 10−5 |
| MFO | 17.282 | 10.747 | 0 | 12.443 | 300.401 | 17.693 | 1.404 × 10−4 |
| PSO | 24.919 | 14.574 | 13.258 | 10.526 | 238.1859 | 19.757 | 1.287 × 10−1 |
| FPA | 9.996 | 15.494 | 8.374 | 2.071 | 267.785 | 13.689 | 2.933 × 10−1 |
| TSA | 13.907 | 9.853 | 8.877 | 4.552 | 65.484 | 20 | 1.961 × 10−4 |
| SCA | 22.737 | 20 | 7.655 | 7.449 | 216.086 | 17.382 | 1.237 × 10−3 |
| True Value | PSO | FPA | TSA | SCA | MFO | IMFO | |
|---|---|---|---|---|---|---|---|
| τmax (Nm) | 15.9 | 19.7568 | 13.6891 | 20 | 17.3818 | 17.6930 | 15.26 |
| Error % | 24.25 | 13.90 | 25.78 | 9.31 | 11.28 | 4.01 | |
| Sk (p.u.) | 0.254 | 0.0242 | 0.1156 | 0.0490 | 0.0743 | 0.102 | 0.245 |
| Error % | 90.47 | 54.48 | 80.71 | 70.75 | 59.84 | 3.54 |
| PSO | FPA | TSA | SCA | MFO | IMFO | |
|---|---|---|---|---|---|---|
| Min. | 1.287 × 10−1 | 2.933 × 10−1 | 1.961 × 10−4 | 1.237 × 10−3 | 1.404 × 10−4 | 7.106 × 10−5 |
| Max. | 3.0070 | 0.7237 | 4.9092 | 0.2916 | 1.3705 | 18.4858 |
| Mean | 0.9922 | 0.3514 | 0.5587 | 0.8834 | 0.4189 | 3.7533 |
| Std. | 1.3903 | 0.1316 | 1.5418 | 0.1402 | 0.6567 | 7.7657 |
| Algorithms | Friedman Ranking | Final Ranking |
|---|---|---|
| IMFO | 1 | 1 |
| MFO | 2.4 | 2 |
| SCA | 4.2 | 4 |
| TSA | 3.2 | 3 |
| FPA | 6.2 | 6 |
| PSO | 5.1 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danin, Z.; Sharma, A.; Averbukh, M.; Meher, A. Improved Moth Flame Optimization Approach for Parameter Estimation of Induction Motor. Energies 2022, 15, 8834. https://doi.org/10.3390/en15238834
Danin Z, Sharma A, Averbukh M, Meher A. Improved Moth Flame Optimization Approach for Parameter Estimation of Induction Motor. Energies. 2022; 15(23):8834. https://doi.org/10.3390/en15238834
Chicago/Turabian StyleDanin, Zekharya, Abhishek Sharma, Moshe Averbukh, and Arabinda Meher. 2022. "Improved Moth Flame Optimization Approach for Parameter Estimation of Induction Motor" Energies 15, no. 23: 8834. https://doi.org/10.3390/en15238834
APA StyleDanin, Z., Sharma, A., Averbukh, M., & Meher, A. (2022). Improved Moth Flame Optimization Approach for Parameter Estimation of Induction Motor. Energies, 15(23), 8834. https://doi.org/10.3390/en15238834








