Improved Moth Flame Optimization Approach for Parameter Estimation of Induction Motor

Abstract

The effective deployment of electrical energy has received attention because of its environmental implications. On the other hand, induction motors are the primary equipment used in many industries. Industrial facilities demand the maximum percentage of energy. This energy demand is determined by the operating circumstances imposed by the internal characteristics of the induction motor. Because internal parameters of an induction motor are not immediately measurable, they must be obtained through an identification process. This paper proposed an improved version of moth flame optimization (IMFO) for the efficient parameter estimation of induction motors. A steady-state equivalent circuit of the induction motor is employed for the simulation. The proposed technique handles the parameter estimation problem better than moth flame optimization (MFO), particle swarm optimization (PSO), the flower pollination algorithm (FPA), the tunicate swarm algorithm (TSA), and the sine cosine algorithm (SCA). The anticipated IMFO reduces the cost function by 49.38% as compared with the basic version of MFO.

1. Introduction

The environmental implications of excessive electricity usage have recently drawn attention in various domains of engineering. As a result, improving machinery and elements with elevated electrical energy usage stages has become a crucial challenge nowadays [1,2].

Induction motors have numerous advantages, including their strength and durability, low cost, low repairs, and ease of operation [3,4]. Alternatively, induction motors account for more than half of the electric energy ingested by industrial plants. Electrical energy ingestion has risen exponentially in recent years due to the widespread use of induction motors. These circumstances created a need to enhance the performance of induction motors, which is primarily determined by their internal parameters. The problem of parameter estimation for induction motors becomes complex because of the nonlinear nature of the equivalent circuit of induction motors [5,6]. Different methods and software have been developed and suggested to find parameters of AC motor equivalent circuits [6,7,8,9,10]. Lu et al. [9] surveyed more than twenty techniques for estimating the efficiency of induction motors regarding aspects of their ease of implementation. In this survey, approaches based on induction motor equivalent circuits are considered the least disruptive. In another study [10], a shaft torque approach is implemented to detect shaft torque and rotor speed from the shaft, eliminating the necessity to estimate losses. It provides the most precise field-efficiency rating but is also the most obtrusive approach.

Different algorithms were proposed (e.g., optimization technique minimizing prediction error [11], upgraded nonlinear least-mean-squares algorithms [12,13], and method of recursive identification [14]) to improve the stability and precision of equivalent parameter calculations. The previously used co-call conventional algorithms suffer from low convergence ability and, therefore, provide the wrong results in many cases. Recently, evolutionary approaches have evolved as the most efficient approach to tackle the challenge of parameter estimation in induction motors. In general, they have outperformed deterministic techniques in terms of precision and reliability under various conditions. Some of the approaches employed in the estimation of parameters in induction motors include particle swarm optimization (PSO) [15,16], artificial immune system (AIS) [17], and genetic algorithms (GA) [18]. Sakthivel et al. employed the bacterial foraging (BF) approach to estimate the parameters of a 5 HP induction motor [19]. The simulation results clearly illustrate the superiority of BF over other evolutionary approaches such as PSO and immune algorithm (IA). The modified shuffled frog-leaping (MSFL) technique is implemented by Perez et al. [20]. The power factor and torque were used as objective functions to minimize the difference between calculated and manufacturers’ data. The outcomes were analyzed and compared to those achieved with differential evolution (DE), GAs, PSO, and SFLA. The MSFL depicted its supremacy in terms of the low value of the objective function and computational time.

In recent times, the electrostatic discharge optimizer (EDO) has been anticipated by researchers [21]. The implemented EDO approach proved its efficient capability when compared to other metaheuristic approaches such as the water cycle algorithm (WCA) and GA. EDO was able to produce zero error between simulated and manufacturers’ data for both cases, i.e., single-cage model and double-cage model. Well-known metaheuristic approaches, as a rule, showed sufficient results compared with conventional methods. However, to date, additional efforts should have been done for improving the sustainability, speediness, and additional accuracy of motor parameters.

In summary, researchers investigated various empirical and metaheuristic techniques for parameter extraction of three-phase induction motors. However, there is the potential to investigate freshly invented, improved, and hybridized algorithms based on the no-free lunch (NFL) theory for parameter extraction of three-phase induction motors. This leads us to build and design an improved metaheuristic method for parameter extraction of induction motors. The efficiency of any optimization algorithm is determined by how efficiently it traverses the search space and swiftly identifies the global optimal solution without becoming caught in the local optimal solution. As a result, this research article provides an improved version of the moth flame optimization technique based on Lévy flight distribution (IMFO). The following are the primary contribution of the current paper:

• An improved version of MFO is proposed for the parameter estimation of a three-phase induction motor based on experimental data.
• The Lévy flight distribution is introduced in the standard version of MFO to increase the exploitation capability.
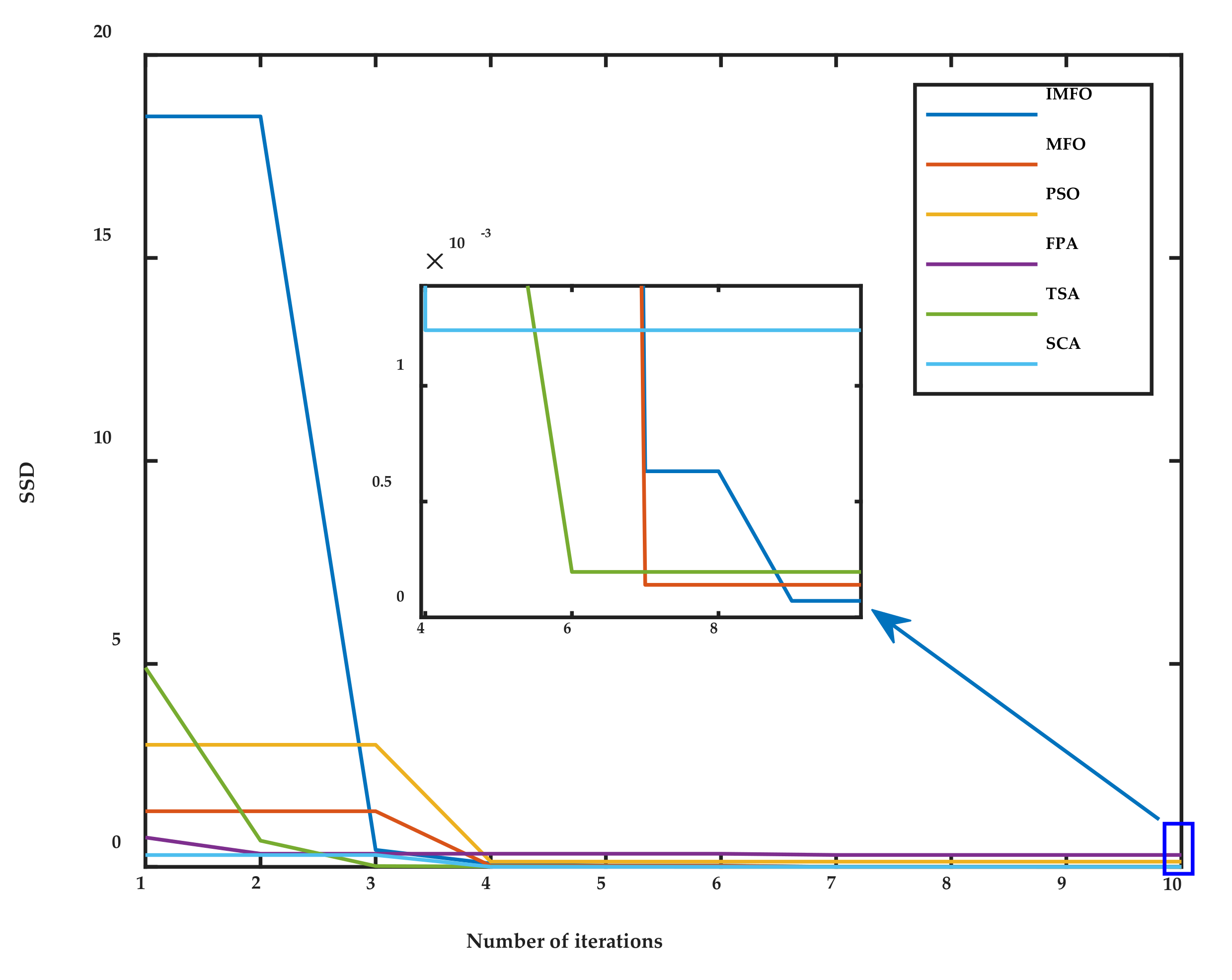
• The proposed approach is evaluated against other recently developed metaheuristics approaches such as TSA, SCA, MFO, FPA, and PSO.

The remaining part of this research investigation is organized as follows: Section 2 gives an overview of the problem formulation. Section 3 outlines the motivation and foundation of the proposed IMFO approach. The implementation of the proposed IMFO is illustrated in Section 4. Section 5 provides the results and discussion, and finally, conclusive remarks on the proposed study are presented in Section 6.

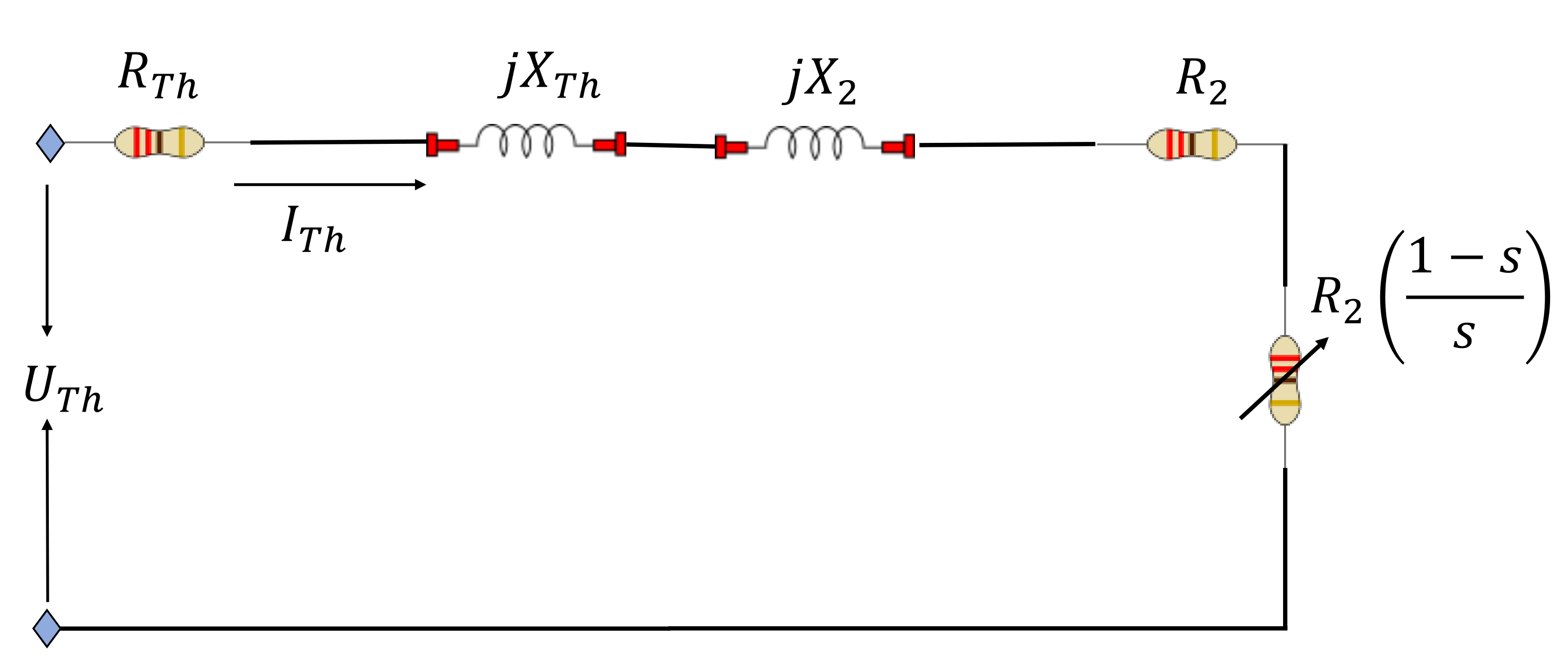
2. Materials and Methods

Alternating current (AC) induction motor functionality can be described in various forms. The most fundamental method to determine the dynamic and steady-state behavior of electrical motors is by the description of electromagnetic interactions between windings. This method was chosen earlier by Kraus et al. [22] and Leonhard [23], and many others. Nevertheless, analytical difficulties force this approach to find more convenient approaches that can be implemented relatively easily but with a high precision of obtained results. Such a method exists and is based on the study of the equivalent motor circuit [24]. An equivalent circuit ensures the development of output and input characteristics: rotation velocity vs. motor torque, input current, power, and power factor. Most applications should be a T-equivalent AC motor network representing stator and be reduced to stator rotor circuits, as shown in Figure 1.

The motor diagram includes equivalent resistances and inductive reactance of stator $R_1$, $X_1$, and rotor $R_2/s$, $X_2$, as well as the reactance of a stator magnetizing branch X_m. Parameter s designates motor velocity slip as a relative backlog of motor velocity vs. synchronous speed. For the convenience of representing rotor losses separately from an output motor power, the resistance $R_2/s$ is divided into two resistive components, $R_2$, determining resistive rotor losses and $R_2\left(1-s\right)/s$ defining output motor power. The equivalent circuit (Figure 1) ensures the assessment of input motor parameters as:

$${\left(I_{\mathit{in}}\right)}_{\mathit{ph}}=\frac{U_{\mathit{ph}}}{Z_{\mathit{in}}}$$

(1)

$$Z_{\mathit{in}}=R_1+{\mathit{jX}}_1+\frac{{\mathit{jX}}_m\left(\frac{R_2}{s}+{\mathit{jX}}_2\right)}{\frac{R_2}{s}+\left({\mathit{jX}}_m+X_2\right)}=R_1+{\mathit{jX}}_1+\frac{{\mathit{jX}}_m\left(R_2+{\mathit{jX}}_{2}s\right)}{R_2+\mathit{js}\left(X_m+X_2\right)}$$

(2)

$$P_{\mathit{in}}=3{\left(I_{\mathit{in}}\right)}_{\mathit{ph}}\cdot U_{\mathit{ph}}\cdot \mathit{cos}\phi$$

(3)

$$\mathit{cos}\phi =\mathit{cos}\left(\mathit{arg}\left(Z_{\mathit{in}}\right)\right)$$

(4)

where $\mathit{cos}\phi$ represents the power factor, $P_{\mathit{in}}$ denotes the input power, ${(I_{\mathit{in}})}_{\mathit{ph}}$ signifies the input phase current, and $U_{\mathit{ph}}$ and $Z_{\mathit{in}}$ are known as phase voltage and input impedance, respectively.

However, the calculations of output characteristics with the T-equivalent diagram are relatively complicated since there is a need to combine a system of equations describing two parallel branches: one of a magnetizing circuit and another of the output circuit. The Thevenin approach [25] application can be recommended for facilitating the complexity of parameter estimation. The Thevenin theorem suggests a transformation of the initial T-diagram to a simpler single-branch circuit, as shown in Figure 2.

Thevenin voltage ($U_{\mathit{Th}}$), resistance ($R_{\mathit{Th}}$), and reactance ($X_{\mathit{Th}}$) are calculated as per [25]:

$$U_{\mathit{Th}}=\frac{X_m}{X_m+X_1}=\gamma ; R_{\mathit{Th}}=R_1{\left(\frac{X_m}{X_m+X_1}\right)}^2=R_1\cdot {\gamma }^2; X_{\mathit{Th}}=X_1$$

(5)

where coefficient γ is used for the convenience of the representation of Thevenin parameters. The output characteristics of a motor can be calculated by using the following expressions:

$${\tau }_{\mathit{ind}}=\frac{\frac{3U_{\mathit{Th}}^2{R}_{2}s}{{\omega }_S}}{{\left(s{R}_{\mathit{Th}}+R_2\right)}^2+s^2{\left(X_{\mathit{Th}}+X_2\right)}^2}$$

(6)

where, ${\tau }_{\mathit{ind}}$ signifies the output motor torque, and slip s of a motor speed is calculated as:

$$s=1-\frac{{\omega }_m}{{\omega }_s}$$

(7)

The benefits of the equivalent circuit approach mentioned above can be useful if and only if all equivalent parameters are determined and well-known. The task of a parameters assessment involves complex computation, and until now, none of the developed methods can be considered absolutely priority and final. Below, deterministic approaches are compared with different heuristic strategies showing significant advantages for solving the aforementioned task. Among them, we represent an improved version of MFO providing better convergence and accuracy.

3. Objective Function

The primary target of equivalent circuit parameter extraction is to discover optimized values of parameters (i.e., $R_1$, $R_2$, $X_1$, $X_2$, $X_m$, and ${\tau }_{\max }$) that reduce the discrepancies between a computed and measured value of torque regarding motor velocity. In accordance, the objective function has been established on the basis of a Least-Mean-Square approach (LMS) applicable in plenty of applications [26], which represents the sum of squares deviations which are calculated as the difference between measured and calculated torque. The main objective of optimal searching is to obtain the parameters set, providing the minimum of the established objective function. The initial selection of parameters and their modifications through the searching procedure is carried out with each of the heuristic’s approaches analyzed in this work. The objective function is as follows:

$$Z={\displaystyle \sum }_i^N{\left({\tau }_i-\frac{\frac{3U_{\mathit{Th}}^2{R}_{2}s}{{\omega }_S}}{{\left(s{R}_{\mathit{Th}}+R_2\right)}^2+s^2{\left(X_{\mathit{Th}}+X_2\right)}^2}\right)}^2\to \mathit{MIN}$$

(8)

where $N$ signifies the total number of observations, $U_{\mathit{Th}}$ defines Thevenin voltage, $R_{\mathit{Th}}$ signifies the resistance, $X_{\mathit{Th}}$ represents reactance, ${\omega }_S$ synchronous speed, $R_2$ represents rotor resistance, s denotes slip, and ${\tau }_i$ denotes the measured value of torque.

4. Improved Moth Flame Optimization

4.1. Moth Flame Optimization

In 2015, Mirjalili et al. anticipated the moth flame optimization (MFO) algorithm for solving optimization problems related to engineering [27]. The MFO algorithm is driven by the unique night navigation methods of moths. They have learned to fly at night by utilizing moonlight. They navigate via a process known as transverse orientation. The moth moves in a straight line over a large distance by maintaining a constant angle with respect to the moon. However, the moth becomes trapped in a spiral pattern around ambient light and eventually converges on it. In the search space, a random swarm of moths is created. Their locations are adjusted in relation to the flame in a spiral pattern so that the moth’s movement does not surpass the search space. Moths are known to travel in all orientations in a hyper ellipse around the flame. Because the motion of moths towards the flame causes the algorithm to become caught in local optima, each moth’s position with its corresponding flame is adjusted. This makes each moth go around more than one flame and makes it less likely for local optima stagnation to happen. The following equation is utilized to compute the number of flames.

$$\mathit{flame} \mathit{number}=\mathit{round} \left(\left(N-L\right)\times \frac{N-1}{T}\right)$$

(9)

where N represents the maximum number of flames, T denotes the maximum number of iterations, and L signifies the current number of iterations.

The position of each moth, with respect to a flame, is adjusted according to the following equation:

$$K_i=S\left(K_i, F_j\right)$$

(10)

where $K_i$ stands for the i^th moth, $S$ represents a spiral function, and $F_j$ denotes the location of j^th flame.

The spiral function ($S)$ is defined as follows:

$$S\left(K_i,F_j\right)=d_i\times e^{\mathit{at}}\times \mathit{cos}\left(2\pi t\right)+F_j$$

(11)

where $a$ denotes the constant for maintaining the shape of the logarithm spiral, $d_i$ signifies the distance between the j^th flame and the i^th moth, and $t$ defines the random number between −1 and +1.

The value of $d_i$ is computed by using Equation (12):

$$d_i=\left|F_j-K_i \right|$$

(12)

where $K_i$ stands for the location of i^th moth, $F_j$ signifies the location of j^th flame, and the distance between j^th flame and i^th moth is denoted by $d_i$. The navigation movement of the moths around the flames is illustrated in Figure 3.

4.2. Lévy Flight Distribution

Benoît Mandelbrot, a scientist, introduced the concept of Lévy’s flight to define the step sizes of various durations [27]. He also anticipated the concept of Cauchy and Rayleigh flights for step sizes with Cauchy and ordinary distributions. Lévy flight is a non-Gaussian probabilistic random process in which the step lengths are selected by the Lévy distribution. The following is an outline of the mathematical framework of Lévy’s flight:

The Lévy distribution is described as follows:

$$L \left(s\right)~{\left|s\right|}^{-1-\beta }$$

(13)

where $\beta$ signifies the random integer value between 0 and 2, and $s$ illustrates the step size.

The value of step size $s$ is estimated by Equation (14).

$$s=\frac{u}{{\left|v\right|}^{\frac{1}{\beta }}}$$

(14)

where $u$ and $v$ define the normal distribution.

4.3. Improved Moth Flame Optimization (IMFO)

The proposed improved moth flame optimization (IMFO) is discussed in this section. Any metaheuristic algorithm’s efficiency when solving any complex optimization problem is primarily determined by how effectively the algorithm explores each area of the search space, as well as how effectively the algorithm exploits the most promising areas explored during the exploration phase. Most of the metaheuristic algorithms struggled to achieve harmony between these two essential stages and so failed to find the optimum solution in the search space. Hybridization and enhancement of the established algorithms are the only two notable ways to maintain a reasonable trade-off between these two stages.

MFO is a scalable and easy-to-implement algorithm that has been effectively evaluated on a variety of scientific and engineering challenges. The MFO algorithm, on the other hand, has several disadvantages, such as being caught in a local optimal solution and having a sluggish convergence speed. As specified by the No Free Lunch theorem [28], no technique can tackle all optimization problems. In this regard, an improved version of the moth flame optimization technique is proposed in this research article by incorporating the Lévy flight mechanism in the exploitation phase. The proposed modification eliminates the above-stated disadvantages and can obtain the optimal solution for complex optimization problems such as the parameter estimation of the induction motor. The flow chart of the proposed IMFO is illustrated in Figure 4. Algorithm 1 illustrates the pseudo code for the IMFO algorithm.

Algorithm 1. Pseudo-code for improved moth flame optimization (IMFO) algorithm.

Initialization of location of moths in the search space While(iteration <= Maximum iteration) Update the number of flames by utilizing Equation (9) OM = Fitness Function (Equation (8)) ifiteration = 1    F = sort(M);    OF = sort (OM); else    F = sort (Kt−1, Kt);    OF = sort (Kt−1, Kt); end  for i = 1: n     for j = 1: d      Calculate D using Equation (12) with respect to the corresponding moth      Update K(i,j) using Equations (10), (11) and (13) with respect to the corresponding moth      end end

5. Results and Discussion

5.1. Parameter Estimation of Induction Motor

The proposed IMFO approach for parameter estimation is evaluated on a 1 kW three-phase induction motor. To assess and evaluate the effectiveness of the proposed IMFO algorithm, a comparative analysis with moth flame optimization (MFO) [27], PSO [29], the flower pollination algorithm (FPA) [30], the tunicate swarm algorithm (TSA) [31], and the sine cosine algorithm (SCA) [32] was conducted. The number of objective function evaluations is kept similar in all approaches to perform a valid comparison among the selected metaheuristics algorithms.

Several parameters must be defined for the proposed IMFO implementation, including the number of moths or population size, the number of iterations, and a constant (b). Whereas the number of moths is taken as 30, the number of iterations is taken as 10, and the value of the constant (b) is defined as 1. These parameters are precisely chosen to ensure the efficient performance of IMFO. The value of all parameters utilized in the simulations are shown in

Table 1. The parameter configuration of all compared algorithms.

Algorithm	Parameter	Value
IMFO	Constant parameter (b)	1
	Number of moths	30
	Number of iterations	10
MFO	Constant parameter (b)	1
	Population size	30
	Number of iterations	10
PSO	C1	1.5
	C2	1.5
	Number of particles	30
	Wmin	0.4
	Wmax	0.9
FPA	Coefficient value (a)	2
	Switch probability (p)	0.8
	Population size	30
	Number of iterations	10
TSA	Constant parameter (Pmin)	1
	Constant parameter (Pmax)	4
	Population size	30
	Number of iterations	10
SCA	Controlling parameter (r1)	[0, 2]
	Population size	30
	Number of iterations	10

.

Table 2. Range of all parameters.

Parameter	Lower Bound	Upper Bound
$R_1$	0	30
$R_2$	0	20
$X_1$	0	35
$X_2$	0	35
$X_m$	0	340
${\tau }_{\max }$	0	20

shows the upper and lower bounds for all six parameters of the three-phase induction motor. All tests are run on MATLAB 2021a, Windows 10 64-bit, with an Intel Core i5 processor operating at 4.8 GHz with 8 GB of RAM. For a true assessment, all algorithms are assessed using the same number of search agents, i.e., 30 for a total of 10 runs.

Table 3. Optimized value of all parameters.

Algorithms	${\mathit{R}}_1 \left(\mathsf{\Omega }\right)$	${\mathit{R}}_2 \left(\mathsf{\Omega }\right)$	${\mathit{X}}_1 \left(\mathsf{\Omega }\right)$	${\mathit{X}}_2 \left(\mathsf{\Omega }\right)$	${\mathit{X}}_{\mathit{m}} \left(\mathsf{\Omega }\right)$	${\mathit{\tau }}_{\max } \left(\mathbf{Nm}\right)$	SSD
IMFO	27.381	15.638	15.259	15.259	230.692	15.262	7.106 × 10−5
MFO	17.282	10.747	0	12.443	300.401	17.693	1.404 × 10−4
PSO	24.919	14.574	13.258	10.526	238.1859	19.757	1.287 × 10−1
FPA	9.996	15.494	8.374	2.071	267.785	13.689	2.933 × 10−1
TSA	13.907	9.853	8.877	4.552	65.484	20	1.961 × 10−4
SCA	22.737	20	7.655	7.449	216.086	17.382	1.237 × 10−3

illustrates the optimized value of all the parameters. It is very evident from Table 3 that the proposed IMFO approach gives the most optimized value of all the parameters with the least value of SSD (7.1059 × 10⁻⁵).

Table 4. Error of all compared algorithms.

	True Value	PSO	FPA	TSA	SCA	MFO	IMFO
τmax (Nm)	15.9	19.7568	13.6891	20	17.3818	17.6930	15.26
Error %		24.25	13.90	25.78	9.31	11.28	4.01
Sk (p.u.)	0.254	0.0242	0.1156	0.0490	0.0743	0.102	0.245
Error %		90.47	54.48	80.71	70.75	59.84	3.54

depicts the percentage of error between experimental and simulated values.

The torque vs. slip characteristic is redrawn based on the optimized value of all parameters and is illustrated in Figure 5. In Figure 5, solid line represents theoretical values while shapes illustrate the measured values. It is very clear from Figure 5 that the proposed IMFO approach obtains a good coincidence between measured and simulated values of torque and critical slip as compared to other metaheuristics approaches. This suggests that the anticipated IMFO approach outperforms other methods.

5.2. Convergence Analysis

Figure 6 depicts the convergence curves of the equivalent circuit for three phase induction motor. Figure 6 specifies that the proposed IMFO algorithm surpasses the MFO, PSO, FPA, TSA, and SCA algorithms in terms of convergence speed and offers a genuine outcome for the same amount of function evaluations (i.e., 10).

The proposed IMFO algorithm obtains the least value of SSD (7.106 × 10⁻⁵). At the same time, the MFO and TSA provide the second-best SSD values of 1.404 × 10⁻⁴ and 1.961 × 10⁻⁴, respectively. The rationale for this is that the intensification or exploitation of the prior solutions of these techniques is less. The worst value of SSD is provided by the SCA, PSO, and FPA as 1.237 × 10⁻³, 1.287 × 10⁻¹, and 2.933 × 10⁻¹, respectively. The SCA, PSO, and FPA show their poor performance because of getting trapped in the local minima. More iterations and search agents are required to achieve the results of IMFO, and this will increase the computational cost.

5.3. Statistical Analysis

This section presents statistical assessments based on minimum, standard deviation, maximum, and mean in terms of SSD for all previously mentioned approaches, as well as a comparison with the precision and reliability of the different algorithms in a maximum of ten runs, as demonstrated in

Table 5. Statistical analysis for all algorithms.

	PSO	FPA	TSA	SCA	MFO	IMFO
Min.	1.287 × 10−1	2.933 × 10−1	1.961 × 10−4	1.237 × 10−3	1.404 × 10−4	7.106 × 10−5
Max.	3.0070	0.7237	4.9092	0.2916	1.3705	18.4858
Mean	0.9922	0.3514	0.5587	0.8834	0.4189	3.7533
Std.	1.3903	0.1316	1.5418	0.1402	0.6567	7.7657

Min.: Minimum, Max.: Maximum, Std.: Standard.

.

The determination of the precision of the algorithms is based on the comparison between the SSD mean value and its standard deviation. Both these parameters should have been computed previously. This provides the ability to assess the trustworthiness of the specific method. The results of the statistical study show that the proposed IMFO approach is the most accurate and useful for finding equivalent parameters since it has the lowest standard deviation. The superiority of the proposed IMFO algorithm lies in avoiding the local optimal solution and fast convergence speed as compared to other metaheuristic algorithms. The Friedman ranking test results are shown in

Table 6. Friedman ranking test for all compared metaheuristic algorithm.

Algorithms	Friedman Ranking	Final Ranking
IMFO	1	1
MFO	2.4	2
SCA	4.2	4
TSA	3.2	3
FPA	6.2	6
PSO	5.1	5

. It is very clear from Table 6 that proposed IMFO algorithm achieves the best ranking followed by MFO, TSA, SCA, PSO, and FPA.

5.4. Computational Time

Figure 7 depicts the average execution time of each algorithm for the equivalent circuit of a three-phase induction motor. In comparison to MFO, SCA, TSA, FPA, and PSO, the suggested IMFO algorithm takes about 10.9 s to execute, whereas FPA takes about 18.23 s. This analysis demonstrates that the Lévy flight mechanism improves the accuracy of the basic version of the MFO algorithm. Additionally, other improvements can be done to solve multi-objective issues.

6. Conclusions

This article emphasizes the substantial use of heuristic algorithms for finding parameters of the AC motor equivalent circuit. The presented work proposes an improved version of the original heuristic approach, namely moth flame optimization (MFO), for the estimation of induction motor parameters from experimental data. The suggested method considers a set of experimental torque-speed points measured in laboratory test. Based on these measured points, the application of the Kloss approach provides the magnitudes of maximum torque and critical slip. Further, maximum torque and critical slip values together with the Thevenin transformation ensure the final formulation of the objective function with the aim of reducing the difference between the experimental data and those that were obtained theoretically with the application of the simulating procedure. The essence of the improvement in moth flame optimization was the usage of Lévy flight distribution, which was incorporated during the exploitation phase of MFO to avoid the local minima. The usage of Lévy flight distribution considerably increases the accuracy of the conventional MFO and the estimation of motor parameters. The simulation results indicate the supremacy of the proposed IMFO approach as compared with other metaheuristic approaches. The results of comprehensive analysis between different metaheuristic algorithms showed that the developed algorithm is faster than MFO by 1.15 times, SCA by 1.43 times, TSA by 1.31 times, FPA by 1.67 times, and PSO by 1.31 times. Moreover, the proposed algorithm gives much better and more accurate results for maximum torque and critical slip values.

In the future, the efficiency of the proposed IMFO approach can be improved further in terms of fast convergence rate and low computational time by utilizing other metaheuristic approaches.