Numerical Simulation of the Combination of Novel Spiral Fin and Phase Change Material for Cylindrical Lithium-Ion Batteries in Passive Thermal Management
Abstract
:1. Introduction
2. Numerical Modelling
2.1. Physical Model
2.2. Assumptions and Governing Equations
- The physical properties of various materials inside the battery are consistent and isotropic.
- Joule heat is the main source of heat produced by batteries, ignoring the effect of reversible entropy heat generation.
- The thermal conductivity and specific heat capacity of the single battery and various performance parameters of the battery will not change due to changes in battery temperature and residual state of charge (SOC).
- The heat generation inside the battery is uniform.
- The solid and liquid phases of the PCM are homogeneous and isotropic.
- The density of the PCM is approximately determined by Boussinesq, and other thermophysical properties are constant and uniform. The Boussinesq model will take into account buoyancy during natural convection.
- The gravitational acceleration is constant 9.81 m/s2 in the negative Z-axis direction.
- Based on these assumptions, the governing equations are as follows:
- The energy equation for the battery can be expressed as [52]
2.3. Boundary Conditions and Calculation Steps
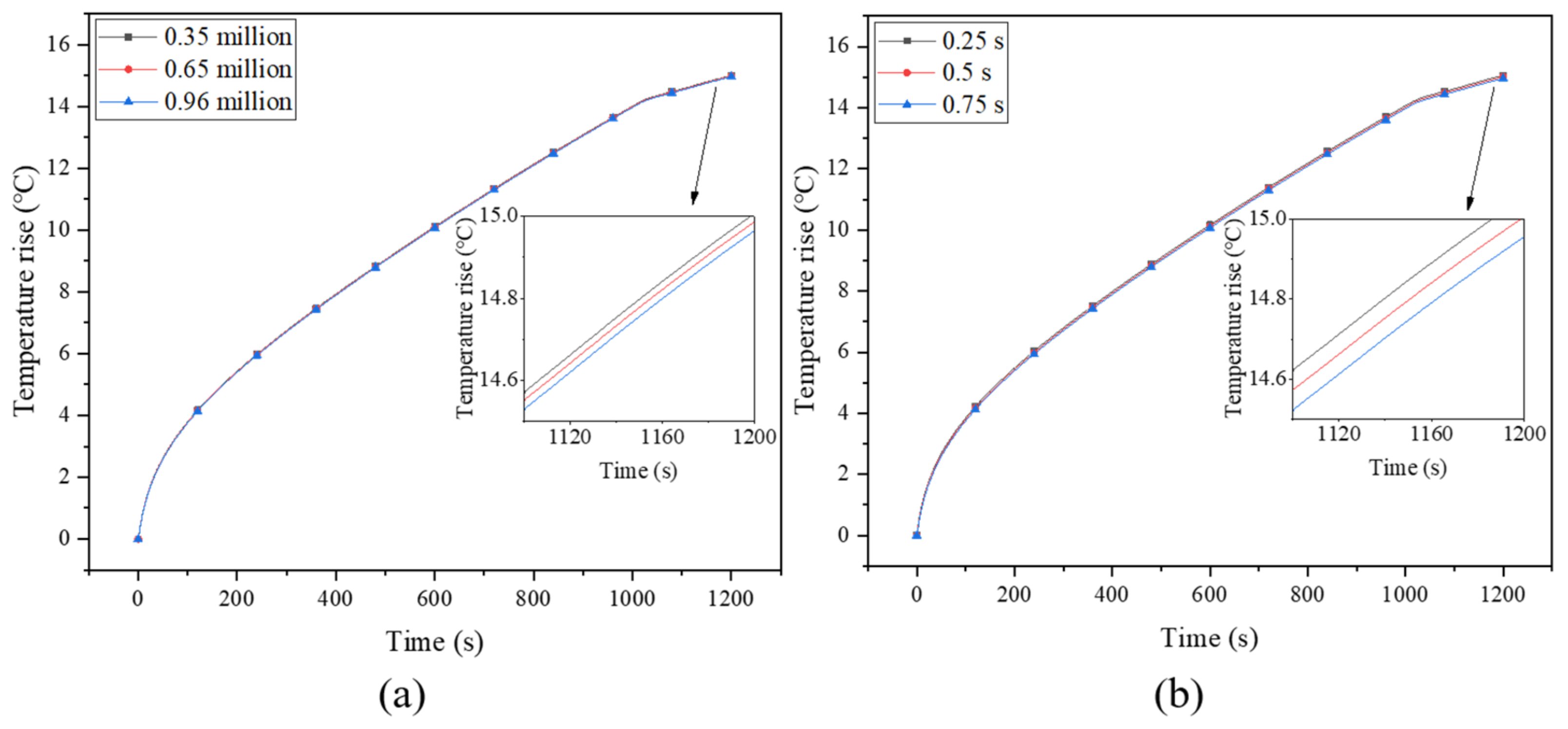
2.4. Grid Independence Test
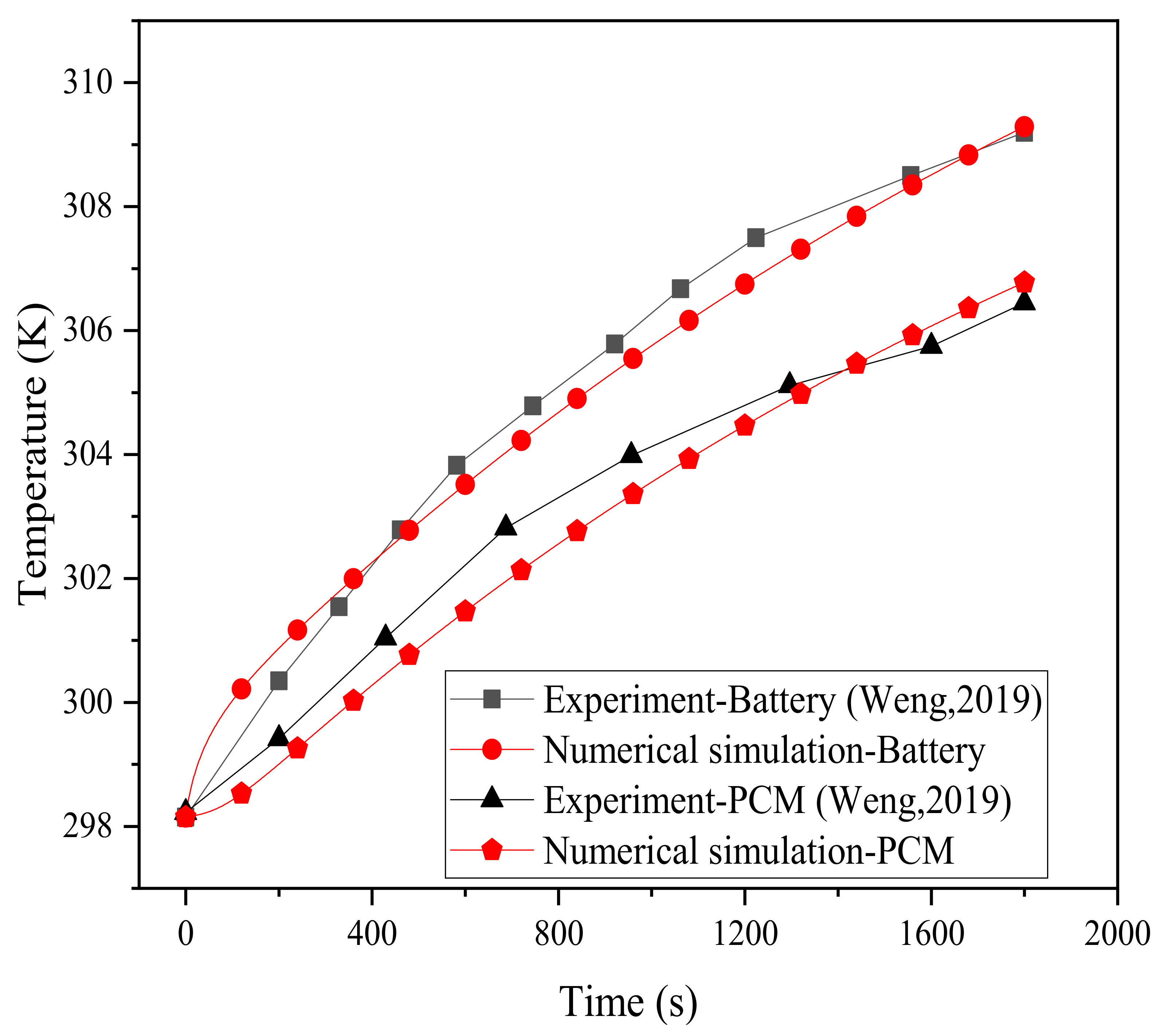
2.5. Model Validation
3. Results
3.1. The Effectiveness of Pure PCM
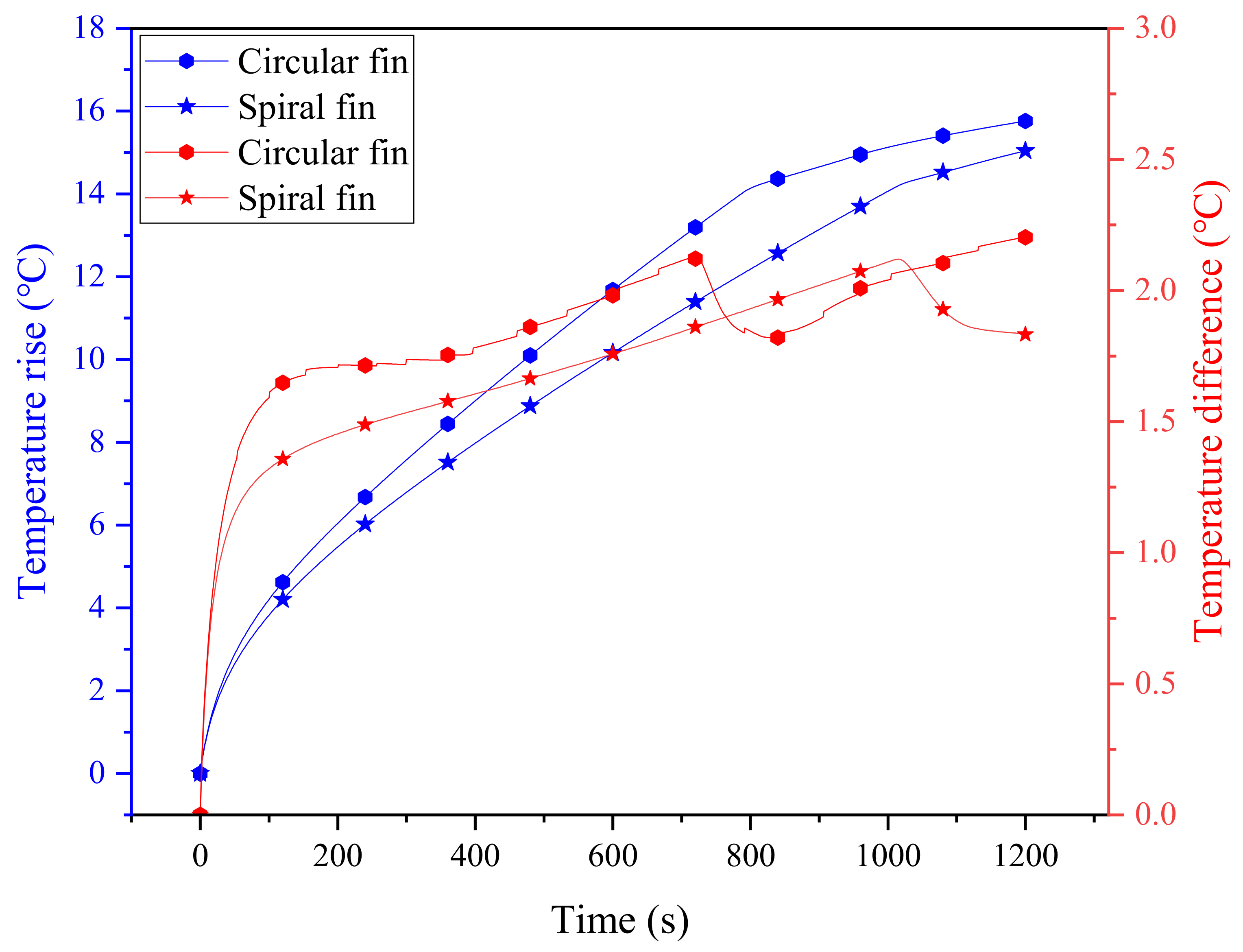
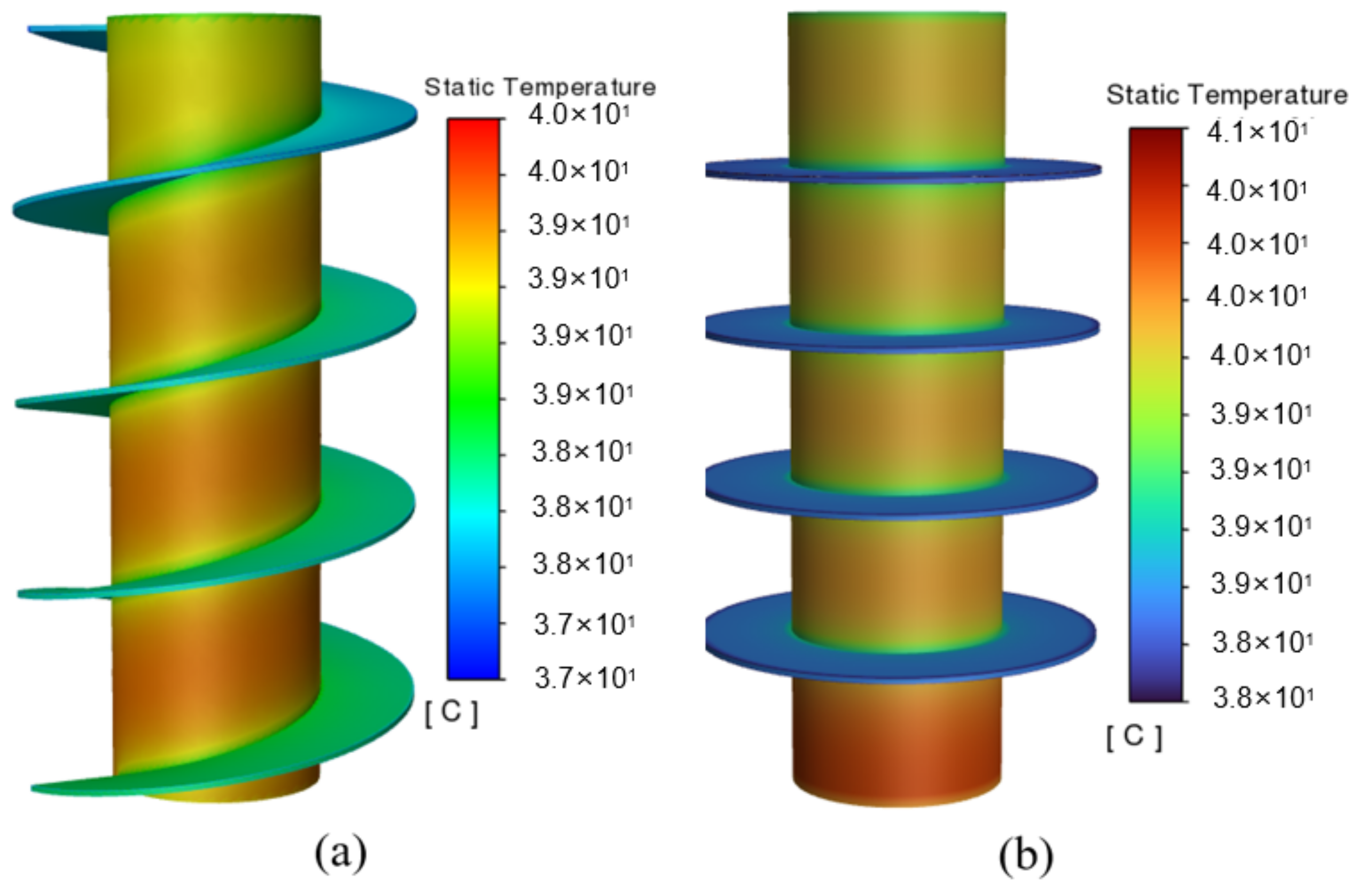
3.2. Comparison of Circular and Spiral Fins
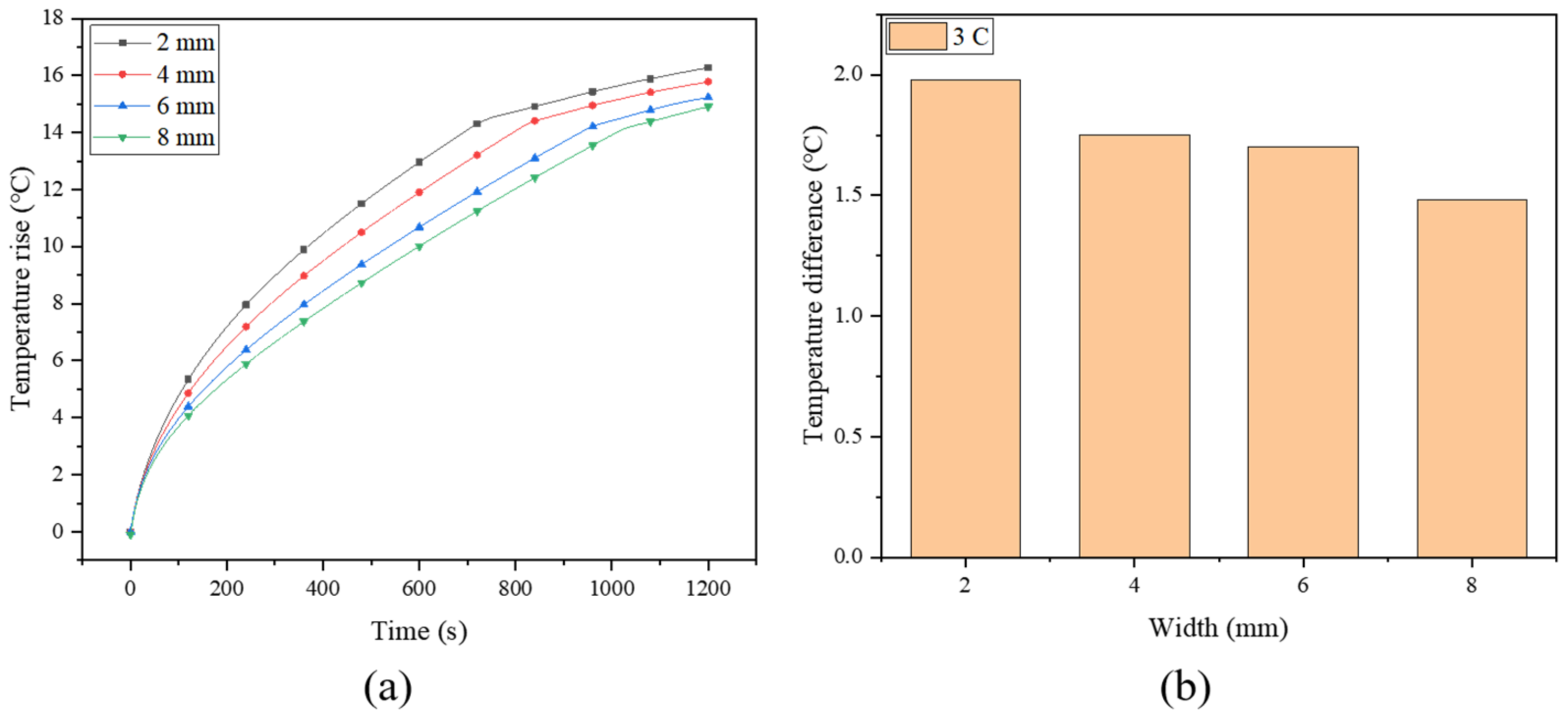
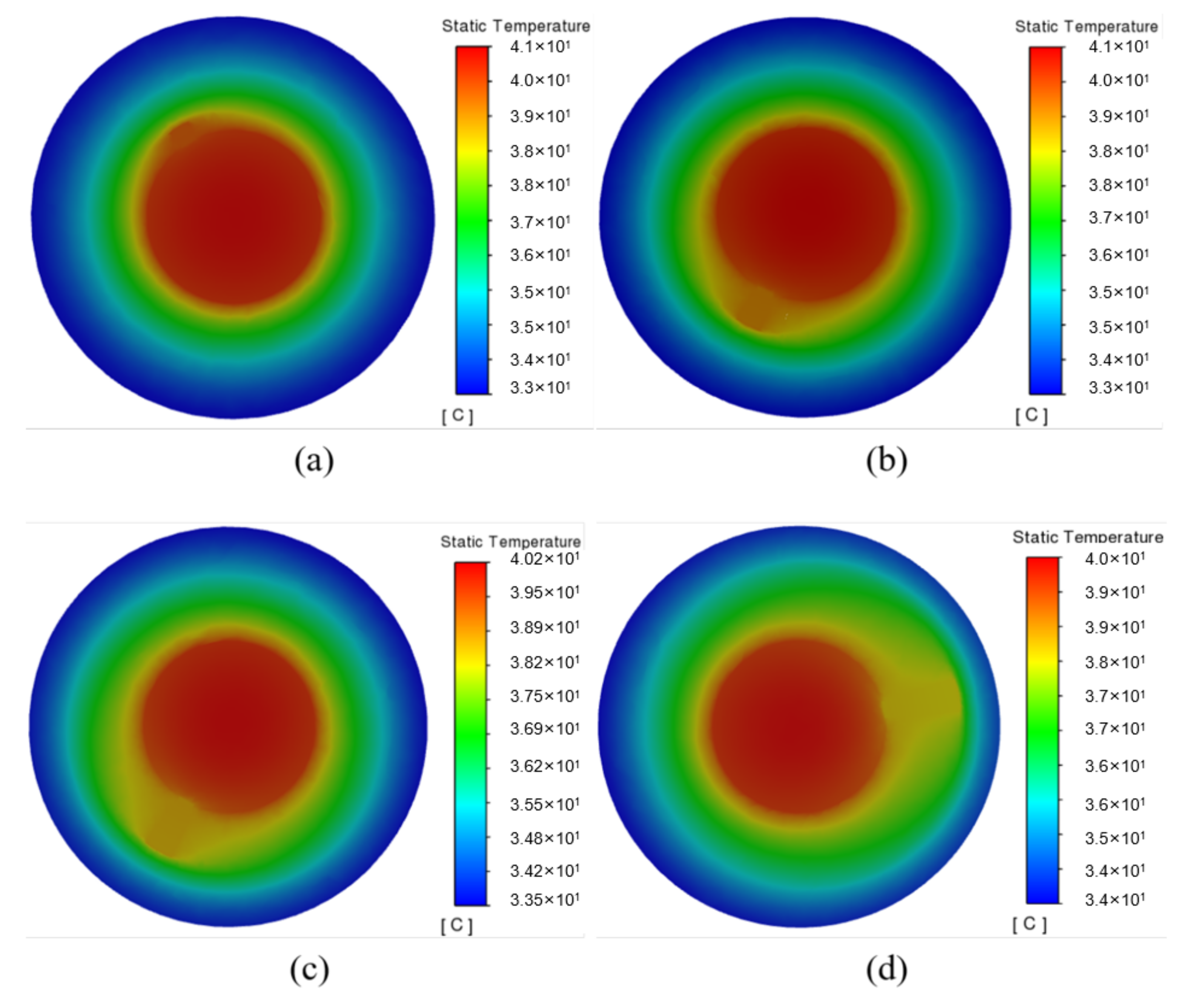
3.3. Influence of the Width of the Spiral Fin
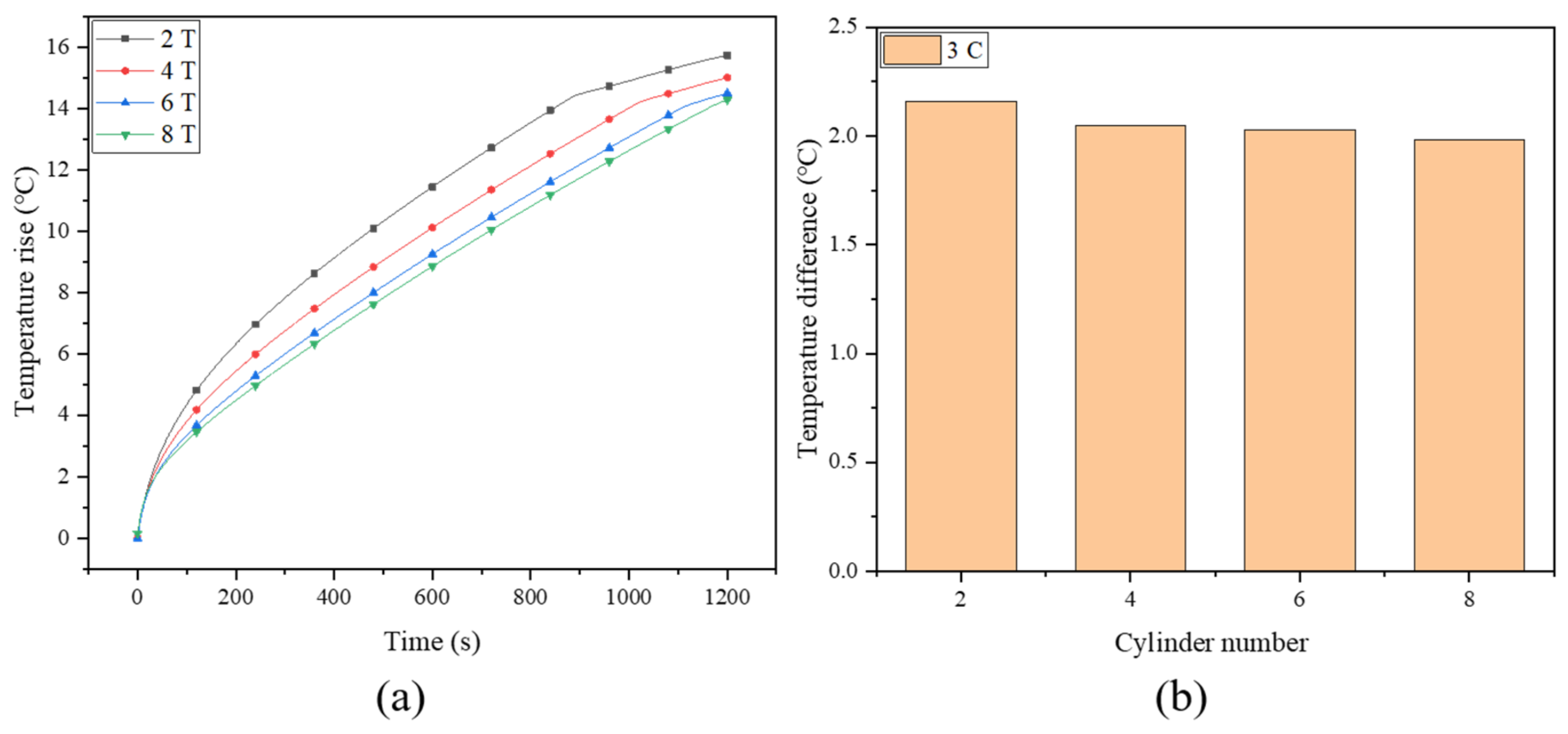
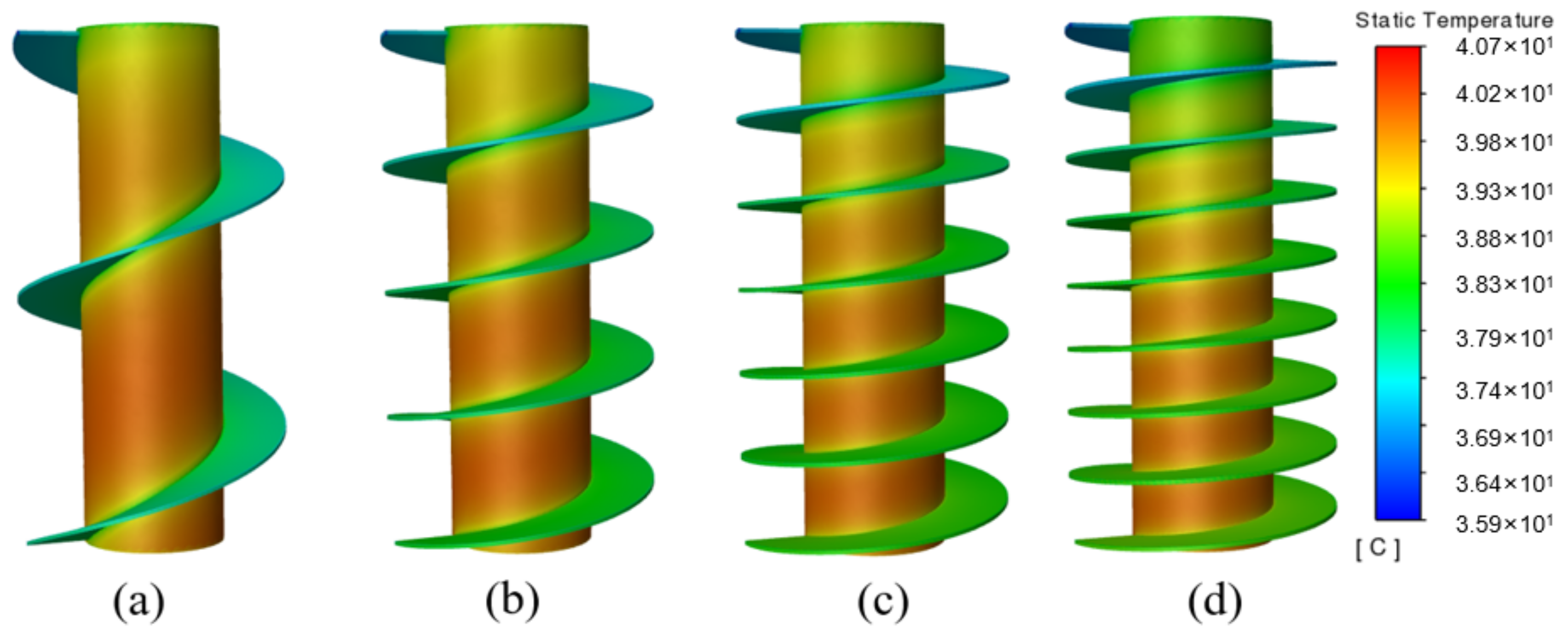
3.4. Influence of the Number of Spiral Turns
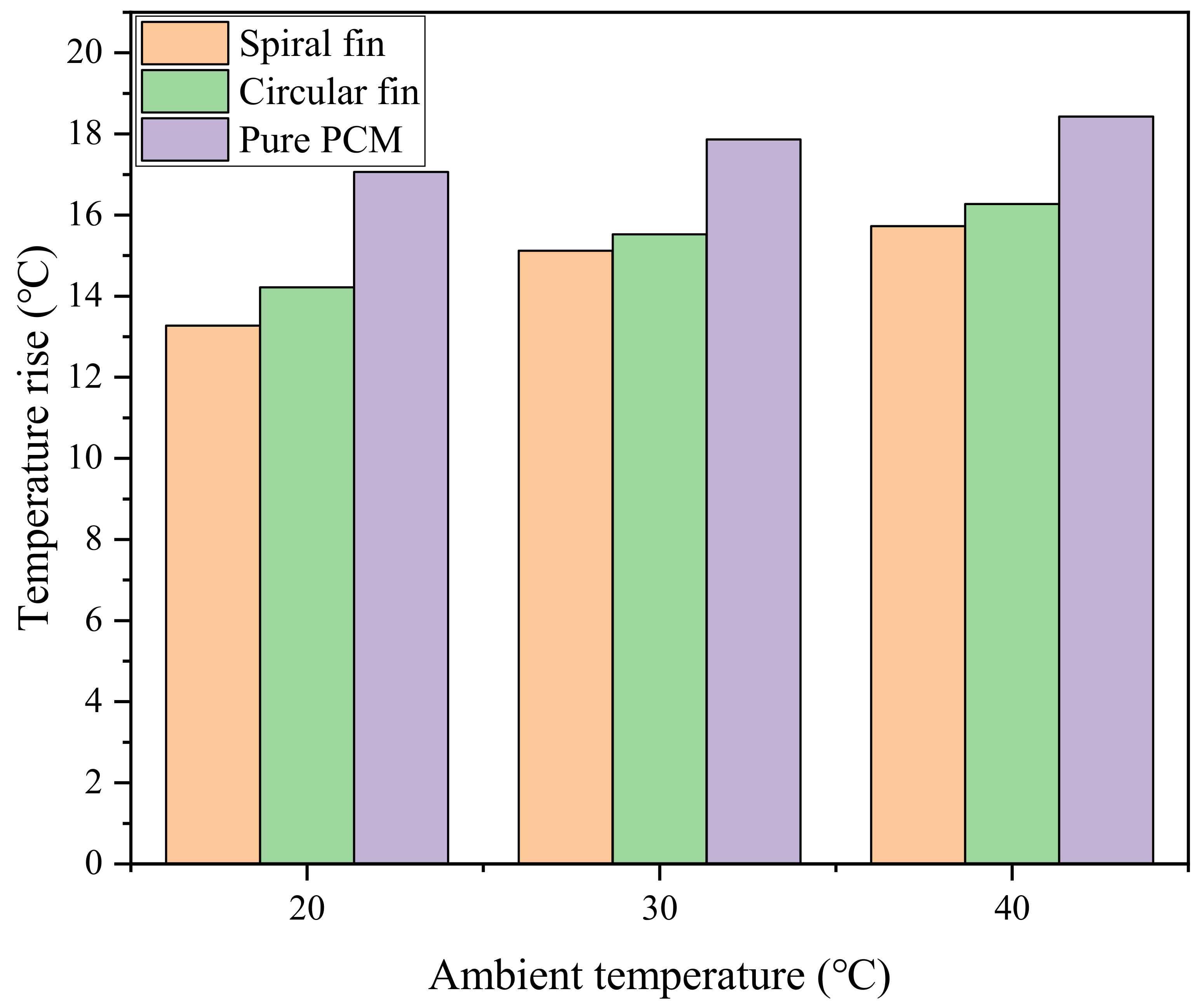
3.5. Influence of Ambient Temperature
4. Conclusions
- 1.
- Compared with circular fins, a spiral fin of the same line length can reduce the maximum temperature of the battery by 0.72 °C. The most important point is that the spiral fin showed a greater advantage in improving the temperature uniformity of the battery, which made the temperature difference decrease by 16.8%.
- 2.
- Compared with the finless system, when the width of the spiral fin was 2, 4, 6 and 8 mm, the maximum temperature of the battery decreased by 4%, 8.3%, 11.9% and 14.2%, respectively.
- 3.
- When the number of turns of the fin increased from 2 T to 8 T, the maximum temperature of the battery decreased from 40.88 °C to 39.28 °C. Moreover, when the number of turns increased from 6 T to 8 T, the temperature drop was no longer obvious, being only 0.22 °C.
- 4.
- When the ambient temperature was 20 °C, 30 °C and 40 °C, the maximum temperature rise of the PCM-spiral optimization system decreased by 3.78 °C, 2.74 °C and 2.71 °C, respectively, compared with the pure PCM system, and by 0.95 °C, 0.41 °C and 0.55 °C, respectively, compared with the PCM-circular system. This shows that the PCM-spiral fin system has certain advantages even in a high-temperature environment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shahbaz, M.; Raghutla, C.; Chittedi, K.R.; Jiao, Z.; Vo, X.V. The Effect of Renewable Energy Consumption on Economic Growth: Evidence from the Renewable Energy Country Attractive Index. Energy 2020, 207, 118162. [Google Scholar] [CrossRef]
- Xu, F.; Zhai, Y.; Zhang, E.; Liu, Q.; Jiang, G.; Xu, X.; Qiu, Y.; Liu, X.; Wang, H.; Kaskel, S. Ultrastable Surface-Dominated Pseudocapacitive Potassium Storage Enabled by Edge-Enriched N-Doped Porous Carbon Nanosheets. Angew. Chem. Int. Ed. Engl. 2020, 59, 19460–19467. [Google Scholar] [CrossRef] [PubMed]
- Tran, M.-K.; Akinsanya, M.; Panchal, S.; Fraser, R.; Fowler, M. Design of a Hybrid Electric Vehicle Powertrain for Performance Optimization Considering Various Powertrain Components and Configurations. Vehicles 2020, 3, 20–32. [Google Scholar] [CrossRef]
- Saw, L.H.; Poon, H.M.; Thiam, H.S.; Cai, Z.; Chong, W.T.; Pambudi, N.A.; King, Y.J. Novel Thermal Management System Using Mist Cooling for Lithium-Ion Battery Packs. Appl. Energy 2018, 223, 146–158. [Google Scholar] [CrossRef] [Green Version]
- Lander, L.; Kallitsis, E.; Hales, A.; Edge, J.S.; Korre, A.; Offer, G. Cost and Carbon Footprint Reduction of Electric Vehicle Lithium-Ion Batteries through Efficient Thermal Management. Appl. Energy 2021, 289, 116737. [Google Scholar] [CrossRef]
- Farag, M.; Sweity, H.; Fleckenstein, M.; Habibi, S. Combined Electrochemical, Heat Generation, and Thermal Model for Large Prismatic Lithium-Ion Batteries in Real-Time Applications. J. Power Sources 2017, 360, 618–633. [Google Scholar] [CrossRef]
- Weng, J.; Ouyang, D.; Yang, X.; Chen, M.; Zhang, G.; Wang, J. Alleviation of Thermal Runaway Propagation in Thermal Management Modules Using Aerogel Felt Coupled with Flame-Retarded Phase Change Material. Energy Convers. Manag. 2019, 200, 112071. [Google Scholar] [CrossRef]
- Wu, W.; Wu, W.; Wang, S. Form-Stable and Thermally Induced Flexible Composite Phase Change Material for Thermal Energy Storage and Thermal Management Applications. Appl. Energy 2019, 236, 10–21. [Google Scholar] [CrossRef]
- Malik, M.; Dincer, I.; Rosen, M.A. Review on Use of Phase Change Materials in Battery Thermal Management for Electric and Hybrid Electric Vehicles: Review on Use of PCM in Battery Thermal Management for EV and HEV. Int. J. Energy Res. 2016, 40, 1011–1031. [Google Scholar] [CrossRef]
- Zheng, Y.; Shi, Y.; Huang, Y. Optimisation with Adiabatic Interlayers for Liquid-Dominated Cooling System on Fast Charging Battery Packs. Appl. Therm. Eng. 2019, 147, 636–646. [Google Scholar] [CrossRef]
- Feng, X.; Xu, C.; He, X.; Wang, L.; Zhang, G.; Ouyang, M. Mechanisms for the Evolution of Cell Variations within a LiNixCoyMnzO2/Graphite Lithium-Ion Battery Pack Caused by Temperature Non-Uniformity. J. Clean. Prod. 2018, 205, 447–462. [Google Scholar] [CrossRef]
- Chen, K.; Chen, Y.; She, Y.; Song, M.; Wang, S.; Chen, L. Construction of Effective Symmetrical Air-Cooled System for Battery Thermal Management. Appl. Therm. Eng. 2020, 166, 114679. [Google Scholar] [CrossRef]
- Akinlabi, A.A.H.; Solyali, D. Configuration, Design, and Optimization of Air-Cooled Battery Thermal Management System for Electric Vehicles: A Review. Renew. Sustain. Energy Rev. 2020, 125, 109815. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Q.; Wang, T. Effects of Air-Cooling Structure on Cooling Performance Enhancement of Prismatic Lithium-ion Battery Packs Based on Coupled Electrochemical-thermal Model. Energy Sci. Eng. 2021, 9, 1450–1464. [Google Scholar] [CrossRef]
- Sundin, D.W.; Sponholtz, S. Thermal Management of Li-Ion Batteries with Single-Phase Liquid Immersion Cooling. IEEE Open J. Veh. Technol. 2020, 1, 82–92. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Liu, Y.; Wang, F.; Yang, N.; Liu, X.; Liu, H.; Li, W.; Liu, H.; Huang, B. Performance Analysis of Phase Change Material in Battery Thermal Management with Biomimetic Honeycomb Fin. Appl. Therm. Eng. 2021, 196, 117296. [Google Scholar] [CrossRef]
- Huang, R.; Li, Z.; Hong, W.; Wu, Q.; Yu, X. Experimental and Numerical Study of PCM Thermophysical Parameters on Lithium-Ion Battery Thermal Management. Energy Rep. 2020, 6, 8–19. [Google Scholar] [CrossRef]
- Qin, P.; Liao, M.; Zhang, D.; Liu, Y.; Sun, J.; Wang, Q. Experimental and Numerical Study on a Novel Hybrid Battery Thermal Management System Integrated Forced-Air Convection and Phase Change Material. Energy Convers. Manag. 2019, 195, 1371–1381. [Google Scholar] [CrossRef]
- Jaguemont, J.; Omar, N.; Van den Bossche, P.; Mierlo, J. Phase-Change Materials (PCM) for Automotive Applications: A Review. Appl. Therm. Eng. 2018, 132, 308–320. [Google Scholar] [CrossRef]
- Weng, J.; Ouyang, D.; Yang, X.; Chen, M.; Zhang, G.; Wang, J. Optimization of the Internal Fin in a Phase-Change-Material Module for Battery Thermal Management. Appl. Therm. Eng. 2020, 167, 114698. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, D.; Jiang, L. Advanced thermal management system driven by phase change materials for power lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2022, 159, 112207. [Google Scholar] [CrossRef]
- Hallaj, S.A.; Selman, J.R. A Novel Thermal Management System for Electric Vehicle Batteries Using Phase-Change Material. J. Electrochem. Soc. 2000, 147, 3231. [Google Scholar] [CrossRef]
- Verma, A.; Shashidhara, S.; Rakshit, D. A Comparative Study on Battery Thermal Management Using Phase Change Material (PCM). Therm. Sci. Eng. Prog. 2019, 11, 74–83. [Google Scholar] [CrossRef]
- Liu, J.; Fan, Y.; Xie, Q. Temperature Mitigation Effect of Phase Change Material on Overcharging Lithium-Ion Batteries: An Experimental Study. J. Therm. Anal. Calorim. 2022, 147, 5153–5163. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Min, H.; Li, H.; Li, Q. Performance Investigation of a Passive Battery Thermal Management System Applied with Phase Change Material. J. Energy Storage 2021, 35, 102279. [Google Scholar] [CrossRef]
- Liu, J.; Fan, Y.; Xie, Q. An Experimental Study on the Thermal Performance of Mixed Phase Change Materials-Based Battery Cooling System. J. Energy Storage 2022, 46, 103839. [Google Scholar] [CrossRef]
- Heyhat, M.M.; Mousavi, S.; Siavashi, M. Battery Thermal Management with Thermal Energy Storage Composites of PCM, Metal Foam, Fin and Nanoparticle. J. Energy Storage 2020, 28, 101235. [Google Scholar] [CrossRef]
- Lazrak, A.; Fourmigué, J.-F.; Robin, J.-F. An Innovative Practical Battery Thermal Management System Based on Phase Change Materials: Numerical and Experimental Investigations. Appl. Therm. Eng. 2018, 128, 20–32. [Google Scholar] [CrossRef]
- Siddique, A.R.M.; Mahmud, S.; Heyst, B.V. A Comprehensive Review on a Passive (Phase Change Materials) and an Active (Thermoelectric Cooler) Battery Thermal Management System and Their Limitations. J. Power Sources 2018, 401, 224–237. [Google Scholar] [CrossRef]
- Jiang, G.; Huang, J.; Fu, Y.; Cao, M.; Liu, M. Thermal Optimization of Composite Phase Change Material/Expanded Graphite for Li-Ion Battery Thermal Management. Appl. Therm. Eng. 2016, 108, 1119–1125. [Google Scholar] [CrossRef]
- Zou, D.; Ma, X.; Liu, X.; Zheng, P.; Hu, Y. Thermal Performance Enhancement of Composite Phase Change Materials (PCM) Using Graphene and Carbon Nanotubes as Additives for the Potential Application in Lithium-Ion Power Battery. Int. J. Heat Mass Transf. 2018, 120, 33–41. [Google Scholar] [CrossRef]
- Alipanah, M.; Li, X. Numerical Studies of Lithium-Ion Battery Thermal Management Systems Using Phase Change Materials and Metal Foams. Int. J. Heat Mass Transf. 2016, 102, 1159–1168. [Google Scholar] [CrossRef]
- Buonomo, B.; Ercole, D.; Manca, O.; Menale, F. Thermal Cooling Behaviors of Lithium-Ion Batteries by Metal Foam with Phase Change Materials. Energy Procedia 2018, 148, 1175–1182. [Google Scholar] [CrossRef]
- Zhi, M.; Fan, R.; Yang, X.; Zheng, L.; Yue, S.; Liu, Q.; He, Y. Recent Research Progress on Phase Change Materials for Thermal Management of Lithium-Ion Batteries. J. Energy Storage 2022, 45, 103694. [Google Scholar] [CrossRef]
- Usman, H.; Ali, H.M.; Arshad, A.; Ashraf, M.J.; Khushnood, S.; Janjua, M.M.; Kazi, S.N. An Experimental Study of PCM Based Finned and Un-Finned Heat Sinks for Passive Cooling of Electronics. Heat Mass Transf. 2018, 54, 3587–3598. [Google Scholar] [CrossRef]
- Ali, H.M.; Arshad, A. Experimental Investigation of N-Eicosane Based Circular Pin-Fin Heat Sinks for Passive Cooling of Electronic Devices. Int. J. Heat Mass Transf. 2017, 112, 649–661. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; Xia, X. Experimental Investigation on the Thermal Behavior of Cylindrical Battery with Composite Paraffin and Fin Structure. Int. J. Heat Mass Transf. 2017, 109, 958–970. [Google Scholar] [CrossRef]
- Zheng, N.; Fan, R.; Sun, Z.; Zhou, T. Thermal Management Performance of a Fin-enhanced Phase Change Material System for the Lithium-ion Battery. Int. J. Energy Res. 2020, 44, 7617–7629. [Google Scholar] [CrossRef]
- Fan, R.; Zheng, N.; Sun, Z. Evaluation of Fin Intensified Phase Change Material Systems for Thermal Management of Li-Ion Battery Modules. Int. J. Heat Mass Transf. 2021, 166, 120753. [Google Scholar] [CrossRef]
- Liu, S.; Peng, H.; Hu, Z.; Ling, X.; Huang, J. Solidification Performance of a Latent Heat Storage Unit with Innovative Longitudinal Triangular Fins. Int. J. Heat Mass Transf. 2019, 138, 667–676. [Google Scholar] [CrossRef]
- Skaalum, J.; Groulx, D. Heat Transfer Comparison between Branching and Non-Branching Fins in a Latent Heat Energy Storage System. Int. J. Therm. Sci. 2020, 152, 106331. [Google Scholar] [CrossRef]
- Zhao, C.; Opolot, M.; Liu, M. Numerical study of melting performance enhancement for PCM in a circular enclosure with internal-external fins and metal foams. Int. J. Heat Mass Transf. 2020, 150, 119348. [Google Scholar] [CrossRef]
- Weng, J.; He, Y.; Ouyang, D.; Yang, X.; Zhang, G.; Wang, J. Thermal Performance of PCM and Branch-Structured Fins for Cylindrical Power Battery in a High-Temperature Environment. Energy Convers. Manag. 2019, 200, 112106. [Google Scholar] [CrossRef]
- Hasse, C.; Grenet, M.; Bontemps, A.; Dendievel, R.; Sallée, H. Realization, Test and Modelling of Honeycomb Wallboards Containing a Phase Change Material. Energy Build. 2011, 43, 232–238. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Lu, Z.; Bai, Q. Thermal performance of a shell-and-tube latent heat thermal energy storage unit: Role of circular fins. Appl. Energy 2017, 202, 558–570. [Google Scholar] [CrossRef]
- Farouk, N.; Alotaibi, A.A.; Alshahri, A.H.; Almitani, K.H. Challenges in Incorporating Phase Change Materials into Thermal Control Units for Lithium-Ion Battery Cooling. J. Energy Storage 2022, 49, 104094. [Google Scholar] [CrossRef]
- Sun, Z.; Fan, R.; Yan, F.; Zhou, T.; Zheng, N. Thermal Management of the Lithium-Ion Battery by the Composite PCM-Fin Structures. Int. J. Heat Mass Transf. 2019, 145, 118739. [Google Scholar] [CrossRef]
- Al-abidi, A.A.; Bin Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammed, A.T. CFD Applications for Latent Heat Thermal Energy Storage: A Review. Renew. Sustain. Energy Rev. 2013, 20, 353–363. [Google Scholar] [CrossRef]
- Seddegh, S.; Wang, X.; Henderson, A.D. Numerical Investigation of Heat Transfer Mechanism in a Vertical Shell and Tube Latent Heat Energy Storage System. Appl. Therm. Eng. 2015, 87, 698–706. [Google Scholar] [CrossRef]
- Zhang, F.; Yi, M.; Wang, P.; Liu, C. Optimization Design for Improving Thermal Performance of T-Type Air-Cooled Lithium-Ion Battery Pack. J. Energy Storage 2021, 44, 103464. [Google Scholar] [CrossRef]
- Kong, D.; Peng, R.; Ping, P.; Du, J.; Chen, G.; Wen, J. A Novel Battery Thermal Management System Coupling with PCM and Optimized Controllable Liquid Cooling for Different Ambient Temperatures. Energy Convers. Manag. 2020, 204, 112280. [Google Scholar] [CrossRef]
- Inc A. ANSYS FLUENT 18.0: Theory Guide; ANSYS: Cannonsburg, PA, USA, 2017.
- Mansir, I.B.; Sinaga, N.; Farouk, N.; Aljaghtham, M.; Diyoke, C.; Nguyen, D.D. Numerical Simulation of Dimensions and Arrangement of Triangular Fins Mounted on Cylindrical Lithium-Ion Batteries in Passive Thermal Management. J. Energy Storage 2022, 50, 104392. [Google Scholar] [CrossRef]
- Cao, J.; Ling, Z.; Fang, X.; Zhang, Z. Delayed Liquid Cooling Strategy with Phase Change Material to Achieve High Temperature Uniformity of Li-Ion Battery under High-Rate Discharge. J. Power Sources 2020, 450, 227673. [Google Scholar] [CrossRef]
- Choudhari, V.G.; Dhoble, A.S.; Panchal, S. Numerical Analysis of Different Fin Structures in Phase Change Material Module for Battery Thermal Management System and Its Optimization. Int. J. Heat Mass Transf. 2020, 163, 120434. [Google Scholar] [CrossRef]
- Ambekar, S.; Rath, P.; Bhattacharya, A. A Novel PCM and TCE Based Thermal Management of Battery Module. Therm. Sci. Eng. Prog. 2022, 29, 101196. [Google Scholar] [CrossRef]


| Refs. | Fin Shape | Major Findings |
|---|---|---|
| [37] | rectangular | Eight rectangular fins present the best cooling performance. |
| [38] | rectangular | When the heat production is 15 W, the working time with fins is 61% longer than that without fins. |
| [39] | rectangular | The length and direction of the fin have an effect on heat dissipation, and the heat is quickly transferred to the PCM through the embedded fin. |
| [40] | longitudinal triangular | The total solidification time of PCM is 38.3% shorter than that of rectangular finned structure. |
| [41] | branched | Branching fins impede the natural convection process of heat storage. |
| [42] | tree-like | In the case of foam metal, the melting rate of PCM is lower than that of fin. |
| [43] | X, I, V, Y-shaped | The X-shaped fin reduces the maximum temperature of the battery more effectively due to the large heat dissipation area. |
| [44] | honeycomb plate | The presence of the honeycomb structure reduces the temperature of the heat source. |
| [45] | circular | The insertion of circular fins into the PCM can reduce the melting time by 65%. |
| [46] | circular | The number of fins is increased from 3 to 5, and the temperature of the battery is reduced by 1–1.7 °C. |
| Parameter | Unit | Battery | PCM | Fin | Acrylic |
|---|---|---|---|---|---|
| Size/thickness | mm | 18 × 65 | - | 0.5 | 2 |
| Density | kg/m3 | 2720 | 820 | 2719 | 1215 |
| Heat capacity | J/(kg·K) | 300 | 2000 | 896 | 1300 |
| Coefficient of thermal conductivity | W/(m·K) | 3 | 0.2 | 202.4 | 0.17 |
| Dynamic viscosity | kg/m·s | - | 0.02 | - | - |
| Coefficient of thermal expansion | K−1 | - | 0.0001 | - | - |
| Heat of fusion | J/kg | - | 165,000 | - | - |
| Temperature of the solid phase | K | - | 311.15 | - | - |
| Temperature of the liquid phase | K | - | 316.15 | - | - |
| Nominal capacity | Ah | 2.4 | |||
| Nominal voltage | V | 3.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Ma, Q.; Li, X. Numerical Simulation of the Combination of Novel Spiral Fin and Phase Change Material for Cylindrical Lithium-Ion Batteries in Passive Thermal Management. Energies 2022, 15, 8847. https://doi.org/10.3390/en15238847
Liu J, Ma Q, Li X. Numerical Simulation of the Combination of Novel Spiral Fin and Phase Change Material for Cylindrical Lithium-Ion Batteries in Passive Thermal Management. Energies. 2022; 15(23):8847. https://doi.org/10.3390/en15238847
Chicago/Turabian StyleLiu, Jiahao, Qingwen Ma, and Xianbin Li. 2022. "Numerical Simulation of the Combination of Novel Spiral Fin and Phase Change Material for Cylindrical Lithium-Ion Batteries in Passive Thermal Management" Energies 15, no. 23: 8847. https://doi.org/10.3390/en15238847
APA StyleLiu, J., Ma, Q., & Li, X. (2022). Numerical Simulation of the Combination of Novel Spiral Fin and Phase Change Material for Cylindrical Lithium-Ion Batteries in Passive Thermal Management. Energies, 15(23), 8847. https://doi.org/10.3390/en15238847







