Heat Transfer Intensification in a Heat Exchanger by Means of Twisted Tapes in Rib and Sawtooth Forms
Abstract
1. Introduction
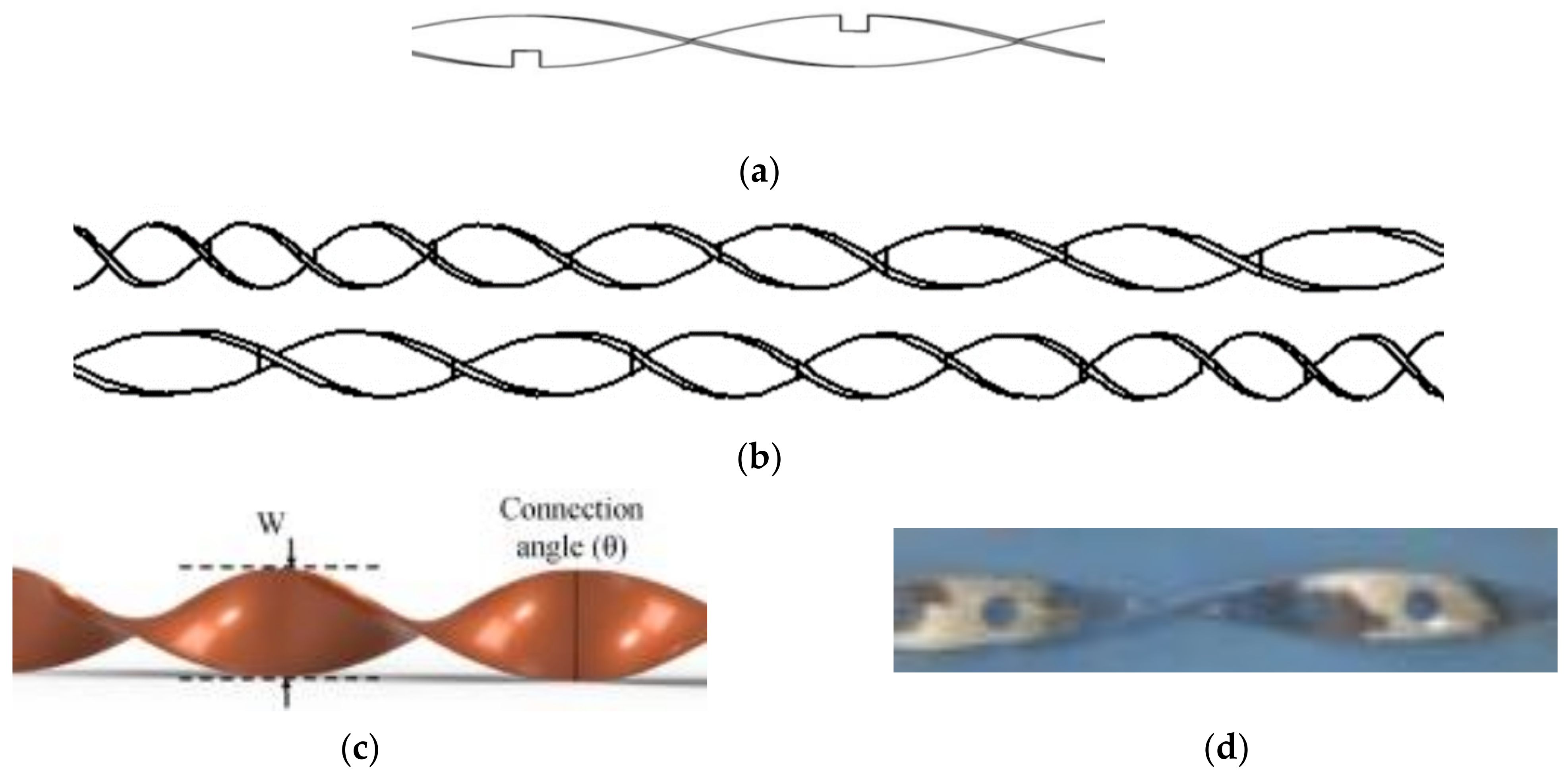
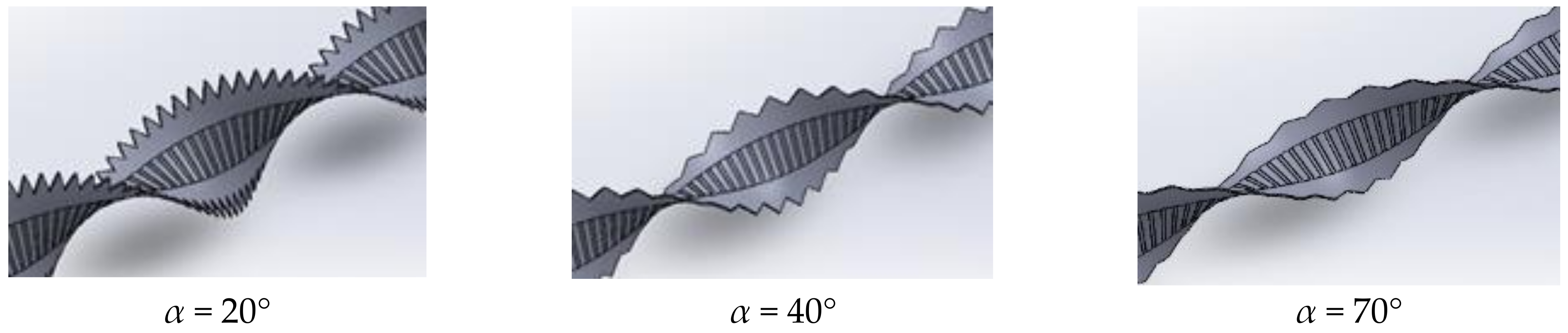
2. Details of Twisted Tapes in Rib and Sawtooth Forms
3. Experimental Setup
4. Data Reduction
5. Confirmatory Data of a Plain Tube
6. Results and Discussion
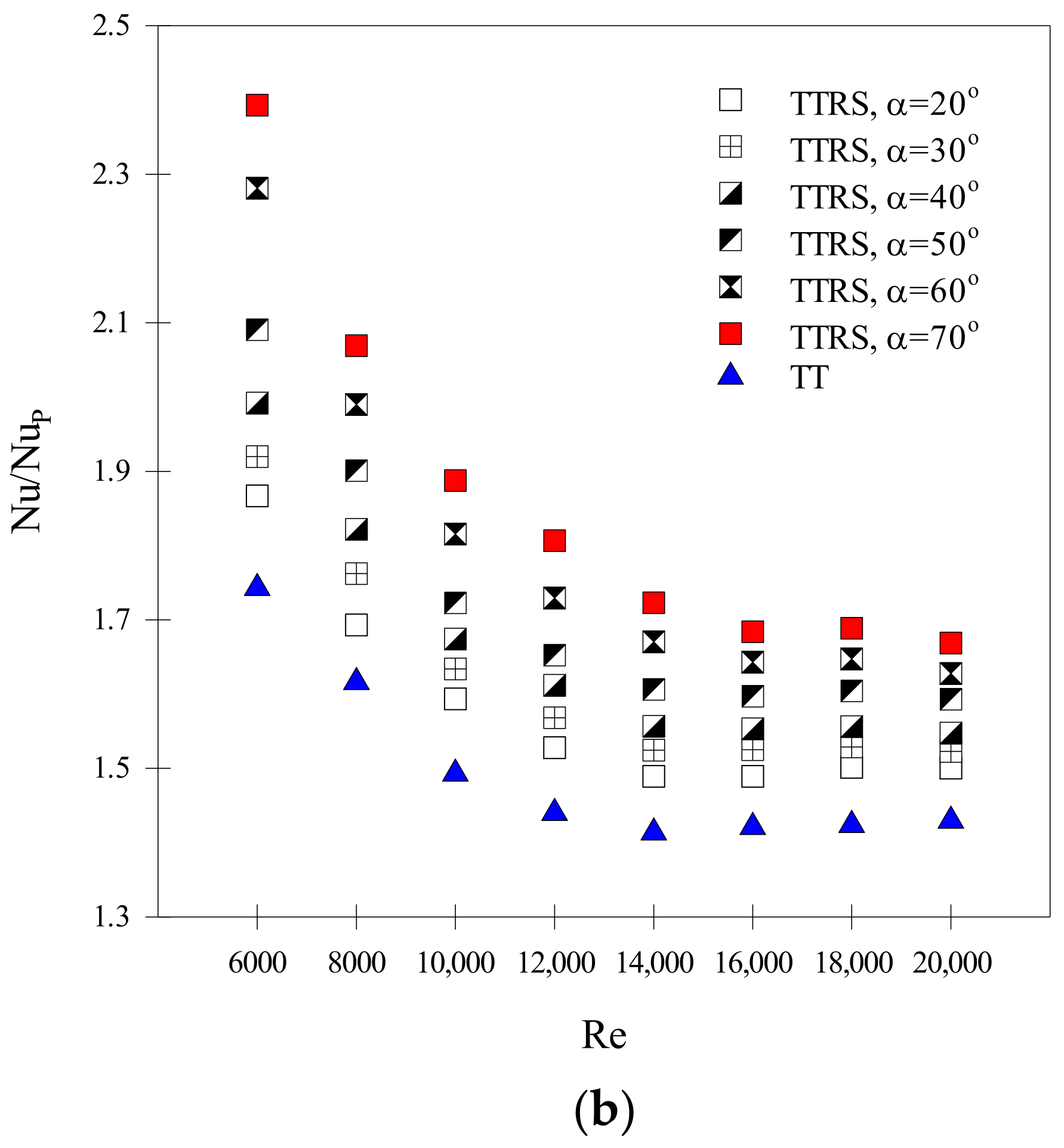
6.1. Heat Transfer Results
6.2. Friction Factor Results
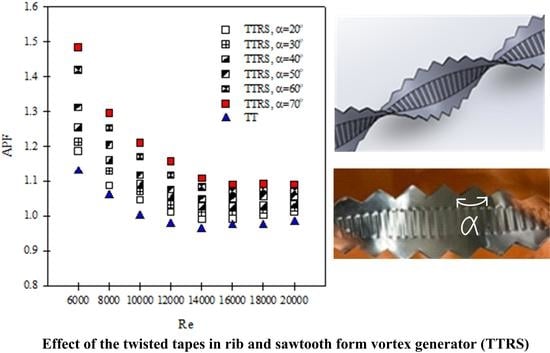
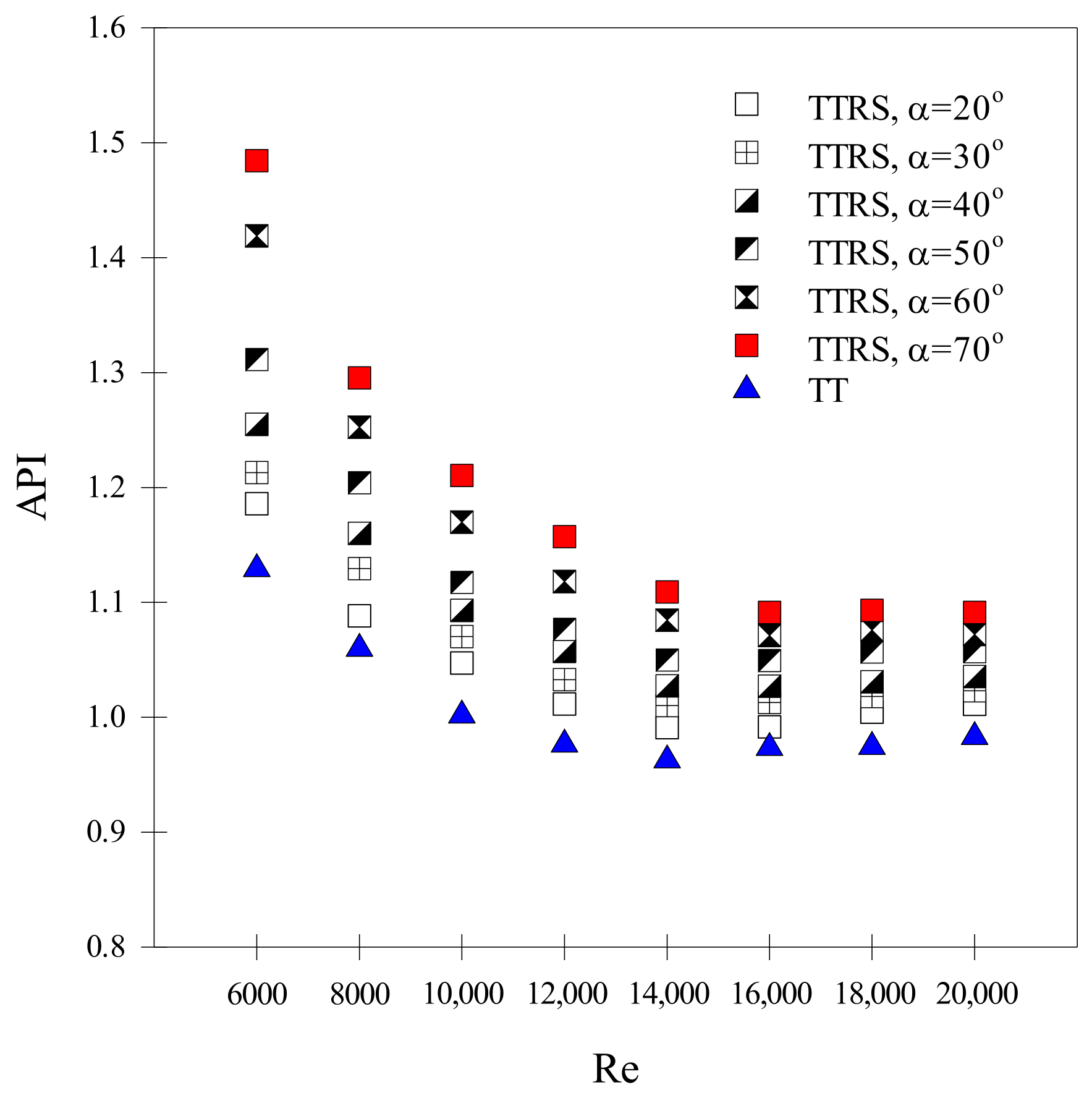
6.3. Aerothermal Performance Results
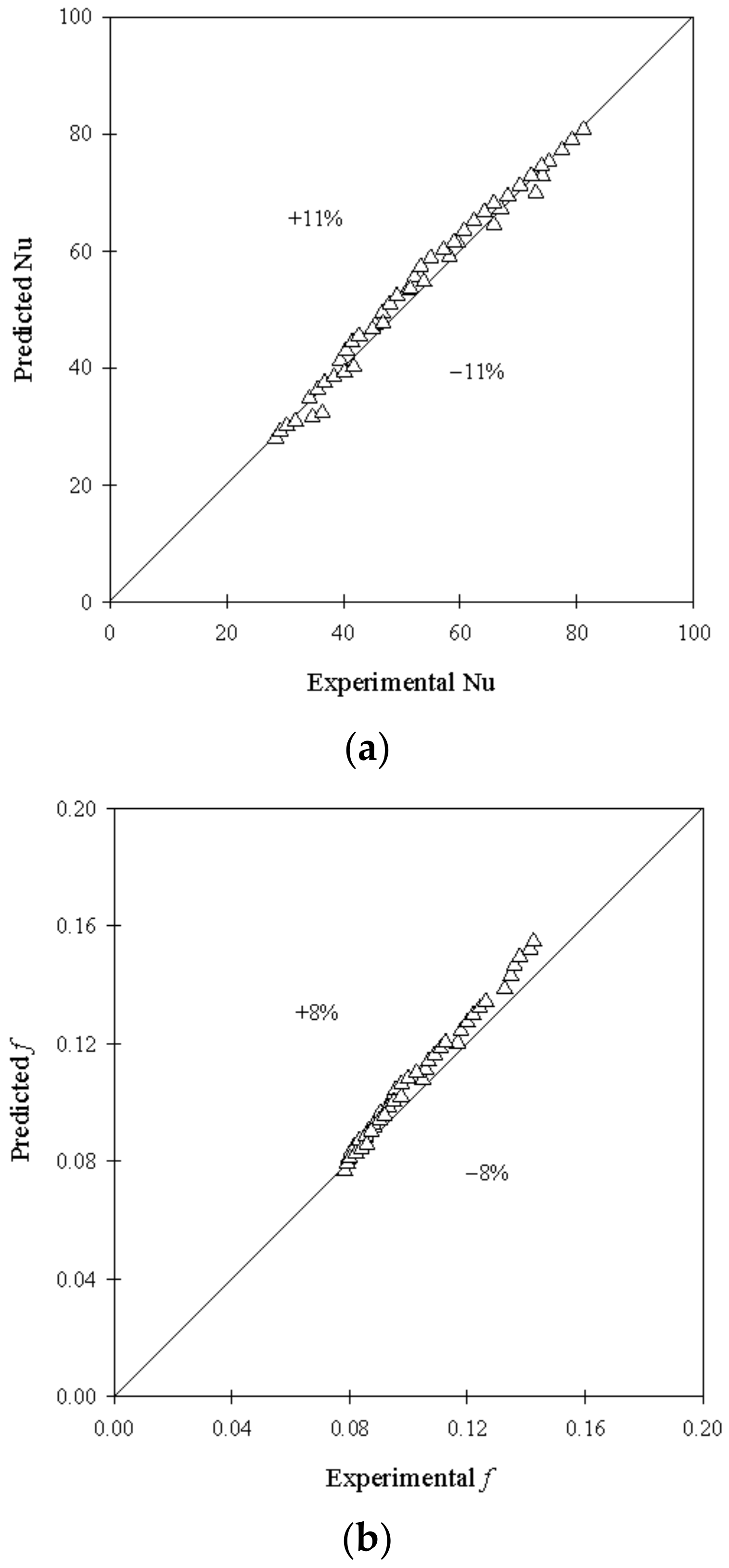
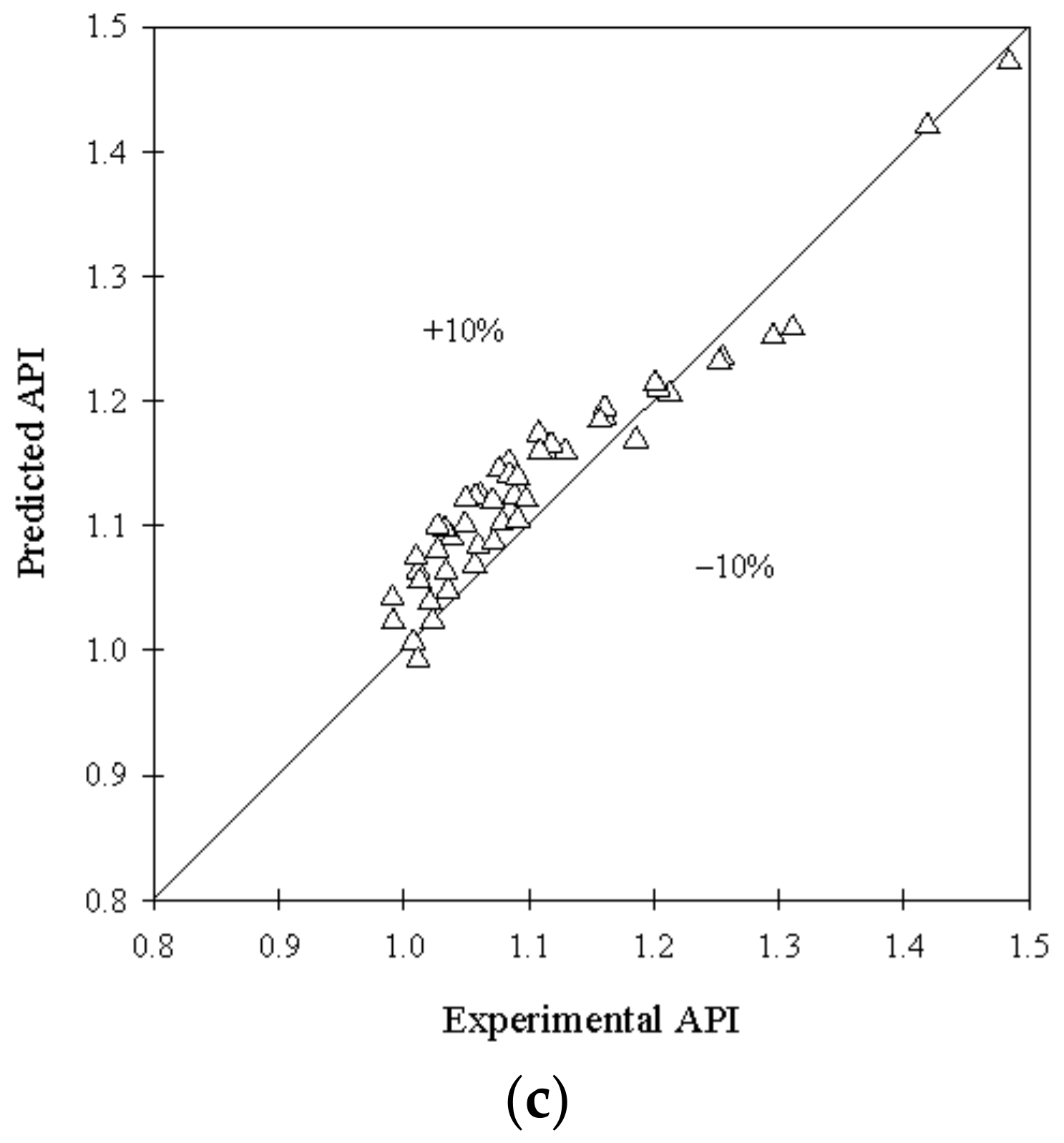
6.4. Empirical Correlations
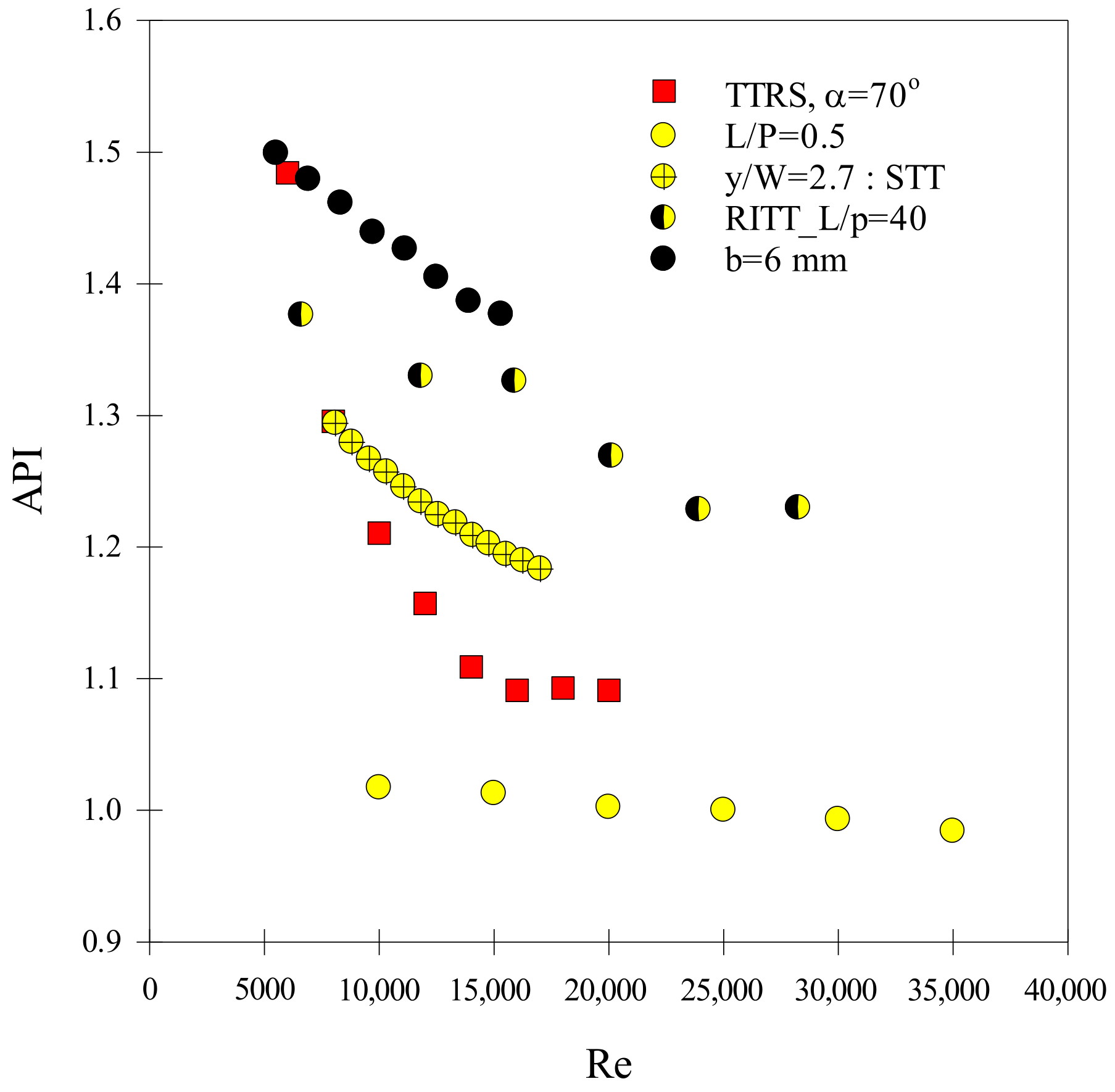
7. Benchmarking
8. Conclusions
- ○
- The TTRSs-generated swirl and turbulence promotes fluid mixing over the wall. This results from the viscous sublayer being disturbed, which greatly improves heat transfer and balances out the increased pressure loss penalty.
- ○
- Twisted tapes in rib and sawtooth form (TTRSs) increase the Nusselt number with a reasonable friction loss penalty. The Nusselt number increases with the sawtooth angle and Re. For a heat exchanger tube with TTRSs installed while α = 20°, 30°, 40°, 50°, 60°, and 70°, the average Nusselt numbers increases are estimated to be 158%, 162%, 166%, 172%, 180%, and 187%, respectively. It is also found that the TTRSs with α = 70° outperform those with α = 20°, 30°, 40°, 50°, and 60° by approximately 1.18, 1.15, 1.12, 1.08, and 1.04 times, respectively.
- ○
- The friction factors caused by TTRS devices with sawtooth angles (α) of 20°, 30°, 40°, 50°, 60°, and 70° are 3.51, 3.55, 3.60, 3.67, 3.75, and 3.82 times greater than those caused by a plain tube alone.
- ○
- The maximum aerothermal performance index (API) was found at α = 70° owing to the dominant effect of increased heat transfer. It is more practical to use TTRSs with larger sawtooth angles at lower Reynolds numbers for energy savings. API values range from 0.99 to 1.19, 1.01 to 1.21, 1.03 to 1.26, 1.05 to 1.31, 1.07 to 1.42, and 1.09 to 1.48 for TTRSs with sawtooth angles (α) of 20°, 30°, 40°, 50°, 60°, and 70°, respectively.
- ○
- Applying twisted tapes in rib and sawtooth form (TTRSs) with appropriate geometries at low Reynolds numbers results in a promising trade-off between enhanced heat transfer and an increased friction loss penalty resulting in a higher API.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | heat transfer area, m2 |
| ca | specific heat of air, J/kg·K |
| D | inner diameter of test tube, m |
| f | friction factor |
| h | average heat transfer coefficient, W/m2·K |
| k | thermal conductivity of fluid, W/m·K |
| L | length of the test tube, m |
| mass flow rate, kg/s | |
| Nu | Nusselt number |
| pressure drop, Pa | |
| Pr | Prandtl number |
| heat transfer rate of air, W | |
| convective heat transfer rate of air, W | |
| Re | Reynolds number |
| average temperature, K | |
| T | temperature, K |
| U | average velocity of air flow, m/s |
| volumetric flow rate, m3/s | |
| Greek symbols | |
| fluid density, kg/m3 | |
| kinematic viscosity, m2/s | |
| Subscripts | |
| a | air |
| b | bulk |
| in | inlet position |
| out | outlet position |
| w | wall |
| p | smooth tube |
| Abbreviations | |
| API | aerothermal performance index |
| TT | typical twisted tape |
| TTRS | twisted tape in a rib and sawtooth form |
References
- Bergles, A.E. Techniques to augment heat transfer. In Handbook of Heat Transfer Applications; Rosenhow, W.M., Ed.; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Marner, W.J.; Bergles, A.E.; Chenoweth, J.M. On the presentation of performance data for enhanced tubes used in shell-and tube heat exchangers. ASME J. Heat Mass Trans. 1983, 105, 358–365. [Google Scholar] [CrossRef]
- Altun, A.H.; Nacak, H.; Canli, E. Effects of trapezoidal and twisted trapezoidal tapes on turbulent heat transfer in tubes. Appl. Therm. Eng. 2022, 211, 118386. [Google Scholar] [CrossRef]
- Wongcharee, K.; Changcharoen, W.; Eiamsa-ard, S. Numerical investigation of flow friction and heat transfer in a channel with various shaped ribs mounted on two opposite ribbed walls. Int. J. Chem. React. 2011, 9, A26. [Google Scholar] [CrossRef]
- Eiamsa-ard, S.; Koolnapadol, N.; Promvonge, P. Heat transfer behavior in a square duct with tandem wire coil element insert. Chin. J. Chem. Eng. 2012, 20, 863–869. [Google Scholar]
- Li, W.; Yu, Z. Heat exchangers for cooling supercritical carbon dioxide and heat transfer enhancement: A review and assessment. Energy Rep. 2021, 7, 4085–4105. [Google Scholar] [CrossRef]
- Acır, A.; Ata, İ. A study of heat transfer enhancement in a new solar air heater having circular type turbulators. J. Energy Inst. 2016, 89, 606–616. [Google Scholar] [CrossRef]
- Nanan, K.; Thianpong, C.; Pimsarn, M.; Chuwattanakul, V.; Eiamsa-Ard, S. Flow and thermal mechanisms in a heat exchanger tube inserted with twisted cross-baffle turbulators. Appl. Therm. Eng. 2017, 114, 130–147. [Google Scholar] [CrossRef]
- Harish, H.; Manjunath, K. Heat and fluid flow behaviors in a laminar tube flow with circular protruded twisted tape inserts. Case Stud. Therm. Eng. 2022, 32, 101880. [Google Scholar]
- Mashayekhi, R.; Eisapour, A.H.; Eisapour, M.; Talebizadehsardari, P.; Rahbari, A. Hydrothermal performance of twisted elliptical tube equipped with twisted tape insert. Int. J. Therm. Sci. 2022, 172, 107233. [Google Scholar] [CrossRef]
- Ajarostaghi, M.; Soheil, S.; Zaboli, M.; Javadi, H.; Badenes, B.; Urchueguia, J.F. A review of recent passive heat transfer enhancement methods. Energies 2022, 15, 986. [Google Scholar] [CrossRef]
- Kaood, A.; Fadodun, O.G. Numerical investigation of turbulent entropy production rate in conical tubes fitted with a twisted-tape insert. Int. Commun. Heat Mass Transf. 2022, 139, 106520. [Google Scholar] [CrossRef]
- Gan, L.; Yang, C.; Zhang, J.; Zong, H.; Xu, B.; Qian, J. Internal flow analysis of a heat transfer enhanced tube with a segmented twisted tape insert. Energies 2020, 13, 207. [Google Scholar]
- Zheng, F.; Liu, S.; Lin, Z.; Nugud, J.; Wang, L.; Chang, L.; Wang, L. Experimental study on heat transfer performances of flat tube bank fin heat exchanger using four different fin patterns. ASME J. Heat Transfer. 2018, 140, 041801. [Google Scholar] [CrossRef]
- Okbaz, A.; Pınarbaşı, A.; Olcay, A.B. Experimental investigation of effect of different tube row-numbers, fin pitches and operating conditions on thermal and hydraulic performances of louvered and wavy finned heat exchangers. Int. J. Therm. Sci. 2020, 151, 106256. [Google Scholar] [CrossRef]
- Rajesh Babu, C.; Kumar, P.; Roy, S.; Kanungo, D. CFD analysis of an economizer for heat transfer enhancement using serrated finned tube equipped with variable fin segments. Mater. Today Proc. 2021, 45, 222–230. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, D.; Sheng, Q.; Hu, M.; Cheng, Y.; Cen, K. Research on gas side performance of staggered fin-tube bundles with different serrated fin geometries. Int. J. Heat Mass Transf. 2020, 152, 119509. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Čikić, A.; Muhič, S.; Stojkov, M. Development of a new type of finned heat exchanger. Tehnički vjesnik/Tech. Gaz. 2017, 24, 1785–1796. [Google Scholar]
- Liu, X.; Yu, J.; Yan, G. An experimental study on the air side heat transfer performance of the perforated fin-tube heat exchangers under the frosting conditions. Appl. Therm. Eng. 2020, 166, 114634. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Muhič, S. Numerical analysis of tube heat exchanger with perforated star-shaped fins. Fluids 2020, 5, 242. [Google Scholar] [CrossRef]
- Wijayanta, A.T.; Pranowo, P.; Mirmanto, M.; Kristiawan, B.; Aziz, M. Internal flow in an enhanced tube having square-cut twisted tape insert. Energies 2019, 12, 306. [Google Scholar] [CrossRef]
- Ahmad, S.; Abdullah, S.; Sopian, K. Numerical and experimental analysis of the thermal performances of SiC/water and Al2O3/water nanofluid inside a circular tube with constant-increased-PR twisted tape. Energies 2020, 13, 2095. [Google Scholar] [CrossRef]
- Kalateh, M.R.; Kianifar, A.; Sardarabadi, M. Energy, exergy, and entropy generation analyses of a water-based photovoltaic thermal system, equipped with clockwise counter-clockwise twisted tapes: An indoor experimental study. Appl. Therm. Eng. 2022, 215, 118906. [Google Scholar] [CrossRef]
- Dagdevir, T.; Ozceyhan, V. An experimental study on heat transfer enhancement and flow characteristics of a tube with plain, perforated and dimpled twisted tape inserts. Int. J. Therm. Sci. 2021, 159, 106564. [Google Scholar] [CrossRef]
- Zhang, H.; Nunayon, S.S.; Alvin, X.J.; Lai, C.K. Pressure drop and nanoparticle deposition characteristics for multiple twisted tape inserts with partitions in turbulent duct flows. Int. J. Heat Mass Transf. 2022, 193, 121474. [Google Scholar] [CrossRef]
- Dagdevir, T.; Ozceyhan, V. A comprehensive second law analysis for a heat exchanger tube equipped with the rod inserted straight and twisted tape and using water/CuO nanofluid. Int. J. Therm. Sci. 2022, 181, 107765. [Google Scholar] [CrossRef]
- Dandoutiya, B.K.; Kumar, A. W-cut twisted tape’s effect on the thermal performance of a double pipe heat exchanger: A numerical study. Case Stud. Therm. Eng. 2022, 34, 102031. [Google Scholar] [CrossRef]
- Xie, C.; Mansir, I.B.; Mahariq, I.; Singh, P.K.; Arsalanloo, A.; Shahzad, R.M.; Jarad, F. Performance boost of a helical heat absorber by utilization of twisted tape turbulator, an experimental investigation. Case Stud. Therm. Eng. 2022, 36, 102240. [Google Scholar] [CrossRef]
- Soltani, M.M.; Gorji-Bandpy, M.; Vaisi, A.; Moosavi, R. Heat transfer augmentation in a double-pipe heat exchanger with dimpled twisted tape inserts: An experimental study. Heat Mass Transf. 2022, 58, 1591–1606. [Google Scholar] [CrossRef]
- Maithani, R.; Kumar, B.; Sharma, S.; Kumar, S.; Kumar, A. Effect of a unique winglet twisted tape insert on thermal and hydraulic properties of tubular heat exchanger. Exp. Heat Transf. 2022, 35, 1077–1098. [Google Scholar] [CrossRef]
- Muneeshwaran, M.; Wen, L.H.; Wang, C.C. Investigation of fouling mitigation using stationary and rotating twisted tapes. Appl. Therm. Eng. 2022, 214, 118896. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Muhič, S.; Čikić, A. Experimental testing of the heat exchanger with star-shaped fins. Int. J. Heat Mass Transf. 2019, 149, 119190. [Google Scholar] [CrossRef]
- Kline, S.J.; McClintock, F.A. Describing Uncertainties in Single Sample Experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, P.D. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Webb, R.L.; Kim, N.H. Principles of Enhanced Heat Transfer, 2nd ed.; Taylor & Francis: New York, NY, USA, 2005. [Google Scholar]






| Instrument | Device Accuracy |
| Resistance temperature detector (RTD) | ±0.001 Ω at 0 °C |
| −130 to +95 °C ±0.05 °C | |
| Hot wire anemometer | ±0.015 m/s, range: 0–50 m/s |
| resolution: 0.01 m/s | |
| Digital differential pressure gauge | ±3.2% for 250 Pa |
| Maximum error in experimental parameters | |
| Parameter | Maximum uncertainty error (%) |
| Reynolds number (Re) | ±5.2 |
| Nusselt number (Nu) | ±8.1 |
| Friction factor (f) | ±7.9 |
| Aerothermal performance index | ±4.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poonpakdee, P.; Samutpraphut, B.; Thianpong, C.; Chokphoemphun, S.; Eiamsa-ard, S.; Maruyama, N.; Hirota, M. Heat Transfer Intensification in a Heat Exchanger by Means of Twisted Tapes in Rib and Sawtooth Forms. Energies 2022, 15, 8855. https://doi.org/10.3390/en15238855
Poonpakdee P, Samutpraphut B, Thianpong C, Chokphoemphun S, Eiamsa-ard S, Maruyama N, Hirota M. Heat Transfer Intensification in a Heat Exchanger by Means of Twisted Tapes in Rib and Sawtooth Forms. Energies. 2022; 15(23):8855. https://doi.org/10.3390/en15238855
Chicago/Turabian StylePoonpakdee, Pasu, Boonsong Samutpraphut, Chinaruk Thianpong, Suriya Chokphoemphun, Smith Eiamsa-ard, Naoki Maruyama, and Masafumi Hirota. 2022. "Heat Transfer Intensification in a Heat Exchanger by Means of Twisted Tapes in Rib and Sawtooth Forms" Energies 15, no. 23: 8855. https://doi.org/10.3390/en15238855
APA StylePoonpakdee, P., Samutpraphut, B., Thianpong, C., Chokphoemphun, S., Eiamsa-ard, S., Maruyama, N., & Hirota, M. (2022). Heat Transfer Intensification in a Heat Exchanger by Means of Twisted Tapes in Rib and Sawtooth Forms. Energies, 15(23), 8855. https://doi.org/10.3390/en15238855