Negative Impact Mitigation on the Power Supply System of a Fans Group with Frequency-Variable Drive
Abstract
1. Introduction
- −
- Improving the aerodynamic characteristics of fans;
- −
- Improving the design of heat exchange sections;
- −
- Improving the algorithms and technical means of fan motor control.
- , —temperature and mass flow rate of gas at the GCP inlet, respectively;
- —temperature and mass flow rate of air through the GCP heat exchange sections;
- —thermal resistance, characterizing the pollution level of the heat exchange surface.
2. Impact of the Typical FCGCP on the Power Supply System
2.1. Basic Theoretical Provisions
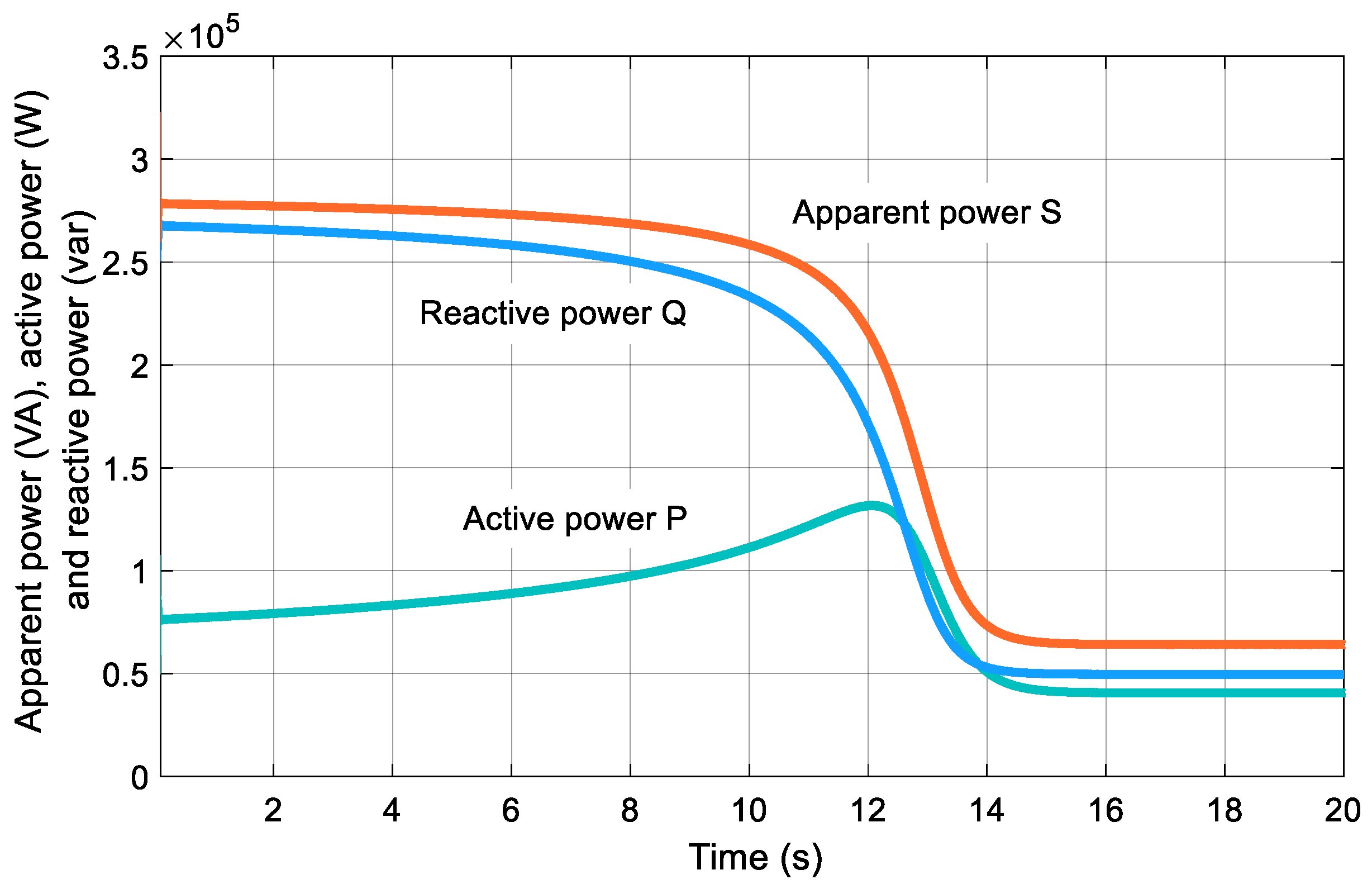
2.2. Modeling the FCGCP Power Supply System
3. Novel Substation Topology for Power Supply to the FCGCP
3.1. Proposed Technical Solution
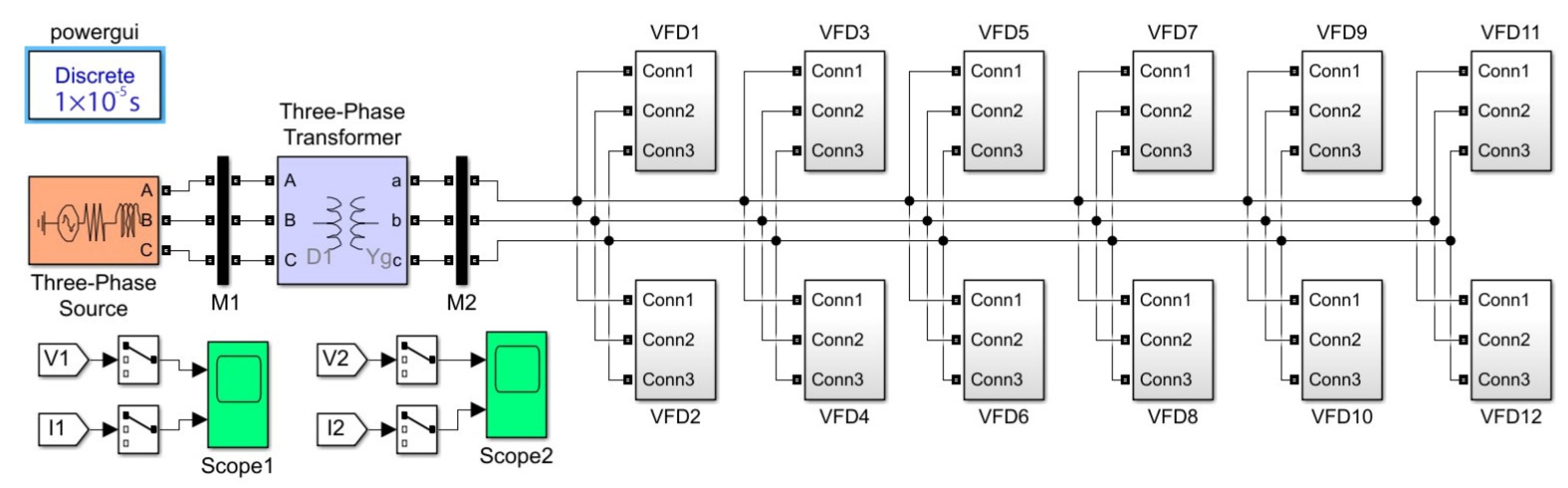
3.2. Simulation of the Proposed Electrical Complex
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | |
| ACU | Air-cooling unit |
| AHF | Active harmonic filter |
| EMC | Electromagnetic compatibility |
| EMF | Electromotive force |
| FC | Frequency converter |
| FCGCP | Frequency-controlled gas cooling plant |
| FFT | Fast Fourier transformation |
| GCP | Gas cooling plant |
| IGBT | Insulated Gate Bipolar Transistors |
| PCC | Point of common coupling |
| TDD | Total demand distortion |
| THD | Total harmonic distortion |
| VFD | Variable-frequency drive |
| Nomenclature | |
| P | Active power |
| Q | Reactive power |
| S | Apparent power |
| Tin | Temperature of gas at the GCP inlet |
| Ggas | Mass flow rate of gas at the GCP inlet |
| Temperature of air through the GCP heat exchange sections | |
| Gair | Mass flow rate of air through the GCP heat exchange sections |
| Thermal resistance | |
| Tout | Gas temperature at the GCP outlet |
| e(t) | Electromotive force |
| v(t) | Voltage on the load |
| vR(t) | Voltage on the resistance |
| vL(t) | Voltage on the inductance |
| i(t) | Current consumed from the grid |
| Grid voltages vector | |
| Grid currents vector | |
| Busbar 0.4 kV voltage vector | |
| Secondary currents vector | |
| f0 | Nominal value of the motor control frequency |
| f | Current value of the motor control frequency |
| P0.k | Rated power of the electric motor |
| Pk | Electric motor power at control frequency f |
| η | Efficiency of the electric motor |
| V2 | RMS voltage on the transformer secondary winding |
| Vd | DC busbar voltage |
| Pd.in | Power consumed by a group of N inverters |
| Rinv.k | Value of the equivalent resistance of the k-th inverter |
| Lsk | Inductance of the line choke |
| Rsk | Resistance of the line choke |
| Ck | Capacitance of the smoothing choke at the rectifier output |
| Ldk | Inductance of the smoothing choke at the rectifier output |
| Rdk | Resistance of the smoothing choke at the rectifier output |
Appendix A
| Parameter | Value | Unit |
|---|---|---|
| Phase-to-phase rated voltage | 10 | kV |
| Frequency | 50 | Hz |
| Source resistance | 0.2…1.33 | Ω |
| Source inductance | (3…18.75) × 10–3 | H |
| Parameter | Value | Unit |
|---|---|---|
| Rated power | 1000 | kVA |
| Frequency | 50 | Hz |
| Winding 1 parameters | ||
| Phase-to-phase rated voltage | 10 | kV |
| Winding resistance | 1.05 | Ω |
| Leakage inductance | 17.5 × 10−3 | H |
| Winding 2 parameters | ||
| Phase-to-phase rated voltage | 0.4 | kV |
| Winding resistance | 0.004 | Ω |
| Leakage inductance | 28 × 10−6 | H |
| Magnetization parameters | ||
| Resistance | 16 × 103 | Ω |
| Inductance | 22.5 | H |
| Parameter | Value | Unit |
|---|---|---|
| Rated power | 1000 | kVA |
| Frequency | 50 | Hz |
| Winding 1 parameters | ||
| Phase-to-phase rated voltage | 10 | kV |
| Winding resistance | 1.05 | Ω |
| Leakage inductance | 17.5 × 10−3 | H |
| Winding 2 parameters | ||
| Phase-to-phase rated voltage | 0.4 | kV |
| Winding resistance | 0.012 | Ω |
| Leakage inductance | 84 × 10−6 | H |
| Winding 3 parameters | ||
| Phase-to-phase rated voltage | 0.4 | kV |
| Winding resistance | 0.004 | Ω |
| Leakage inductance | 28 × 10−6 | H |
| Magnetization parameters | ||
| Resistance | 16 × 103 | Ω |
| Inductance | 22.5 | H |
References
- Kroger, D.G. Air-Cooled Heat Exchangers and Cooling Towers: Thermal-flower Performance Evaluation and Design. Ph.D. Thesis, University of Stellenbosch, Stellenbosch, South Africa, 2004. [Google Scholar]
- Mokhatab, S.; Poe William, A.; Speight, J.G. Handbook of Natural Gas Transmission and Processing–Principles and Practices, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Artyukhov, I.I.; Arshakyan, I.I.; Trimbach, A.A. Analysis of circuits of frequency control of gas-cooling device’s fans. In Proceedings of the International Conference on Actual Problems of Electron Devices Engineering, Saratov, Russia, 24–25 September 2008; pp. 381–389. [Google Scholar] [CrossRef]
- Larabee, J.; Pellegrino, B.; Flick, B. Induction Motor Starting Methods and Issues. In Proceedings of the Record of Conference Papers Industry Applications Society 52nd Annual Petroleum and Chemical Industry Conference, Athens, Greece, 12–14 September 2005; pp. 217–222. [Google Scholar]
- Habyarimana, M.; Dorrell, D.G. Methods to reduce the starting current of an induction motor. In Proceedings of the International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; pp. 34–38. [Google Scholar] [CrossRef]
- Artyukhov, I.I.; Stepanov, S.F.; Arshakyan, I.I.; Korotkov, A.V.; Pogodin, N.V. Dynamic compensation of reactive power at power supply system for air cooler of gases. Promyshlennaya Energ. 2004, 6, 47–51. [Google Scholar]
- Artyukhov, I.I.; Stepanov, S.F.; Mirgorodskaya, E.E.; Mityashin, N.P.; Zemtsov, A.I. Transient Processes with Starting of a Multi-Pole Asynchronous Motor with a Fan on the Shaft. In Proceedings of the 2021 17th Conference on Electrical Machines, Drives and Power Systems (ELMA 2021), Sofia, Bulgaria, 1–4 July 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Abakumov, A.M.; Kuznetsov, P.K.; Stepashkin, I.P. Adaptive automatic control system for air-cooled gas apparatus. J. Phys. Conf. Ser. 2018, 1111, 012031. [Google Scholar] [CrossRef]
- Yanvarev, I.; Vanyashov, A.; Krupnikov, A. Thermal Management Technologies Development for the Gas Transport on the Gas-main Pipeline. Procedia Eng. 2015, 113, 237–243. [Google Scholar] [CrossRef][Green Version]
- Artyukhov, I.; Abakumov, A.; Zemtsov, A.; Yerbayev, Y.; Zakharov, V. Energy Efficiency Analysis of Control Algorithms for Fan Electric Drives in Gas Air-Cooling Plants. In Lecture Notes in Civil Engineering, Proceedings of ICEPP 2021, Kazan, Russia, 26 February 2021; Springer: Cham, Switzerland, 2022; Volume 190, pp. 46–55. [Google Scholar] [CrossRef]
- Artyukhov, I.I.; Stepanov, S.F.; Pylskaya, E.K.; Zemtsov, A.I. Dynamics of Compressed Gas Temperature Stabilization System with Variable-Frequency Drive of Fans in a Gas Air-Cooling Unit. In Proceedings of the International Conference on Electrotechnical Complexes and Systems (ICOECS), Ufa, Russia, 27–30 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Novák, J.; Šimánek, J.; Černý, O.; Doleček, R. EMC of frequency controlled electric drives. Radioengineering 2008, 17, 101–105. [Google Scholar]
- Zare, F.; Soltani, H.; Kumar, D.; Davari, P.; Delpino, H.A.M.; Blaabjerg, F. Harmonic Emissions of Three-Phase Diode Rectifiers in Distribution Networks. IEEE Access 2017, 5, 2819–2833. [Google Scholar] [CrossRef]
- Artyukhov, I.; Bochkareva, I.; Molot, S.; Kalganova, S.; Stepanov, S.; Trigorly, S. Power Quality in Industrial Isolated Gener-ation Power Systems with Powerful Nonlinear Consumers. In Proceedings of the 9th International Scientific Symposium EL-EKTROENERGETIKA 2017, Stará Lesná, Slovak Republic, 12–14 September 2017; pp. 44–49. [Google Scholar]
- Standard 519-2014; IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2014.
- Jaafari, K.A.A.; Poshtan, M.; Beig, A.R. Passive wide spectrum filter for variable speed drives in oil and gas industry. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 1–6. [Google Scholar]
- Park, B.; Lee, J.; Yoo, H.; Jang, G. Harmonic Mitigation Using Passive Harmonic Filters: Case Study in a Steel Mill Power System. Energies 2021, 14, 2278. [Google Scholar] [CrossRef]
- Lumbreras, D.; Gálvez, E.; Collado, A.; Zaragoza, J. Trends in Power Quality, Harmonic Mitigation and Standards for Light and Heavy Industries: A Review. Energies 2020, 13, 5792. [Google Scholar] [CrossRef]
- Špelko, A.; Blažič, B.; Papič, I.; Herman, L. Active Filter Reference Calculations Based on Customers’ Current Harmonic Emissions. Energies 2021, 14, 220. [Google Scholar] [CrossRef]
- Vitoi, L.; Brandao, D.; Tedeschi, E. Active Power Filter Pre-Selection Tool to Enhance the Power Quality in Oil and Gas Platforms. Energies 2021, 14, 1024. [Google Scholar] [CrossRef]
- Raman, R.; Sadhu, P.K.; Kumar, R.; Rangarajan, S.S.; Subramaniam, U.; Collins, E.R.; Senjyu, T. Feasible Evaluation and Implementation of Shunt Active Filter for Harmonic Mitigation in Induction Heating System. Electronics 2022, 11, 3464. [Google Scholar] [CrossRef]
- Shankar, V.A.; Kumar, N.S. Implementation of Shunt Active Filter for Harmonic Compensation in a 3 Phase 3 Wire Distri-bution Network. Energy Procedia 2017, 117, 172–179. [Google Scholar] [CrossRef]
- Hudson, R.; Hong, S.; Hoft, R. Modeling and simulation of a digitally controlled active rectifier for power conditioning. In Proceedings of the of Sixth Annual Applied Power Electronics Conference and Exhibition, Dallas, TX, USA, 10–15 March 1991; pp. 423–429. [Google Scholar] [CrossRef]
- Chimonyo, K.B.; Kumar, K.S.; Kumar, B.K.; Ravi, K. Design and Analysis of Electrical Drives Using Active Front End Converter. In Proceedings of the 2018 Second International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 20–21 April 2018; pp. 115–119. [Google Scholar] [CrossRef]
- Vilberger, M.E.; Kulekina, A.V.; Bakholdin, P.A. The twelfth-pulse rectifier for traction substations of electric transport. IOP Conf. Ser. Earth Environ. Sci. 2017, 87, 032052. [Google Scholar] [CrossRef]
- Qian, G.; Wang, Q.; He, S.; Dai, W.; Wei, N.; Zhou, N. Harmonic Modeling and Analysis for Parallel 12-Pulse Rectifier under Unbalanced Voltage Condition in Frequency-Domain. Energies 2022, 15, 3946. [Google Scholar] [CrossRef]
- Corti, F.; Shehata, A.H.; Laudani, A.; Cardelli, E. Design and Comparison of the Performance of 12-Pulse Rectifiers for Aerospace Applications. Energies 2021, 14, 6312. [Google Scholar] [CrossRef]
- Setlak, L.; Kowalik, R. Examination of Multi-Pulse Rectifiers of PES Systems Used on Airplanes Compliant with the Concept of Electrified Aircraft. Appl. Sci. 2019, 9, 1520. [Google Scholar] [CrossRef]
- Surya, H. The Effect of 12 Pulse Converter Input Transformer Configuration on Harmonics of Input Current. In IOP Conference Series: Materials Science and Engineering; IOP Publishing, Bristol, UK, 2021; Volume 1158. [Google Scholar] [CrossRef]
- Shklyarskiy, Y.; Dobush, I.; Carrizosa, M.J.; Dobush, V.; Skamyin, A. Method for Evaluation of the Utility’s and Consumers’ Contribution to the Current and Voltage Distortions at the PCC. Energies 2021, 14, 8416. [Google Scholar] [CrossRef]















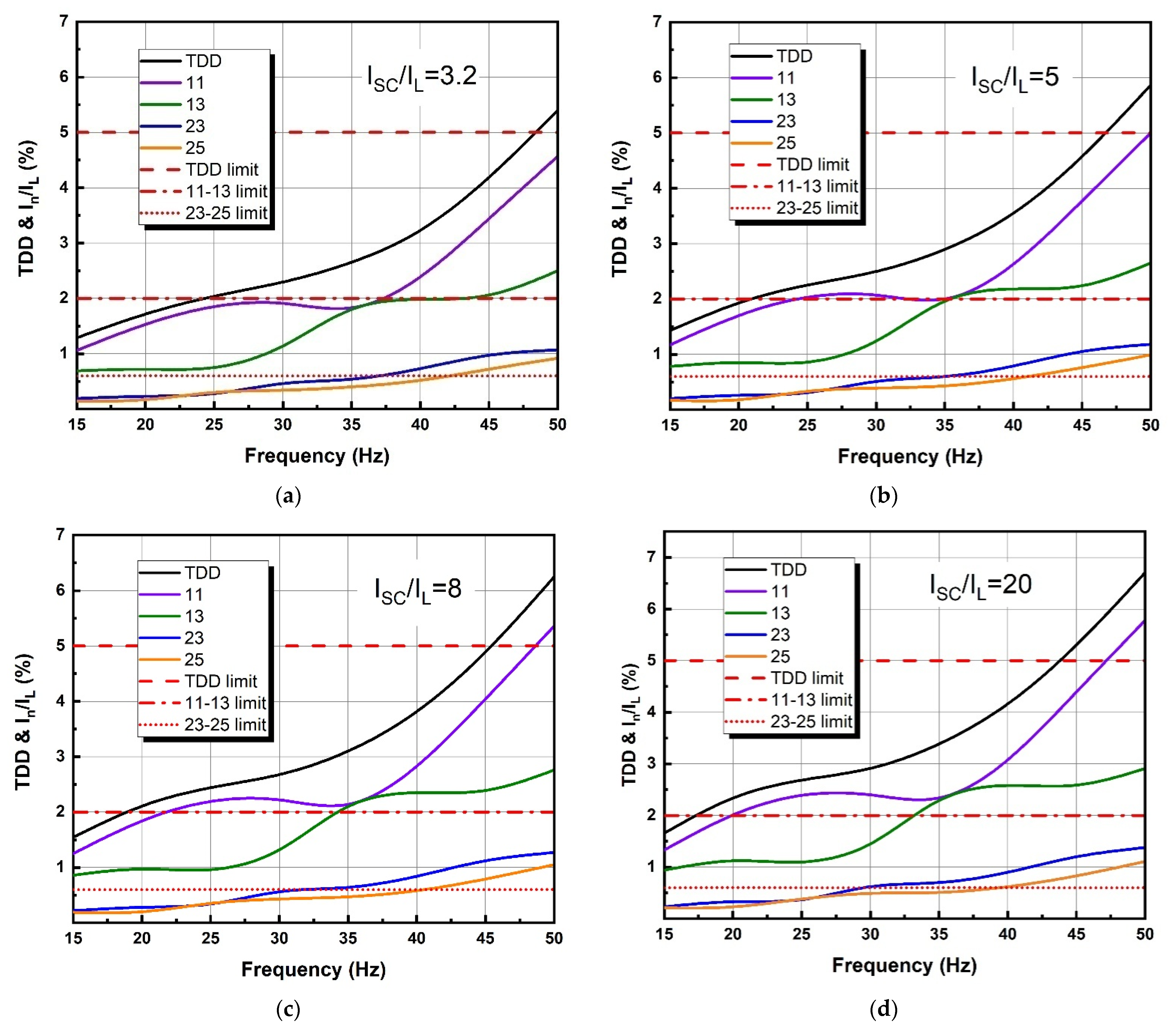


| Individual Harmonic Order (Odd Harmonics) | ||||||
|---|---|---|---|---|---|---|
| ISC/IL | 3 ≤ n < 11 | 11 ≤ n < 17 | 17 ≤ n < 23 | 23 ≤ n < 35 | 35 ≤ n < 50 | TDD |
| <20 | 4.0 | 2.0 | 1.5 | 0.6 | 0.3 | 5.0 |
| 20 < 50 | 7.0 | 3.5 | 2.5 | 1.0 | 0.5 | 8.0 |
| 50 < 100 | 10.0 | 4.5 | 4.0 | 1.5 | 0.7 | 12.0 |
| 100 < 1000 | 12.0 | 5.5 | 5.0 | 2.0 | 1.0 | 15.0 |
| >1000 | 15.0 | 7.0 | 6.0 | 2.5 | 1.4 | 20.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yerbayev, Y.; Artyukhov, I.; Zemtsov, A.; Artyukhov, D.; Molot, S.; Japarova, D.; Zakharov, V. Negative Impact Mitigation on the Power Supply System of a Fans Group with Frequency-Variable Drive. Energies 2022, 15, 8858. https://doi.org/10.3390/en15238858
Yerbayev Y, Artyukhov I, Zemtsov A, Artyukhov D, Molot S, Japarova D, Zakharov V. Negative Impact Mitigation on the Power Supply System of a Fans Group with Frequency-Variable Drive. Energies. 2022; 15(23):8858. https://doi.org/10.3390/en15238858
Chicago/Turabian StyleYerbayev, Yerbol, Ivan Artyukhov, Artem Zemtsov, Denis Artyukhov, Svetlana Molot, Dinara Japarova, and Viktor Zakharov. 2022. "Negative Impact Mitigation on the Power Supply System of a Fans Group with Frequency-Variable Drive" Energies 15, no. 23: 8858. https://doi.org/10.3390/en15238858
APA StyleYerbayev, Y., Artyukhov, I., Zemtsov, A., Artyukhov, D., Molot, S., Japarova, D., & Zakharov, V. (2022). Negative Impact Mitigation on the Power Supply System of a Fans Group with Frequency-Variable Drive. Energies, 15(23), 8858. https://doi.org/10.3390/en15238858









