Sensitivity Analysis of Transcritical CO2 Cycle Performance Regarding Isentropic Efficiencies of Turbomachinery for Low Temperature Heat Sources
Abstract
:1. Introduction
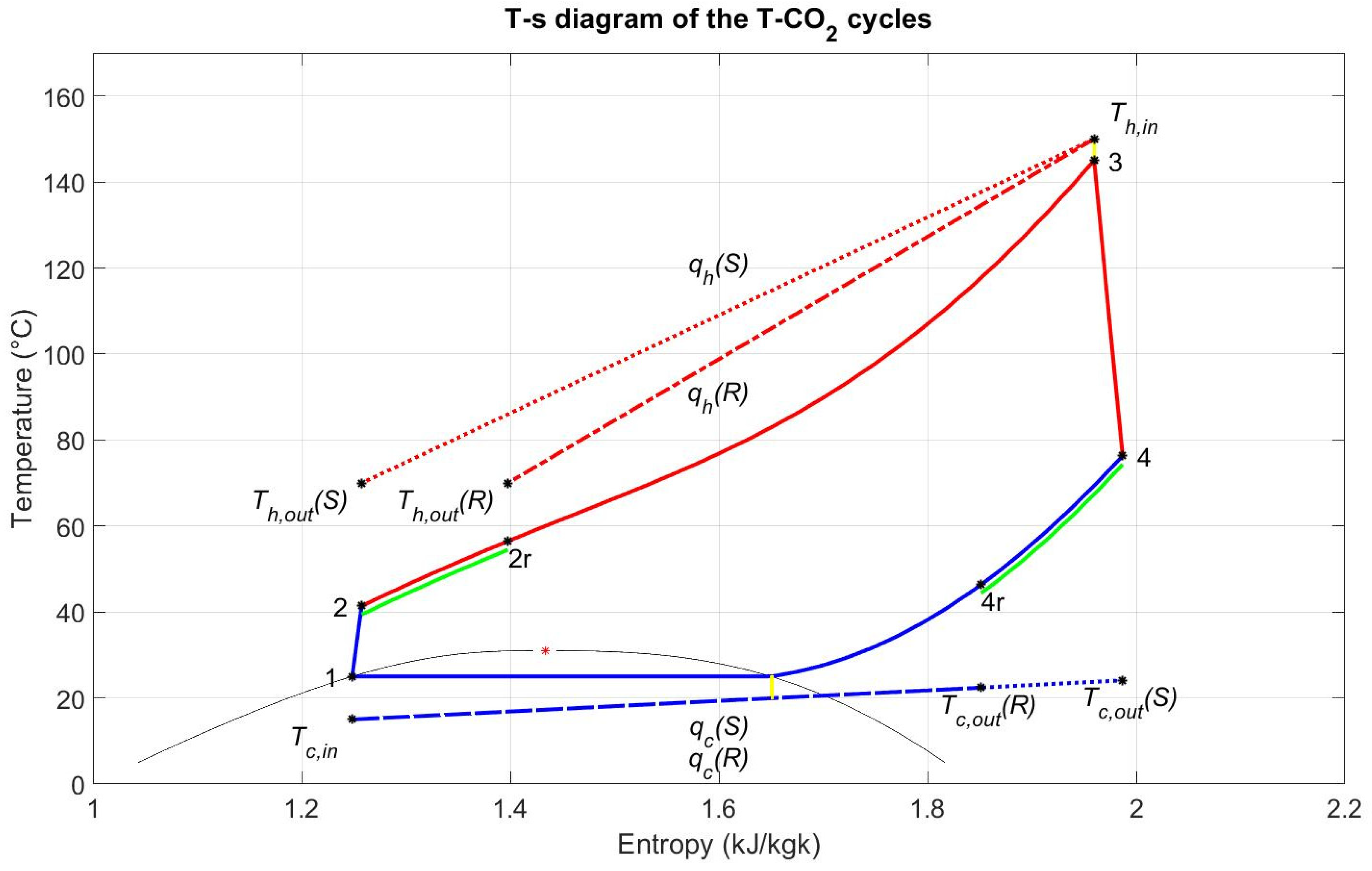
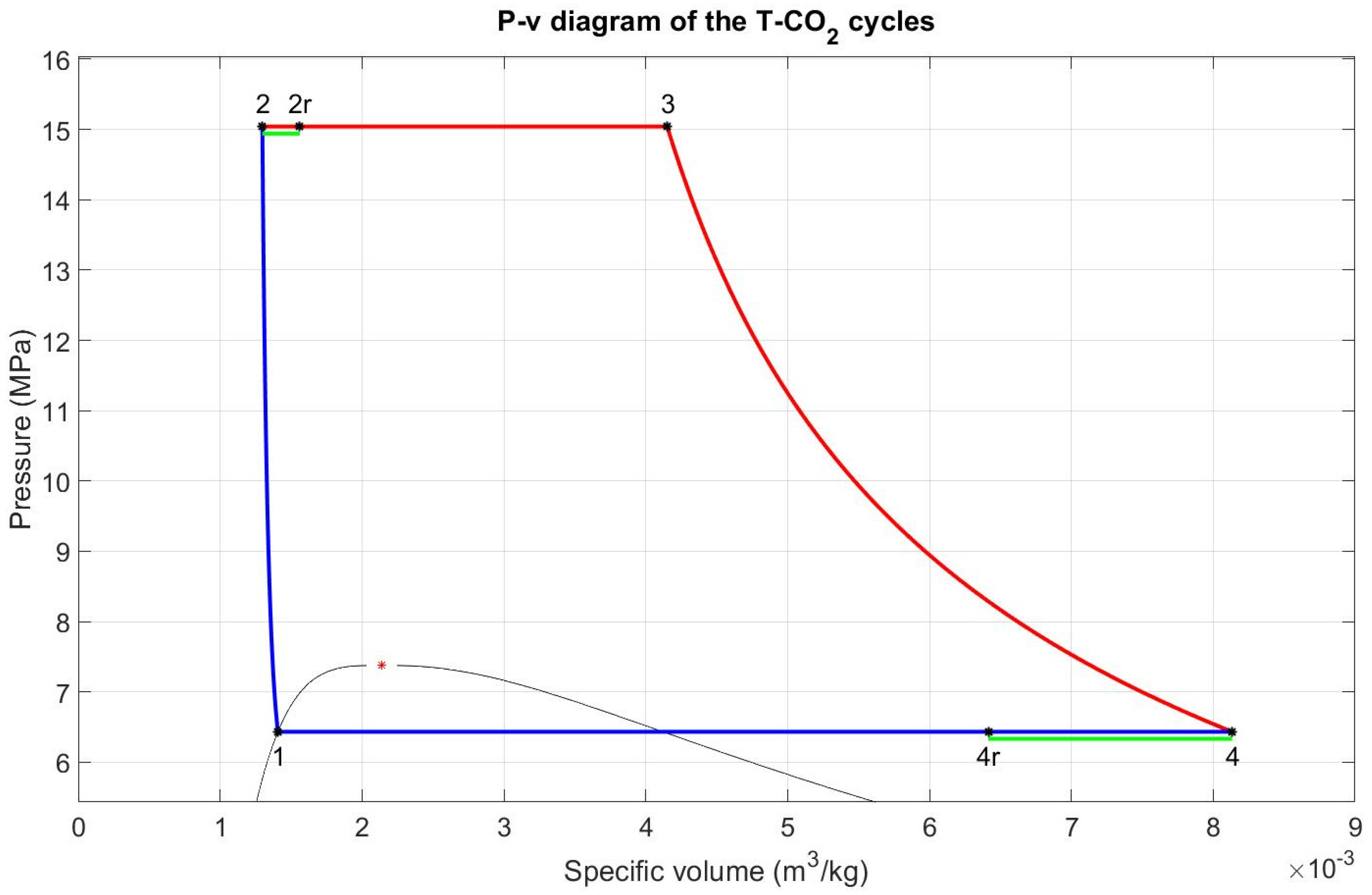
2. Cycle Configurations
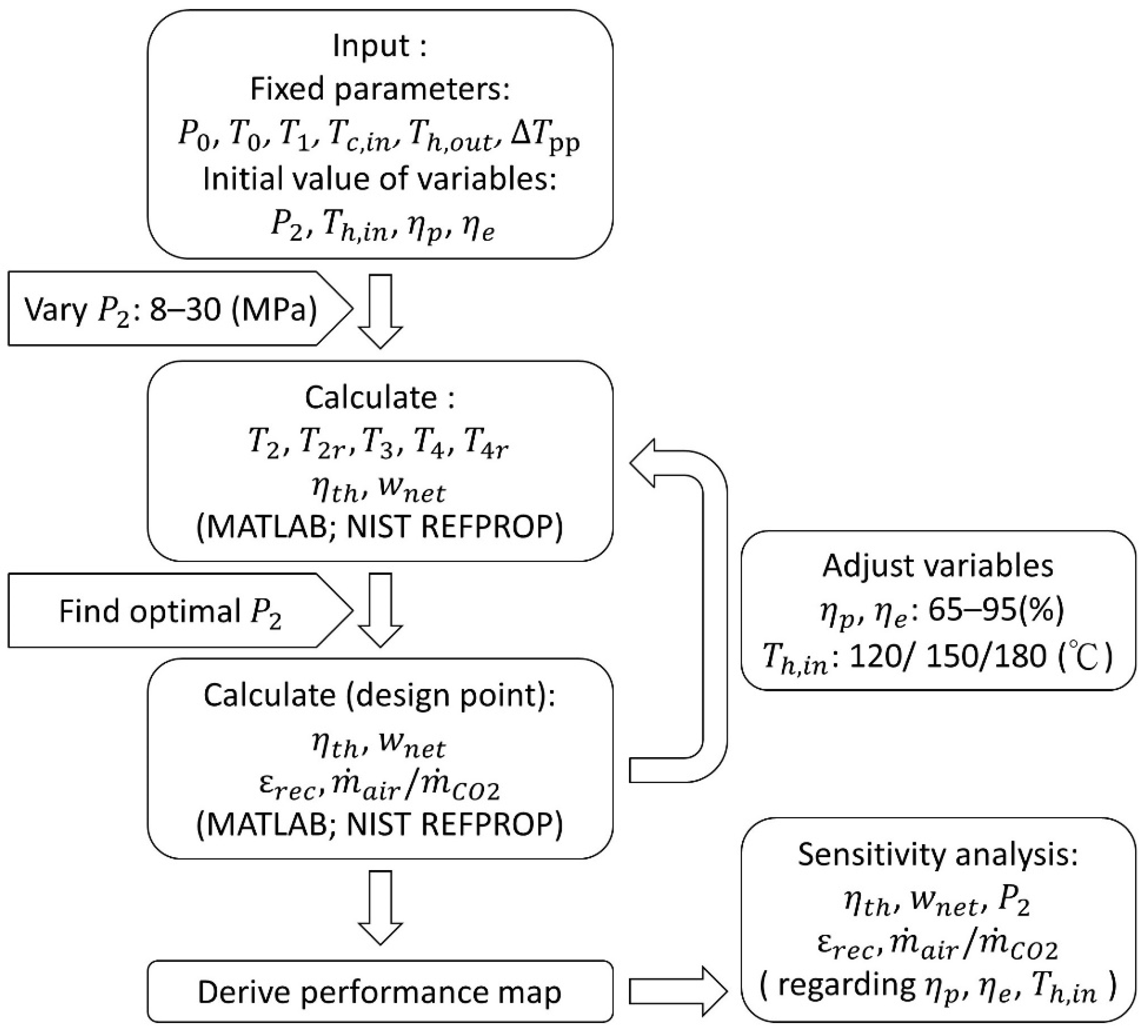
3. Methods
3.1. Energy Analysis
3.2. Simulation Process
3.3. Verification
4. Results and Discussions
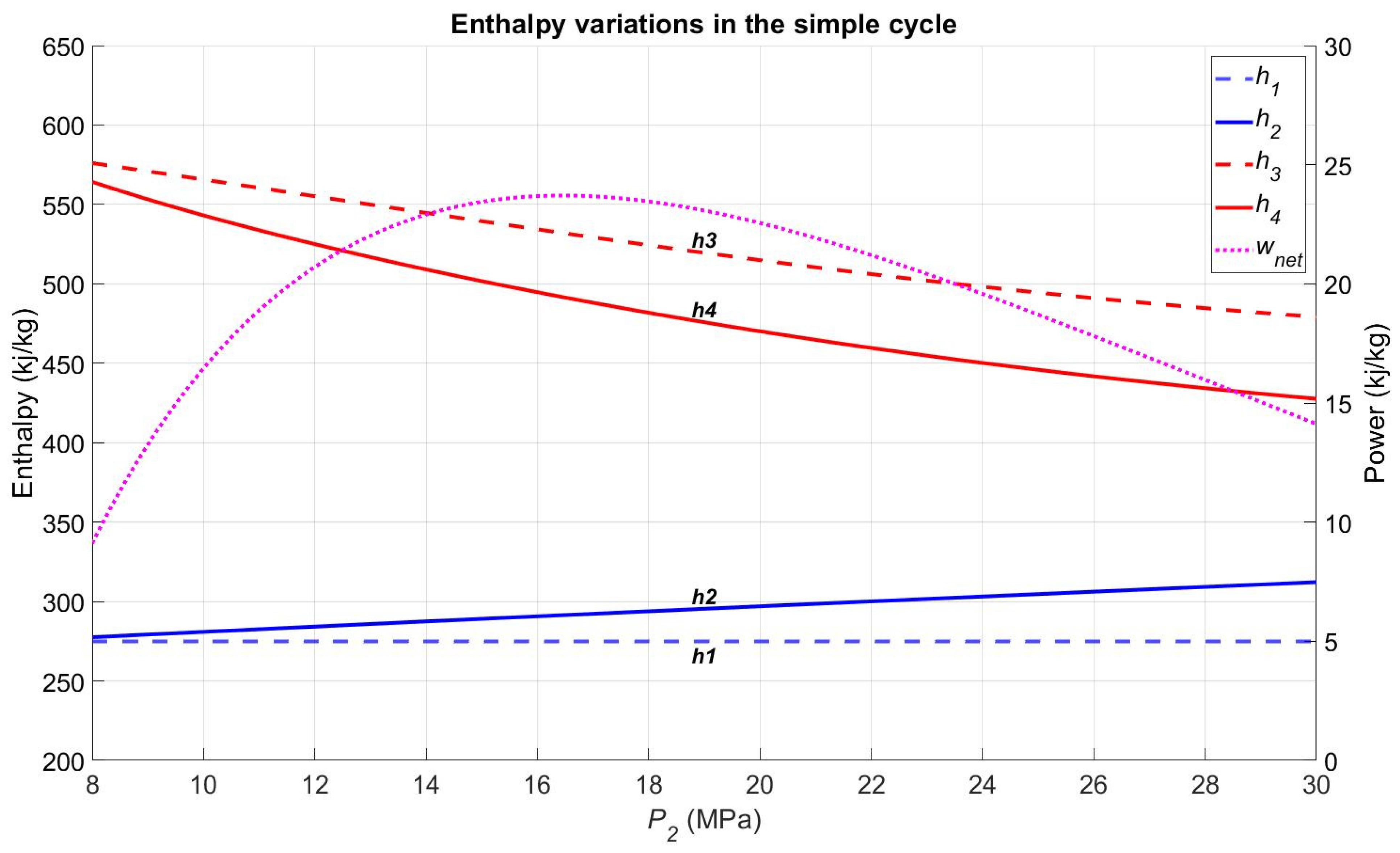
4.1. Simple Cycle
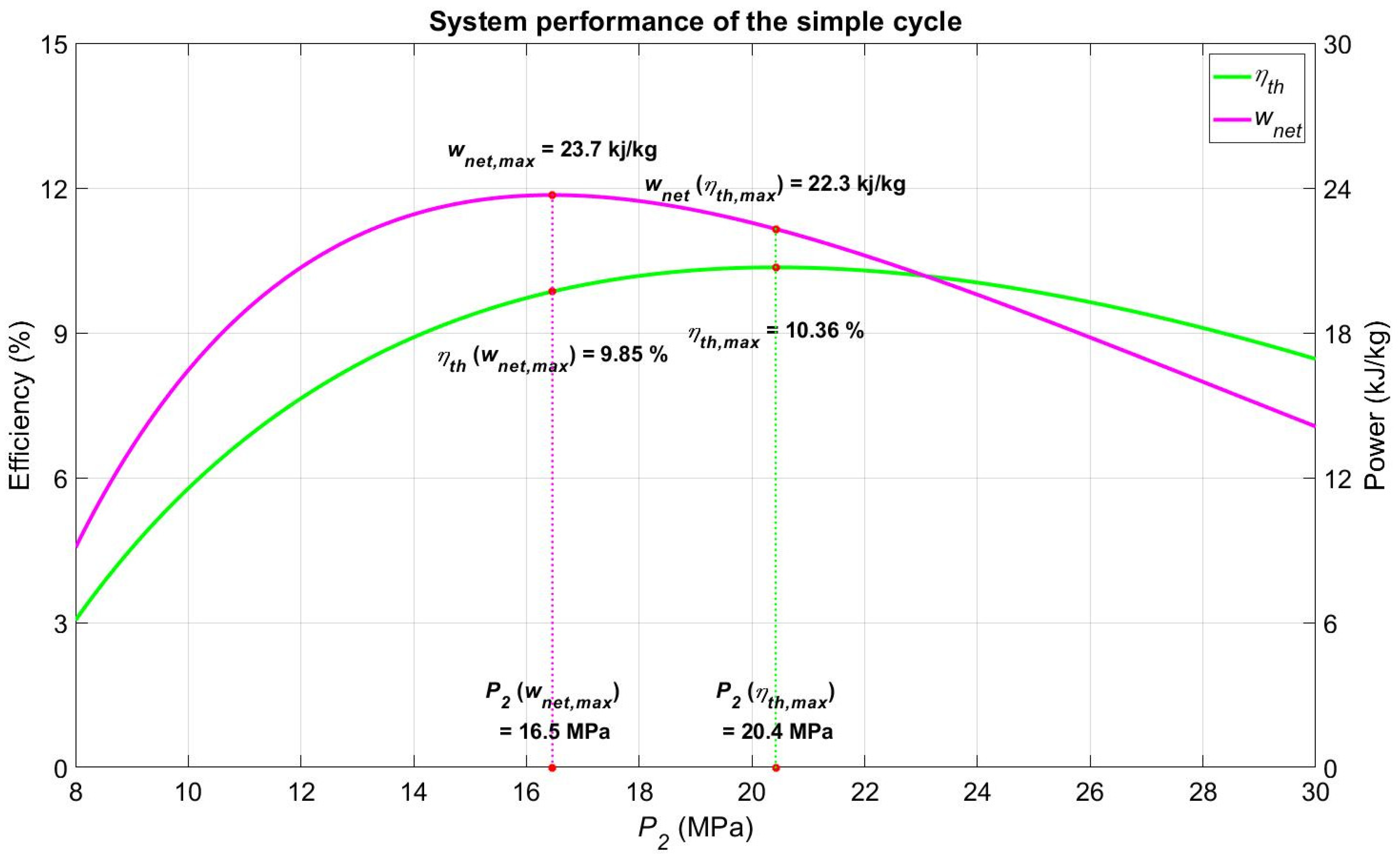
4.1.1. Design Point Setting for the Simple Cycle
4.1.2. Sensitivity Analysis of the Simple Cycle Performance Regarding and
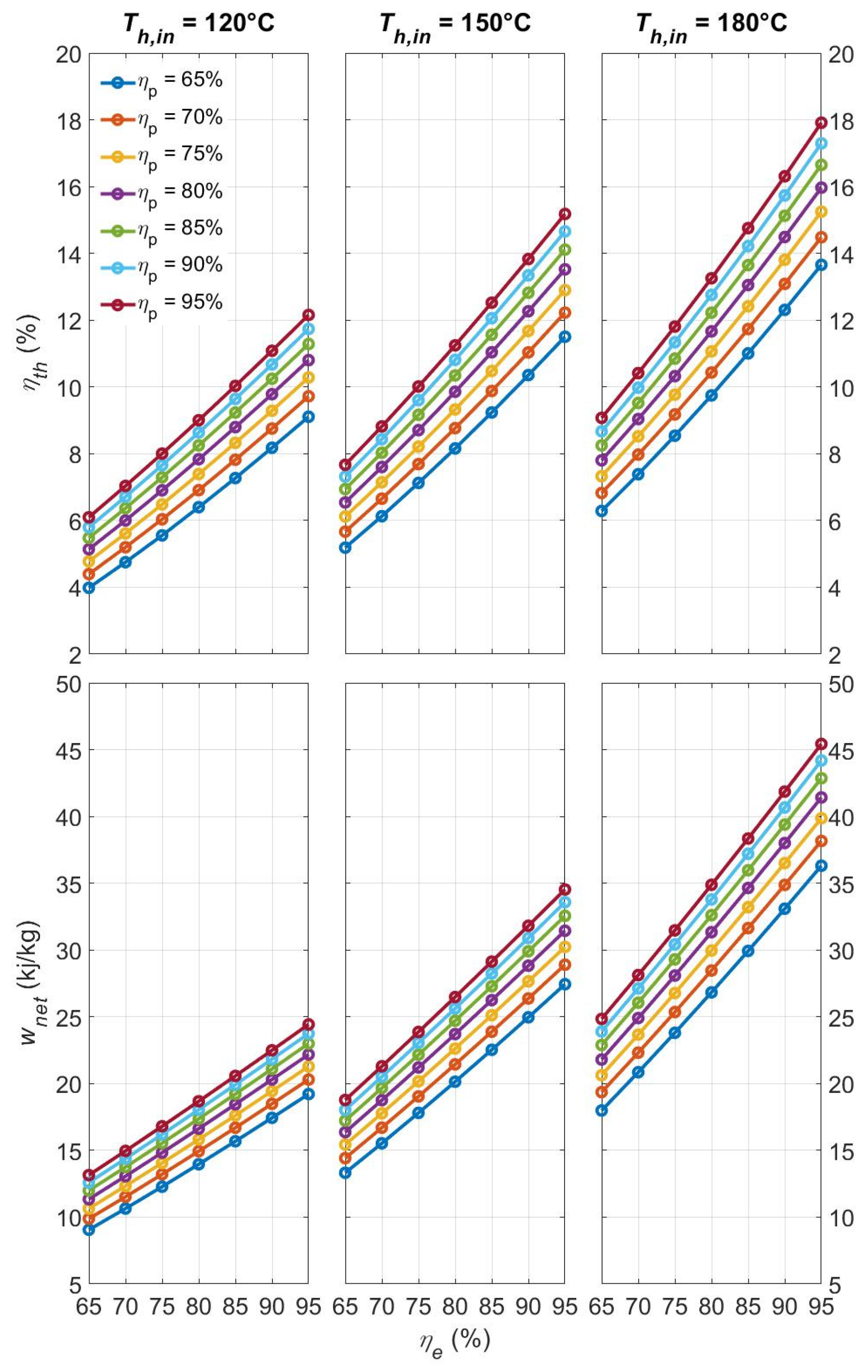
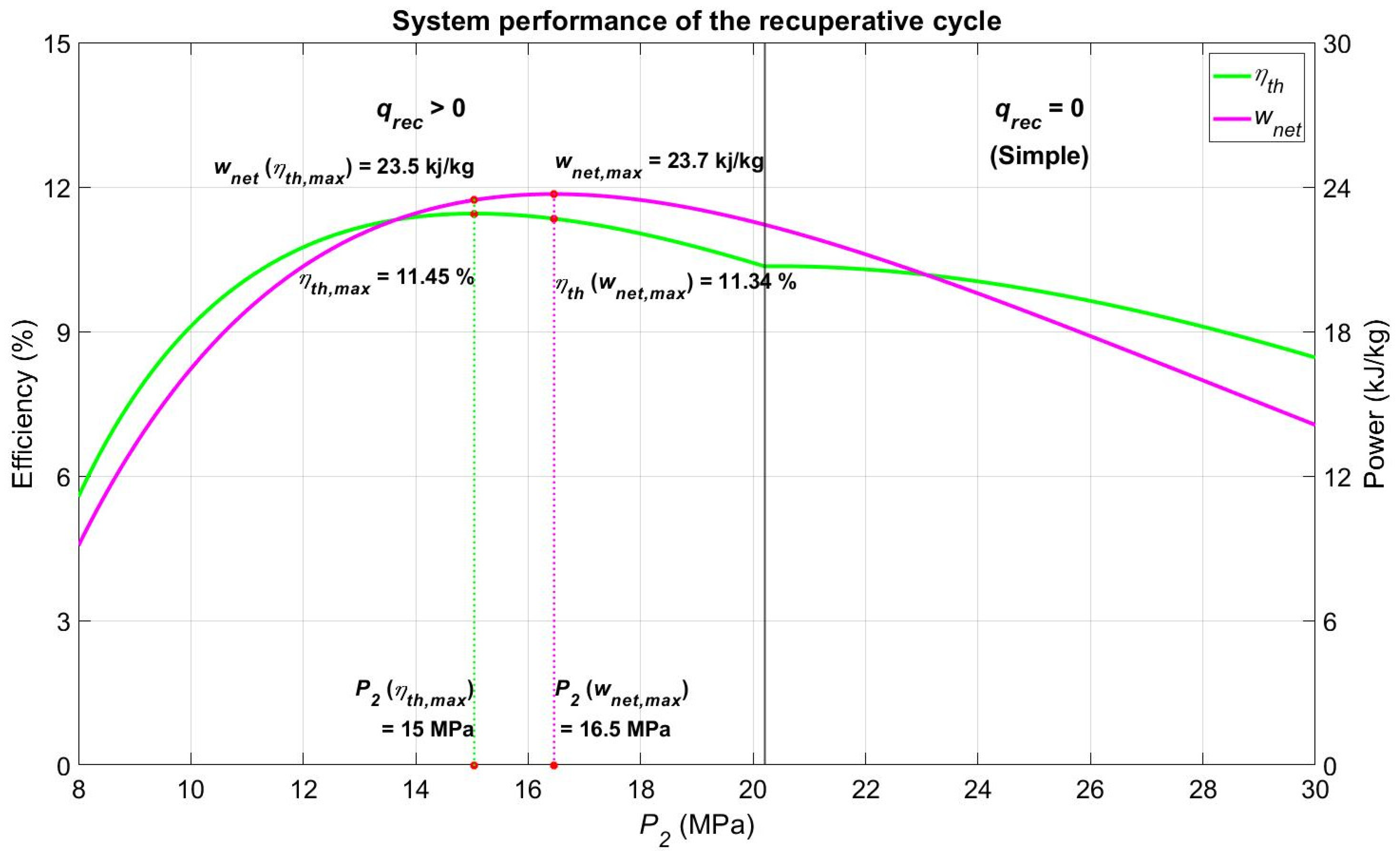
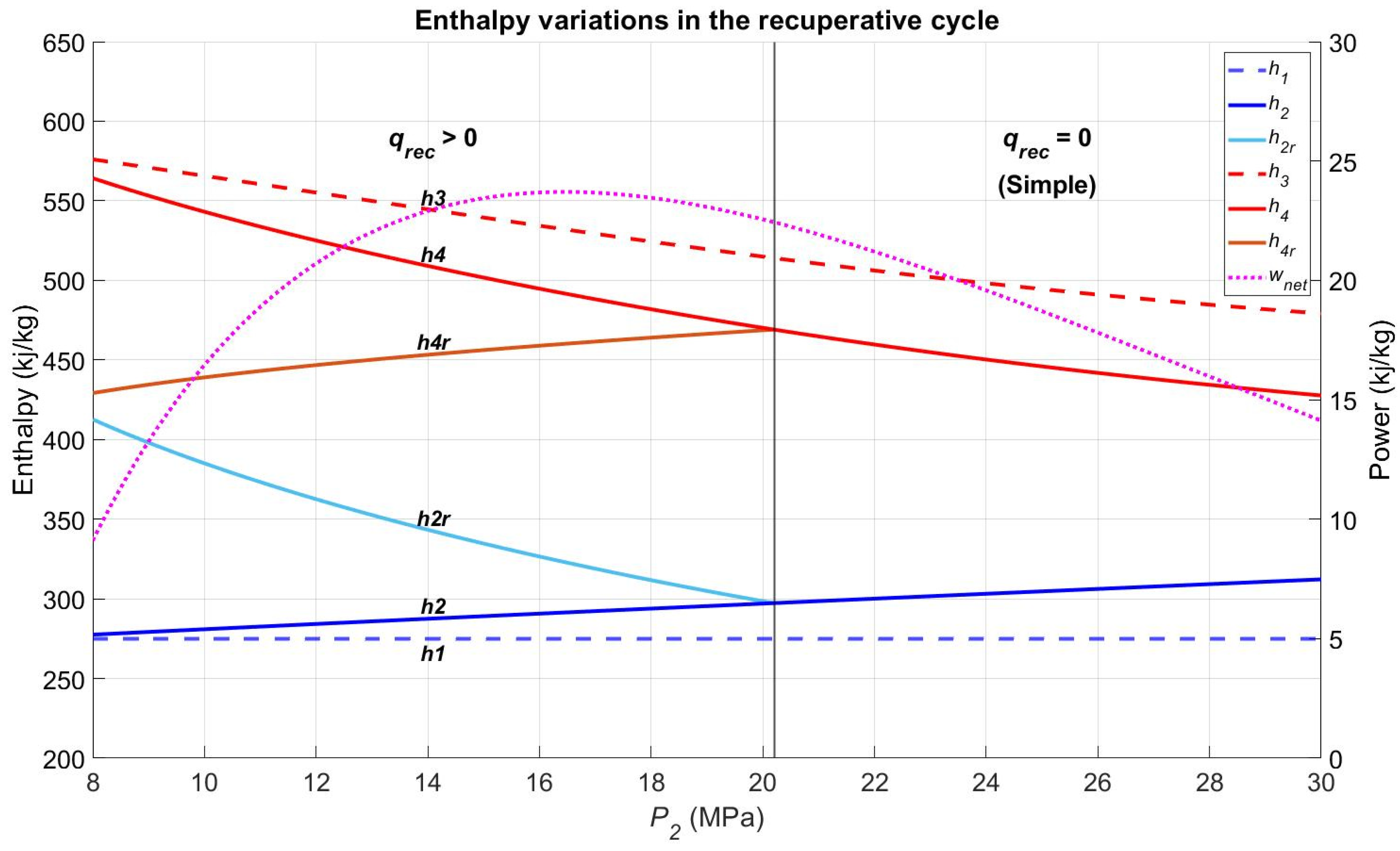
4.2. Recuperative Cycle
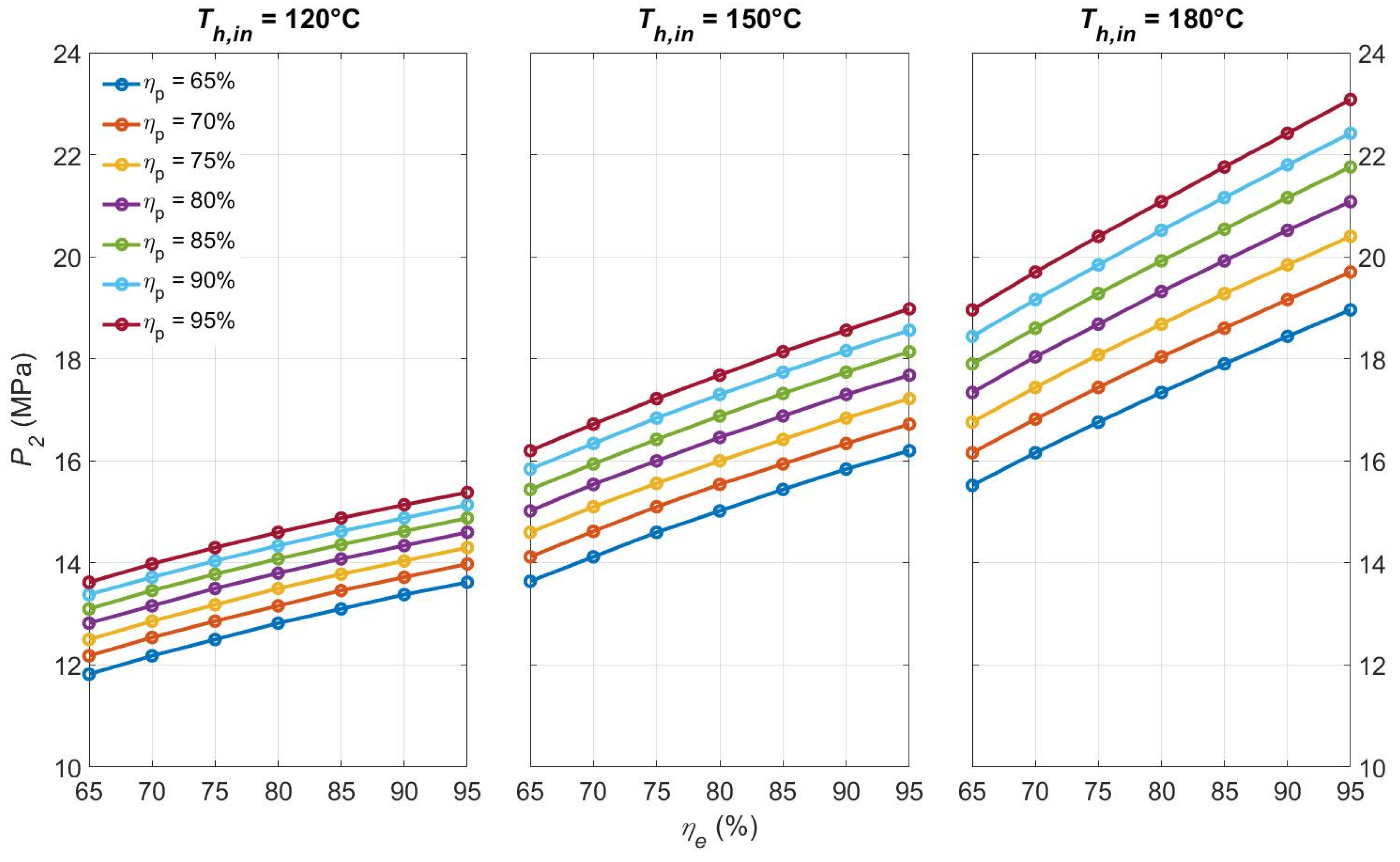
4.2.1. Design Point Setting for the Recuperative Cycle
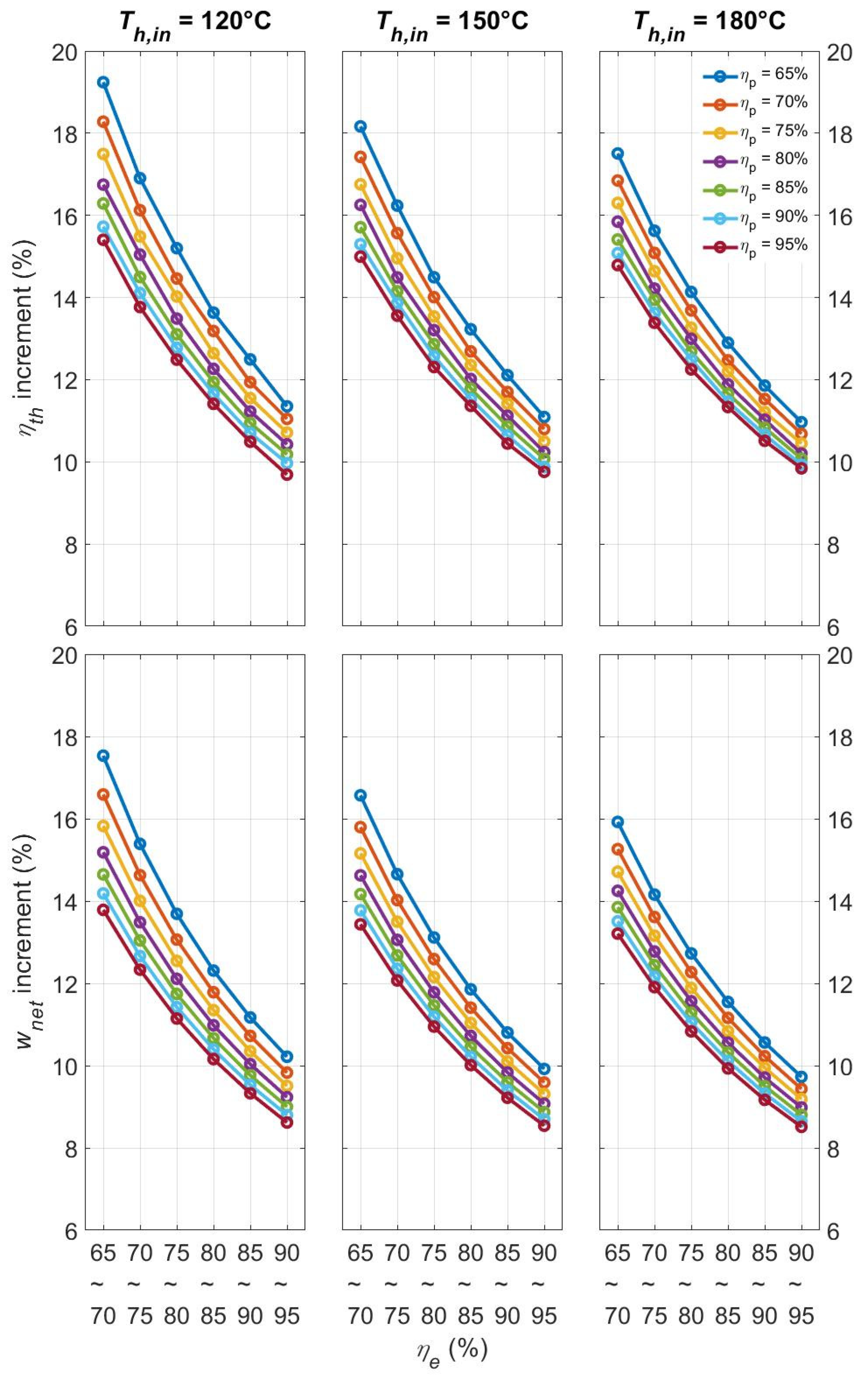
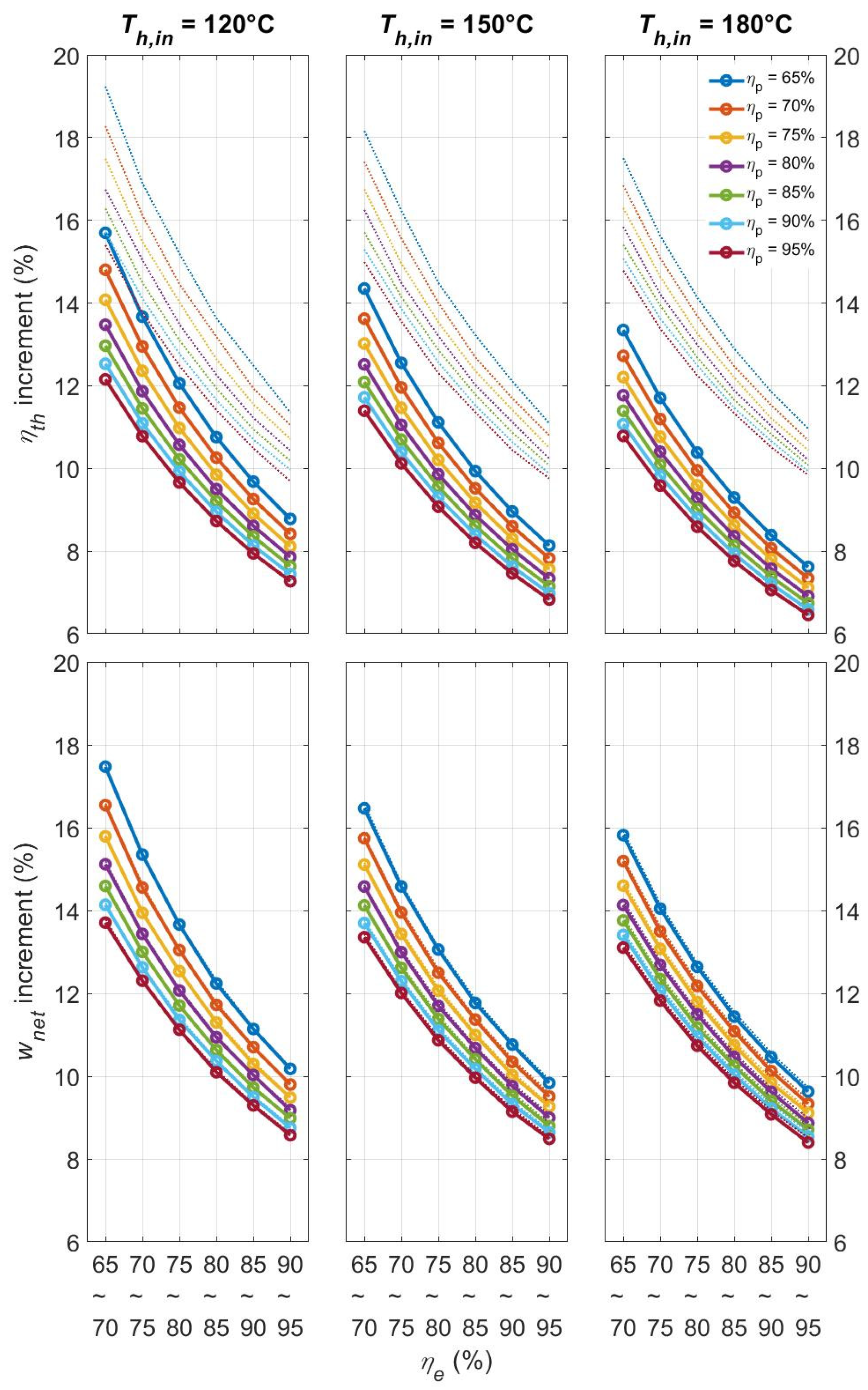
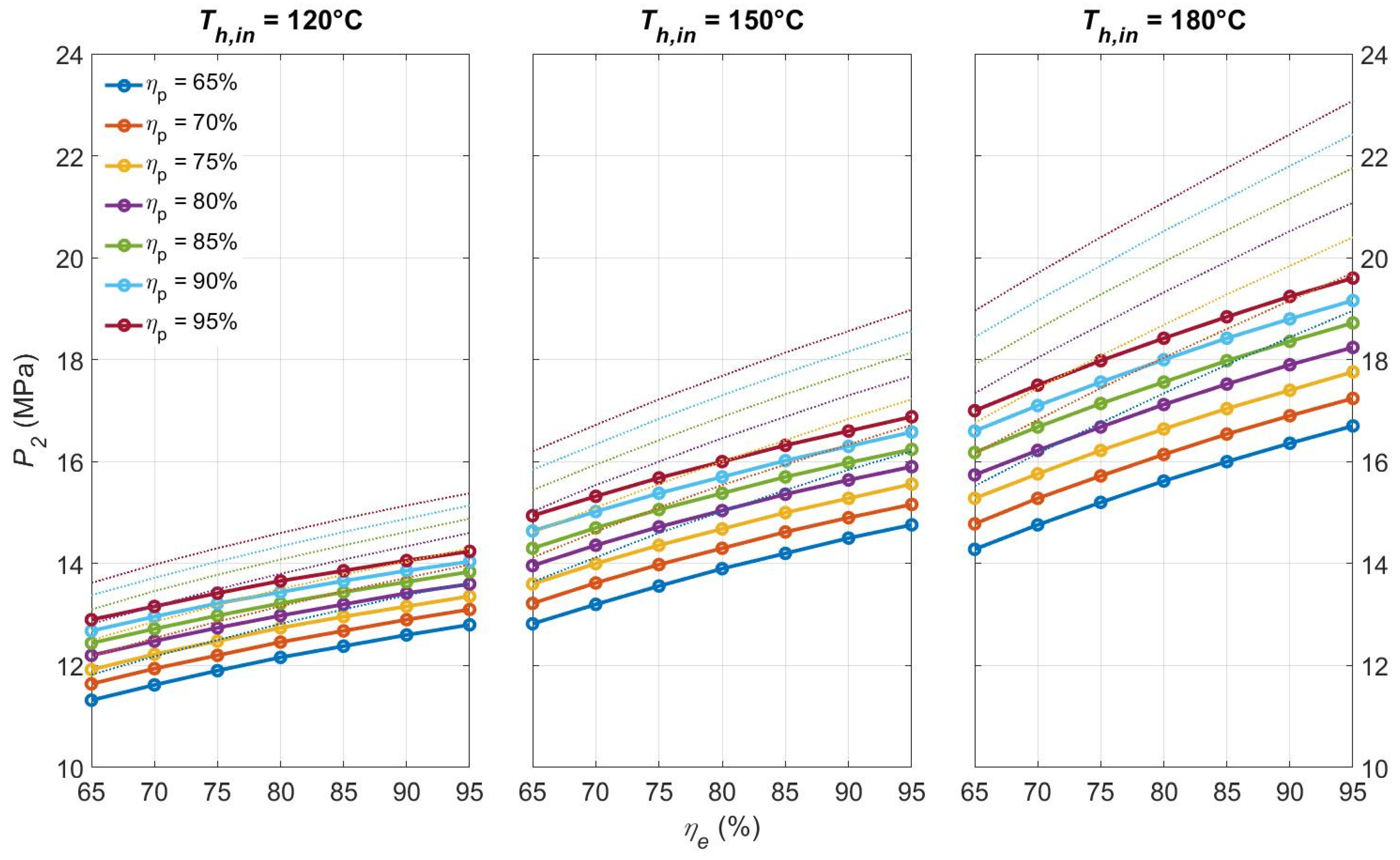
4.2.2. Sensitivity Analysis of the Recuperative Cycle Performance Regarding and
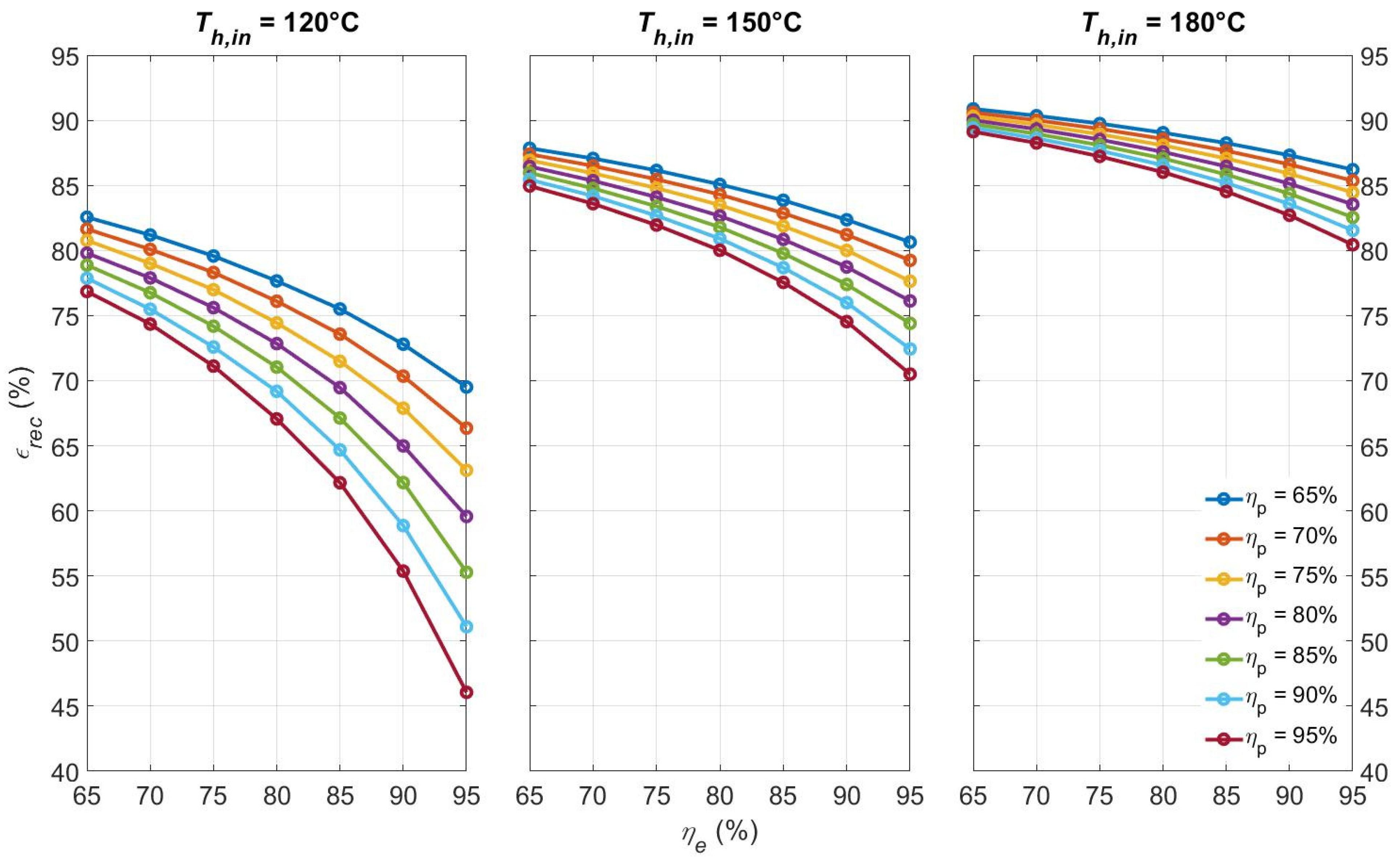
4.2.3. Effectiveness of the Recuperator Regarding and
4.3. Surrounding Conditions
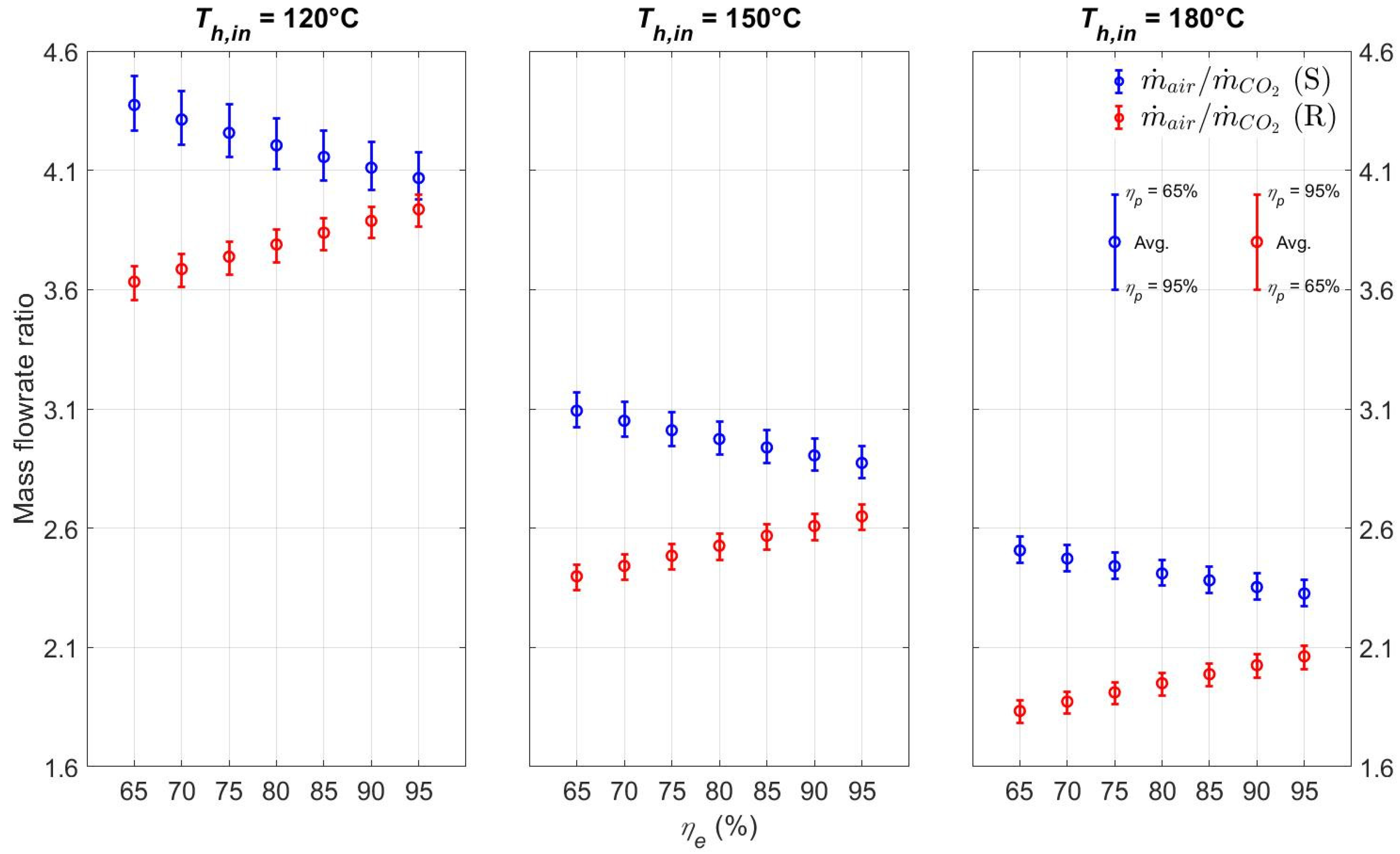
4.3.1. Mass Flow Rate Ratio of Heat Source to CO2
4.3.2. Mass Flow Rate Ratio of the Heat Sink to CO2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| T | Temperature |
| P | Pressure |
| h | Enthalpy |
| Mass flow rate | |
| q | Specific heat transfer rate |
| w | Specific net power output |
| Abbreviations | |
| T-CO2 | Transcritical carbon dioxide |
| ORC | Organic Rankine cycle |
| GWP | Global warming potential |
| ODP | Ozone depletion potential |
| MATLAB | Matrix Laboratory |
| NIST | National Institute of Standards and Technology |
| REFPROP | Reference Fluid Thermodynamic and Transport Properties |
| Greek Symbols | |
| η | Efficiency |
| ε | Effectiveness |
| Subscripts | |
| 0 | Ambient condition |
| 1 | Pump inlet |
| 2 | Pump outlet |
| 3 | Expander inlet |
| 4 | Expander outlet |
| 2r | Recuperator cold side outlet |
| 4r | Recuperator hot side outlet |
| i | State point |
| pp | Pinch point |
| p | Pump |
| h | Heater |
| e | Expander |
| c | Condenser |
| rec | Recuperator |
| s | Isentropic process |
| in | inlet |
| out | outlet |
References
- Chen, Y.; Lundqvist, P.; Johansson, A.; Platell, P. A comparative study of the carbon dioxide transcritical power cycle compared with an organic Rankine cycle with R123 as working fluid in waste heat recovery. Appl. Therm. Eng. 2006, 26, 2142–2147. [Google Scholar] [CrossRef]
- Li, L.; Ge, Y.; Luo, X.; Tassou, S. Thermodynamic analysis and comparison between CO2 transcritical power cycles and R245fa organic Rankine cycles for low grade heat to power energy conversion. Appl. Therm. Eng. 2016, 106, 1290–1299. [Google Scholar] [CrossRef]
- Evans, A.; Strezov, V.; Evans, T.J. Assessment of sustainability indicators for renewable energy technologies. Renew. Sustain. Energy Rev. 2009, 13, 1082–1088. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.J.A.S.I. Investigation of a Novel CO2 Transcritical Organic Rankine Cycle Driven by Parabolic Trough Solar Collectors. Appl. Syst. Innov. 2021, 4, 53. [Google Scholar] [CrossRef]
- Safarian, S.; Aramoun, F.J. Energy and exergy assessments of modified Organic Rankine Cycles (ORCs). Energy Rep. 2015, 1, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Papapetrou, M.; Kosmadakis, G.; Cipollina, A.; La Commare, U.; Micale, G. Industrial waste heat: Estimation of the technically available resource in the EU per industrial sector, temperature level and country. Appl. Therm. Eng. 2018, 138, 207–216. [Google Scholar] [CrossRef]
- Amini, A.; Mirkhani, N.; Pourfard, P.P.; Ashjaee, M.; Khodkar, M.A. Thermo-economic optimization of low-grade waste heat recovery in Yazd combined-cycle power plant (Iran) by a CO2 transcritical Rankine cycle. Energy 2015, 86, 74–84. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, J.; Gao, L. Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery. Energy Convers. Manag. 2009, 50, 576–582. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Z.; Dai, Y.; Ma, S.J. Parametric optimization design for supercritical CO2 power cycle using genetic algorithm and artificial neural network. Appl. Energy 2010, 87, 1317–1324. [Google Scholar] [CrossRef]
- Lecompte, S.; Ntavou, E.; Tchanche, B.; Kosmadakis, G.; Pillai, A.; Manolakos, D.; de Paepe, M. Review of experimental research on supercritical and transcritical thermodynamic cycles designed for heat recovery application. Appl. Sci. 2019, 9, 2571. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Sasaki, S.; Momoki, S. Experimental study for the small capacity organic Rankine cycle to recover the geothermal energy in Obama hot spring resort area. Energy Procedia 2019, 160, 389–395. [Google Scholar] [CrossRef]
- Liu, B.-T.; Chien, K.-H.; Wang, C.-C. Effect of working fluids on organic Rankine cycle for waste heat recovery. Energy 2004, 29, 1207–1217. [Google Scholar] [CrossRef]
- Peris, B.; Navarro-Esbrí, J.; Molés, F.; Mota-Babiloni, A. Experimental study of an ORC (organic Rankine cycle) for low grade waste heat recovery in a ceramic industry. Energy 2015, 85, 534–542. [Google Scholar] [CrossRef]
- Tartière, T.; Astolfi, M. A world overview of the organic Rankine cycle market. Energy Procedia 2017, 129, 2–9. [Google Scholar] [CrossRef]
- Astolfi, M.; Lasala, S.; Macchi, E. Selection Maps For ORC And CO2 Systems For Low-Medium Temperature Heat Sources. Energy Procedia 2017, 129, 971–978. [Google Scholar] [CrossRef]
- Zhang, X.; Cao, M.; Yang, X.; Guo, H.; Wang, J. Economic analysis of organic Rankine cycle using R123 and R245fa as working fluids and a demonstration project report. Appl. Sci. 2019, 9, 288. [Google Scholar] [CrossRef] [Green Version]
- Morrone, P.; Algieri, A. Integrated Geothermal Energy Systems for Small-Scale Combined Heat and Power Production: Energy and Economic Investigation. Appl. Sci. 2020, 10, 6639. [Google Scholar] [CrossRef]
- Calm, J.M.; Hourahan, G.C. Physical, safety, and environmental data for current and alternative refrigerants. In Proceedings of the 23rd International Congress of Refrigeration (ICR2011), Prague, Czech Republic, 21–26 August 2011; pp. 21–26. [Google Scholar]
- Chen, H.; Goswami, D.Y.; Rahman, M.M.; Stefanakos, E.K. A supercritical Rankine cycle using zeotropic mixture working fluids for the conversion of low-grade heat into power. Energy 2011, 36, 549–555. [Google Scholar] [CrossRef]
- Baik, Y.-J.; Kim, M.; Chang, K.C.; Kim, S.J. Power-based performance comparison between carbon dioxide and R125 transcritical cycles for a low-grade heat source. Appl. Energy 2011, 88, 892–898. [Google Scholar] [CrossRef]
- Vélez, F.; Chejne, F.; Antolin, G.; Quijano, A. Theoretical analysis of a transcritical power cycle for power generation from waste energy at low temperature heat source. Energy Convers. Manag. 2012, 60, 188–195. [Google Scholar] [CrossRef]
- Tuo, H. Thermal-economic analysis of a transcritical Rankine power cycle with reheat enhancement for a low-grade heat source. Int. J. Energy Res. 2013, 37, 857–867. [Google Scholar] [CrossRef]
- Sarkar, J. Review and future trends of supercritical CO2 Rankine cycle for low-grade heat conversion. Renew. Sustain. Energy Rev. 2015, 48, 434–451. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Zhang, X.; Fujima, K.; Enomoto, M.; Sawada, N. Solar energy powered Rankine cycle using supercritical CO2. Appl. Therm. Eng. 2006, 26, 2345–2354. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, C.; Favrat, D. Transcritical or supercritical CO2 cycles using both low-and high-temperature heat sources. Energy 2012, 43, 402–415. [Google Scholar] [CrossRef]
- Liu, L.; Yang, Q.; Cui, G. Supercritical carbon dioxide (s-CO2) power cycle for waste heat recovery: A review from thermodynamic perspective. Processes 2020, 8, 1461. [Google Scholar] [CrossRef]
- Cayer, E.; Galanis, N.; Desilets, M.; Nesreddine, H.; Roy, P. Analysis of a carbon dioxide transcritical power cycle using a low temperature source. Appl. Energy 2009, 86, 1055–1063. [Google Scholar] [CrossRef]
- Montes, M.J.; Linares, J.I.; Barbero, R.; Rovira, A. Proposal of a new design of source heat exchanger for the technical feasibility of solar thermal plants coupled to supercritical power cycles. Sol. Energy 2020, 211, 1027–1041. [Google Scholar] [CrossRef]
- Chen, Y.; Lundqvist, P.; Platell, P. Theoretical research of carbon dioxide power cycle application in automobile industry to reduce vehicle’s fuel consumption. Appl. Therm. Eng. 2005, 25, 2041–2053. [Google Scholar] [CrossRef]
- Cayer, E.; Galanis, N.; Nesreddine, H. Parametric study and optimization of a transcritical power cycle using a low temperature source. Appl. Energy 2010, 87, 1349–1357. [Google Scholar] [CrossRef]
- Yoon, S.Y.; Kim, M.J.; Kim, I.S.; Kim, T.S. Comparison of micro gas turbine heat recovery systems using ORC and trans-critical CO2 cycle focusing on off-design performance. Energy Procedia 2017, 129, 987–994. [Google Scholar] [CrossRef]
- Novales, D.; Erkoreka, A.; De la Peña, V.; Herrazti, B. Sensitivity analysis of supercritical CO2 power cycle energy and exergy efficiencies regarding cycle component efficiencies for concentrating solar power. Energy Convers. Manag. 2019, 182, 430–450. [Google Scholar] [CrossRef]
- Salah, S.I.; Khader, M.A.; White, M.T.; Sayma, A.I. Mean-line design of a supercritical CO2 micro axial turbine. Appl. Sci. 2020, 10, 5069. [Google Scholar] [CrossRef]
- Kim, Y.M.; Sohn, J.L.; Yoon, E.S. Supercritical CO2 Rankine cycles for waste heat recovery from gas turbine. Energy 2017, 118, 893–905. [Google Scholar] [CrossRef]
- Kim, Y.-M.; Lee, Y.-D.; Ahn, K.-Y. Parametric Study of a Supercritical CO2 Power Cycle for Waste Heat Recovery with Variation in Cold Temperature and Heat Source Temperature. Energies 2021, 14, 6648. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 9.1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013.
- Autier, E.; Kouadri, A. Optimum for CO2 transcritical power Rankine cycle using exhaust gas from fishing boat diesel engines. IFAC Proc. Vol. 2009, 42, 132–139. [Google Scholar] [CrossRef]

| Literature | (%) | (%) | Literature | (%) | (%) |
|---|---|---|---|---|---|
| Wang et al. [9] | 70 | 75 | Salah et al. [33] | 70 | 80 |
| Velez et al. [21] | 75 | 75 | Chen et al. [1] Amini et al. [7] Chen et al. [29] | 80 | 70 |
| Cayer et al. [27,30] Baik et al. [20] Tuo [22] Kim et al. [34,35] | 80 | 80 | Li et al. [2] Bellos et al. [4] Yoon et al. [31] | 85 | 85 |
| Kim et al. [25] | 90 | 90 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (°C) | 120/150/180 | (K) | 5 |
| (°C) | 70 | (MPa) | 0.1 |
| (°C) | 15 | (MPa) | 8–30 |
| (°C) | 15 | (%) | 65–95 |
| (°C) | 25 | (%) | 65–95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.-H.; Chiang, H.-W.D.; Wang, P.-J. Sensitivity Analysis of Transcritical CO2 Cycle Performance Regarding Isentropic Efficiencies of Turbomachinery for Low Temperature Heat Sources. Energies 2022, 15, 8868. https://doi.org/10.3390/en15238868
Lu K-H, Chiang H-WD, Wang P-J. Sensitivity Analysis of Transcritical CO2 Cycle Performance Regarding Isentropic Efficiencies of Turbomachinery for Low Temperature Heat Sources. Energies. 2022; 15(23):8868. https://doi.org/10.3390/en15238868
Chicago/Turabian StyleLu, Kun-Hsien, Hsiao-Wei D. Chiang, and Pei-Jen Wang. 2022. "Sensitivity Analysis of Transcritical CO2 Cycle Performance Regarding Isentropic Efficiencies of Turbomachinery for Low Temperature Heat Sources" Energies 15, no. 23: 8868. https://doi.org/10.3390/en15238868
APA StyleLu, K.-H., Chiang, H.-W. D., & Wang, P.-J. (2022). Sensitivity Analysis of Transcritical CO2 Cycle Performance Regarding Isentropic Efficiencies of Turbomachinery for Low Temperature Heat Sources. Energies, 15(23), 8868. https://doi.org/10.3390/en15238868







