Flexible Loads Scheduling Algorithms for Renewable Energy Communities

Abstract

Renewable Energy Communities (RECs) are emerging as an effective concept and model to empower the active participation of citizens in the energy transition, not only as energy consumers but also as promoters of environmentally friendly energy generation solutions, particularly through the use of photovoltaic panels. This paper aims to contribute to the management and optimization of individual and community Distributed Energy Resources (DER). The solution follows a price and source-based REC management program, in which consumers’ day-ahead flexible loads (Flex Offers) are shifted according to electricity generation availability, prices, and personal preferences, to balance the grid and incentivize user participation. The heuristic approach used in the proposed algorithms allows for the optimization of energy resources in a distributed edge-and-fog approach with a low computational overhead. The simulations performed using real-world energy consumption and flexibility data of a REC with 50 dwellings show an average cost reduction, taking into consideration all the seasons of the year, of 6.5%, with a peak of 12.2% reduction in the summer, and an average increase of 32.6% in individual self-consumption. In addition, the case study demonstrates promising results regarding grid load balancing and the introduction of intra-community energy trading.

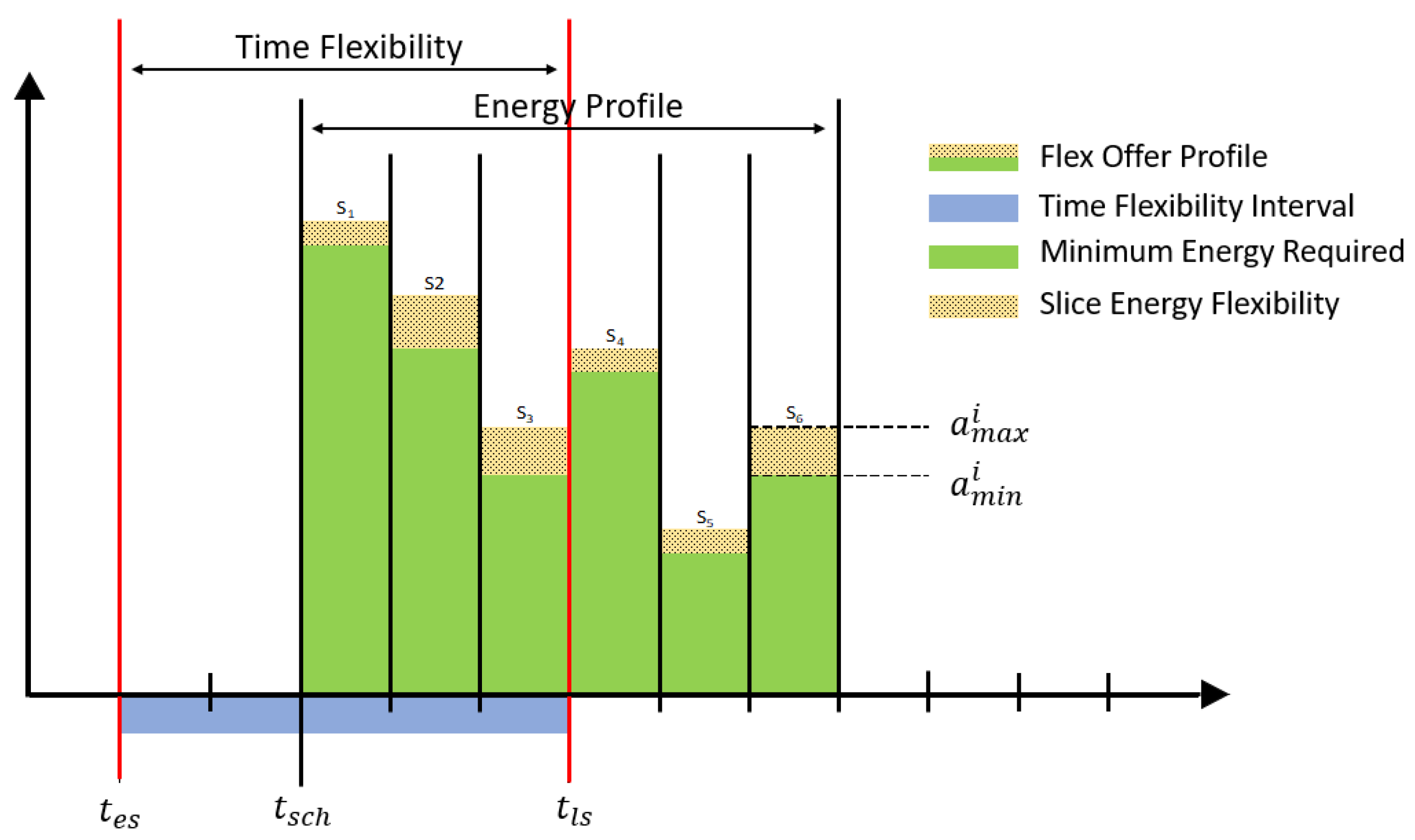
1. Introduction

Traditional energy grids have been heavily dependent on the burning of fossil fuels, such as coal or natural gas, to generate electricity. This type of electricity production therefore has a negative impact on the environment, while also posing geopolitical challenges for countries that must rely upon others for obtaining these vital resources. In addition, energy generation at plants distant from consumers leads to losses in its distribution infrastructure, diminishing efficiency and increasing running costs [1].

Renewable Energy Sources (RES) emerge as a green, reliable, and economically viable solution for electricity production. Given the replenishable nature of its sources, such as the sun and wind, RES enables citizens and governments to become more self-sufficient, as the energy can be produced on an individual basis in a distributed manner. Distributed Energy Resources (DER) are closer to consumers, which also substantially reduces traditional distribution losses and the energy costs of consumers, which incentivizes the use of RES. As a result, the adoption of renewable energy has significantly increased, with its growth forecast to speed up in the next five years [2]. Households, office dwellings, and factories also play an increasingly prominent role in this transition [3], by installing photovoltaic panels to satisfy their own energy needs and injecting their surplus production into the grid. Such end-users are now being designated as prosumers, as they take on the role of both producers and consumers of energy simultaneously.

However, the high penetration of RES poses new difficulties to grid operators in managing and maintaining the necessary grid balance, as there is a time imbalance between peak demand and RES production due to the highly fluctuating operation characteristic of these sources. In addition, at certain times of the year, namely spring and summer, there is an overgeneration risk which may force grid operators to curtail RES or implement negative electricity prices to force demand upwards, leading to higher operating costs and thus reducing both the environmental and economic benefits of renewable sources.

Energy Flexibility Management offers a partial solution to this problem, minimizing the impact of the introduction of RES in energy grids and preserving its economic and environmental benefits. Renewable Energy Communities (REC) offer a powerful framework in which energy sharing between members is possible and where Flexibility Management can be further explored. In this context, Flexigy [4], the project in which this research work has been conducted, aimed to develop an integrated platform for managing the energy flexibility of consumers and prosumers belonging to a REC.

This paper builds on the three-level smart-grid architecture for REC management introduced in [5], detailing the algorithms developed, whose main aim is to schedule the energy flexibility of home appliances, considering the member preferences and the consumption profiles of the appliances with the corresponding flexibilities. The scheduling is performed at each of three architectural levels: (i) at the prosumer level (on a single house or office dwelling), (ii) at REC level (to which the prosumer belongs), and (iii) at the grid level. This paper’s contribution focuses on delivering fast and scalable algorithms that do not use excessive computing resources so that they can be applied closer to the end-user on an edge-and-fog low-cost computing platform, while maintaining a high level of optimization with benefits for the users and the environment.

The proposed method is validated using a dataset composed of the energy flexibility profiles, consumption, and production of fifty dwellings. The data were collected during different seasons on real-world appliances during the project. Finally, the results are presented and the benefits of the solution are thoroughly analyzed.

This paper is organized in multiple sections. Section 2 presents the state-of-the-art concepts and projects related to demand-side response and energy flexibility. Section 3 gives an overview of the developed system model. Section 4 details the flex offer scheduling algorithms. Section 5 presents and discusses the results obtained from a real-world simulation. Section 6 addresses the main conclusions and future work.

2. State of the Art

The EU has committed to reducing 55% of net greenhouse gas emissions [6], integrating more than 40% of Renewable Energy Sources (RES) [7], and improving energy efficiency by 32.5% [8] by 2030. Critical to achieving these targets is the large-scale penetration of intermittent RES and the increase in the electrification of sectors such as transportation and heating [9]. Balancing energy supply demand in the RES-dominated energy landscape requires the involvement of individual consumers in Demand-Side Management (DSM) [10].

The spread of Distributed Energy Resources (DERs), smart IoT home appliances, and advancements in information and communication technologies (ICT) has led to the emergence of smart grids, which enable the participation of individual consumers in existing and emerging electricity markets through DSM applications [11,12,13]. The scientific literature on the state of the art of DSM includes many interesting studies. For example, in [14], the authors examined the benefits of DSM in smart grids, while [11] focused on the developments of energy scheduling and communication technologies for DSM. The authors in [9,15] regarded the implementation of DSM in smart grids as one of the most innovative strategies for optimizing the use of the existing grid, delaying and avoiding grid expansion, and integrating intermittent RES, while electrifying transport and buildings. Furthermore, Smart Energy Europe (smarten), a European business association integrating the consumer-driven solutions of the clean energy transition, and Det Norske Veritas (DNV) in their Demand-Side Flexibility (DSF) among other benefits, calculated €71 billion and €300 billion, respectively, in direct and indirect cost benefits to the consumers [16].

Furthermore, the importance of DSF is highlighted by the Clean Energy Package (CEP) issued in June 2019 by the European Union (EU) [17]. The CEP consists of a set of Directives and Regulations on energy efficiency [8], RES integration [8], energy performance in buildings [18], governance, and common rules for the electricity market [19]. The CEP has laid down ambitious goals for the coming decades and empowers final energy end users, both consumers and prosumers, to be grouped in Energy Communities (EC) to help Europe in becoming the world’s first carbon-neutral continent by 2050.

Simply put, RECs, as defined in CEP [17], represent a novel social construct and concept that can enable their members (consumers and prosumers) to share and benefit from local RES and eventually engage in electricity markets. RECs are groups of geographically close citizens (consumers and prosumers), managing a wide range of heterogeneous energy assets, such as RES, storage technologies including home and EV batteries, home appliances, and other types of load. RECs can participate in numerous activities [9] such as engaging in distributed energy generation as a strategy to reduce costs (self-production and sharing), optimizing the use of renewables for collective self-consumption schemes, and offering flexible services to local system operators in order to avoid grid expansion or other market operators, by taking advantage of the flexibility of several electrical appliances (e.g., water heaters, HVAC systems, dishwashers) and storage. The authors in [20] present a systematic literature review of the history, definitions, programs, and future development opportunities in Demand Response (DR). In addition, the authors discuss the introduction of smart energy communities as a new DR participant with considerable load flexibility. Regarding the quantification of DSF potential, authors in [21,22] analyzed device-level energy consumption data from several different households and concluded that, on average, 50% of the energy demand from the household comes from flexible devices. Furthermore, several studies have demonstrated the demand reduction and shifting potential of flexible energy devices through the scheduling of residential appliances, particularly of wet devices [23,24,25], heat pumps (HP) [26,27,28,29,30], and electric vehicles (EV) [31,32,33,34,35].

The activation of the DSF can enable the optimization of energy generation and consumption resources by scheduling the DSF, based on electricity generation availability, prices, and user personal preferences. With such a motivation, many schemes for scheduling energy generation and consumption resources have been proposed. For instance, direct centralized control of flexible devices has been widely put forward for optimizing the use of individual and community DERs. This type of centralized control system has been implemented to directly control the energy consumption of devices at an individual or an aggregated level to reduce user cost [25,32,36], to level peak loads [12,31,37], or to generate financial benefits to the distribution utilities [38]. Authors in [23] introduced a novel framework enabling system operators to access DR from HVAC systems in a timeframe suitable for operating reserves. In this study, washing machines, dishwashers, and tumble dryers equipped with communication modules were considered smart appliances. In [12], the authors implemented a power scheduling method to reduce both the electricity cost and Peak-to-Average Ratio (PAR), thus strengthening the stability of the entire electricity system.

Domestic thermal loads such as thermal accumulators and HVAC systems have been the target of research as flexible resources for DR used in ECs. These devices can be used to store excess electricity production such as thermal energy, taking into consideration the limits of user comfort and the capacity of appliances. The authors in [39] present a peak shaving solution that predicts water usage profiles from dwelling load patterns, computes thermal losses to determine the water temperature in the tank, and consequently forecasts an optimal consumption profile. Moreover, [40] applies a fuzzy adaptive competitive algorithm as a load control model for scheduling AC units while minimizing the user’s thermal comfort, while [41] introduces a model predictive control (MPC) algorithm to schedule a dwelling AC unit considering variable weather, occupancy, and electricity prices. [42] introduces a nonlinear optimization model for the scheduling of typical home appliances with a time-of-use electricity tariff, while [43] assesses the impacts of time-of-use tariffs on residential electricity demand and peak shifting.

In addition, [43] approaches residential day-ahead energy scheduling for DR in smart grids by formulating an optimization problem that, based on the service provider’s electricity prices given ahead of time, presents a solution with the desired trade-off between cost and comfort. However, the report only tests six appliances (three schedulable and three non-schedulable), leading to concerns of solution applicability in real-world energy communities with hundreds of scheduling devices which results in major computational and time requirements to solve the optimization problem. This has been one of our main concerns for the algorithms proposed in this paper. In the literature [11,12,23,24,25,26,29] and [31,32,36,37,42,44,45], the energy scheduling problem has been solved using many methods such as linear programming, the particle swarm optimization (PSO) method, and game theory. Normally, the equations for most of these optimization problems are nonlinear, so the authors in [12] prefer approaches such as genetic algorithms to solve this type of optimization problem. Moreover, the authors in [46] propose an adaptive day-ahead load optimization and control solution with an edge-and-fog Internet of Things (IoT) architecture.

Despite tremendous flexibility potential and energy community members’ readiness to provide flexibility in their energy consumption, several significant challenges exist that have been either only been partially tackled or remain unexplored:

• A general representation of the flexibility, generalized to all device types, is lacking.
• A simple, modular, and generalized solution/process which can extract flexibility information from all device types with minimal user intervention is still lacking [47].
• Novel, lightweight, scalable, and real-time flexibility scheduling algorithms to manage and optimize individual and community Distributed Energy Resources (DER) need to be developed [48].
• The economic assessment of the benefits of activating demand flexibility in various scenarios, taking into consideration energy exchanges inside the energy community in connection with upstream markets, needs to be investigated.

In the Flexigy project, we tackled the issue of the flexibility representation and extraction challenge by adopting the FlexOffer model (previously introduced in the Mirabel and TOTALFLEX projects [49]) to describe the energy flexibility which can be aggregated and exchanged across several actors and markets.

As reviewed, various works have addressed small-demand flexibility scheduling. However, most of them rely on heavy optimization algorithms that require large computing resources and may take a long computing time when scheduling real-world energy communities with hundreds or thousands of devices, in multiple communities.

The heuristic approach used in the algorithms proposed in this paper allows for the optimization of energy resources in a distributed edge-and-fog computing architecture with low computational overhead. As such, our median-term goals focus on delivering an integrated platform for the management and optimization of RECs, unifying dwelling-Level DR, user energy flexibility, and peer-to-peer community energy sharing, while maintaining a distributed edge-and-fog architecture with low computational requirements.

3. System Model and Architecture

In this study, we consider a REC where a set of prosumers can share the excess production energy between themselves and the utility grid, to promote renewable energy consumption and minimize overall costs. As described in detail in [5] in each prosumer house, there are smart devices capable of switching on and off some appliances and recording their consumption in 15-min time slices (TSs), or smaller. These devices communicate with an edge or cloud device where scheduling decisions are taken to optimize local consumption according to (i) each prosumer profile/strategy; (ii) the energy flexibility of the monitored appliances, and (iii) the electricity prices for the day ahead.

The following sections present the energy flexibility and Flex-Offer (FO) concepts and an overview of the prosumer profiles, which were the basis for the development of the algorithms. In addition, the system architecture is reviewed.

3.1. Energy Flexibility

Energy flexibility, which is the capability to shift the activation of certain loads (appliances), thus changing the overall consumption profile of a facility (home) is the key concept behind the development of the scheduling algorithms.

By taking advantage of these algorithms, the platform can schedule the activation of certain loads in order to optimize the usage of locally generated energy in individual and collective terms.

3.1.1. Flex Offer Concept

This work is based on the Flex-Offer (FO) concept, which was introduced in [50]. In its simplest form, a FO is a standardized model to represent a generic energy flexibility abstraction expressing an amount of energy or an energy profile, a duration, a price, the earliest start time, and the latest start time. Three FO examples follow:

• “Consumption of 5 kWh during 3 h between 01:00 and 05:00, for a price of 0.25 €/kWh”;
• “Consumption follows the energy profile in Figure 1, no price specified”.

In these cases, the FO represents flexible electric loads (e.g., charging electric vehicles, heat pumps, and equipment for domestic use) and production units (e.g., discharging batteries, and photovoltaic panels).

A FO can be formally defined as a tuple:

$$f\_def=(\left[t_{es, }{t}_{ls}\right], ⟨s^1, s^2\dots ., s^s\rangle ),$$

(1)

where:

$$s^i={\left[a_{min}^i, a_{max}^i\right]}_{}$$

In Equation (1), t_es represents the earlier start time and t_ls represents the latest start time for the FO. The second parameter is a list that contains a sequence of slices s that represent the energy profile of the device. Each one of these slices sⁱ is an energy range between aⁱ_min and aⁱ_max, usually represented in kWh, which can be positive if the device consumes energy or negative if the device produces energy. We assume that the duration of each slice is a 1-time unit, adjustable to multiple sampling frequencies. In our use-case power, consumption/production is sampled at 15 min intervals and defined by TimeSliceSize.

The main interest of a FOs is in having it scheduled using several criteria. The main result is that scheduled FO will also have its scheduling, i.e., the time at which the device should be turned on t_sch.

Consequently, Equation (1) can be updated as in Equation (2):

$$f\_sch=(\left[t_{es, }{t}_{ls},t_{sch}\right], ⟨s^1, s^2\dots ., s^s\rangle )$$

(2)

Figure 1 displays a visual representation of a FO energy profile and respective scheduling with the t_es and the t_ls defining a time flexibility interval. The FO energy requirements are represented by energy slices (s_i). The slice energy flexibility is detailed by the difference between the aⁱ_min and aⁱ_max. The t_sch represents the time at which the FO was scheduled.

3.1.2. Device Flexibility and Flex Offers Types

In terms of flexibility, devices can be categorized according to two factors, present in Figure 1: (i) slice energy flexibility and (ii) time flexibility. More specifically, three distinct kinds of devices are defined, originating from the three different types of FO used in this work:

• Fixed Devices are devices whose consumption period and amount of energy consumed cannot be modified (e.g., televisions and lights). Fixed FOs are used to translate these devices into the system. A fixed FO can be formally restricted by:

  $$t_{sch}=t_{es} and s^i{a}_{min}^i=s^i{a}_{max}^i{}_{}$$

  (3)
• Shiftable Devices are time-flexible devices, meaning that the consumption time can be shifted within certain limits without modifying the load profile (e.g., washing machines and dishwashers). These devices offer an opportunity to optimize grid load management. Shiftable FOs translate shiftable devices into the system. A Shiftable FO is subject to:

  $$t_{es}\le t_{sch}\le t_{ls} and s^i{a}_{min}^i=s^i{a}_{max}^i{}_{}$$

  (4)
• Elastic Devices are the most flexible, being fully adjustable in terms of usage time and instantaneous power consumption (e.g., heater, electric car). Similar to shiftable devices, elastic devices provide grid load management capabilities to a greater extent. Elastic FOs translate elastic devices into the system. An Elastic FO is restricted by:

  $$t_{es}\le t_{sch}\le t_{ls}$$

  (5)

3.2. Prosumer Profiles

Prosumer profiles, introduced in [5], are defined so that each prosumer can customize their objectives according to what best fits their goals and beliefs when participating in a REC. From an energy consumption point of view, there are three distinct profiles from which a prosumer can choose:

• Bold Profile the consumer only wants to maximize its renewable energy consumption, regardless of the electricity price;
• Cautious Profile the consumer wants to buy energy always at the lowest total cost possible, whatever its source;
• Local Community Supporter Profile the consumer maximizes REC consumption irrespective of its price.

From the energy production side, the strategy for selling the prosumer excess production can be one of the following:

• Go-Ahead Profile the producer wants to sell all his renewable electricity generation.
• Tactical Profile the producer only wants to sell his surplus renewable generation after optimizing self-consumption.

3.3. System Architecture

As stated before, the developed algorithms follow the three-level approach introduced in [5]. This architecture aims to integrate prosumer profiles in the scheduling solution while allowing for a distributed edge-and-fog implementation of community energy management. The levels of this architecture are the following:

• Level 1—Prosumer level: executed for each prosumer to minimize the energy costs and maximize the individual renewable energy self-consumption.
• Level 2—Local community level: executed at the REC level to minimize overall energy costs and optimize the renewable energy-based supply via peer-to-peer energy trading and collective renewable self-consumption.
• Level 3—Grid level: groups small-scale flex-offers at the REC level or between RECs to respond to specific market requests from different stakeholders.

Figure 2 presents the system architecture from a logical point of view. Level 1, depicted in green in Figure 2, represents each prosumer dwelling with energy consumption from multiple home appliances, and, eventually, energy self-production from PV panels or other renewable sources. At this level, the system collects the flexibility of different appliances on the prosumer premises, expresses this flexibility as FOs, and optimizes individual self-consumption according to prosumer profiles. The algorithm can be run directly at the prosumer house (e.g., IoT hub) in an edge computation approach, retaining data confidentiality and effectively distributing computing, as it does not need to be run on the cloud. FOs left unscheduled at this level at each edge node (each prosumer) are then sent to the fog computer, handling community needs at level 2.

Level 2, illustrated by a red dashed line in Figure 2, represents a REC connected to a single medium-to-low-voltage energy transformer. At this level, all the FOs generated at the community dwellings (level 1), including the FOs partially or not fully scheduled at Level 1, are scheduled using the REC aggregated self-production. Once again, this algorithm can be run in a distributed manner at the fog level (e.g., a fog device implemented at each community). After the scheduling is performed by the algorithms operating at this level, the schedule of the community FOs is sent to the edge nodes, which will orchestrate the devices accordingly.

Finally, level 3, depicted in blue in Figure 2, aggregates the different REC communities FOs, which were not fully or were partially fulfilled at level 1 or 2, and sells those aggregate FOs directly on a flexibility market. Aggregation is required to generate FOs with a higher power, which can be offered on balancing markets [51]. This level can be run on cloud servers, where one or more communities are combined.

4. Flex Offer Scheduling Algorithms

Following the introduced energy flexibility concept, user profiles, and architecture, algorithms for the three scheduling levels are detailed in the following sections.

4.1. Level 1

Level 1 is executed for all FOs from prosumers who have chosen the tactical profile and aim to maximize their energy self-consumption while minimizing the total cost. We assume that the cost of self-consumption is zero. The diagram in Figure 3 depicts the workflow of the level 1 algorithm.

This level only includes prosumers with a tactical profile, which have self-production capabilities. As such, the first step of level 1 algorithms, which might be running in an edge device inside the prosumer dwelling, is to forecast the day-ahead self-production. Once forecast, the algorithm fetches community and grid prices for the day ahead from the REC fog device. Note that by changing the desired timespan while fetching information (predicted prices and production), the algorithm can easily be changed to schedule the next 48 h, or even only the next 6 h. This means that the algorithm can be re-run to confirm its schedule during the day.

Moreover, a forecast of the dwellings’ unpredictable consumptions is generated so that the system can reserve part of the user production for unpredictable energy consumption (e.g., turning on a computer, using a vacuum cleaner, or turning on the lights). This way, the self-produced energy consumption is always maximized at the prosumer level.

Finally, the production profile is updated according to the scheduled consumption. In the following sections, the algorithms developed to schedule the distinct types of FOs at level 1 are presented.

4.1.1. Level 1 Schedule of Fixed FOs

Algorithm 1 describes the solution designed to schedule fixed FO consumption in an optimized manner by using the prosumer self-produced energy, block 3.2 in Figure 3. Since self-produced energy is free for the prosumer, it is always more advantageous, for any buyer profile, to use the maximum self-produced energy possible when a FO is of type fixed FO. As such, this algorithm tries to always schedule the maximum forecasted self-produced energy at any given time.

Algorithm 1: schedSelfConsumptionFixedFO algorithm used at Level 1 to schedule Fixed FOs.
	Input:
		fo—Consumption Fixed FO
		prod—Multidimensional array containing: (i) user production and, (ii) energy prices for each time slice
		prosumer—Prosumer
	Output:
		prod—The updated prosumer production profile
1	Function schedSelfConsumFixedFO (fo, prod, prosumer)
2		t <- fo.tes
3		eProfile <- fo.getEProfile2Sched()
4		sched <- new Schedule(fo.tes)
5		For each eSlice in eProfile Do
6			e2Sched <- getMaxEConsum(prod, t, eSlice)
7			If e2Sched > 0 Then
8				sched.AddSlice(t, e2Schedule)
9			End if
10			t <- t + TimeSliceSize
11		End for
12		prod <- scheduleFO(sched, prod, fo)
13		Return prod
14	End

Given that a Fixed FO has no energy flexibility, its earliest start time (t_es) is considered the scheduling Time (t_schd) (line 2). In line 3 the Fixed Flex Offer consumption profile is fetched from a database to an auxiliary variable—eProfile. Moreover, a new schedule object name sched, is created (line 4), with its start time set to the FO t_es.

Next, for each energy slice of the FO energy profile, the algorithm verifies how much energy consumption can be scheduled using self-production (line 6). If some or all the energy can be scheduled using its self-production, a slice is added to the schedule (line 8). This slice specifies the time, energy amount, and price of the scheduled energy consumption. Finally, in the scheduleFO method (line 12), both the FO and the production energy profile are updated, discounting the energy scheduled, and the FO schedule is saved. Note that if fixed FO cannot be fully fulfilled by the self-production of the prosumer at level 1, the remaining energy needs are stated in a transformed fixed FO that will be scheduled at level 2 and, eventually, at level 3.

4.1.2. Level 1 Schedule of Shiftable FOs

Algorithm 2 describes the algorithm designed to schedule shiftable FOs, also at level 1, block 3.3 in Figure 3. At this level, the biggest concern was not only to maximize self-consumption on all occasions but also that the algorithm should reflect the prosumer buyer profile. In effect, it can be more monetarily rewarding for a user with a cautious buyer profile to schedule the FO with less self-consumption if the price paid for the surplus is significantly less at that slice, instead of having more self-produced energy but ending up paying more for the surplus scheduled at level 2.

As such, the approach shown in Algorithm 2 focuses on prosumers’ buyer profiles, as it heuristically tries to find the best fit for FO consumption.

Algorithm 2: schedSelfConsumpShiftableFO
	Input:
		fo—Consumption Shiftable FO prod—Multidimensional array containing: (i) user production and, (ii) energy prices for each time slice
		prosumer—Prosumer
	Output:
		prod—The updated production profile
1	Function schedSelfConsumShiftableFO (fo, prod, prosumer)
2		cost <- MAXVALUE
3		sched <- new Schedule(fo.tes)
4		For i = fo.tes; i < fo.tls; i = i + TimeSliceSize Do
5			t <- i
6			auxSched <- new Schedule(i)
7			sum <- 0
8			eProfile <- fo.getEProfile2Schedule()
9			For each eSlice in eProfile Do
10				e2Sched <- getMaxEConsum(prod, t, eSlice)
11				consumSurplus = eSlice.energy − e2Sched
12				sum = sum + checkProfileCost(consumSurplus, t, eSlice, prosumer)
13				auxSched.AddSlice(t, e2Sched)
14				t <- t + TimeSliceSize
15			End for
16			If sum < cost Then
17				sched <- auxSched
18				cost <- sum
19			End If
20		End for
21		prod <- scheduleFO(sched, prod, fo)
22		Return prod
23	End

A cycle is executed to check which of the time slices comprised between the FO t_es and t_ls is more financially advantageous for scheduling the start of the FO execution (t_sch) (lines 5 to 20).

At the start of the loop, a set of auxiliary variables is created each time a new candidate t_sch is evaluated (lines 5 to 8). Next, the solution price is determined by calculating the price of the energy surplus of each time slice (lines 9 to 15). To determine it, the algorithm starts by finding the maximum self-produced energy that can be consumed by the slice and consequently the consumption surplus. Then, with the help of the checkProfileCost method (line 12), the electricity consumption price is summed to the total price of the solution.

The checkProfileCost method is the solution presented in this work to be able to optimize the level 1 self-consumption solution without disregarding either the electricity prices at other levels or the prosumer buyer profiles. This method uses the forecast of day-ahead prices and calculates the cost for the prosumer based on its profile:

• For users with a cautious profile, the cost returned at any given time is calculated based on the cost of the surplus energy multiplied by the grid price for that time. As such, an estimate for the scheduling of surplus energy at higher levels is returned.
• For users with a community supporter profile, the cost returned at any given time is calculated based on the cost of the surplus energy multiplied by the REC day-ahead prices at that time.
• For users with a bold profile, the cost is how much non-renewable energy is consumed in surplus of self-consumption. As such, the method returns the total amount of surplus energy in this case.
• Finally, if the cost of the solution being evaluated (either price or amount of surplus energy) is lower than the cost of the previously saved schedule (line 16), both the schedule and cost variables are updated with the new solution values (lines 17 and 18).

After the best schedule is found, the scheduleFO method saves it and updates the FO and the self-production energy profile accordingly, subtracting the energy scheduled at each slice from the slice available energy.

4.1.3. Level 1 Schedule of Elastic FOs

This study also focuses on bringing environmental benefits and optimizing the operational cost of elastic devices such as thermal accumulators and air conditioners by scheduling their day-ahead energy consumption according to their time-of-use tariffs and the prosumer profiles. Future work will be developed concerning battery storage and other forms of elastic energy flexibility. Algorithm 3 details the heuristic algorithm designed to create a FO for elastic devices, which is later scheduled at the same level as a fixed FO.

Algorithm 3: schedElasticDevi
	Input:
		prosumer—The prosumer to which the device belongs
		tMax—Maximum temperature defined by the user to maintain his comfort
		tMin—Minimum temperature defined by the user to maintain his comfort
		tStart—Temperature at the start
		prices—List with the energy self-production values of the user and energy prices of the different grid suppliers available.
		powerCom—average power consumption per time slice.
	Output:
		FO—The created fixed FO for scheduling
1	Function generateHeuristicElasticEProfile
2		t <- new Date(0,0,0)
3		temp <- tStart
4		totalCost <- 0
5		While (auxtime < end) Do
6			nextCoolDownTime = getNextCoolDownTime(tMin, temp, t)
7			If isLowestPriceUntilNextCooldown(nextCoolDownTime, prices)Then
8				newTemp <- calculateNewTemp()
9				If newTemp < tMax Then
10					temp <- heatUp ()
11					consump.add(powerCon, t)
12				Else
13					temp <- coolDown()
14				End
15			Else
16				temp <- coolDown()
17			End
18			t <- t + TimeSliceSize
19		End While
20		FO <- new FO(fixed, consumptions)
21		Return FO
22	End

The heuristic approach to solve elastic device scheduling can be simply explained as an attempt to use the thermal appliance as a conditioned thermal battery.

For example, a client has a water heater that must maintain water between a specified comfort range of temperatures, t_min, and t_max. Our approach focuses on heating up the water at the slices with the lowest price before the water cools down below t_min. However, the water cannot be heated up above t_max. If the water is below t_min, the algorithm heats up regardless of the price, until the desired comfort levels have been met.

When a client has self-production, for example, the most cost and environmentally effective way to use his energy resources are to use surplus energy, which is free, to heat up water, successfully storing renewable energy as heat.

Algorithm 3 does exactly that. First, a set of auxiliary variables are created (lines 2 to 4), including a variable holding the actual temperature of the device. Then, in a loop (lines 5 to 19) each time slice is examined, as follows. First, the next cool-down time is calculated (line 6), based on temperature change equations previously inserted on the system for this specific device.

The cooldown time is the predicted time at which it is forecast that the temperature of the water goes below t_min. Note that the calculation of the forecast of the cooldown time can be improved over time, for example with client hot water consumption patterns. This way the algorithm can more efficiently calculate the cooldown time and maintain comfort temperatures, whilst optimizing energy consumption.

Next, the program checks if the current slice price is the lowest by the cooldown time (line 7). If so, energy is used to heat up water, and the new temperature is calculated. Otherwise, no energy is used, and the water continues to cool down (line 13). Finally (lines 20 and 21), a new fixed FO is created and returned to be scheduled with algorithm 1 with the consumptions scheduled by this algorithm. Note that it results in a fixed FO since the start time is already defined, resulting in a FO without time flexibility, but it can maintain some consumption flexibility.

The main result of the level 1 schedule can be a set of unscheduled FOs, together with another set of partially fulfilled FOs, which change from being flexible or elastic to fixed FO. Alternatively, it is also possible that all FOs from a prosumer are fulfilled, and no further scheduling is performed for FOs from this prosumer. A mix of both alternatives is also possible.

4.2. Level 2

Level 2 starts by getting the users’ production surplus to generate a community energy production profile. It then collects and shuffles in random order all unscheduled FOs of level 1. An FO is considered unscheduled when there is still energy left unscheduled. Finally, the FOs pending from the previous level are scheduled according to the prosumer buyer profile and the FO type (steps 1.4, 1.5, and 1.6 in the diagram in Figure 4).

Note that in this level, the FO scheduling order is randomly selected, addressing the equity problem that may arise from scheduling always in the same order, as the first to be scheduled may benefit more from a large community excess production available than the last (considering that a typical RES does not produce enough energy to satisfy the consumption of all REC members). Note again that by changing the desired timespan while fetching information (community production profile), the algorithm can be easily changed to schedule the desired number of ahead hours.

4.2.1. Level 2 Schedule of Fixed FOs

Algorithm 4 presents the pseudocode designed to schedule fixed FOs at level 2 (block 1.4 in Figure 4), which are scheduled before other types, given their reduced flexibility. This algorithm takes into account the user profile and schedules energy consumption according to it.

Algorithm 4. schedLevel2FixedFO
	Input:
		fo—Consumption Fixed FO
		prod—Multidimensional array containing: (i) community production, (ii) energy prices for each time slice
	Output:
		prod—Updated production profile
1	Function schedFixedFO (fo, prod)
2		t <- fo.tes
3		sched <- new Schedule(t)
4		2eProfile <- fo.getEProfile2Sched()
5		prosumer <- getFOProsumer(fo)
6		For each eSlice in eProfile Do
7			e2Sched <- eSlice.energy
8			sched <- schedSlice(t, e2Sched, prosumer, prod, sched)
9			t <- t + TimeSliceSize
10		End for
11		prod <- scheduleFO(sched, prod, fo)
12		Return prod
13	End

Once again, since a fixed FO has no energy flexibility, its t_es is also the resulting scheduling time t_sch (line 2). The algorithm then initializes an auxiliary variable with a new schedule object, with its start time set to the FO tes (line 3), the FO energy consumption profile (line 4), and with the user buyer profile (line 5). Next, the algorithm schedules each energy slice of the FO energy profile using the schedSlice method.

The schedSlice method guarantees an adequate energy schedule according to the user profile. It uses the forecast of day-ahead prices and calculates the cost for the prosumer based on their profile:

• For users with a cautious profile, the schedule returned at any given time is calculated based on the slice energy multiplied by the lowest price at that time.
• For users with a community supporter profile, the schedule returned at any given time is calculated based on the slice energy multiplied by the REC day-ahead prices at that time.
• For users with a bold profile, the schedule is calculated based on the slice energy multiplied by the cheapest available renewable energy source.

Finally, in the scheduleFO method, both the FO and the production energy profile are updated, discounting the energy scheduled, and the FO schedule is saved in the database.

4.2.2. Level 2 Schedule of Shiftable FOs

Algorithm 5 describes the pseudocode designed to schedule the level 2 shiftable FOs (block 1.5 in Figure 4), This algorithm takes into account the user profile and schedules energy consumption by minimizing the cost of the schedule given the user flexibility.

Algorithm 5. schedLevel2ShiftableFO
	Input:
		fo—Consumption Shiftable FO
		prod—Multidimensional array containing: (i) community production, (ii) energy prices for each time slice
	Output:
		prod—Updated production profile
1	Function schedShiftableFO (fo, prod)
2		consumPrice <- MAXVALUE
3		eProfile <- fo.getEProfile2Schedule()
4		sched <- new Schedule(fo.start)
5		prosumer <- getFOProsumer(fo)
6		For i = fo.tes; i < fo.tls; i = i + TimeSliceSize Do
7			t <- i
8			auxSched <- new Schedule(i)
9			sum <- 0
10			eProfile <- fo.getEProfile2Sched()
11			For each eSlice in eProfile Do
12				e2Sched <- eSlice.energy
13				auxSched <- schedSlice(t, e2Sched, prosumer, prod, auxSched)
14				sum <- sum + auxSched.getPrice(t)
15				t <- t + TimeSliceSize
16			End for
17			If sum < consumPrice Then
18				sched <- auxSched
19				consumPrice <- sum
20			End If
21		End for
22		prod <- scheduleFO(sched, prod, fo)
23		Return prod
24	End

First, a set of auxiliary variables are created. At the start of the loop (lines 6 to 21), a set of auxiliary variables is created each time a new candidate t_sch is evaluated (lines 7 to 10). Next, each possible solution price is determined by calculating the price of the energy of each time slice (lines 11 to 16). To determine this, the algorithm uses the schedSlice method presented before. Finally, if the cost of the solution being evaluated is lower than the cost of the previously saved schedule (line 17), both the schedule and cost variables are updated with the new solution values (lines 18 and 19).

After the best schedule is found, the scheduleFO method saves it and updates the FO and the self-production energy profile, accordingly, discounting the energy scheduled, and the FO schedule is saved in the database.

4.2.3. Level 2 Schedule of Elastic FOs

As described previously in Section 4.1.3. the elastic scheduling algorithms are executed at level 1 for the users with forecasted self-production available. For the elastic devices of all other users, the scheduling is done at level 2. The algorithm used is similar to the one used at level 1, and consequently it will not be described here.

4.3. Level 3

The level 3 algorithms schedule FO at the grid level, but they are out of the scope of this paper as this topic has been extensively researched before.

These algorithms work by aggregating small FOs into large FO which can be scheduled at the grid level or submitted to a flexible market. This schema allows the participation of small consumers in DR, which otherwise would not have a significant impact on energy grid balancing as traditionally energy-intensive industrial users and large customers have by intentionally modifying their consumption patterns.

The authors in [52] theorize about a voluntary local flexibility market where users sell their flexibility, which is then grouped by energy aggregators and sold, reducing costs for all involved stakeholders.

For example, ref. [15] introduces an optimal scheduling algorithm based on load constraints linked to the dwelling occupant’s comfort. Similarly, [16] uses aggregation of energy flexibility expressed by market players as the key to balancing energy supply and demand. After their creation and acceptance, the FOs are aggregated, preserving their flexibility. Afterwards, the scheduling is performed based on forecasts to achieve a greater balance of the grid. Next, the FOs are disaggregated and returned to the prosumer. Once the execution is carried out, billing is conducted and, depending on the benefits of the FO for the utility company, an incentive may be provided to the prosumer.

5. Case Study

This section presents the case study used to test the algorithms and evaluate a set of environmental objectives and economic benefits accomplished through the introduction of management and optimization of REC members’ energy consumption and production. The scheduling is accomplished taking into consideration stated members energy flexibility.

5.1. Simulation Approach and Test Data

The simulations carried out follow the approach illustrated in Figure 5. At first, the system is fed with data relating to historical energy consumption patterns, energy prices, weather information, and users’ FOs for the next day. Finally, the system outputs the user’s FOs schedule according to the algorithm presented in this paper, which maximizes the consumption of both user and REC self-production energy, while meeting the users’ preferences.

Setting energy prices is not the subject of this paper, and as such, the prices for the simulation were obtained from the Iberian wholesale energy market (OMIE) [53]. OMIE is the nominated electricity market operator for managing and setting the Iberian Peninsula’s day-ahead (24 h) and intraday electricity markets. Given that price prediction is published for the next 24 h at the most, the prices for the simulation were set at a 15-min granularity within a 24 h timespan. After consulting experts working in the implementation of REC from a business standpoint, the energy transactions inside the REC were set at 80% of the OMIE price, a 20% discount compared to OMIE prices.

Finally, to evaluate the effectiveness of the scheduling algorithm, the average of the daily price was considered as the flatline tariff for energy consumption, enabling the comparison between the cost before and after the application of the scheduling algorithms. Figure 6 shows the energy prices per kWh used in the simulations during a day in all four seasons. The simulations analyze the performance and results of the algorithm in the summer, spring, autumn, and winter days in central Portugal. User consumption flexibility is based on real-world data collected with the help of smart-energy meters for 50 different dwellings. The testing data accounts for a total of 137 consumption FOs, of which 42 are fixed FOs corresponding to consumptions of computers and fridges, 71 are shiftable FOs characterizing the flexibility of appliances such as washing machines and dishwashers, and 24 are elastic FOs describing the flexibility of water heaters. The same consumption Flex Offers were considered for all seasonal simulations to facilitate a comparison of the results.

However, the solar production was adjusted to values captured during a day, also in central Portugal, in July, May, October, and December, respectively. The energy prices were also changed by values corresponding to the respective timespans, collected from OMIE. Furthermore, during simulations, three different test scenarios were studied, regarding the amount of self-production FOs in a REC.

• Scenario 1: 20% of the REC dwellings have self-production.
• Scenario 2: 40% of the REC dwellings have self-production.
• Scenario 3: 60% of the REC dwellings have self-production.

The testing data also encompasses a mix of all user/prosumer profiles. From a buyer perspective, there were 22 cautious, 19 bold, and 9 local community supporters. From a supplier point of view, there were 44 tactical and 6 go-ahead profiles.

Table 1. Summary of case study test data.

Number of Dwellings	50 Dwellings
Dwellings with Self-Energy Production	(1) 10 dwellings (20%)
	(2) 20 dwellings (40%)
	(3) 30 dwellings (60%)
Number of Fixed FOs	42
Number of Shiftable FOs	71
Number of Elastic FOs	24
Types of Prosumer Buyer Profiles	22 Cautious
	19 Bold
	9 Community Supporter
Types of Prosumer Supplier Profile	44 Tactical
	6 Go-Ahead

summarizes the testbed data information. Note that the control case, with which the results of the algorithms are compared, is based on the usual electricity consumption time and number of dwellings without energy flexibility scheduling. In other words, the control case is the normal operation of a dwelling throughout a day.

5.2. Evaluation KPIs

To access the degree of accomplishment of both the environmental and financial objectives of the project, three Key Performance Indicators (KPIs) are assessed during the results section.

• KPI 1 User self-consumption—This environment-oriented KPI measures the total amount of user energy self-consumption of each community member with available self-production, and compares, by percentage, the values before and after the algorithms were applied. Note that users with go-ahead profiles are not considered, since all their self-production is sold, and its surplus consumption is not optimized by the algorithms. KPI 1 is key to evaluating to what degree individual flexibility and self-consumption optimization (level 1) are implemented.
• KPI 2 REC consumption—This environment-oriented KPI measures, by percentage, how much of the total energy consumption in the REC comes from intra-community energy trading after level 2 algorithms are applied. This KPI is crucial to access the degree to which the intra-community optimization (level 2) of energy resources is working.
• KPI 3 User total energy cost—This financial-oriented KPI quantifies the total spending on the energy of each community member with a cautious buyer profile, and compares, by percentage, the values before and after the algorithms were applied. KPI 3 is only applied to cautious users, due to their profile objectives, and these must reduce energy costs. Users with a go-ahead buyer profile are not considered for this indicator, as selling all their self-produced energy due to contractual terms impedes cost optimization. Also, note that the total cost regards only consumption cost since the profit made by selling self-production to other REC members is not considered in the scope of these results.
• KPI 4 Computational cost—This performance-oriented KPI measures the time, in seconds, to calculate the average run time the algorithms take to access their low computational overhead.

5.3. Results and Evaluation

After applying the scheduling algorithms, the results obtained show a significant improvement, both economically and environmentally, not only for end-users but also for all involved players in the energy market value chain. The results are compared to the situation before the algorithms are applied, which is as described in the Section 5.1, the usual electricity consumption time and number of dwellings without energy flexibility scheduling. First, the results of a summer day simulation are examined in detail. Finally, the results obtained for scenario 3 during other seasons (spring, autumn, and winter) are compared to the results obtained during the summer.

5.3.1. Summer Day Simulation Results

Table 2. Increase of user energy self-consumption (KPI 1) during the summer.

Scenario	KPI 1—Average Increase of User Self Consumption (%) during a Summer Day
1	37.3%
2	18.4%
3	29.3%

depicts the average increase in user self-consumption before and after the algorithms were applied (KPI 1), for each test case scenario during a summer day.

These results show that an increase in self-consumption was achieved by all test case scenarios, as, on average, each user consumed 28.3% more self-produced energy after the algorithms presented in this paper, mainly level 1, was applied to their dwelling. Figure 7 shows in more detail the KPI 1 results attained for each user in test scenario 3 during a summer day.

There is an overall increase in self-consumption among community members. However, some show a decrease, such as the users in dwellings B5 and B22. These situations are explained by the cautious buyer profile chosen by these users, which prioritize total energy cost minimization, proof that the algorithms are properly handling different user profiles. The algorithms take that fact into consideration, and schedule their FOs at the lowest price possible, even if it means consuming less self-produced energy at hours when energy costs are higher, as leftovers would lead to a higher total cost. The financial benefits are analyzed below; the same dwellings, B5 and B22, for example, show a decrease in total energy cost, as expected. Also note that not all cautious users experience a decrease in self-consumption, which is the case of B47 and B50, with an increase in self-consumption of 31% and 141%, respectively, which shows that even cost-oriented users can benefit from the environmentally friendly nature of the optimization.

Table 3. REC consumption increases after scheduling for each test case scenario of the simulation during a summer day.

Scenario	KPI 2—Community Consumption after Scheduling (% of Total Consumption) during a Summer Day
1	16.5%
2	25.7%
3	28.3%

shows the increase in the total REC energy production, which is consumed by REC members, for each test case scenario.

When examining KPI 2 in the case study during a summer day, results show that for the three test scenarios, an average of 23.5% of the total consumption registered in the REC was satisfied by intra-community energy trading. The results also show that the higher the number of self-producing users, the higher the community consumption achieved. In scenario 3, where 60% of the houses have self-production, approximately 28% of the total energy consumed in the community came from energy produced by other members of the community. Figure 8 shows, for test scenario 3 of a summer day, the percentage of the total energy consumption from each energy source before and after the algorithms were applied.

As seen in the results of KPI 1 and KPI 2, REC members’ renewable self-consumption is optimized according to their profiles, and a significant intra-community renewable-based consumption is achieved. Not only do they increase the integration of distributed RES in the grid, leading to higher renewable energy consumption, but also, as the energy is consumed locally, our approach helps to reduce energy transmission losses, accomplishing and validating the environmental benefits of the proposed algorithms in a REC.

Table 4. Average reduction, by percentage, of each prosumer total energy cost during a summer day simulation.

Scenario	KPI 3—Average Reduction of Users’ Total Energy Cost (%) during a Summer Day
1	9.2%
2	10.6%
3	12.2%

depicts the average reduction of users’ total energy cost before and after the algorithms were applied, for each test case scenario during a summer day.

These results show a reduction in the total energy cost in all test case scenarios, as on average, each user consumption cost is 10.6% less after the algorithms presented in this paper are applied to optimize their energy needs. Figure 9 details the total cost before and after for some of the users in test scenario 3. As projected, the graph shows an overall reduction in users’ total energy cost. As mentioned before, users with cautious profiles, who had reduced their self-consumption before, such as the users in B5 and B22, now show a reduction in their total energy cost, attaining their profile objectives. If examining the KPI 3 is extended to users with a bold buyer profile, such as B10 and B20, both saw their energy total cost increasing. However, since the bold profile aims to maximize renewable energy consumption regardless of the cost, their personal objectives were accomplished.

5.3.2. Seasonal Results

During different times of the year, conditions change, such as daylight hours and climate, and lead to different production profiles and production flexibility. To access the effectiveness of the algorithms under these conditions, seasonal solar production was adjusted to values captured in a day in May, October, and December. The energy prices were also changed accordingly, as depicted in Figure 6. The results obtained show that, for scenario 3, the algorithm fulfills its promise and delivers a value proposition for the users in every season analyzed (see Table 5). The result analysis shows three key points:

• Despite the season, every simulation showed both an average increase in self-consumption between self-producing members and a reduction in price for users which mainly focuses on the total cost of the solution.
• The higher the intra-community consumption, the higher the reduction in the total cost, which proves that REC can not only be an environmentally friendly solution for diminishing energy losses through transmission, but can also be profitable for its members.
• Seasons with more sunlight hours achieved the lowest average increase in user self-consumption, and months where sunlight hours are reduced achieved the most increase in self-consumption. This can be explained by the nature of energy flexibility and its core benefits. In the summer, a user who leaves home early and usually runs his washing machine before leaving, at 7:30 am, is using the energy generated by its solar panels unawares, which are already producing energy due to the longer daylight hours. However, if the user carries out the same routine in the winter, it might not utilize any solar production at that time. So, when the user specifies to the system the flexibility of use all morning, the algorithms can better harness solar production, which translates to a bigger increase, on average, in the use of solar production during these months.

Table 5. Comparison of KPIs for test case scenario 3 simulation during different seasons.

Season	KPI 1—Average Increase of User Self Consumption (%)	KPI 2—Community Consumption after Scheduling (% of Total Consumption)	KPI 3—Average Reduction of Users’ Total Energy Cost (%)
Summer	29.3	28.3	12.2
Autumn	46.9	21.2	7.1
Winter	32.7	13.9	2.5
Spring	21.5	17.7	4.1

Table 5. Comparison of KPIs for test case scenario 3 simulation during different seasons.

Season	KPI 1—Average Increase of User Self Consumption (%)	KPI 2—Community Consumption after Scheduling (% of Total Consumption)	KPI 3—Average Reduction of Users’ Total Energy Cost (%)
Summer	29.3	28.3	12.2
Autumn	46.9	21.2	7.1
Winter	32.7	13.9	2.5
Spring	21.5	17.7	4.1

5.3.3. Computational Tests

The simulations of the previous case studies were run in a centralized manner, where both levels 1 and 2 were executed sequentially in the same machine. Note that parallelization of the level 1 of each consumer is possible but was not considered in these results. The hardware and software on which the simulations were run have the following characteristics and services:

• Processor-Intel Core i7-8550U CPU @ 1.80 GHz 1.99 GHz
• RAM-8.00 GB
• Programming language-C#
• Database-SQL Server (the biggest time bottleneck during the simulations)

Figure 10 shows the average time taken, in seconds, to schedule both level 1 and level 2 from REC with 1 dwelling, 5 dwellings, 10 dwellings, and increments of 10 dwellings until a total of 50 dwellings is scheduled.

Consider also that level 1 can be distributed among several computers, in an edge architecture, as presented in Section 3. This decentralization of level 1 can significantly reduce the time taken to schedule the REC FOs by lowering processing requirements and enabling decentralized parallelization of computing resources. During our simulations, level 1 executed for optimizing the user self-consumption takes, on average, 3.37 s to run. Once level 1 is scheduled, level 2 can be executed at the REC fog computer. On average, for 50 dwellings, level 2 took 124 s.

6. Conclusions

The energy produced from RES has emerged as a green, reliable, and environmentally friendly solution for the replacement of traditional energy production methods, which are heavily dependent on the burning of fossil fuels. Moreover, RES, such as sun and wind, can be individually harnessed by citizens, allowing for energy self-sufficiency, and the reduction of transmission losses. As a result, RECs are emerging as an effective concept and model to empower the active involvement of citizens in the energy transition as promoters of RES and participation in the energy markets.

This paper aimed to contribute to the management, scheduling, and optimization of individual and community energy consumption and production in a REC. It follows a previous REC architecture and introduces heuristic algorithms that aim to address the economic and social needs of different players. The algorithms are organized in a distributed edge-and-fog approach and are designed for low computational overhead.

The test case scenario carried out with 50 REC members aimed to simulate a real-world community, with diverse buyer and supplier profiles, energy flexibility, and production capabilities. The results demonstrate very promising results, for every season of the year, encouraging the use of RES, and helping producers reduce the initial investment pay-out time not only by maximizing the use of self-produced energy but also by selling the energy surplus to other community members at a profitable price. The test case scenario also demonstrated the low computational overhead of the algorithms presented when applied in a decentralized edge-and-fog architecture. These results mean that this service can be applied closer to the end-user in an edge-and-fog low-cost implementation, while maintaining a high level of optimization and benefits for the users.

The algorithms are currently being updated to take into consideration the scheduling of optimized battery energy storage and consumption and the introduction of electric vehicles in a vehicle-to-grid fashion. Future work should evaluate these algorithms against real-world implementations, with a more diversified list of dwellings, appliances, flexibilities, and other seasonal data. Future work should also encompass a strong economic analysis of scenarios for business implementation purposes.