Insights into the Thermal Performance of Underground High Voltage Electricity Transmission Lines through Thermo-Hydraulic Modelling
Abstract
:1. Introduction
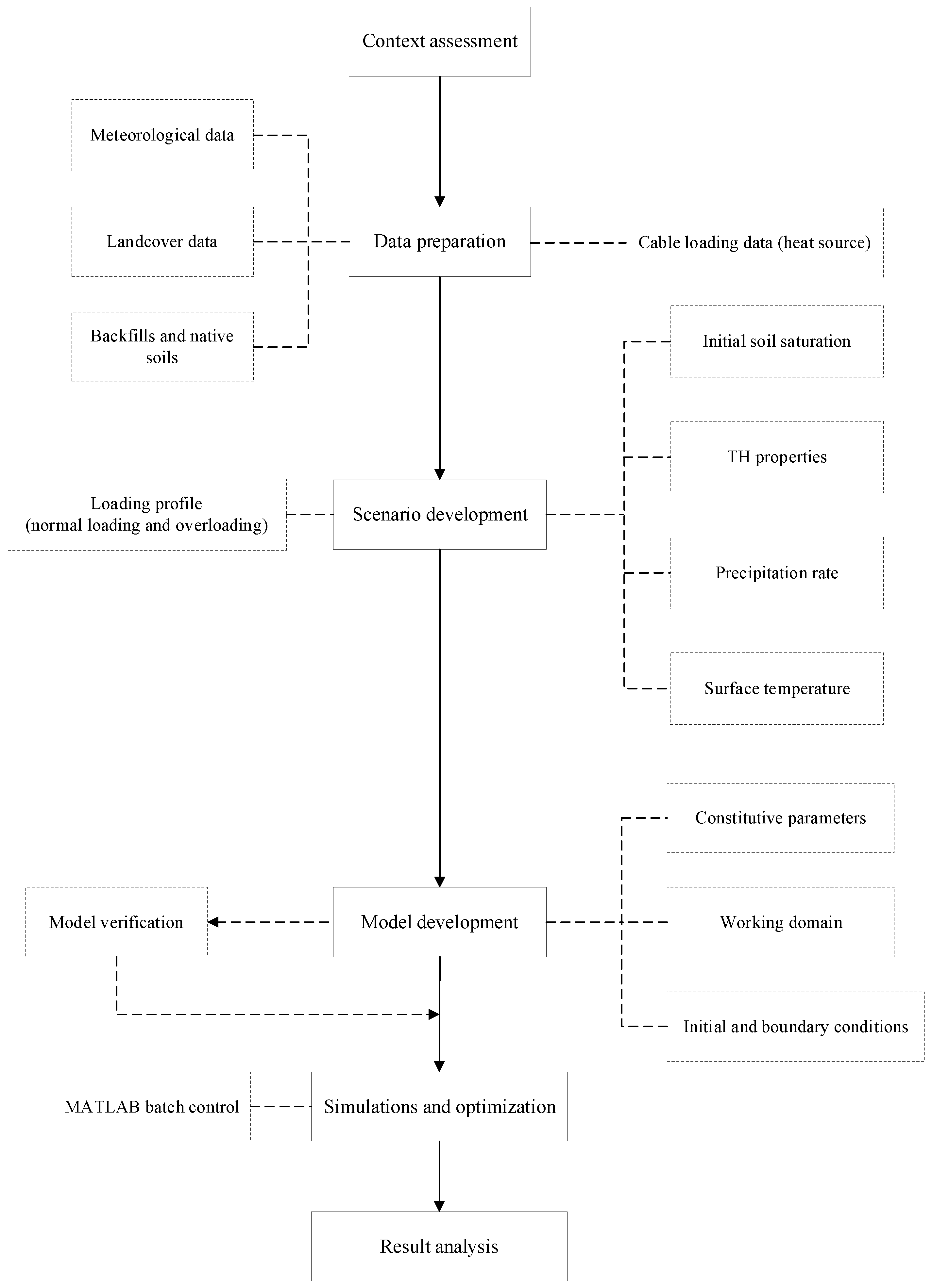
2. Methodology and Theoretical Formulations
2.1. Heat Transfer
2.2. Moisture and Air Transfers
2.3. Heat and Moisture Flow Coupling
2.3.1. Thermal Conductivity
2.3.2. Water Retention Characteristics
2.3.3. Unsaturated Phase Conductivities
3. Data Preparation
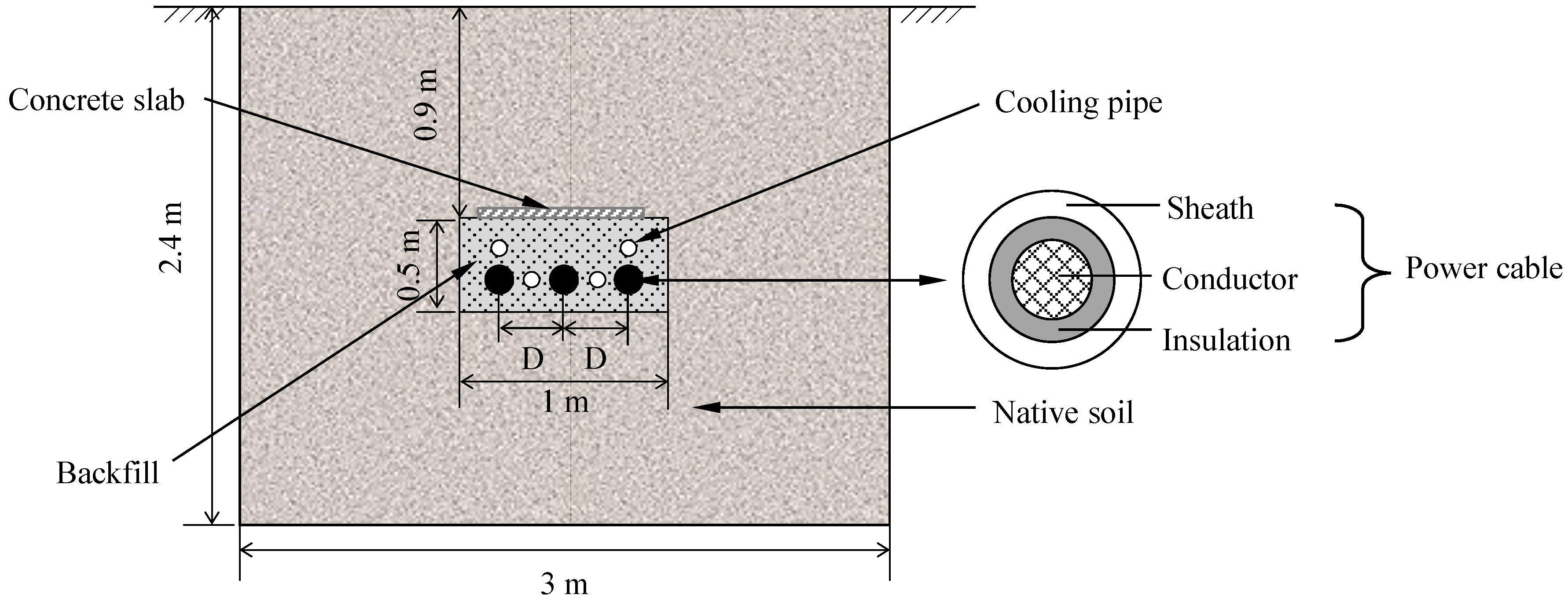
3.1. Cable and Location Information
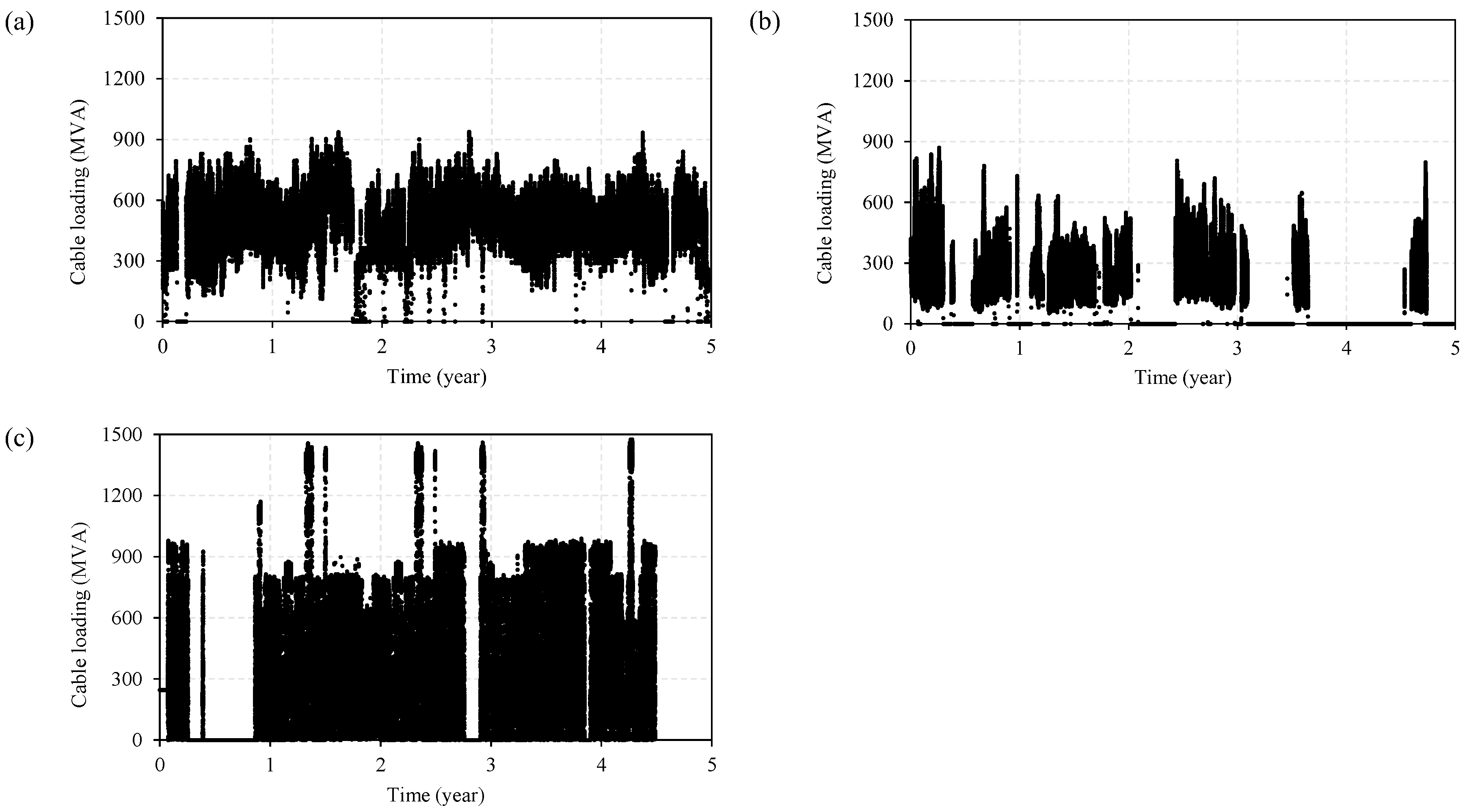
3.2. Loading Data and Heat Flux
3.3. Ground Condition Data
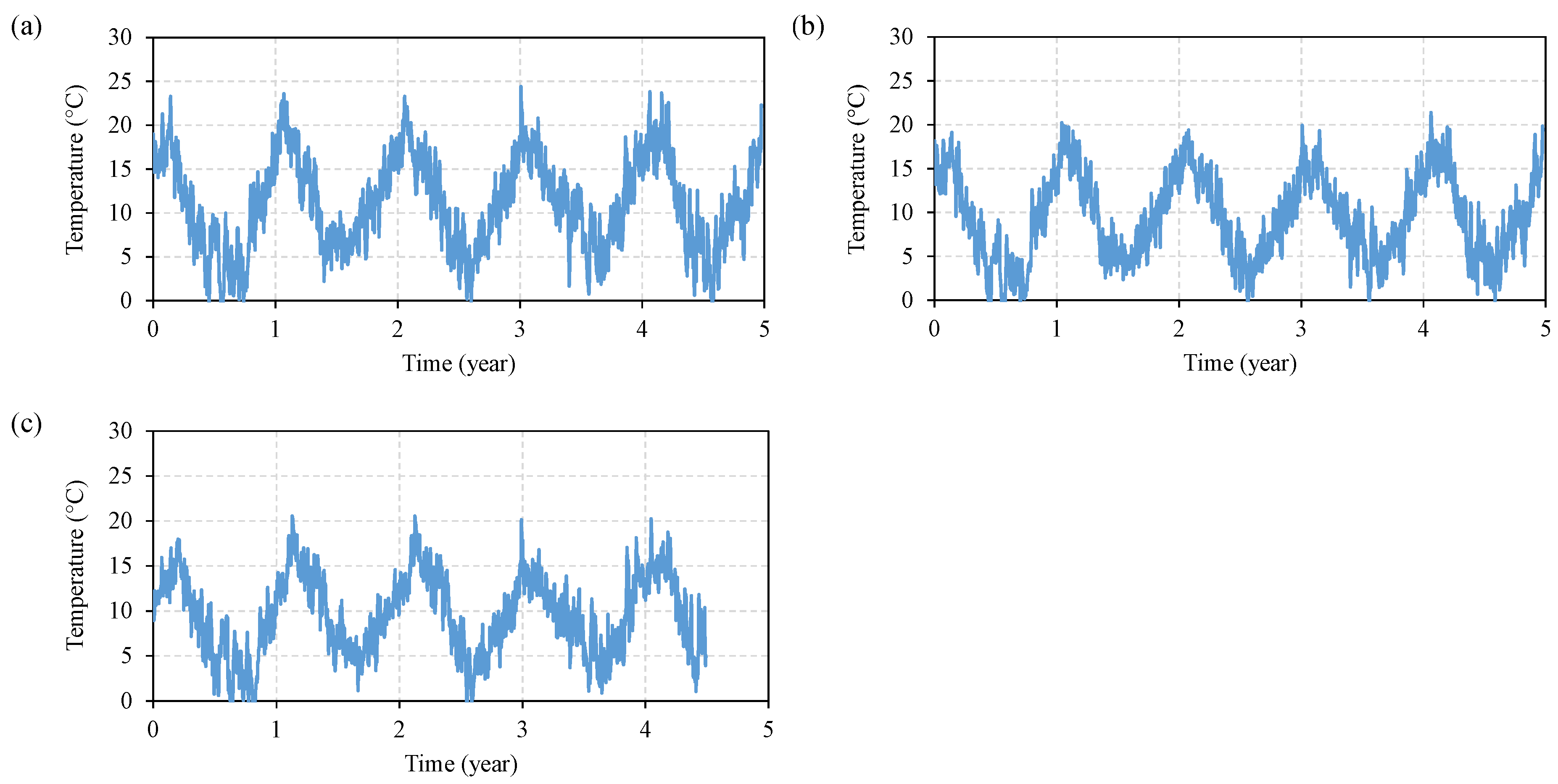
3.4. Climatic Data
4. Model Development and Verification
4.1. Scenarios and Soil Parameters
4.1.1. Native Soil Parameters
4.1.2. Backfill Parameters
4.2. Spatial Representation and Meshing
4.3. Initial and Boundary Conditions
4.4. TH-Model Verification
5. Results and Discussion
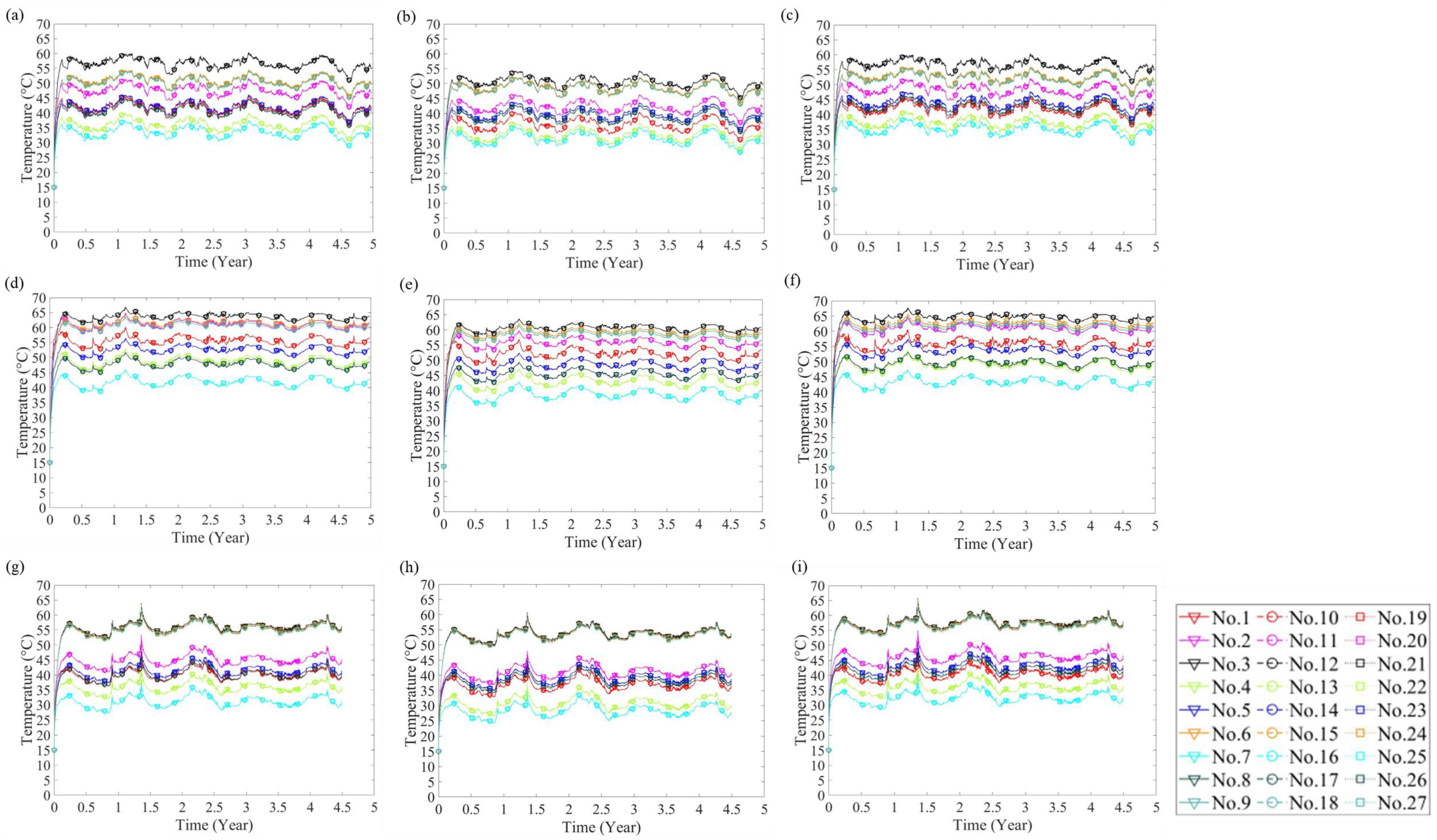
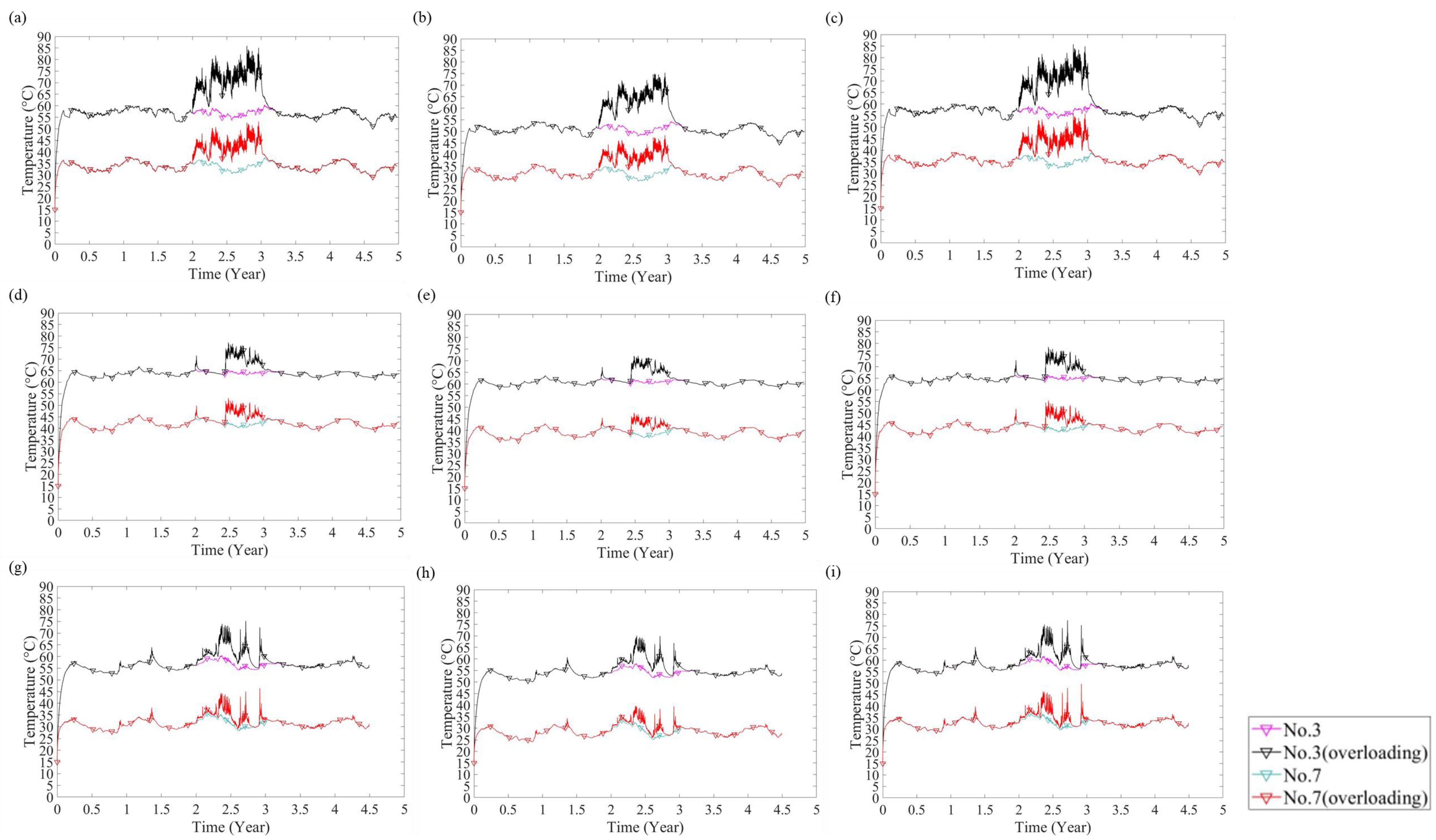
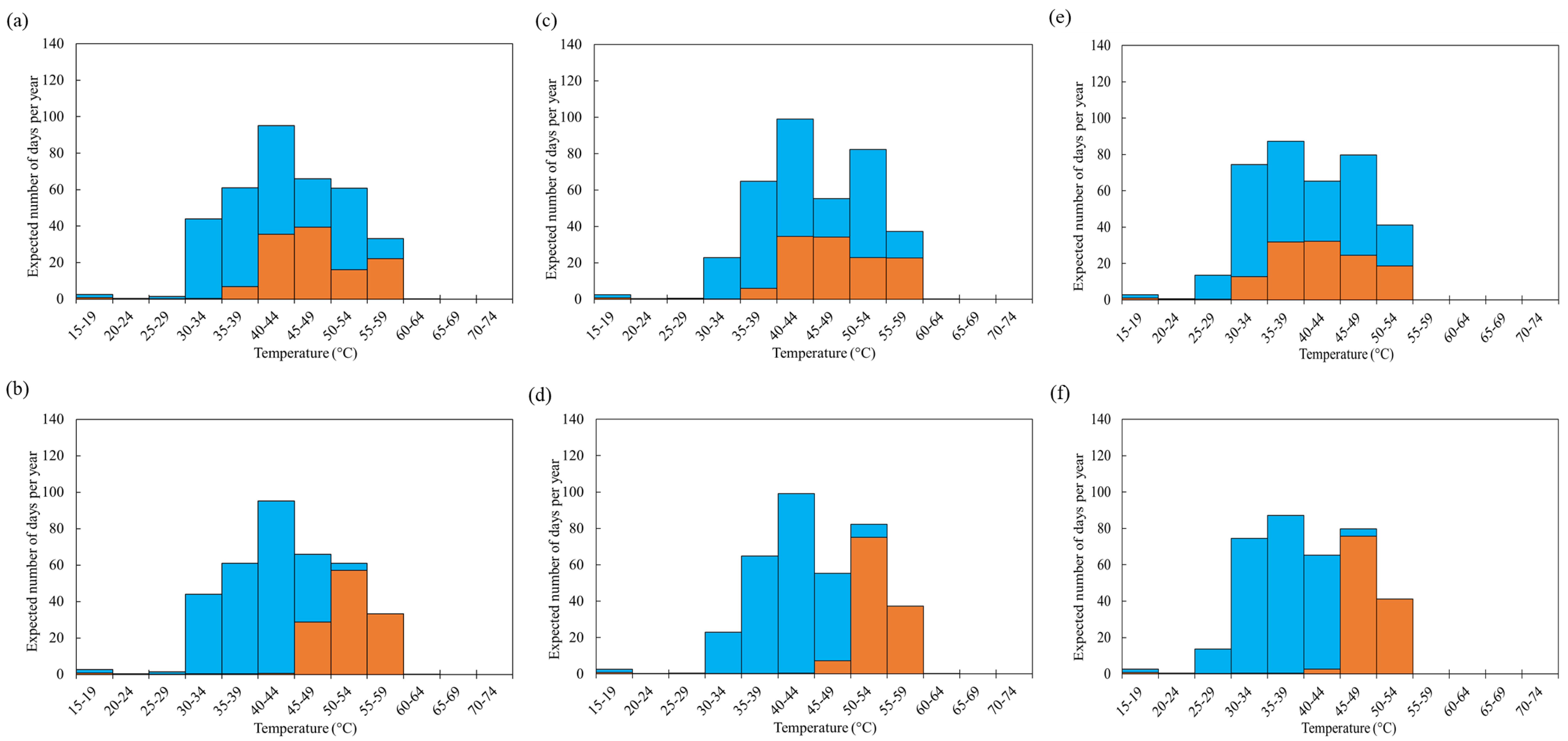
5.1. Cable Thermal Behaviour
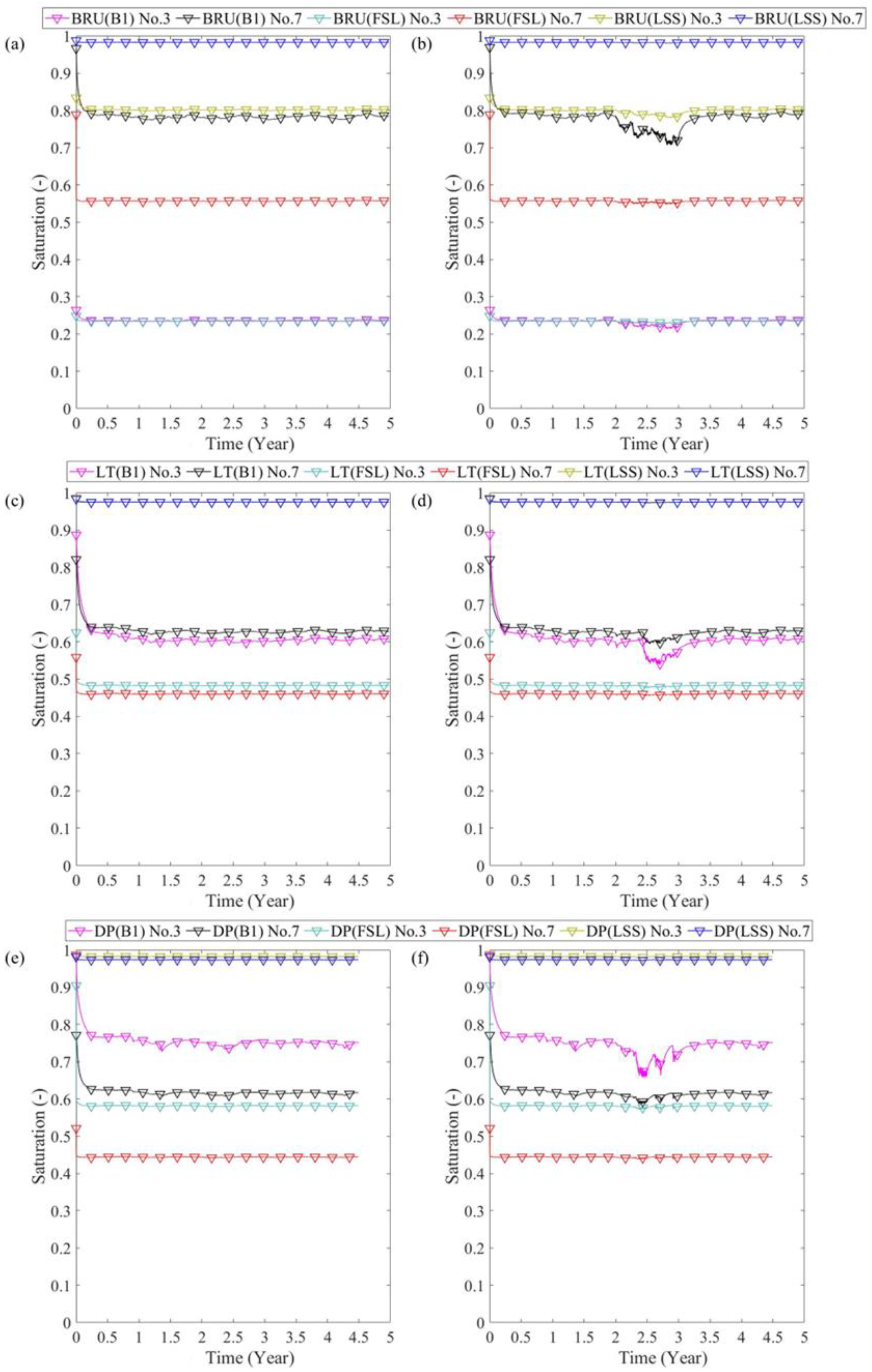
5.2. Hydraulic Behaviour of Backfill
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. World Energy Outlook 2021. Available online: https://www.iea.org/reports/world-energy-outlook-2021 (accessed on 21 January 2021).
- Yang, L.; Qiu, W.; Huang, J.; Hao, Y.; Fu, M.; Hou, S.; Li, L. Comparison of conductor-temperature calculations based on different radial-position-temperature detections for high-voltage power cable. Energies 2018, 11, 117. [Google Scholar] [CrossRef] [Green Version]
- Czapp, S.; Ratkowski, F. Optimization of thermal backfill configurations for desired high-voltage power cables ampacity. Energies 2021, 14, 1452. [Google Scholar] [CrossRef]
- Movasat, M.; Tomac, I. Assessment of physical properties of water repellent soils. J. Geotech. Geoenviron. Eng. 2021, 147, 06021010. [Google Scholar] [CrossRef]
- Ahmad, S.; Rizvi, Z.H.; Arp, J.C.C.; Wuttke, F.; Tirth, V.; Islam, S. Evolution of temperature field around underground power cable for static and cyclic heating. Energies 2021, 14, 8191. [Google Scholar] [CrossRef]
- Verschaffel-Drefke, C.; Schedel, M.; Balzer, C.; Hinrichsen, V.; Sass, I. Heat dissipation in variable underground power cable beddings: Experiences from a real scale field experiment. Energies 2021, 14, 7189. [Google Scholar] [CrossRef]
- Shafagh, I.; Shepley, P.; Shepherd, W.; Loveridge, F.; Schellart, A.; Tait, S.; Rees, S.J. Thermal energy transfer around buried pipe infrastructure. Geomech. Energy Environ. 2022, 29, 100273. [Google Scholar] [CrossRef]
- Anders, G.J.; Radhakrishna, H.S. Power cable thermal analysis with consideration of heat and moisture transfer in the soil. IEEE Trans. Power Deliv. 1988, 3, 1280–1288. [Google Scholar] [CrossRef]
- Hwang, C.C.; Jiang, Y.H. Extensions to the finite element method for thermal analysis of underground cable systems. Electr. Power Syst. Res. 2003, 64, 159–164. [Google Scholar] [CrossRef]
- Gouda, O.E.; El Dein, A.Z.; Amer, G.M. Effect of the formation of the dry zone around underground power cables on their ratings. IEEE Trans. Power Deliv. 2011, 26, 972–978. [Google Scholar] [CrossRef]
- De Lieto Vollaro, R.; Fontana, L.; Vallati, A. Thermal analysis of underground electrical power cables buried in non-homogeneous soils. Appl. Therm. Eng. 2011, 31, 772–778. [Google Scholar] [CrossRef]
- Papagiannopoulos, I.; Chatziathanasiou, V.; Exizidis, L.; Andreou, G.T.; De Mey, G.; Więcek, B. Behaviour of the thermal impedance of buried power cables. Int. J. Electr. Power Energy Syst. 2013, 44, 383–387. [Google Scholar] [CrossRef]
- Chatziathanasiou, V.; Chatzipanagiotou, P.; Papagiannopoulos, I.; De Mey, G.; Więcek, B. Dynamic thermal analysis of underground medium power cables using thermal impedance, time constant distribution and structure function. Appl. Therm. Eng. 2013, 60, 256–260. [Google Scholar] [CrossRef]
- De Lieto Vollaro, R.; Fontana, L.; Vallati, A. Experimental study of thermal field deriving from an underground electrical power cable buried in non-homogeneous soils. Appl. Therm. Eng. 2014, 62, 390–397. [Google Scholar] [CrossRef]
- Kroener, E.; Vallati, A.; Bittelli, M. Numerical simulation of coupled heat, liquid water and water vapor in soils for heat dissipation of underground electrical power cables. Appl. Therm. Eng. 2014, 70, 510–523. [Google Scholar] [CrossRef]
- Wiecek, B.; De Mey, G.; Chatziathanasiou, V.; Papagiannakis, A.; Theodosoglou, I. Harmonic analysis of dynamic thermal problems in high voltage overhead transmission lines and buried cables. Int. J. Electr. Power Energy Syst. 2014, 58, 199–205. [Google Scholar] [CrossRef]
- Ocłoń, P.; Cisek, P.; Pilarczyk, M.; Taler, D. Numerical simulation of heat dissipation processes in underground power cable system situated in thermal backfill and buried in a multilayered soil. Energy Convers. Manag. 2015, 95, 352–370. [Google Scholar] [CrossRef]
- Hughes, T.J.; Henstock, T.J.; Pilgrim, J.A.; Dix, J.K.; Gernon, T.M.; Thompson, C.E. Effect of sediment properties on the thermal performance of submarine HV cables. IEEE Trans. Power Deliv. 2015, 30, 2443–2450. [Google Scholar] [CrossRef]
- Thomas, H.R.; He, Y. Analysis of coupled heat, moisture and air transfer in a deformable unsaturated soil. Geotechnique 1995, 45, 677–689. [Google Scholar] [CrossRef]
- Thomas, H.R.; Sansom, M.R. Fully coupled analysis of heat, moisture, and air transfer in unsaturated soil. J. Eng. Mech. 1995, 121, 392–405. [Google Scholar] [CrossRef]
- Thomas, H.R.; Rees, S.W. Measured and simulated heat transfer to foundation soils. Géotechnique 2009, 59, 365–375. [Google Scholar] [CrossRef]
- Thomas, H.R. Modelling two-dimensional heat and moisture transfer in unsaturated soils, including gravity effects. Int. J. Numer. Anal. Methods Geomech. 1985, 9, 573–588. [Google Scholar] [CrossRef]
- Thomas, H.R.; King, S.D. Coupled temperature/capillary potential variations in unsaturated soil. J. Eng. Mech. 1991, 117, 2475–2491. [Google Scholar] [CrossRef]
- Thomas, H.R.; He, Y.; Onofrei, C. An examination of the validation of a model of the hydro/thermo/mechanical behaviour of engineered clay barriers. Int. J. Numer. Anal. Methods Geomech. 1998, 22, 49–71. [Google Scholar] [CrossRef]
- Thomas, H.R.; Cleall, P.; Li, Y.C.; Harris, C.; Kern-Luetschg, M. Modelling of cryogenic processes in permafrost and seasonally frozen soils. Geotechnique 2009, 59, 173–184. [Google Scholar] [CrossRef]
- Hosking, L.J.; Thomas, H.R.; Sedighi, M. A dual porosity model of high-pressure gas flow for geoenergy applications. Can. Geotech. J. 2018, 55, 839–851. [Google Scholar] [CrossRef] [Green Version]
- Ewen, J.; Thomas, H.R. Heating unsaturated medium sand. Geotechnique 1989, 39, 455–470. [Google Scholar] [CrossRef]
- Philip, J.R.; De Vries, D.A. Moisture movement in porous materials under temperature gradients. EOS Trans. Am. Geophys. Union 1957, 38, 222–232. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Parker, J.C.; Lenhard, R.J.; Kuppusamy, T. A parametric model for constitutive properties governing multiphase flow in porous media. Water Resour. Res. 1987, 23, 618–624. [Google Scholar] [CrossRef]
- Central Electricity Generating Board. Contract: TC/ST/C5388. Beddington-Rowdown. Surrey; The National Grid Company plc: London, UK, 1986. [Google Scholar]
- International Electrotechnical Commission. Electric Cables—Calculation of the Current Rating; International Electrotechnical Commission: Geneva, Switzerland, 2006. [Google Scholar]
- IEC 60287-2-1; Electric Cables-Calculation of the Current Rating—Part 2: Thermal Resistance—Section 1: Calculation of the Thermal Resistance. IEC: Geneva, Switzerland, 1995.
- CIGRE. Cable Systems Electrical Characteristics. Technical Brochure of Working Group WG B1.30; CIGRE: Paris, France, 2013. [Google Scholar]
- CIGRE. A Guide for Rating Calculations of Insulated Cables. Technical Brochure of Working Group B1.35 on Cable Ratings; CIGRE: Paris, France, 2015. [Google Scholar]
- Engineering Toolbox. Permeability. Available online: https://www.engineeringtoolbox.com/permeability-d_1923.html (accessed on 21 January 2021).
- Lindström, L. Evaluating Impact on Ampacity According to IEC-60287 Regarding Thermally Unfavourable Placement of Power Cables; KTH: Stockholm, Sweden, 2011. [Google Scholar]
- The National Grid Company plc. Current Ratings for Cables. Technical Guidance Note TGN(T)067. Surrey; The National Grid Company plc: London, UK, 1996. [Google Scholar]
- Malusis, M.A.; Yeom, S.; Evans, J.C. Hydraulic conductivity of model soil–bentonite backfills subjected to wet–dry cycling. Can. Geotech. J. 2011, 48, 1198–1211. [Google Scholar] [CrossRef]
- Sandford, R.J.; Swan, F.K.; Thomas, H.R. An Investigation into Temporary Flowable Backfills: Liquid Soil Technology; Geoenvironmental Research Centre, Cardiff University: Cardiff, UK, 2019. [Google Scholar]
- Hruška, M.; Clauser, C.; De Doncker, R.W. The effect of drying around power cables on the vadose zone temperature. Vadose Zone J. 2018, 17, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Ragab, R.; Rosier, P.; Dixon, A.; Bromley, J.; Cooper, J.D. Experimental study of water fluxes in a residential area: 2. Road infiltration, runoff and evaporation. Hydrol. Process. 2003, 17, 2423–2437. [Google Scholar] [CrossRef]
- Ramier, D.; Berthier, E.; Andrieu, H. An urban lysimeter to assess runoff losses on asphalt concrete plates. Phys. Chem. Earth Parts A/B/C 2004, 29, 839–847. [Google Scholar] [CrossRef]
- Ramier, D.; Berthier, E.; Andrieu, H. The hydrological behaviour of urban streets: Long-term observations and modelling of runoff losses and rainfall–runoff transformation. Hydrol. Process. 2011, 25, 2161–2178. [Google Scholar] [CrossRef]
- Redfern, T.W.; Macdonald, N.; Kjeldsen, T.R.; Miller, J.D.; Reynard, N. Current understanding of hydrological processes on common urban surfaces. Prog. Phys. Geogr. 2016, 40, 699–713. [Google Scholar] [CrossRef] [Green Version]
- Angrill, S.; Petit-Boix, A.; Morales-Pinzón, T.; Josa, A.; Rieradevall, J.; Gabarrell, X. Urban rainwater runoff quantity and quality—A potential endogenous resource in cities? J. Environ. Manag. 2017, 189, 14–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Busby, J. Thermal conductivity and diffusivity estimations for shallow geothermal systems. Q. J. Eng. Geol. Hydrogeol. 2016, 49, 138–146. [Google Scholar] [CrossRef]
- USDA. U.S. Salinity Laboratory. Available online: https://www.ars.usda.gov/pacific-west-area/riverside-ca/agricultural-water-efficiency-and-salinity-research-unit/docs/model/rosetta-class-average-hydraulic-parameters/ (accessed on 21 January 2021).

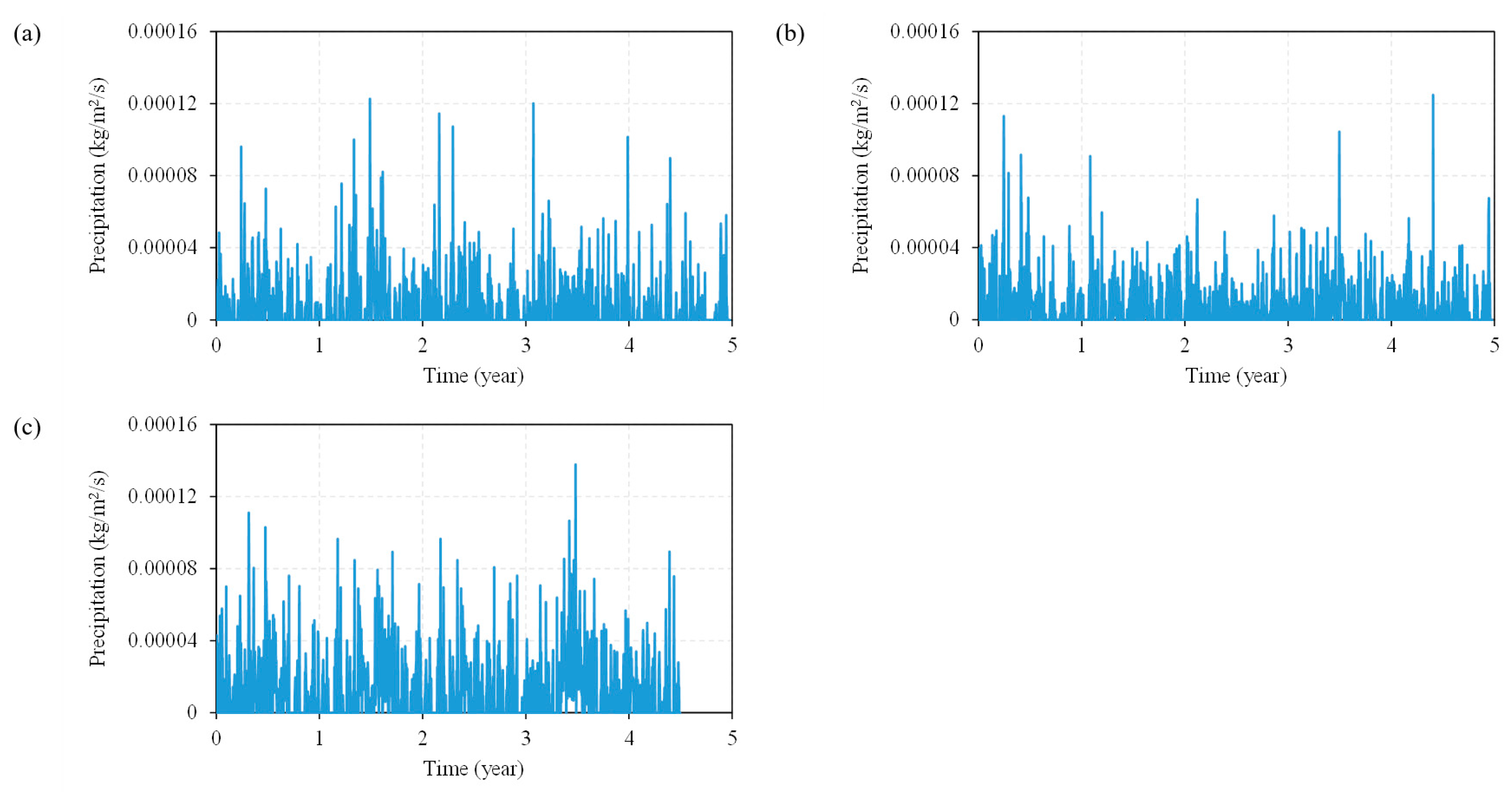
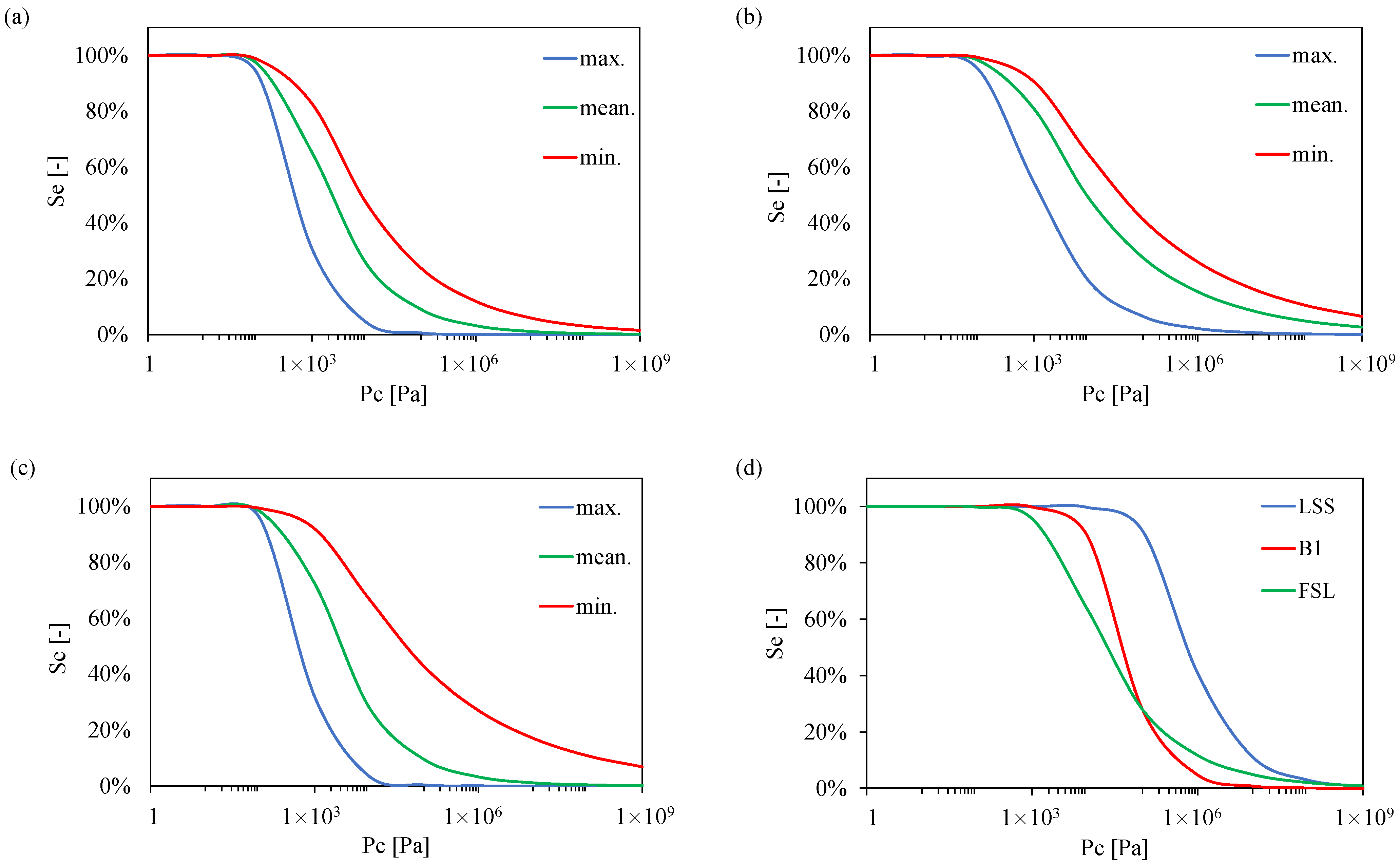
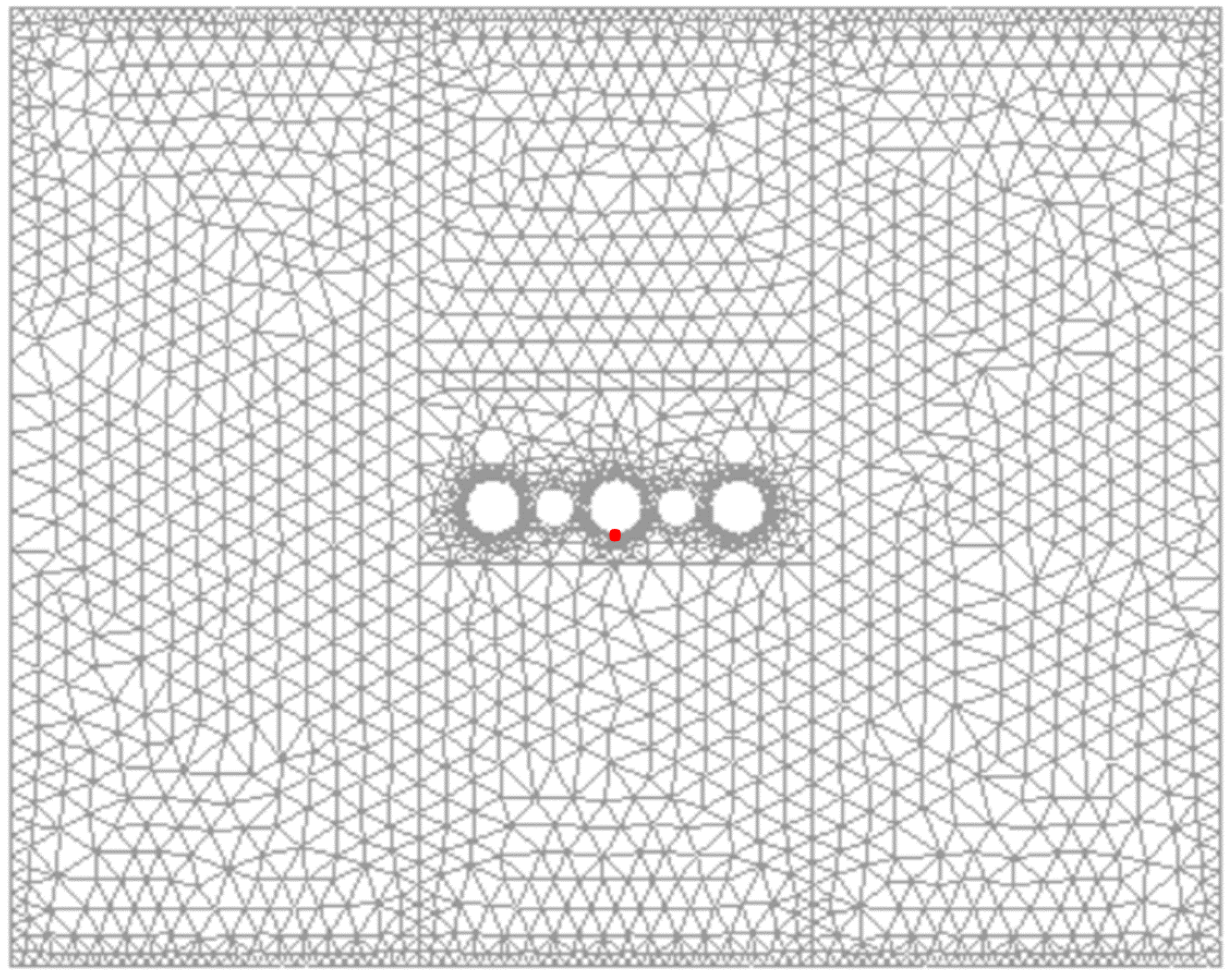
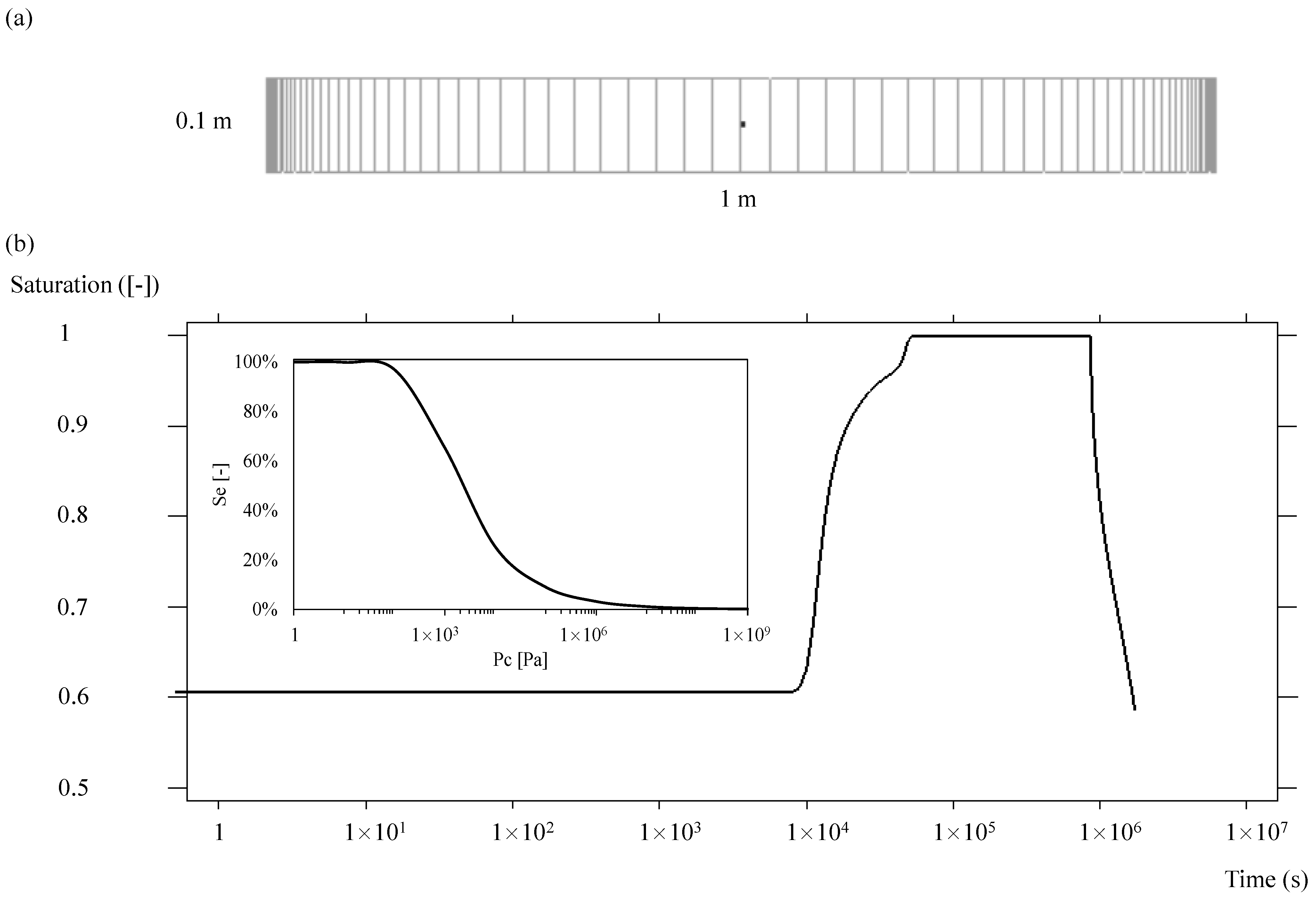
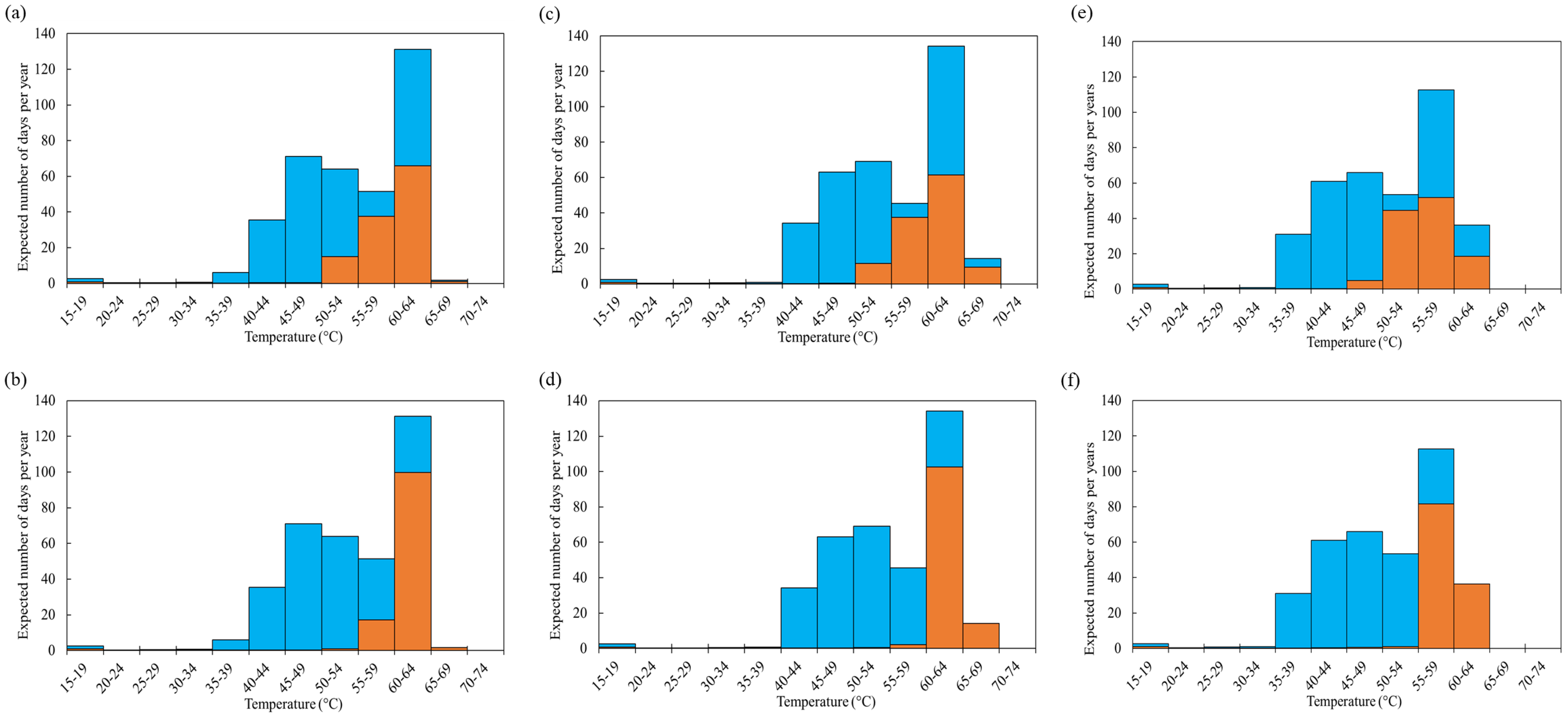
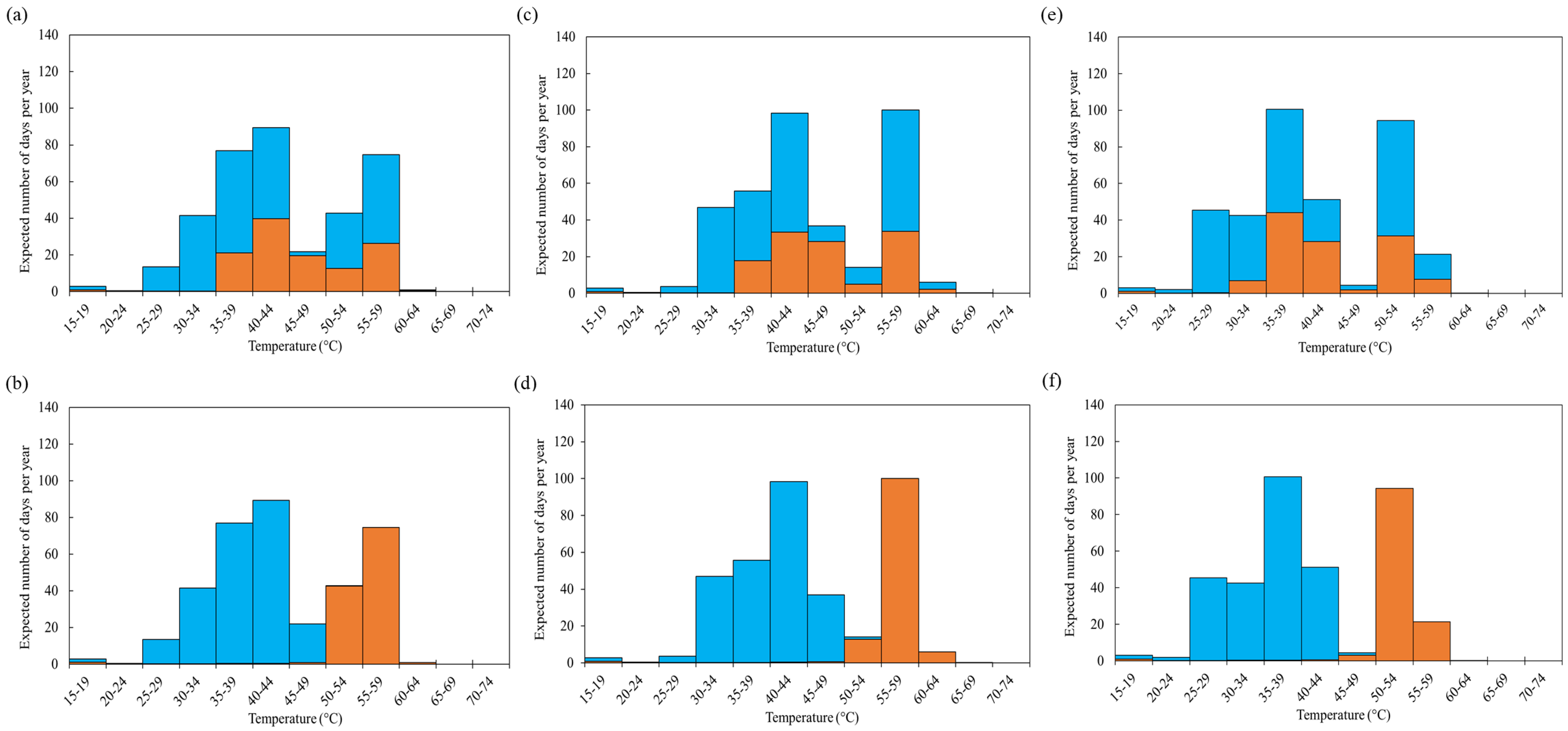
| Circuit Name (Location) | Cable Type | Cable Section Length (km) | Single Core (mm2) (OD, mm) | Loading Condition (kV) |
|---|---|---|---|---|
| Beddington–Rowdown (BRU) | XLPE | 10.068 | 2000 (135) | 400 |
| Lackenby–Thornton (LT) | Oil-filled | 11.568 | 2000 (135) | 400 |
| Dinorwig–Pentir (DP) | Oil-filled | 10.757 | 2000 (135) | 400 |
| Parameter | Unit | Equation/Reference | Value |
|---|---|---|---|
| Conductor resistivity (Cu), | Ωm | [34] | 1.84 |
| Proximity effect coefficient, | - | [34] | 1.07 |
| Angular frequency, | 1/s | [35] | 439.82 |
| Relative magnetic permeability, | H/m | [36] | 1.26 × 10−6 |
| Skin effect coefficient, | - | [34] | 1 |
| Proximity effect coefficient, | - | [34] | 1 |
| Phase to Earth Voltage | kV | 400/√3 [37] | 2.31 × 105 |
| Loss angle (power dissipation factor), | - | [34] | 0.003 |
| Dataset | Cable Location | ||
|---|---|---|---|
| BRU | LT | DP | |
| Native soil type | Sandy loam | Clay | Loam |
| Groundwater depth | 2 m | >30 m | >2 m |
| Ground Water Flooding potential | Potential for groundwater flooding | Not prone/Limited potential/potential to groundwater flooding | Potential for groundwater flooding |
| Bedrock Permeability | High | Low | Low |
| Scenario | Parameters | Precipitation | Saturation |
|---|---|---|---|
| 1 | Min | Min | Min |
| 2 | Mean | Min | Min |
| 3 | Max | Min | Min |
| 4 | Min | Min | Mean |
| 5 | Mean | Min | Mean |
| 6 | Max | Min | Mean |
| 7 | Min | Min | Max |
| 8 | Mean | Min | Max |
| 9 | Max | Min | Max |
| 10 | Min | Mean | Min |
| 11 | Mean | Mean | Min |
| 12 | Max | Mean | Min |
| 13 | Min | Mean | Mean |
| 14 | Mean | Mean | Mean |
| 15 | Max | Mean | Mean |
| 16 | Min | Mean | Max |
| 17 | Mean | Mean | Max |
| 18 | Max | Mean | Max |
| 19 | Min | Max | Min |
| 20 | Mean | Max | Min |
| 21 | Max | Max | Min |
| 22 | Min | Max | Mean |
| 23 | Mean | Max | Mean |
| 24 | Max | Max | Mean |
| 25 | Min | Max | Max |
| 26 | Mean | Max | Max |
| 27 | Max | Max | Max |
| Location | Native Soil | (kg/m3) | (J/(kg K)) | (W/(mK)) |
|---|---|---|---|---|
| BRU | Sandy loam | 2620 | 793.69 | 3.81 |
| DP | Loam | 2660 | 788.91 | 3.82 |
| LT | Clay | 2600 | 796.72 | 1.96 |
| Parameter (min) | Parameter (mean) | Parameter (max) | ||
|---|---|---|---|---|
| Native soil (sandy loam) | (Pa) at | −78,209 | 39,399 | −65,206 |
| (Pa) at | 84,249 | 96,104 | 100,068 | |
| (Pa) at | 97,271 | 99,803 | 100,814 | |
| (cm−1) | 0.12 | 0.21 | 0.36 | |
| 1.3 | 1.45 | 1.87 | ||
| 0.23 | 0.31 | 0.47 | ||
| 0.01 | 0.04 | 0.09 | ||
| 0.30 | 0.39 | 0.47 | ||
| (m/s) | 6.99 × 10−6 | 1.35 × 10−5 | 2.62 × 10−5 | |
| (m/s) | 5.14 × 10−7 | 9.95 × 10−7 | 1.93 × 10−7 | |
| (Pa) | 101,325 | 101,325 | 101,325 | |
| (K) | 288.15 | 288.15 | 288.15 | |
| Backfill | (Pa) at | −78,209 | 39,399 | −65,206 |
| (Pa) at | 84,249 | 96,104 | 100,068 | |
| (Pa) at | 97,271 | 99,803 | 100,814 |
| Parameter (min) | Parameter (mean) | Parameter (max) | ||
|---|---|---|---|---|
| Native soil (clay) | (Pa) at | −6,150,000 | −386,553 | 90,589 |
| (Pa) at | −34,454 | 76,522 | 99,173 | |
| (Pa) at | 85,934 | 96,945 | 100,539 | |
| (cm−1) | 0.08 | 0.16 | 0.32 | |
| 1.20 | 1.25 | 1.47 | ||
| 0.17 | 0.20 | 0.32 | ||
| 0.01 | 0.01 | 0.01 | ||
| 0.38 | 0.46 | 0.54 | ||
| (m/s) | 3.56 × 10−6 | 8.94 × 10−6 | 2.24 × 10−5 | |
| (m/s) | 2.62 × 10−7 | 6.58 × 10−7 | 1.65 × 10−6 | |
| (Pa) | 101,325 | 101,325 | 101,325 | |
| (K) | 288.15 | 288.15 | 288.15 | |
| Backfill | (Pa) at | −6,150,000 | −386,553 | 90,589 |
| (Pa) at | −34,454 | 76,522 | 99,173 | |
| (Pa) at | 85,934 | 96,945 | 100,539 |
| Parameter (min) | Parameter (mean) | Parameter (max) | ||
|---|---|---|---|---|
| Native soil (loam) | (Pa) at | −878,9679 | 75,734 | 99,515 |
| (Pa) at | −71,989 | 96,394 | 100,530 | |
| (Pa) at | 82,286 | 99,545 | 100,874 | |
| (cm−1) | 0.07 | 0.14 | 0.29 | |
| 1.20 | 1.47 | 1.99 | ||
| 0.17 | 0.32 | 0.50 | ||
| 0.01 | 0.01 | 0.01 | ||
| 0.30 | 0.40 | 0.50 | ||
| (m/s) | 3.26 × 10−6 | 8.19 × 10−6 | 2.06 × 10−5 | |
| (m/s) | 2.40 × 10−7 | 6.02 × 10−7 | 1.51 × 10−6 | |
| (Pa) | 101,325 | 101,325 | 101,325 | |
| (K) | 288.15 | 288.15 | 288.15 | |
| Backfill | (Pa) at | −8,789,679 | 75,734 | 99,515 |
| (Pa) at | −71,989 | 96,394 | 100,530 | |
| (Pa) at | 82,286 | 99,545 | 100,874 |
| Backfill | (cm−1) | (m/s) | (m/s) | ||
| Liquid Soil Sand (LSS) | 4.33 × 10−4 | 1.58 | 0.37 | 2.30 × 10−10 | 1.69 × 10−11 |
| sand-bentonite (B1) | 4.84 × 10−3 | 1.78 | 0.44 | 2.60 × 10−10 | 1.91 × 10−11 |
| fine sandy loam (FSL) | 2.77 × 10−2 | 1.38 | 0.28 | 3.96 × 10−6 | 2.91 × 10−7 |
| Backfill | (kg/m3) | (J/(kg K)) | (W/(mK)) | ||
| Liquid Soil Sand (LSS) | 2896.9 | 1779.1 | 9.09 | 0.01 | 0.35 |
| sand-bentonite (B1) | 2896.9 | 1779.1 | 9.09 | 0.04 | 0.44 |
| fine sandy loam (FSL) | 2896.9 | 1779.1 | 9.09 | 0.01 | 0.45 |
| Upstream Boundary Conditions (Left Side) | Initial Conditions | Downstream Boundary Conditions (Right Side) |
|---|---|---|
| PAP flux: 0 (kg/m2/s) (0 ≤ t ≤ 10 days) PAP flux: linear increase from 0 to 1 × 10−4 (kg/m2/s) (10 ≤ t ≤ 20 days) | = −1421 Pa = 100 Pa = 288.15 K | = 100 Pa = 100 Pa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Zagorščak, R.; Sandford, R.J.; Cwikowski, O.N.; Yanushkevich, A.; Thomas, H.R. Insights into the Thermal Performance of Underground High Voltage Electricity Transmission Lines through Thermo-Hydraulic Modelling. Energies 2022, 15, 8897. https://doi.org/10.3390/en15238897
Liu K, Zagorščak R, Sandford RJ, Cwikowski ON, Yanushkevich A, Thomas HR. Insights into the Thermal Performance of Underground High Voltage Electricity Transmission Lines through Thermo-Hydraulic Modelling. Energies. 2022; 15(23):8897. https://doi.org/10.3390/en15238897
Chicago/Turabian StyleLiu, Kui, Renato Zagorščak, Richard J. Sandford, Oliver N. Cwikowski, Alexander Yanushkevich, and Hywel R. Thomas. 2022. "Insights into the Thermal Performance of Underground High Voltage Electricity Transmission Lines through Thermo-Hydraulic Modelling" Energies 15, no. 23: 8897. https://doi.org/10.3390/en15238897
APA StyleLiu, K., Zagorščak, R., Sandford, R. J., Cwikowski, O. N., Yanushkevich, A., & Thomas, H. R. (2022). Insights into the Thermal Performance of Underground High Voltage Electricity Transmission Lines through Thermo-Hydraulic Modelling. Energies, 15(23), 8897. https://doi.org/10.3390/en15238897







