Review on Model Based Design of Advanced Control Algorithms for Cogging Torque Reduction in Power Drive Systems

Abstract

This review of the state of the art aims to collect the description and main research results in the field of development and validation of control algorithms with the main purpose to solve the problem of cogging torque and main sources of electromagnetic torque ripple. In particular, we focus on electric drives for advanced and modern mechatronic applications such as industrial automation, robotics, and automotive applications, with special emphasis on work that exploits model-based design. A great added value of this paper is to explicitly show the operational steps required for the model-based design design of optimized control algorithms for electric drives where it is necessary to make up for electromagnetic torque oscillations due to the main sources of ripple, particularly cogging torque. The ultimate goal of this paper is to provide researchers approaching this particular problem with a comprehensive collection of the most effective solutions reported in the state of the art and also a summary for effectively applying the model-based design methodology.

1. Introduction

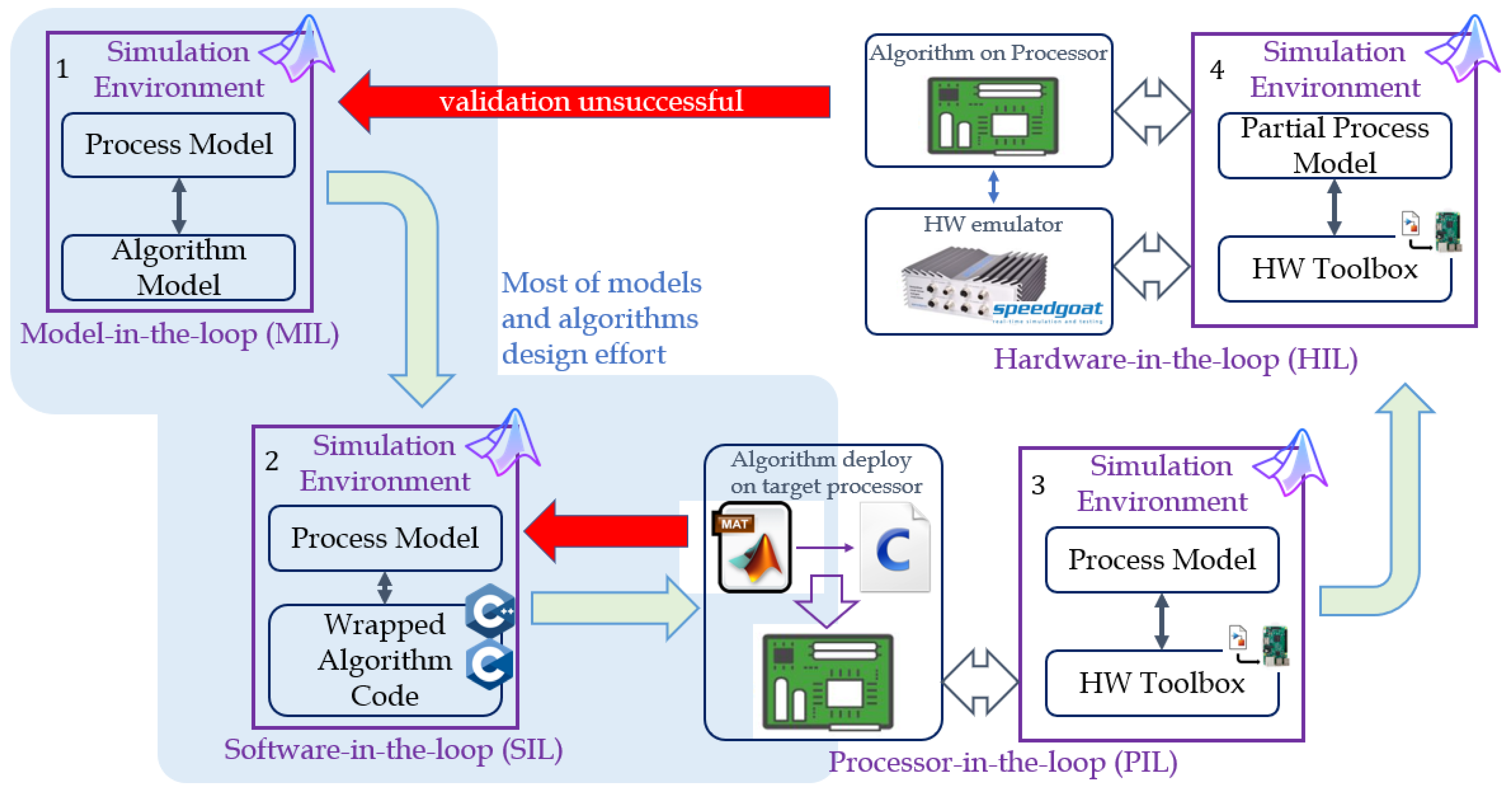
1.1. Brief Introduction to MBD for Mechatronics

This state-of-the-art review focuses on a very specific topic such as the development of advanced algorithms for reducing cogging torque and major sources of electromagnetic torque disturbance in which MBD is exploited as a design paradigm.

As is well known, the use of MBD enables superior results to be achieved in the project phases, in which various aspects need to be evaluated upstream of the realization of a prototype, on which it will later be possible to concretize and refine the results.

The MBD approach has become particularly popular in the design of control algorithms for the automation of processes and dynamic systems of particular industrial interest [1,2].

Through the MBD approach, the risks associated with testing under critical operating conditions can be reduced, decreasing validation time and optimizing implementation steps [3].

So, MBD can be exploited to evaluate the choice of control techniques, numerical optimization criteria, operational approximations, modeling of phenomena at different levels of detail, computational complexity, cost-benefit ratio, preliminary evaluation of the required embedded platform, final integration on micro-controller/processor, etc. [4,5,6].

In addition, there are advanced tools implementing the MBD paradigm that make it easy to use for design and subsequent integration on electronic systems of interest, greatly speeding up implementation time.

Figure 1 schematically recalls the stages of the MBD paradigm.

Model-in-the-Loop (MIL) is the first step in the modeling-based development chain, in which both the control and monitoring algorithms and the physical plant or process are implemented through a set of mathematical equations and/or formalisms, in a simulation environment, such as MATLAB/Simulink.

It is an essential step, as it allows us to make an exhaustive study of the system and of the interaction with the blocks that implement the algorithms, especially from the point of view of the operating space, verifying the functioning in various operating conditions and the consequences in their variations [7].

Software-in-the-Loop (SIL) is a process in which the actual Production Software Code, which in general can derive from developments prior to the adoption of MBD techniques, and therefore not necessarily self-generated code, is incorporated into a simulation environment that contains the mathematical models of the physical system.

This is done to allow for the inclusion of software features for which no templates exist or to allow for faster simulation runs, as part of the functional blocks are already written in low-level C / C ++ code. Therefore, SIL is defined as the inclusion of compiled production software code in a simulation model [8].

Processor-in-the-Loop (PIL) is the process in which the control and monitoring system is compiled and downloaded into an integrated target processor, ergo an embedded platform with micro-controller/processor with specifications consistent with that selected for the final mechatronic system and communicates directly with the model of the plant via standard communications such as Ethernet.

In this phase of the MBD validation process, hardware toolboxes are referred to as SW infrastructures that allow interaction between the simulation environment and the low-level environment, such as micro-controller or micro-processor. Among the most widely used in automotive and industrial automation is support for NXP’s evaluation boards [9]. This allows designers to validate their control algorithm even in the absence of the physical process, by exploiting the simulated model, which interacts with the embedded code on the embedded system.

In this case, I/O devices are not used for communication, so unlike the RCP phase there is no verification of the interactions between the Embedded system and the physical process or part of it being tested [10].

Hardware-in-the-Loop (HIL) indicates the testing technique of electronic control units by connecting them to special benches that reproduce in a more or less complete way the electro-mechanical and electronic system of the process.

The purpose of the HIL tests is to use the benches to anticipate the checks on components, subsystems and systems already in the design and prototyping phase, without waiting for the availability of the final product for which they are intended.

In fact, the real components installed respond to the simulated signals as if they were operating in a real environment, since they are not able to distinguish signals coming from a physical environment from those produced by software models.

In this way, the HIL method makes it possible to reproduce the most diverse operating conditions with the benches and observing the behavior of the system and of the individual elements [11].

In this phase of validating control algorithms, one often has to deal with the problem of only having part of the physical process to be controlled. To increase the degree of validation with respect to the PIL phase, hardware emulators are often used. These devices, such as the widely used Speedgoat systems [12], are able to provide HW interfaces for system and process models, supplying currents and voltages instead of sensors and actuators of the final process. This allows designers to further test the validity of the algorithms by “getting closer” to the physical process with respect to PIL testing (as schematically reported in Figure 2).

1.2. Contributions

Many reviews of the state of the art regarding the reduction of Cogging Torque in Synchronous/Brushless motors by physical modification techniques can be found in the literature, but there are none regarding control techniques.

In this review, we focus on works that propose advanced control techniques for reducing cogging torque and major sources of torque disturbance. The development of the control techniques proposed in this work takes advantage of the MBD approach, which, as discussed above, is the most efficient and flexible. Compared with the reviews in the literature, our most relevant contributions are:

• Focus on the problem of cogging torque reduction by advanced control technique validated through MBD approach;
• Collect the most recent state-of-the-art work on this topic;
• Critical analysis of the control techniques proposed by various authors, with the aim of providing suggestions for implementation and improvement of the reported results.

1.3. Paper Organization

The rest of the manuscript is organized into the following Sections: Section II explains the cogging torque problem in detail by reporting the main approaches and methods used for mathematical modeling in the context of control algorithm design; Section III gives details of mathematical modeling and integration in a simulation environment of the main components of electric drives in modern mechatronic systems; Section IV describes the most commonly used control techniques for solving the cogging torque problem by listing their advantages and disadvantages; and Section V gives final conclusions and a discussion of possible future developments.

2. Cogging Torque’s Details and Modeling

2.1. Reasons for Control Design in Cogging Torque Reduction

Given the enormous potential of this methodology, MBD is increasingly being used to increase the efficiency of individual components of an entire mechatronic process.

It can safely be said that the mechatronic processes of strongest industrial interest are physical electro-mechanical in nature, so among the most decisive components for maximum efficiency of the entire process are definitely electrical drives.

It can certainly be said that, by now, modern drives for advanced mechatronic applications mostly exploit Permanent Magnet Synchronous Motors (PMSM) and Brushless motors.

They have the most advantageous inertia/torque ratio, high efficiencies, physically robust characteristics, and are the most versatile for use at both very low and high speeds.

As is well known, among the inherent problems of using Synchronous/Brushless motors is torque ripple due to cogging torque, which causes undesirable oscillations, lowering performance both for low-speed applications where high accuracy in positioning control is required, and in speed control applications where unwelcome noise is generated.

There are some papers in the literature in which a very specific design is proposed with the aim of mitigating the effect of oscillations due to this physical phenomenon, but these have met with little success in practice [13,14,15].

This is mainly due to the fact that such solutions are based on physical modifications applicable only in some specific configurations, relating to Synchronous motors suitable mainly for applications in which moderate electromagnetic torque is required, since the underlying concept is to limit the amount of permanent magnets, arranging them so that the stator–rotor magnetic interaction is reduced, but effectively reducing the torque deliverable by the machine (see Figure 3).

The most promising results have been achieved by design of control algorithms, which are capable of compensating for cogging torque, which for all intents and purposes is an additive disturbance signal with respect to electromagnetic torque, so control techniques are effective in compensating for it.

MBD being the best among advanced algorithm development and validation approaches, research in recent years sees the application of this paradigm for efficient resolution of this type of problem as well.

2.2. Cogging Torque Modeling Approaches

As anticipated, cogging torque is an intrinsic phenomenon of permanent magnet synchronous motors and Brushless motors, both radial and axial flux, related to the magnetic interaction between the main parts of the electrical machine, such as stator and rotor.

The phenomenon is present in both synchronous motor configurations, with magnets superficial to the rotor and internal to the rotor iron, and Brushless, causing the same effect, i.e., electromagnetic torque disturbance.

The problem is intrinsic, as it depends on the unavoidable variation of the equivalent reluctance of the enclosing magnetic path of the magnetic flux concatenated with the stator iron through the air gap and produced by the permanent magnets themselves.

By manually rotating the rotor axis, it is possible to perceive this phenomenon as preferential angular positioning, at some angular positions “attractive” and at some angles ”repulsive”.

The phenomenon occurs even in the absence of power supply to the electrical machine, so it is interpreted as an additive disturbance with respect to the electromagnetic torque, due to the phase currents (and from the angular position).

In addition, due to the total symmetry of the ferromagnetic structure of electric machines, the alternation of the ”repulsive” effect and the ”attractive” effect due to the variation of the air gap, i.e., the magnetic reluctance, compensate each other along the entire round angle. This allows the intuition that cogging torque is a zero mean phenomenon.

In Figure 4, the concept of alternating “attractive” and “repulsive” phase is shown for a surface magnet synchronous motor configuration; the concept is the same for all configurations.

It represents the behavior in the proximity of the preferential angular position, i.e., the position where naturally the concatenated magnetic flux tends to align the teeth of the stator slots with the magnets arranged on the rotor.

In the direction of rotation, the force generated by the concatenated magnetic flux (in the direction tangential to the rotor surface) alternates between positive and negative signs depending on whether the angular position is less or greater than the preferential position itself.

Obviously, the magnetic force is composed of a tangential component, which is the actual cause of cogging torque, and a normal component, which, however, is absorbed by the structure without any effect on the relative rotation between stator and rotor.

The application of advanced control techniques to reduce this inherent effect appears to be the best approach. Following the MBD design standard, a first step is certainly to make an estimate of the cogging torque by means of a mathematical model.

In the literature, the most widely used approaches that have been shown to be usable in the context of control algorithms, with the best results being closed form modeling and the online estimation.

Works in the literature that focus on mathematical modeling of cogging torque in closed form start from the equivalent energy representation of the machine, via an equivalent magnetic circuit. This highlights the angular position dependence of the stored magnetic power budget.

This relationship is further highlighted in the dependence of magnetic reluctance, due to the fact (described intuitively above) that the air gap varies its amplitude during relative rotation between stator and rotor [16,17,18,19,20,21].

Referring to Figure 5, it is possible to quantify the magnetic energy stored by the ferromagnetic structure as given in Equation (1).

$$W_m=\frac{1}{2}{L}_{eq}{I}^2+\frac{1}{2}{R}_{eq}\left({\theta }_m\right){{\varphi }^2}_{rs}+NI{\varphi }_{rg}$$

(1)

$W_m$ denotes the magnetic energy stored by the electrical machine, both under energized and not energized conditions. With $L_{eq}$ we denote the stator inductance of the equivalent circuit of the internal windings, I the phase current; $R_{eq}$ the equivalent magnetic reluctance associated with the magnetic induction circuit at the mechanical air gap; and with N we denote the number of windings per stator phase. Finally, ${\varphi }_{rs}$ and ${\varphi }_{rg}$ denote the components of the magnetic flux concatenated through the air gap between the stator and rotor.

It follows that the cogging torque is defined as the derivative of magnetic energy with respect to angular position, in the absence of power, that is, at zero electric current in the machine windings. In Equation (2), the relationship between magnetic energy and cogging torque is given.

$$T_{cog}=-\frac{\partial W_m(I=0)}{\partial {\theta }_m}=-\frac{1}{2}{{\varphi }^2}_{rs}\frac{\partial R_{eq}\left({\theta }_m\right)}{\partial {\theta }_m}$$

(2)

In Equation (2), the term $\frac{\partial W_m(I=0)}{\partial {\theta }_m}$ denotes the partial derivative of the magnetization energy with respect to the angular position of the rotor, calculated under the condition that the electrical machine is not powered by any energy source.

The exact expression of the cogging torque depends on the square of the magnetic flux intensity concatenated with the air gap ${\varphi }_{rs}$, and the derivative of the equivalent magnetic reluctance, a function of angular position.

Note that ${\varphi }_{rs}$ depends on the physical characteristics of the permanent magnets, i.e., the magnetic material used, while $R_{eq}$ depends substantially on geometrical factors, thus on the shape of the stator slots as well as on the arrangement of the permanent magnets themselves. Since this is all known information, this is an analytical representation in closed form.

This is the most widely used approach by researchers focusing on control algorithms because of the simplicity of integrating the cogging torque model, being precisely in closed form it can be integrated into the mechanical balance of rotor rotation.

Moreover, it is easy to validate through dedicated SW tools for finite element analysis that do not require the presence of the machine but only design information, which is often the case in advanced design activities typical of innovative companies exploiting R&D.

Another widely used approach, especially in the presence of the prototype electrical machine, is to use a test pod for direct measurement [22]. A typical test bench for cogging torque measurement is shown in Figure 6.

The typical measuring bench basically consists of two electric motors and a torque sensor (normally a torque transducer).

Through the first motor, which is called MASTER, we impose the motion of the second motor, called SLAVE, of which we are interested in recording the data inherent in the torque at the shaft by means of the torque transducer.

Since the Slave is “dragged” by the Master, its stator windings will not be current flowing, and this means that the torque measured by the torque transducer coincides with the Cogging Torque.

The important thing about this measurement is that it is made in the steady state of speed since the contribution of inertial actions due to acceleration transients must be avoided.

In fact, the measurement made in this way is the simplest procedure for obtaining a cogging torque profile that can be exploited in eventual modeling with a greater degree of accuracy describing the dynamic behavior of the machine and the design of a feedback law to compensate for such disturbance.

The result of the measurement is usually a set of data representing the measured cogging torque at different angular positions. This allows a closed-form model to be derived by approximation procedure, by harmonic analysis [23] or polynomial [24], as reported in Equation (3).

$$T_{cog}=\sum _{i=0}^{N_h}{A}_{k}cos\left(k\frac{{\theta }_m}{{\theta }_{cog}}+a_k\right)+B_{k}sin\left(k\frac{{\theta }_m}{{\theta }_{cog}}+b_k\right)$$

(3)

where $A_k,B_k,a_k$ and $b_k$ are harmonic development parameters, while ${\theta }_{cog}$ is the angular period of the cogging pair, which depends on geometrical and construction factors, such as the number of stator slots and teeth, the number of permanent magnets and type of rotor iron arrangement (information known a priori).

Other works base the estimation of cogging torque on artificial intelligence models, neural networks and machine learning [25,26]. Few works, however, combine artificial intelligence models with control algorithms.

The main reason is certainly to reduce the overall computational complexity of the automatic cogging pair reduction system, and of course to reduce the storage space, which is usually the weak point of AI models compared to other approaches.

3. Synchronous Motor and Advanced Electric Power Drives Modeling

3.1. Fundamental Components of Electric Power Drives in Mechatronics

Another key step in the MBD approach is certainly accurate modeling of the electrical machine and drive components, including inverter, modulation system and implemented load.

A block diagram for the architecture of an electric drive for mechatronic applications is shown in Figure 7. The fundamental components of the system and their function are shown below.

• Static power converters: these are used to convert the electrical power regime to that which is useful for driving the electrical machine through the inverter. Configurations typically found in mechatronic systems of industrial interest are AC/DC converters to handle direct power from the mains or DC/DC converters to handle the DC bus level provided by a constant source, such as a Li-ion battery.
• Modulation system: conceptually separate from the system that integrates the control algorithm, but often implemented on the same embedded platform, it is the union of algorithm and HW interface for direct management of the inverter mosfets. The control algorithm typically provides a duty-cycle equivalent signal, which is converted into switching logic by the switching system, to manage the state of the inverter and power the electrical machine accordingly.
• Inverter: the electronic circuit that physically manages the (bidirectional) power transfer from the power source (DC side) to the electrical machine (AC side). The state of the inverter is decided by the modulation system. Conceptually, the inverter is a combinatorial logic network with $2^3$ combinations (in the three-phase case).
• Control system: the embedded platform on which the logic related to the feedback control algorithm is integrated. In modern embedded systems it coexists with the modulation system and cooperates via SW drivers. In the sensorless configuration, such a system also integrates the angular position/velocity estimation algorithm by exploiting direct measurement of electric current (from inverter or motor phase).
• Transduction system: the set of devices for measuring the physical quantities of primary interest for managing the electric drive. Typically it consists of:

  -

  Temperature sensors, placed at “critical” points, such as the electrical machine and static converters, which are subject to high currents and therefore need to be monitored for losses due to the Joule effect.

  -

  Position and angular velocity sensors: placed on the rotor axis if we are talking about encoders/resolvers or placed inside the structure if we are talking about hall effect sensors.

  -

  Voltage/current sensors: typically placed on the inverter, since motor phases and inverter branches are necessarily traversed by the same current.

3.2. Synchronous Motor Modeling including Cogging Torque

The mathematical model of the synchronous motor is typically derived by applying the unified theory of electrical machines, which states that any electrical machine is dynamically describable by an equivalent electrical and magnetic circuit [27].

Permanent-magnet synchronous motors of interest in mechatronic applications, where it is required to solve the cogging torque problem, are to date three-phase motors, so the following are the fundamental points of modeling for three-phase machines [28,29]. Note that the dynamic model is formally unchanged whether the machines have radial magnetic flux or axial magnetic flux.

In Equation (4), the dynamic balance of phase voltages of the electrical machine is given. The vector $\overrightarrow{U}$ represents the triad of supply voltages, referred to the neutral of the equivalent circuit, the term $R_s\overrightarrow{I}$ represents the losses in the stator circuit, and the term $\frac{d\overrightarrow{Psi}}{dt}$ represents the voltage drop due to the phenomena of self and mute induction and the electromechanical energy conversion phenomenon, mainly due to the presence of the permanent magnets.

$$\overrightarrow{U}=\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]=R_s\left[\begin{array}{c}{I}_a\\ I_b\\ I_c\end{array}\right]+\frac{d}{dt}\left[\begin{array}{c}{\Psi }_a\\ {\Psi }_b\\ {\Psi }_c\end{array}\right]=R_s\overrightarrow{I}+\frac{d\overrightarrow{\Psi }}{dt}$$

(4)

In Equation (5) are given the main components of the concatenated magnetic flux, denoted by the vector $\overrightarrow{\Psi }$. The vectors ${\overrightarrow{\Psi }}_{AI}$ and ${\overrightarrow{\Psi }}_{MI}$ denote the magnetic flux vectors generated by the phenomena of self and mutual induction, respectively, and the vector ${\overrightarrow{\Psi }}_{PM}$ denotes the magnetic flux vector produced by the magnets concatenated at the air gap.

$I_a,I_b$ and $I_c$ denote the components of the current vector (three-phase reference); $U_a,U_b$ and $U_c$ denote the components of the phase voltage vector (three-phase axes); and ${\Psi }_a,{\Psi }_b$ and ${\Psi }_c$ are the components of the concatenated magnetic flux vector, taking into account both self and mutual induction at the mechanical air gap. $R_s$ is the stator circuit electrical resistance.

$$\overrightarrow{\Psi }={\overrightarrow{\Psi }}_{AI}+{\overrightarrow{\Psi }}_{MI}+{\overrightarrow{\Psi }}_{PM}=L_{eq}\overrightarrow{I}+k_{\Psi }\left[\begin{array}{c}cos\left(p\theta \right)\\ cos\left(p\theta -\frac{2\pi }{3}\right)\\ cos\left(p\theta -\frac{4\pi }{3}\right)\end{array}\right]=L_{eq}\overrightarrow{I}+k_{\Psi }\overrightarrow{C}\left(\theta \right)$$

(5)

Note that the magnetic flux vectors of self and mutual induction can be grouped in the term $L_{eq}\overrightarrow{I}$, where $L_{eq}$ appropriately integrates the inductive coefficients of self and mutual induction.

In addition, the flux vector of permanent magnets ${\overrightarrow{\Psi }}_{PM}$ depends on the coefficient $k_{\Psi }$, indicating its intensity, which is a function of the ferromagnetic material used and the geometric arrangement, and depends formally on the angular position, as discussed above.

Combining Equation (4) and Equation (5), we derive the dynamical equilibrium of currents in the explicit form, in which the link between electrical ($\overrightarrow{U}$ and $\overrightarrow{I}$) and mechanical ($\theta$ and $\omega$) variables is evident. Equation (6) is the equation in vector form of the electrical dynamics of the Synchronous machine.

$$\overrightarrow{U}=R_s\overrightarrow{I}+L_{eq}\frac{d\overrightarrow{I}}{dt}+\frac{d{\overrightarrow{\Psi }}_{PM}}{dt}=R_s\overrightarrow{I}+L_{eq}\frac{d\overrightarrow{I}}{dt}+k_{\Psi }p\frac{d\theta }{dt}\frac{\partial \overrightarrow{C}\left(\theta \right)}{\partial \theta }=R_s\overrightarrow{I}+L_{eq}\frac{d\overrightarrow{I}}{dt}+\omega \overrightarrow{E}\left(\theta \right)$$

(6)

Equation (7) represents the balance of power terms, the meaning of which is explained below.

• The term $P_{in}$ denotes the power absorbed by the machine and is formally defined as the scalar product between voltage vector $\overrightarrow{U}$ and current vector $\overrightarrow{I}$.
• The term $P_{joule}$ denotes the heating losses of the windings, which, as is known from physics, depend on the resistance of the circuit and the square of the modulus of the current, formally $R_s<\overrightarrow{I},\overrightarrow{I}>=R_s{|\overrightarrow{I}|}^2$.
• The term $P_{magnetic}$ represents the magnetic power stored in the equivalent circuit and due exclusively to self and mutual induction phenomena; formally $L_{eq}<\frac{d\overrightarrow{I}}{dt},\overrightarrow{I}>$.
• The term $P_{mechanical}$ represents the mechanical power delivered by the machine, against electromechanical conversion (Lentz’s law). For Synchronous motors, it depends on the angular position, via the counter-electro motion force $\overrightarrow{E}\left(\theta \right)$ (more precisely its gradient), the electric current, and of course the angular speed.

$$P_{in}=<\overrightarrow{U},\overrightarrow{I}>=R_s<\overrightarrow{I},\overrightarrow{I}>+L_{eq}<\frac{d\overrightarrow{I}}{dt},\overrightarrow{I}>+\omega <\overrightarrow{E}\left(\theta \right),\overrightarrow{I}>=P_{joule}+P_{magnetic}+P_{mechanic}$$

(7)

The most relevant term for dynamic modeling purposes is the contribution of the mechanical power output, which as we know is the product of electro-magnetic torque and rotor angular speed. Equation (8) shows the expression of the electro-magnetic torque, in the three-phase reference system.

$$T_{em}=<\overrightarrow{E}\left(\theta \right),\overrightarrow{I}>=-p{k}_{\Psi }\sum _{k=1}^{3}sin\left(p\theta -\frac{2(1-k)\pi }{3}\right)I_k$$

(8)

Equation (9) represents the dynamic rotational equilibrium for the rotor axis. Note that the second member of the equation represents the superposition of the contributions of electromagnetic torque $T_{em}$, Cogging torque $T_{cog}$ and resistant torque associated with the mechanical load $T_{load}$. The parameters $J_r$ and $b_r$ represent the rotor moment of inertia and the coefficient of friction, respectively.

$$J_r\frac{d\omega }{dt}+b_r\omega =J_r\frac{d^2\theta }{d{t}^2}+b_r\frac{d\theta }{dt}=T_{em}+T_{cog}-T_{load}$$

(9)

An example of integration with block diagrams is shown in Figure 8, of the interaction between the set of differential equation representing the electrical balance of the phases of the electric motor and the differential equation representing the dynamic rotational balance of the rotor.

Note how the output of one dynamic subsystem turns out to be the input for the other, defining a ”recursive” dependence. Specifically, the electrical subsystem has the components of the voltage vector, position and angular velocity as inputs. The mechanical subsystem has as inputs, derived from the electrical subsystem, the currents (which in fact define the electromagnetic torque).

Figure 9 and Figure 10 show the block diagrams, realized in the Simulink environment, of the dynamic subsystems describing the behavior of the electric motor. In Figure 9, note how the current dynamics of each phase is excited by the relative electro-motor control force component, which is a function of angular velocity and angular position.

Figure 10 shows that the mechanical equilibrium is activated from the electromagnetic torque, a function of phase currents and angular position. Note how the cogging torque model (red box in Figure 10) is inserted as an additive disturbance with respect to the electromagnetic torque.

To avoid the direct dependence of the electromagnetic torque expression on the angular position, the coordinate transformations are defined in Equation (10). The matrix $B_{\alpha \beta }$ defines the Blondel transformation, while the matrix $P_{dq}\left(\theta \right)$ formalizes the Park transformation.

$$B_{\alpha \beta }=\frac{2}{3}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right]P_{dq}\left(\theta \right)=\left[\begin{array}{ccc}cos\left(\theta \right)& -sin\left(\theta \right)& 0\\ sin\left(\theta \right)& cos\left(\theta \right)& 0\\ 0& 0& 1\end{array}\right]$$

(10)

Note that the Blondel transformation is basically the matrix form of the coordinate change due to the definition of space vector [30], which defines the decomposition of the three-phase vector ${\overrightarrow{X}}_{abc}={[X_a,X_b,X_c]}^T$ in the Gauss plane, as given in Equation (11).

$$X_{\alpha \beta }=\frac{2}{3}\left(X_a+X_b{e}^{j\frac{2\pi }{3}}+X_c{e}^{j\frac{4\pi }{3}}\right)=X_{\alpha }+j{X}_{\beta }$$

(11)

Combining the previous equation with the definition of homopolar component (typically used in electrical engineering) $X_{om}=\frac{X_a+X_b+X_c}{3}$, we obtain perfect equivalence with the Blondel transformation. Note that $X_{om}=0$ for symmetric and balanced systems (such as electric motors), defining a formally passive transformation.

Through the introduced coordinate transformations, we obtain the mathematical model that is exploited for the design of the control algorithms, given in Equation (12).

$$\left\{\begin{array}{c}{U}_d=R_s{I}_d+L_{eq}\frac{d{I}_d}{dt}-p\omega L_{eq}{I}_q\\ U_q=R_s{I}_q+L_{eq}\frac{d{I}_q}{dt}+p\omega (L_{eq}{I}_d+k_{\Psi })\\ \frac{d\theta }{dt}=\omega \\ J_r\frac{d\omega }{dt}+b_r\omega =T_{em}^{dq}+T_{cog}-T_{load}\\ T_{em}^{dq}=\frac{3}{2}p{k}_{\Psi }{I}_q\end{array}\right.$$

(12)

3.3. Modulation System in Advanced Power Drives

SVM (Space-Vector-Modulation) modulation is now the most widely used modulation technique, as it provides better performance than classical PWM (Pulse-Width-Modulation) based techniques.

As shown in Figure 11, reference is made to a classical configuration of an inverter with impressed voltage, connected to a three-phase load, which represents the equivalent circuit of the electrical machine in this specific case.

In the figure, $V_{d}s$ has been used to denote the DC voltage, which is managed to modulate the inverter legs so as to energize the motor phases appropriately. The phase currents, which obviously coincide with those of the inverter branches, are referred to as $I_a,I_b$ and $I_c$.

Note that the drive voltages of the inverter, denoted by $V_{leg,a},V_{leg,b}$ and $V_{leg,c}$, are referred to the ground reference of the inverter circuit, unlike the phase voltages, denoted by $V_a,V_b$ and $V_c$, which are obviously referred to the star center of the stator windings.

Calling $V_{no}$ the potential difference between the star-center reference n and the ground reference o, it is possible to find the expressions of the phase voltages of the electrical machine as a function of the inverter leg voltages, as expressed in Equations (13) and (14).

$$V_{leg,a}+V_{leg,b}+V_{leg,c}=V_a+V_b+V_c+3V_{no}⟶V_{no}=\frac{V_{leg,a}+V_{leg,b}+V_{leg,c}}{3}$$

(13)

$$\begin{array}{c}\hfill V_a=\frac{2}{3}{V}_{leg,a}-\frac{1}{3}(V_{leg,b}+V_{leg,c})\\ \hfill V_b=\frac{2}{3}{V}_{leg,b}-\frac{1}{3}(V_{leg,a}+V_{leg,c})\\ \hfill V_c=\frac{2}{3}{V}_{leg,c}-\frac{1}{3}(V_{leg,a}+V_{leg,b})\end{array}$$

(14)

From these equations, the phase voltages corresponding to the possible state combinations of the inverter, resulting from modulation, are derived.

Table 1. Summary of the possible space vectors for three-phase inverter.

Space Vector	State Leg A	State Leg B	State Leg C	${\mathit{V}}_{\mathit{a}}$	${\mathit{V}}_{\mathit{b}}$	${\mathit{V}}_{\mathit{c}}$
$V_0$	0	0	0	0	0	0
$V_1$	1	0	0	$\frac{2V_{dc}}{3}$	$-\frac{V_{dc}}{3}$	$-\frac{V_{dc}}{3}$
$V_2$	1	1	0	$\frac{V_{dc}}{3}$	$\frac{V_{dc}}{3}$	$-\frac{2V_{dc}}{3}$
$V_3$	0	1	0	$\frac{V_{dc}}{3}$	$\frac{2V_{dc}}{3}$	$-\frac{V_{dc}}{3}$
$V_4$	0	1	1	$-\frac{2V_{dc}}{3}$	$\frac{V_{dc}}{3}$	$\frac{V_{dc}}{3}$
$V_5$	0	0	1	$-\frac{V_{dc}}{3}$	$-\frac{V_{dc}}{3}$	$\frac{2V_{dc}}{3}$
$V_6$	1	0	1	$\frac{V_{dc}}{3}$	$-\frac{2V_{dc}}{3}$	$\frac{V_{dc}}{3}$
$V_7$	1	1	1	0	0	0

shows for each combination of inverter modulation signals the corresponding trio of phase voltages. Each triad actually corresponds to a sector of the SVM modulation.

Note that applying the definition of space vector to the eight triads corresponding to the possible eight states of the inverter, we obtain the vectors $V_0,...,V_7$, which are positioned on the vertices of a hexagon in the Gauss complex plane.

These vectors, as shown in Figure 12, delimit the sectors with which the SVM modulation algorithm selects the most suitable state of the inverter, so that the desired voltage is averaged over the switching period $T_{sw}$.

From the control system, a vector of voltages (referenced to the star center) is generated typically in the Park $dq$ reference system. After the inverse transformation to obtain the control triad in three-phase axes, the definition of space vector is applied via the Blondel transformation, the result of which is the vector $V_{\alpha \beta }^{*}$.

As shown in Figure 13, the control vector is instantaneously placed in one of the sectors of the modulation hexagon. The objective of SVM modulation is to reproduce the vector calculated by the control system, in mean value within the switching period, by partitioning the modulation vectors, as expressed in Equation (15).

$${\overrightarrow{V}}_{\alpha \beta }^{*}=\frac{1}{T_{sw}}\left(T_1{\overrightarrow{V}}_1+T_2{\overrightarrow{V}}_2+T_0{\overrightarrow{V}}_0+T_7{\overrightarrow{V}}_7\right)$$

(15)

By $T_1,T_2,T_0,T_7$, we have indicated the portions of the switching period in which the inverter is brought into a certain state by modulation. Note that the terms $\frac{T_i}{T_{sw}}$ have the same meaning as the duty-cycle for the PWM technique.

Note, as schematized in Figure 14, that in order to integrate the SVM modulation, the triplet $U_{abc}$ is transformed so that the vector $V_{\alpha \beta }^{*}$ can be calculated. The modulus and angle are then extrapolated so that we can work out which sector is in the modulation hexagon. The selection of the sector and the calculation of the distribution times is done (for example) by a state machine.

Figure 15 shows the Simulink diagram of a possible implementation of an SVM algorithm for an ideal inverter (with instantaneous switching) in a simulation environment. In particular, it is shown how to realize the selection of each sector and the allocation of modulation states by means of a state machine realized with STATEFLOW.

3.4. Complete Dynamics Modeling including Cogging Torque

The last (but not least) fundamental component to be mathematically modeled is the electrical machine load. Mechatronic systems of industrial interest are mostly physical–electromechanical in nature. This allows the dynamics of the system implemented by permanent-magnet synchronous motors to be represented through the Lagrangian formalism [31].

$$\begin{array}{cc}\hfill L(q,\dot{q})& =K(q,\dot{q})-U\left(q\right)=\sum _i{K}_i(q,\dot{q})-\sum _j{U}_j\left(q\right)\hfill \\ \hfill & =\sum _i\frac{1}{2}\left(M_i{\left|\overrightarrow{v}(q,\dot{q})\right|}^2+{\overrightarrow{\omega }}_i^T(q,\dot{q})J_i\left(q\right){\overrightarrow{\omega }}_i(q,\dot{q})\right)-\sum _j{M}_i<\overrightarrow{g},{\overrightarrow{P}}_i>\hfill \end{array}$$

(16)

Equation (16) reports the definition of the Lagrangian function $L$ as the difference between the total kinetic energy of the system $K$ and the potential energy $U$. The vector $q={[q_1,...,q_n]}^T$ is composed of the Lagrangian variables, ergo the variables needed to describe the dynamics of the system.

The dynamics of the system can be derived by application of the variations method, from which the following equation is derived.

$$\frac{d}{dt}\frac{\partial L(q,\dot{q})}{\partial {\dot{q}}_i}-\frac{\partial L(q,\dot{q})}{\partial q}=Q_i^T=\sum _i<{\overrightarrow{F}}_{ext,i},\frac{\partial {\overrightarrow{P}}_i\left(q\right)}{\partial q_i}>+\sum _j<{\overrightarrow{T}}_{ext,j},\frac{\partial {\overrightarrow{\alpha }}_i\left(q\right)}{\partial q_i}>$$

(17)

The term $Q_i$ represents the superposition of the non-conservative external effects; ${\overrightarrow{F}}_{ext,i}$ and ${\overrightarrow{T}}_{ext,j}$ are external, non-conservative forces and torques, respectively, applied to the system; ${\overrightarrow{P}}_i$ is the point of application of the force, and ${\alpha }_i$ is the angle subject to change under the action of the torque.

$$M(\overrightarrow{q})\ddot{\overrightarrow{q}}+C(\overrightarrow{q},\dot{\overrightarrow{q}})\dot{\overrightarrow{q}}+G(\overrightarrow{q})=\Gamma (\overrightarrow{q}){\overrightarrow{F}}_{act}-J^T(\overrightarrow{q}){\overrightarrow{F}}_{env}$$

(18)

Compactly, it is possible to rewrite the set of dynamic equations as in Equation (18), where $M(\overrightarrow{q})$ is the inertia matrix, $C(\overrightarrow{q})$ is the matrix of Coriolis terms, $G(\overrightarrow{q})$ is the vector of gravitational and potential terms, $\Gamma (\overrightarrow{q})$ is the matrix that maps the action of the actuators ${\overrightarrow{F}}_{act}$ into the dynamics of the variables $\overrightarrow{q}$, $J(\overrightarrow{q})$ is the analytic Jacobian, and finally ${\overrightarrow{F}}_{env}$ represents the effect of non-conservative external forces.

Note that combining the model of the implemented system in Equation (18) with the mathematical model of the electrical machine in Equation (12) we obtain the final mathematical model, which allows us to design control algorithms for electro-mechanical systems that inherently takes into account the presence of the cogging torque.

4. Most Used Algorithms for Cogging Torque Reduction

The latest work in the literature, concerning the design of algorithms and control systems capable of compensating for cogging torque in Permanent Magnet Synchronous Motors dedicated to advanced mechatronic applications, has shown that the most effective techniques are precisely those in which the mathematical model of cogging torque can be handled as an internal detail in the overall model.

4.1. Model Predictive Control

In the MPC approach, the current control action is computed online rather than using a pre-computed, online, control law. A model predictive controller uses, at each sampling instant, the plant’s current input and output measurements, the plant’s current state, and the plant’s model to:

• Calculate, over a finite horizon, a future control sequence that optimizes a given performance index and satisfies constraints on the control action;
• Use the first control in the sequence as the plant’s input.

The MPC strategy is illustrated in Figure 16, where $N_p$ is the prediction horizon, $u(t+k\mid t)$ is the predicted control action at $t+k$ given $u\left(t\right)$. Similarly, $y(t+k\mid t)$ is the predicted output at $t+k$ given $y\left(t\right)$.

We consider a discretized model of a dynamic system of the form of Equation (19).

$$\begin{array}{cc}\hfill \mathit{x}(k+1)& =\mathbf{\Phi }\mathit{x}\left(k\right)+\mathbf{\Gamma }\mathit{u}\left(k\right)\hfill \\ \hfill \mathit{y}\left(k\right)& =\mathit{C}\mathit{x}\left(k\right)\hfill \end{array}$$

(19)

where $\Phi \in {\mathbb{R}}^{n\times n},\Gamma \in {\mathbb{R}}^{n\times m}$, and $C\in {\mathbb{R}}^{p\times n}$. Applying the backward difference operator, $\Delta x(k+1)=\mathit{x}(k+1)-x\left(k\right)$ is derived Equation (20).

$$\begin{array}{cc}\hfill \Delta \mathit{x}(k+1)& =\Phi \Delta \mathit{x}\left(k\right)+\Gamma \Delta \mathit{u}\left(k\right)\hfill \\ \hfill \Delta \mathit{y}(k+1)& =\mathit{y}(k+1)-\mathit{y}\left(k\right)\hfill \\ \hfill & =\mathit{C}\mathit{x}(k+1)-\mathit{C}\mathit{x}\left(k\right)\hfill \\ \hfill & =\mathit{C}\Delta \mathit{x}(k+1)\hfill \end{array}$$

(20)

where $\Delta \mathit{u}(k+1)=\mathit{u}(k+1)-\mathit{u}\left(k\right)$. With further algebraic manipulation it is obtained the matrix form of augmented state form dynamics in Equation (21).

$$\begin{array}{cc}\hfill {\mathit{x}}_a(k+1)\left[\begin{array}{c}\Delta \mathit{x}(k+1)\\ \mathit{y}(k+1)\end{array}\right]& =\left[\begin{array}{cc}\Phi & O\\ C\Phi & {\mathit{I}}_p\end{array}\right]\left[\begin{array}{c}\Delta \mathit{x}\left(k\right)\\ \mathit{y}\left(k\right)\end{array}\right]+\left[\begin{array}{c}\Gamma \\ C\Gamma \end{array}\right]\Delta \mathit{u}\left(k\right)={\mathbf{\Phi }}_a{\mathit{x}}_a\left(k\right)+{\mathbf{\Gamma }}_a\Delta \mathit{u}\left(k\right)\hfill \\ \hfill \mathit{y}\left(k\right)& =\left[\begin{array}{cc}O\hfill & {\mathit{I}}_p\hfill \end{array}\right]\left[\begin{array}{c}\Delta \mathit{x}\left(k\right)\\ \mathit{y}\left(k\right)\end{array}\right]={\mathit{C}}_a{\mathit{x}}_a\left(k\right)\hfill \end{array}$$

(21)

Suppose now that the state vector ${\mathit{x}}_a$ at each sampling time, k, is available to us. Our control objective is to construct a control sequence as the follows.

$$\Delta \mathit{u}\left(k\right),\Delta \mathit{u}(k+1),\dots ,\Delta \mathit{u}\left(k+N_p-1\right)$$

(22)

where $N_p$ is the prediction horizon, such that a given cost function and constraints are satisfied. The above control sequence will result in a predicted sequence of the augmented state vectors.

$${\mathit{x}}_a(k+1\mid k),{\mathit{x}}_a(k+2\mid k),\dots ,{\mathit{x}}_a\left(k+N_p\mid k\right)$$

(23)

which can then be used to compute predicted sequence of the plant’s outputs.

$$\mathit{y}(k+1\mid k),\mathit{y}(k+2\mid k),\dots ,\mathit{y}\left(k+N_p\mid k\right)$$

(24)

Using the above information it is possible to compute the control sequence of Equation (22) and then apply $\mathit{u}\left(k\right)$ to the plant to generate $\mathit{x}(k+1)$. Repeating the process again, using $\mathit{x}(k+1)$ as an initial condition to compute $\mathit{u}(k+1)$, and so on.

Most of the work in which MPC is used to reduce cogging torque, the approach of constructing the control sequence assuming known linearized model parameters is used Since the linearized model is derived by approximation from Equations (12) and (18), it contains the information about the extrapolated cogging model.

In the following, it is reported the approach to construct $\mathit{u}\left(k\right)$ given $\mathit{x}\left(k\right)$. Figure 17 represents schematically the MPC architecture. Using the plant model parameters and the measurement of ${\mathit{x}}_a\left(k\right)$ is evaluated the augmented states over the prediction horizon successively applying the recursion formula, obtaining the set of equations in Equations (25).

$$\begin{array}{cc}\hfill {\mathit{x}}_a(k+1\mid k)=& {\mathbf{\Phi }}_a{\mathit{x}}_a\left(k\right)+{\mathbf{\Gamma }}_a\Delta \mathit{u}\left(k\right)\hfill \\ \hfill {\mathit{x}}_a(k+2\mid k)=& {\mathbf{\Phi }}_a{\mathit{x}}_a(k+1\mid k)+{\mathbf{\Gamma }}_a\Delta \mathit{u}(k+1)\hfill \\ \hfill & ={\mathbf{\Phi }}_a^2{\mathit{x}}_a\left(k\right)+{\mathbf{\Phi }}_a{\mathbf{\Gamma }}_a\Delta \mathit{u}\left(k\right)+{\mathbf{\Gamma }}_a\Delta \mathit{u}(k+1)\hfill \\ \hfill & ⋮\hfill \\ \hfill {\mathit{x}}_a\left(k+N_p\mid k\right)=& {\mathbf{\Phi }}_a^{N_p}{\mathit{x}}_a\left(k\right)+{\mathbf{\Phi }}_a^{N_p-1}{\mathbf{\Gamma }}_a\Delta \mathit{u}\left(k\right)+\cdots +{\mathbf{\Gamma }}_a\Delta \mathit{u}\left(k+N_p-1\right)\hfill \end{array}$$

(25)

In matrix form, it is possible to compact as in Equation (26).

$$\left[\begin{array}{c}{\mathit{x}}_a(k+1\mid k)\\ {\mathit{x}}_a(k+2\mid k)\\ ⋮\\ {\mathit{x}}_a\left(k+N_p\mid k\right)\end{array}\right]=\left[\begin{array}{c}{\mathbf{\Phi }}_a\\ {\mathbf{\Phi }}_a^2\\ ⋮\\ {\mathbf{\Phi }}_a^{N_p}\end{array}\right]{\mathit{x}}_a\left(k\right)+\left[\begin{array}{cccc}{\Gamma }_a& & & \\ {\mathbf{\Phi }}_a{\Gamma }_a& {\Gamma }_a& & \\ ⋮& & \ddots & \\ {\mathbf{\Phi }}_a^{N_p-1}{\Gamma }_a& & \cdots & {\Gamma }_a\end{array}\right]\left[\begin{array}{c}\Delta \mathit{u}\left(k\right)\\ \Delta \mathit{u}(k+1)\\ ⋮\\ \Delta \mathit{u}\left(k+N_p-1\right)\end{array}\right]$$

(26)

$$\begin{array}{cc}\hfill \mathit{Y}=\left[\begin{array}{c}\mathit{y}(k+1\mid k)\\ \mathit{y}(k+2\mid k)\\ ⋮\\ \mathit{y}\left(k+N_p\mid k\right)\end{array}\right]& =\left[\begin{array}{c}{\mathit{C}}_a{\mathit{x}}_a(k+1\mid k)\\ {\mathit{C}}_a{\mathit{x}}_a(k+2\mid k)\\ ⋮\\ {\mathit{C}}_a{\mathit{x}}_a\left(k+N_p\mid k\right)\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}{C}_a{\Phi }_a\\ C_a{\Phi }_a^2\\ ⋮\\ C_a{\Phi }_a^{N_p}\end{array}\right]x_a\left(k\right)\hfill \\ \hfill & +\left[\begin{array}{cccc}{C}_a{\Gamma }_a& & & \\ C_a{\Phi }_a{\Gamma }_a& C_a{\Gamma }_a& & \\ ⋮& & \ddots & \\ C_a{\Phi }_a^{N_p-1}{\Gamma }_a& & \cdots & C_a{\Gamma }_a\end{array}\right]\left[\begin{array}{c}\Delta \mathit{u}\left(k\right)\\ \Delta \mathit{u}(k+1)\\ ⋮\\ \Delta \mathit{u}\left(k+N_p-1\right)\end{array}\right]\hfill \\ & =\mathit{W}{\mathit{x}}_a\left(k\right)+\mathit{Z}\Delta \mathit{u}\left(k\right)\hfill \end{array}$$

(27)

Equation (27) describes the dependence of the sequence of future output vectors, in the prediction horizon, as a function of the increased state vectors, in that prediction horizon, and as a function of the change in the control vector. This equation is decisive in solving the optimization problem, which is formalized in the following.

$$\begin{array}{c}J(\Delta \mathit{U})=\frac{1}{2}{\left({\mathit{r}}_p-\mathit{Y}\right)}^{\top }\mathit{Q}\left({\mathit{r}}_p-\mathit{Y}\right)+\frac{1}{2}\Delta {\mathit{U}}^{\top }\mathit{R}\Delta \mathit{U}\\ {\mathit{Y}}^{min}\le \mathit{Y}\le {\mathit{Y}}^{max}\\ {\mathit{U}}^{min}\le \mathit{U}\le {\mathit{U}}^{max}\end{array}$$

(28)

Equation (28) represents the cost functional that is minimized to derive the predictive sequence of optimal control, according to the criterion defined precisely by $J(\Delta u)$.

$$\begin{array}{cc}\hfill \Delta \mathit{u}\left(k\right)& =\stackrel{N_p\mathrm{block}\mathrm{matrices}}{\overbrace{\left[\begin{array}{cc}{\mathit{I}}_m\hfill & \mathit{O}\cdots \mathit{O}\hfill \end{array}\right]}}{\left(\mathit{R}+{\mathit{Z}}^{\top }\mathit{Q}\mathit{Z}\right)}^{-1}{\mathit{Z}}^{\top }\mathit{Q}\left({\mathit{r}}_p-\mathit{W}{\mathit{x}}_a\right)\hfill \\ \hfill & ={\mathit{K}}_{\mathit{r}}{\mathit{r}}_p-{\mathit{K}}_{\mathit{x}}\Delta \mathit{x}\left(k\right)-{\mathit{K}}_{\mathit{y}}\mathit{y}\left(k\right)\hfill \end{array}$$

(29)

For the control vector to be optimal and meet all operational constraints on the control and output variables, minimization of the functional is associated with an optimizer based, for example, on gradient descent algorithm or Newtonian methods.

As can be understood from the procedure for constructing the control vector, MPC actually acts as a LQR (Linear-Quadratic-Regulator) controller in which it is possible to explicitly insert operational constraints on the controlled and control variables.

This represents an enormous advantage over the classical optimal control approach, as the control system solution can take into account the realistic constraints of the physical system to be controlled, and furthermore, there is the certainty that the control vector provides (sub-)optimal action in each of its components, being the result of evaluation over successive time windows.

On the other hand, MPC requires a very high computational effort, which is not always suitable for micro-controller-based embedded systems.

This is because at each step of the algorithm, an internal simulation is run, which exploits the mathematical model of the physical process to predict behavior and to be able to calculate a control vector, which will be optimal over that simulated time window.

Thus, the system on which the algorithm is integrated must be able to simulate $N_p$ steps of the process model, within a single numerical integration step.

Another small disadvantage is that MPC is still an optimal control technique based on the mathematical model, so it is very sensitive to model uncertainties.

It is, however, very much used in the context of cogging torque reduction, as the ability to correctly model the electrical machine and the cogging phenomenon is quite optimized, leaving little room for model uncertainties that the feedback control may not be able to handle [32,33,34,35].

4.2. Feedback Linearization Control

Another widely used control technique is Feedback Linearization Control (FLC), which takes advantage of differential geometry theory to directly handle model dynamics in a nonlinear form.

In order to apply the control vector design technique by Feedback Linearization, it is necessary that the mathematical model of the mechatronic system of interest be in the state form called ”similar in control”, as given in Equation (30), where the vector field $f\left(x\right)$ is called drift vector, while the $g_k\left(x\right)$ is the control vectors field.

$$\begin{array}{c}\frac{dx}{dt}=F(x,u)=f\left(x\right)+\sum _k{g}_k\left(x\right)u_k;x_0=x\left(t_0\right)\\ y_l=H_l(x,u)=h_l\left(x\right)\end{array}$$

(30)

Being able to handle the inherent non-linearities of the mathematical model in the generic state form of Equation (30), the resulting control law by definition contains information about the cogging pair, via the model chosen to represent it.

$$\begin{array}{c}\frac{d{h}_i}{dt}=\frac{\partial h_i}{\partial x}\frac{\partial x}{\partial t}=\frac{\partial h_i}{\partial x}\left(\overrightarrow{f}+\sum _{k=1}^{n_u}{\overrightarrow{g}}_k{u}_k\right)=\frac{\partial h_i}{\partial x}\overrightarrow{f}=L_f{h}_i\\ ...\\ \frac{d^{{\mu }_i}{h}_i}{d{t}^{{\mu }_i}}=\frac{d}{dt}\left({L_f}^{{\mu }_i-1}\right)=\frac{\partial }{\partial x}\left({L_f}^{{\mu }_i-1}\right)\left(\overrightarrow{f}+\sum _{k=1}^{n_u}{\overrightarrow{g}}_k{u}_k\right)={L_f}^{{\mu }_i}{h}_i+\sum _{k=1}^{n_u}{L}_{g_k}{L_f}^{{\mu }_i-1}{h}_i{u}_k\end{array}$$

(31)

The operative procedure for applying feedback linearization involves deriving the control outputs as many times as necessary to obtain expressions in which the contributions of the control variables appear. In Equation (31), the expression of the derivative ${\mu }_i$ for the $i$ control output is given in general form. We denote the relative degree for the output $i$ by ${\mu }_i$, with the condition that $\sum {\mu }_i\le n_x$.

$$\begin{array}{c}\left[\begin{array}{c}{L_f}^{{\mu }_1}{h}_1\\ {L_f}^{{\mu }_2}{h}_2\\ ...\\ {L_f}^{{\mu }_l}{h}_l\end{array}\right]+\left[\begin{array}{ccc}{L}_{g_1}{L_f}^{{\mu }_1-1}{h}_1& ...& L_{g_m}{L_f}^{{\mu }_1-1}{h}_1\\ L_{g_1}{L_f}^{{\mu }_2-1}{h}_2& ...& L_{g_m}{L_f}^{{\mu }_2-1}{h}_2\\ ...& ...& ...\\ L_{g_1}{L_f}^{{\mu }_l-1}{h}_l& ...& L_{g_m}{L_f}^{{\mu }_1-l}{h}_l\end{array}\right]\overrightarrow{u}=\overrightarrow{v}=\overrightarrow{\Gamma }(\overrightarrow{x})+\Sigma (\overrightarrow{x})\overrightarrow{u}\\ \\ \overrightarrow{u}={\Sigma }^{+}(\overrightarrow{x})\left(\overrightarrow{v}-\overrightarrow{\Gamma }(\overrightarrow{x})\right)+\left(I-{\Sigma }^{+}(\overrightarrow{x})\Sigma (\overrightarrow{x})\right)\lambda \end{array}$$

(32)

Proceeding with the derivation of each control output, in general we obtain the matrix expression given in Equation (32), where with $L_{g_i}{L}_f{h}_j(\overrightarrow{x})=\frac{\partial }{\partial \overrightarrow{x}}\left(\frac{\partial h_j}{\partial \overrightarrow{x}}\overrightarrow{}f\right){\overrightarrow{g}}_i$ is the Lie derivative of the function $h_j$ in the directions of the vector fields $\overrightarrow{f}$ and ${\overrightarrow{g}}_i$, respectively.

$$\begin{array}{c}\dot{\overrightarrow{z}}=\left[\begin{array}{ccccc}{A}_1& 0& 0& ...& 0\\ 0& A_2& 0& ...& 0\\ ...& ...& ...& ...& ...\\ 0& 0& 0& ...& A_l\end{array}\right]\overrightarrow{z}+\left[\begin{array}{cccc}{B}_1& 0& ...& 0\\ 0& B_2& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& B_l\end{array}\right]\overrightarrow{v}\\ \\ \overrightarrow{z}=\left[\begin{array}{c}{\overrightarrow{z}}_1\\ {\overrightarrow{z}}_2\\ ...\\ {\overrightarrow{z}}_l\end{array}\right];{\overrightarrow{z}}_i=\left[\begin{array}{c}{h}_i\\ L_f{h}_i\\ ...\\ {L_f}^{{\mu }_i-1}\end{array}\right];A_i=\left[\begin{array}{cccccc}0& 1& 0& 0& ...& 0\\ 0& 0& 1& 0& ...& 0\\ ...& ...& ...& ...& ...& ...\\ 0& 0& 0& 0& ...& 1\\ 0& 0& 0& 0& ...& 0\end{array}\right];B_i=\left[\begin{array}{c}0\\ 0\\ ...\\ 0\\ 1\end{array}\right]\end{array}$$

(33)

The feedback linearization procedure results in a change of coordinates in which the dynamics of the new state vector is linear, as shown in Equations (33). Note that the state representation in addition to being linear represents a chain of integrators, consequently the pair $(A_i,B_i)$ turns out to be completely reachable/controllable $\forall i$.

$$\overrightarrow{\tilde{z}}=\left[\begin{array}{c}\overrightarrow{z}\\ \overrightarrow{\sigma }\left(\overrightarrow{x}\right)\end{array}\right]with\overrightarrow{\sigma }\left(\overrightarrow{x}\right)s.t\frac{\partial \overrightarrow{\tilde{z}}}{\partial \overrightarrow{x}}\ne 0$$

(34)

In general, a change of basis with reduction of the cardinality of the state space is obtained. Formally, this requires that certain mathematical conditions are fulfilled, which define the criterion of zero dynamics [36]. The first condition is given in Equation (34), where we impose that the Jacobian of the base change is formally lawful (invertible). This means that the completion $\overrightarrow{\sigma }(\overrightarrow{x})\in R^{n_x-\sum {\mu }_i}$ will have to be constructed appropriately to satisfy the condition.

$$\dot{\overrightarrow{\sigma }}\left(\overrightarrow{x}\right)=\overrightarrow{\gamma }\left(\overrightarrow{z},\overrightarrow{\sigma }\right)+\overrightarrow{\xi }\left(\overrightarrow{z},\overrightarrow{\sigma }\right)v$$

(35)

The completion vector $\overrightarrow{\sigma }\left(\overrightarrow{x}\right)$ will in general have a non-linear state representation, dependent on both the new and old state variables and also on the new control vector, as given in Equation (35).

$$L_{g_k}{\sigma }_i=0\forall i,k\to \dot{\overrightarrow{\sigma }}\left(\overrightarrow{x}\right)=\overrightarrow{\gamma }\left(\overrightarrow{z},\overrightarrow{\sigma }\right)\to \dot{\overrightarrow{\sigma }}\left(\overrightarrow{x}\right)=\overrightarrow{\gamma }\left(0,\overrightarrow{\sigma }\right)A.S.$$

(36)

The second condition, given in Equation (36), serves to eliminate the contribution of the new control vector v from the dynamics of the vector $\overrightarrow{\sigma }$. In this way, it is possible to implement the zero-dynamics criterion, which guarantees us that even in the case of a reduction of the cardinality of the state space, the vector v constructed by means of a feedback linearization technique is able to asymptotically stabilize even the state variables that serve only to make the base change formally lawful. In the above equation, “A.S” means asymptotically stable.

The FLC-based control synthesis approach is schematized in Figure 18. Note that two control “loops” can be identified, one external and one internal. The inner one consists of the nonlinear terms based on the Lie derivative calculus, shown earlier, which is intended to map the control action of the outer loop into the representation space of the nonlinear dynamical system. The outer loop exploits the change of coordinates to the linear representation domain. In fact, the outer loop is dedicated to reducing the error between the reference and the output of the system, and is realized by linear control techniques.

As can be seen from the operating procedure for constructing the control vector using the FLC technique, the greatest advantage of this method is that it can handle highly non-linear dynamic models, being able to include very realistic details in the model itself, such as the cogging torque in this particular case.

Some inconvenience arises when the relative degree of the system is much less than the cardinality of the state space associated with the starting model. In this case, one must choose a base change completion that is invertible, so as to make it formally acceptable.

However, it can be said that in practical cases it is always possible to construct performance outputs such that they return a relative degree equal to (or slightly less than) the dimension of the state vector of the initial non-linear model.

For electro-mechanical systems of industrial interest, such as in robotics and industrial automation, dynamic system models are also found to have suitable formal properties for the application of this control methodology, which is why it is one of the most widely used control techniques by designers of algorithms and control systems [37,38,39,40,41,42].

4.3. Resonant Control

Control techniques based on the concept of resonance are often used by designers to resolve and attenuate the presence of periodic disturbances, whose pulsation/frequency can be measured or estimated with reasonable accuracy. In fact, resonant type controllers are well suited to the rejection of additive disturbances in sinusoidal form, as is the case with cogging torque.

This is the reason why some works in the literature are based on the use of resonant techniques, such as PR (Proportional Resonant) and PIR (Proportional Integral Resonant). Since cogging torque is an additive disturbance compared to electro-magnetic disturbance with periodic comparing often analyzed by harmonic models, it proves to be a rather efficient technique under certain types of conditions.

The transfer function shown in Equation (37) represents the Laplace transform domain implementation (for SISO = Single-Input-Single-Output systems) of a PR (Proportional-Resonant) type controller.

$$G_C\left(s\right)=K_p+\frac{2K_{i}s}{s^2+{\omega }_0^2}$$

(37)

$K_p$ denotes the proportional gain, $K_i$ denotes the gain obtained when the additive disturbance on the output has exactly the pole pulsation of the transfer function ${\omega }_0$, known as the resonance pulsation or maximum feedback gain.

In Equation (38) is shown the version that is most often taken into account for integration convenience. Since the previous equation contains complex conjugate poles, in order to facilitate discretization and thus implementation in low-level code, a damping factor is often inserted, which also improves the controller’s response, making it less abrupt and consequently requiring less control effort.

$$G_C\left(s\right)=G_{Cp}\left(s\right)+G_{Cr}\left(s\right)=K_p+\frac{2K_i{\omega }_{c}s}{s^2+2{\omega }_{c}s+{\omega }_0^2}$$

(38)

The pulse ${\omega }_c$ is called the cut-off pulse and differs from ${\omega }_0$ obviously, in practice ${\omega }_c<{\omega }_0$. Having inserted a damping factor, the disturbance pulse and the resonant filter within the control now differ, so the feedback gain will not be maximum at the same time as the disturbance pulse. Theoretically, disturbance rejection is less efficient than the ideal PR case, but in practice we find that performance is virtually equivalent, also benefiting from smoother control action.

Equation (39) represents a possible implementation of the resonant PR controller by discretization. In particular, by simply using a bi-linear transformation, one obtains a discrete system that is not strictly proper (which in the discrete domain continues to make physical sense).

$$G_{Cr}\left(z\right)=\frac{Y\left(z\right)}{E\left(z\right)}=\frac{a_1\left(1-z^{-2}\right)}{b_0+b_1{z}^{-1}+b_2{z}^{-2}}\mathrm{with}\begin{array}{cc}\hfill & a_1=4K_i{T}_s{\omega }_c\hfill \\ \hfill & b_0=T_s^2{\omega }_0^2+4T_s{\omega }_c+4\hfill \\ \hfill & b_1=2T_s^2{\omega }_0^2-8\hfill \\ \hfill & b_2=T_s^2{\omega }_0^2-4T_s{\omega }_c+4\hfill \end{array}$$

(39)

Applying the inverse Z-transform yields the finite difference equation (or recursive equation) shown in Equation (40). The implementation on a microcontroller therefore requires memory to be kept of two steps prior to the current one.

$$y\left(k\right)=\frac{1}{b_0}\left[a_1·e\left(k\right)-a_1·e(k-2)-b_1·y(k-1)-b_2·y(k-2)\right]$$

(40)

Figure 19 shows how to realize a block diagram equivalent to the PR controller in the form of a Z-transformed transfer function, Simulink environment, using only ’native’ blocks.

The tuning of resonant controller parameters is quite easy to achieve in practice, which is why it is among the most frequently used techniques by control algorithm designers for this type of problem. The most commonly used technique is that of forced oscillations, often accompanied by the classic Ziegler–Nichols table [43,44,45,46,47,48]. Due to the ease of development and integration on an embedded platform, it is also one of the most widely used control techniques in power and control electronics in general [49,50,51], not only in electrical drives.

4.4. Others Control Techniques

Few other works in the literature exploit adaptive control techniques for cogging torque reduction in servo drives for mechatronic systems [52,53,54,55].

Adaptive control in general can be divided into direct approach and indirect approaches:

• Direct Adaptive Control: in this case, the mathematical model of the physical system is taken as known and the control action is adapted by going to change its online parameters;
• Indirect Adaptive Control: in this case, a simplified model, such as a linearized version, is used as a basis, going to modify its parameters based on the error between the actual measurements and the model’s prediction, also modifying a posterior the controller parameters that must be adapted accordingly.

Figure 20 shows the principle diagrams of both approaches of adaptive control. In both cases, it is possible to derive a control law that incorporates cogging torque information, reason why it was deemed appropriate to include this approach among the techniques that can be practically used.

In the case of direct adaptive control, one of the cogging pair models previously discussed can be exploited. To exploit online adaptive paradigms usually use error-corrector learning algorithms such as gradient descent, which work best on linear models. So in the case of indirect adaptive control, if the estimation of cogging torque-related parameters is based on the linearized model, the compensation may not be as efficient as in the direct case.

Very few works in the literature exploit the Sliding Mode control technique instead, which is classified as variable structure control [56,57]. It is based on the mathematical concept of region of attraction so as to derive a control law that typically depends on the sign of the hyperplane describing that region of attraction.

The main problem with this control technique is that it works well when the system model has slight non-linearities and a relative degree (the number of times the output must be derived to obtain an expression containing the control variables) of unity. It is used side-by-side with other types of controllers because, in any case, it is based on a mathematical model of the motor in which it is actually possible to incorporate the cogging torque information to be compensated by the resulting control action.

4.5. Final Considerations

4.5.1. Model Predictive Control

Main advantages:

• Easy way of dealing with constraints on controls and states;
• High performance controllers and accurate;
• No need to generate solutions for the whole time-horizon;
• Flexibility: managing any model, any optimal objective function;
• Includes cogging torque information directly in the control law.

Main disadvantages:

• High computational complexity (poorly suited to typical embedded systems);
• Problems of robustness with respect to uncertainties in the reference mathematical model;
• Strict dependence on the dynamic model.

4.5.2. Feedback Linearization Control

Main advantages:

• Management of highly non-linear models;
• Joint use of other highly effective techniques on stationary linear systems;
• Fully algebraic control law (no on-line recursion required);
• Includes information on cogging torque through the most accurate model possible (optimizing compensation);
• Relative simplicity of implementation;
• Robust respect to the model parameters uncertainty.

Main disadvantages:

• Strict dependence on the mathematical modeling;
• Does not inherently manage operational constraints on dynamic variables.

4.5.3. Resonant Controller

Main advantages:

• Good ability to handle sinusoidal disturbances (as the cogging torque);
• Relative easy to tune;
• Simple to implement in embedded system.

Main disadvantages:

• Strongly dependent on the operating condition under which the control coefficients are chosen;
• Does not exploit completely the cogging torque modeling.

4.5.4. Adaptive and Sliding Mode Controllers

The main advantage is related to a relatively small computational complexity (more about the sliding mode technique).

The main disadvantages are:

• Inherent problems of convergence and numerical stability;
• Partial or ineffective use of the cogging torque model.

5. Conclusions

This paper proposed a discussion of how to apply the MBD approach in the context of the design of control systems and algorithms for cogging torque reduction, a rather hot topic for advanced mechatronic applications where high efficiency and performance is required, and especially a topic of current research on the control of permanent magnet electric machines.

During this review of the state of the art, the problem of torque cogging was analyzed in detail justifying the importance of addressing this issue through control algorithms in order to realize flexible and scalable solutions for various mechatronic applications and systems.

Popular mathematical modeling methodologies were presented with a view to being able to exploit cogging torque information directly in the design of control algorithms.

It was shown how to carry out mathematical modeling and in a simulated environment, of the components of the mechatronic system: the electric motor, presenting an overview of the dynamic model that integrates the cogging torque into the mechanical equilibrium; the modulation system, now based almost exclusively on SVM technique, presenting the theoretical principles and a possible integration in a simulated environment, with a view to successfully apply MBD validation of the control algorithms, in the most realistic simulation possible; the mechanical load part and the connection with the dynamics of the machine to derive the most complete mathematical model possible.

The most popular control techniques for this type of problem were then analyzed, in particular to those presented in the most recent literature articles and which showed the most promising results. The purpose is to give an overview of the algorithms by discussing their advantages and disadvantages, which were summarized in a table.

The analysis led to the statement that MPC and FLC are certainly the most efficient control algorithms. On the one hand, MPC incorporates the ability to handle the operational constraints of the problem, ensuring that the control action is physically achievable by the system components, and on the other hand, FLC’s ability to handle inherently nonlinear systems, the complete information about the cogging pair and to have an inherent robustness to parametric uncertainties.

It is expected that future work will exploit the strengths of these two control techniques, taking advantage of FLC’s architecture characterized by a linear outer loop and nonlinear inner loop. Since MPC works excellently with discretized linear systems, an innovative idea could be to transform the mathematical model representation that includes the cogging pair, with nonlinear dynamics, into an equivalently linear model, and to apply MPC in the outer loop, further ensuring that the final control action respects the physical constraints of the drive.