Study of Rotation Effect on Nanofluid Natural Convection and Heat Transfer by the Immersed Boundary-Lattice Boltzmann Method
Abstract
1. Introduction
2. Problem Statement and Mathematical Model
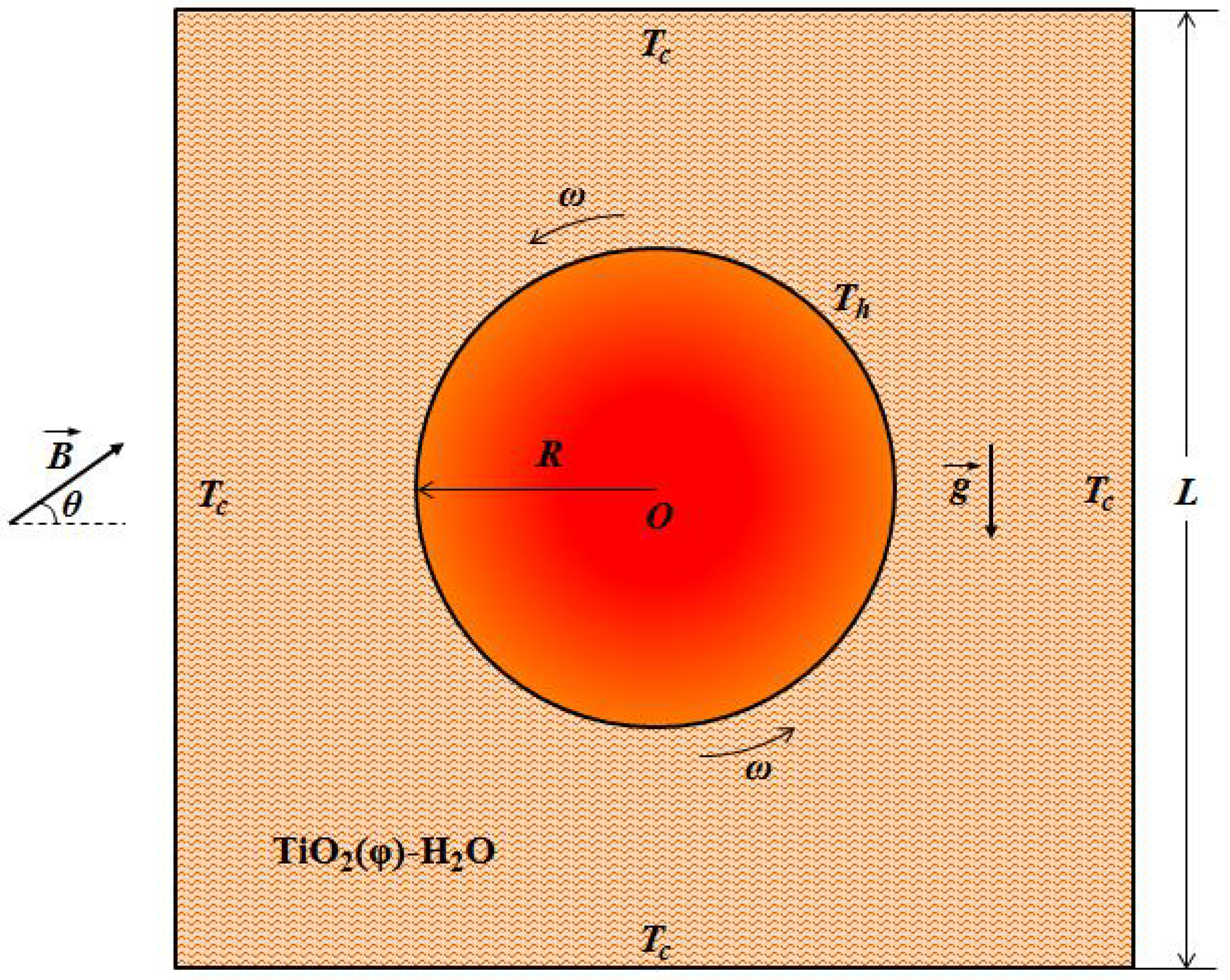
2.1. Problem Statement
2.2. Thermophysical Properties of TiO2-H2O
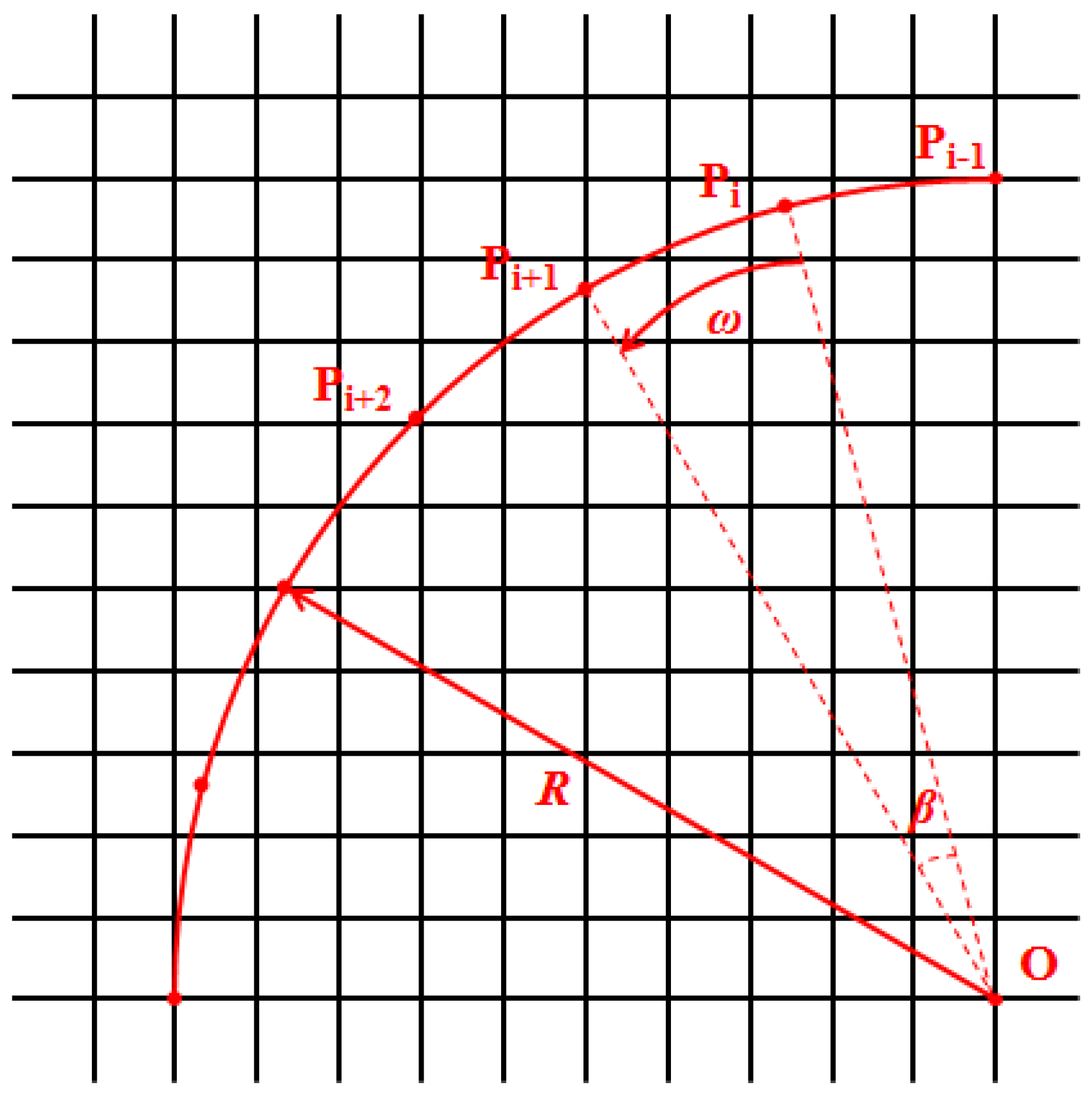
2.3. Immersed Boundary-Lattice Boltzmann Method (IB-LBM)
2.4. Minimum Angular Velocity and Dimensionless Rotational Speed
3. Code Validation and Grid Independence
4. Results and Discussion
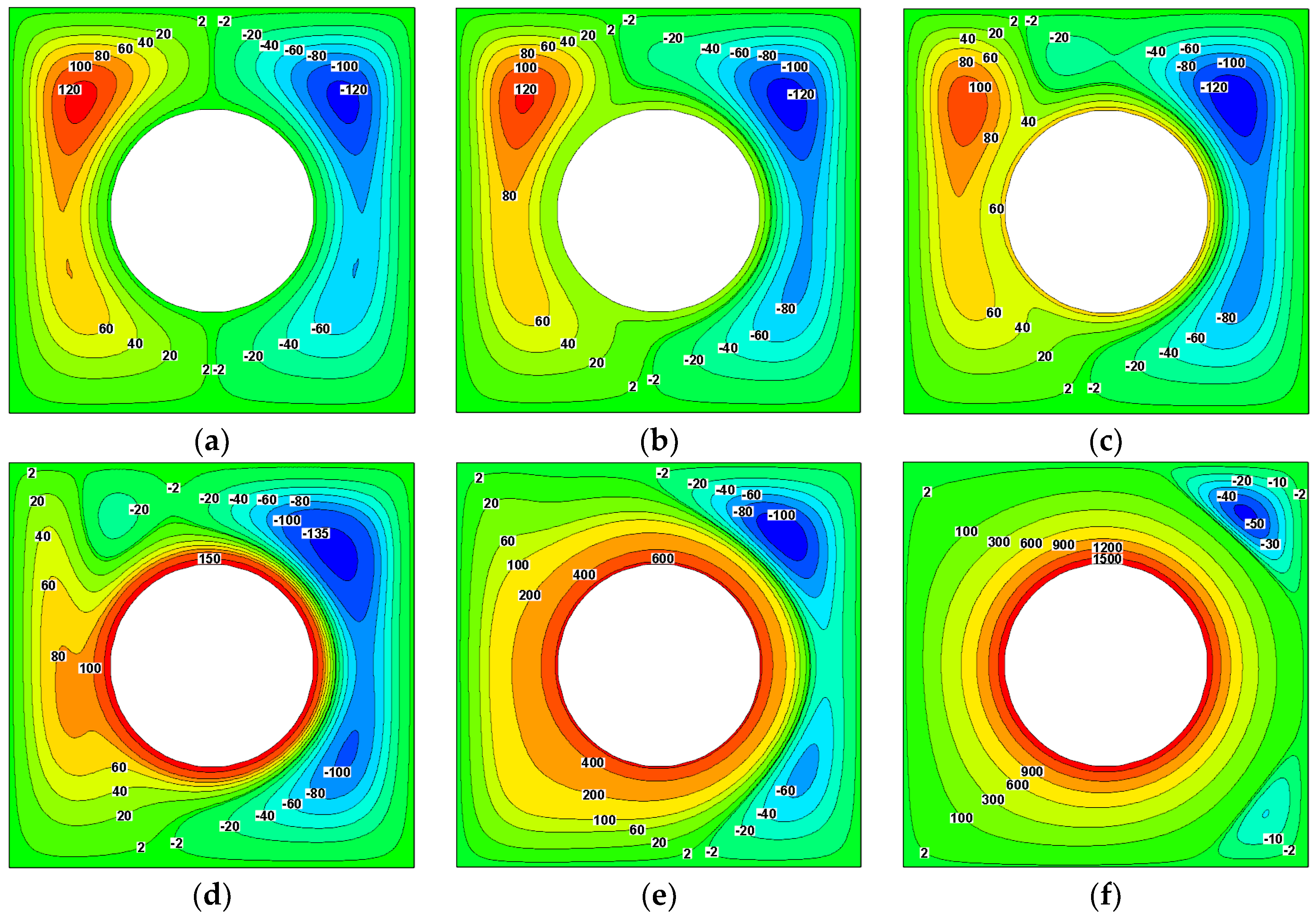
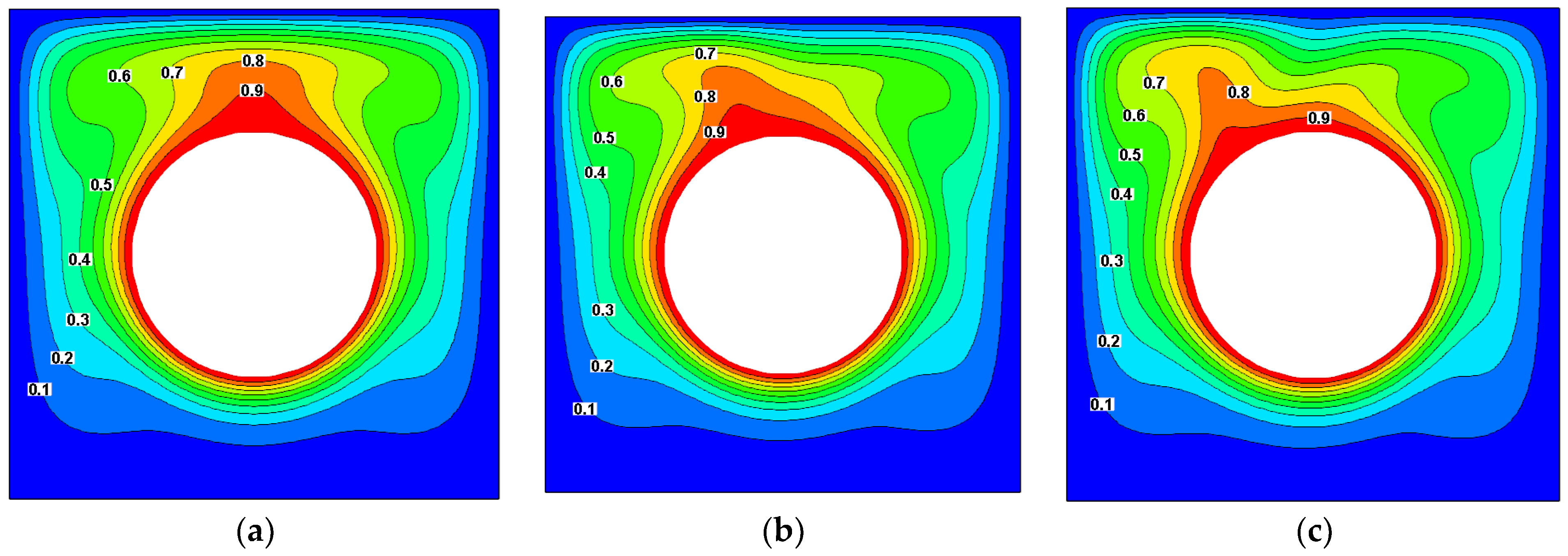
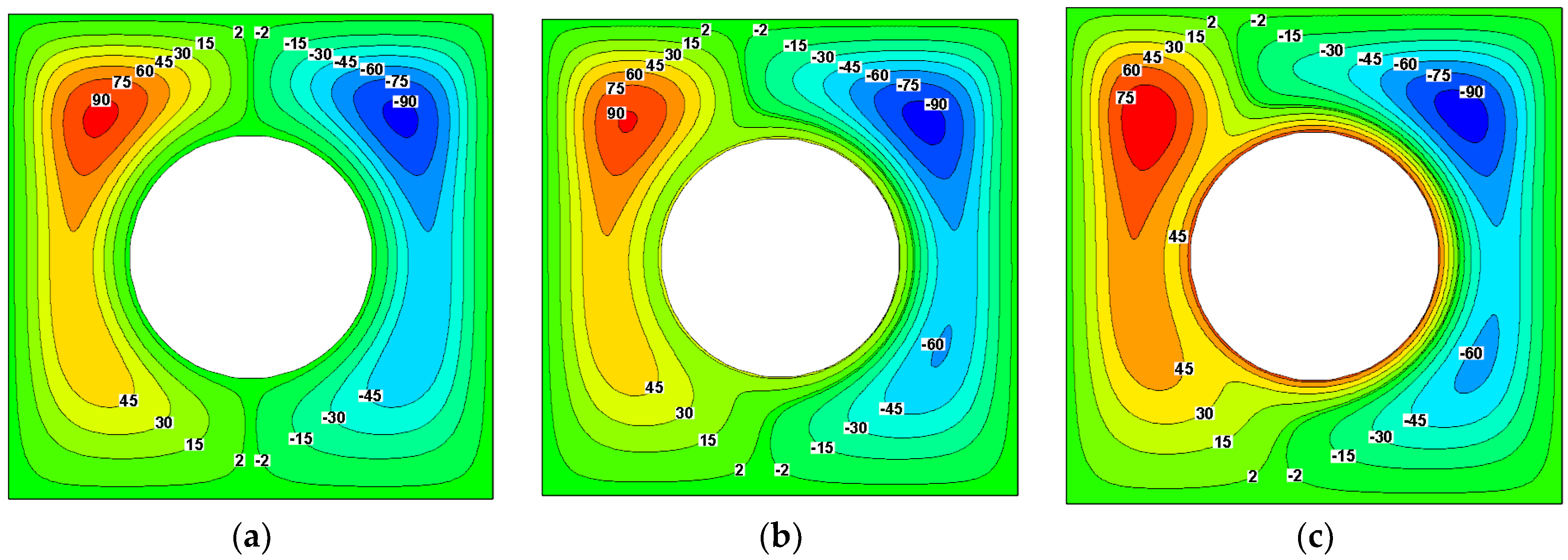
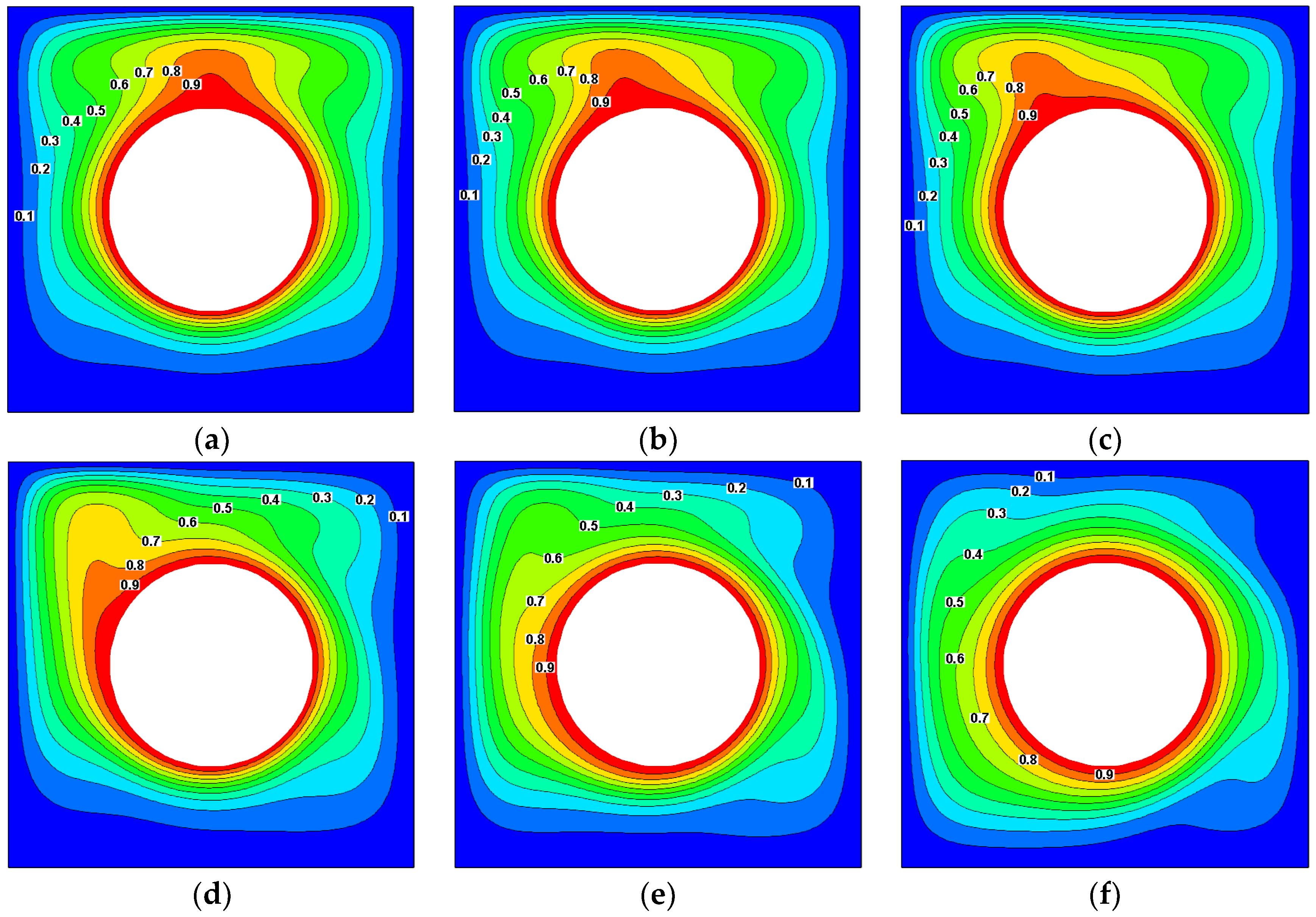
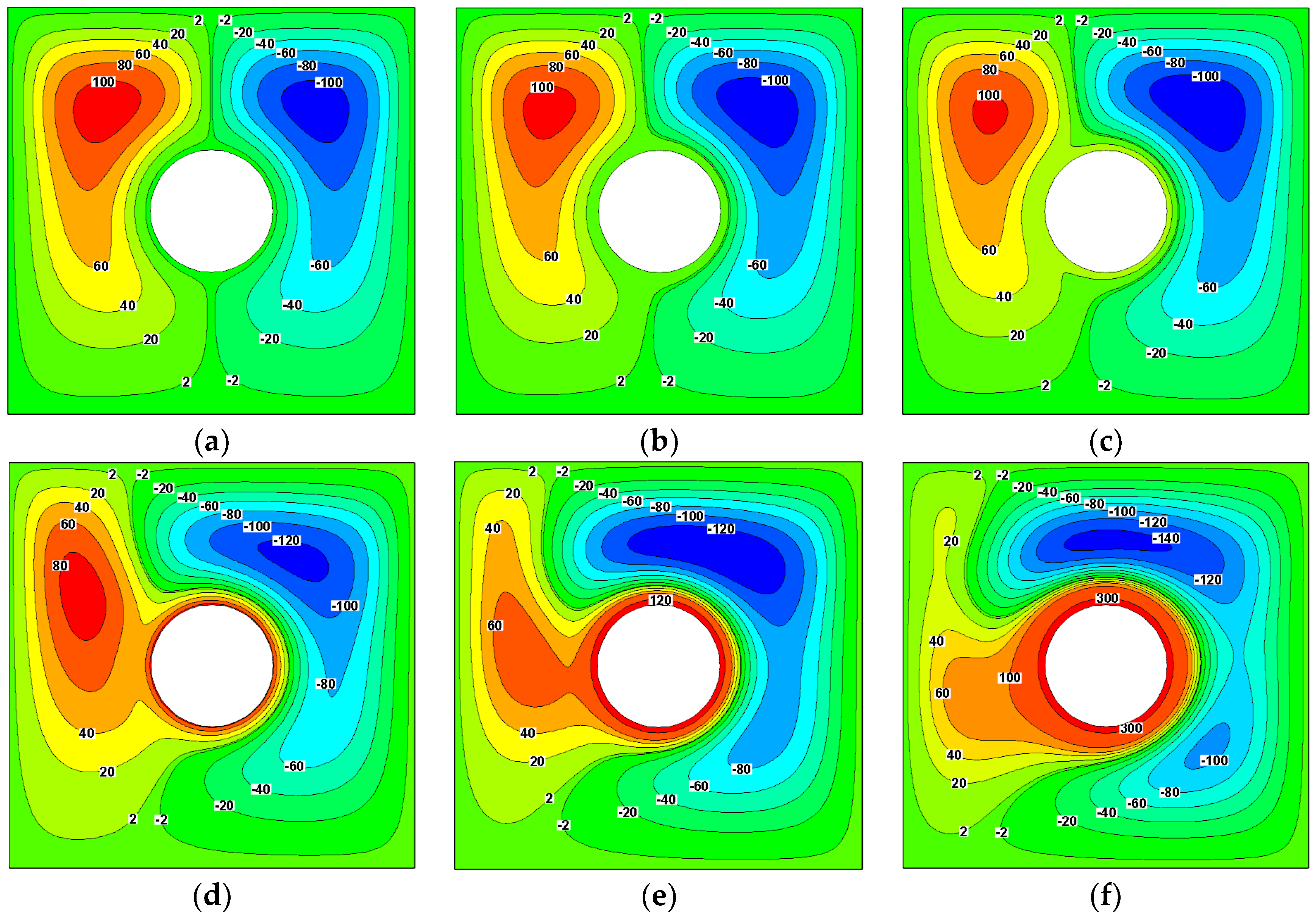
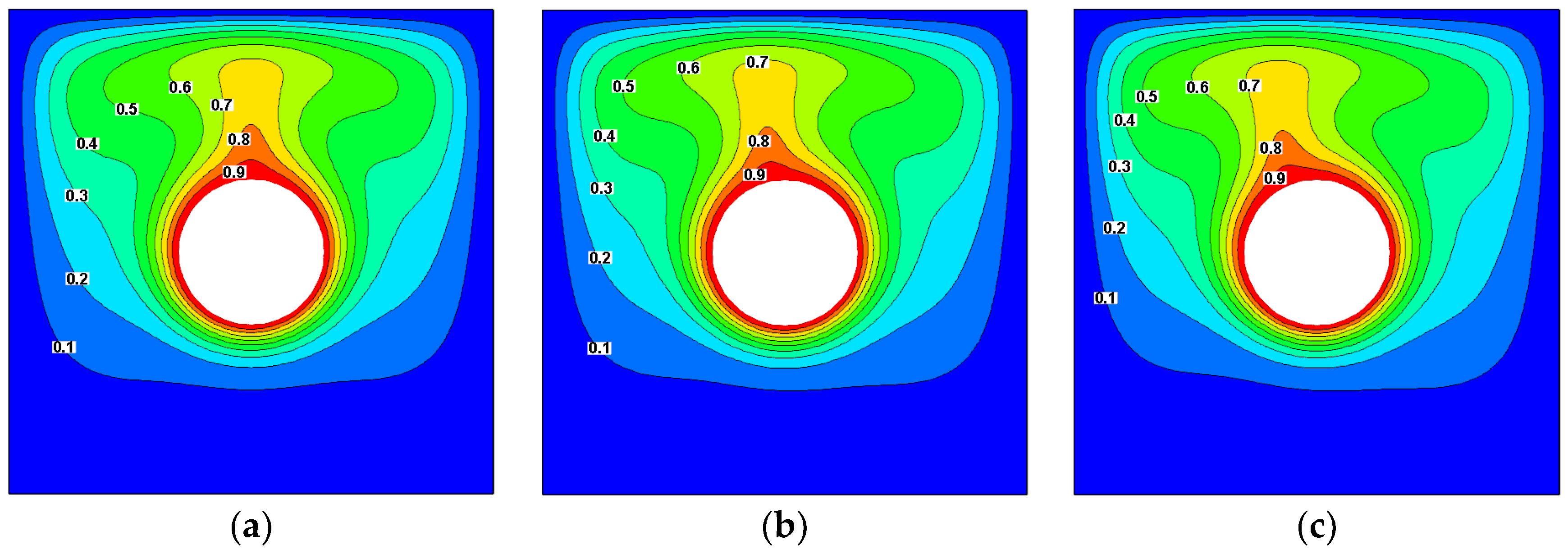
4.1. Effect of Rotational Speed on Streamlines and Isothermals
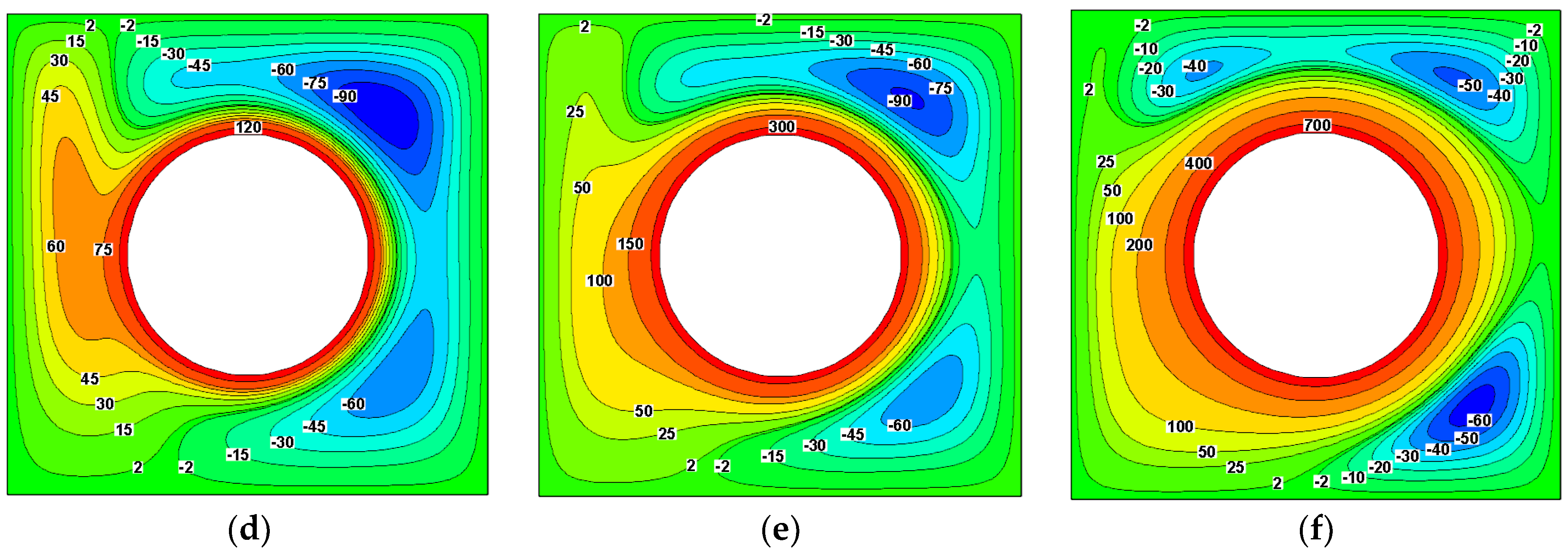
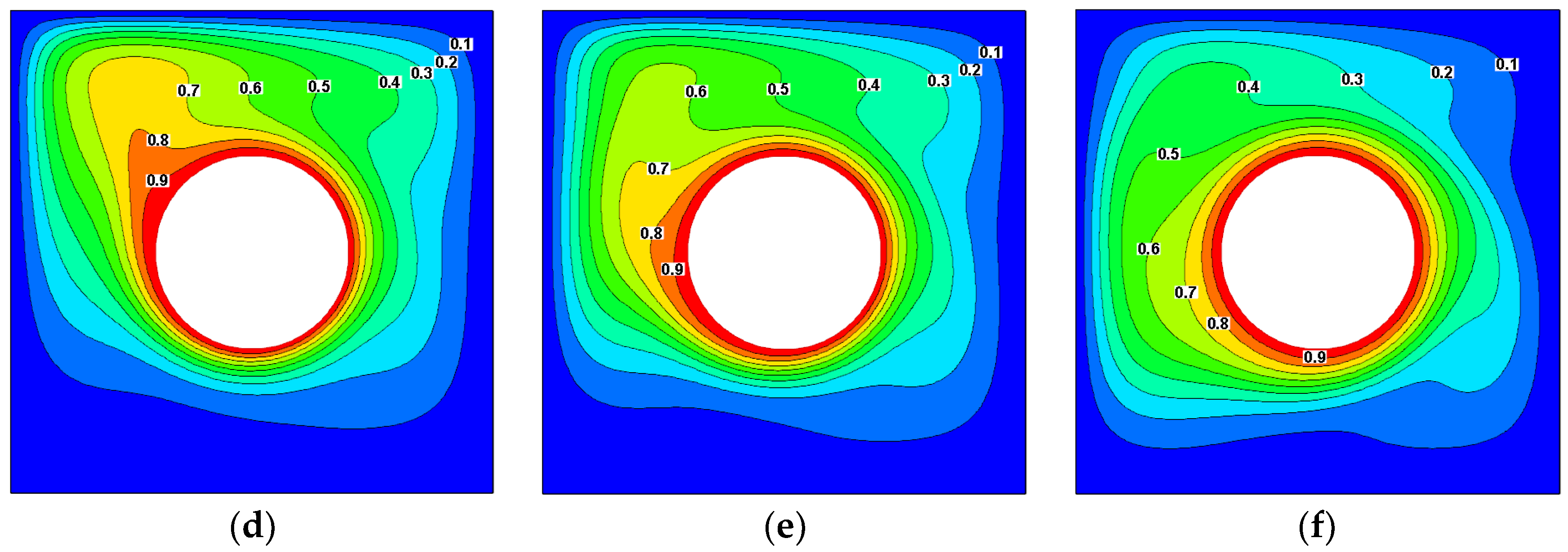
4.2. Effect of Magnetic Field on Streamlines and Isothermals
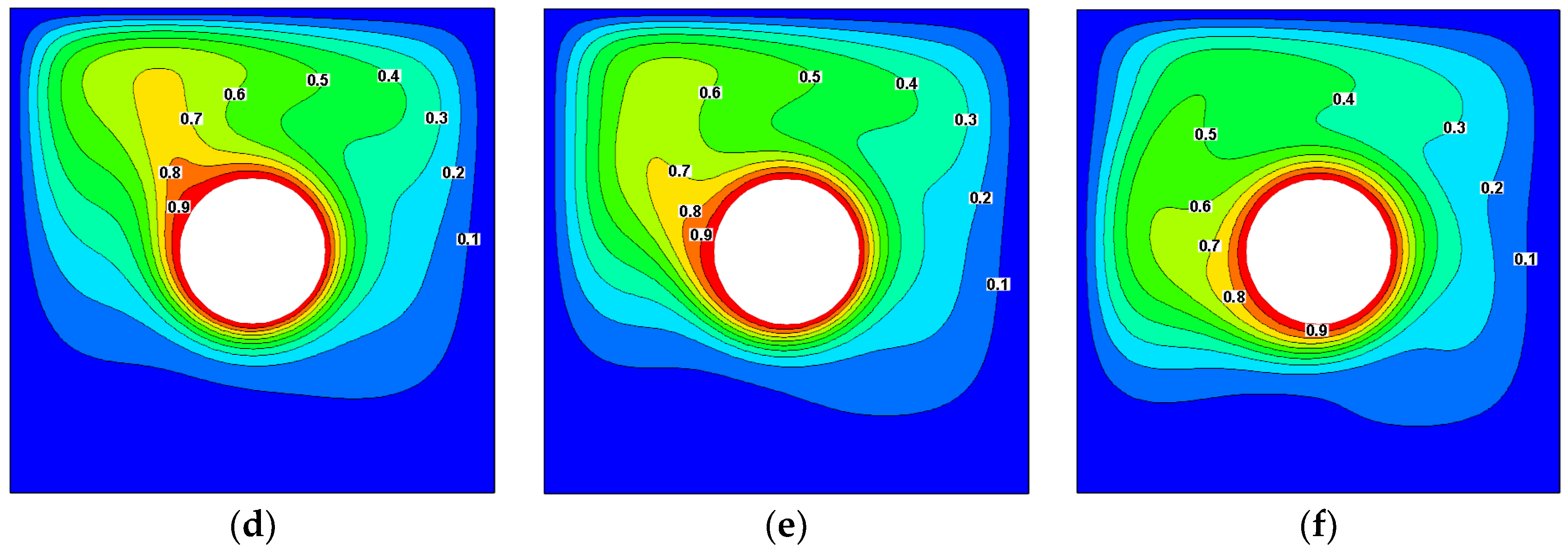
4.3. Effect of Aspect Ratio on Streamlines and Isothermals
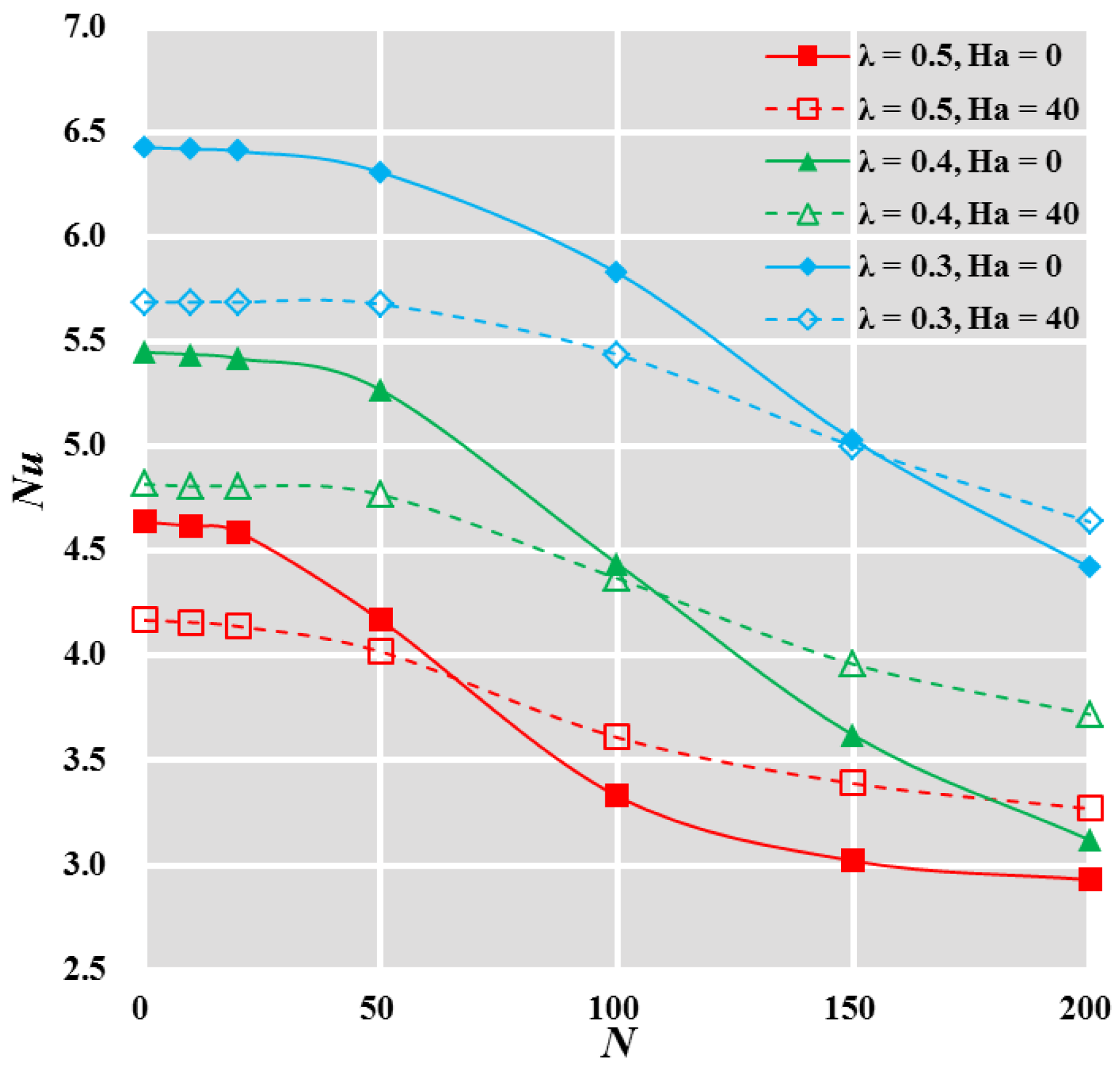
4.4. Effect of Rotational Speed on Average Nusselt Number
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ashorynejad, H.R.; Zarghami, A. Magnetohydrodynamics flow and heat transfer of Cu-water nanofluid through a partially porous wavy channel. Int. J. Heat Mass Transf. 2018, 119, 247–258. [Google Scholar] [CrossRef]
- Tayebi, T.; Chamkha, A.J. Entropy generation analysis due to MHD natural convection flow in a cavity occupied with hybrid nanofluid and equipped with a conducting hollow cylinder. J. Therm. Anal. Calorim. 2020, 139, 2165–2179. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Ismael, M.A.; Chamkha, A.J.; Hashim, I. Mixed convection of Al2O3-water nanofluid in a double lid-driven square cavity with a solid inner insert using Buongiorno’s two-phase model. Int. J. Heat Mass Transf. 2018, 119, 939–961. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Tayebi, T.; Chamkha, A.J.; Ganji, D.D. Natural convection analysis in a square enclosure with a wavy circular heater under magnetic field and nanoparticles. J. Therm. Anal. Calorim. 2020, 139, 661–671. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Ismael, M.A.; Chamkha, A.J.; Hashim, I.; Abulkhair, H. Unsteady flow and entropy analysis of nanofluids inside cubic porous container holding inserted body and wavy bottom wall. Int. J. Mech. Sci. 2021, 193, 106161. [Google Scholar] [CrossRef]
- Radwan, A.; Ahmed, M. Thermal management of concentrator photovoltaic systems using microchannel heat sink with nanofluids. Sol. Energy 2018, 171, 229–246. [Google Scholar] [CrossRef]
- Chamkha, A.; Ismael, M.; Kasaeipoor, A.; Armaghani, T. Entropy generation and natural convection of CuO-water nanofluid in C-shaped cavity under magnetic field. Entropy 2016, 18, 50. [Google Scholar] [CrossRef]
- Tayebi, T.; Chamkha, A.J. Entropy generation analysis during MHD natural convection flow of hybrid nanofluid in a square cavity containing a corrugated conducting block. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 1115–1136. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Ismael, M.A.; Chamkha, A.J. Mixed convection in superposed nanofluid and porous layers in square enclosure with inner rotating cylinder. Int. J. Mech. Sci. 2017, 124–125, 95–108. [Google Scholar] [CrossRef]
- Hu, Y.; Li, D.; Shu, S.; Niu, X. Natural convection in a nano fluid-filled eccentric annulus with constant heat flux wall: A lattice Boltzmann study with immersed boundary method. Int. Commun. Heat Mass Transf. 2017, 86, 262–273. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Mejri, I.; Abbassi, M.A.; Omri, A. Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with linear temperature distribution. Powder Technol. 2014, 256, 257–271. [Google Scholar] [CrossRef]
- Sathiyamoorthy, M.; Chamkha, A. Effect of magnetic field on natural convection flow in a liquid gallium filled square cavity for linearly heated side wall(s). Int. J. Therm. Sci. 2010, 49, 1856–1865. [Google Scholar] [CrossRef]
- Izadi, S.; Armaghani, T.; Ghasemiasl, R.; Chamkha, A.J.; Molana, M. A comprehensive review on mixed convection of nanofluids in various shapes of enclosures. Powder Technol. 2019, 343, 880–907. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Gedik, E.; Chamkha, A.J.; Hashim, I. Impacts of heated rotating inner cylinder and two-phase nanofluid model on entropy generation and mixed convection in a square cavity. Heat Mass Transf. Und Stoffuebertragung 2020, 56, 321–338. [Google Scholar] [CrossRef]
- Upadhya, S.M.; Devi, R.L.V.R.; Raju, C.S.K.; Ali, H.M. Magnetohydrodynamic nonlinear thermal convection nanofluid flow over a radiated porous rotating disk with internal heating. J. Therm. Anal. Calorim. 2020, 143, 1973–1984. [Google Scholar] [CrossRef]
- Jeyabalan, S.R.; Chertovskih, R.; Gama, S.; Zheligovsky, V. Nonlinear Large-Scale Perturbations of Steady Thermal Convective Dynamo Regimes in a Plane Layer of Electrically Conducting Fluid Rotating about the Vertical Axis. Mathematics 2022, 10, 2957. [Google Scholar] [CrossRef]
- Chertovskih, R.; Gama, S.M.A.; Podvigina, O.; Zheligovsky, V. Dependence of magnetic field generation by thermal convection on the rotation rate: A case study. Phys. D Nonlinear Phenom. 2010, 239, 1188–1209. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D. Lattice Boltzmann method for MHD natural convection heat transfer using nanofluid. Powder Technol. 2014, 254, 82–93. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C. Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications. J. Comput. Phys. 2009, 228, 1963–1979. [Google Scholar] [CrossRef]
- Hu, Y.; Li, D.; Shu, S.; Niu, X. Immersed boundary-lattice Boltzmann simulation of natural convection in a square enclosure with a cylinder covered by porous layer. Int. J. Heat Mass Transf. 2016, 92, 1166–1170. [Google Scholar] [CrossRef]
- Li, D.; Zhang, H.; Ye, P.; Yu, Z. Natural convection of power-law nanofluid in a square enclosure with a circular cylinder: An immersed boundary-lattice boltzmann study. Int. J. Mod. Phys. C 2018, 29, 1850105. [Google Scholar] [CrossRef]
- Kang, S.K.; Hassan, Y.A. A comparative study of direct-forcing immersed boundary-lattice Boltzmann methods for stationary complex boundaries. Int. J. Numer. Methods Fluids 2011, 66, 1132–1158. [Google Scholar] [CrossRef]
- Chamkha, A.J. MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects. Appl. Math. Model. 1997, 21, 603–609. [Google Scholar] [CrossRef]
- Veera Krishna, M.; Ameer Ahamad, N.; Chamkha, A.J. Hall and ion slip impacts on unsteady MHD convective rotating flow of heat generating/absorbing second grade fluid. Alex. Eng. J. 2021, 60, 845–858. [Google Scholar] [CrossRef]
- Veerakrishna, M.; Subba Reddy, G.; Chamkha, A.J. Hall effects on unsteady MHD oscillatory free convective flow of second grade fluid through porous medium between two vertical plates. Phys. Fluids 2018, 30, 23106. [Google Scholar] [CrossRef]
- Krasnov, D.S.; Zienicke, E.; Zikanov, O.; Boeck, T.; Thess, A. Numerical study of the instability of the Hartmann layer. J. Fluid Mech. 2004, 504, 183–211. [Google Scholar] [CrossRef]
- Rahmati, A.R.; Tahery, A.A. Numerical study of nanofluid natural convection in a square cavity with a hot obstacle using lattice Boltzmann method. Alex. Eng. J. 2018, 57, 1271–1286. [Google Scholar] [CrossRef]
- Vijaybabu, T.R.; Dhinakaran, S. MHD Natural convection around a permeable triangular cylinder inside a square enclosure filled with Al2O3−H2O nanofluid: An LBM study. Int. J. Mech. Sci. 2019, 153–154, 500–516. [Google Scholar] [CrossRef]
- Lai, T.; Liu, X.; Xue, S.; Xu, J.; He, M.; Zhang, Y. Extension of Ergun equation for the calculation of the flow resistance in porous media with higher porosity and open-celled structure. Appl. Therm. Eng. 2020, 173, 115262. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific: Singapore, 2013. [Google Scholar]
- Zarghami, A.; Di Francesco, S.; Biscarini, C. Porous substrate effects on thermal flows through a rev-scale finite volume lattice boltzmann model. Int. J. Mod. Phys. C 2014, 25, 1350086. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Vajravelu, K. Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al2O3-water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder. Int. J. Heat Mass Transf. 2015, 80, 16–25. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C.; Zhao, N. Simulation of thermal flow problems via a hybrid immersed boundary-lattice Boltzmann method. J. Appl. Math. 2012, 2012, 161484. [Google Scholar] [CrossRef]
- Dong, B.; Zhou, X.; Zhang, Y.; Chen, C.; Li, W. Numerical simulation of thermal flow of power-law fluids using lattice Boltzmann method on non-orthogonal grids. Int. J. Heat Mass Transf. 2018, 126, 293–305. [Google Scholar] [CrossRef]
- Fu, J.; Zhang, T.; Li, M.; Li, S.; Zhong, X.; Liu, X. Study on flow and heat transfer characteristics of porous media in engine particulate filters based on lattice Boltzmann method. Energies 2019, 12, 3319. [Google Scholar] [CrossRef]
- Kang, X.; Liao, Q.; Zhu, X.; Yang, Y. Non-equilibrium extrapolation method in the lattice Boltzmann simulations of flows with curved boundaries (non-equilibrium extrapolation of LBM). Appl. Therm. Eng. 2010, 30, 1790–1796. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, Q.; Zhu, X.; Wang, H.; Wu, R.; Lee, D.J. Lattice Boltzmann simulation of substrate flow past a cylinder with PSB biofilm for bio-hydrogen production. Int. J. Hydrogen Energy 2011, 36, 14031–14040. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Z.; Qian, Y.; Guo, W. Study on bifurcation and dual solutions in natural convection in a horizontal annulus with rotating inner cylinder using thermal immersed boundary-lattice Boltzmann method. Entropy 2018, 20, 733. [Google Scholar] [CrossRef]




| ρ (kg·m−3) | cp (J·kg−1·K−1) | k (W·m−1·K−1) | μ (Pa·s) | |
|---|---|---|---|---|
| H2O | 995.7 | 4179.8 | 0.614 | 0.797 × 10−3 |
| TiO2 | 4250.0 | 686.2 | 8.954 | - |
| Grid | 120 × 120 | 160 × 160 | 200 × 200 | 240 × 240 | 280 × 280 |
|---|---|---|---|---|---|
| Nu | 3.96 | 4.11 | 4.17 | 4.18 | 4.18 |
| Relative change | - | 3.79% | 1.46% | 0.02% | 0.00% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, T.; Xu, J.; Liu, X.; He, M. Study of Rotation Effect on Nanofluid Natural Convection and Heat Transfer by the Immersed Boundary-Lattice Boltzmann Method. Energies 2022, 15, 9019. https://doi.org/10.3390/en15239019
Lai T, Xu J, Liu X, He M. Study of Rotation Effect on Nanofluid Natural Convection and Heat Transfer by the Immersed Boundary-Lattice Boltzmann Method. Energies. 2022; 15(23):9019. https://doi.org/10.3390/en15239019
Chicago/Turabian StyleLai, Tianwang, Jimin Xu, Xiangyang Liu, and Maogang He. 2022. "Study of Rotation Effect on Nanofluid Natural Convection and Heat Transfer by the Immersed Boundary-Lattice Boltzmann Method" Energies 15, no. 23: 9019. https://doi.org/10.3390/en15239019
APA StyleLai, T., Xu, J., Liu, X., & He, M. (2022). Study of Rotation Effect on Nanofluid Natural Convection and Heat Transfer by the Immersed Boundary-Lattice Boltzmann Method. Energies, 15(23), 9019. https://doi.org/10.3390/en15239019






