Analysis of the Effects of Grid-Connected Charging/Discharging Stations on Relay Protection
Abstract
:1. Introduction
2. Analysis of Influence of Charging and Discharging Station Access on Relay Protection of Distribution Network
2.1. Impact Analysis of Electric Vehicle Charging Load
2.2. Analysis of Fault Characteristics
2.3. Influence Analysis of Positive Sequence Fault Component
- a.
- positive sequence fault component direction element
- b.
- Effects of charging/discharging station connected to the grid on directional components
3. Relay Protection Scheme
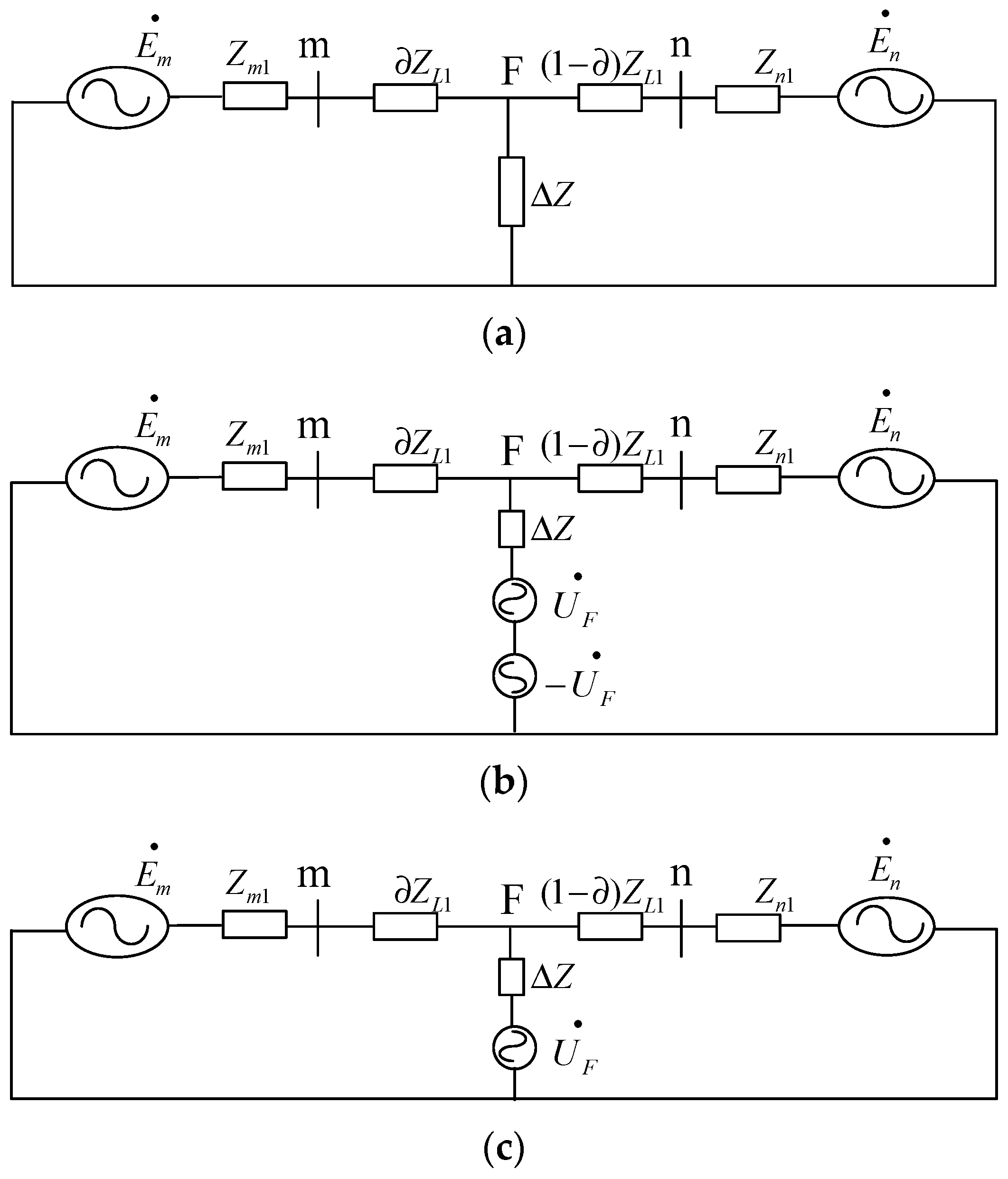
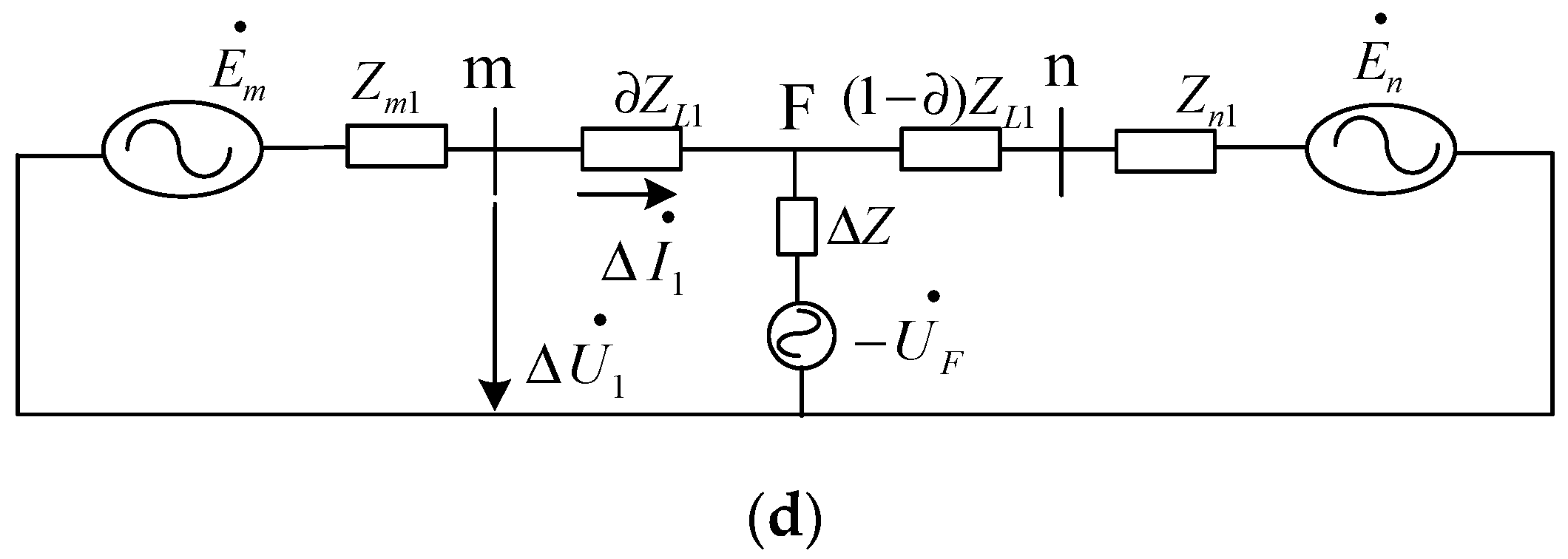
3.1. Based on Fault Component Positive Sequence Integrated Impedance Protection Principle
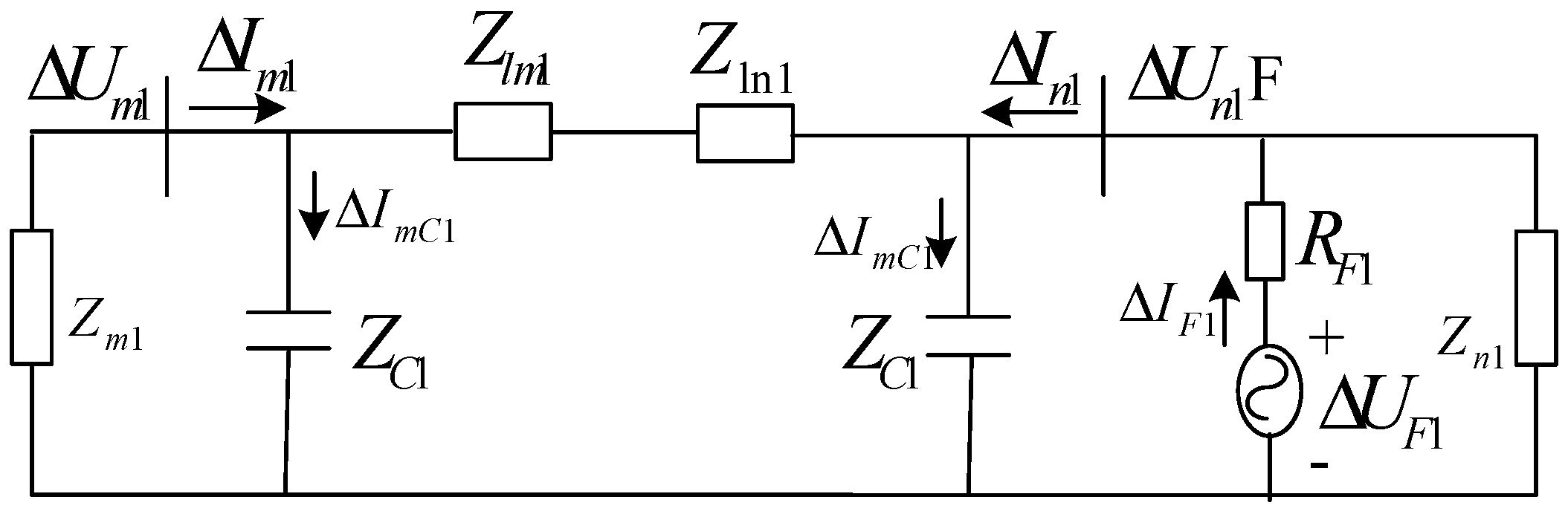
3.1.1. Positive Sequence Integrated Impedance of Fault Component in an Out-of-Zone Fault
3.1.2. Positive Sequence Integrated Impedance of Fault Components in the In-Zone Fault
3.1.3. Positive Sequence Integrated Impedance of Fault Component in the Fault Zone
3.2. Performance Analysis
- (1)
- The differential impedance of the positive sequence fault component is constructed by analyzing the different amplitudes of the sum of measured impedance of the protection at both ends of the feeder when the fault occurs inside and outside the zone: .
- (2)
- The positive sequence integrated impedance can effectively determine the impedance of the internal fault of the line within the range of the vertical differential protection and is not affected by the fault of the grid-connected equipment.
- (3)
- The positive sequence comprehensive impedance depends on the voltage-to-current ratio of the positive sequence fault component after the fault occurs, and the calculated results are approximately the same at any time during the steady state period of the fault. Therefore, the protection elements at both ends of the feeder are not required to consider whether synchronous sampling and the data window are synchronized during differential protection, which is suitable for fault analysis and feeder protection under the grid-connected operation of large-scale charging and discharging stations.
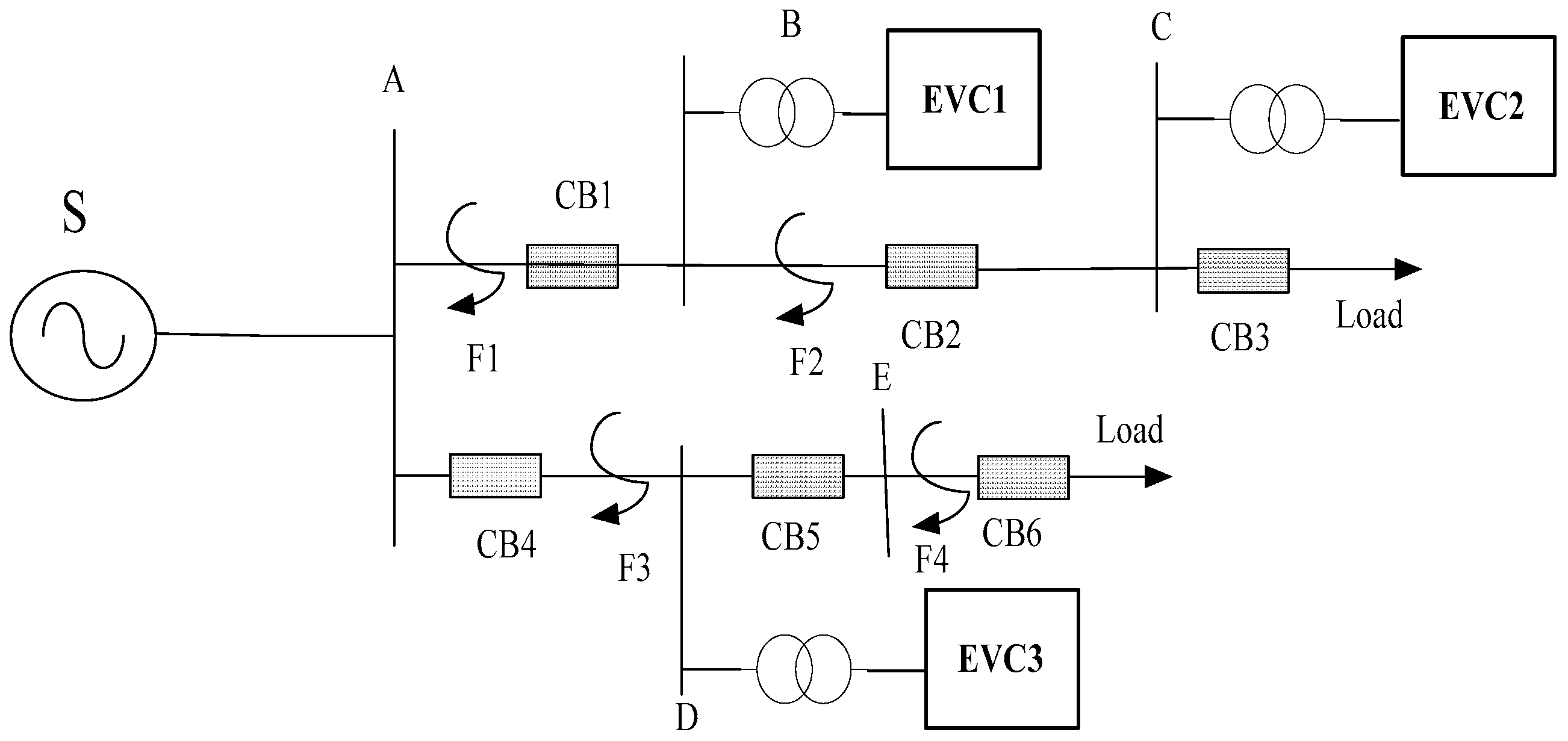
4. Simulation Verification
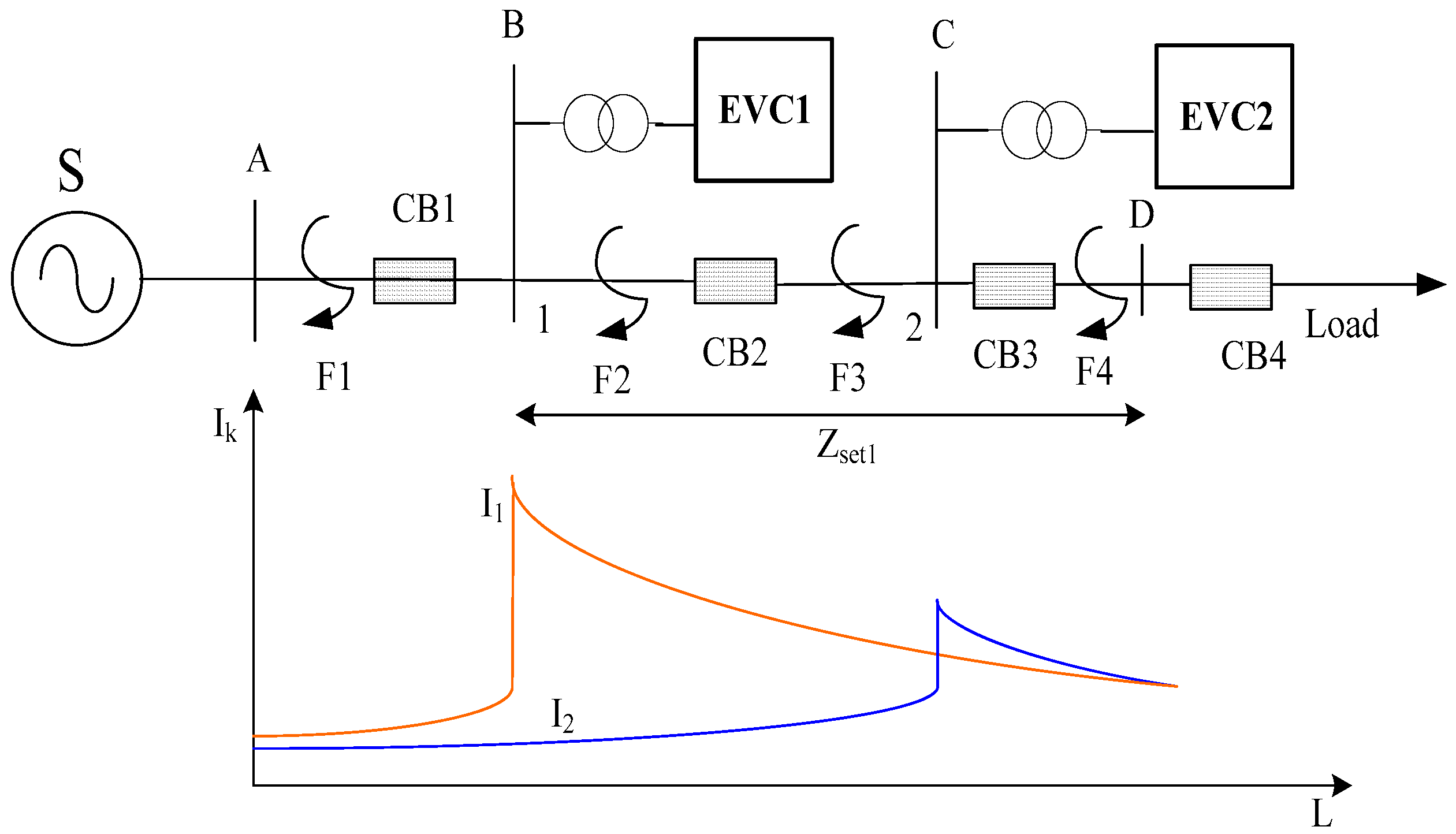
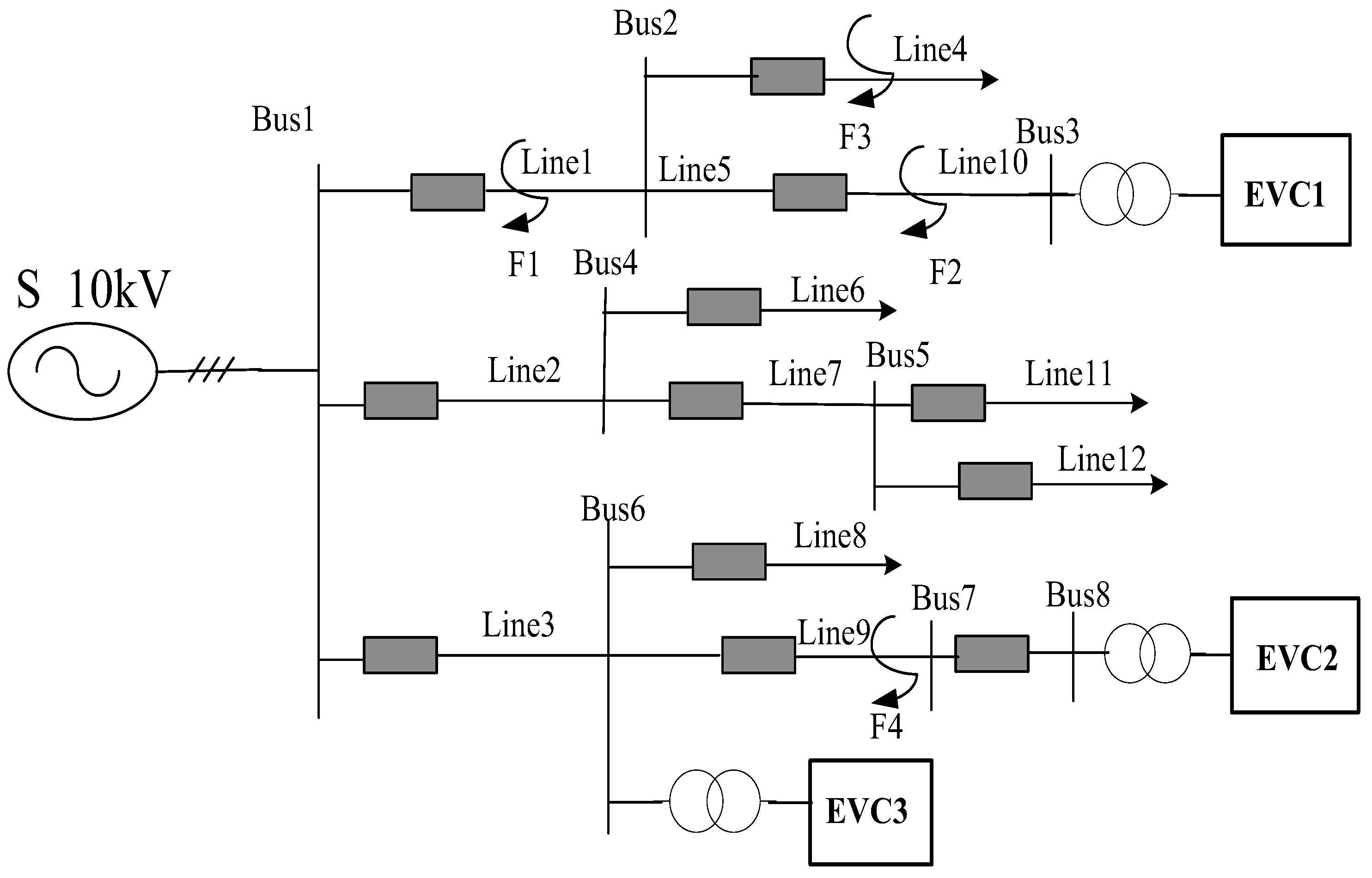
4.1. Simulation Structure and Parameters
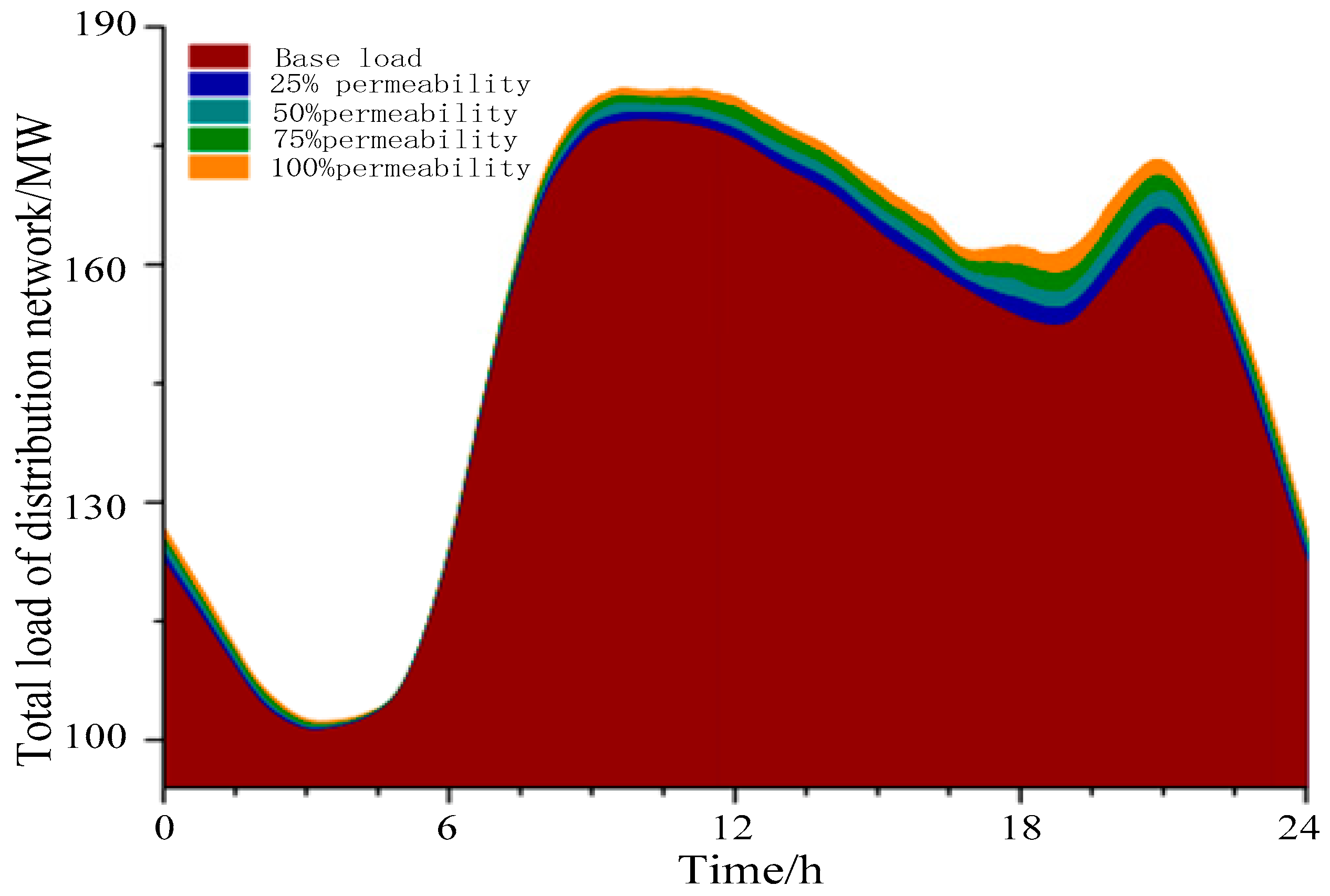
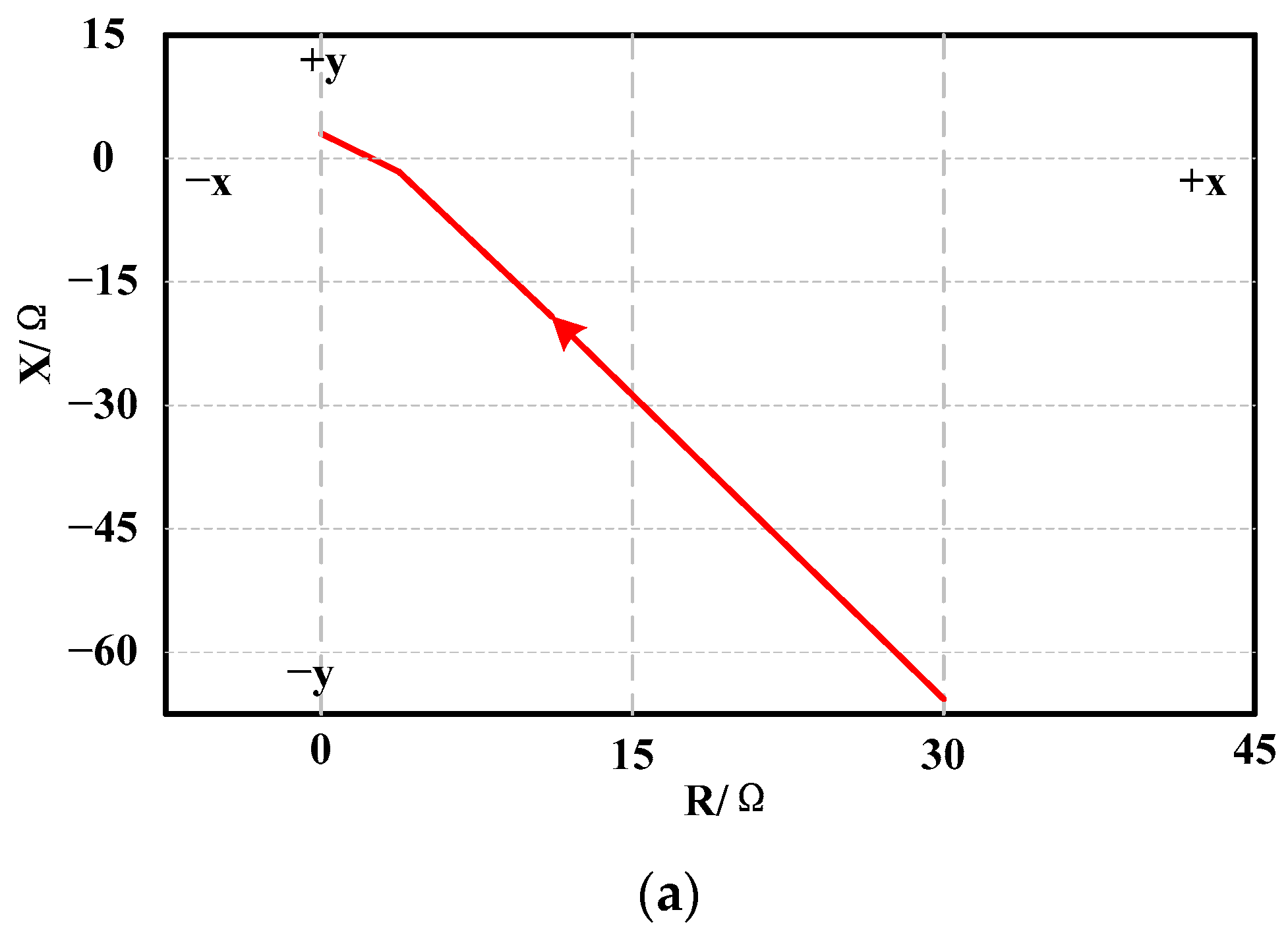
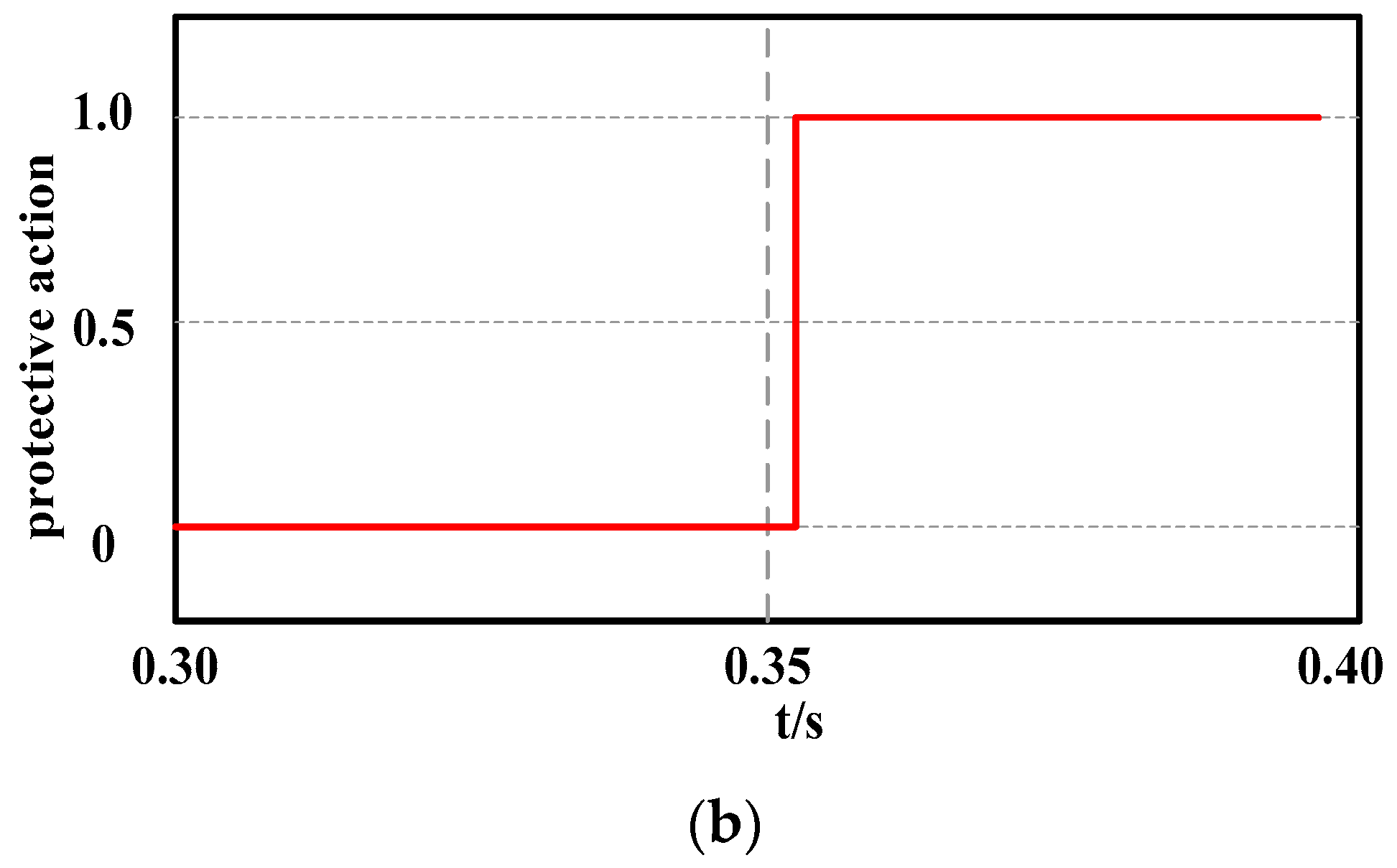
4.2. Simulation Results
- a.
- Influence of charging station access on load of distribution network
- b.
- Protection action result
5. Conclusions
- (1)
- The large-capacity charging and discharging stations are connected to the distribution network, which changes the generation and fault characteristics of the short-circuit current. The original single-radiation power supply network will be changed to a double-terminal or multi-terminal network due to the access of large-capacity charging and discharging stations, which will bring many adverse effects to the relay protection device of the distribution network. The relay protection configuration of grid-connected charging and discharging stations not only needs to consider the fault characteristics of charging and discharging stations themselves but must also consider the effects on the fault characteristics of a distribution network.
- (2)
- This paper analyzes the short-circuit fault characteristics of charging and discharging stations connected to the grid. Different fault situations have different fault characteristics, and the impact on distribution network protection is also different, with focus on the analysis of the impact on the positive sequence fault components. Under the influence of fault characteristic analysis, the principle of the positive sequence integrated impedance longitudinal protection is proposed. Under different fault conditions, the amplitude characteristics of the positive sequence impedance inside and outside the zone, and the positive sequence impedance differential protection criterion with braking characteristics, are studied and analyzed.
- (3)
- By adding the effects of transition resistance to the protection criterion in the simulation and calculation process, the simulation results verify the applicability of the protection principle.
- (4)
- The research results show that the vertical protection principle based on positive sequence comprehensive impedance offers a certain practicality for the protection of distribution networks with large-capacity, charge–discharge stations. The protection principle has high sensitivity and is generally unaffected by transition resistance, which provides theoretical support for the improvement of grid-connection protection of large-capacity, charging/discharging stations.
Author Contributions
Funding
Conflicts of Interest
References
- Fan, J.L.; Zhang, Y.J.; Wang, B. The impact of urbanization on residential energy consumption in China: An aggregated and disaggregated analysis. Renew. Sustain. Energy Rev. 2017, 75, 220–233. [Google Scholar] [CrossRef]
- Li, W.; Long, R.; Chen, H. Consumers’ evaluation of national new energy vehicle policy in China: An analysis based on a four paradigm model. Energy Policy 2016, 99, 33–41. [Google Scholar] [CrossRef]
- Li, Y.M.; Zhang, Q.; Liu, B.Y.; McLellan, B.; Gao, Y.; Tang, Y.Y. Substitution effect of New-Energy Vehicle Credit Program and Corporate Average Fuel Consumption Regulation for Green-Car Subsidy. Energy 2018, 152, 223–236. [Google Scholar] [CrossRef]
- Bradley, T.; Quinn, C. Analysis of plug-in hybrid electric vehicle utility factors. J. Power Sources 2010, 195, 5399–5408. [Google Scholar] [CrossRef]
- Thomas, C.E.S. Transportation options in a carbon constrained world: Hybrids, plug-in hybrids, biofuels, fuel electric vehicles, and battery electric vehicles. Int. J. Hydrogen Energy 2009, 34, 9279–9296. [Google Scholar] [CrossRef]
- Shuang, G.; Chau, K.T.; Chan, C.C.; Diyun, W. Loss Analysis of Vehicle-To-Grid Operation. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; IEEE Computer Society: Washing, DC, USA, 2010; pp. 1–6. [Google Scholar]
- Jenkins, S.D.; Rossmaier, J.; Ferdowsi, M. Utilization and effect of plug-in hybrid electric vehicles in the united states power grid. In Proceedings of the IEEE Vehicle and Propulsion Conference (VPPC), Harbin, China, 3–5 September 2008. [Google Scholar]
- Staats, P.T.; Grady, W.M.; Arapostathis, A.; Thallam, R.S. A statistical analysis of the effect of electric vehicle battery charging on distribution system harmonic voltages. IEEE Trans Power Deliv. 2010, 13, 640–646. [Google Scholar] [CrossRef]
- Schlee, J.; Mousseau, A.; Eggebraaten, J.; Johnson, B.; Hess, H.; Johnson, B. The Effects of Plug-In Electric Vehicles on a Small Distribution Grid. In Proceedings of the 41st North American Power Symposium, Starkville, MS, USA, 4–6 October 2009; IEEE Computer Society: Washing, DC, USA, 2009; pp. 1–6. [Google Scholar]
- Kroposki, B.; Pink, C.; DeBlasio, R. Benefits of power electronic interfaces for distributed energy systems. IEEE Trans. Energy Convers. 2010, 25, 901–908. [Google Scholar] [CrossRef] [Green Version]
- Zhong, C.; Ming, D.; Jianhui, S. Modeling and control for large capacity battery energy storage system. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 1429–1436. [Google Scholar]
- Ma, J.; Li, J.; Wang, Z. An adaptive distance protection scheme for dis-tribution system with distributed generation. In Proceedings of the Inter-National Conference on Critical Infrastructure, Beijing, China, 20–22 September 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–4. [Google Scholar]
- Jiali, H.; Zheng, N.G. Novel principle of pilot differential relay protection of transmission lines. In Proceedings of the 4th International Conference on Power Transmission & Distribution Technology, Changsha, China, 21–23 April 2003. [Google Scholar]
- Xiaohua, L.; Xianggen, Y.; Deshu, C.; Gang, W. Theoretical analysis of differential protection based on sampled values. In Proceedings of the International Conference on Power System Technology, Chongqing, China, 22–26 October 2006. [Google Scholar]
- Acha, S.; Green, T.C.; Shah, N. Effects of optimised plug-in hybrid vehicle charging strategies on electric distribution network losses. In Proceedings of the 2010 IEEE PES Transmission and Distribution Conference and Exposition, New Orleans, LA, USA, 19–22 April 2010. [Google Scholar]
- Mohammed, A.H.; Illindala, M.S. The influence of inverter-based DGs and their controllers on distribution network protection. IEEE Trans. Ind. Appl. 2014, 50, 2928–2937. [Google Scholar]
- Plet, C.A.; Graovac, M.; Green, T.C.; Iravani, R. Fault response of grid-connected inverter dominated networks. In Proceedings of the Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–8. [Google Scholar]
- Pradhan, A.K.; Routray, A.; Madhan, G.S. Fault direction estimation in radial distribution system using phase change in sequence current. IEEE Trans. Power Deliv. 2007, 22, 2065–2071. [Google Scholar] [CrossRef]
- Haron, A.R.; Mohamed, A.; Shareef, H.; Zayandehroodi, H. Analysis and solutions of overcurrent protection issues in a microgrid. In Proceedings of the 2012 IEEE International Conference on Power and Energy, Kota Kinabalu, Malaysia, 2–5 December 2012; pp. 644–649. [Google Scholar]
- Gao, Y.B.; Zeng, J.S.; Qiu, P.; Lu, Y.; Huang, X.M.; Xu, X.D. A protection scheme of Ac side faults of DC distribution system. Appl. Mech. Mater. 2004, 3570, 107–111. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Fu, G.; Li, B. Directional protection based on fault component energy function in micro-grid. In Proceedings of the 2012 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Tianjin, China, 21–24 May 2012; pp. 1–5. [Google Scholar]
- Junyent-Ferre, A.; Gomis-Bellmunt, O.; Green, T.C.; Soto-Sanchez, D.E. Current control reference calculation issues for the operation of renewable source grid interface VSCs under unbalanced voltage sags. IEEE Trans. Power Electron. 2011, 26, 3744–3753. [Google Scholar] [CrossRef]
- Kumar, D.S.; Srinivasan, D.; Reindl, T. A fast and scalable protection scheme for distribution networks with distributed generation. IEEE Trans. Power Deliv. 2016, 31, 67–75. [Google Scholar] [CrossRef]
- Wang, F.; Duarte, J.L.; Hendrix, M.A.M. Design and analysis of active power control strategies for distributed generation inverters under unbalanced grid faults. IET Gener. Transm. Distrib. 2010, 4, 905–916. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, P.; Timbus, A.V.; Teodorescu, R.; Liserre, M.; Blaabjerg, F. Flexible active power control of distributed power generation systems during grid faults. IEEE Trans. Ind. Electron. 2007, 54, 2583–2592. [Google Scholar] [CrossRef]
- Ng, C.H.; Ran, L.; Bumby, J. Unbalanced grid fault ride through control for a wind turbine inverter. In Proceedings of the Industry Applications Conference, New Orleans, LA, USA, 23–27 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 154–164. [Google Scholar]
- Coffele, F.; Booth, C.; Dyśko, A. An adaptive overcurrent protection scheme for distribution networks. IEEE Trans. Power Deliv. 2015, 30, 561–568. [Google Scholar] [CrossRef]
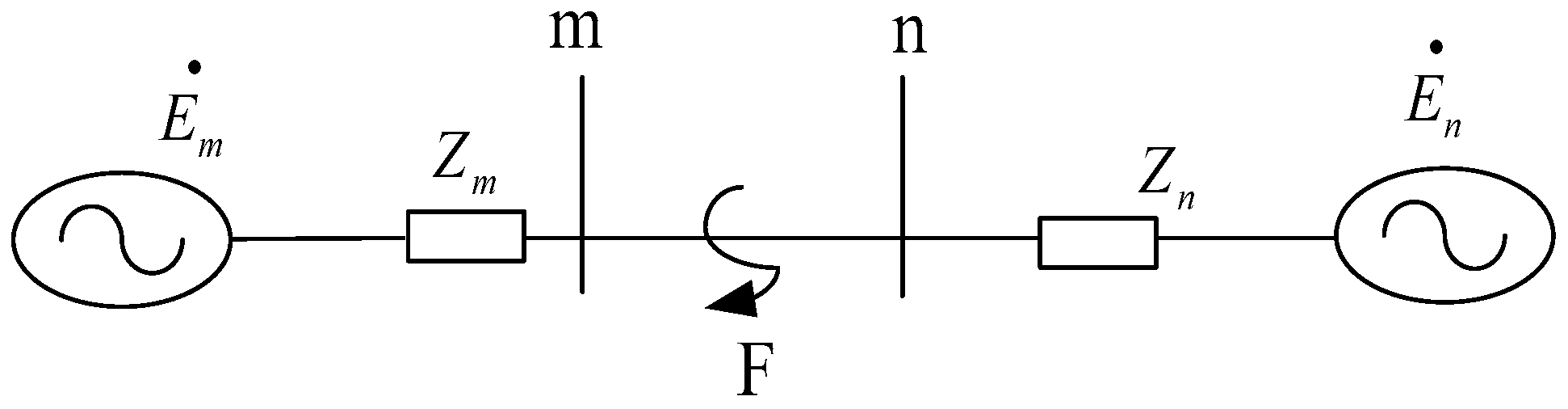
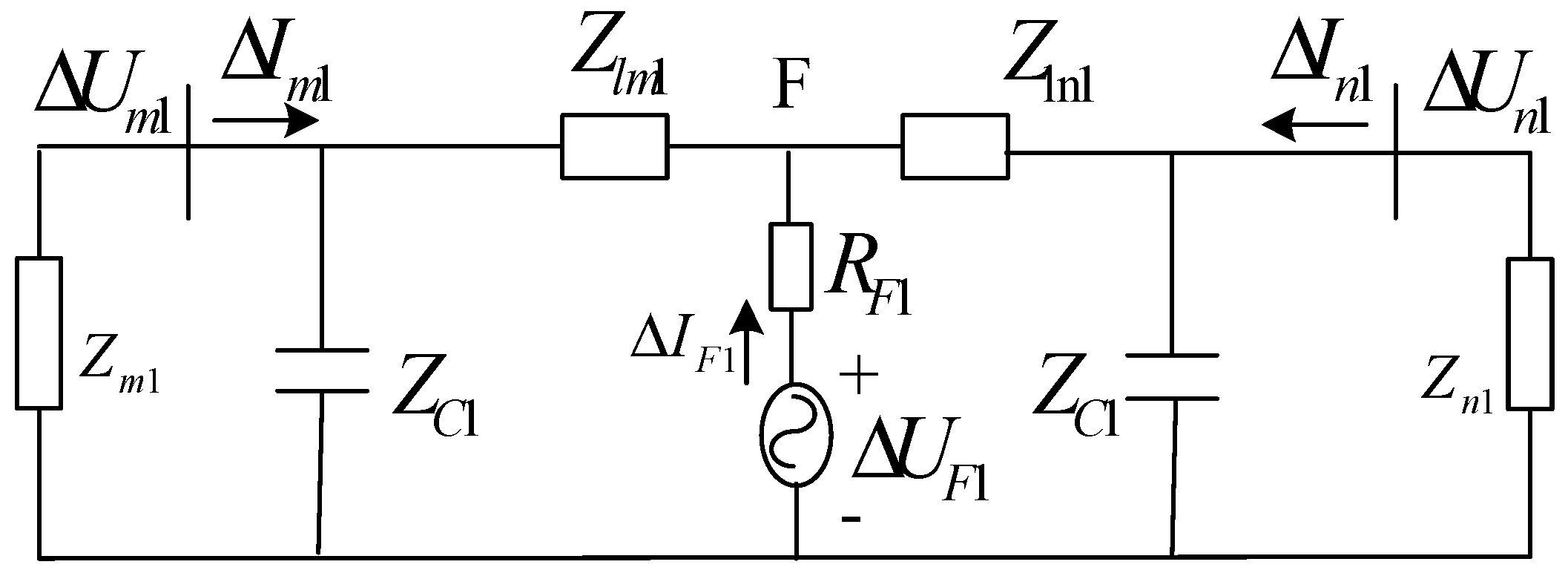
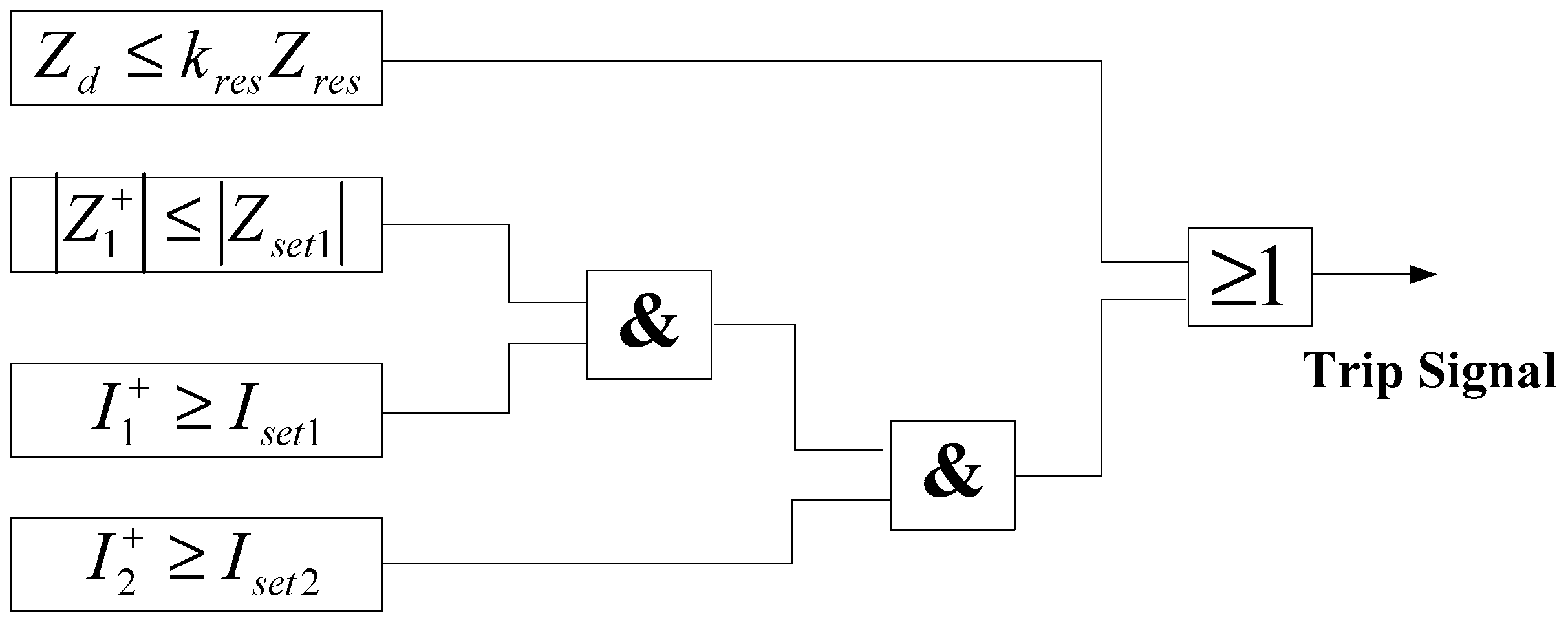
| Fault Type | ΔZ |
|---|---|
| Single phase earth fault | Z2 + Z0 |
| Two-phase ground fault | Z2//Z0 |
| Two-phase short-circuit fault | Z2 |
| Three-phase short-circuit fault | 0 |
| Permeability of Water | Maximum Load/MW | Time of Maximum Load/h | Minimum Load/MW | Minimum Load Time/h | Peak Valley Difference/MW | Peak Valley Differential/% |
|---|---|---|---|---|---|---|
| 0% | 173.55 | 9:58 | 104.96 | 3:09 | 68.59 | 39.52 |
| 25% | 175.43 | 10:03 | 105.17 | 3:13 | 70.26 | 40.05 |
| 50% | 177.30 | 9:51 | 105.25 | 3:11 | 72.05 | 40.64 |
| 75% | 179.18 | 9:46 | 105.32 | 3:14 | 73.86 | 41.22 |
| 100% | 180.55 | 9:35 | 106.10 | 3:15 | 74.45 | 41.24 |
| Fault Location | Fault Type | Transition Resistance/Ω | Positive Sequence Integrated Impedance/Ω | Braking Coefficient/k | Brake Impedance/Ω | Time/s | Sensitivity | Decision Outcome |
|---|---|---|---|---|---|---|---|---|
| F1 | ABC | 4.95 | 0.05 | 0.36 | 51.92 | 0.311 | 1.23 | Out-of-area fault |
| F1 | BC | 0.02 | 0.02 | 0.36 | 22.38 | 0.313 | 1.26 | Out-of-area fault |
| F1 | CAG | 4.95 | 0.04 | 0.36 | 55.62 | 0.320 | 1.34 | Out-of-area fault |
| F2 | AB | 4.95 | 47.57 | 0.36 | 0.25 | 0.285 | 1.29 | In-area fault |
| F2 | ABG | 0.02 | 23.18 | 0.36 | 0.12 | 0.293 | 1.43 | In-area fault |
| F2 | CA | 0.02 | 24.25 | 0.36 | 0.06 | 0.289 | 1.37 | In-area fault |
| F3 | CA | 0.02 | 0.01 | 0.36 | 2.56 | 0.316 | 1.31 | Out-of-area fault |
| F3 | CA | 1.05 | 0.03 | 0.36 | 4.41 | 0.318 | 1.35 | Out-of-area fault |
| F4 | ABG | 9.95 | 0.02 | 0.36 | 63.42 | 0.316 | 1.32 | Out-of-area fault |
| F4 | CAG | 0.02 | 0.01 | 0.36 | 41.64 | 0.314 | 1.28 | Out-of-area fault |
| Fault Location | Fault Type | Transition Resistance/Ω | Positive Sequence Integrated Impedance/Ω | Braking Coefficient/k | Brake Impedance/Ω | Time/s | Sensitivity | Decision Outcome |
|---|---|---|---|---|---|---|---|---|
| F1 | ABC | 4.95 | 50.15 | 0.36 | 92.42 | 0.315 | 1.37 | Out-of-area fault |
| F1 | BC | 0.02 | 11.35 | 0.36 | 46.22 | 0.305 | 1.31 | Out-of-area fault |
| F1 | CAG | 4.95 | 55.38 | 0.36 | 98.62 | 0.311 | 1.35 | Out-of-area fault |
| F2 | AB | 4.95 | 52.85 | 0.36 | 91.84 | 0.298 | 1.29 | Out-of-area fault |
| F2 | CA | 0.02 | 30.16 | 0.36 | 74.58 | 0.316 | 1.41 | Out-of-area fault |
| F4 | CAG | 9.95 | 99.84 | 0.36 | 0.26 | 0.291 | 1.26 | In-area fault |
| F4 | CAG | 0.02 | 23.65 | 0.36 | 0.32 | 0.295 | 1.28 | In-area fault |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Ma, J.; Shang, L.; Chen, S. Analysis of the Effects of Grid-Connected Charging/Discharging Stations on Relay Protection. Energies 2022, 15, 9065. https://doi.org/10.3390/en15239065
Wang Q, Ma J, Shang L, Chen S. Analysis of the Effects of Grid-Connected Charging/Discharging Stations on Relay Protection. Energies. 2022; 15(23):9065. https://doi.org/10.3390/en15239065
Chicago/Turabian StyleWang, Qingjie, Jing Ma, Lei Shang, and Shuangyin Chen. 2022. "Analysis of the Effects of Grid-Connected Charging/Discharging Stations on Relay Protection" Energies 15, no. 23: 9065. https://doi.org/10.3390/en15239065
APA StyleWang, Q., Ma, J., Shang, L., & Chen, S. (2022). Analysis of the Effects of Grid-Connected Charging/Discharging Stations on Relay Protection. Energies, 15(23), 9065. https://doi.org/10.3390/en15239065






