Experimental and Prenemilary Numerical Evaluation of Pressure Drops under the Conditions of the Stratified Gas-Liquid Flow in a Horizontal Pipe Filled with Metal Foam
Abstract
1. Introduction
2. Experimental Set-Up
2.1. Metal Foam
2.2. Measuring Set-Up
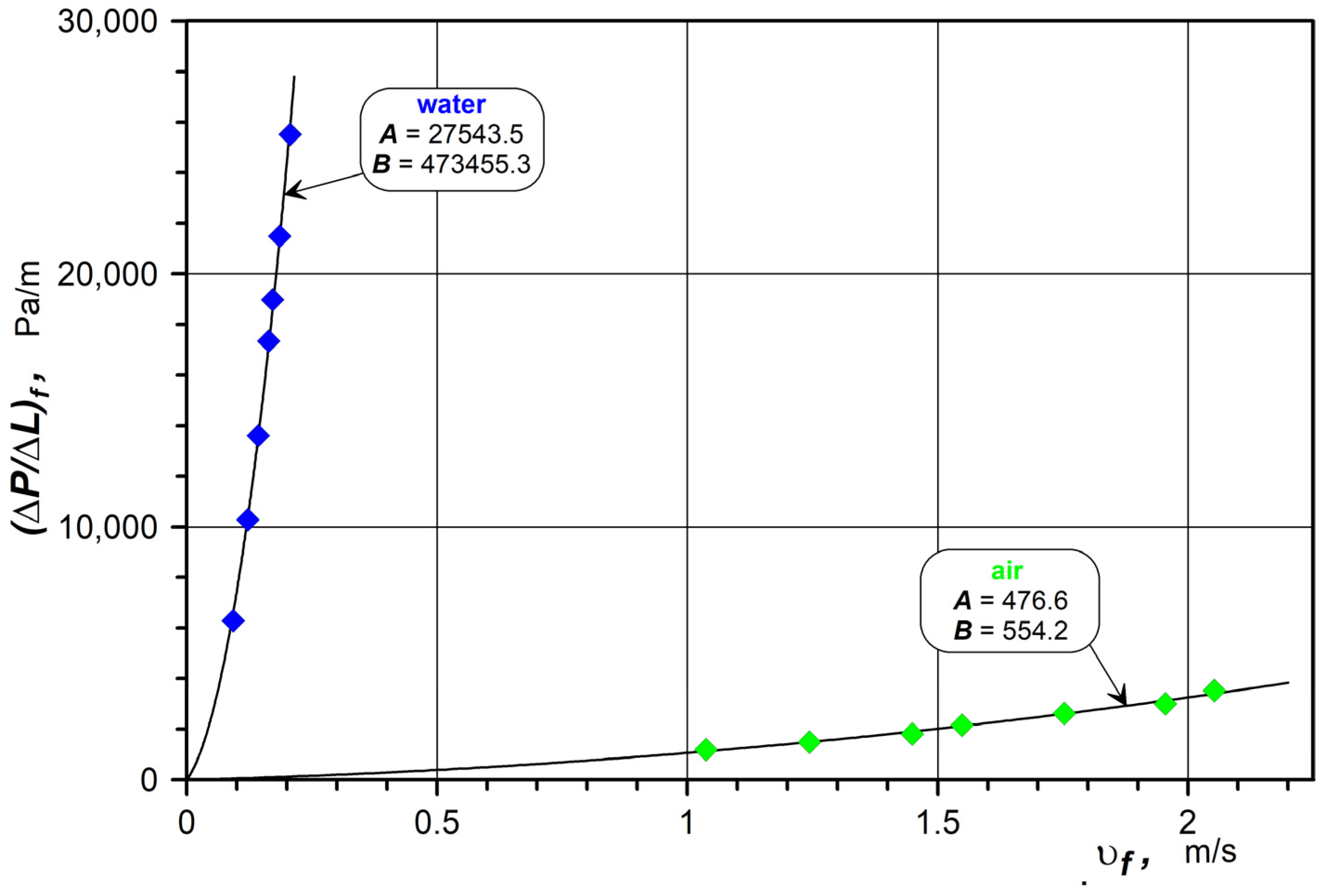
2.3. Selection of Flow Rates and Results of Measurements
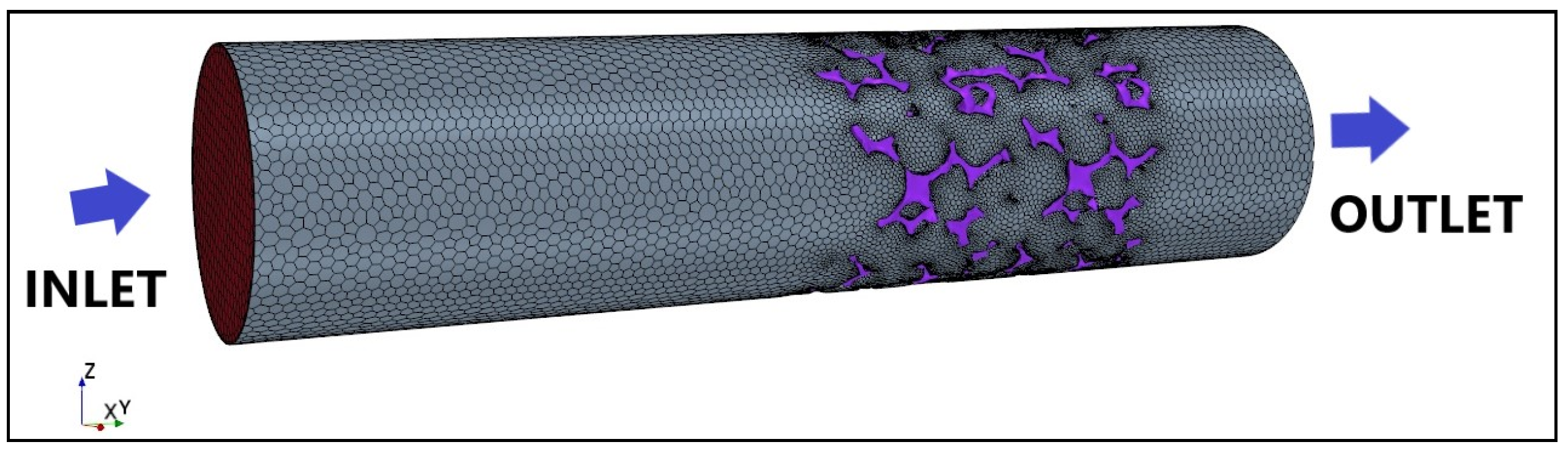
3. Numerical Study
- a—area vector, m2
- g—gravitational acceleration, m/s2
- mij—mass transfer rate to phase i from phase j, kg/s
- mji—mass transfer rate to phase j from phase i, kg/s
- p—pressure, assumed to be equal in all phases, Pa
- t—time, s
- Fint—internal forces (including user-defined potential force), N
- M—interphase momentum transfer per unit volume, N⋅s/m3
- Siα—phase momentum source term, N/m3
- Ti—molecular stresses, Pa
- Tit—turbulent stresses, Pa
- V—volume, m3
- α—specific phase volume fraction, -
- v—velocity, m/s
- ρ—density, kg/m3
4. Results and Discussion
4.1. Experimental Results
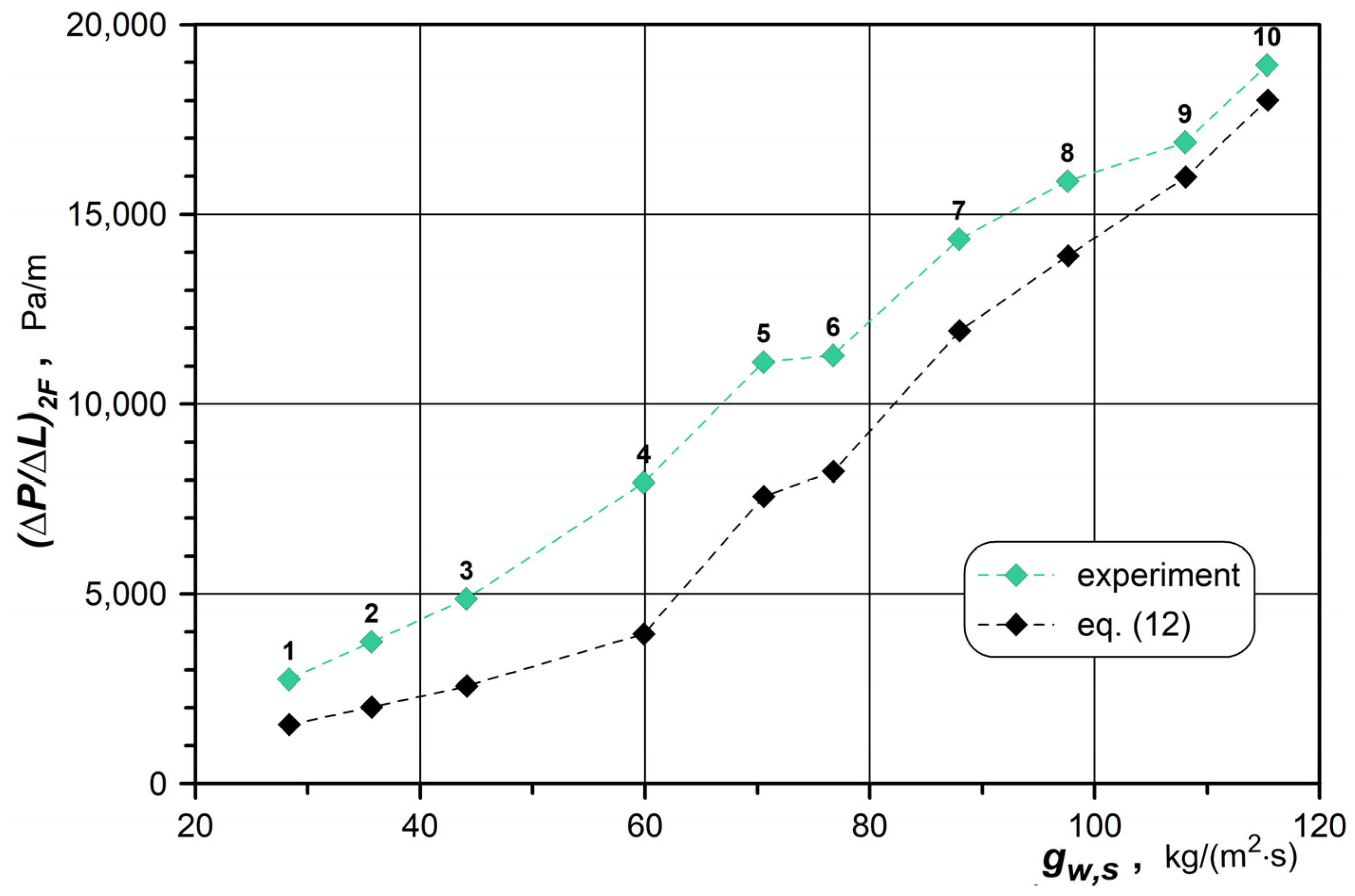
4.2. Numerical Results
5. Conclusions
- The presence of metal foam in the pipe leads to a multiple increase in the gas-liquid two-phase pressure drop.Comment: This increase is particularly visible when it is compared to the pressure drop that accompanies two-phase mixture flow in a hollow tube, in the form of stratified pattern. In this case, one can forecast a decrease in the total energy efficiency of the heat exchanger, rather than its increase. However, it may be expedient to provide a short length of foam in the inlet section of the pipe. It will then mainly perform the function of a flow turbulator, and not a specific rib inside the flow pipe.
- The empirical equations applied to forecast the flow resistance in the foam layer take on complex forms.Comment: In addition, they sometimes require the inputs of parameter values, which need to be determined individually based on experimentation. This fact makes the practical use of these equations difficult; however, it results from the very complex and peculiar internal structure of the metal foam. When its structure is described only with the PPI value, this proves to be insufficient, both in terms of identification of the course of flow and thermal phenomena.
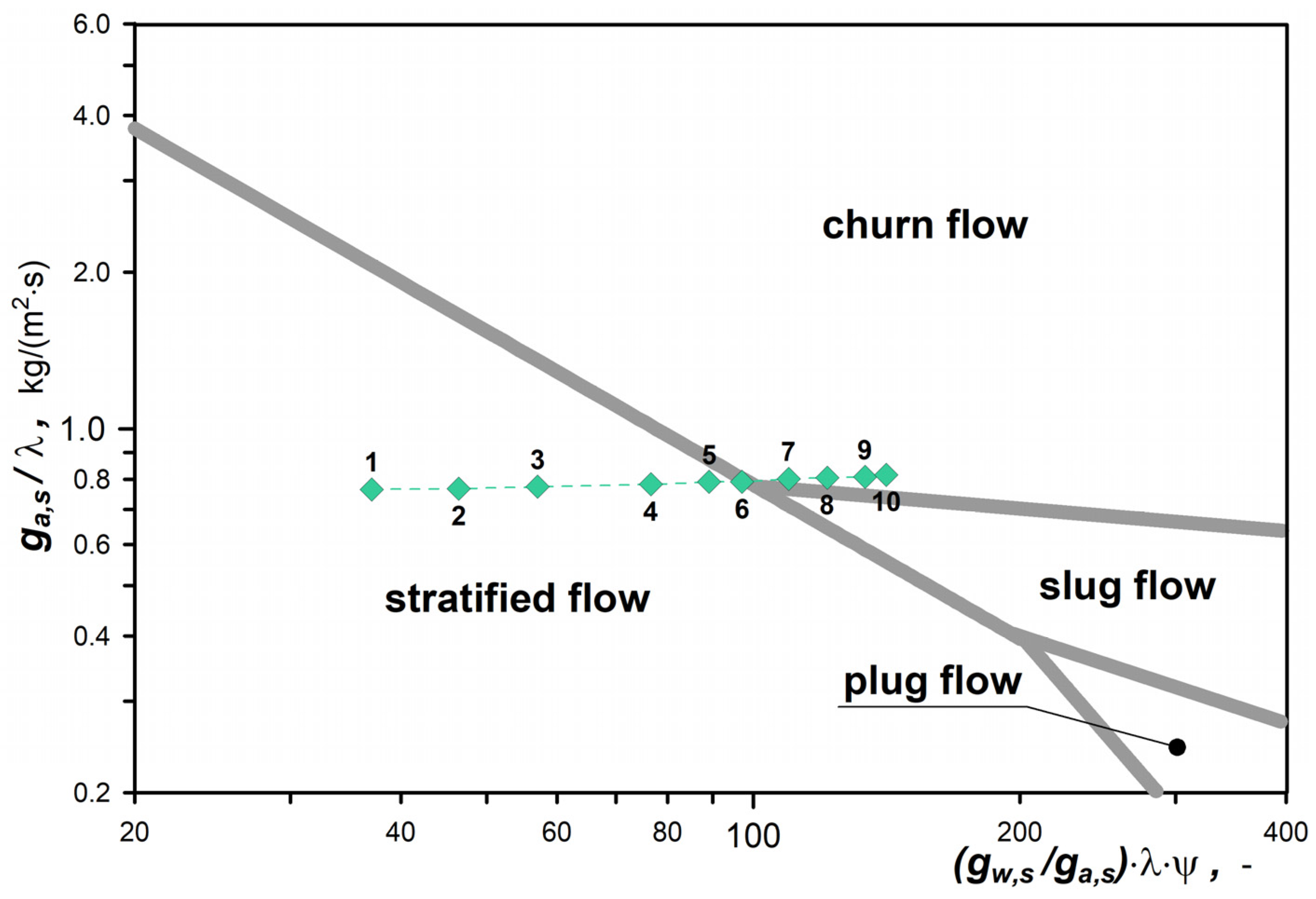
- The mere fact of installing metal foam in a pipe does not guarantee that a sufficiently large disturbance of the stratified flow pattern is obtained, and thus the effect of enhanced mixing of the phases achieved.Comment: In order to forecast the type of gas-liquid two-phase pattern formed in a pipe containing foam packing, one should generate maps of flow patterns developed specifically for a particular case.
- The main difficulty in the methodology of numerical simulation of flow through the foam packing is associated with the adequate representation of its actual internal structure.Comment: In the place of theoretical models generated for granular layers, it is more suitable to apply 3D images generated by means of computer microtomography. However, even in such a case, it is not possible to represent suitably the roughness of the surface of the solid body (metal), and thus take it into account in the simulations to represent the interface between two-phase mixture and the metal packing during flow through the foam.
- Interfacial slip should be taken into account in the procedures applied in the numerical modeling of two-phase flow in a pipe with foam packing.Comment: However, we should remember that its value is different than the flow in an empty pipe. For this reason, the level of gas packing in the foam skeleton, as well as liquid volume, is also different. Its actual volume ratio may also be determined by the type of foam material (type of metal or non-metallic material), and in particular, the wettability of its surface by the liquid.
- A variety of numerical modeling techniques can serve as effective tools in assessing the disturbance of two-phase flow pattern in a pipe with foam packing, as the procedure is very difficult to be executed experimentally.Comment: In the case when it is unfeasible or non-advisable to conduct laboratory research, the results of numerical calculations can also be applied in forecasting pressure drops. The resulting values are similar to those that can be indicated by the accessible empirical equations (with regard to the case discussed here). However, the execution of numerical calculations requires access to dedicated software and a computer with sufficient computing power; however, this does not guarantee the short duration of simulations anyway. In addition, their results often require additional processing. All this means that the application of numerical simulations when actual flow systems are designed may turn out to be as time-consuming and cost-effective as the experimental studies that can offer the most reliable results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| d | diameter, m |
| f | friction factor, − |
| g | mass flux, kg/(m2·s) |
| x | measured quantity (overall) |
| Da | Darcy number, − |
| G | mass flow rate, kg/s |
| K | foam permeability, m2 |
| L | length, m |
| M | molar mass, kg/kmol |
| P | pressure, Pa |
| R | specific gas constant (for air: 288.3), J/(kg·K)) |
| Re | Reynolds number, − |
| V | volume flow rate, m3/s |
| T | temperature, K (°C) |
| XLM | Lockart-Martinelli parameter, − |
| Greek symbols | |
| λ, ψ | correction of phase properties, − |
| η | viscosity, Pa·s |
| ρ | density, kg/m3 |
| σ | surface tension, N/m |
| υ | velocity, m/s |
| ΔΠ | flow resistance (drop pressure), Pa |
| ΔΛ | length increment, m |
| Subscripts | |
| a | air |
| atm | atmospheric |
| c | cell |
| cl | computed value |
| e | equivalent parameter |
| efp | empty flow pipe |
| f | fluid |
| fp | flow pipe |
| g | gas |
| in | inlet |
| l | liquid |
| ms | measured value |
| out | outlet |
| p | pore |
| r | reference value |
| rot | rotameter |
| s | superficial value (apparent) |
| w | water |
References
- Evans, A.; Hutchinson, J.; Ashby, M. Multifunctionality of cellular metal systems. Prog. Mater. Sci. 1998, 43, 171–221. [Google Scholar] [CrossRef]
- De Schampheleire, S.; De Jaeger, P.; De Kerpel, K.; Ameel, B.; Huisseune, H.; De Paepe, M. How to Study Thermal Applications of Open-Cell Metal Foam: Experiments and Computational Fluid Dynamics. Materials 2016, 9, 94. [Google Scholar] [CrossRef] [PubMed]
- Paek, J.W.; Kang, B.H.; Kim, S.Y.; Hyun, J.M. Effective Thermal Conductivity and Permeability of Aluminum Foam Materials. Int. J. Thermophys. 2000, 21, 453–464. [Google Scholar] [CrossRef]
- Banhart, J. Manufacture, characterisation and application of cellular metals and metal foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Tadrist, L.; Miscevic, M.; Rahli, O.; Topin, F. About the use of fibrous materials in compact heat exchangers. Exp. Therm. Fluid Sci. 2004, 28, 193–199. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, H.; Sun, S.; Ding, G. Heat transfer measurements and correlation of refrigerant flow boiling in tube filled with copper foam. Int. J. Refrig. 2014, 38, 215–226. [Google Scholar] [CrossRef]
- Abadi, G.B.; Moon, C.; Kim, K.C. Experimental study on single-phase heat transfer and pressure drop of refrigerants in a plate heat exchanger with metal-foam-filled channels. Appl. Therm. Eng. 2016, 102, 423–431. [Google Scholar] [CrossRef]
- Hooman, K.; Chumpia, A.; Jadhav, P.; Rudolph, V. Metal Foam Heat Exchanger for Dry Cooling. Final Report for ANLEC Project 5-0710-0063. 2013. Available online: https://www.globalccsinstitute.com/archive/hub/publications/120141/metal-foam-heat-exchanger-dry-cooling.pdf (accessed on 10 October 2022).
- Abadi, G.B.; Kim, K.C. Experimental heat transfer and pressure drop in a metal-foam-filled tube heat exchanger. Exp. Therm. Fluid Sci. 2017, 82, 42–49. [Google Scholar] [CrossRef]
- Ji, W.-T.; Li, Z.-Y.; Qu, Z.-G.; Guo, J.-F.; Zhang, D.-C.; He, Y.-L.; Tao, W.-Q. Film condensing heat transfer of R134a on single horizontal tube coated with open cell copper foam. Appl. Therm. Eng. 2015, 76, 335–343. [Google Scholar] [CrossRef]
- Bağcı, Ö.; Dukhan, N. Experimental hydrodynamics of high-porosity metal foam: Effect of pore density. Int. J. Heat Mass Transf. 2016, 103, 879–885. [Google Scholar] [CrossRef]
- Kouidri, A.; Madani, B. Experimental hydrodynamic study of flow through metallic foams: Flow regime transitions and surface roughness influence. Mech. Mater. 2016, 99, 79–87. [Google Scholar] [CrossRef]
- Wang, H.; Guo, L. Experimental investigation on pressure drop and heat transfer in metal foam filled tubes under convective boundary condition. Chem. Eng. Sci. 2016, 155, 438–448. [Google Scholar] [CrossRef]
- Hu, H.; Zhu, Y.; Ding, G.; Sun, S. Effect of oil on two-phase pressure drop of refrigerant flow boiling inside circular tubes filled with metal foam. Int. J. Refrig. 2012, 36, 516–526. [Google Scholar] [CrossRef]
- Hu, H.; Zhu, Y.; Peng, H.; Ding, G.; Sun, S. Effect of tube diameter on pressure drop characteristics of refrigerant–oil mixture flow boiling inside metal-foam filled tubes. Appl. Therm. Eng. 2014, 62, 433–443. [Google Scholar] [CrossRef]
- Ji, X.; Xu, J. Experimental study on the two-phase pressure drop in copper foams. Heat Mass Transf. 2012, 48, 153–164. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, H.; Sun, S.; Ding, G. Flow boiling of refrigerant in horizontal metal-foam filled tubes: Part 1—Two-phase flow pattern visualization. Int. J. Heat Mass Transf. 2015, 91, 446–453. [Google Scholar] [CrossRef]
- Tourvieille, J.-N.; Philippe, R.; de Bellefon, C. Milli-channel with metal foams under an applied gas–liquid periodic flow: External mass transfer performance and pressure drop. Chem. Eng. J. 2015, 267, 332–346. [Google Scholar] [CrossRef]
- Lai, Z.; Hu, H.; Ding, G. Effect of porosity on heat transfer and pressure drop characteristics of wet air in hydrophobic metal foam under dehumidifying conditions. Exp. Therm. Fluid Sci. 2018, 96, 90–100. [Google Scholar] [CrossRef]
- Wu, Z.; Caliot, C.; Bai, F.; Flamant, G.; Wang, Z.; Zhang, J.; Tian, C. Experimental and numerical studies of the pressure drop in ceramic foams for volumetric solar receiver applications. Appl. Energy 2010, 87, 504–513. [Google Scholar] [CrossRef]
- Bai, M.; Chung, J. Analytical and numerical prediction of heat transfer and pressure drop in open-cell metal foams. Int. J. Therm. Sci. 2011, 50, 869–880. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, Y.; Tong, Q. Numerical investigation of pressure drop and heat transfer through open cell foams with 3D Laguerre-Voronoi model. Int. J. Heat Mass Transf. 2017, 113, 819–839. [Google Scholar] [CrossRef]
- Diani, A.; Bodla, K.K.; Rossetto, L.; Garimella, S.V. Numerical Analysis of Air Flow through Metal Foams. Energy Procedia 2014, 45, 645–652. [Google Scholar] [CrossRef]
- Diani, A.; Bodla, K.K.; Rossetto, L.; Garimella, S.V. Numerical investigation of pressure drop and heat transfer through re-constructed metal foams and comparison against experiments. Int. J. Heat Mass Transf. 2015, 88, 508–515. [Google Scholar] [CrossRef]
- Ambrosio, G.; Bianco, N.; Chiu, W.K.; Iasiello, M.; Naso, V.; Oliviero, M. The effect of open-cell metal foams strut shape on convection heat transfer and pressure drop. Appl. Therm. Eng. 2016, 103, 333–343. [Google Scholar] [CrossRef]
- Dyga, R.; Brol, S. Pressure Drops in Two-Phase Gas–Liquid Flow through Channels Filled with Open-Cell Metal Foams. Energies 2021, 14, 2419. [Google Scholar] [CrossRef]
- Hapanowicz, J. Proposition of non-standard method useful for viscosity measurements of unstable two-phase systems coupled with examples of its application. Measurement 2020, 164, 108113. [Google Scholar] [CrossRef]
- Baker, O. Simultaneous flow of oil and gas. Oil Gas J. 1954, 53, 185–195. [Google Scholar]
- Troniewski, L.; Ulbrich, R. The analysis of flow regime maps of two-phase gas-liquid flow in pipes. Chem. Eng. Sci. 1984, 39, 1213–1224. [Google Scholar] [CrossRef]
- Dyga, R.; Płaczek, M. Influence of Hydrodynamic Conditions on the Type and Area of Occurrence of Gas–Liquid Flow Patterns in the Flow through Open–Cell Foams. Materials 2020, 13, 3254. [Google Scholar] [CrossRef]
- Lockhart, R.W.; Martinelli, R.C. Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Prog. 1949, 45, 39–48. [Google Scholar]
- Chisholm, D. A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow. Int. J. Heat Mass Transf. 1967, 10, 1767–1778. [Google Scholar] [CrossRef]
- Shi, J.; Zheng, G.; Chen, Z. Experimental investigation on flow condensation in horizontal tubes filled with annular metal foam. Int. J. Heat Mass Transf. 2017, 116, 920–930. [Google Scholar] [CrossRef]
- Tourvieille, J.-N.; Philippe, R.; de Bellefon, C. Milli-channel with metal foams under an applied gas–liquid periodic flow: Flow patterns, residence time distribution and pulsing properties. Chem. Eng. Sci. 2015, 126, 406–426. [Google Scholar] [CrossRef]
- Siemens PLM Software: UserGuide_13.06. Siemcenter STAR-CCM+. Available online: https://community.sw.siemens.com/s/question/0D54O000061xpUOSAY/simcenter-starccm-user-guide-tutorials-knowledge-base-and-tech-support (accessed on 2 November 2022).
- Dyga, R. Wymiana Ciepła i Hydrodynamika Przepływu Przez Piany Metalowe; Studies and Monographs 420; Publishing House of the Opole University of Technology: Opole, Poland, 2015; ISBN 978-83-65235-16-9. (In Polish) [Google Scholar]
- Boomsma, K.; Poulikakos, D.; Ventikos, Y. Simulations of flow through open cell metal foams using an idealized periodic cell structure. Int. J. Heat Fluid Flow 2003, 24, 825–834. [Google Scholar] [CrossRef]
- Płaczek, M.; Dyga, R.; Witczak, S. Experimental investigation of void fraction in horizontal air-water flow through FeCrAlY foam. Procedia Eng. 2012, 42, 690–703. [Google Scholar] [CrossRef][Green Version]
- Rong, J.; Zhang, T.; Qiu, F.; Xu, J.; Zhu, Y.; Yang, D.; Dai, Y. Design and preparation of efficient, stable and superhydrophobic copper foam membrane for selective oil absorption and consecutive oil–water separation. Mater. Des. 2018, 142, 83–92. [Google Scholar] [CrossRef]







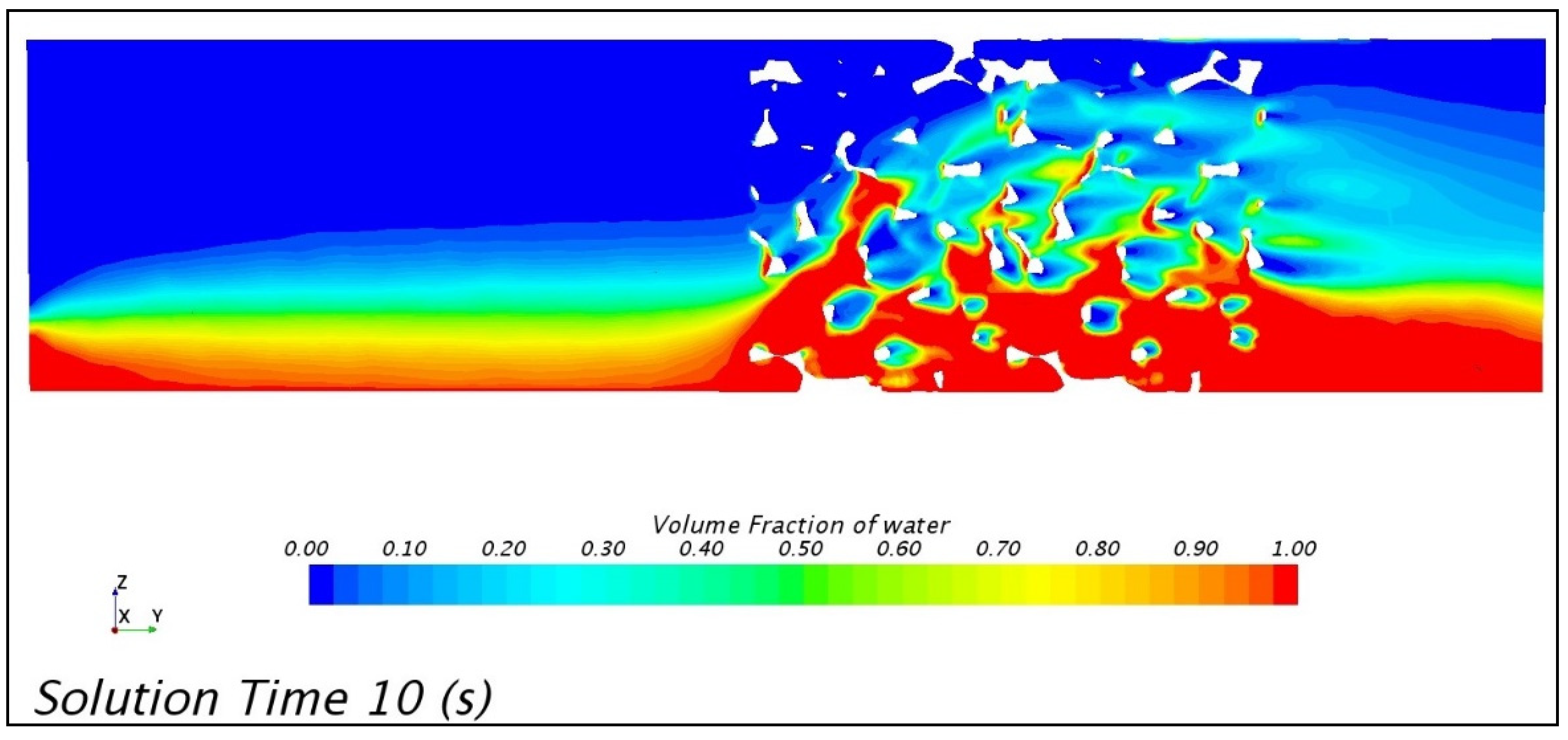
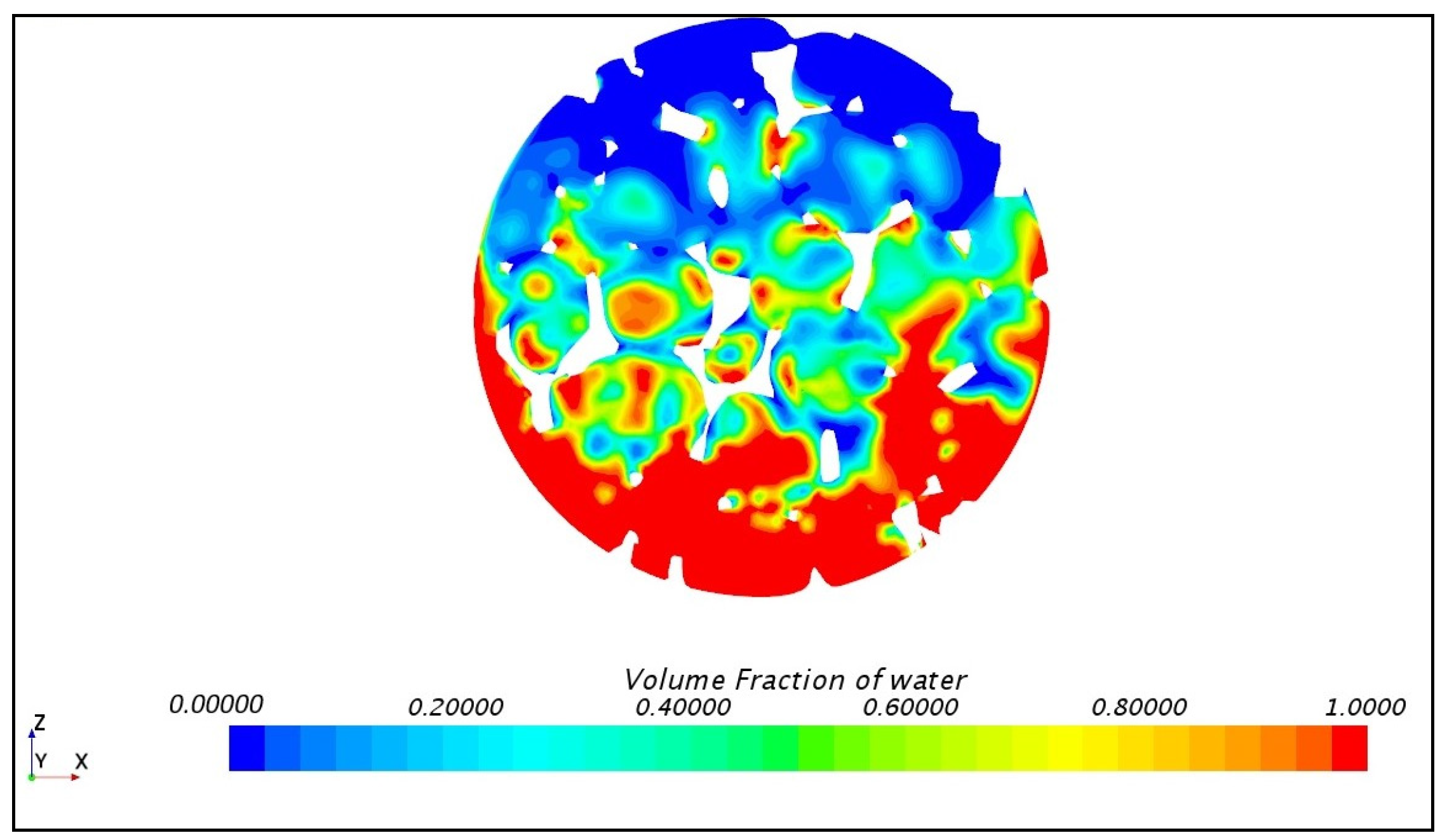

| Parameter | Own Research | According to [26] |
|---|---|---|
| type of metal | Aluminium | Aluminium |
| PPI | 40 | 40 |
| ε, − | 0.930 | 0.929 |
| dp, mm | 1.20 | 0.82 |
| dc, mm | 2.00 | 2.38 |
| de = dp·ε/(1 − ε), mm | 15.9 | 10.7 |
| Ka, m2 | 0.382 × 10−7 | 0.659 × 10−7 |
| Kw, m2 | 0.363 × 10−7 | 0.765 × 10−7 |
| Point No. | ga,s | ρa | ηa | gw,s | ρw | ηw | Pin | (∆P/∆L)2F |
|---|---|---|---|---|---|---|---|---|
| kg/(m2·s) | kg/m3 | Pa·s | kg/(m2·s) | kg/m3 | Pa·s | Pa | Pa/m | |
| 1 | 0.7648 | 1.201 | 18.4 × 10−6 | 28.34 | 996.9 | 9 × 10−4 | 102,822 | 2751 |
| 2 | 0.7675 | 1.209 | 18.4 × 10−6 | 35.66 | 996.9 | 9 × 10−4 | 103,491 | 3740 |
| 3 | 0.7740 | 1.230 | 18.4 × 10−6 | 44.12 | 996.9 | 9 × 10−4 | 105,197 | 4874 |
| 4 | 0.7824 | 1.257 | 18.4 × 10−6 | 59.90 | 996.9 | 9 × 10−4 | 107,343 | 7930 |
| 5 | 0.7913 | 1.286 | 18.4 × 10−6 | 70.56 | 996.9 | 9 × 10−4 | 109,647 | 11,115 |
| 6 | 0.7906 | 1.283 | 18.4 × 10−6 | 76.75 | 996.9 | 9 × 10−4 | 109,438 | 11,289 |
| 7 | 0.8021 | 1.321 | 18.4 × 10−6 | 87.97 | 996.9 | 9 × 10−4 | 112,509 | 14,348 |
| 8 | 0.8054 | 1.332 | 18.4 × 10−6 | 97.64 | 996.9 | 9 × 10−4 | 113,366 | 15,874 |
| 9 | 0.8086 | 1.342 | 18.4 × 10−6 | 108.09 | 996.9 | 9 × 10−4 | 114,204 | 16,901 |
| 10 | 0.8165 | 1.369 | 18.4 × 10−6 | 115.38 | 996.9 | 9 × 10−4 | 116,374 | 18,933 |
| Flow Pattern | B | b1 | b2 | C | c1 | c2 | D |
|---|---|---|---|---|---|---|---|
| stratified | 0.125 | 0.25 | −0.25 | 0.0001 | 0.20 | 0.33 | 0.33 |
| plug, slug, churn | 0.070 | 0.50 | −0.25 | 0.0018 | 0.45 | 0.66 | 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hapanowicz, J.; Szydłowska, A.; Wydrych, J. Experimental and Prenemilary Numerical Evaluation of Pressure Drops under the Conditions of the Stratified Gas-Liquid Flow in a Horizontal Pipe Filled with Metal Foam. Energies 2022, 15, 9068. https://doi.org/10.3390/en15239068
Hapanowicz J, Szydłowska A, Wydrych J. Experimental and Prenemilary Numerical Evaluation of Pressure Drops under the Conditions of the Stratified Gas-Liquid Flow in a Horizontal Pipe Filled with Metal Foam. Energies. 2022; 15(23):9068. https://doi.org/10.3390/en15239068
Chicago/Turabian StyleHapanowicz, Jerzy, Adriana Szydłowska, and Jacek Wydrych. 2022. "Experimental and Prenemilary Numerical Evaluation of Pressure Drops under the Conditions of the Stratified Gas-Liquid Flow in a Horizontal Pipe Filled with Metal Foam" Energies 15, no. 23: 9068. https://doi.org/10.3390/en15239068
APA StyleHapanowicz, J., Szydłowska, A., & Wydrych, J. (2022). Experimental and Prenemilary Numerical Evaluation of Pressure Drops under the Conditions of the Stratified Gas-Liquid Flow in a Horizontal Pipe Filled with Metal Foam. Energies, 15(23), 9068. https://doi.org/10.3390/en15239068








